2013年中考数学知识点 三角形专题专练 相似三角形判定经典习题20道(无答案)
中考数学总复习《相似三角形的判定》专题训练(含答案)

相似三角形的判定 一 、填空题 1.在ABC△和DEF△中,22ABDEACDFAD,,,如果ABC△的周长是16,
面积是12,那么DEF△的周长、面积依次为 . 2.如图,在矩形ABCD中,1AB,2BC将其折叠使AB落在对角线AC上,得到折痕AE,那么BE的长度为
3.如图,矩形AOCB的两边OC、OA分别位于x轴、y轴上,点B的坐标为20B,53,D是AB边上的点,将ADO△沿直线OD翻折,使A点恰好落在对角线OB上的点E处,若点E在一反比例函数的图象上,那么该函数的解析式是 .
二 、解答题 4.如图,DEBC∥,且DBAE,若510ABAC,,求AE的长.
5.如图,已知四边形ABCD是平行四边形.求证:MEFMBA△∽△.
FEDCB
A
OyxEAB
CD
ED
CB
A 6.已知ABC△的三条边长分别为2、5、6,DEF△的三条边长分别为20、8、24,这两个三角形是否相似?为什么? 7.如图所示,在RtABC△中,90A,6AB,8AC,D、E分别是边ABAC、
的中点,点P从点D出发沿DE方向运动,过点P作PQBC于Q,过点Q作QRBA∥交AC于R,当点Q与点C重合时,点P停止运动,设,BQxQRy. (1)求点D到BC的距离DH的长; (2)求y关于x的函数关系式(不要求写出自变量的取值范围).
8.如图,已知O是ABC△内一点,DEF、、分另是OAOBOC、、的中点.求证:ABCDEF△∽△.
9.已知,如图,D为ABC△内一点连结,EDAD,以BC为边在ABC△外作,CBEABDBCEBAD.求证:DBEABC△∽△.
MFEDC
BA
ERP
QH
A
BCD
OFE
A
BCD 10.如图所示,ABCD∥,,ADBC交于点,EF为BC上一点,且EAFC. 求证:(1)EAFB;(2)2AFFEFB.
11.如图,在ABC△中,ADBC,垂足为D,且CEBE,垂足为E,交BA的延长线于点E.求证:BDEBAC△∽△.
2013中考全等三角形证明经典50题

ADB C1、已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD1. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB2. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠23. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC4. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C5. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE6. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求ADADBCBA CDF2 1 ECDBA7. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB8. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠29. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC10. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C11. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
求证:BC=AB+DC 。
13.已知:AB//ED ,∠EAB=∠BDE ,AF=CD ,EF=BC ,求证:∠F=∠C14. 已知:AB=CD ,∠A=∠D ,求证:∠B=∠CBA CDF2 1 ECDBDCBAFEA15. P 是∠BAC 平分线AD 上一点,AC>AB ,求证:PC-PB<AC-AB16. 已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BE17. 已知,E 是AB 中点,AF=BD ,BD=5,AC=7,求DC18.(5分)如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC . 19.(5分)如图,OM 平分∠POQ ,MA ⊥OP ,MB ⊥OQ ,A 、B 为垂足,AB 交OM 于点N .求证:∠OAB =∠OBA20.(5分)如图,已知AD ∥BC ,∠P AB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB .21.(6分)如图,△ABC 中,AD 是∠CAB 的平分线,且AB =AC +CD ,求证:∠C =2∠B22.(6分)如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC于E ,BF ⊥AC 于F ,若AB =CD ,AF =CE ,BD 交AC 于点M .(1)求证:MB =MD ,ME =MF(2)当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.23.(7分)已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点, (1)求证:△AED ≌△EBC .(2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):P DACBFAED C BP E D CB A OEDCBADC BA24.(7分)如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F . 求证:BD =2CE . 25、(10分)如图:DF=CE ,AD=BC ,∠D=∠C 。
初三数学相似三角形经典题(含答案)

相似三角形经典习题例1 从下面这些三角形中,选出相似的三角形.例2 已知:如图,ABCD 中,2:1:=EB AE ,求AEF ∆与CDF ∆的周长的比,若是2cm 6=∆AEF S ,求CDF S ∆.例3 如图,已知ABD ∆∽ACE ∆,求证:ABC ∆∽ADE ∆.例4 以下命题中哪些是正确的,哪些是错误的?(1)所有的直角三角形都相似. (2)所有的等腰三角形都相似.(3)所有的等腰直角三角形都相似. (4)所有的等边三角形都相似.例5 如图,D 点是ABC ∆的边AC 上的一点,过D 点画线段DE ,使点E 在ABC ∆的边上,而且点D 、点E 和ABC ∆的一个极点组成的小三角形与ABC ∆相似.尽可能多地画出知足条件的图形,并说明线段DE 的画法.例6 如图,一人拿着一支刻有厘米分画的小尺,站在距电线杆约30米的地址,把手臂向前伸直,小尺竖直,看到尺上约12个分画恰好遮住电线杆,已知手臂长约60厘米,求电线杆的高.例7 如图,小明为了测量一高楼MN 的高,在离N 点20m 的A 处放了一个平面镜,小明沿NA 后退到C 点,正好从镜中看到楼顶M 点,假设5.1=AC m ,小明的眼睛离地面的高度为,请你帮忙小明计算一下楼房的高度(精准到).例8 格点图中的两个三角形是不是是相似三角形,说明理由.例9 依照以下各组条件,判定ABC ∆和C B A '''∆是不是相似,并说明理由:(1),cm 4,cm 5.2,cm 5.3===CA BC AB cm 28,cm 5.17,cm 5.24=''=''=''A C C B B A .(2)︒='∠︒='∠︒=∠︒=∠35,44,104,35A C B A .(3)︒='∠=''=''︒=∠==48,3.1,5.1,48,6.2,3B C B B A B BC AB .例10 如图,以下每一个图形中,存不存在相似的三角形,若是存在,把它们用字母表示出来,并简要说明识别的依照.例11 已知:如图,在ABC ∆中,BD A AC AB ,36,︒=∠=是角平分线,试利用三角形相似的关系说明AC DC AD ⋅=2.例12 已知ABC ∆的三边长别离为五、1二、13,与其相似的C B A '''∆的最大边长为26,求C B A '''∆的面积S .例13 在一次数学活动课上,教师让同窗们到操场上测量旗杆的高度,然后回来交流各自的测量方式.小芳的测量方式是:拿一根高米的竹竿直立在离旗杆27米的C 处(如图),然后沿BC 方向走到D 处,这时目测旗杆顶部A 与竹竿顶部E 恰好在同一直线上,又测得C 、D 两点的距离为3米,小芳的目高为米,如此即可明白旗杆的高.你以为这种测量方式是不是可行?请说明理由.例14.如图,为了估算河的宽度,咱们能够在河对岸选定一个目标作为点A ,再在河的这一边选点B 和C ,使BC AB ⊥,然后再选点E ,使BC EC ⊥,确信BC 与AE 的交点为D ,测得120=BD 米,60=DC 米,50=EC 米,你能求出两岸之间AB 的大致距离吗?例15.如图,为了求出海岛上的山峰AB 的高度,在D 和F 处树立标杆DC 和FE ,标杆的高都是3丈,相隔1000步(1步等于5尺),而且AB 、CD 和EF 在同一平面内,从标杆DC 退后123步的G 处,可看到山峰A 和标杆顶端C 在一直线上,从标杆FE 退后127步的H 处,可看到山峰A 和标杆顶端E 在一直线上.求山峰的高度AB 及它和标杆CD 的水平距离BD 各是多少?(古代问题)例16 如图,已知△ABC 的边AB =32,AC =2,BC 边上的高AD =3.(1)求BC 的长;(2)若是有一个正方形的边在AB 上,另外两个极点别离在AC ,BC 上,求那个正方形的面积.。
中考数学《相似三角形》知识点及练习题

相似三角形一. 知识梳理1.平行线分线段成比例定理定理:两条直线被三条平行线所截,所得的对应线段成比例。
推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
2.相似三角形定义:三角对应相等、三边对应成比例的两个三角形叫做相似三角形。
相似比:相似三角形对应边的比叫做相似比。
3.相似三角形的判定平行法:平行于三角形一边的直线和其他两边相交,所得的三角形与原三角形相似。
两角法:两角分别相等的两个三角形相似。
边角法:两边成比例且夹角相等的两个三角形相似。
三边法:三边对应成比例的两个三角形相似。
4.相似三角形的性质①相似三角形的对应角相等,对应边成比例;②相似三角形对应边上高的比,对应边上中线的比与对应角平分线的比都等于相似比;③相似三角形周长的比等于相似比;④相似三角形面积的比等于相似比的平方。
5.位似图形定义:如果两个图形不仅相似,而且对应顶点的连线相交于一点,那么这样的两个图形叫做位似图形,这个点叫做位似中心。
这时的相似比又叫位似比6. 黄金分割:点C 把线段AB 分成两条线段AC 和BC,如果ACBC AB AC =,那么称线段AB 被点C 黄金分割,点C 叫做线段AB 的黄金分割点,AC 与AB 的比叫做黄金比. 1:618.0215:≈-=AB AC 二.课后作业1.下列图形中不一定属于相似形的是( )A.两个圆B.两个等边三角形C.两个正方形D.两个矩形2.如果两个相似三角形的面积比是1∶4,那么它们的周长比是( )A. 1∶16B. 1∶4C. 1∶6D. 1∶23.已知△ABC ∽△DEF ,且AB:DE=1:2,则△ABC 的周长与△DEF 的周长之比( )A.1:2B.1:4C.2:1D.4:14.如图,给出下列条件:其中,不能单独判定△ABC∽△ACD 的条件为( )A.∠B=∠ACDB.∠ADC=∠ACBC.AC CD =AB BCD.AC AD =AB AC5.如图,DE ∥BC ,且AD=2,BD=5,则△ADE 与△ABC 的相似比为( )A.2:5B.5:2C.2:7D.7:26.如图,在△ABC 中,DE ∥BC ,AD=2,AE=3,BD=4,则AC=( ) A.7 B.8 C.9 D.10 E A D CB A BC DE7.已知△ABC ∽△DEF ,且它们的周长之比为1:2,那么它们的相似比为 。
(完整版)初中三角形相似证明练习题
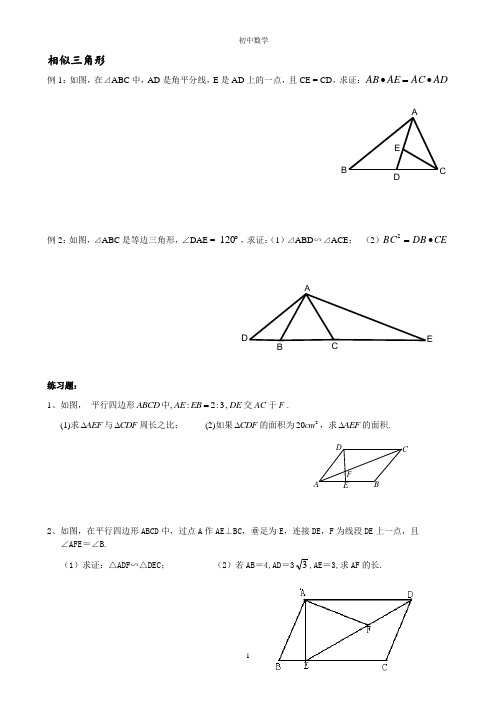
相似三角形例1:如图,在⊿ABC 中,AD 是角平分线,E 是AD 上的一点,且CE = CD ,求证:AD AC AE AB •=•例2:如图,⊿ABC 是等边三角形,∠DAE = ︒120,求证:(1)⊿ABD ∽⊿ACE ; (2)CE DB BC •=2练习题:1、如图, 平行四边形ABCD 中,:2:3AE EB =,DE 交AC 于F .(1)求AEF ∆与CDF ∆周长之比; (2)如果CDF ∆的面积为220cm ,求AEF ∆的面积.2、如图,在平行四边形ABCD 中,过点A 作AE ⊥BC ,垂足为E ,连接DE ,F 为线段DE 上一点,且 ∠AFE =∠B.(1)求证:△ADF ∽△DEC ; (2)若AB =4,AD =33,AE =3,求AF 的长.AB CDEAB CDE A BECD F3、如图,在△ABC 中,D 是BC 边上一点,E 是AC 边上一点.且满足AD =AB ,∠ADE =∠C . (1)求证:∠AED =∠ADC ,∠DEC =∠B ; (2)求证:AB 2=AE •AC .4、在□ABCD 中,∠EAC=∠D ,试说明AC ·BE=AE ·CD5、如图,在∆ABC 中,AD 是∠BAC 的外角平分线,CE ∥AB ,求证:AC AD DE AB •=•ABCDEFBDCE真题再现1.如图,在正方形ABCD中,E是CD的中点,点F在BC上,且FC=14BC。
图中相似三角形共有【】A.1对B.2对C.3对D.4对2.将一副三角板如图放置。
若AE∥BC,则∠AFD= 0。
3.如图,为测量学校围墙外直立电线杆AB的高度,小亮在操场上点C处直立高3m的竹竿CD,然后退到点E处,此时恰好看到竹竿顶端D与电线杆顶端B重合;小亮又在点C1处直立高3m的竹竿C1D1,然后退到点E1处,此时恰好看到竹竿顶端D1与电线杆顶端B重合。
小亮的眼睛离地面高度EF=1.5m,量得CE=2m,EC1=6m,C1E1=3m。
2013届初三数学课时专题训练--相似三角形及应用参考答案

2013届初三数学课时专题训练相似三角形及应用参考答案一、选择题二、填空题1、10.52、43、104、605、246、20104183⎪⎭⎫⎝⎛⋅(或3214023⎪⎭⎫ ⎝⎛)7、∠A=∠D 8、7.00(若写7不扣分) 9、433- 10、①,③,④ 11、144; 12、1213、712或2; 14、40 15、)cm (542=∆CDF S 16、高为6米17、3.215.1206.1≈÷⨯=MN (m ). 18、两岸间AB 大致相距100米. 19、1506=AB 米,30750=BD 步, 20、解得d =306.三、解答题(共4题,每题20分,共80分) 1、解:(1)在Rt △ABC 中,由AB =1,BC =21得 AC =22)21(1+=25∵BC =CD ,AE =AD∴AE =AC -AD =215-.(2)∠EAG =36°,理由如下: ∵FA =FE =AB =1,AE =215-∴FAAE =215-∴△FAE 是黄金三角形∴∠F =36°,∠AEF =72° ∵AE =AG ,FA =FE∴∠FAE =∠FEA =∠AGE ∴△AEG ∽△FEA∴∠EAG =∠F =36°.2、解:(1)如上图,由AD ⊥BC ,由勾股定理得BD =3,DC =1,所以BC =BD +DC =3+1=4.如下图,同理可求BD =3,DC =1,所以BC =BD -CD =3-1=2.(2)如下图,由题目中的图知BC =4,且162)32(2222=+=+AC AB ,162=BC ,∴222BC AC AB =+.所以△ABC 是直角三角形.由AE G F 是正方形,设G F =x ,则FC =2-x ,∵G F ∥AB ,∴AC FCAB GF =,即2232x x -=. ∴33-=x ,∴3612)33(2-=-=AEGF S 正方形. 如下图,当BC =2,AC =2,△ABC 是等腰三角形,作CP ⊥AB 于P ,∴AP =321=AB ,在Rt △APC 中,由勾股定理得CP =1,∵GH ∥AB ,∴△C GH ∽△CBA ,∵xx x -=132,32132+=x ∴121348156)32132(2-=+=GFEH S 正方形 因此,正方形的面积为3612-或121348156-.3、解:(1)∆ABE ∽∆DAE , ∆ABE ∽∆DCA∵∠BAE =∠BAD +45°,∠CDA =∠BAD +45∴∠BAE =∠CDA 又∠B =∠C =45° ∴∆ABE ∽∆DCA(2)∵∆ABE ∽∆DCA ∴CDBACA BE = 由依题意可知CA =BA =2∴nm22=∴m=n2自变量n 的取值范围为1<n<2.∵m=n2 ∴m=n=2∵OB =OC =21BC =1∴OE =OD =2-1 ∴D (1-2, 0)∴BD =OB -OD =1-(2-1)=2-2=CE , DE =BC -2BD =2-2(2-2)=22-2 ∵BD 2+CE 2=2 BD 2=2(2-2)2=12-82, DE 2=(22-2)2= 12-82 ∴BD 2+CE 2=DE 2 (4)成立证明:如图,将∆ACE 绕点A 顺时针旋转90°至∆ABH 的位置,则CE =HB ,AE =AH , ∠ABH =∠C =45°,旋转角∠EAH =90°.连接HD ,在∆EAD∵AE =AH , ∠HAD =AD =AD .∴∆EAD ≌∆HAD∴DH =DE又∠HBD =∠ABH +∴BD 2+HB 2=DH 2即BD 2+CE 2=DE 24、(1)证明:∵AD =CD ,∴AF =CF ,∠DFA =DFC ∵∠DAB =∠DAF +∠CAB =90°,∠CAB +∠B =90°,∴∠DCF =∠DAF =∠B 在Rt △DCF 和Rt △ABC 中,∠DFC =∠ACB =90°,∠DCF =∠B ∴△DCF ∽△ABC ∴CD CF AB CB =,即CD AF AB CB=.∴AB ·AF =CB ·CD (2)解:①∵AB =15,BC =9,∠ACB =90°,∴AC =12,∴CF =AF =6∴1(9)2y x =+×6=3x +27(x >0)②∵BC =9(定值),∴△PBC 的周长最小,就是PB +PC 最小.由(1)可知,点C 关于直线DE 的对称点是点A ,∴PB +PC =PB +PA ,故只要求PB +PA 最小.显然当P 、A 、B 三点共线时PB +PA 最小.此时DP =DE ,PB +PA =AB. 由(1),∠ADF =∠FAE ,∠DFA =∠ACB =90°,地△DAF ∽△ABC.EF ∥BC ,得AE =BE =12AB =152,EF =92.∴AF ∶BC =AD ∶AB ,即6∶9=AD ∶15.∴AD =10. Rt △ADF 中,AD =10,AF =6,∴DF =8.∴DE =DF +FE =8+92=252.∴当x =252时,△PBC 的周长最小,此时y =12925、(1)∵∠ACB =90°,∴AC =.∵S =12AB CP ⋅⋅=12AC BC ⋅⋅,∴CP =AC BC AB ⋅=403050⨯=24.在Rt △CPM 中,∵sin ∠EMP =1213, ∴1213CP CM =. ∴CM =1312CP =132412⨯=26.(2)由△APE ∽△ACB ,得PE AP BC AC =,即3040PE x =,∴PE =34x . 在Rt △MPE 中,∵sin ∠EMP =1213,∴1213PE ME =.∴EM =1312PE =133124x ⨯=13x .∴PM =PN =516x .∵AP +PN +NB =50,∴x +516x +y =50.∴y =215016x -+(0 < x < 32).(3) 第三问:由于给出对应顶点,那么解法一可以直接运用相似和三角比求出对应边长再列比例式求解。
初中数学相似三角形专项练习题目
初中数学相似三角形专项练习题目第18.1课时 相似三角形一.填空题(基础)1. 如图,ABC ∆∽MNP ∆,则它们的对应角分别是A ∠与∠___M__,∠B 与∠___N__,C∠与∠___P__;对应边成比例的是________=_________=_________;若AB=2.7cm,cmMN 9.0=,cmMP 1=,则相似比=_________,=BC _________cm .BAGFEDCBANPMC (第2题)(第1题)2. 如图,四边形ABCD 中,AD ∥EF ∥BC ,AC 交EF 于G .图中能相似的三角形共有_______对,它们分别是_________、___________,小明通过这两对相似三角形推出了比例式:ABBEAD FG =,对不对,为什么? 二.填空题3. 如图,ABC ∆和DEF ∆的三边长分别为7、2、6和12、4、14,且两三角形相似,则A ∠与∠_____,∠B 与∠_____,C ∠与∠_____,)()()(AC DF AB ==。
(第5题)(第4题)(第3题)CGFED CBAFEBAEFDCB A4. 如图,ABC ∆∽AEF ∆,写出三对对应角:_________=_________,_________=________, ________=_________,并且)()()()()(==AF ,若ABC ∆与AEF∆的相似比是3:2,cm EF 8=,则________=BC 。
5. 如图,ABC ∆中,点D 在BC 上,EF ∥BC ,分别交AB 、AC 、AD 于点E 、F 、G ,图中共有______对相似三角形,它们是______________________________________.6. 如图,平行四边形ABCD中,,上的一点,是43=EC BE BC E ,于点交F BD AE =BF 的值。
及,求DF DABEcm 6FB三.选择题1.下列命题中不正确的是( )A .如果两个三角形全等,那么这两个三角形相似。
相似三角形的判定及习题
相似三角形的判定练习1、相似三角形1)定义:如果两个三角形中,三角对应相等,三边对应成比例,那么这两个三角形叫做相似三角形。
几种特殊三角形的相似关系:两个全等三角形一定相似。
两个等腰直角三角形一定相似。
两个等边三角形一定相似。
两个直角三角形和两个等腰三角形不一定相似。
补充:对于多边形而言,所有圆相似;所有正多边形相似(如正四边形、正五边形等等);2)性质:两个相似三角形中,对应角相等、对应边成比例。
3)相似比:两个相似三角形的对应边的比,叫做这两个三角形的相似比。
如△ABC与△DEF相似,记作△ABC ∽△DEF。
相似比为k。
4)判定:①定义法:对应角相等,对应边成比例的两个三角形相似。
②三角形相似的预备定理:平行于三角形一边的直线和其它两边相交,所构成的三角形与原三角形相似。
三角形相似的判定定理:判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.简述为:两角对应相等,两三角形相似.(此定理用的最多)判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.简述为:两边对应成比例且夹角相等,两三角形相似.判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似.简述为:三边对应成比例,两三角形相似.直角三角形相似判定定理:○1.斜边与一条直角边对应成比例的两直角三角形相似。
○2.直角三角形被斜边上的高分成的两个直角三角形与原直角三角形相似,并且分成的两个直角三角形也相似。
补充一:直角三角形中的相似问题:斜边的高分直角三角形所成的两个直角三角形与原直角三角形相似.射影定理:CD²=AD·BD,AC²=AD·AB,BC²=BD·BA(在直角三角形的计算和证明中有广泛的应用).补充二:三角形相似的判定定理推论推论一:顶角或底角相等的两个等腰三角形相似。
中考专题专题复习——相似三角形(含详解)
E ABD C中考专题专题复习——相似三角形1.如果532x =,那么x 的值是( ) A . 310 B .215 C .152 D .1032.如果4:7:2x =,那么x 的值是( )A .14B .78 C .67 D .723.已知:四条线段a 、b 、c 、d 之间有如下关系a ∶b= c ∶d ,且a =12,b=8,c=15,则线段d= 10 .4.如图,在△ABC 中,DE ∥BC ,DF ∥AC ,则下列比例式一定成立的是( )A .AE DE EC BC =B .AE CF AC BC = C .AD BF ABBC=D .DE DF BCAC=5.如图,在ΔABC 中,D 、E 分别是AB 、AC 边上的中点,连接DE , 那么ΔADE 与ΔABC 的面积之比是A .1:16B .1:9C .1:4D .1:26.如图,在△ABC 中,D 、E 两点分别在AB 、AC 边上,且DE ∥BC .若3:2:=BC DE ,则ABC ADE S S ∆∆:为的值为 A. 4:9 B. 9:4 C. 3:2 D. 3:27.已知:ABC ∆中,E D ,分别是AC AB ,的中点,16=∆ABC S 2cm ,则=∆ADE S ( )A .216cm B .212cmC .28cmD . 24cm8.已知ABC DEF △∽△,AB :DE =2:1,且ABC △的周长为16,则DEF △的周长为 A .4 B .6C .8D .32(第2题)E D CBA9. 如果两个相似三角形的相似比是1:2,那么这两个相似三角形的周长比是 .10. 如图,在△ABC 中,DE ∥AB 分别交AC ,BC 于点D ,E , 若AD =2,CD =3,则△CDE 与△CAB 的周长比为 .11.已知两个相似三角形的周长比是1:3,它们的面积比是 12.如果两个相似三角形的相似比是1︰2,那么它们的面积比是_______.13. 如图,平行四边形ABCD 中,E 为DC 的中点,DEF △的面积为2,则△ABF 的面积为A .2B .C .6D .814. 已知:2:3,a b = 那么下列等式中成立的是A .32a b =B .23a b =C .52a b b +=D .13a b b -=15. 如图,在△ABC 中,点D 、E 分别在AB 、AC 边上,DE ∥BC ,若AD =6,BD =2,AE =9,则EC 的长是A .8B .6C .4D .316.如图,在△ABC 中,点D 、E 分别在AB 、AC 边上,DE ∥BC ,若 AD :DB =1:2,AE =2,则AC = .17.如图,在ABC ∆中,D 是AB 边上一点,连接CD . 要使ACD ∆与ABC ∆相似, 应添加的条件是 . (只需写出一个条件即可)18.如图,在等边ABC △中,P 为BC 上一点,D 为AC 上一点,且60APD ∠=︒,2BP =,43CD =,则ABC △的边长为 ( ) A.3B.4C.5D.6AB CDA BCPD60DCBAE DCBAAC E B6题图19.已知:如图,在ABC △中,D 是AC 上一点,联结BD ,且∠ABD =∠ACB . (1)求证:△ABD ∽△ACB ;(2)若AD =5,AB = 7,求AC 的长.20.如图,等边△ABC 的边长为3,点P 为BC 边上一点,且BP =1,点D 为AC 上一点;若∠APD =60°,则CD 长是 A.43 B.23 C.21 D.3221.如图,在△ABC 中,∠C =90º,D 是AC 上一点,DE ⊥AB 于点=6,DE =3,则AE的长为A .3B .4C .5D .622.已知:如图,在Rt △ABC 中,∠C =90°,∠ABC =60°,AC D 为CB 延长线上一点,且BD =2AB . 求AD 的长.23. 如图,在ABC △中,90C =∠,在AB 边上取一点D ,使BD BC =,过D 作DE AB ⊥交AC 于E ,86AC BC ==,.求DE 的长.ADBD CBAEDA B24. 已知:如图,在△ABC 中,D 、E 两点分别在AC 、AB 两边上,ABC ADE ∠=∠,3,7==AD AB , 2.7AE =,求AC 的长.25.已知:如图,在△ABC 中,AB =AC = 5,BC = 8, D ,E 分别为BC ,AB 边上一点,∠ADE =∠C . (1)求证:△BDE ∽△CAD ; (2)若CD =2,求BE 的长.26.如图,在Rt △ABC 中,∠CAB =90°,AD 是∠CAB 的平分线,tan B =21,则CD ∶DB =27. 已知:如图,在△ABC 中,AD ⊥BC 于点D ,CE ⊥AB 于点E ,BE=2AE ,且AD=6sin ∠BCE=13. 求CE 的长.F EDC B AABCDM28.如图,在平行四边形ABCD 中,E 为边AD 延长线上的一点,且D 为AE 的黄金分割点,即12AD AE =,BE 交DC 于点F,已知1AB =,求CF 的长 .29.(本小题满分6分)已知:如图,在梯形ABCD 中,AB ∥DC ,AB=2,DC=5,BC=3,AC 与BD 相交于点M ,且DM=207. (1)求证:△AMB ∽△CMD ;(2)求∠BDC 的正弦值.30. 如图,在矩形ABCD 中,E 为BC 上一点,DF ⊥AE 于点F .(1)求证:ΔABE ∽ΔDFA ;(2)若AB=6,AD=12,BE=8,求DF 的长.31.如图,直角梯形ABCD 中,∠ADC =90°,AD ∥BC ,点E 在BC 上,点F 在AC 上, ∠DFC =∠AEB .(1)求证:△ADF ∽△CAE ;(2)当AD =8,DC =6,点E 、F 分别是BC 、 AC 的中点时,求直角梯形ABCD 面积.(第18题)FEDCBA32.已知Rt △ABC 中,AC =3,BC = 4,过直角顶点C 作CA 1⊥A B ,垂足为A 1,再过A 1作A 1C 1⊥BC , 垂足为C 1,过C 1作C 1A 2⊥AB ,垂足为A 2,再过A 2作A 2C 2⊥BC ,垂足为C 2,…,这样一直做下去, 得到了一组线段CA 1,A 1C 1,C 1A 2,…, 则CA 1= ,8999C A A C .33.如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ACB 和△DCE 的顶点都在格点上.求证:△ACB ∽△DCE .34. 如图,已知每个小方格都是边长为1的正方形,我们称每个小正方形的顶点为格点,以格点为顶点的图形称为格点图形. 图中的△ABC 是一个格点三角形.(1)请你在第一象限内画出格点△AB 1C 1, 使得△AB 1C 1∽△ABC ,且△AB 1C 1与△ABC 的相似比为3:1; (2)写出B 1、C 1两点的坐标.35. 如图,在8×4的矩形网格中,每格小正方形的边长都是1,若△ABC 的三个顶点在图中相应的格点上,则 tan ∠ACB 的值为( ).x87 6 5 432 11 2 3 4 5 6 7 8 BC A 0 yA .1B .13C .12D . 2236.如图,将△ABC 的三边分别扩大一倍得到△111A B C(顶点均在格点上),若它们是以P 点为位似中心的 位似图形,则P 点的坐标是( ). A .(4,3)-- B .(3,3)-- C .(4,4)-- D .(3,4)--37.如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.已知,ABC △的顶点都在格点上,︒=∠90C ,8=AC ,4=BC ,若在边AC 上以某个格点E 为端点画出长是52的线段EF ,使线段另一端点F 恰好落在边BC 上,且线段EF 与点C 构成的三角形与ABC △相似,请你在图中画出线段EF (不必说明理由).38.如图,将△ABC 的三边分别扩大一倍得到△111A B C (顶点 均在格点上),若它们是以P 点为位似中心的位似图形,则P 点的坐标是( ).A .(4,3)--B .(3,3)--C .(4,4)--D .(3,4)--39.如图,A ,B ,C 三点均为格点,△ABC 与△A ′B ′C ′关于y 轴对称.(1) 画出△A ′B ′C ′;(2) 如果△ABC 边上任意一点M 的坐标为()x y ,, 那么它的对应点M ' 的坐标是 .第18题ACBxyCABAC40. 如图,在5×6的网格图中,△ABC 的顶点A 、B 、C 在格点(每个小正方形的顶点)上,请在网格图中画一个..△1A 1B 1C ,使△1A 1B 1C ∽△ABC (相似比不为1),且点1A 、1B 、1C 必须在格点上.。
(2021年整理)2013年中考数学重难点相似三角形知能综合检测(含解析)
(完整)2013年中考数学重难点相似三角形知能综合检测(含解析) 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整)2013年中考数学重难点相似三角形知能综合检测(含解析))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整)2013年中考数学重难点相似三角形知能综合检测(含解析)的全部内容。
相似三角形一、选择题(每小题4分,共12分)1.如图,点F是ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论错误的是( )(A)ED DFEA AB=(B)DE EFBC FB=(C)BC BFDE BE=(D)BF BCBE AE=2。
已知如图(1),(2)中各有两个三角形,其边长和角的度数已在图上标注,图(2)中AB,CD交于O点,对于各图中的两个三角形而言,下列说法正确的是( )(A)都相似(B)都不相似(C)只有(1)相似(D)只有(2)相似3。
(2011·河北中考)如图,在△ABC中,∠C=90°,BC=6,D,E分别在AB,AC上,将△ABC 沿DE折叠,使点A落在点A′处,若A′为CE的中点,则折痕DE的长为( )(A)12(B)2 (C)3 (D)4二、填空题(每小题4分,共12分)4.(2012·重庆中考)已知△ABC∽△DEF,△ABC的周长为3,△DEF的周长为1,则△ABC与△DEF的面积之比为_______。
5.(2011·青海中考)如图,△ABC是一块锐角三角形的材料,边BC=120 mm,高AD=80 mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,这个正方形零件的边长是_______mm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
2013年中考初中数学知识点:三角形【专题专练】 相似三角形
判定经典习题20道
1、如图,在ABC中,点D在ABC内,已知AEACDEBCADAB.求证:
ACEABD
.
E
D
C
B
A
2、如图,D是ABC的边AC上一点,CBD的平分线交AC于点E,ABAE.求证:
ACADAE
2
.
E
D
C
B
A
3、如图,BD、CE是ABC的两条高,AM是BAC的平分线,交BC于M,交
DE
于N,求证:(1);DEBCANAM(2).ECBEDB
M
N
E
D
C
B
A
4、如图,在ABC中,D为BC的中点,ACAD,BCDE,与AB相交于点E,
EC
与AD相交于点F,求证:(1)ABC∽FCD;(2)FDAF.
2
E
F
D
CB
A
4、在ABC中,ACAB,点D在AB上,点E在AC的延长线上,DE交BC于F,
求证:.FEDFCEBD
F
E
D
C
B
A
5、如图,在ABC中,ACAB,ACBD于D,求证:ACCDBC22.
D
C
B
A
6、如图,在ABC中,cmAB8,cmBC16.点P从点A开始,沿AB边向点B以
scm/2
的速度移动;点Q从点B开始,沿边BC向点scm/4以的速度移动,如果P、Q同时出发,
经过几秒钟,PBQ与ABC相似?
P
C
A
Q
B
7、如图,在ABC中,90ACB,AD为边BC上的中线,ADCP于P,求证:
3
BDABPBAD
.
D
P
C
A
B
8、如图,在ABC中,90BAC,BCAD于D,E为AC的中点,ED、AB的
延长线交于点F,求证:DFACAFAB.
F
E
D
C
A
B
9、如图,P是正方形ABCD的边BC上一点,PCBP3.M是CD的中点,
APMN
于N,求证:PNANMN2.
N
M
D
P
C
A
B
10、在ABC中,AM是BAC的平分线,AM的垂直平分线DN交BC,的延长线于N,
求证:CNBNMN2.
N
M
D
C
A
B
11、AD、CE是ABC的两条高,F是AB上一点,ADAF,BCFG//交AC于G.
求证:CEFG.
4
G
F
E
D
C
A
B
11、在ABC中,ABAC,AD是中线,P是AD上一点,过点C作BACF//,交
BP
延长线于F,BF交AC于点E,求证:PFPEBP2.
F
E
D
P
C
A
B
12、如图,在正方形ABCD中,M、N分别在AB、BC上,且BNBM,
MCBP
于P,连结DP、NP.求证:PDPN.
N
M
DPCA
B
13、在ABC中,90ACB,ABCD于D,P是CD中点,AP延长线交BC于Q,
ABQR
于R.求证:QBQCQR2.
Q
RED
P
C
A
B
14、如图,在ABC中,90C,3AC,4BC,点E在直角边AC上(点E与
A、C两点均不重合),点F在斜边AB上(点F与A、B
两点均不重合).
(1)若EF平分ABCRt的周长,设AE的长为x,试用含x的代数式表示AEF的面
积;
(2)是否存在线段EF,将ABCRt的周长和面积同时平分?若存在,求出此时AE的
5
长,若不存在,说明理由.
F
E
C
A
B
15、在梯形ABCD中,BCADEF////,求证:FHEG.
H
G
F
E
D
C
A
B
16在ABC中,ACAB,ACAB,D是AC的中点,连结BD,过A作
BDAE
交BC于E,求证:ECBE2.
G
E
D
C
A
B
17、如图,D、F分别为ABC边AB,AC上的点,且3:2::FACFDBAD,连
DF交BC的延长线于E
,则FDEF:的值?
E
F
D
C
B
A
18、如图,在ABC中,90BAC,BCAD于D点,E是BC边上的一个动点(不
与B,C重合),ABEF,ACEG,垂足分别为F,G.(1)求证:
ADCGCDEG;(2)FD与DG
是否垂直?若垂直,请证明;若不垂直,请说明理
由;(3)当ACAB时,为等腰直角三角形吗?并说明理由.
6
G
EFD
C
B
A
G
E
F
D
C
B
A
19、(1)如图1,在ABC中,BCDE//,点Q在BC上,AQ交DE于点P,求证:
PEBQQCDP
.
(2)如图2和图3,在ABC中,90BAC,正方形DEFG的四个顶点在
ABC
的边上,连接AG、AF,分别交DE于M、N两点.
①如图2,若1ACAB,则______;MN
②如图3,求证:ENDMMN2.
(图1)
E
Q
P
D
CB
A
(图2)
N
M
F
GEDCB
A
(图3)
N
M
FG
E
D
C
B
A
20. 如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-4,0),点B的坐标是(0,b)
(b>0).P是直线AB上的一个动点,作 PC⊥x轴,垂足为C。记点P关于y轴的对称点为
P´(点P´不在y轴上),连结PP´, P´A, P´C.设点P的横坐标为a。
(1)当b=3时,
○1求直线AB的解析式;
○2若点P´的坐标是(-1,m),求m的值;
(2)若点P在第一象限,记直线AB与P´C的交点为D。当P´D:DC=1:3时,求a的值;
(3)是否同时存在a,b,使△P´CA为等腰直角三角形?若存在,请直接写出所有满足要求
7
的a,b的值;若不存在,请说明理由。
