2斜线在平面内的射影、直线
9正射影和垂线定理
90°
C
45°
D
补充作业:
1.点P在△ABC的射影为O,
P
且PA、PB、PC两两垂直,
求证:O为△ABC的垂心
A
C O
B H
2.平面α 内有一个正六边形,
它的中心是O,边长为2cm, OH⊥α ,OH=4cm,求点H到
这个六边形顶点和边的距离。
A D B
O C
如图,在空间四边形ACBP中, PA⊥面ABC, AC⊥BC,
A1
a
D A
α
β C
B
面ABCD →面α 面 → 面 αβ 面ABCD B1BCC 面 1→ 直线 直线A A11C C→ →斜线 斜线 a a 直线 直线B AB 1B →垂线 b
D B C A1 D1 C1
B1
AB1C内
∴BD1⊥平面AB1C
三垂线定理的逆定理
线射垂直
α
P A O
a
?
α
P
线斜垂直
O
A
a
平面内的一条直线和 平面的一条斜线在平 面内的射影垂直
平面内的一条直 线和平面的一条 斜线垂直
三垂线定理的逆定理
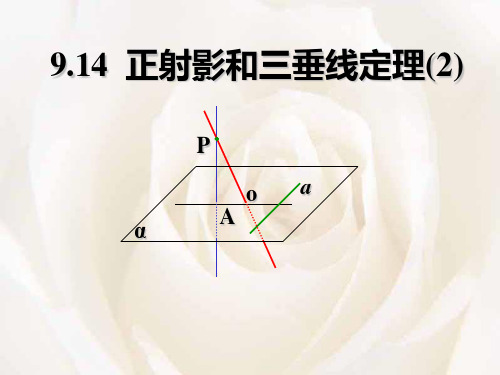
在平面内的一条直线,如果和这个平面的一 条斜线垂直,那么,它也和这条斜线的射影垂直。 P
这个六边形顶点和边的距离。
A D B
O
C
三垂线定理
例3、一段笔直的道路旁有一条河,河对岸有电塔AB, 高15m,只有测角器和皮尺作测量工具,不过河怎样求出 电塔顶A与道路的距离? 解:在道边取一点C, 使BC与道边所成水平角等于90°, 再在道边取一点D, 使水平角CDB等于45°, 测得C、D的距离等于20m A
B
直线与平面所成的角的定义

直线与平面所成的角的定义:
①直线和平面所成的角有三种:
a.斜线和平面所成的角:一条直线与平面α相交,但不和α垂直,这条直线叫做平面α的斜线.斜线与α的交点叫做斜足,过斜线上斜足以外的点向平面引垂线,过垂足与斜足的直线叫做斜线在平面α内的射影,平面的一条斜线和它在平面上的射影所成的锐角,叫做这条直线和这个平面所成的角.
b.垂线与平面所成的角:一条直线垂直于平面,则它们所成的角是直角。
c.一条直线和平面平行,或在平面内,则它们所成的角为00.
②取值范围:00≤θ≤900.
求斜线与平面所成角的思路类似于求异面直线所成角:“一作,二证,三计算”
最小角定理:
斜线和它在平面内的射影所成的角(即线面角),是斜线和这个平面内的所有直线所成角中最小的角。
求直线与平面所成的角的方法:
(1)找角:求直线与平面所成角的一般过程:①通过射影转化法,作出直线与平面所成的角;
②在三角形中求角的大小.
(2)向量法:设PA是平面α的斜线,,向量n为平面α的法向量,设PA与平面α所成的角为θ,则。
三垂线定理(中学课件201909)
一基础训练题
1)P是边长为a的正六边形ABCDEF所在平面外一点,
PA⊥AB, PA⊥AF。为求P与CD的距离,作PQ⊥CD
于Q点,则
() C
A、Q为CD的中点
B、Q与D重合
C、 Q与C重合
D、以上都不对
2)在正方体AC1中,E、G分别是AA1和CC1的中点, F在
AB上,且C1E⊥EF, 则EF与GD所成的角的大小为( D )
能否求出电塔顶与道路的距离?
B
90°
C
45°
D
例题5,长方体ABCD-A1B1C1D1中,AB=a。 BC=BB1=b。求点C到直线AB1的距离
D1 C1
A1 B1
D
C
A
B
例 如果一个角所在平面外一点到角的两边距离相等, 那么这一点在平面上的射影在这个角的平分线上。
已知:∠BAC在平面内,点P,PE⊥AB, P
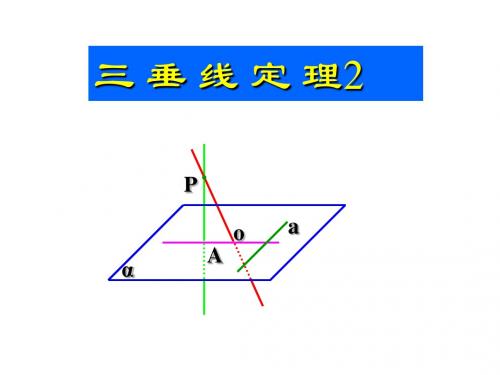
三 垂 线 定 理2
P
oa
α
A
二、两个基本定理回顾
1,三垂线定理:在平面内的一条直线,和这个平面 的一条斜线的射影垂直,那么它也和这条斜线垂直。
OA是PA在平面内的射影
P
a
a
a OA
OA α
a PA
2,三垂线定理的逆定理 在平面内的一条直线,如果和这个平面的一
条斜线垂直,那么,它也和这条斜线的射影垂直。
A
D B
C
例题2,在正方体AC1中,EF是异面直线AC与A1D的
公垂线,求证EF//BD1
D1 C1
A1 B1
E
D AF
C B
例题4 设PA、PB、PC两两互相垂直,且PA=3,PB=4, PC=6,求点P到平面ABC的距离。
直线、平面垂直的判定及其性质

直线、平面垂直的判定及其性质知识要点梳理知识点一、直线和平面垂直的定义与判定1.直线和平面垂直定义如果直线和平面内的任意一条直线都垂直,我们就说直线与平面互相垂直,记作.直线叫平面的垂线;平面叫直线的垂面;垂线和平面的交点叫垂足.2.直线和平面垂直的判定定理判定定理:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.知识点二、斜线、射影、直线与平面所成的角一条直线和一个平面相交,但不和这个平面垂直,这条直线叫做这个平面的斜线.过斜线上斜足外的一点间平面引垂线,过垂足和斜足的直线叫做斜线在这个平面内的射影.平面的一条斜线和它在平面上的射影90],叫做这条直线和这个平面所成的角.所成的锐角[00至0知识点三、二面角1.二面角定义平面内的一条直线把平面分成两部分,这两部分通常称为半平面.从一条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫二面角的棱,这两个半平面叫做二面角的面.2.二面角的平面角在二面角的棱上任取一点,以该点为垂足,在两个半平面内分别作垂直于棱的射线,则这两条射线构成的角叫做二面角的平面角.二面角的大小可以用它的平面角来度量,二面角的平面角是多少度,就说这个二面角是多少度.平面角是180]直角的二面角叫做直二面角二面角范围是[00至0知识点四、平面与平面垂直的定义与判定1.平面与平面垂直定义两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面垂直. 表示方法:平面与垂直,记作.2.平面与平面垂直的判定定理判定定理:一个平面过另一个平面的垂线,则这两个平面垂直. 符号语言: 图形语言:知识点五、直线与平面垂直的性质1.基本性质一条直线垂直于一个平面,那么这条直线垂直于这个平面内的所有直线.2.性质定理1垂直于同一个平面的两条直线平行.2垂直于同一条直线的两个平面平行知识点六、平面与平面垂直的性质性质定理:两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.如果两个平面互相垂直那么经过第一个平面内的一点垂直于第二个平面的直线在第一个平面内 例1 在三棱锥P A B C -中,侧面PAC 与面ABC 垂直,3PA PB PC ===.求证:A B B C ⊥; 设23AB BC ==,求A C 与平面PBC 所成角的大小.例2 如图,直角A B C △所在平面外一点S ,且SA SB SC ==,点D 为斜边A C 的中点.求证:SD ⊥平面ABC ;若A B B C =,求证:B D ⊥面S A C .例3 在正方体ABCD-A1B1C1D1中.(1)求直线A1B 和平面ABCD 所成的角;(2)求直线A1B 和平面A1B1CD 所成的角.例4如图所示,河堤斜面与水平面所成二面角为300,堤面上有一条直道CD ,它与堤角的水平线AB 的夹角为450 ,沿这条直道从堤脚C 向上行走10m 到达E 处,此时人升高了多少m ?例5 在四面体ABCD 中,已知AC ⊥BD,∠ BAC= ∠CAD=45°,∠BAD=60°,求证:平面ABC ⊥平面ACD.例6四棱锥P-ABCD 的底面是矩形,AB=2,侧面PAB 是等边三角形,且侧面PAB ⊥底面ABCD.证明:侧面PAB ⊥侧面PBC ;(2)求侧棱PC 与底面ABCD 所成的角A B C DE一、选择题1.两异面直线在平面α内的射影()A.相交直线 B.平行直线 C.一条直线—个点 D.以上三种情况均有可能2.在下列四个命题中,假命题为()A.如果一条直线垂直于平面内的无数条直线,那么这条直线和这个平面垂直B.垂直于三角形两边的直线必垂直于第三边C.过点A垂直于直线a的所有直线都在过点A垂直于a的平面内D.如果三条共点直线两两垂直,那么其中一条直线垂直于另两条直线确定的平面3.已知P是四边形ABCD所在平面外一点且P在平面ABCD内的射影在四边形ABCD内,若P到这四边形各边的距离相等,那么这个四边形是()A.圆内接四边形 B.矩形 C.圆外切四边形 D.平行四边形4.在△ABC中,AB=AC=5,BC=6,PA⊥平面ABC,PA=8,则P到BC的距离等于()A.5 B.52 C.35 D.455.A、B两点相距4cm,且A、B与平面a的距离分别为3cm和1cm,则AB与平面a所成角的大小是()A.30°B.60°C.90°D.30°或90°6. 直线a不垂直于平面α,则α内与a垂直的直线有()A.0条B.1条C.无数条D.α内所有直线7. 已知三条直线m,n,l,三个平面α,β,γ.下面四个命题中,正确的是()A.αγαββγ⊥⎫⇒⎬⊥⎭//B.mll mββ⎫⇒⊥⎬⊥⎭//C.mm nnγγ⎫⇒⎬⎭//////D.mm nnγγ⊥⎫⇒⎬⊥⎭//8. 设a,b是异面直线,下列命题正确的是()A.过不在a,b上的一点P一定可以作一条直线和a,b都相交B.过不在a,b上的一点P一定可以作一个平面和a,b垂直C.过a一定可以作一个平面与b垂直D.过a一定可以作一个平面与b平行二、填空题1.AB是平面α的斜线段,其长为a,它在平面α内的射影A′B的长为b,则垂线A′A_________.2.如果直线l、m与平面α、β、γ满足:l=β∩γ,l⊥α,mα和m⊥γ,现给出以下四个结论:α∥γ且l⊥m;②αγ且m∥β③αβ且l⊥m;④αγ且l⊥m;其中正确的为“________”3.给出以下四个命题(1)两条平行直线在同一平面内的射影一定是平行直线;(2)两条相交直线在同一平面内的射影一定是相交直线;(3)两条异面直线在同一平面内的射影—定是两条相交直线;(4)一个锐角在平面内的射影一定是锐角.其中假命题的共有_________个.4. αβ,是两个不同的平面,m n ,是平面α及β之外的两条不同的直线,给出四个论断: m n ⊥①;αβ⊥②;n β⊥③;m α⊥④.以其中三个论断作为条件,余下的一个论断作为结论,写出你认为正确的一个命题__________.5 设O 为平行四边形A B C D 对角线的交点,P 为平面A C 外一点且有P A P C =,PB PD =,则P O 与平面A B C D 的关系是_____________.6.设三棱锥P A B C -的顶点P 在底面ABC 内射影O (在A B C △内部,即过P 作P O ⊥底面ABC ,交于O ),且到三个侧面的距离相等,则O 是A B C △的______心.三、解答题1如图所示,平面α∥平面β,点A ∈α,C ∈α,点B ∈β,D ∈β,点E ,F 分别在线段AB ,CD 上,且AE ∶EB=CF ∶FD.求证:EF ∥β;(2)若E ,F 分别是AB ,CD 的中点,AC=4,BD=6且AC ,BD 所成的角为60°,求EF 的长2在正三棱柱ABC ﹣A1B1C1中,侧棱长为,底面三角形的边长为1,则BC1与侧面ACC1A1所成的角是3.三棱锥 P-ABC 中,PC ⊥平面ABC ,PC =32 ,D 是 BC 的中点,且△ADC 是边长为 2的正三角形,求二面角 P-AB -C 的大小。
2[1].3.2平面与平面垂直的判定
![2[1].3.2平面与平面垂直的判定](https://img.taocdn.com/s3/m/4f36fdd9d15abe23482f4db2.png)
F
D1 A1 C1 B1 A1 D1 O H C1 G B1
(1) )
(2) )
六、两个平面互相垂直的定义
两个平面相交, 两个平面相交,如果它们所成的二面角 是直二面角,就说这两个平面相互垂直 两个平面相互垂直. 是直二面角,就说这两个平面相互垂直.
β
β
α
记作: 记作:
α
α ⊥β
七、面面垂直的判定定理: 面面垂直的判定定理:
注意: 注意:
α A
二面角的平面角的三个特征: 二面角的平面角的三个特征: 2.线在面内 3.与棱垂直
1.点在棱上
平面角是直角的二面角叫做直二面角
l
O B
β
练习: 练习: 指出下列各图中的二面角的平面角: 指出下列各图中的二面角的平面角:
正方体 A’C中 D’ A’ D A 二面角B--B’C--A 二面角 B B’ O C B E O C D C’ A
经典例题讲解
如图, 是 的直径, 垂直⊙ 所在的平面 所在的平面, 是 例1 如图,AB是⊙O的直径,PA垂直⊙O所在的平面,C是 的直径 圆周上不同于A,B的任意一点, 的任意一点, 圆周上不同于 的任意一点 求证:平面 求证:平面PAC⊥平面 ⊥平面PBC. . 又已知条件, 设 所在平面为 证明: 证明: ⊙O所在平面为α,又已知条件, PA⊥α,BC在α内,所以PA⊥BC. ⊥ 在 所以 因为点C是圆周上不同于 因为点 是圆周上不同于A,B的任意 是圆周上不同于 的任意 一点,AB是⊙O的直径, 一点, 是 的直径, 的直径 所以, 是直角, 所以,∠BCA是直角,即BC⊥AC. 是直角 又因为PA与 是 又因为 与AC是△PAC所在平面内的 所在平面内的 两条相交直线,所以BC⊥平面PAC. 两条相交直线,所以 ⊥平面 又因为BC在平面 又因为 在平面PBC内,所以,平面 在平面 内 所以, PAC⊥平面 ⊥平面PBC.
8.4 直线、平面垂直的判定和性质

面PBD,又AC⊂平面PAC,所以平面PAC⊥平面PBD.
(2)易知∠PDB即为二面角P-AC-B的平面角,所以∠PDB=60°. 作BO⊥PD于O,连接AO,由(1)知BO⊥平面PAC,所以∠BAO即为直线AB
与平面PAC所成的角.令AB=2a,则BD= 3a,BO= 3 BD= 3 a,所以sin∠
在空间内,从平面外一点向这个平面所引的垂线段和斜线段中:(1)垂线
段最短;(2)射影相等的两条斜线段相等,两条斜线段相等,它们的射影也
相等;(3)射影较长的斜线段也较长,较长的斜线段的射影也较长.这就是
垂线段和斜线段长定理,应当注意:定理中涉及的垂线段和斜线段都是
从平面外同一点引出的,缺少这个条件,结论不成立.
(2)解法一:空间向量法. 如图,由(1)知,DE⊥DC,过D作DF⊥平面ABCD,则DE,DC,DF两两垂直, 分别以DE,DC,DF所在直线为x轴,y轴,z轴建立空间直角坐标系D-xyz,
则D(0,0,0),A(1,-1,0),B(1,1,0),C(0,1,0),可求得S
1 2
,
0,
3 2,连接PO,OB,OC,∵△PAD为正三角形,∴ PO⊥AD,∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,∴PO⊥ 平面ABCD,∴PO∥MB,∵PO=MB= 3 ,故四边形OPMB为矩形,∴PO⊥ PM,同理,PO⊥PN,∴PO⊥平面PMN,又PO⊂平面PAD,∴平面PAD⊥平 面PMN.
2.点到平面的距离、线到面的距离 (1)从平面外一点引平面的一条垂线,这个点和垂足间的距离,叫做这个 点到这个平面的距离. (2)一条直线和一个平面平行时,这条直线上任意一点到这个平面的距 离,叫做这条直线和这个平面的距离. 3.斜线在平面内的射影 (1)从斜线上斜足以外的一点向平面引垂线,过垂足与斜足的直线叫做 斜线在这个平面内的射影,垂足与斜足间的线段叫做这个点到平面的斜 线段在这个平面内的射影. (2)斜线上任意一点在平面上的射影一定在斜线的射影上. 4.垂线段和斜线段长定理
直线与平面垂直的判定定理 ppt课件
l
l m,l n
m
,
n
l
//
mA
mI n A
n
②该定理作用:“线线垂直线面垂直”
③应用该定理,关键是证明在平面内有两条相交直线与已知直线
垂直,至于这两条直线是否与已知直线有公共点则是无关紧要的.
例 如图,已知 a//b,a,求证:b.
证明:在平面 内作两条相交直线m,n.
因为直线 a,
又QB1D1I DD1=D1
A1
A 1C 1面 D B B 1D 1
A 1 C 1 B D 1 , A 1 C 1 D B 1
D
C1 B1
C
另证: QDD1 面A1B1C1D1,DD1 面DBB1D1
面A1B1C1D1 面DBB1D1
A
B
又Q面A1B1C1D1I 面DBB1D1 B1D1,
且A1C1 面A1B1C1D1,A1C1 B1D1
C C1
B
α
B1
1.直线与平面垂直的定义
(1)如果一条直线 l和一个平面内的任意一条直线都垂直, 则称直线 l与平面互相垂直,记作 l . 直线 l 叫做平面 的垂线,平面 叫做直线 l的垂面.
它们惟一的公共点P叫做垂足.
画法:通常把直线画成与表示平面的 平行四边形的一边垂直.
注1: ①定义中的“任意一条直线”与“所有直线”是同义词,但与 “无数条直线”不同.
A1C1 面DBB1D1
小结论: 正方体中,面的对角线垂直于过另一条面的对角线的对角面; 正方体中,异面的体对角线和面对角线互相垂直.
练 如图为直四棱柱A B C D A 'B 'C 'D '(侧棱与底面垂直
9.4.2 正射影和三垂线定理
③
如果将定理“在 平面内”的条件去掉, 结论仍然成立吗?
例如:当 b⊥ 时, b⊥OA
但 b不垂直于OP
P
b
直线a 一定要在平面内, 如果 a 不在平面内,定理 就不一定成立。
O
a
α
A
三垂线定理
说明:
1、三垂线定理描述的是PO(斜线)、AO(射
影)、a(直线)之间的垂直关系。 2、a与PO可以相交,也可以异面。 3、三垂线定理的实质是平面的一条斜线和 平面内的一条直线垂直的判定定理。
BC⊥AM
(3) 在正方体AC1中,
D1 A1 B1
C1
求证:A1C⊥BC1 , A1C⊥B1D1
证明: ∵在正方体AC1中
D
A D1 B1 D A B B
C
A1B1⊥面BCC1B1且BC1 ⊥B1C
由三垂线定理知
∴B1C是A1C在面BCC1B1上的射影
C1
A1
A1C⊥BC1
同理可证, A1C⊥B1D1
例1 直接利用三垂线定理证明下列各题:
(1) 已知:PA⊥正方形ABCD所在平面,O为对角线BD的中点 求证:PO⊥BD,PC⊥BD
(2) 已知:PA⊥平面PBC,PB=PC,M是BC的中点, 求证:BC⊥AM (3) 已知:在正方体AC1中,求证:A1C⊥B1D1,A1C⊥BC1
P
A B D
P C
同理,AC⊥BD
AC是PC在ABCD上的射影
平面ABCD
∴ PO⊥BD
∴ PC⊥BD
(2) 已知:PA⊥平面PBC,PB=PC,
P
M是BC的中点,
求证:BC⊥AM 证明: ∵ PA⊥平面PBC
平面的垂线、平面的垂线段
5、求斜线与平面所成角的步骤: (1)过斜线上不同于斜足的点作平面 的垂线(选择可作垂线的点); (2)连接垂足与斜足,找到斜线 在该 平面上的射影; (3)构造以垂线段、斜线段、斜线段 的射影为边的直角三角形,在此直角 三角形中以斜足为顶点的锐角是斜线 与平面所成的角,解此直角三角形。
O
P
O A
(4)PC⊥AB,PA⊥BC, PB⊥AC
(5)PA⊥PB,PB⊥PC,PC⊥PA
O
从平面外同一点向该平面能作多少条垂线段和斜线段?
有且只有一条 有无数条
从平面外同一点向这个平面所引的垂线段和斜线段中:
(1)垂线段唯一存在且最短; (2)射影相等的两条斜线段相等, 射影较长的斜线段也较长; (3)相等的斜线段的射影相等, 较长的斜线段的射影也较长。
.P
1、过点P引直线m的垂线,垂足为O, m 则垂足O叫做点P在直线 m上的射影
O
2、过点P引平面的垂线,垂足为O, 则垂足O叫做点P在平面上的射影
· P
O
3、平面的斜线在该平面内的射影: 从斜线上斜足O1以外的点P引平面的垂线, 过垂足O2和斜足O1的直线叫做斜线在该平面内的射影, 垂足和斜足间的线段叫做 斜线段在该平面内的射影。
如果直线m与平面相交且垂直,交点 为O,则直线m叫做平面的垂线,交点O 叫做垂足,
垂线m上的任意一点P与垂足O 间的线段PO叫做平面的垂线段 过空间一点的面的垂线及垂线段有且只有一条
如果直线n与平面相交且不垂直,交 点为M,则直线n叫做平面的斜线,交点 M叫做斜足,
斜线n上任意一点N与斜足之间的线段叫做平面的斜线段。 过空间一点的面的斜线和斜线段有无数条
P
A
ห้องสมุดไป่ตู้
直线、平面垂直的判定及其性质
例 1、如图,已知点 P 为平面 ABC 外一点,PA⊥BC,PC⊥AB,求证:PB⊥AC.
证明:过 P 作 PO⊥平面 ABC 于 O,连接 OA、OB、OC.
∵PO⊥平面 ABC,BC 平面 ABC,
∴PO⊥BC. 又∵PA⊥BC,∴BC⊥平面 PAO.
解:连接 BC1 交 B1C 于点 O,连接 A1O. 设正方体的棱长为 a, 因为 A1B1⊥B1C1,A1B1⊥B1B,所以 A1B1⊥平面 BCC1B1. 所以 A1B1⊥BC1. 又因为 BC1⊥B1C,所以 BC1⊥平面 A1B1CD. 所以 A1O 为斜线 A1B 在平面 A1B1CD 内的射影,∠BA1O 为直线 A1B 与平面 A1B1CD
直线与平面垂直的判定
日常生活中,我们对直线与平面垂直有很多感性认识,比如,旗杆与地 面的位置关系,大桥的桥柱与水面的位置关系等,都给我们以直线与平面垂 直的印象. 问题1:如果一条直线垂直于一个平面的无数条直线,那么这条直线是否与这 个平面垂直?举例说明.
在阳光下观察直立于地面的旗杆及它在地面的影子.随着时间的变化,尽 管影子BC的位置在移动,但是旗杆AB所在直线始终与BC所在直线垂直.也就 是说,旗杆AB所在直线与地面内任意一条不过点B的直线B′C′也是垂直的.
∵BD∥NA,∴AC1⊥NA. 又由 BD⊥AC,可知 NA⊥AC, ∴∠C1AC 就是平面 AFC1 与平面 ABCD 所成二面角的平面角或补角.
在 Rt△ C1AC 中,tan∠C1AC= C1C 1 ,故∠C1AC=30°. CA 3
∴平面 AFC1 与平面 ABCD 所成二面角的大小为 30°或 150°.
