压力角计算及公式
压力角计算公式

2.2滚子摆动从动件盘形凸轮机构的设计如图2所示滚子摆动从动件盘形凸轮机构,摆杆摆动中心C ,杆长为l ,机架OC 长为b ,从动件处于起始位置时,滚子中心处于B 0点,摆杆与机架OC 之间的夹角为0ψ,当凸轮转过ϕ角后,从动件摆过ψ角,滚子中心处于B 点。
分析代换后的平面连杆机构OABC ,得从动杆BC 上B 点位移、速度、加速度矢量式:0()()(π)OA OA AB AB l l b l θθψψ+-=--e e i e(9)式中2220arccos()2b l b r lbψ+-= ()()(π)OA OA AB AB AB b o l l l ωθωθωψψ+=--g g g (10)22200()()()(π)(π)OA OA AB AB AB AB AB AB b b l l l l l ωθωθεθεψψωψψ--+=------e e g g e (11)注意,在文献[1]』中,从动件的角速度、角加速度在回程时为负,推程时为正,而此处逆时针为正,顺时针为负,所以引用公式时,须添加负号。
据矢量方程式(8)(9)(10)式推导可得:00(1)sin()tan (1)cos()bABbl b l ωψψωθωψψω-+=--+ 当tan 0AB θ≥时,arctan(tan )AB AB θθ=当tan 0AB θ<时,πarctan(tan )AB AB θθ=+20200cos (1)cos()cos (1)cos()sin()b AB AB AB b b AB AB AB b l l b l l ωθψψθωωεθψψθψψθωω⎡⎤--++⎢⎥⎣⎦=--+++++AB 杆的方向亦即从动件受力方向,从动件运动垂直于CB 杆方向,凸轮机构压力角为:π2o AB a ψψθ=--- (12)图2摆动滚子盘形凸轮机构的演化Fig.2 Evolution of disk cam with oscillating rollerM 点处曲率半径为AB l r τρ=-即:20200cos (1)cos()cos (1)cos()sin()b AB AB b b AB AB AB b l r b l l τωθψψθωρωεθψψθψψθωω⎡⎤--++⎢⎥⎣⎦=---+++++ (13)凸轮实际廓线上M 点的向径为:(π)()o AB b l r τψψθ=+---r'i e e将该向径反方向旋转ϕ角,即得凸轮处于初始位置时点M 的向径:()(π)()o AB b l r τϕψψϕθϕ=-+-----r e e e (14)将式(14)分别点乘i j 和,得凸轮实际廓线的直角坐标方程:cos cos()cos()sin sin()sin()o AB o AB x b l r y b l r ττϕψψϕθϕϕψψϕθϕ=-++--⎫⎬=-+++--⎭(15)。
30度压力角渐开线花键设计公式
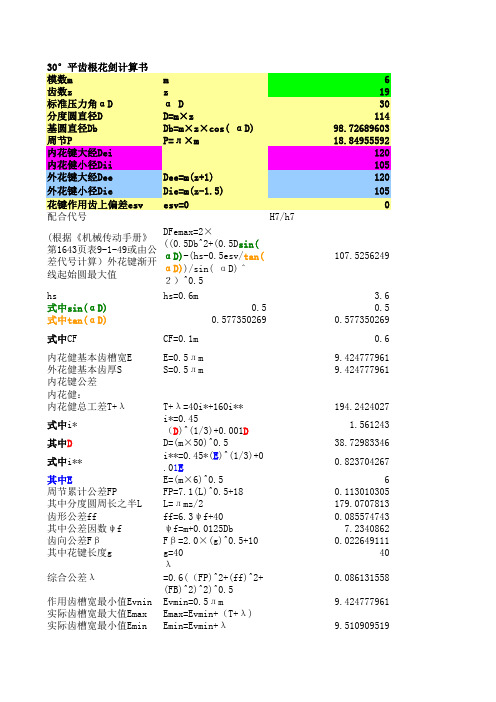
30°平齿根花剑计算书模数m m6齿数z z19标准压力角αDα D30分度圆直径D D=m×z114基圆直径Db Db=m×z×cos( αD)98.72689603周节P P=л×m18.84955592内花键大经Dei120内花健小径Dii105外花键大经Dee Dee=m(z+1)120外花键小径Die Die=m(z-1.5)105花键作用齿上偏差esv esv=00配合代号H7/h7(根据《机械传动手册》第1643页表9-1-49或由公差代号计算)外花键渐开线起始圆最大值DFemax=2×((0.5Db^2+(0.5D sin(αD)-(hs-0.5esv/tan(αD))/sin( αD)^2)^0.5107.5256249hs hs=0.6m 3.6式中sin(αD)0.50.5式中tan(αD)0.5773502690.577350269式中CF CF=0.1m0.6内花健基本齿槽宽E E=0.5лm9.424777961外花健基本齿厚S S=0.5лm9.424777961内花键公差内花健:内花健总工差T+λT+λ=40i*+160i**194.2424027式中i*i*=0.45(D)^(1/3)+0.001D1.561243其中D D=(m×50)^0.538.72983346式中i**i**=0.45*(E)^(1/3)+0.01E0.823704267其中E E=(m×6)^0.56周节累计公差FP FP=7.1(L)^0.5+180.113010305其中分度圆周长之半L L=лmz/2179.0707813齿形公差ff ff=6.3ψf+400.085574743其中公差因数ψfψf=m+0.0125Db7.2340862齿向公差FβFβ=2.0×(g)^0.5+100.022649111其中花键长度g g=4040综合公差λλ=0.6((FP)^2+(ff)^2+(FB)^2)^2)^0.50.086131558作用齿槽宽最小值Evnin Evmin=0.5лm9.424777961实际齿槽宽最大值Emax Emax=Evmin+(T+λ)实际齿槽宽最小值Emin Emin=Evmin+λ9.510909519作用齿槽宽最大值Evmax Evmax=Emax-λ 4.804868442外花键大经Dee Dee=m(z1+)120外花键小径Die Die=m(z-1.5)105外花键公差T+λT+λ=40i*+160i**式中i*i*=0.45(D)^(1/3)+0.001D其中D D=(m×50)^0.5式中i**i**=0.45*(E)^(1/3)+0 .01E周节累计公差FP其中分度圆周长之半L 齿形公差ff其中公差因数ψf齿向公差Fβ其中花键长度g综合公差λ作用齿宽最小值Evnin 实际齿宽最大值Emax 实际齿宽最小值Emin 作用齿宽最大值Evmax 外花键公差T+λ120 105179 4.891179。
凸轮机构基本参数的设计

凸轮机构基本参数的设计前节所先容的几何法和解析法设计凸轮轮廓曲线,其基圆半径r0、直动从动件的偏距e或摆动从动件与凸轮的中心距a、滚子半径rT等基本参数都是预先给定的。
本节将从凸轮机构的传动效率、运动是否失真、结构是否紧凑等方面讨论上述参数的确定方法。
1 凸轮机构的压力角和自锁图示为偏置尖底直动从动件盘形凸轮机构在推程的一个位置。
Q为从动件上作用的载荷(包括工作阻力、重力、弹簧力和惯性力)。
当不考虑摩擦时,凸轮作用于从动件的驱动力F是沿法线方向传递的。
此力可分解为沿从动件运动方向的有用分力F'和使从动件紧压导路的有害分力F''。
驱动力F与有用分力F'之间的夹角a(或接触点法线与从动件上力作用点速度方向所夹的锐角)称为凸轮机构在图示位置时的压力角。
显然,压力角是衡量有用分力F'与有害分力F''之比的重要参数。
压力角a愈大,有害分力F''愈大,由F''引起的导路中的摩擦阻力也愈大,故凸轮推动从动件所需的驱动力也就愈大。
当a增大到某一数值时,因F''而引起的摩擦阻力将会超过有用分力F',这时无论凸轮给从动件的驱动力多大,都不能推动从动件,这种现象称为机构出现自锁。
机构开始出现自锁的压力角alim称为极限压力角,它的数值与支承间的跨距l2、悬臂长度l1、接触面间的摩擦系数和润滑条件等有关。
实践说明,当a增大到接近alim时,即使尚未发生自锁,也会导致驱动力急剧增大,轮廓严重磨损、效率迅速降低。
因此,实际设计中规定了压力角的许用值[a]。
对摆动从动件,通常取[a]=40~50;对直动从动件通常取[a]=30~40。
滚子接触、润滑良好和支承有较好刚性时取数据的上限;否则取下限。
对于力锁合式凸轮机构,其从动件的回程是由弹簧等外力驱动的,而不是由凸轮驱动的,所以不会出现自锁。
因此,力锁合式凸轮机构的回程压力角可以很大,其许用值可取[a]=70~80。
曲柄滑块四杆机构压力角传动角的定义及其计算课件

传动角定义及作用
定义
在平面连杆机构中,主动件与从动件开始相对运动时的两个共线位置之间的夹角。
作用
衡量机构的传动性能,传动角越大,机构的传动性能越好,效率越高。
影响压力角和传动角的因素
01
曲柄长度
02
连杆长度
03
滑块位置
04
压力角传动角计算方法论述
压力角计算方法
定义
计算公式 注意事项
传动角计算方法
定义
传动角是指在曲柄滑块四杆机构 中,主动件通过连杆传递给从动 件的力的方向与从动件运动方向
之间所夹的锐角。
计算公式
传动角γ可通过余弦函数计算, γ=arccos((lAB^2+lBC^2-
lAC^2)/(2lAB·lBC)),其中lAB、 lBC和lAC分别为曲柄、连杆和滑
块的长度。
注意事项
在计算传动角时,需确保所取角 度为锐角,并注意机构的运动方
实验目的
验证曲柄滑块四杆机构压力角传动角的定义,探究机构运动过程中压力角和传动角的变化规律,提高理论知识的 实践应用能力。
方案制定
搭建曲柄滑块四杆机构实验台,通过调整机构参数和运动速度,采集不同位置下的压力角和传动角数据,进行对 比分析。
数据采集与整理方法论述
数据采集方法
采用光电传感器和角度传感器实时采集 机构运动过程中的压力角和传动角数据, 确保数据的准确性和实时性。
曲柄滑块四杆机构定义
01
02
03
04
块四杆机构工作原理
旋转运动转换为直线运动
传动比与行程速度变化
曲柄滑块四杆机构类型
对心曲柄滑块机构 偏置曲柄滑块机构
03
压力角传动角概念及影响因素
渐开线圆柱外齿轮常用参数及其计算公式

项目
代号
计算公式及说明
7
基圆螺旋角
tan = tan cos
法面变位系数
8
9
变位系数
齿顶高系数
端面变位系数
法面齿顶高系数
∗
ℎ
端面齿顶高系数
ℎ∗
法面径向间隙系
10
径向间隙系数
(齿顶隙系数)
数
端面径向间隙系
数
∗
∗
= cos
ℎ∗ = ℎ∗ cos
序号
项目
代号
量柱(球)测量距
24
中心距
重合度
=
端面重合度
25
计算公式及说明
齿线重合度
α
cos
cos
=
=
1
2
1
2
cos
mod
1 + 2 =
2
1 + 2
2 cos
1 tan 1 − tan + 2 tan 2 − tan
渐开线圆柱外齿轮常用参数及其计算公式
序号
项目
代号
1
齿数
1、齿轮一周所含的轮齿的个数;
2
分度圆螺旋角
1、 斜齿轮中,不同圆周上的螺旋角是不同的;
2、 设计图纸中给出的是分度圆上的螺旋角;
法面模数
3
4
模数
端面模数
法面压力角
压力角
(齿形角)
端面压力角
5
分度圆直径
6
基圆直径
计算公式及说明
齿轮系数计算公式

齿轮系数计算公式(国标齿轮压力角普遍为cos20°)名称代号计算公式齿数Z齿数模数m m=p/πm=齿距/π分度圆直径 d d=mz(齿中径) d=模数X齿数压力角cosαcosα=(W1-W)/3.14mW =跨K个齿的公法线长度W1=跨K+1个齿的公法线长度基圆直径d b d b= d X cosα(两齿轮运行中形成的线)d b=分度圆直径X压力角齿顶圆直径da da=(Z+2)mda=(齿数+2)X模数齿根圆直径df df= (Z-2.5)mdf= (齿数-2.5)X模数齿顶高ha ha=ha*mha=ha*模数(常用ha*=1)(短齿ha*=0.8)顶隙 c c=c*mc=c*模数(常用c*=0.25)(短齿c*=0.3)齿根高hf hf=ha+c=(ha*+c*)m=1.25m齿高h h=ha+hf=m+1.25m=2.25m齿距P P=mπP=模数Xπ齿厚S槽宽e S=e=P/2中心距(与齿轮副合配)a a=d1/2+d2/2=(Z1+Z2)m/2(d1代表一个齿轮的分度圆直径,d2代表另一个齿轮的分度圆直径)(Z1代表一个齿轮的齿数,Z2代表另一个齿轮的齿数)(m代表齿轮模数)模数选择优先选择(1 1.25 1.5 2 2.5 3 4 5 6 8 10 12 14 16 20 2532 40 50)可以选用(1.75 2.25 2.75 3.5 4.5 5.5 7 9 14 18 22 28 26 45)尽可能不用(3.25 3.75 6.5 11 30)压力角选择米制:20°14.5°15°17.5°22.5°25°28°30°英制:20°14.5°15°其次16°17°17.5°22.5°25°cos20=0.9397 cos30=0.866 cos45=0.7071美标与日标跟国标一样的,可能他们比较多的采用“节径”这个概念,我们相应来说比较多的用的是“模数”。
渐开线内花键压力角的测算方法

M2 =2(A2 +R 2)=M1 +2(R 2 -R1 )(si n -1 α+1 )(2) 而当花键轴键数为奇数时 , 如图 2 所示 , 则可
得 M 2 =2[ A2 co s(90°/z )+R2] =M1 +2(R2 -R1 )[ cos(90°/z )/sin α+1] (3) 式(1)、(2)用来计算偶数齿时 M 值的换算 , 式
(编辑 若 禾)
作者单位 :陕西省柴油机厂 邮政编码 :咸阳市 · 713800 收稿日期 :1999 年 6 月
16 2000 /6
38 卷 第 430 期
梯形花键轴 M 值的换算
◆叶国丰 ◆王 静
在加工梯形花键轴时 , 有时会因无图纸中所标 注的直径圆棒而无法检测 M 值 , 因此 , 如何用现有 相近的直径圆棒来替代检测 , 并准确换算出替代圆 棒的检测值 M , 就成为解决问题的关键 。
1 换算公式推导
当花键轴键数为偶数时 , 可绘制出如图 1 所示 的几何图形 , 并根据它计算出新圆棒检测产品的 M 值 。图中 β 值是齿形角的 1/2 , M1 为已知值 , R1 是 产品图纸要求的检测用圆棒半径 , R 2 是现有圆棒 半径 , A1 是图纸规定用圆棒中心到被检齿轮圆心 的距离 , A 2 是现有圆棒中心到被检齿轮圆心的距 离 , M 2 是现有圆棒检测被检齿轮的 M 值(待求)。
4 结论
①式(4)是以 ΔMR i为变量的 αi 的单调连续函 数 , 因此 , 测量时必须确保 M R 1 、 MR 2 的精度 , 才能 保证 αi 的准确度 。
②通过对投影放大齿形影像描点和作图 , 量出
两组圆间距 MR i 。这一方法的准确度取决于渐开线 内花键齿形本身的加工精度 、放大影像和描点的质 量以及几何作图的技巧和准确度 。
锥齿轮螺旋角计算公式

锥齿轮螺旋角计算公式
齿形角其实就是齿轮分度圆上的压力角,如果是斜齿轮,有段面齿形角和法向齿形角,以法向齿形角为标准,两者满足tan(法向压力角)= tan(端面压力角) * cos(螺旋角),蜗杆齿形角概念类似。
渐开线上任一点法向压力的方向线(即渐开线上该点的法线)和该点速度方向的夹角称为该点的压力角。
压力角在整个渐开线上都存在,并且不断变化,及从齿根圆到齿顶圆都存在。
说不清楚了,上图
AK是渐开线,αk是压力角,可以看出从A点到K点压力角是不同的(图上是K点处的压力角)。
压力角是可以求的,但是实际生产中有约定俗成的标准,基本都是分度圆上20°标准齿轮,及齿形角为20°的标准齿轮,渐开线上其他位置压力角用处不大也不需要特殊求解。
螺旋角基本都是斜齿轮和锥齿轮上应用的概念,圆柱螺旋线的切线与通过切点的圆柱面直母线之间所夹的锐角,圆锥螺旋线的切线与通过切点的圆锥面直母线之间所夹的锐角,都叫螺旋角,通常说的螺旋角其实是分度圆上的螺旋角。
上图
图二可能更直观一点
如果要计算螺旋角齿顶圆直径da=mz/cos β+2m 分度圆直径d=mz/cos β 两齿轮啮合的中心距A=m(z1+z2)/cos β 等等这些都可以推出来(斜齿轮为例)。
导程角一般说明于螺纹和蜗杆,用于螺纹也叫“螺纹升角”,是在中径圆柱或中径圆锥上螺旋线的切线与垂直于螺纹轴线的平面的夹角。
在蜗轮蜗杆传动中,蜗杆导程角是蜗杆分度圆柱上螺旋线的切线与蜗杆端面之间的夹角。
如图
φ即为导程角计算公式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
压力角是不计算摩擦力的情况下,受力方向和运动方向所夹的锐角。
压力角是若不考虑各运动副中的摩擦力及构件重力和惯性力的影响,机构运动时从动件所受的驱动力的方向线与该力作用点的速度
方向线之间的夹角。
概述
编辑本段
压力角(pressure angle)(α):若不考虑各运动副中的摩擦力及构件重力和惯性力的影响,作用于点C的力P与点C速度方向之间所夹
的锐角.
与压力角相联系的还有传动角(γ).
压力角越大,传动角就越小.也就意味着压力角越大,其传动效率越低.所以设计过程中应当使压力角小.
原理
编辑本段
在平面连杆机构中不计摩擦和构件的惯性的情况下,机构运动时从动件所受的驱动力的方向线与该力作用点的速度方向线之间的
夹角。在曲柄摇杆机构中(图1),主动件通过连杆作用在摇杆上的力P沿BC方向,力作用点C?的速度vC的方向垂直CD,这两方向
线所夹的角?α为压力角。压力角α越大,P在vC方向能作功的有效分力就越小,传动越困难。压力角的余角γ 称为传动角。机构
的压力角或传动角是评价机构动力学指标之一,设计机构时应限制其最大压力角或最小传动角。对于齿轮传动(图2),压力角?α也
是从动轮齿上所受驱动力P的方向线与P力作用点C?的速度vC方向线之间的夹角α,压力角α的大小随着轮齿啮合位置的不同而
变化。压力角
压力角
如果知道模数根据公式: m=(W1-W)/3.14cosα 就可以算出来 m-模数 W1-----跨k+1个齿的公法线长度 W-----跨K个齿的
公法线长度 α-----压力角
分度圆直径d分=mz 齿顶高h顶=m 齿顶圆直径D顶=d分+2h定=m(z+2)??齿根高h根=1.25m 全齿高h=h顶+h根=2.25m 周节
t=πm。
可以看出m是齿轮齿数计算的 一个基本参数
模数歌“标准模数用处大,设计计算都用它,齿轮大小随着它,模数越大受力?力的方向和运动方向的夹角叫做压力角。
同一条渐开线上位置不同,压力角就不一样,接近基圆压力角较小,离基圆越远,压力角越大,即越接近渐开线起点,压力角越
小,基圆上的 渐开线上点的压力角为零。
分度圆上的 压力角20°
如果分度圆的压力角越小,其基圆离分度圆就很近,这样齿根变短且齿根很瘦,牙齿所能承载的力量较小,如果分度圆压力角>
20°,基圆离分度圆就远了,齿根也厚了,壮实有力了,但是齿顶变尖了且传动费劲了,不过为了加强牙齿力量有时也采用大压力
角(如汽车上的某些齿轮α=22.2°.
我国规定分度圆标准压力角是20°
压力角歌“齿形压力角各处不一样,标准压力角20°定在分圆上,增大压力角齿顶变尖根变壮”。
2.2滚子摆动从动件盘形凸轮机构的设计
如图2所示滚子摆动从动件盘形凸轮
机构,摆杆摆动中心C,杆长为l,机架OC
长为b,从动件处于起始位置时,滚子中心
处于B0点,摆杆与机架OC之间的夹角为
0
,当凸轮转过角后,从动件摆过
角,滚子中心处于B点。
分析代换后的平面连杆机构OABC,
得从动杆BC上B点位移、速度、加速度矢
量式:
0()()(π)OAOAABAB
llbleeie
(9)
式中2220arccos()2blbrlb
()()(π)OAOAABABABbolllggg
(10)
222
00()()()(π)(π)OAOAABABABABABABbb
llllleegge
(11)
注意,在文献[1]』中,从动件的角速度、角加速度在回程时为负,推程时为正,而此处逆时针为正,顺时针
为负,所以引用公式时,须添加负号。
据矢量方程式(8)(9)(10)式推导可得:
当tan0AB时,arctan(tan)ABAB
当tan0AB时,πarctan(tan)ABAB
AB杆的方向亦即从动件受力方向,从动件运动垂直于CB杆方向,凸轮机构压力角为:
π
2
oAB
a
(12)
M点处曲率半径为ABlr即:
2
0200cos(1)cos()cos(1)cos()sin()bABAB
bb
ABABAB
blrbll
(13)
图2摆动滚子盘形凸轮机构的演化
Fig.2 Evolution of disk cam with oscillating roller follower
凸轮实际廓线上M点的向径为:
将该向径反方向旋转角,即得凸轮处于初始位置时点M的向径:
()(π)()oABblrreee
(14)
将式(14)分别点乘ij和,得凸轮实际廓线的直角坐标方程:
coscos()cos()sinsin()sin()oABoABxblryblr
(15)
