相似三角形典型例题精选
九年级数学相似三角形典型例题

九年级数学相似三角形典型例题一、利用相似三角形的判定定理证明相似例1:已知:在△ABC和△DEF中,∠A = ∠D = 60°,AB = 4,AC = 8,DE = 2,DF = 4。
求证:△ABC∽△DEF。
解析:1. 我们看相似三角形的判定定理。
对于两个三角形,如果它们的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似。
2. 在本题中:计算公式,公式。
并且已知∠A = ∠D = 60°。
因为公式且∠A = ∠D,所以根据相似三角形判定定理中的“两边对应成比例且夹角相等的两个三角形相似”,可以得出△ABC∽△DEF。
二、相似三角形性质的应用(求边长)例2:已知△ABC∽△A'B'C',相似比为公式,若AB = 6,则A'B'的长为多少?解析:1. 因为相似三角形对应边成比例。
设A'B' = 公式。
已知相似比公式。
2. 又已知公式,AB = 6,所以公式。
通过交叉相乘可得:公式。
即公式,解得公式,所以A'B'的长为9。
三、利用相似三角形解决实际问题(测量高度)例3:在同一时刻,身高1.6米的小强在阳光下的影长为0.8米,一棵大树的影长为4.8米,求这棵大树的高度。
解析:1. 因为在同一时刻,太阳光下不同物体的高度和影长成正比。
设大树的高度为公式米。
可以得到两个相似三角形,一个是由小强及其影子构成,另一个是由大树及其影子构成。
2. 根据相似三角形的性质,对应边成比例。
则公式。
交叉相乘可得:公式。
计算得公式,解得公式米。
所以这棵大树的高度是9.6米。
史上最全!!!!相似三角形难题精选

相似三角形难题精选模块一:相似三角形中的动点问题如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.(1)当t为何值时,AD=AB,并求出此时DE的长度;(2)当△DEG与△ACB相似时,求t的值.如图,在△ABC中,ABC=90°,AB=6m,BC=8m,动点P以2m/s的速度从A点出发,沿AC 向点C移动.同时,动点Q以1m/s的速度从C点出发,沿CB向点B移动.当其中有一点到达终点时,它们都停止移动.设移动的时间为t秒.(1)①当t=2.5s时,求△CPQ的面积;②求△CPQ的面积S(平方米)关于时间t(秒)的函数解析式;(2)在P,Q移动的过程中,当△CPQ为等腰三角形时,求出t的值.如图1,在Rt△ABC中,ACB=90°,AC=6,BC=8,点D在边AB上运动,DE平分CDB交边BC于点E,EM⊥BD,垂足为M,EN⊥CD,垂足为N.(1)当AD=CD时,求证:DE∥AC;(2)探究:AD为何值时,△BME与△CNE相似?如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm 的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,当P点到达B点时,Q点随之停止运动.设运动的时间为x.(1)当x为何值时,PQ∥BC?(2)△APQ与△CQB能否相似?若能,求出AP的长;若不能,请说明理由.如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从A开始向点B以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0<t<6)。
相似三角形经典题型

相似三角形经典题型一、相似三角形的判定定理相关题型1. 题目已知在△ABC和△A'B'C'中,∠A = 50°,AB = 3cm,AC = 4cm,∠A'= 50°,A'B'= 6cm,A'C' = 8cm。
判断这两个三角形是否相似。
解析根据相似三角形的判定定理:如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似。
在△ABC和△A'B'C'中,(AB)/(A'B')=(3)/(6)=(1)/(2),(AC)/(A'C')=(4)/(8)=(1)/(2),且∠A = ∠A' = 50°。
所以△ABC∽△A'B'C'。
2. 题目如图,在四边形ABCD中,∠B = ∠ACD,AB = 6,BC = 4,AC = 5,CD=(7)/(2),求AD的长。
解析因为∠B = ∠ACD,且(AB)/(AC)=(6)/(5),(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7),(AC)/(AD)未知。
又因为(AB)/(AC)=(6)/(5),(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7),不满足三边对应成比例。
但是由∠B = ∠ACD,(AB)/(AC)=(6)/(5),(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7),可以尝试证明△ABC和△ACD相似。
因为∠B = ∠ACD,(AB)/(AC)=(6)/(5),(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7),这里我们重新计算(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7)是错误的,应该是(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7),(AB)/(AC)=(6)/(5),(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7)(AB)/(AC)=(6)/(5),(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7)(AB)/(AC)=(BC)/(CD)所以△ABC∽△DCA。
相似三角形练习题及答案

相似三角形练习题及答案在初中数学中,相似三角形是一个很重要的概念。
相似三角形具有相同的形状,但是尺寸不同。
理解相似三角形的性质对于解决几何问题和计算三角形的边长和角度非常有帮助。
下面是一些相似三角形的练习题,帮助你巩固对该概念的理解,并附有答案供参考。
练习题一:已知△ABC和△DEF相似,且AB = 6cm,AC = 8cm,BC = 12cm。
若DE = 9cm,求DF和EF的长度。
练习题二:△ABC和△PQR中,∠B = ∠Q,AB = 5cm,BC = 8cm,PQ = 6cm,若AC = 10cm,求PR的长度。
练习题三:已知△ABC和△DEF相似,DE = 4.5cm,EF = 6cm,BC = 12cm,若AC = 8cm,求△ABC和△DEF的周长比。
练习题四:在△ABC中,∠B = 90°,AB = 9cm,BC = 12cm。
点D是BC的中点,于BC上作DE ⊥ BC,DE = 3cm。
求△ADE和△ABC的周长比。
练习题五:已知△ABC和△DEF相似,AB = 10cm,BC = 12cm,AC = 15cm,EF = 6cm,若△DEF的面积为18平方厘米,求△ABC的面积。
答案及解析如下:练习题一:由相似三角形的性质可知,相似三角形的边长之比相等。
设DF = x,EF = y。
根据题意可写出比例:AB/DE = AC/EF = BC/DF代入已知值,得到:6/9 = 8/y = 12/x解得:x = 16cm,y = 12cm因此,DF = 16cm,EF = 12cm。
练习题二:由相似三角形的性质可知,相似三角形的边长之比相等。
设PR = x。
根据题意可写出比例:AB/PQ = AC/PR = BC/QR代入已知值,得到:5/6 = 10/x = 8/(6 + x)解得:x = 15cm因此,PR = 15cm。
练习题三:由相似三角形的性质可知,相似三角形的边长之比相等。
相似三角形典型例题30道

相似三角形典型例题30道1: 在△ABC中,DE是平行于BC的线段,且AD/DB = 2/3。
求DE/BC的比值。
2: 已知△PQR与△XYZ相似,PQ = 6,XY = 9,求QR 与YZ的比值。
3: 在△ABC中,D、E分别是AB、AC上的点,且DE平行于BC,已知AD = 3,DB = 6,求AE与EC的比值。
4: 已知两个相似三角形的面积比为4:9,求它们对应边的比。
5: 在△XYZ中,MN是平行于XY的线段,且XM = 4,MY = 6,求MN/XY的比值。
6: 在△ABC中,AD是BC的中线,且AE是AB的延长线,若AE与BC相交于点F,求AF与FB的比值。
7: 在△DEF中,GH平行于EF,已知DE = 8,DF = 10,求GH/EF的比值。
8: 在一个相似三角形中,若大三角形的周长是36,小三角形的周长是24,求它们的面积比。
9: 在△JKL中,MN平行于JK,若JM = 3,MK = 5,求MN/JK的比值。
10: 如果两个相似三角形的对应边长分别为5和15,求它们的面积比。
11: 在△ABC中,AD是BC的中线,且DE平行于BC,已知AD = 4,BC = 8,求DE的长度。
12: 已知相似三角形的对应边长比为1:4,求它们的周长比。
13: 在△PQR中,S是PQ的中点,若ST平行于QR,求PS与PQ的比值。
14: 在相似三角形中,若小三角形的每条边长为5,大三角形的对应边长为15,求它们的面积比。
15: 在一个三角形中,若一条边的延长线与另一边的平行线相交,则形成的两小三角形与原三角形相似,求相似比。
16: 在△XYZ中,若XY = 10,XZ = 15,YZ = 12,求△XYZ的周长。
17: 已知△ABC与△DEF相似,若AB = 4,DE = 8,求AC与DF的比值。
18: 在△GHI中,JK平行于GH,若GJ = 5,GH = 20,求JK的长度。
19: 在相似三角形中,若一个三角形的面积是36,另一个三角形的面积是144,求其对应边的比。
(完整版)相似三角形经典模型总结及例题分类.doc
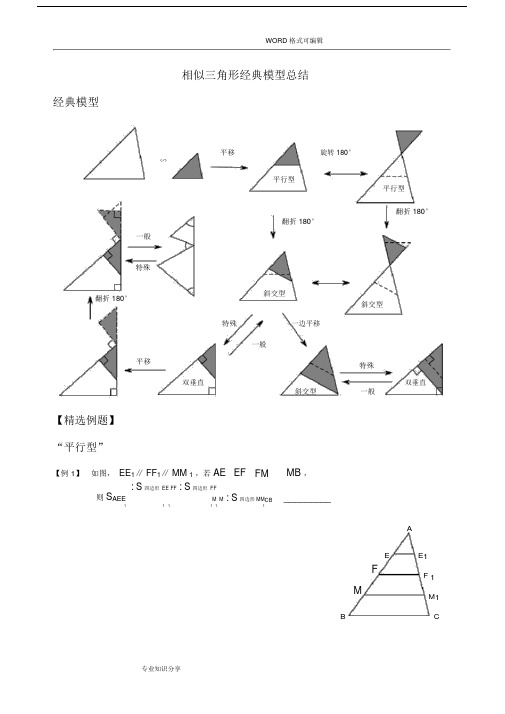
WORD 格式可编辑相似三角形经典模型总结经典模型平移旋转 180°∽平行型平行型翻折 180°翻折 180°一般特殊翻折 180°斜交型斜交型特殊一边平移一般平移特殊双垂直斜交型双垂直一般【精选例题】“平行型”【例 1】如图,EE1∥FF1∥MM1,若AE EF FM MB ,则S AEE : S四边形EE FF : S四边形FFM M : S四边形 MM C B _________1 1 1 1 1 1AE E1FF 1MM1B CWORD 格式可编辑【例 2】如图,AD∥EF∥MN∥BC,若AD 9,BC 18 , AE:EM :MB 2:3:4,则EF _____ , MN _____A DE FMNB C【例 3】已知,P为平行四边形ABCD 对角线, AC 上一点,过点P 的直线与 AD , BC , CD 的延长线, AB 的延长线分别相交于点 E , F , G , H求证: PE PHPF PGG D CE PFA B H【例 4】已知:在ABC 中, D 为 AB 中点, E 为 AC 上一点,且AE2, BE、 CD相交于点 F ,求BF的值ECEF ADF EB C【例 5】已知:在ABC 中, AD 1AB,延长 BC到F ,使CF1BC,连接 FD交 AC于点 E 2 3求证:① DE EF ② AE 2CEADEB专业知识分享【例 6】已知:D,E为三角形ABC 中 AB 、BC 边上的点,连接 DE 并延长交 AC 的延长线于点 F ,BD: DE AB: AC求证:CEF 为等腰三角形ACDEB F【例7】如图,已知 AB / / EF / /CD ,若 AB a , CD b , EF c ,求证:11 1 .c a bACEB F D【例 8】如图,找出S ABD、 S BED、 S BCD之间的关系,并证明你的结论.CAEB F D【例 9】如图,四边形ABCD中,B D90M是AC上一点,ME AD于点EMF BC,,于点 F 求证:MFME 1AB CDDEMA CFB【例 10】如图,在ABC 中, D 是 AC 边的中点,过 D 作直线 EF 交 AB 于 E ,交 BC 的延长线于 F 求证: AE BF BE CFAEDBC F 【例 11】如图,在线段AB 上,取一点 C ,以 AC , CB 为底在 AB 同侧作两个顶角相等的等腰三角形ADC 和CEB, AE交 CD于点 P, BD交 CE于点Q,求证: CP CQDEP QA C B【例 12】阅读并解答问题 .在给定的锐角三角形ABC 中,求作一个正方形DEFG,使 D, E落在 BC边上, F , G分别落在AC , AB 边上,作法如下:ABC 两边上的正方形D'E'F 'G'如图,第一步:画一个有三个顶点落在第二步:连接 BF ' 并延长交 AC 于点 F第三步:过 F 点作 FE BC ,垂足为点 E第四步:过 F 点作 FG∥BC 交 AB 于点 G第五步:过 G 点作 GD BC ,垂足为点 D四边形 DEFG 即为所求作的正方形问题:⑴证明上述所作的四边形DEFG 为正方形⑵在 ABC 中,如果BC 6 3,ABC 45 , BAC 75 ,求上述正方形DEFG 的边长AG FG'F'E CWORD 格式可编辑“平行旋转型”图形梳理:E'F'AAAF'E'AEF'EFFFEE'FEF'BCBCBBCAEF 旋转到 AE ‘ F ’CAEF 旋转到 AE ‘ F ’AEF 旋转到 AE ‘ F ’AEF 旋转到AE ‘F ’特殊情况: B 、 E'、 F '共线AAEF' EF'E'FE'FBC B CAEF 旋转到 AE ‘ F ’ AEF 旋转到 AE ‘ F ’C , E', F '共线E'AE'AEFEF'FF'BCBCAEF 旋转到 AE ‘ F ’AEF 旋转到 AE ‘ F ’【例 13】已知梯形 ABCD , AD ∥BC ,对角线AC 、 BD 互相垂直,则①证明: AD 2 BC 2AB 2 CD 2ADOB CWORD 格式可编辑【例 14】当AOD ,以点 O 为旋转中心,逆时针旋转度(090 ),问上面的结论是否成立,请说明理由DAOB C【例 15】(全国初中数学联赛武汉选拔赛试题)如图,四边形ABCD 和 BEFG 均为正方形,求AG : DF : CE_________.A DGFB CE“斜交型”【例 16】如图,ABC 中, D 在 AB 上,且 DE∥BC 交 AC 于 E , F 在 AD 上,且 AD2AF AB ,求证:AEF :ACDAFD EB C【例 17】如图,等边三角形ABC中,D,E分别在BC,AB上,且CE BE ,AD ,CE 相交于 M ,求证 : EAM : ECAAEMB DC AGF BE【例 18】如图,四边形ABCD 的对角线相交于点O ,BAC CDB ,求证:DAC CBDADOB C【例 19】如图,设ABBCCA,则 1 2 吗?AD DE EAA1 DE2B C【例 20】在锐角三角形ABC 中, AD , CE 分别为 BC , AB 边上的高,ABC 和BDE 的面积分别等于 18和 2 , DE 2,求 AC 边上的高AEB D C【例 21】如图,在等边ABC 的边 BC 上取点 D ,使BD 1,作CH AD,H为垂足,连结BH。
相似三角形30道经典题

相似三角形30道经典题英文回答:1. Theorem: If two triangles are similar, then their corresponding sides are proportional.2. Corollary: If two triangles have two pairs of corresponding sides proportional, then they are similar.3. Theorem: If two triangles have three pairs of corresponding angles congruent, then they are similar.4. Corollary: If two triangles have two pairs of corresponding angles congruent, then the third pair is also congruent, and the triangles are similar.5. Theorem: The ratio of the areas of two similar triangles is equal to the square of the ratio of any two corresponding sides.6. Corollary: The ratio of the areas of two similar triangles is equal to the square of the ratio of any two corresponding altitudes.7. Theorem: If a line parallel to one side of a triangle divides another side into two segments, then the ratio of the lengths of the segments is equal to the ratio of the corresponding sides of the triangle.8. Corollary: If a line parallel to the base of a triangle divides the other two sides into segments, then the ratios of the lengths of the segments are equal to the ratio of the corresponding sides of the triangle.9. Theorem: If a line parallel to one side of a triangle divides the area of the triangle into two parts, then the ratio of the areas of the parts is equal to the ratio of the corresponding sides of the triangle.10. Corollary: If a line parallel to the base of a triangle divides the area of the triangle into two parts, then the ratios of the areas of the parts are equal to theratio of the corresponding sides of the triangle.11. Theorem: The sum of the interior angles of a triangle is 180 degrees.12. Corollary: The sum of the exterior angles of a triangle is 360 degrees.13. Theorem: The Pythagorean Theorem: For a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.14. Corollary: The converse of the Pythagorean Theorem: If the square of one side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.15. Theorem: The Law of Cosines: For any triangle, the square of one side is equal to the sum of the squares of the other two sides minus twice the product of the other two sides and the cosine of the included angle.16. Corollary: The Law of Sines: For any triangle, the ratio of the sine of one angle to the length of theopposite side is equal to the ratio of the sine of anyother angle to the length of its opposite side.17. Theorem: The area of a triangle is equal to halfthe product of the base and height.18. Corollary: The area of a triangle is equal to half the product of two sides and the sine of the included angle.19. Theorem: The perimeter of a triangle is equal tothe sum of the lengths of its three sides.20. Corollary: The perimeter of a triangle is equal to the sum of the lengths of two sides plus the length of the third side.21. Theorem: If a triangle is equilateral, then its angles are all equal to 60 degrees.22. Corollary: If a triangle has two sides equal, thenits angles opposite the equal sides are equal.23. Theorem: If a triangle has two angles equal, thenits sides opposite the equal angles are equal.24. Corollary: If a triangle has three equal sides,then its angles are all equal to 60 degrees.25. Theorem: If a triangle has a right angle, then its other two angles are acute.26. Corollary: If a triangle has an obtuse angle, then its other two angles are acute.27. Theorem: If a triangle has two adjacent sides equal, then the angle opposite the equal sides is greater than the other angles.28. Corollary: If a triangle has two adjacent sides unequal, then the angle opposite the greater side isgreater than the angle opposite the smaller side.29. Theorem: If a triangle has two adjacent angles equal, then the sides opposite the equal angles are equal.30. Corollary: If a triangle has two adjacent angles unequal, then the side opposite the greater angle isgreater than the side opposite the smaller angle.中文回答:1. 定理,如果两个三角形相似,那么它们对应边的比值相等。
相似三角形判定典型例题

PE N
因为PN∥BC,所以△APN∽ △ABC
所以 因此
AE AD 80–x
=
=
PN xBC ,得
B QD
x=48(毫米)。答:-------。
M
C
80
120
12.如图,正方形ABCD的边长为8,E是AB的中
点,点M,N分别在BC,CD上,且CM=2,则当
CN=__1___或_4___时,△CMN与△ADE形状相同
复习课
1.已知:如图,△ABC中,P是AB边上的一点, 连结CP.满足什么条件时△ ACP∽△ABC?
解:⑴∵∠A= ∠A,∴当∠1= ∠ACB
(或∠2= ∠B)时,△ ACP∽△ABC A
⑵ ∵∠A= ∠A, ∴当AC:AP=AB:AC时, B
P1
4
2
C
△ ACP∽△ABC
答:当∠1= ∠ACB 或∠2= ∠B
a
解:⑴∵ ∠1=∠D=90° b a
1
∴当 A C C B 时,即当 a B D 时,
CB BD
△ABC∽ △CDB,∴ B D
a2
b
⑵∵ ∠1=∠D=90°
∴当
AC BC
AB BD
时,即当
b a
△ABC∽ △BDC, ∴BD
2
2
ba
时,
BD
2
2
ab
a
b
典型例题
7.如图为三个并列的边长相同 的正方形,试说明:
。
A
D
A
D
E
N
B
MC
解:当CN=1时,
AD AE 2 CM CN 1
△CMN∽△ADE
E
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相似三角形的判定与性质综合运用经典题型
考点一:相似三角形的判定与性质:
例1、如图,△PCD 是等边三角形,A 、C 、D 、B 在同一直线上,且∠APB=120°.
求证:⑴△PAC ∽△BPD ;⑵ CD 2 =AC ·BD.
例2、如图,在等腰△ABC 中, ∠BAC=90°,AB=AC=1,点D 是BC 边上的一个动点(不与B 、C 重合〕,在AC 上取一点E ,使∠ADE=45°
〔1〕求证:△ABD ∽△DCE ;
〔2〕设BD=x ,AE=y ,求y 关于x 函数关系式及自变量x 值范围,并求出当x 为何值时AE 取得最小值?
〔3〕在AC 上是否存在点E ,使得△ADE 为等腰三角形?假设存在,求AE 的长;假设不存在,请说明理由?
例3、如下图,在平行四边形ABCD 中,过点A 作AE ⊥BC ,垂足为E ,连接DE ,F 为线段DE 上一点,且∠AFE=∠B :
1〕求证:△ADF ∽△DEC ;
2〕假设AB=4,33 AD ,AE=3,求AF 的长。
A B
C D
F
考点二:射影定理:
例4、如图,在Rt ΔABC 中,∠ACB=90°,CD ⊥AB 于D ,CD=4cm,AD=8cm,求AC 、BC 及BD 的长。
例5、如图,正方形ABCD ,E 是AB 的中点,F 是AD 上的一点,且AF=14
AD ,EG ⊥CF 于点G , 〔1〕求证:△AEF ∽△BCE ; 〔2〕试说明:EG 2=CG ·FG.
例6、:如下图的一张矩形纸片ABCD 〔AD>AB 〕,将纸片折叠一次,使点A 与点C 重合,再展开,折痕EF 交AD 边于E ,交BC 边于F ,分别连结AF 和CE .
〔1〕求证:四边形AFCE 是菱形;
〔2〕假设AE=10cm ,△ABF 的面积为24cm 2,求△ABF 的周长;
〔3〕在线段AC 上是否存在一点P ,使得2AE 2
=AC ·AP ?假设存在,请说明点P 的位置,并予以证明;假设不存在,请说明理由.
A B C D E
F
G
考点三:相似之共线线段的比例问题:
例7、如图,P 为平行四边形ABCD 的对角线AC 上一点,过P 的直线与AD 、BC 、CD 的延长线、AB 的延长线分别相交于点E 、F 、G 、H. 求证:PG PH PF PE
例8、如图,点P 是菱形ABCD 的对角线BD 上一点,连接CP 并延长,交AD 于点E ,交BA 的延长线于点F .
〔1〕求证:PC 2=PE •PF ;
〔2〕假设菱形边长为8,PE=2,EF=6,求FB 的长.
例9、如图,CD 是Rt △ABC 斜边上的高,E 为AC 的中点,ED 交CB 的延长线于F . 求证:BD •CF=CD •DF .
例10、如图:在等边三角形ABC 中,点D 、E 分别是AB 、BC 延长线上的点,且BD=CE ,直线CD 与AE 相交于点F .
〔1〕求证:DC=AE ;
〔2〕求证:AD 2=DC •DF .
例11、如图,E是矩形ABCD的边BC上一点,EF⊥AE,EF分别交AC,CD于点M,F,BG⊥AC,垂足为G,BG交AE于点H.
〔1〕找出与△ABH相似的三角形,并证明;
〔2〕假设E是BC中点,BC=2AB,AB=2,求EM的长.
例12、如图,四边形ABCD、DEFG都是正方形,连接AE、CG,AE与CG相交于点M,CG与AD 相交于点N.
求证:〔1〕AE=CG;〔2〕AN•DN=CN•MN.
例13、如图,在Rt△ABC中,CD是斜边AB上的高,点M在CD上,DH⊥BM且与AC的延长线交于点E.求证:
〔1〕△AED∽△CBM;〔2〕AE•CM=AC•CD.
例14、如图,△ABC是直角三角形,∠ACB=90°,CD⊥AB于D,E是AC的中点,ED的延长线与CB的延长线交于点F.
〔1〕求证:FD2=FB•FC;
〔2〕假设G是BC的中点,连接GD,GD与EF垂直吗?并说明理由.
例15、如图,四边形ABCD、CDEF、EFGH都是正方形.
(1)⊿ACF与⊿ACG相似吗?说说你的理由.
(2)求∠1+∠2的度数.
考点四:相似三角形的实际应用:
例16、如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成矩形零件,使一边在BC上,其余两个顶点分别在边AB、AC上.
〔1〕假设这个矩形是正方形,那么边长是多少?
〔2〕假设这个矩形的长PQ是宽PN的2倍,那么边长是多少?
例17、左,右并排的两棵大树的高分别是AB=8m和CD=12m,两树的根部的距离BD=5m。
一个身高1.6m的人沿着正对着两棵树的一条水平直路从左向右前进,当他与左边较低的树的距离小于多少时,就不能看见右边较高的树的顶端点C?
例18、两颗树的高度分别为AB=6m,CD=8m,两树的根部间的距离AC=4m,小强沿着正对这两棵树的方向从左向右前进,如果小强的眼睛与地面的距离为1.6m,当小强与树AB的距离小于多少时,就不能看到树CD的树顶D?
例19、小亮想利用太阳光下的影子测量校园内一棵大树的高,小亮发现因大树靠近学校围墙,大树的影子不全落在地面上,如下图,经测量,墙上影高CD=1.5m,地面影长BC=10m.假设此时1米高的标杆的影长恰好为2m.请你求出这棵大树AB的高度.
例20、如图,九年级的数学活动课上,小明发现电线杆AB的影子落在土坡的坡面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30°角,且此时测得1米杆的影长为2米,求电线杆的高度.
例21、如图,有一路灯杆AB〔底部B不能直接到达〕,在灯光下,小明在点D处测得自己的影长DF=3m,沿BD方向到达点F处再测得自己得影长FG=4m,如果小明的身高为1.6m,求路灯杆AB的高度.
考点五:相似三角形中的动点问题:
例22、在矩形ABCD中,AB=12cm,AD=6cm,点P沿AB边从点A开始向点B以2cm/秒的速度移动,点Q沿DA边从点D开始向点A以1cm/秒的速度移动,如果P、Q同时出发,用t〔秒〕表示运动时间〔0≤t≤6〕,那么当t为何值时,△APQ与△ABD相似?说明理由.
例23、如图,在△ABC中,∠B=90°,AB=6米,BC=8米,动点P以2米/秒的速度从A点出发,沿AC向点C移动.同时,动点Q以1米/秒的速度从C点出发,沿CB向点B移动.当其中有一点到达终点时,它们都停止移动.设移动的时间为t秒.
〔1〕①当t=2.5秒时,求△CPQ的面积;②求△CPQ的面积S〔平方米〕关于时间t〔秒〕的函数解析式;
〔2〕在P,Q移动的过程中,当△CPQ为等腰三角形时,写出t的值。
例24、如下图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm 的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.
〔1〕当x为何值时,PQ∥BC;
〔2〕当S△BCQ:S△ABC=1:3 ,求S△BPQ:S△ABC的值;
〔3〕△APQ能否与△CQB相似?假设能,求出AP的长;假设不能,请说明理由.
例25、如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标为〔6,0〕,〔6,8〕.动点M、N分别从O、B同时出发,都以每秒1个单位的速度运动,其中,点M沿OA向终点A 运动,点N沿BC向终点C运动,过点N作NP⊥BC,交AC于点P,连接MP,动点运动了x 秒.
〔1〕用含x的代数式表示P的坐标〔直接写出答案〕;
〔2〕设y=S四边形OMPC,求y的最小值,并求此时x的值;
〔3〕是否存在x的值,使以P、A、M为顶点的三角形与△AOC相似?假设存在,请求出x 的值;假设不存在,请说明理由.
例26、如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF⊥AE于F.
〔1〕求证:△PFA∽△ABE;
〔2〕当点P在射线AD上运动时,设PA=x,是否存在实数x,使以P、F、E为顶点的三角形也与△ABE相似?假设存在,请求出x的值;假设不存在,请说明理由.
例27、如图,在平面直角坐标系中,Rt△AOB的两条直角边OA、OB分别在y轴和x轴上,并且OA、OB的长分别是方程x2﹣7x+12=0的两根〔OA<OB〕,动点P从点A开始在线段AO 上以每秒1个单位长度的速度向点0运动;同时,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动,设点P、Q运动的时间为t秒.
〔1〕求A、B两点的坐标;
〔2〕求当t为何值时,△APQ与△AOB相似;
〔3〕当t=2时,在坐标平面内,是否存在点M,使以A、P、Q、M为顶点的四边形是平行四边形?假设存在,求出M点的坐标;假设不存在,请说明理由.
本文档局部内容来源于网络,如有内容侵权请告知删除,感谢您的配合!。
