2020年高考押题预测卷03(新课标Ⅱ卷)-文科数学(参考答案)
2020年高考押题预测卷01(新课标Ⅱ卷)-文科数学(全解全析)

2020年高考押题预测卷01【新课标Ⅱ卷】文科数学·全解全析1.【答案】B【解析】因为集合{}{}2log 01,A x x x x =>=>{}{}223013B x x x x x =--<=-<<, 所以{}()11,A B x x ⋃=>-=-+∞,故选B. 2.【答案】A【解析】22(1)(1)22(1)1(1)111(1)(1)i i i i i i z i i i z i i ii ----⋅-=+⇒====--=--+++⋅-, 所以1z i =--==,故本题选A.3.【答案】A【解析】命题“0x ∀>,tan sin x x >”为全称命题,其否定为“0x ∃>,tan sin x x ≤”,故选:A. 4.【答案】D【解析】试题分析:由0a b ⋅=r r ,1a =r ,2b =r 可知BD =()144555BD BA AD AB a b =∴==-u u u r u u u r u u u r u u u r r r 5.【答案】C【解析】对数函数3log y x =为()0,∞+上的增函数,则331log log 105a =<=; 对数函数13log y x =为()0,∞+上的减函数,则113311log log 153b =>=;指数函数3xy =为R 上的增函数,则103033-<<,即01c <<.因此,b c a >>.故选:C. 6.【答案】B【解析】由图可知,含有两个及以上阳爻的卦有巽、离、兑、乾四卦,取出两卦的基本事件有(巽,离),(巽,兑),(巽,乾),(离,兑),(离,乾),(兑,乾)共6个,其中符合条件的基本事件有(巽,离), (巽,兑),(离,兑)共3个,所以,所求的概率3162P ==.故选:B. 7.【答案】A【解析】令21x e =,则22222122111ln 1e f e e e e ⎛⎫== ⎪+⎝⎭--,再取1x e=,则12211ln 1f ee e e⎛⎫== ⎪⎝⎭--,显然22221e e e<+,故排除选项B 、C ;再取x e =时,()220ln 12f e e e e ==>---,又当x →+∞时,()0f x →,故排除选项D.故选:A.8.【答案】B【解析】由题意几何体原图为正四棱台,底面的边长分别为2和6,高为2,所以几何体体积1104(436233V =+⨯=.故选B 9.【答案】D【解析】执行程序框图,可得0S =,2n =,满足条件,12S =,4n =,满足条件,113244S =+=,6n =,满足条件,1111124612S =++=,8n =,由题意,此时应该不满足条件,退出循环,输出S 的值为11228123⨯=.故选D . 10.【答案】B【解析】()()ln f x x x ax =-Q ,(0,)x ∈+∞,()ln 21f x x ax '∴=-+,Q 函数()()ln f x x x ax =-有且仅有一个极值点,ln 210x ax ∴-+=在(0,)x ∈+∞上只有一个根,即ln 12x ax +=只有一个正根,即ln 12x a x+=只有一个正根, 令ln 1x y x +=,则由2ln 0xy x-'==可得1x =, 当01x <<时,0y '>,当1x <时,0y '<, 故ln 1x y x+=在(0,1)上递增,在(1,)+∞递减, 当1x =时,函数的极大值也是函数的最大值为1,(1,)x ∈+∞时,ln 10x y x+=>, 当0x →时,y →-∞,所以当21a =或20a ≤时,2y a =与ln 1x y x+=图象只有一个交点, 即方程ln 12x a x+=只有一个根,故12a =或0a ≤,当12a =时,()ln 10f x x x '=-+=,可得1x =,且()0f x '≤,1x =不是函数极值点,故舍去.所以0a ≤故选:B11.【答案】B【解析】不妨设过点()2,0F c 作b y x a =的垂线,其方程为()ay x c b=--, 由()b y x a a y xc b ⎧=⎪⎪⎨⎪=--⎪⎩解得2a x c =,ab y c =,即2,a ab P c c ⎛⎫ ⎪⎝⎭,由16PF OP =,所以有22224222226a b a a a b c c c cc ⎛⎫⎛⎫++=+ ⎪ ⎪⎝⎭⎝⎭, 化简得223a c =,所以离心率3==ce a.故选:B. 12.【答案】C【解析】()ln x f x x =Q ,()()ln xx x x x e g x f e e e===,由于()111ln 0x f x k x ==<,则11ln 001x x <⇒<<,同理可知,20x <, 函数()y f x =的定义域为()0,∞+,()21ln 0xf x x-'=>对()0,1x ∀∈恒成立,所以,函数()y f x =在区间()0,1上单调递增,同理可知,函数()y g x =在区间(),0-∞上单调递增,()()()212x f x g x f e ∴==,则21x x e =,()22221x x x g x k x e ∴===,则2221k k x e k e x ⎛⎫= ⎪⎝⎭, 构造函数()2kh k k e =,其中k 0<,则()()()222kkh k k k e k k e '=+=+.当2k <-时,()0h k '>,此时函数()y h k =单调递增;当20k -<<时,()0h k '<,此时函数()y h k =单调递减.所以,()()2max 42h k h e=-=.故选:C. 13.【答案】210-【解析】因344ππα<<,故,所以,,应填2-. 14.【答案】17365【解析】以点B 为原点,BC 为x 轴,建立如图所示的平面直角坐标系,则:(0,0)B ,(0,3)A ,(6,0)C ,(6,3)D ,设(,)E x y ,(1)(,3),(6,3)AE x y AC =-=-u u u r u u u r ,∴1(,3)(6,3)(2,1)3x y -=-=-,∴231x y =⎧⎨-=-⎩,解得22x y =⎧⎨=⎩,∴(2,2),(4,1)E ED =u u u r ,∴17ED =; (2)Q 0BE AC =u u u r u u u r g ,∴BE AC ⊥u u u r u u u r,且35AC =,cos 355BCA ∠==, ∴655EC =⨯=,且3CD =,cos 355DCE ∠==,∴在CDE ∆中,根据余弦定理得:2221441172cos 9235555DE EC CD EC CD DCE =+-⋅⋅∠=+-⨯⨯⨯=, ∴365DE =.故答案为:36517,.15.【答案】230x y -+=【解析】设PM x =,则5,3MC PC ==,在PMC ∆中,由余弦定理,得295cos 23x MPC x +-∠=⋅⋅ 22633x x =+≥,当且仅当2x =时,等号成立,此时MPC ∠最大,且222PC PM MC =+, 故PM MC ⊥,又20212MC k -==--,所以12PM k =,故PM 所在直线的方程为12(1)2y x -=-,即230x y -+=.故答案为:230x y -+=. 16.【答案】323π【解析】如图所示:设球心为O ,ABC △所在圆面的圆心为1O ,则1OO ⊥平面ABC ;因为6BA BC ==2ABC π∠=,所以ABC △是等腰直角三角形,所以1O 是AC 中点;所以当三棱锥体积最大时,P 为射线1O O 与球的交点,所以113p ABC ABC V PO S -=⋅⋅V ;因为16632ABC S ==V ,设球的半径为R ,所以2221113PO PO OO R R AO R R =+=+-=-(213333R R ⋅-⋅=,解得:2R =,所以球的体积为:343233R ππ=. 17.(本小题满分12分)【答案】(1)21n a n =-;(2)21n nT n =+ 【解析】(1)依题意有2(1)4n n a S +=① 当1n =时,21(1)0a -=,得11a =; (2分) 当2n ≥时,211(1)4n n a S --+=② (4分)有①-②得11()(2)0n n n n a a a a --+--=,因为0n a >,∴11020n n n n a a a a --+>⇒--=(2)n ≥, ∴{}n a 成等差数列,得21n a n =-. (6分) (2)111()22121n b n n =--+, (8分) 1211111111(1)(1)2335212122121n n nT b b b n n n n =+++=-+-++-=-=-+++L L (12分)18.(本小题满分12分)【答案】(1)见解析;(2)23【解析】(1)因为PAB △为等腰直角三角形,所以PA PB ⊥.BC ⊥平面PAB ,PA ⊂平面PAB ,所以BC PA ⊥.PA PBPA BCPA BC PB B ⊥⎧⎪⊥⇒⊥⎨⎪⋂=⎩平面PBC . (4分) (2)取AB 的中点O ,连接PO ,DO .因为PAB △和DAB V 均为等腰三角形,所以PO AB ⊥,⊥DO AB . 因为BC ⊥平面PAB ,PO ⊂平面PAB ,所以PO BC ⊥.PO AB PO BCPO AB BC B ⊥⎧⎪⊥⇒⊥⎨⎪⋂=⎩平面ABCD . (6分) 在RT PAO V 中,1PO AO ==,所以112PA =+=在RT DAO V 中,1AO =,5AD =512DO =-=.又因为⊥DO AB ,CB AB ⊥,2DO BC ==, (8分) 所以四边形BCDO 为矩形,即1CD =,112ADC S CD DO =⨯⨯=V . 在RT PDO V 中,1PO =,2DO =,所以2125PD =+=. 因为在PAD △中,2PA =,5PD AD ==所以221232(5)()222PAD S =-=V . (10分) 设点C 到平面PAD 的距离为d , 因为C PAD P ADC V V --=,即13111323d ⨯⨯=⨯⨯,23d =. (12分)19.(本小题满分12分)【答案】(1)ˆ20200y x =-+;(2)6.5元.【解析】(1)由题意得,x =16×(6+6.2+6.4+6.6+6.8+7)=6.5, y =16×(80+74+73+70+65+58)=70; (2分)则()61()5 1.20.30 1.5614iii x x y y =--=------=-∑,621()0.250.090.010.010.090.250.7i i x x =-=+++++=∑; (6分) 所以142007ˆ.b-==- ,() 7020 6.5200ˆˆay bx =-=--⨯= 所以所求回归直线方程为20200ˆy x =-+. (8分) (2)由题意可得,()()()3202ˆ003P yx x x =-=-+-, (10分) 整理得P =-20(x -6.5)2+245,当x =6.5时,P 取得最大值为245;所以要使收益达到最大,应将价格定位6.5元. (12分) 20.(本小题满分12分) 【答案】(1)221(0)4x y y +=≠(2)存在;25λ=【解析】(1)设(, )B x y ,则(,)C x y --,又(2,0)A ,212212244y y y k k x x x -∴⋅=⋅==-----.2214x y ∴+=,又斜率存在,2x ∴≠±∴点B 的轨迹方程是221(0)4x y y +=≠. (4分)(2)联立122(2),1,4y k x x y =⋅-⎧⎪⎨+=⎪⎩得2222111(41)164(41)0k x k x k +-+-= 解得:211122112(41)4,21441()B B B k k x y k x k k --==-=++,12102041B BCB y k k x k --∴==--. (6分) 联立122(2),4,y k x x y =⋅-⎧⎨+=⎩得2222111(1)44(1)0k x k x k +-+-=.解得:21122112(1)4,11E E k k x y k k --==++ (10分) 121056415EF E E y k k k x --∴==-+22,55B E FC F E B C k k k k ∴=∴=, ∴存在常数25,使得25BC EF k k =. (12分) 21.(本小题满分12分)【答案】(1)见解析(2)见解析【解析】(1)函数定义域为R 因为()1()1xxf x ae x f x ae '=-+∴=-, 当0a ≤时,()0f x '<恒成立,()f x 在R 上单调递减; (2分) 当0a >时,令()0f x '=得ln x a =-.当ln x a <-时,()0f x '<,当ln x a >-时,()0f x '> (4分) 综上:当0a ≤时单调递减区间为(,)-∞+∞,无增区间; (5分) 当0a >时,增区间为(ln ,)a -+∞,减区间为(,ln )a -∞-, (2)由(1)知当0a >时,()f x 在ln x a =-时取得极小值, ()f x 的极小值为(ln )2ln f a a -=+. (7分)设函数11()2ln (3)ln 1g x x x x x=+--=+- 21()(0)x g x x x -'=> (9分)当01x <<的()0g x '<;()g x 单调递减;当1x >时()0g x '>;()g x 单调递增; 故min ()(1)0g x g ==,即()(1)0g x g ≥=,所以01()3f x a≥-. (12分) 22.(本小题满分10分)选修4-4:坐标系与参数方程【答案】(1)24,10y x x =--=(2)16【解析】(1)24,4x t y t⎧=⎨=⎩消去参数t 可得2:4C y x =, (3分)因为cos sin xy ρθρθ=⎧⎨=⎩,所以:10l x -=; (6分)(2)法一:∵直线l 经过拋物线焦点(1,0),又倾斜角是30°,∴可设直线l的参数方程是1,12x y t ⎧=+⎪⎪⎨⎪=⎪⎩(t 是参数), (8分)代入抛物线方程得2160t --=.设直线l 和抛物线交于A B 、两点且它们对应的参数分别为12,t t,则121216t t t t ⎧+=⎪⎨=-⎪⎩ (10分) 12||16AB t t =-====; (12分)法二:抛物线C 的焦点是(1,0)F 且在直线l 上,设l 交抛物线于1122(,),(,)A x y B x y联立抛物线方程和直线方程2410y xx ⎧=⎪⎨-=⎪⎩,消y 得21410x x -+=,所以1214x x +=,所以12||14216AB x x p =++=+=. (12分) 23.(本小题满分10分)选修4-5:不等式选讲【答案】(1){|3M x x =-„或3}x ….(2)证明见解析 【解析】(1)当1a =时,()|1||-1|f x x x =++()6|1||1|6f x x x ⇔++-厖 (2分)当1x -„时,116,3,3x x x x ---+-∴-厔? 当11x -<<时,116x x +-+…不成立,∴x ∴∈∅ 当1x …时,116,3,3x x x x ++-∴厖?. 综上得不等式的解集{|3M x x =-„或3}x …. (6分) (2)111()||||||f x x a x a a a a a =++-+=+… ,||3a M a ∈∴Q …,令||t a =,则3t …,而1y t t=+在[3,)+∞是单调增的∴当3t =时,min 110333y =+= ∴当a M ∈时,10()3f x …. (12分)。
2020年高考押题预测卷03(新课标Ⅱ卷)-理科数学(参考答案)

所以曲线 C1 的极坐标方程为: 4cos . 曲线 C2 : 2 3cos 2sin ,即 2 2 3cos 2sin ,
则 C2 的直角坐标方程为: x 3 2 y 12 4 .
(Ⅱ)直线 l 的直角坐标方程为 y 3 x , 3
所以 l 的极坐标方程为 5 R .
6z2
0
,
令 z2 4 得 x2 3 , y2 0 ,即 n2 3, 0, 4 ,
所以 cos n1, n2
n1 n2 n1 n2
3 2 4
3 3014 4
3 2
2
12
32 42
5 61 61 ,
设二面角 A NF C 的大小为 ,则 精品资料公众号:卷洞洞 侵权删
公众号:卷洞洞
~
cos
cos
n1, n2
5 61 61
所以二面角 A NF C 余弦值为 5 61 . 61
19.(本小题满分 12 分)
【解析】(1)因为抛物线 C 上的点到准线的最小距离为 2 ,所以 p 2 ,解得 p 4 . 2
故抛物线 C 的方程为 y2 8x ;
(2)由(1)知焦点为 F 2, 0 .
6 精品资料公众号:卷洞洞 侵权删
公众号:卷洞洞
~
联立
5 6
,得 A 2 3 ,
4cos
联立
5 6
,得 B 4 ,
2 3cos 2sin
AB A B 4 2 3 .
解法二:(Ⅰ)同解法一
(Ⅱ)直线 l 的直角坐标方程为 y 3 x , 3
联立
y 3x 3
,解得 A 3, 3 ,
y2
,则
y1
y2
8 k
2020年高考数学押题导航卷文科数学-01(新课标Ⅱ卷)(解析版)

押题导航卷01(新课标Ⅱ卷)文科数学一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)1.若集合}0|{≥=x x B ,且A B A =I ,则集合A 可能是( )。
A 、}2,1{B 、}1|{≤x xC 、}1,0,1{-D 、R 【答案】A【解析】∵集合}0|{≥=x x B ,且A B A =I ,∴B A ⊆,故A 答案}2,1{满足要求,故选A 。
2.已知i 为虚数单位,复数iz -=25,则复数z 在复平面内对应的点位于( )。
A 、第一象限 B 、第二象限 C 、第三象限 D 、第四象限 【答案】D 【解析】i i i i i z +=+-+=-=2)2)(2()2(525,i z -=2, 复数z 在复平面内对应的点为)1,2(-,表示第四象限的点,故选D 。
3.从某校高三年级随机抽取一个班,对该班50名学生的高校招生体检表中视力情况进行统计,其结果的频率分布直方图如图所示:若某高校A 专业对视力的要求在9.0以上,则该班学生中能报A 专业的人数为( )。
A 、20B 、22C 、25D 、30 【答案】A【解析】202.0)25.075.000.1(50=⨯++⨯,故选A 。
4.已知函数)(x f 是定义在R 上的偶函数,且在),0(+∞上单调递增,则( )。
A 、)2()13log ()3(6.03f f f <-<-B 、)13log ()2()3(36.0-<<-f f f C 、)3()13log ()2(36.0-<-<f f f D 、)13log ()3()2(36.0-<-<f f f【答案】C【解析】∵)(x f 定义在R 上的偶函数,∴)3()3(f f =-,)13(log )13log (33f f =-, 又2212226.016.00<<⇒<<,313log 227log 13log 9log 3333<<⇒<<,∴313log 236.0<<,∴)3()13log ()2(36.0-<-<f f f ,故选C 。
2020年高考数学全国卷2-文科数学试题参考答案

2020年普通高等学校招生全国统一考试 ( 文科) 数 学 试题参考答案
1 . D 2 . A 3 . C 4 . B 5 . D 6 . B 7 . C 8 . B 9 . B 10 . A 11 . C
2 =
1-
a x
+l
n
a x
(x - a )2
.
取c = - 1 得h (x ) = 2l nx - 2x + 2 ,h (1 ) = 0 , 则由(1 ) 知, 当x ≠1 时,h (x ) < 0 , 即1 - x +l nx < 0 .
故当x
∈(0 ,a
) , (a
, + ∞) 时,1 -
a x
≤
3 2
或x
≥121
.
(2 ) 因为f (x ) = | x - a 2| + | x - 2a + 1| ≥| a 2 - 2a + 1| = (a - 1 )2 , 故当(a - 1 )2 ≥4 , 即| a - 1| ≥2 时,f (x ) ≥4 . 所以当a ≥3 或a ≤- 1 时,f (x ) ≥4 . 当- 1 <a < 3 时,f (a 2 ) = | a 2 - 2a + 1| = (a - 1 )2 < 4 . 所以a 的取值范围是( - ∞, - 1 ] ∪[3 , + ∞) .
y 2 =4 .
故C 2 的普通方程为x 2 - y 2 =4 .
2020年普通高等学校招生伯乐马押题考试(二)文科数学试卷及答案解析.

2020年普通高等学校招生伯乐马押题考试(二)文科数学试卷注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题1.已知全集U Z =,集合,{}1,0,1,2A =-,{}220B x Z x x =∈--<,则()UAB =( ) A.{}1,2B.{}1,0-C.{}0,1D.{}1,2-2.已知复数z 满足92i14iz +=+,则在复平面内z 对应的点位于( ) A.第一象限B.第二象限C.第三象限D.第四三象限3.已知双曲线22221y x a b-=(0a >,0b >)的顶点到渐近线的距离与焦点到渐近线的距离之比为13,则该双曲线的离心率为( )B.3C.4.为了得到函数21cos cos 2y x x x =-的图像,可以将函数cos 2y x =的图像( ) A.向左平移π6个单位长度 B.向右平移π3个单位长度 C.向右平移π6个单位长度 D.向左平移π3个单位长度 5.记不等式组10,10,10,x y x y y +-≤⎧⎪-+≥⎨⎪+≥⎩的解集为D ,(),x y D ∃∈,使2x y a +≥成立,则实数a 的取值范围是( ) A.(],3-∞ B.(],5-∞-C.[]5,3-D.[)3,+∞6.函数||2sin ()x xf x e =在[π-,]π的图象大致为( )A. B.C. D.7.已知圆C :221x y +=,点M 为直线260x y --=上一动点,过点M 向圆C 作切线MA ,MB ,A ,B 为切点,则直线AB 经过定点( )A.11,36⎛⎫-⎪⎝⎭B.11,36⎛⎫- ⎪⎝⎭C.11,63⎛⎫-⎪⎝⎭D.11,63⎛⎫-⎪⎝⎭8.函数()sin cos f x x x ωω=-()0ω>在区间()0,π内有三个零点,则ω的值可能为( ) A.2B.3C.4D.59.中央电视台总台推出的《中国诗词大会》节目以“赏中华诗词、寻文化基因、品生活之美”为宗旨,邀请全国各个年龄段、各个领域的诗词爱好者共同参与诗词知识竞赛,现组委会要从甲、乙等五位候选参赛者中随机选取2人进行比拼,则甲、乙二人至少有一人被选上的概率为( ) A.0.6B.0.7C.0.8D.0.910.已知n S 是等比数列{}n a 的前n 项和,若3S ,9S ,6S 成等差数列,且252m a a a +=,则m =( ) A.6B.7C.8D.911.正方体1111ABCD A B C D -的棱长为a ,M 为1CC 的中点,N 为线段1DD 上靠近1D 的一个三等分点,设过点B ,M ,N 的平面把正方体的棱1AA 所在直线交于点Q ,则线段AQ 的长为( )A.8a B.6a C.4a D.3a 12.各项均为实数的等差数列的公差为2,其首项的平方与其余各项之和不超过33,则这样的数列至多有( ) A.5项B.6项C.7项D.8项第II 卷(非选择题)请点击修改第II 卷的文字说明二、填空题(题型注释)13.把一个大金属球表面涂漆,共需1.5公斤油漆.若把这个大金属球熔化制成为64个大小都相同的小金属球,不记损耗,将这些小金属球表面都涂漆,则需要用油漆______公斤. 14.已知抛物线24y x =的焦点为F ,P 为抛物线上一动点,定点()1,1A ,则PAF △周长最小值为______.15.已知等腰直角三角形ABC 中,1AB AC ==,()1,2,3,,8i M i =⋅⋅⋅顺次为线段BC 的九等分点,则9i i AM AM -⋅的最大值为______.16.平行于x 轴的直线与函数()ln ,0,e ,0,x x f x x x>⎧⎪=⎨-<⎪⎩的图像交于A ,B 两点,则线段AB 长度的最小值为______.三、解答题(题型注释)17.在ABC ∆中,角,,A B C 的对边分别是,,a b c 2sin 2cos 2B CC c +=. (1)求角A 的大小;(2)若7a =,ABC ∆的面积是4,求ABC ∆的周长. 18.如图,在四棱锥P ABCD -中, 90ABC ACD ∠=∠=, BAC ∠ 60CAD =∠=, PA ⊥平面ABCD , 2,1PA AB ==.设,M N 分别为,PD AD 的中点. (1)求证:平面CMN ∥平面PAB ; (2)求三棱锥P ABM -的体积.19.已知椭圆C :22221x y a b +=(0a b >>)的一个顶点为()0,1,离心率e =(1)求椭圆C 的标准方程;(2)斜率为k 的直线l 与椭圆C 交于不同的两点M ,N ,若椭圆上存在点P ,使得OP OM ON =+,其中O 是坐标原点,求OMN 的面积.20.某基地蔬菜大棚采用水培、无土栽培方式种植各类蔬菜.过去50周的资料显示,该地周光照量X (小时)都在30小时以上,其中不足50小时的周数有5周,不低于50小时且不超过70小时的周数有35周,超过70小时的周数有10周.根据统计,该基地的西红柿增加量y (百斤)与使用某种液体肥料x (千克)之间对应数据为如图所示的折线图.(1)依据数据的折线图,是否可用线性回归模型拟合y 与x 的关系?请计算相关系数r 并加以说明(精确到0.01).(若|r|>0.75,则线性相关程度很高,可用线性回归模型拟合)(2)蔬菜大棚对光照要求较大,某光照控制仪商家为该基地提供了部分光照控制仪,但每若某台光照控制仪运行,则该台光照控制仪周利润为3000元;若某台光照控制仪未运行,则该台光照控制仪周亏损1000元.若商家安装了3台光照控制仪,求商家在过去50周周总利润的平均值. 附:相关系数公式r=∑(x −x)(y −y)ni=1√∑(x i −x)2n i=1√∑(y i −y)2ni=1,参考数据√0.3≈0.55,.21.已知函数()22ln f x ax x =-,()()212g x a x =-+.(1)若R a ∈,讨论函数()f x 的单调性;(2)若N a ∈,对于任意的()0,x ∈+∞,()()f x g x ≥恒成立,求a 的最小值.22.在直角坐标系xOy 中,曲线1C 的参数方程为1,22,2x t y ⎧=⎪⎪⎨⎪=-+⎪⎩(t 为参数).以坐标原点为极点,以x 轴正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为2sin ρθ=,若点A 的极坐标为15π,6ρ⎛⎫-⎪⎝⎭,点B 的极坐标为23π,4ρ⎛⎫ ⎪⎝⎭.(1)写出曲线1C 的极坐标方程和曲线2C 的直角坐标方程; (2)若点1A C ∈,2B C ∈,求AOB 的面积.23.已知()12f x x x a =++-,()123g x x x =+--.(1)若()12f x a ≥-恒成立,求实数a 的取值范围; (2)若存在实数1x ,2x ,使得()()12f x g x =成立,求实数a 的取值范围.参考答案1.D【解析】1.先求出集合B ,再求得集合B 的补集,由集合的交集运算可得选项.{}{}{}2201201B x Z x x x Z x =∈--<=∈-<<=,,所以{}0,1UB x Z x x =∈≠≠,又{}1,0,1,2A =-,所以()UA B ={}1,2-,故选:D. 2.A【解析】2.运用复数的除法运算化简得到z ,z ,可得到选项.()()()()92i 14i 92i 17341214i 14i 14i 17iz i +-+-====-++-,所以1+2z i =, 故在复平面内z 对应的点位于第一象限. 故选:A. 3.B【解析】3.分别求出顶点到渐近线的距离、焦点到渐近线的距离,列出关于,,a b c 的方程,再结合222c a b =+ ,即可求得离心率的值.由题意知:取双曲线的顶点(0,)A a 、焦点坐标(0,)F c , 取渐近线方程为ay x b=,也即是0ax by -= ,顶点到渐近线的距离为1abd c==,焦点到渐近线的距离为1d b == ,1213ab d a c d b c ∴===, 3ce a∴== ,4.B【解析】4.结合二倍角公式和降幂公式化简得22c 1cos cos 2os 23y x x x x π⎛⎫- ⎪=⎝-⎭=,再结合平移法则即可求解.211cos 211cos cos 22cos 22222x y x x x x x x +=+-=-+=-= 22sin 2cos 2cos 2cos 2cos 2626333x x x x x ππππππ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-=--=-=-=- ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦,由函数平移法则可知,将函数cos 2y x =的图像向右平移3π个长度单位即可得到cos 23x π⎛⎫- ⎪⎝⎭,故选:B 5.A【解析】5.令2z x y =+,求出z 的最大值,max a z ≤ 即可. 可行域如图所示由1010x y y +-=⎧⎨+=⎩ 得 (2,1)A -,当2z x y =+过(2,1)A -时,max 2213z =⨯-=,故选:A 6.A【解析】6.根据函数奇偶性,对称性,单调性和最值之间的关系进行判断即可. 解:||||2sin()2sin ()()x x x xf x f x e e ---==-=-,则函数()f x 是奇函数, 则图象关于原点对称,故排除D . 当(0,)x π∈时,)4()xx f x e π+'=,则当(0,)4x π∈时,()0f x '>,函数()f x 为增函数,(4x π∈,)π时,()0f x '<,函数()f x 为减函数,则当4x π=时,()f x取得极大值同时也是最大值4422()14f e e πππ==<,故选:A . 7.D【解析】7.根据题意设M 的坐标为(26,)M m m +,由切线的性质得点A 、B 在以OM 为直径的圆C 上,求出圆的方程,将两个圆的方程相减求出公共弦AB 所在的直线方程,再求出直线AB 过的定点坐标.解:因为M 是直线260x y --=的任一点,所以设(26,)M m m +, 因为圆221x y +=的两条切线MA 、MB ,切点分别为A 、B , 所以OA MA ⊥,OB MB ⊥,则点A 、B 在以OM 为直径的圆C 上,即AB 是圆O 和圆C 的公共弦, 则圆心C 的坐标是(3m +,)2m ,且半径的平方是222(26)4m m r ++=,所以圆C 的方程是2222(26)(3)()24m m m x m y ++--+-=,①又221x y +=,②,②-①得,(26)10m x my ++-=,即公共弦AB 所在的直线方程是:(26)10m x my ++-=, 即(2)(61)0m x y x ++-=,由61020x x y -=⎧⎨+=⎩得16x =,13y =-,所以直线AB 恒过定点1(6,1)3-,故选:D . 8.B【解析】8.由辅助角公式可得())4f x x πω=-.由0πx <<,可得444x πππωωπ-<-<-.根据()f x 在区间()0,π内有三个零点,可得234ππωππ<-≤,求出ω的取值范围,即得答案.()sin cos )4f x x x x πωωω=-=-. 0,0,444x x πππωπωωπ><<∴-<-<-,函数()f x 在区间()0,π内有三个零点,91323,444ππωππω∴<-≤∴<≤. 故选:B . 9.B【解析】9.先计算出甲、乙二人都没有被选上的概率,由对立事件的概率可得出答案总的基本事件个数为2510C =,甲、乙二人都没有被选上的基本事件有233C =,∴ 甲、乙二人都没有被选上的概率为232530.310C C ==,则甲、乙二人至少有一人被选上的概率为10.30.7-=, 故选:B 10.C【解析】10.利用等比数列的基本量,转化已知条件,利用整体代换,即可求得结果. 不妨设数列{}n a 的公比为q , 因为3S ,9S ,6S 成等差数列, 故可得3692S S S +=,当1q =时,11918a a =,解得10a =(舍) 当1q ≠时, 即()()()3691111112111a q a q a q qqq---+=---整理可得()363210q q q --=, 也即()()332110qq +-=,解得31q =(舍),312q =-. 252m a a a +=等价于412m q q q -+=,也即32?1122m q q -+==, 解得214m q-=,又312q =-. 故可得26m -=,则8m =. 故选:C 11.B【解析】11.根据四点共面找出点Q 的位置,即可求出AQ 的长度. 如图所示,过A 作AE BM 交1DD 于点E ,则E 是1DD 的中点, 过N 作NTAE 交1AA 于点T ,则NT BM ,B ∴,M ,N ,T 四点共面,所以点Q 与点T 重合,11111236AQ AE D E D N a a a ∴==-=-=. 故选: B 12.C【解析】12.本题考查等差数列求和公式,写出首项的平方与其余各项之和的表达式,利用一个数的平方最小为0,解不等式即可.设等差数列为{}n a ,则21133n a S a +-≤,2111(1)2332n n a na a -∴++⨯-≤ , 211(1)(1)33a n a n n ∴+-+-≤,211(1)(31)()3324n n n a --+∴++≤, 为了使n 尽量大,故211()02n a -+=, (1)(31)334n n -+∴≤,(1)(31)132n n ∴-+≤,当6n =时,519132⨯< , 当7n =时,622132⨯= ,max 7n = ,故选:C 13.6【解析】13.设大金属球的半径为R ,小金属球的半径为r ,根据体积相等建立等量关系式,然后求出64个小球的表面积之和,从而得出答案.设大金属球的半径为R ,小金属球的半径为r ,由33446433R r ππ=⨯ ,可得14r R =, 64个小球的表面积之和为2264444()r R ππ⨯=⨯由题意得:大金属球表面为24R π需要1.5公斤油漆,4 1.56∴⨯=(公斤)故答案为:6 14.3【解析】14.求PAF ∆周长的最小值,即求||||PA PF +的最小值.设点P 在准线上的射影为D ,则根据抛物线的定义,可知||||PF PD =.因此问题转化为求||||PA PD +的最小值,根据平面几何知识,当D 、P 、A 三点共线时||||PA PD +最小,从而可得结果 求PAF ∆周长的最小值,即求||||PA PF +的最小值, 设点P 在准线上的射影为D , 根据抛物线的定义,可知||||PF PD =因此,||||PA PF +的最小值,即||||PA PD +的最小值根据平面几何知识,可得当D ,P ,A 三点共线时||||PA PD +最小, 因此的最小值为(1)112A x --=+=, ||1AF =,所以PAF ∆周长的最小值为213+=, 故答案为:3.15.4081【解析】15.先建立平面直角坐标系,求出点的坐标,将9i i AM AM -⋅用坐标表示出来,再求出最大值. 如图建立平面直角坐标系等腰直角三角形ABC 中,1AB AC ==,BC ∴= ,19i i M M M A -∴ ,2(922i AM =--,92(9)(922i i AM --=--,92)()(((929222i i i i AM AM AM --⋅==-⋅-+-⨯- 22222(9)81981i i i i =-+=-- , 4i ∴=或5i =时9i i AM AM -⋅最大,此时29240(494)8181i i AM AM -⋅=--⨯=. 故答案为:408116.2e【解析】16.画出函数图像,数形结合构造函数,利用导数判断函数单调性并求函数最值即可. 根据题意,画出()f x 的图象如下所示:令()f x t =,(0)t >,故可得lnx t =,解得t x e =;e t x -=,解得e x t=-. 故可得(),,,te A e t B t t ⎛⎫- ⎪⎝⎭,(0)t >,故()teAB g t e t==+,(0)t >, 故可得()2te g t e t ='-,()30te g t e t'=+>'恒成立, 故()g t '是单调递增函数,且()10g '=,关于()0g t '<在()0,1成立,()0g t '>在()1,+∞成立, 故()g t 在()0,1单调递减,在()1,+∞单调递增, 故()()12min g t g e e e ==+=. 即AB 的最小值为2e . 故答案为:2e . 17.(1)23π;(2)15【解析】17.(12sin 2sin sin2A A C C =,化简得到tan 2A=(2)根据面积得到15bc =,再根据余弦定理得到8+=b c ,计算得到周长. (1)在ABC 中,A B C π++=,所以cos cos sin 222B C A Aπ+-==,2sin 2sin sin 2A A C C =,因为sin 0C ≠22sin 2A A =,所以2cos 2sin 222A A A =,又sin 02A ≠sin 22A A =,所以tan2A =,易知0,022A A ππ<<<<,所以23A π=,故23A π=.(2)由题意得1sin 2bc A ==,得15bc =, 由余弦定理,得22222cos 49b c bc A b c bc +-=++=, 即()249b c bc +-=,所以()21549,8b c b c +-=+=, 故ABC 的周长为15a b c ++=.18.(1)证明见解析 (2)三棱锥P ABM -的体积V =【解析】18.试题分析:(1)由中位线定理可得MN ∥PA ⇒ MN ∥平面PAB . 再证得60ACN BAC CN ∠=∠=∥ABCN ∥平面PAB ⇒平面CMN ∥平面PAB ; (2)由(1)知,平面CMN ∥平面PAB ⇒点M 到平面PAB 的距离等于点C 到平面PAB 的距离⇒ 3M PAB C PAB P ABC V V V V ---====. 试题解析:(1)证明:∵,M N 分别为,PD AD 的中点, 则MN ∥PA . 又∵MN ⊄平面PAB , PA ⊂平面PAB , ∴MN ∥平面PAB .在Rt ACD ∆中, 60,CAD CN AN ∠==,∴ 60ACN ∠=.又∵60BAC ∠=, ∴CN ∥AB .∵CN ⊄平面PAB , AB ⊂平面PAB ,∴ CN ∥平面PAB .又∵CN MN N ⋂=, ∴平面CMN ∥平面PAB . (2)由(1)知,平面CMN ∥平面PAB ,∴点M 到平面PAB 的距离等于点C 到平面PAB 的距离.由已知, 1AB =, 90ABC ∠=, 60BAC ∠=,∴BC =,∴三棱锥P ABM -的体积111232M PAB C PAB P ABC V V V V ---====⨯⨯=19.(1)2214x y +=;(2【解析】19.(1)根据已知条件,列出方程,即可求得,,a b c ,则问题得解;(2)设出直线方程y kx m =+,联立椭圆方程,利用韦达定理和已知条件,即可求得,k m 的关系,再求弦长以及三角形面积,则问题得解.(1)根据题意,显然1,c b a ==, 结合222a b c =+, 解得2224,1,3a b c ===,故椭圆方程为:2214x y +=.(2)设直线l 的方程为y kx m =+, 联立椭圆方程可得()222148440k x kmx m +++-=, 则()()2222Δ64414440k mk m =-+->,即2241k m +>设,M N 两点的坐标为()()1122,,,x y x y ,故可得()2121222418,1414m km x x x x k k--+==++ 则()121222214my y k x x m k+=++=+ 因为OP OM ON =+, 故可得2282,1414P Pkm mx y k k -==++, 又点P 在椭圆上,故可得222282441414km m k k -⎛⎫⎛⎫+= ⎪ ⎪++⎝⎭⎝⎭,整理可得:22414k m +=.故MN ===又()0,0到直线y kx m =+的距离d =故三角形OMN 的面积12S MN d=⨯⨯12=221214k =⨯+=即三角形OMN 20.(1)可用线性回归模型拟合y 与x 的关系(2)商家在过去50周周总利润的平均值为4600元【解析】20.试题分析:(1)由折线图,可得x̅,y ̅,依次算得∑(x i −x)25i=1,∑(y i −5j=1y)2,∑(x i −x)(y i −y)5i=1,可求得r =√910≈0.95>0.75, 所以可用线性回归模型拟合y 与x 的关系.(2)分别计算安装1台,2台时所获周利润值(期望值),数值大的为所选择。
2020年高考数学(文)原创终极押题卷(新课标ⅠⅡⅢ卷) (考试版)
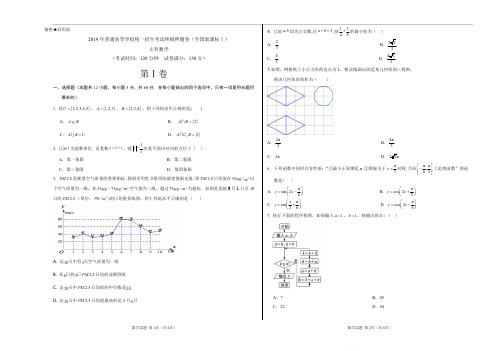
k0
2.706
20.(本小题满分 12 分)
3.841
6.635
10.828
已知椭圆
C
:
x2 a2
y2 b2
1(a
b
0) 的左、右焦点分别为 F1、F2 ,过点 F2 且垂直于 x 轴的直线截椭圆形成
的弦长为
2 ,且椭圆 C 的离心率为
2 2
,过点
F1
的直线 l
与椭圆 C
交于
M,
N
两点.
(Ⅰ)求椭圆 C 的标准方程;
B. f 3 f 20.6 f log313 D. f 20.6 f 3 f log313
二、填空题(本题共 4 小题,每小题 5 分,共 20 分)
13. 已知向量 a , b ,满足 a b 2 ,且 b (1, 3) ,则 a在b方向上的投影为 ______________.
4.
已知 a,b 均为正实数,且 a b 3 ,则 1 1 的最小值为( ab
)
A.
2 3
B. 2 2 3
C. 4 3
D. 4 2 3
5.如图,网格纸上小正方形的边长为 1,粗实线画出的是某几何体的三视图,
则该几何体的体积为( )
A. 2π 3
[:]
B. 4π 3
C. 2π
D. 2 5π
6.下列函数中同时具有性质:“①最小正周期是
(Ⅲ)现全班学生中有 40%是女生,其中 3 个女生的每周平均体育锻炼时间不超过 4 小时.若每周平均体
育锻炼时间超过 4 小时称为经常锻炼,问:有没有 90%的把握说明,经常锻炼与否与性别有关?
附:
K
2
a
nad bc 2 bc d a c
2020届高考实战3套卷全国卷(二)数学(文)试题答案
4c2
c2
2c
2c
1
7c2
,
A F1
7c ,
2
参考答案
根据点 A 在双曲线上,得 A F1 A F 2 a ,
即 7 c c 2 a ,所以 e c
a
9. 【答案】B
7 1 .故选 C.
3
【解析】由 a ln x x 可得 a x x 0 且 x 1 ,
ln x
设 g x x ,则 g x ln x 1 ,
8
长度,得到 g ( x ) c o s [ 2 ( x
π )
π ] cos(2 x
π ) ,则 g ( x ) 的
8 12
3
最小正周期为 π,A 错误;由 x [0 ,
π ]
,可得 2 x
π
π [
,
4π ]
,
2
3 33
显然 g ( x ) 在区间 [0 , π ] 上不单调, B 错误;当 x π 时,
ln x
ln x 2
易知 g x 在 0 , 1 和 1 , e 上单调递减,
在 e , 上单调递增,所以 g x 的极小
值为 g e e ,作出 g x 的大致图象如图
所示,由图可知当 a e , 时,函数
f x 有两个不动点. 故选 B.
10.【答案】D 【解析】如图所示,取 A B , A C 的中点 D , E ,
2
2
∵ π 0.1 4 0.1 4 0.5 2 ,∴ c a ,∴ c a b .故选 B.
7. 【答案】D 【解析】因为甲、乙的陈述都只对了一半,所以若乙的陈述 中“甲走桃花峪登山线路”正确,则甲的陈述全部错误,与题 意不符,故乙的陈述中,“甲走桃花峪登山线路”不正确, “丙走红门盘道徒步线路”正确,故甲的陈述中,“乙走桃花 峪登山线路”正确,丙的陈述中,“甲走天烛峰登山线路”正 确.故选 D.
2020年高考押题预测卷02(新课标Ⅲ卷)-文科数学(考试版)
A.5
B.4
C.3
D.2
10.已知三棱锥 D﹣ABC 的外接球的表面积为 128π, 晦 晦耀 , 耀
,则三棱锥 D﹣ABC 体积
的最大值为( )
흐
晦崕
A.
B.
C.
D.
11.若关于 x 的不等式 4x3+ax﹣1≤0 对任意 x∈[﹣1,1]都成立,则实数 a 的取值范围是( )
A.[﹣4,﹣3]
B.{﹣3}
A.[0,1]
B. 晦,
C. ,
D.(﹣∞,1]
k0
2.072
2.706
3.841
5.024
6.635
7.879
10.828
第Ⅱ卷
19.(本小题满分 12 分)[来源:学科网ZXXK]
不
二、填空题(本题共 4 小题,每小题 5 分,共 20 分)
13.已知向量
, , h, (其中 m 为实数),若
,则 m=
在如图所示的五面体 ABCDEF 中,四边形 ABCD 为菱形,且∠DAB=60°,EF∥平面 ABCD,EA=ED=
[来源:学_科_网 Z_X_X_K]
晦 25,则 k=
.
三、解答题(本大题共 6 小题,共 70 分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分 12 分)
AB=2EF=2,M 为 BC 中点 . (1)求证:FM∥平面 BDE; (2)若平面 ADE⊥平面 ABCD,求 F 到平面 BDE 的距离.
日自倍,松竹何日而长等,如图是源于其思想的一个程序框图,若输入的 a,b 分别为 3,1,则输出的
n 等于( )
一、选择题(本题共 12 小题,每小题 5 分,共 60 分.在每小题给出的四个选项中,只有一项是符合题目 要求的)
2020年普通高等学校招生全国统一考试(新课标Ⅱ卷)数学文科
绝密★启用前2020年普通高等学校招生全国统一考试(新课标Ⅱ卷)文科数学注意事项:1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前考生将自己的姓名、准考证号填写在答题卡上。
2. 回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号框涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号框。
写在本试卷上无效。
3. 答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。
4. 考试结束,将试题卷和答题卡一并交回。
第Ⅰ卷一、选择题:本大题共12小题。
每小题5分,在每个小题给出的四个选项中,只有一项是符合要求的。
(1)已知集合M={x|-3<X<1},N={-3,-2,-1,0,1},则M∩N= (A){-2,-1,0,1}(B){-3,-2,-1,0}(C){-2,-1,0} (D){-3,-2,-1 }(2)||=(A)2(B)2 (C)(D)1(3)设x,y满足约束条件,则z=2x-3y的最小值是(A)(B)-6 (C)(D)-(4)△ABC的内角A,B,C的对边分别为a,b,c,已知b=2,B=,C=,则△ABC的面积为(A)2+2 (B)(C)2(D)-1(5)设椭圆C:+=1(a>b>0)的左、右焦点分别为F1、F2,P是C上的点PF2⊥F1F2,∠PF1F2=30。
,则C的离心率为(A)(B)(C)(D)(6)已知sin2α=,则cos2(α+)=(A)(B)(C)(D)(7)执行右面的程序框图,如果输入的N=4,那么输出的S=(A)1(B)1+(C)1++++(D)1++++(8)设a=log32,b=log52,c=log23,则(A)a>c>b (B)b>c>a (C)c>b>a (D)c>a>b (9)一个四面体的顶点在点间直角坐系O-xyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx平面为投影面,则得到的正视图可为(A)(B)(C)(D)( 10)设抛物线C:y2=4x的焦点为F,直线L过F且与C交于A, B两点.若|AF|=3|BF|,则L的方程为(A)y=x-1或y=-x+1 (B)y=(X-1)或y=-(x-1)(C)y=(x-1)或y=-(x-1)(D)y=(x-1)或y=-(x-1)(11)已知函数f(x)=x3+ax2+bx+c ,下列结论中错误的是(A)(B)函数y=f(x)的图像是中心对称图形(C)若x0是f(x)的极小值点,则f(x)在区间(-∞,x0)单调递减(D)若x0是f(x)的极值点,则f’(x0)=0(12)若存在正数x使2x(x-a)<1成立,则a 的取值范围是(A)(-∞,+∞)(B)(-2, +∞) (C)(0, +∞) (D)(-1,+∞)第Ⅱ卷本卷包括必考题和选考题两部分。
2020年高考押题预测卷03(新课标Ⅱ卷)-理科数学(参考答案)
2020年高考押题预测卷03【新课标Ⅱ卷】理科数学·参考答案13. [21,)e -+∞ 14. 0,2p ⎛⎫ ⎪⎝⎭ =y x 15. 179 16.①②④ 17.(本小题满分12分)【解析】(1)∵121n n S S +-=∴()1121n n S S ++=+,*n N ∈ 因为111a S ==,所以可推出10n S +>.故1121n n S S ++=+,即{}1n S +为等比数列. ∵112S +=,公比为2∴12n n S +=,即21n n S =-,∵1121n n S --=-,当2n ≥时,112n n n n a S S --=-=,11a =也满足此式, ∴12n na ;(2) 因为12n n n n n b a -==,01112222n n n T -=++⋅⋅⋅+ ∴121122222n n n T =++⋅⋅⋅+,两式相减得:011111122222222n n n nn n T -+=++⋅⋅⋅+-=- 即1242n n n T -+=-,代入1250n n T n -⋅=+,得2260n n --=.令()226xf x x =--(1x ≥),()2ln 210xf x '=->在[)1,x ∈+∞成立,∴()226xf x x =--,()1,x ∈+∞为增函数,而()()540f f ⋅<,所以不存在正整数n 使得1250n n T n -⋅=+成立.18.(本小题满分12分)【解析】证明:(1)因为底面ABCD 为正方形,所以8AD AB == 又因为6PA =,10PD =,满足222PA AD PD +=, 所以PA AD ⊥又PA AB ⊥,AD ⊂面ABCD ,AB面ABCD ,AB AD A ⋂=,所以PA ⊥面ABCD .又因为PA ⊂面PAF ,所以,面PAF ⊥面ABCD .(2)由(1)知AB ,AD ,AP 两两垂直,以A 为坐标原点,以AB ,AD ,AP 分别为x ,y ,z 轴建系如图所示,则()0,0,0A ,()0,0,6P ,()8,0,0B ,()8,8,0C ,()0,8,0D 则()4,4,3N ,()8,4,0F . 所以()8,4,0AF =,()4,4,3AN =,()0,8,0BC =,()8,8,6PC =-,设面ANF 法向量为()1111,,n x y z =,则由1100n AF n AN ⎧⋅=⎪⎨⋅=⎪⎩得111118404430x y x y z +=⎧⎨++=⎩,令11z =得134x =,132y =-,即133,,142n ⎛⎫=- ⎪⎝⎭; 同理,设面PBC 的法向量为()2222,,n x y z =, 则由2200n PC n BC ⎧⋅=⎪⎨⋅=⎪⎩得2222886080x y z y +-=⎧⎨=⎩,令24z =得23x =,20y =,即()23,0,4n =,所以12122212222330145614cos ,3313442n n n n n n ⨯++⨯⋅<>===⎛⎫⎛⎫+-+⨯+ ⎪ ⎪⎝⎭⎝⎭, 设二面角A NF C --的大小为θ,则12cos cos ,n n θ=-<>=所以二面角A NF C --余弦值为61-. 19.(本小题满分12分)【解析】(1)因为抛物线C 上的点到准线的最小距离为2,所以22p=,解得4p =. 故抛物线C 的方程为28y x =; (2)由(1)知焦点为()2,0F .由已知可得AB DE ⊥,所以两直线AB 、DE 的斜率都存在且均不为0. 设直线AB 的斜率为k ,则直线CD 的斜率为1k-, 故直线AB 的方程为()2y k x =-.联立方程组()282y x y k x ⎧=⎪⎨=-⎪⎩,消去x ,整理得28160ky y k --=.设点()11,A x y 、()22,B x y ,则128y y k+=. 因为(),M M M x y 为弦AB 的中点,所以()12142M y y y k=+=. 由()2M M y k x =-,得2422M M y x k k =+=+,故点2442,M kk ⎛⎫+ ⎪⎝⎭.同理,可得()242,4N k k +-.故NF =MF ==.所以2111616||1632k k MF NF k k ⎛⎫+⋅==⋅=+≥⨯= ⎪ ⎪⎝⎭, 当且仅当1k k=,即1k =±时,等号成立. 所以MF NF ⋅的最小值为32. 20.(本小题满分12分)【解析】(1)国家一线队共6名队员,二线队共4名队员.选派4人参加比赛, 基本事件总数410n C =,恰好有3名国家一线队队员参加比赛包含的基本事件个数3164m C C =,∴恰好有3名国家一线队队员参加比赛的概率p 3164410821C C m n C ===. (2)X 的取值为0,1,2,3,4,()1014P X ==, ()8121P X ==,()327P X ==,()4335P X ==,()14210P X==,∴X 的分布列为:(3)4:1获胜的概率3128327P ⎛⎫== ⎪⎝⎭, 4:2获胜的概率2223212833327P C ⎛⎫=⨯⨯⨯=⎪⎝⎭,4:3获胜的概率222342121633381P C ⎛⎫⎛⎫=⨯⨯⨯= ⎪ ⎪⎝⎭⎝⎭,所以林高远获得冠军的概率为1236481P P P P =++=. 21.(本小题满分12分)【解析】(1)依题意0x >,当0a =时,1()(1)f x b x'=-+ ①当1b ≤-时,()0f x '>恒成立,此时()f x 在定义域上单调递增;②当1b >-时,若10,1x b ⎛⎫∈ ⎪+⎝⎭,()0f x '>;若1,1x b ⎛⎫∈+∞⎪+⎝⎭,()0f x '< 故此时()f x 的单调增、减区间分别为10,1b ⎛⎫ ⎪+⎝⎭、1,1b ⎛⎫+∞⎪+⎝⎭(2)由1()21f x ax a b x'=-+--,又(1)0f =, 故()f x 在1x =处取得极大值,从而()01f '=,即1210,a a b -+--==-b a进而得1()221f x ax a x '=-+-=(21)(1)ax x x +-- 当0a ≥时,若1,1x e ⎡⎫∈⎪⎢⎣⎭,()0f x '>则;若(]1,x e ∈,则()0f x '<.所以()=(1)0f x f =最大值 故0a ≥符合题意当0a <时,依题意,有112()0a f e ⎧->⎪⎨⎪≤⎩即2122(1)a e a e ⎧>-⎪⎪⎨-⎪≥-⎪⎩,故此时220(1)e a e -≤<- 综上所求实数a 的范围为22(1)e a e -≥-22.(本小题满分10分)选修4-4:坐标系与参数方程【解析】解法一:(Ⅰ)曲线1C :222x cos y sin θθ=+⎧⎨=⎩(θ为参数)可化为直角坐标方程:()2224x y -+=,即2240x y x +-=, 可得24cos 0ρρθ-=,所以曲线1C 的极坐标方程为:4cos ρθ=.曲线2C:2sin ρθθ=-,即2cos 2sin ρθρθ=-, 则2C的直角坐标方程为:(()2214x y -++=. (Ⅱ)直线l的直角坐标方程为y x =, 所以l 的极坐标方程为()56R πθρ=∈.联立564cos πθρθ⎧=⎪⎨⎪=⎩,得A ρ=-联立562sin πθρθθ⎧=⎪⎨⎪=-⎩,得4B ρ=-,4A B AB ρρ=-=-.解法二:(Ⅰ)同解法一(Ⅱ)直线l的直角坐标方程为3y x =-,联立22340y x x x y ⎧=-⎪⎨⎪-+=⎩,解得(3,A ,联立(()2214y x x y ⎧=⎪⎪⎨⎪-++=⎪⎩,解得()2B -,所以4AB ==-23.(本小题满分10分)选修4-5:不等式选讲【解析】(1)①当12x <时,()324f x x =-+≤ 2132x ∴-≤<②当112x ≤<时,()4f x x =≤ 112x ∴≤<③当1x ≥时,()324f x x =-≤ 12x ∴≤≤ 综上:()4f x ≤的解集为223x x ⎧⎫-≤≤⎨⎬⎩⎭(2)法一:由(1)可知()132,21,1232,1x x f x x x x x ⎧-+<⎪⎪⎪=≤<⎨⎪-≥⎪⎪⎩()min 12f x ∴=即12m =又*,,a b c R ∈且12a b c ++= 则2221a b c ++=,设x y z ===222x y xy +≥ 2222121222xy x y a b a b ∴≤+=+++=++同理:2222yz b c ≤++,2222zx c a ≤++2222222222228xy yz zx a b b c c a ∴++≤++++++++=()2222222212121812x y z x y z xy yz zx a b c ∴++=+++++≤++++++=x y z ∴++≤≤当且仅当16a b c ===时取得最大值法二:由(1)可知()132,21,1232,1x x f x x x x x ⎧-+<⎪⎪⎪=≤<⎨⎪-≥⎪⎪⎩()min 12f x ∴=即12m =又*,,a b c R ∈且12a b c ++==4442121213332222a b c ⎫++++++⎪≤++⎪ ⎪⎝⎭当且仅当16a b c ===时取得最大值法三:由(1)可知()132,21,1232,1x x f x x x x x ⎧-+<⎪⎪⎪=≤<⎨⎪-≥⎪⎪⎩()min 12f x ∴=即12m =12a b c ∴++= 2121214a b c ∴+++++=由柯西不等式可知:()())2222222111111++⨯++≥++即:)211121++≤≤当且仅当212121a b c +=+=+即16a b c ===时,取得最大值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年高考押题预测卷03【新课标Ⅱ卷】文科数学·参考答案13.[21,)e -+∞ 14.0,2p ⎛⎫ ⎪⎝⎭ =2y x ±15.17916.①②④17.(本小题满分12分)【解析】(1)∵121n n S S +-= ∴()1121n n S S ++=+,*n N ∈ 因为111a S ==,所以可推出10n S +>.故1121n n S S ++=+,即{}1n S +为等比数列. ∵112S +=,公比为2∴12n n S +=,即21n n S =-,∵1121n n S --=-,当2n ≥时,112n n n n a S S --=-=,11a =也满足此式,∴12n n a -=;(2) 因为12n n n n n b a -==,01112222n n n T -=++⋅⋅⋅+ ∴121122222n n n T =++⋅⋅⋅+,两式相减得:011111122222222n n n n n n T -+=++⋅⋅⋅+-=- 即1242n n n T -+=-,代入1250n n T n -⋅=+,得2260n n --=.令()226xf x x =--(1x ≥),()2ln 210xf x '=->在[)1,x ∈+∞成立,∴()226xf x x =--,()1,x ∈+∞为增函数,而()()540f f ⋅<,所以不存在正整数n 使得1250n n T n -⋅=+成立.18.(本小题满分12分)【解析】(Ⅰ)取PA 中点G ,连FG ,GD , 由11//,,//,22FG AB FG AB ED AB ED AB ==,可得//,FG ED FG ED =, 可得EDGF 是平行四边形,则//EF DG ,又PD ⊥平面ABCD ,∴平面PAD ⊥平面ABCD ,∵AB AD AB ⊥⇒⊥平面PAD ,AB ⊂平面PAB ,∴平面PAB ⊥平面PAD , ∵PD AD =,G 是PA 中点,则DG PA ⊥,而DG ⊂平面PAD DG ⇒⊥平面PAB , 而//EF DG ,∴EF ⊥平面PAB . (Ⅱ)根据三棱锥的体积公式, 得12P AEF B AEF F BAE P BAE V V V V ----===1123BAE S PD ∆=⨯⨯⨯ 111332324=⨯⨯⨯=. 19.(本小题满分12分)【解析】(1)因为抛物线C 上的点到准线的最小距离为2,所以22p=,解得4p =. 故抛物线C 的方程为28y x =; (2)由(1)知焦点为()2,0F .由已知可得AB DE ⊥,所以两直线AB 、DE 的斜率都存在且均不为0. 设直线AB 的斜率为k ,则直线CD 的斜率为1k-, 故直线AB 的方程为()2y k x =-.联立方程组()282y x y k x ⎧=⎪⎨=-⎪⎩,消去x ,整理得28160ky y k --=.设点()11,A x y 、()22,B x y ,则128y y k+=. 因为(),M M M x y 为弦AB 的中点,所以()12142M y y y k=+=.由()2M M y k x =-,得2422M M y x k k =+=+,故点2442,M kk ⎛⎫+ ⎪⎝⎭.同理,可得()242,4N k k +-.故NF =MF ==.所以2111616||1632k k MF NF k k ⎛⎫+⋅==⋅=+≥⨯= ⎪ ⎪⎝⎭, 当且仅当1k k=,即1k =±时,等号成立. 所以MF NF ⋅的最小值为32. 20.(本小题满分12分)【解析】(1)依题意,100300500700c b m n ====,,,. 在本次的实验中,2K的观测值2K21000(400200300100)47.61910.828700300500500⨯⨯-⨯=≈>⨯⨯⨯.∴在犯错误的概率不超过0.1%的前提下,认为对共享产品的态度与性别有关系;(2)依题意,应该从认为共享产品对生活无益的女性中抽取4人,记为A B C D ,,,,从认为共享产品对生活无益的男性中抽取2人,记为a ,b .从以上6人中随机抽取2人,所有的情况为:(,),(,),(,),(,),(,),(,),(,)A B A C A D A a A b B C B D (),B a ,(,),(,),(,),(,),(,),(,),(,)B b C D C a C b D a D b a b ,共15种,其中满足条件的为(,),(,),(,),(,),(,),(,),(,),(,)A a A b B a B b C a C b D a D b 共8种情况,故所求概率815P =; 21.(本小题满分12分)【解析】(1)依题意0x >,当0a =时,1()(1)f x b x'=-+ ①当1b ≤-时,()0f x '>恒成立,此时()f x 在定义域上单调递增; ②当1b >-时,若10,1x b ⎛⎫∈ ⎪+⎝⎭,()0f x '>;若1,1x b ⎛⎫∈+∞⎪+⎝⎭,()0f x '< 故此时()f x 的单调增、减区间分别为10,1b ⎛⎫ ⎪+⎝⎭、1,1b ⎛⎫+∞⎪+⎝⎭(2)由1()21f x ax a b x'=-+--,又(1)0f =, 故()f x 在1x =处取得极大值,从而()01f '=,即1210,a a b -+--==-b a进而得1()221f x ax a x '=-+-=(21)(1)ax x x +-- 当0a ≥时,若1,1x e ⎡⎫∈⎪⎢⎣⎭,()0f x '>则;若(]1,x e ∈,则()0f x '<.所以()=(1)0f x f =最大值 故0a ≥符合题意当0a <时,依题意,有112()0a f e ⎧->⎪⎨⎪≤⎩即2122(1)a e a e ⎧>-⎪⎪⎨-⎪≥-⎪⎩,故此时220(1)e a e -≤<- 综上所求实数a 的范围为22(1)e a e -≥-22.(本小题满分10分)选修4-4:坐标系与参数方程【解析】解法一:(Ⅰ)曲线1C :222x cos y sin θθ=+⎧⎨=⎩(θ为参数)可化为直角坐标方程:()2224x y -+=,即2240x y x +-=, 可得24cos 0ρρθ-=,所以曲线1C 的极坐标方程为:4cos ρθ=.曲线2C:2sin ρθθ=-,即2cos 2sin ρθρθ=-, 则2C的直角坐标方程为:(()2214x y -++=. (Ⅱ)直线l的直角坐标方程为y x =, 所以l 的极坐标方程为()56R πθρ=∈. 联立564cos πθρθ⎧=⎪⎨⎪=⎩,得A ρ=-联立562sin πθρθθ⎧=⎪⎨⎪=-⎩,得4B ρ=-,4A B AB ρρ=-=-.解法二:(Ⅰ)同解法一(Ⅱ)直线l的直角坐标方程为y x =,联立2240y x x x y ⎧=⎪⎨⎪-+=⎩,解得(3,A ,联立(()2214y x x y ⎧=⎪⎪⎨⎪-++=⎪⎩,解得()2B -, 所以4AB ==-23.(本小题满分10分)选修4-5:不等式选讲【解析】(1)①当12x <时,()324f x x =-+≤ 2132x ∴-≤<②当112x ≤<时,()4f x x =≤ 112x ∴≤<③当1x ≥时,()324f x x =-≤ 12x ∴≤≤ 综上:()4f x ≤的解集为223x x ⎧⎫-≤≤⎨⎬⎩⎭(2)法一:由(1)可知()132,21,1232,1x x f x x x x x ⎧-+<⎪⎪⎪=≤<⎨⎪-≥⎪⎪⎩()min 12f x ∴=即12m =又*,,a b c R ∈且12a b c ++=则2221a b c ++=,设x y z ===222x y xy +≥Q 2222121222xy x y a b a b ∴≤+=+++=++同理:2222yz b c ≤++,2222zx c a ≤++2222222222228xy yz zx a b b c c a ∴++≤++++++++=()2222222212121812x y z x y z xy yz zx a b c ∴++=+++++≤++++++=x y z ∴++≤≤当且仅当16a b c ===时取得最大值法二:由(1)可知()132,21,1232,1x x f x x x x x ⎧-+<⎪⎪⎪=≤<⎨⎪-≥⎪⎪⎩()min 12f x ∴=即12m =又*,,a b c R ∈且12a b c ++=2=444212121333222a b c ⎫++++++⎪≤++⎪ ⎪⎝⎭当且仅当16a b c ===时取得最大值法三:由(1)可知()132,21,1232,1x x f x x x x x ⎧-+<⎪⎪⎪=≤<⎨⎪-≥⎪⎪⎩()min 12f x ∴=即12m =,12a b c ∴++=,2121214a b c ∴+++++=由柯西不等式可知:()())2222222111111++⨯++≥++即:)211121++≤≤当且仅当212121a b c +=+=+即16a b c ===时,取得最大值。
