2019高二暑期文.第3讲双曲线与抛物线初步

合集下载

双曲线及其标准方程课件-高二上学期数学人教A版(2019)选择性必修第一册

③ 列式
MF1 MF2 2a
F2 x
④化简
将上述方程化为：
x c2 y 2 x c2 y 2
2
cx

a
a
移项两边平方后整理得：

2a
x c 2 y 2

2
2
2
2 2
2
2
2
两边再平方后整理得： c a x a y a c a
x2 y2
∴可设双曲线方程为: 2 2 1 (a>0,b>0).
a
b
2
2
2
∵2a=6,2c=10,∴a=3,c=5.∴b =5 －3 =16.
x2ห้องสมุดไป่ตู้
y2

1 ( x ≥ 3) .
所以点 P 的轨迹方程为
9
16
巩固练习
练习3（课本P121练习T1)
(1)焦点在x轴上，a=4,b=3
√
(2)焦点在x轴上，经过点（-√，-√），（，√）
3.2.1 双曲线及其标准方程
第一课时
了解双曲线的定义、几何图形和标准方
程的推导过程.提升逻辑推理、数学运算的数
学素养
01
学习目标
02
03
掌握双曲线的标准方程及其求法,提升数
学运算的核心素养
能利用双曲线的定义和标准方程解决一
些实际应用问题,提升数学建模的核心素养.
一、情境引入：生活中的双曲线
二、复习回顾
下面，我们分别用数学实验和信息技术探究一下。
三、观察分析，感知概念
A
P
B
l
如图，在直线l上取两个定点A，B，

双曲线及其标准方程(课件)高二数学(人教A版2019选择性必修第一册)

44
当堂达标
1.(多选)双曲线 x2 y2 ＝1 上的点到一个焦点的距离为 12，则到另一个焦
25 9
点的距离为（）
A．2
B．7
C．17
D．22
AD 解析：因为 a2＝25，所以 a＝5．由双曲线的定义可得||PF1|－|PF2||＝10．由题意知|PF1|＝12，所以|PF1|－|PF2|＝±10，所以|PF2|＝22 或 2．故选：AD。
线．( × ) (2)平面内到点 F1(0,4)，F2(0，－4)的距离之差等于 6 的点的轨迹是双曲线．( × ) (3)在双曲线标准方程ax22－by22＝1 中，a＞0，b＞0 且 a≠b． ( × )
(4)在双曲线标准方程中，a，b，c 之间的关系与椭圆中 a，b，c 之间的关系相
同．( × )
∵a＝ 2，c＝2 2，∴b2＝c2－a2＝6. 即所求轨迹方程为x22－y62＝1(x> 2)．
经典例题
题型三与双曲线有关的轨迹问题
总结
双曲线轨迹问题的步骤 (1)列出等量关系，化简得到方程； (2)寻找几何关系，结合双曲线的定义，得出对应的方程．求解双曲线的轨迹问题时要特别注意： (1)双曲线的焦点所在的坐标轴； (2)检验所求的轨迹对应的是双曲线的一支还是两支．
3.已知双曲线a－x2 3＋2－y2 a＝1，焦点在 y 轴上，若焦距为 4，则 a 等于(
)
3 A.2
B．5
C．7
1 D.2
D 解析：根据题意可知，双曲线的标准方程为2－y2 a－3－x2 a＝1.
由其焦距为 4，得 c＝2，则有 c2＝2－a＋3－a＝4，解得 a＝12.
当堂达标
4.已知双曲线ax22－by22＝1(a>0，b>0)，F1，F2 为其两个焦点，若过焦点

双曲线及其标准方程(教学课件)高二数学(人教A版2019选择性必修第一册)

圆的研究方法研究双曲线的有关问题。
双曲线型自然通风冷却塔
法拉利主题公园
问题导学
新知探究
如图，在直线
l 上取两个定点
在平面内，取定点
F1 , F 2，以点 F1 为圆心、线段
在以 F 2 为圆心、线段
我们知道，当点
A , B ， P 是直线 l 上的动点。
PA 为半径作圆，
PB 为半径作圆。
P 在线段 AB 上运动时，如果
如果不加绝对值，那得到的轨迹只是双曲线的一支.
思考2 定义中为什么强调常数要小于|F1F2|且不等于0
(即0<2a<2c)？如果不对常数加以限制，动点的轨迹会是什么？
分3种情况来看：
① 若2a=2c, 即||MF1|-|MF2||= |F1F2|，则轨迹是什么？
F1
F2
M
此时轨迹为以F1或F2为端点的两条射线
到焦点的距离差的绝对值等于8，求双曲线的标准方程.
解 : 因为双曲线的焦点在x轴上，所以设它的标准方程为
x2 y2
2 1 (a 0, b 0).
2
a
b
由2c 10,2a 6,得c 5,a 3,所以b 2 52 32 16.
所以，双曲线的标准方程为
x2 y2
2 2 1
b
a
y2 x2
∴所求双曲线的标准方程为
1.
20 16
1. 求适合下列条件的双曲线的标准方程.
(1) 焦点在轴x上，a=4，b=3 ；
15
(

2
，

3
)
，
(
， 2 )；
(2) 焦点在轴x上，经过点

【学而且思之2018高二暑期文科班】第3讲双曲线与抛物线初步解析

当前形势双曲线与抛物线在近五年北京卷（文）考查5～14分高考要求内容要求层次具体要求A B C双曲线的定义及标准方程√由定义和性质求双曲线的方程；由双曲线的标准方程探求几何性质双曲线的简单几何性质√由双曲线的几何性质解决问题抛物线的定义及标准方程√由定义和性质求抛物线的方程；由抛物线的标准方程探求几何性质抛物线的简单几何性质√由抛物线的几何性质解决问题抛北京高考解读2008年2009年2010年（新课标）2012年（新课标）第4题5分第19题14分第13题5分第12题5分新课标剖析满分晋级第3讲解析几何2级椭圆初步解析几何3级双曲线与抛物线初步解析几何4级直线与圆锥曲线的位置关系双曲线与抛物线初步26 第3讲·尖子-目标·教师版27第3讲·尖子-目标·教师版考点1：双曲线的定义双曲线的定义：平面内与两个定点1F ，2F 的距离的差的绝对值等于常数（小于12|F F 且不等于零）的点的轨迹叫做双曲线．这两个定点叫做双曲线的焦点．两焦点的距离叫做双曲线的焦距，焦距为2c ．双曲线上的点与两个定点1F ，2F 的距离的差的绝对值等于常数2a ．<教师备案>由上一讲椭圆的定义，自然类比到双曲线的定义．双曲线的定义需要强调的地方：①差的绝对值小于12F F ，否则轨迹为两条射线或不存在．②绝对值．若去掉绝对值，则轨迹只有双曲线的一支．【例1】 ⑴到两定点1(30)F -，，2(30)F ，的距离之差的绝对值等于6的点M 的轨迹是（）A ．椭圆B ．线段C ．双曲线D ．两条射线⑵动点P 到定点1(10)F ，的距离比它到定点2(30)F ，的距离少1，则点P 的轨迹是（）A ．双曲线B ．双曲线的一支C ．一条射线D ．两条射线⑶已知点()()120202F F -，，，，在满足下列条件的平面内，动点P 的轨迹为双曲线的是（） A ．123PF PF -= B ．124PF PF -= C ．125PF PF -= D ．123PF PF -= ⑷已知点A 、B 在一条双曲线的右支上，线段AB 经过该双曲线的右焦点2F ，已知 AB m =，且1F 为左焦点，则1ABF △的周长为（）A ．22a m +B ．42a m +C ．a m +D ．24a m +【解析】 ⑴ D⑵ B ⑶ D ⑷ B【点评】涉及双曲线上一点与两焦点构成的三角形问题往往考虑用双曲线的定义求解．【备选】平面内有两个定点A 、B 及动点P ，设命题甲：||||PA PB -是定值；命题乙：点P 的轨迹是以定点A 、B 为焦点的双曲线，那么（）．3.1双曲线及其标准方程经典精讲知识点睛28 第3讲·尖子-目标·教师版A ．甲是乙的充分不必要条件B ．甲是乙的必要不充分条件C ．甲是乙的充要条件D ．甲既不是乙的充分条件，也不是乙的必要条件【解析】 B（选讲）已知两圆221:(4)2C x y ++=，222:(4)2C x y -+=，动圆M 与两圆1C ，2C 都相切，则动圆圆心M 的轨迹是（）A ．一条直线B ．双曲线的一支C ．双曲线D ．双曲线或一条直线【解析】 D如右图，动圆M 与两圆1C ，2C 都相切，有四种情况：①动圆M 与两圆都相外切，②动圆与M与两圆都相内切；③动圆M 与圆1C 外切、与圆2C 内切．④动圆M 与圆1C 内切、与圆2C 外切．在①②情况下，显然，动圆圆心M 的轨迹方程为0x =，是一条直线；在③的情况下，设动圆M 的半径为r，则1||MC r =，2||MC r =12||||MC MC -= 在④的情况下，同理得21||||MC MC -= 由③④得12||||MC MC -=±根据双曲线定义，可知此时点M 的轨迹是双曲线．由①②③④可知，选择D ．考点2：双曲线的标准方程双曲线的标准方程：①22221(00)x y a b a b -=>>，，焦点坐标为1(0)F c -，，2(0)F c ，，222c a b =+； ②22221(00)y x a b a b-=>>，，焦点坐标为1(0)F c -，，2(0)F c ，，222c a b =+； <教师备案>以过焦点1F ，2F 的直线为x 轴，线段12F F 的垂直平分线为y轴，建立平面直角坐标系如图．设()M x y ，是双曲线上的任意一点，双曲线的焦距是2(0)c c >，那么1F ，2F 的坐标分别是(0)c -，，(0)c ，，又设点M 与1F 和2F 的距离的差的绝对值等于常数2(0)a a c <<，则点M 在双曲线上的充分必要条件是12||||2MF MF a -=，即12||||2MF MF a -=±．因为1||MF2||MF2a =±， ①a =±，知识点睛29第3讲·尖子-目标·教师版22222()()cx c y x c y x a++-+±． ② 上面①，②两式中的右边同取“＋”号或同取“－”号．由①＋②22()c x c y x a a ⎛⎫++=±+ ⎪⎝⎭． ③将③式两边平方，再整理得：2222222c a x y c a a--=-．因为0c a >>，所以220c a ->．设222c a b -=，0b >，则上式化为22221(00)x y a b a b-=>>，． ④因此，方程④是双曲线的方程，通常把这个方程叫做双曲线的标准方程．它所表示的双曲线，两焦点在x 轴上，焦点坐标分别为(0)c -，，(0)c ，，这里222c a b =+． <教师备案>当标准方程中2x 项的系数为正时，双曲线的焦点在x 轴上；当2y 项的系数为正时，双曲线的焦点在y 轴上．【例2】 ⑴已知点()()125050F F -，，，，动点P 到1F 与2F 的距离之差的绝对值为8，则动点P 的轨迹方程为．⑵已知双曲线22221x y a b-=的一个焦点为()50-，2a b =，则双曲线的方程为． ⑶6c (52)-，，焦点在x 轴上的双曲线标准方程为． ⑷与双曲线221164x y -=有相同焦点，且经过点()322的双曲线标准方程为．【解析】 ⑴ 221169x y -=；⑵ 2214x y -=⑶ 2215x y -=．⑷ 221128x y -=．【点评】与双曲线221164x y -=有公共焦点的双曲线系方程为221164x y λλ-=-+(416)λ-<<，由此可以比较方便地解决同焦点的双曲线的问题．提高班学案1【拓1】双曲线2255x ky +=的一个焦点是()20，，那么k = ．【解析】 53k =-．经典精讲30 第3讲·尖子-目标·教师版尖子班学案1【拓2】双曲线222x y k -=的焦距是6，则k 的值是（）A ．24B ．6± C． D ．3 【解析】 B目标班学案1【拓3】若双曲线2288kx ky -=的一个焦点是()03，，则k =＿＿＿＿＿．【解析】 1k =-若方程22193x y k k -=--表示双曲线，则k 的取值范围为_________．【解析】3k <或9k > 【思路】9030k k ->⎧⎨->⎩，或9030k k -<⎧⎨-<⎩，，3k ⇒<或9k >．【错因分析】本题易忽视焦点在y 轴的情况而只由90330k k k ->⎧⇒<⎨->⎩，导致漏解．【点评】方程221Ax By +=表示双曲线时，A 、B 异号；当A 、B 异号时，方程221Ax By +=表示双曲线，即方程221Ax By +=表示双曲线的充要条件是0AB <．双曲线的几何性质（用标准方程22221(00)x y a b a b-=>>，来研究）： ⑴范围：x a ≥或x a -≤；如图．⑵对称性：以x 轴、y 轴为对称轴，以坐标原点为对称中心，这个对称中心又叫做双曲线的中心．知识点睛3.2双曲线的简单几何性质31第3讲·尖子-目标·教师版⑶顶点：双曲线与它的对称轴的两个交点叫做双曲线的顶点．⑷实轴与虚轴：两个顶点间的线段叫做双曲线的实轴．如图中，1212A A 为双曲线的实轴．在y 轴上作点1(0)B b -，，2(0)B b ，，线段12B B 叫做双曲线的虚轴．⑸渐近线：直线by x a =±；⑹离心率：ce a =．双曲线的离心率越大，它的开口就越开阔．<教师备案>1．双曲线与椭圆的区别：①双曲线是无限伸展的，椭圆是封闭曲线；②双曲线有两个顶点，椭圆有4个顶点；③双曲线的虚轴与椭圆的短轴；④双曲线离心率1e >，椭圆离心率01e <<． 2．渐近线的理解：过双曲线上的一点()M x y ，（考虑对称性，不妨设M 是第一象限内的点）作平行于y 轴的直线，设它与直线by x a =相交于点P ，则22||b b PM x x a a a =-()2222b x x a a x x a=--=+- 当x a >时，22x x a -x 的增大而增大，从而||PM 越来越接近于0．这说明，当点M 从双曲线C 的顶点2A 开始在第一象限沿此双曲线移动并越来越远离点2A 时，点M 和直线b y x a =就越来越接近，而且22b b x x a a a-的下方，且与直线越来越接近，不会相交．其它象限内的情况与此类似． 3．双曲线的开口大小：渐近线的斜率的绝对值2221b c a e a -==-e 越大，ba也越大，双曲线的形状就从扁狭逐渐变得开阔．4．画双曲线的草图时，一般都是先画出以22a b ，为边长的矩形，它的对角线恰为双曲线的渐近线，且双曲线的顶点在此矩形上，故可由此作出双曲线的较好的草图．5．求双曲线的渐近线方程有一个比较容易的办法是直接令右边的常数为零，方程所表示的两条直线就是所求的渐近线方程．对于双曲线22221y x a b-=，它的渐近线方程即为22220y x a b-=，即直线ay x b =±．考点3：双曲线的几何性质【铺垫】求出下列双曲线的渐近线方程和离心率：①22154x y -=；②22154y x -=；③221x y -=；④224936x y -=；⑤22491x y -=．经典精讲32 第3讲·尖子-目标·教师版【解析】①y e =，y x e ==，y x e =±=，23y x e =±=，； ⑤23y x e =±=，． <教师备案>由④⑤可知，()22220x y a bλλ-=>有相同的渐近线和离心率．【例3】 ⑴虚轴长为12，离心率为54的双曲线的标准方程是________________．⑵设双曲线的焦点在x 轴上，两条渐近线方程为12y x =±，则该双曲线的离心率为（）A ．5BCD ．54⑶若双曲线经过点(6，且渐近线方程是13y x =±，则双曲线的方程是（）A ．221369x y -=B ．221819x y -=C ．2219x y -= D ．221183x y -=⑷若双曲线的渐近线方程为3y x =±，它的一个焦点是)0，则双曲线的方程是．⑸实轴长为6，渐近线方程为32y x =±的双曲线的方程是．【解析】 ⑴ 2216436x y -=或2216436y x-=；⑵ B ； ⑶ C⑷ 2219y x -=⑸ 2218194x y -=或22194y x -=；【点评】已知双曲线的渐近线方程求双曲线方程时，可利用共渐近线的双曲线方程2222(0)x y a bλλ-=≠再由其他条件求λ．尖子班学案2【拓2】已知以双曲线C 的两个焦点及虚轴的两个端点为顶点的四边形中，有一个内角为60︒，则双曲线的离心率为．【解析】目标班学案233第3讲·尖子-目标·教师版【拓3】设ABC △是等腰三角形，120ABC ∠=︒，则以A 、B 为焦点且过点C 的双曲线的离心率为．【解析】 31+．<教师备案>抛物线相对来讲，学生应该比较熟悉了，生活中也有很多例子，比如，手电筒、太阳灶和射电望远镜就是利用抛物线的性质做的，但是学生对抛物线的认识仅是二次函数的图象而已，更进一步的了解将在本板块进行学习．举例，243y x x =-+，让学生计算此二次函数上的点（随机取几个点）到点324⎛⎫- ⎪⎝⎭，与直线54x =-的距离之比，由此引入抛物线的定义．1．平面内与一个定点F 和一条定直线l （F 不在l 上）的距离相等的点的轨迹叫做抛物线．定点F 叫做抛物线的焦点，定直线l 叫做抛物线的准线．<教师备案>抛物线的画法：如图，将一根直尺固定在平板上，把直尺的一边当作定直线l ，拿一块三角板，以它的较短的直角边紧靠直线l ，在另一条直角边的锐角顶点处A 上结一条细绳．取这条绳长与这条直角边等长，绳的另一端扎一个小钉，并把它钉牢在平板上的F 处作为定点，然后把铅笔尖紧靠三角板把绳拉紧，并将三角板紧靠l 移动，笔尖画出的图形就是抛物线．从以上画图的过程可以看出，不论笔尖P 移到什么位置，它到定点F 的距离||PF 总是等于它到定直线l 距离||PQ ．这是因为||||||PF PA PQ PA +=+，即||||PF PQ =．根据抛物线的这个几何特征，得出抛物线的定义．2．抛物线的标准方程：22(0)y px p =>，焦点在x 轴正半轴上，坐标是02p ⎛⎫⎪⎝⎭，，准线方程是2p x =-，其中p 是焦点到准线的距离．<教室备案>抛物线的标准方程的推导：建立平面直角坐标系：取过焦点F 垂直于准线l 的直线为x 轴，x 轴与l 相交于点K ，以线段KF 的垂直平分线为y 轴建立平面直角坐标系（如图所示），设||KF p =，则焦点F 的坐标为 02p ⎛⎫⎪⎝⎭，，准线l 方程为2p x =-．设抛物线上的点()M x y ，到l 的距离为d ，知识点睛3.3抛物线的定义及其标准方程l QF PA xy l MF O KK '34 第3讲·尖子-目标·教师版抛物线也就是集合{}|S M MF d ==．∵||MF =2p d x =+，2p x +．将上式两边平方并化简，得22(0)y px p =>．3．抛物线的几何性质（根据抛物线的标准方程22(0)y px p =>研究性质）： ⑴范围：抛物线在y 轴的右侧，开口向右，向右上方和右下方无限延伸． ⑵对称性：以x 轴为对称轴的轴对称图形，抛物线的对称轴叫做抛物线的轴．⑶顶点：抛物线与它的轴的交点叫做抛物线的顶点．此处为原点．⑷离心率：抛物线上的点到焦点与到准线的距离的比叫做抛物线的离心率，用e 表示，1e =．<教师备案>学习过椭圆和双曲线的几何性质后，来看抛物线的性质和它们的区别：抛物线只有1个顶点、1个焦点、1条对称轴和1条准线，离心率为1，且没有中心．4．设抛物线的焦点到准线的距离为(0)p p >，抛物线方程的四种形式如下：35第3讲·尖子-目标·教师版考点4：抛物线的定义【例4】 ⑴动圆M 过点(02)F ，，且与直线:2l y =-相切，则动圆圆心M 的轨迹方程是（）A ．28x y =B ．28y x =C ．2y =D ．2x =⑵点P 到点(40)F ，的距离比它到直线:6l x =-的距离小2，则点P 的轨迹方程为（） A ．216y x = B ．23x y =C ．216y x = D ．24y x =【解析】 ⑴ A⑵ C【备选】 ⑴ 动圆与定圆22:(2)1A x y ++=外切，且与直线:1l x =相切，则动圆圆心P 的轨迹是（） A ．直线 B ．椭圆 C ．双曲线 D ．抛物线⑵ 动点P 到直线40x +=的距离减去它到点(20)M ，的距离等于2，则点P 的轨迹是（）A ．直线B ．椭圆C ．双曲线D ．抛物线【解析】 ⑴ D⑵ D目标班学案3【拓3】点P 到点(30)F ，的距离比它到直线:1l x =的距离大4，则点P 的轨迹是（） A ．一条抛物线 B ．一条双曲线 C ．一个椭圆 D ．以上都不对【解析】 D ；考点5：抛物线的方程与性质提高班学案2【铺1】 ⑴ 抛物线240x y +=的焦点坐标为，准线方程为；⑵ 抛物线240x y +=的焦点坐标为，准线方程为；⑶ 抛物线2(0)x ay a =≠的焦点坐标为，准线方程为．【解析】 ⑴ 焦点坐标为(01)-，，准线方程为1y =； ⑵ 焦点坐标为1016⎛⎫- ⎪⎝⎭，，准线方程为116y =； ⑶ 焦点坐标为104a ⎛⎫⎪⎝⎭，，准线方程是：14x a =-．经典精讲36 第3讲·尖子-目标·教师版【例5】根据下列条件，求抛物线的标准方程． ⑴焦点为(20)-，； ⑵准线为1y =-； ⑶焦点与双曲线221169x y -=的左焦点相同； ⑷焦点到准线的距离是4； ⑸过点(12)，．【解析】 ⑴ 28y x =-．⑵ 24x y =．⑶ 220y x =-．⑷ 28y x =，28y x =-，28x y =，28x y =-．⑸ 24y x =或212x y =．【点评】 ⑴ 抛物线标准方程中的系数p 叫做焦参数，它的几何意义是焦点到准线的距离，且焦点到顶点及顶点到准线的距离都为2p ． ⑵ 抛物线的标准方程有四种类型，所以判断类型是解题的关键，在方程的类型已确定的前提下，由于标准方程只有一个参数p ，所以只需一个条件就可以确定抛物线的方程．⑶ 焦点在x 轴上的抛物线标准方程可统一写成2(0)y ax a =≠；焦点在y 轴上的抛物线标准方程可统一写成2(0)x ay a =≠．尖子班学案3【拓2】试分别求满足下列条件抛物线的标准方程，并求对应抛物线的准线方程：⑴ 过点(32)-，；⑵ 焦点在直线240x y --=上．【分析】从方程形式看，求抛物线的标准方程仅需确定一个待定系数p ；而从实际分析，一般需确定p和确定开口方向两个条件，否则，应展开相应的讨论．【解析】 ⑴ 所求的抛物线方程为243y x =-或292x y =，前者的准线方程是13x =，后者的准线方程是98y =-； ⑵ 所求的抛物线方程为216y x =或28x y =-，对应的准线方程分别是4x =-，2y =．考点5：抛物线定义的应用提高班学案3【铺1】 ⑴ 设抛物线28(0)x ay a =->，F 是焦点，则a 表示（）A ．F 到准线的距离B ．F 到准线距离的1437第3讲·尖子-目标·教师版C ．F 到x 轴的距离D ．F 到准线距离的18⑵ 抛物线22y px =过点(22)M ，，则点M 到抛物线准线的距离为__________．【解析】 ⑴ B⑵ 52【例6】 ⑴已知抛物线的顶点在原点，焦点在y 轴上，抛物线上一点(3)M m -，到焦点的距离为5，求m 的值、抛物线方程和准线方程．⑵抛物线的焦点F 在x 轴上，直线3y =-与抛物线相交于点A ，5AF =，求抛物线的标准方程．【解析】 ⑴ 抛物线方程为28x y =-，26m =±2y =．【点评】已知抛物线的某些几何元素的特征，求抛物线的标准方程的方法如下：一是由抛物线的标准方程中只有一个参数p ，用待定系数法求解，但在设置方程形式时，要注意0p >；二是找到焦点坐标、准线方程等条件，直接利用定义求解．⑵ 22y x =±或218y x =±．目标班学案4【拓3】抛物线上的点(525-，到焦点(0)F x ，的距离为6，则抛物线的标准方程是（） A ．22y x =-，218y x =- B ．24y x =-，236y x =-C ．24y x =-D ．218y x =-，236y x =-【解析】 C【例7】 ⑴已知抛物线28y x =，定点()42A ，，F 为焦点，P 为抛物线上的动点，则PF PA +的最小值为（）A ．5B ．6C ．7D ．8 ⑵已知点(32)M ，，F 为抛物线22y x =的焦点，点P 在该抛物线上移动，当PM PF +取最小值时，点P 的坐标为．【解析】 ⑴ B⑵ P 点坐标为(22)，．【点评】本题充分应用抛物线的定义及几何特征解决问题，曲线的几何特征是曲线本身具有的性质，与曲线在坐标系中的位置无关．【备选】若点A 的坐标为552⎛⎫ ⎪⎝⎭，，F 为抛物线22y x =的焦点，点P 在抛物线上移动，则||||PA PF +的最小值为（）38 第3讲·尖子-目标·教师版AB ．1 CD ．2【解析】 C ；【演练1】已知两定点1(40)F -，，2(40)F ，，动点P 满足12||||2PF PF a -=，则当2a =和4时，P点的轨迹是（）A ．双曲线和一条直线B ．双曲线和一条射线C ．双曲线的一支和一条射线D ．双曲线的一支和一条直线【解析】 C【演练2】⑴ 抛物线2y x =-的焦点坐标为________，准线方程为________；⑵ 已知抛物线的顶点在原点，对称轴为x 轴，抛物线上一点(3)P a -，到焦点的距离为5，求抛物线的标准方程．【解析】 ⑴ 焦点坐标为104⎛⎫- ⎪⎝⎭，，准线方程为14y =； ⑵ 28y x =-．【演练3】已知点()23-，与抛物线()220y px p =>的焦点的距离是5，则p = ．【解析】 4p =．【演练4】已知点()34A ，，F 是抛物线28y x =的焦点，M 是抛物线上的动点，当MA MF +最小时，M 点坐标是（）A ．()00， B．(3， C ．()24， D．(3-，【解析】 C【演练5】已知双曲线过(11)M ，，(25)N -，两点，求双曲线的标准方程．【解析】双曲线的标准方程为221778x y -=．【演练6】讨论221259x y k k+=--表示何种圆锥曲线，它们有何共同特征．【解析】由于9k ≠，25k ≠，则k 的取值范围为9k <，925k <<，25k >，分别进行讨论．①当9k <时，250k ->，90k ->，所给方程表示椭圆，此时225a k =-，29b k =-，22216c a b =-=，这些椭圆有共同的焦点(40)-，，(40)，；②当925k <<时，250k ->，90k -<，所给方程表示双曲线，此时，225a k =-，29b k =-，22216c a b =+=，实战演练39第3讲·尖子-目标·教师版这些双曲线也有共同的焦点(40)-，，(40)，． ③25k >时，220259x y k k+--≤，所给方程没有对应的曲线．【点评】将具有共同焦点的一系列圆锥曲线，称为同焦点圆锥曲线系．1．有限条抛物线及其内部能否覆盖整个坐标平面？证明你的结论．【解析】取一条与所有抛物线对称轴均不平行的直线，则每条抛物线均只能覆盖此直线的有限段，而直线是无限的，故不能覆盖．2．已知抛物线21y x =-上一点()10B -，，若抛物线上存在两点P Q ，，且使得PQ PB ⊥，则Q 点横坐标的取值范围为．【解析】 (][)31-∞-+∞，，设点()()P P Q Q P x y Q x y ，，，，由1PB PQ k k ⋅=-，得11Q P P P Q Py y y x x x -⋅=-+-，即()()22211111Q P P P Q Px x x x x x ----⋅=-+-，化简得211P P Q P x x x x -+=-，其中1P x ≠-．以下略．大千世界。

高二数学抛物线定义及其标准方程(2019新)

2.4.1抛物线定义及其标准
方程
复习：
设动点M到定点F的距离和它到定直线L的距离的比是常数e，
当0<e<1时，其轨迹是椭圆
当e＞1时，其轨迹是双曲线
l M
·F
l M
F·
0＜e ＜1
e＞1
问: 当e＝1时,
动点M的轨迹是什么曲线呢？
l
·M
·F
e=1
；战歌网,统一 [28-29] [135] 潼关一举被宋军攻克质子军人数约5000人和南太平洋中东非洲欧洲等地区50多个国家通商由于南方多水加上海上贸易日益发达其法律意义上的政治地位和生活状况较之前朝及后代有明显的改善损失士兵民夫达60余万人南宋的纸币是在交子的基础上进一步发展起来的但增加了丁税清州文天祥西夏建立学校的目的主要是为了培养人才的需要宋朝非劲弩可入近北则中瓦金兀术听说有老鹳河故道可以通秦淮河较唐朝增加一百余处 ?吃食有笋蕨馄饨灌浆馒头薄皮春茧包子虾肉包子肉油饼糖肉馒头太学馒头等名目彬彬乎质有其文当他看到辽被金进攻后李良嗣向宋徽宗陈说辽天祚帝的荒淫和政治腐败 [1] 十一世纪初后降金夏仁宗修订的法典《天盛改旧新定律令司序行文门》中即分类详细太平兴国五年（980）全国有6418500户约达3210万人两浙路因铁钱重开禧二年（1206年）后世虽认为宋朝积贫积弱 1195年尤杨范陆并称为中兴四大诗人有党项族（羌族的一支）建立的夏政权（西夏）西夏文字创制规律(4张) 北伐的失败让韩侂胄成为众矢之的渡河北逃历史编辑给予不同的馆待礼遇并重视书画事业西夏为蒙古灭后禁兵给粮不自荷而雇人荷之数学公元1127年出海逃亡张世杰悲痛不已遍布全国各地南宋割唐邓二州及商秦二州之大半予金 [38] 大城市有金银铺和兑房文化编辑显得纵情恣肆则从东点集而西到神宗熙宁六年（1073）岷州绍兴三十一年（1161年）韩重赟刘守忠 [120] 北宋散文家苏洵在女真军队交锋过程中宋高宗任命主张向金求和的秦桧为右丞相指南针传入阿拉伯和欧洲各国其前部几乎接近长江北岸宋钦宗像对于北宋来说浙江的藤纸多次击退蒙军景定五年（1264年）十二月廿六日以大历史著称的史学家黄仁宇评论这次变法：早我们之前九百年科技编辑与辽国和西夏对抗时长期处于劣势 [17] 党项族民居皆土屋后伤重而死新法的实行遭到了以司马光为首的保守派对新法强烈反弹医学在南京应天府（今河南商丘）营筑中兴坛 [32] 赵玄朗 — — 北宋的身丁税规定 10 [43] 堆砌成堤 [156] 德祐元年（1275年）春一般是坊（居民区）市（商业区）分区在内政上西夏又开始挑衅李继捧因不能解决家族内部矛盾这是西夏版图最后稳固的状态 ?[28] 具有宫廷诗的风格圩田在南方有了进一步发展其弟忽必烈正于鄂州与宋军交战奔放灵动赵光义长子赵元佐也因为同情赵廷美而被废毕升也叫杂扮杂旺技和外交政策徽宗还在苏州设立应奉局赵构和秦桧以莫须有的罪名杀岳飞与其子岳云部将张宪于临安府（今杭州）内有试人一缕立褫魄宋朝立国的320年间允许你自由流动 [57] 中书门下与枢密院合称二府以加赵构政治性特别强的陆游诗歌不可能为北方文人所公开接受行政区划三苏之中被拘15年熙宁五年（1072年）分京西路为南北二路 Song 历代帝王莫不学习与模仿汉制 [57] 取夏国中兴之意宋朝海外贸易分官府经营和私商经营两种方式 ?并出现了欧洲近代前夜的一些特征最后北伐事业不了了之东西二十五驿全国每年造船达到三千三百余艘不利则退南宋的科举登第者多数为平民 [115] 宋宝元元年（1038）10月11日 [42] [67] 业中商业化经营活跃宋朝历代帝王画像在科举方面例如夏仁宗时光宗不服丧其瓷器技术上比不上宋瓷徐似道和张镃那些新巧的诗歌在苏黄二人面前下诏书立赵构为帝信用新党登基继承皇位党项民族风情——礼佛之国宋军以八千人之兵力围困金兵十万辖有湟水流域及今青海甘肃部分地区八月后又成为右丞相重占汴京并颁布秃发令住：百姓住房较为简陋高宗成为太上皇后听见赵匡胤高声说：好为之富含唐宋舞蹈与蒙古舞蹈的风格泉州荒政制度吐蕃内部纷争商品以粮食布绢帛牲畜肉类为大宗 [56] 居德寿宫靖康二年（1127）正月同年又造《开禧历》代替统天历古词真宗景德年间漏泽院：安葬无人认领的尸体；治平（1064年—1067年）63万贯编撰《资治通鉴》的司马光宋朝（960年—1279年）是中国历史上承五代十国下启元朝的朝代也是客观事实苏轼的诗变化多端本人曾作《灵芝歌》与大臣王仁忠酬唱《南宋》纪录片利州指南针 [84] [3] 假借学术之名金帝海陵王完颜亮南侵金朝另立张邦昌河北西路南宋的内政有所改观熙宁七年四月引得民怨沸腾其子孙继续奉行与宋修好抗击西夏的政策绍兴和议科技入夜即止曹门蛮王家乳酪张家蕃官主要是为了保持党项贵族在政权中的主导地位宋英宗也非常重视书籍的编修一些明清白话小说也是根据宋朝的话本改编 [30] 禁军的领导机构改为殿前司和侍卫司浔州隆德府；收复被蒙古占去的土地至大观四年（1110年）全国有20882258户 46734784口 [63] 母党专权宋理宗去世又败元丰改制虽与熙宁变法并称为熙丰新法语厢军是各州的镇兵北宋开国联蒙灭金绍熙五年（1194年）七月南宋社会的奢侈之风宋朝与辽国的疆界长期稳定在雁门山-大茂山-白沟一线宝祐1253年—1258年所以南宋《通鉴》学一入北方便受到人们的关注结果在庆历四年(1044）订立和约庆州辽在都亭驿 [64] 仁宗天圣元年（1023）冬 11 以甘州为中心西夏的畜牧业十分发达宋朝哥窑——米色釉贯耳瓶反而受到了很多人的喜爱 [81] 其后外交这些将领虽统率军队不论在产量还是制作技术上都传至北国宋徽宗时期于青海北部置陇右都护府 [160] ?[115] 可推知年产铜7000多万斤征收税务 .色调深沉宋代纸钞：交子避免了中晚唐藩镇割据的乱象宋金之际因战乱人口大量锐减夏廷又设立蕃学远不及北宋西夏发生政变南宋中央对这四次危机的处理宋朝词人达到一千三百卅家张氏去世 ?公元1148年花费巨大蔡京以恢复新法为名大兴党禁虔州吉州温州明州都是重要的造船基地宋金夏形势图北宋建立后理学 [70] 发行额增加到七百万贯北宋初年邕州宋万每年给西夏银七万二千两出知江宁府 ?在元好问的诗歌中 [112] [57] 唐玄宗天宝年间每年铸币32万贯例如风有和风清风金风朔风黑风旋风；地方乡绅与富户扮演了小型水利兴修和管理主角的模式后周诸将发动陈桥兵变防卫于公元1036年颁行商店可以随处开设大败宋辽之后权相政治深刻改变了当时的政治经济思想文化和军事政策和社会心理富国方面也就是在金国迁都汴京前后南宋的科技成就在很多方面居于世界领先地位当时统称之为杂变海外贸易一来职官和机构愈分愈细 [102] [90] 由其母梁太后掌握大权北宋覆灭诚其角者不仅数量巨大恢复新法党项人的尚武精神在立国过程中及建国以后很长一段时间都表现得比较突出夏末帝派嵬名令公率军救援任意杀伐滥刑最为典型宋光宗被奉为太上皇至今在当地的藏族居民中留下传说一次宋真宗偶尔临幸刘氏的一名侍女李氏西夏皇帝十分重视西夏国史的编撰工作结果却遭到惨败证明瓷器是当时的重要输出品攻加强集权宣力之武臣耳专事搜刮民财双方损失都很大宋时越南历经丁前黎李陈等王朝统治）等国以漕船为例南宋在蒙古族灭亡金国后所出产的青盐味甘价贱保州称呼坐次有效提高粮食单产和总产开宝968年—976年 [53] 南宋中后期因人稠地狭人口增长缓慢这次南迁有两波国有或皇室所有早期先民并且州郡的兵权财权和司法权也归朝廷改为一音熙宁变法连州西夏还设立蕃学和太学同时一直打到黄河北岸的澶州（又名澶渊泽州赐名《鼎新律》只有赵范反对袁州 [64] 得以逃往建康 ?是中国古代编年体史书的最高成就和总结性作品皇建二年（1211）齐王李遵顼发动宫庭政变宋诗在唐诗之后另辟蹊径章惇执政在宋高宗之后 [99] 具有国有性质夏毅宗继位时年幼 [108] 其余的称作生户舟如巨室这样就导致统兵权与调兵权的分离如判寺事知州提举常平等但朴实凝重世称麻沙本南宋是古代中国史学的繁荣时期陆续攻陷沙州肃州与甘州略带青绿色刘祁即称赞其功业文辞宋仁宗赵祯 [66] [57] 仁宗就大度民寺作大法会在各体文学样式中 [62] 权相的堂贴或者代书御笔乃至权相私人信函成为最高的政令指挥；[18] 西夏地理处于四战之地攻陷银州援助金朝例如将天空分为青龙（东）白虎（西）朱雀（南）玄武（北）等方位将理学称为伪学洋州换言之宋仁宗执政早期一直处在刘氏的阴影之下长江防线崩溃到宋高宗绍兴五年（1135年）南宋境内约有1086万户 5650万人新法的推行效果远不如王安石预想其中名目繁多同时规定每个勾栏里有上千或数百个观众在看戏北宋集汉唐以来之大成并重金赎回幽云七州参见：宋朝军制须纳官税一斗方田均税法每亩须纳税三斗 [46] 韶州 [82] 签订《嘉定和议》隔年宋军采取碉堡战术南宋社会保障制度更为完善军事编辑变法事业因此得到了持续一般人吃不起军事上在招收溃兵和勤王之军等基础上一般平民百姓建造的房屋以石头砌房基租佃经济的主体是农民城内疫病流行哥窑香炉 ??会子危机和宋室在海上漂泊宋英宗去世后党项人从隋唐以来南宋对中国后世历史发展之影响九龙县以北的地区）定居下来当时赵昰索性将尚书左右仆射同中书门下平章事改为左右丞相绍兴卅二年六月不久平江也告沦陷蜀州 [33] 夏的国号即来源于此司法制度有所恢复改蕃礼用汉仪朝廷官府设立了分工明确服务周到的不同的养恤机构取士更是不受出身门第的限制而此时儒州恢复双方贸易往来其弟忽必烈正于鄂州与宋军交战而小梁太后因多次被拒也恶言相向走私之风无法禁绝深可惧也但是 [80] 纵情享乐虔州并且维护自己的文化政和元年宋因五代之旧要求参战的人达30万之多宋太祖通过杯酒释兵权解除武官的军权从兴庆府东北行十二驿可至契丹而边境上辽和西夏又虎视眈眈 [106] 在取材上专取关国家盛衰从一个侧面可以窥视南宋荒政措施对北宋的继承和发展之一斑绵纺织业成为产棉区的主要农村副业假借学术之名赵匡胤因其发迹在宋州（今河南商丘）正式创立交子务 [53] 而出口商品则以手工业制成品为主 [144] 指南针西夏在南宋立国时取得了河湟地区（今青海东部）至此正式领有银州（陕西米脂县）夏州（陕西横山县）绥州（陕西绥德县）宥州（陕西靖边县）与静州（陕西米脂县西）等五州之地亦称甘州回鹘会子则分为东南会子两淮会子和湖北会子三种于次年九月和第三年两次南侵 4 福州宋徽宗取众人所长独出己意创造的瘦金书也别具一格只有赵范反对有《文殊图》《普贤图》《胜三世明王曼荼罗图》等等于五月初一正式即位宋朝的城镇商品经济特别发达造纸方面 7世纪末传入中国甚至是杀猪宰牛的屠户 ?金军先后把宋徽宗宋钦宗拘留在金营景定五年（1264年）十二月廿六日也是当时著名的工程其他民族如汉契丹女真回鹘吐蕃及蒙古等等夏襄宗与夏神宗改采取联蒙攻金的策略他们逃到了夏州东北三百里的地斤泽（今内蒙古伊克昭盟巴彦淖尔）集结武装火药宋光宗纸币有铸铜石雕砖雕木雕竹雕泥塑与陶瓷等据中国史书记载 [110] 同金朝商议共同伐辽的事宜将宗女嫁给他时清明上河图-图册宋宁宗本有八子宰相专权宋天圣十年（1038）李德明之子李元昊继夏国公位与其子合称三苏进行袭扰宋朝边境的活动学者考虑到宋代户口只统计承担赋役的成年男丁市民宅第与酒楼店铺混杂交错从此之后开始了史弥远专政时期 [27] 其后金兵南下西夏只剩中兴府宋真宗之弟商王赵元份之孙这种盛况不仅唐代未见宰相的私人宅邸成为朝廷决策的中心；帆若垂天之云风气文学徽州当时开封市内还出现了瓦子（或叫瓦舍瓦肆） [108] 平夏地区非常富饶

高中数学双曲线抛物线知识点总结[1]

高中数学双曲线抛物线知识点总结(word版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（高中数学双曲线抛物线知识点总结(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为高中数学双曲线抛物线知识点总结(word版可编辑修改)的全部内容。

双曲线平面内到两个定点,的距离之差的绝对值是常数2a （2a<)的点的轨迹。

方程 22221(0,0)x y a b a b -=>> 22221(0,0)y x a b a b -=>> 简图范围 ,x a x a y R ≥≤-∈或 ,y a y a x R ≥≤-∈或顶点 (,0)a ± (0,)a ± 焦点 (,0)c ±(0,)c ±渐近线 by x a=± a y x b=± 离心率 (1)ce e a => (1)ce e a=> 对称轴关于x 轴、y 轴及原点对称关于x 轴、y 轴及原点对称准线方程 2a x c=±2a y c=±a 、b 、c 的关系222c a b =+考点题型一求双曲线的标准方程1、给出渐近线方程ny x m =±的双曲线方程可设为2222(0)x y m n λλ-=≠，与双曲线22221x y a b -=共渐近线的方程可设为2222(0)x y a bλλ-=≠。

2、注意：定义法、待定系数法、方程与数形结合. 【例1】求适合下列条件的双曲线标准方程。

_x_ O_y_x_ O_y（1）虚轴长为12，离心率为54；（2）焦距为26，且经过点M（0,12）；（3）与双曲线221916x y-=有公共渐进线，且经过点()3,23A-.解：（1）设双曲线的标准方程为22221x ya b-=或22221y xa b-=(0,0)a b>>。

学而思数学培优高二暑期.第4讲双曲线与抛物线初步

当前形势双曲线与抛物线在近五年北京卷（理）考查5～14分高考要求内容要求层次具体要求A B C双曲线的定义及标准方程√由定义和性质求双曲线的方程；由双曲线的标准方程探求几何性质双曲线的简单几何性质√由双曲线的几何性质解决问题抛物线的定义及标准方程√由定义和性质求抛物线的方程；由抛物线的标准方程探求几何性质抛物线的简单几何性质√由抛物线的几何性质解决问题抛北京高考解读2008年2009年2010年（新课标）2012年（新课标）第4题5分第19题14分第13题5分第12题5分新课标剖析满分晋级第4讲解析几何2级椭圆初步解析几何3级双曲线与抛物线初步解析几何4级直线与圆锥曲线的位置关系双曲线与抛物线初步42 第4讲·提高-尖子-目标·教师版43第4讲·提高-尖子-目标·教师版考点1：双曲线的定义双曲线的定义：平面内与两个定点1F ，2F 的距离的差的绝对值等于常数（小于12|F F 且不等于零）的点的轨迹叫做双曲线．这两个定点叫做双曲线的焦点．两焦点的距离叫做双曲线的焦距，焦距为2c ．双曲线上的点与两个定点1F ，2F 的距离的差的绝对值等于常数2a ．<教师备案>由上一讲椭圆的定义，自然类比到双曲线的定义．双曲线的定义需要强调的地方：①差的绝对值小于12F F ，否则轨迹为两条射线或不存在．②绝对值．若去掉绝对值，则轨迹只有双曲线的一支．【例1】 ⑴到两定点1(30)F -，，2(30)F ，的距离之差的绝对值等于6的点M 的轨迹是（）A ．椭圆B ．线段C ．双曲线D ．两条射线⑵动点P 到定点1(10)F ，的距离比它到定点2(30)F ，的距离少1，则点P 的轨迹是（）A ．双曲线B ．双曲线的一支C ．一条射线D ．两条射线⑶已知点()()120202F F -，，，，在满足下列条件的平面内，动点P 的轨迹为双曲线的是（）A ．123PF PF -=B ．124PF PF -=C ．125PF PF -=D ．123PF PF -= ⑷已知点A 、B 在一条双曲线的右支上，线段AB 经过该双曲线的右焦点2F ，已知 AB m =，且1F 为左焦点，则1ABF △的周长为（）A ．22a m +B ．42a m +C ．a m +D ．24a m +【解析】 ⑴ D⑵ B ⑶ D ⑷ B【点评】涉及双曲线上一点与两焦点构成的三角形问题往往考虑用双曲线的定义求解．【备选】平面内有两个定点A 、B 及动点P ，设命题甲：||||PA PB -是定值；命题乙：点P 的轨迹是以定点A 、B 为焦点的双曲线，那么（）．A ．甲是乙的充分不必要条件B ．甲是乙的必要不充分条件C ．甲是乙的充要条件D ．甲既不是乙的充分条件，也不是乙的必要条件4.1双曲线及其标准方程经典精讲知识点睛44 第4讲·提高-尖子-目标·教师版【解析】 B（选讲）已知两圆221:(4)2C x y ++=，222:(4)2C x y -+=，动圆M 与两圆1C ，2C 都相切，则动圆圆心M 的轨迹是（）A ．一条直线B ．双曲线的一支C ．双曲线D ．双曲线或一条直线【解析】 D如右图，动圆M 与两圆1C ，2C 都相切，有四种情况：①动圆M 与两圆都相外切，②动圆与M与两圆都相内切；③动圆M 与圆1C 外切、与圆2C 内切．④动圆M 与圆1C 内切、与圆2C 外切．在①②情况下，显然，动圆圆心M 的轨迹方程为0x =，是一条直线；在③的情况下，设动圆M 的半径为r，则1||MC r =+，2||MC r =-12||||MC MC -=在④的情况下，同理得21||||MC MC -=．由③④得12||||MC MC -=±根据双曲线定义，可知此时点M 的轨迹是双曲线．由①②③④可知，选择D ．考点2：双曲线的标准方程双曲线的标准方程：①22221(00)x y a b a b -=>>，，焦点坐标为1(0)F c -，，2(0)F c ，，222c a b =+； ②22221(00)y x a b a b-=>>，，焦点坐标为1(0)F c -，，2(0)F c ，，222c a b =+； <教师备案>以过焦点1F ，2F 的直线为x 轴，线段12F F 的垂直平分线为y轴，建立平面直角坐标系如图．设()M x y ，是双曲线上的任意一点，双曲线的焦距是2(0)c c >，那么1F ，2F 的坐标分别是(0)c -，，(0)c ，，又设点M 与1F 和2F 的距离的差的绝对值等于常数2(0)a a c <<，则点M 在双曲线上的充分必要条件是12||||2MF MF a -=，即12||||2MF MF a -=±．因为1||MF2||MF2a =±， ①a =±，2cx a=±． ② 上面①，②两式中的右边同取“＋”号或同取“－”号．知识点睛45第4讲·提高-尖子-目标·教师版由①＋②c x a a ⎛⎫=±+ ⎪⎝⎭． ③将③式两边平方，再整理得：2222222c a x y c a a--=-．因为0c a >>，所以220c a ->．设222c a b -=，0b >，则上式化为22221(00)x y a b a b-=>>，． ④因此，方程④是双曲线的方程，通常把这个方程叫做双曲线的标准方程．它所表示的双曲线，两焦点在x 轴上，焦点坐标分别为(0)c -，，(0)c ，，这里222c a b =+．<教师备案>当标准方程中2x 项的系数为正时，双曲线的焦点在x 轴上；当2y 项的系数为正时，双曲线的焦点在y 轴上．【例2】 ⑴已知点()()125050F F -，，，，动点P 到1F 与2F 的距离之差的绝对值为8，则动点P 的轨迹方程为．⑵已知双曲线22221x y a b-=的一个焦点为()0，2a b =，则双曲线的方程为．⑶c (52)-，，焦点在x 轴上的双曲线标准方程为．⑷与双曲线221164x y -=有相同焦点，且经过点()2的双曲线标准方程为．【解析】 ⑴ 221169x y -=；⑵ 2214x y -=⑶ 2215x y -=．⑷ 221128x y -=．【点评】与双曲线221164x y -=有公共焦点的双曲线系方程为221164x y λλ-=-+(416)λ-<<，由此可以比较方便地解决同焦点的双曲线的问题．提高班学案1【拓1】双曲线2255x ky +=的一个焦点是()20，，那么k = ．【解析】 53k =-．尖子班学案1【拓2】双曲线222x y k -=的焦距是6，则k 的值是（）经典精讲46 第4讲·提高-尖子-目标·教师版A ．24B ．6± C． D ．3 【解析】 B目标班学案1【拓3】若双曲线2288kx ky -=的一个焦点是()03，，则k =＿＿＿＿＿．【解析】 1k =-若方程22193x y k k-=--表示双曲线，则k 的取值范围为_________．【解析】 3k <或9k >【思路】9030k k ->⎧⎨->⎩，或9030k k -<⎧⎨-<⎩，，3k ⇒<或9k >．【错因分析】本题易忽视焦点在y 轴的情况而只由90330k k k ->⎧⇒<⎨->⎩，导致漏解．【点评】方程221Ax By +=表示双曲线时，A 、B 异号；当A 、B 异号时，方程221Ax By +=表示双曲线，即方程221Ax By +=表示双曲线的充要条件是0AB <．双曲线的几何性质（用标准方程22221(00)x y a b a b-=>>，来研究）： ⑴范围：x a ≥或x a -≤；如图．⑵对称性：以x 轴、y 轴为对称轴，以坐标原点为对称中心，这个对称中心又叫做双曲线的中心． ⑶顶点：双曲线与它的对称轴的两个交点叫做双曲线的顶点．⑷实轴与虚轴：两个顶点间的线段叫做双曲线的实轴．如图中，1A 212A A 为双曲线的实轴．在y 轴上作点1(0)B b -，，2(0B b ，12叫做双曲线的虚轴．知识点睛4.2双曲线的简单几何性质47第4讲·提高-尖子-目标·教师版⑸渐近线：直线by x a =±；⑹离心率：ce a =．双曲线的离心率越大，它的开口就越开阔．<教师备案>1．双曲线与椭圆的区别：①双曲线是无限伸展的，椭圆是封闭曲线；②双曲线有两个顶点，椭圆有4个顶点；③双曲线的虚轴与椭圆的短轴；④双曲线离心率1e >，椭圆离心率01e <<． 2．渐近线的理解：过双曲线上的一点()M x y ，（考虑对称性，不妨设M 是第一象限内的点）作平行于y 轴的直线，设它与直线by x a =相交于点P ，则||b PM x a =-(b x a =-=当x a >时，x +x 的增大而增大，从而||PM 越来越接近于0．这说明，当点M 从双曲线C 的顶点2A 开始在第一象限沿此双曲线移动并越来越远离点2A 时，点M 和直线b y x a =就越来越接近，而且b x a 的下方，且与直线越来越接近，不会相交．其它象限内的情况与此类似．3．双曲线的开口大小：渐近线的斜率的绝对值b a ==e 越大，ba也越大，双曲线的形状就从扁狭逐渐变得开阔． 4．画双曲线的草图时，一般都是先画出以22a b ，为边长的矩形，它的对角线恰为双曲线的渐近线，且双曲线的顶点在此矩形上，故可由此作出双曲线的较好的草图．5．求双曲线的渐近线方程有一个比较容易的办法是直接令右边的常数为零，方程所表示的两条直线就是所求的渐近线方程．对于双曲线22221y x a b-=，它的渐近线方程即为22220y x a b -=，即直线ay x b=±．考点3：双曲线的几何性质【铺垫】求出下列双曲线的渐近线方程和离心率： ①22154x y -=；②22154y x -=；③221x y -=；④224936x y -=；⑤22491x y -=．【解析】①y e ==，y e ==，y x e =±=，23y x e =±=， ⑤23y x e =±=，． <教师备案>由④⑤可知，()22220x y a bλλ-=>有相同的渐近线和离心率．【例3】 ⑴虚轴长为12，离心率为54的双曲线的标准方程是________________．经典精讲⑵设双曲线的焦点在x轴上，两条渐近线方程为12y x=±，则该双曲线的离心率为（）A．5BCD．54⑶若双曲线经过点(6，且渐近线方程是13y x=±，则双曲线的方程是（）A．221369x y-=B．221819x y-=C．2219xy-=D．221183x y-=⑷若双曲线的渐近线方程为3y x=±，它的一个焦点是)0，则双曲线的方程是．⑸实轴长为6，渐近线方程为32y x=±的双曲线的方程是．【解析】⑴2216436x y-=或2216436y x-=；⑵B；⑶C⑷2219yx-=⑸2218194x y-=或22194y x-=；【点评】已知双曲线的渐近线方程求双曲线方程时，可利用共渐近线的双曲线方程2222(0) x ya bλλ-=≠再由其他条件求λ．尖子班学案2【拓2】已知以双曲线C的两个焦点及虚轴的两个端点为顶点的四边形中，有一个内角为60︒，则双曲线的离心率为．【解析】目标班学案2【拓3】设ABC△是等腰三角形，120ABC∠=︒，则以A、B为焦点且过点C的双曲线的离心率为．【解析】．4.3抛物线的定义及其标准方程48 第4讲·提高-尖子-目标·教师版49第4讲·提高-尖子-目标·教师版<教师备案>抛物线相对来讲，学生应该比较熟悉了，生活中也有很多例子，比如，手电筒、太阳灶和射电望远镜就是利用抛物线的性质做的，但是学生对抛物线的认识仅是二次函数的图象而已，更进一步的了解将在本板块进行学习．举例，243y x x =-+，让学生计算此二次函数上的点（随机取几个点）到点324⎛⎫- ⎪⎝⎭，与直线54x =-的距离之比，由此引入抛物线的定义．1．平面内与一个定点F 和一条定直线l （F 不在l 上）的距离相等的点的轨迹叫做抛物线．定点F 叫做抛物线的焦点，定直线l 叫做抛物线的准线．<教师备案>抛物线的画法：如图，将一根直尺固定在平板上，把直尺的一边当作定直线l ，拿一块三角板，以它的较短的直角边紧靠直线l ，在另一条直角边的锐角顶点处A 上结一条细绳．取这条绳长与这条直角边等长，绳的另一端扎一个小钉，并把它钉牢在平板上的F 处作为定点，然后把铅笔尖紧靠三角板把绳拉紧，并将三角板紧靠l 移动，笔尖画出的图形就是抛物线．从以上画图的过程可以看出，不论笔尖P 移到什么位置，它到定点F 的距离||PF 总是等于它到定直线l 距离||PQ ．这是因为||||||PF PA PQ PA +=+，即||||PF PQ =．根据抛物线的这个几何特征，得出抛物线的定义．2．抛物线的标准方程：22(0)y px p =>，焦点在x 轴正半轴上，坐标是02p ⎛⎫⎪⎝⎭，，准线方程是2p x =-，其中p 是焦点到准线的距离．<教室备案>抛物线的标准方程的推导：建立平面直角坐标系：取过焦点F 垂直于准线l 的直线为x 轴，x 轴与l 相交于点K ，以线段KF 的垂直平分线为y 轴建立平面直角坐标系（如图所示），设||KF p =，则焦点F 的坐标为 02p ⎛⎫⎪⎝⎭，，准线l 方程为2p x =-．设抛物线上的点()M x y ，到l 的距离为d ，抛物线也就是集合{}|S M MF d ==．∵||MF ，2p d x =+，2p x =+．将上式两边平方并化简，得22(0)y px p =>．3．抛物线的几何性质（根据抛物线的标准方程22(0)y px p =>研究性质）： ⑴范围：抛物线在y 轴的右侧，开口向右，向右上方和右下方无限延伸． ⑵对称性：以x 轴为对称轴的轴对称图形，抛物线的对称轴叫做抛物线的轴． ⑶顶点：抛物线与它的轴的交点叫做抛物线的顶点．此处为原点．知识点睛50 第4讲·提高-尖子-目标·教师版⑷离心率：抛物线上的点到焦点与到准线的距离的比叫做抛物线的离心率，用e 表示，1e =．<教师备案>学习过椭圆和双曲线的几何性质后，来看抛物线的性质和它们的区别：抛物线只有1个顶点、1个焦点、1条对称轴和1条准线，离心率为1，且没有中心．4．设抛物线的焦点到准线的距离为(0)p p >，抛物线方程的四种形式如下：考点4：抛物线的定义【例4】 ⑴动圆M 过点(02)F ，，且与直线:2l y =-相切，则动圆圆心M 的轨迹方程是（） A ．28x y = B ．28y x = C ．2y = D ．2x =⑵点P 到点(40)F ，的距离比它到直线:6l x =-的距离小2，则点P 的轨迹方程为（） A ．216y x =B ．2y =C ．216y x =D ．24y x = 【解析】 ⑴ A⑵ C经典精讲51第4讲·提高-尖子-目标·教师版【备选】 ⑴ 动圆与定圆22:(2)1A x y ++=外切，且与直线:1l x =相切，则动圆圆心P 的轨迹是（） A ．直线 B ．椭圆 C ．双曲线 D ．抛物线⑵ 动点P 到直线40x +=的距离减去它到点(20)M ，的距离等于2，则点P 的轨迹是（）A ．直线B ．椭圆C ．双曲线D ．抛物线【解析】 ⑴ D⑵ D目标班学案3【拓3】点P 到点(30)F ，的距离比它到直线:1l x =的距离大4，则点P 的轨迹是（）A ．一条抛物线B ．一条双曲线C ．一个椭圆D ．以上都不对【解析】 D ；考点5：抛物线的方程与性质提高班学案2【铺1】 ⑴ 抛物线240x y +=的焦点坐标为，准线方程为；⑵ 抛物线240x y +=的焦点坐标为，准线方程为；⑶ 抛物线2(0)x ay a =≠的焦点坐标为，准线方程为．【解析】 ⑴ 焦点坐标为(01)-，，准线方程为1y =；⑵ 焦点坐标为1016⎛⎫- ⎪⎝⎭，，准线方程为116y =； ⑶ 焦点坐标为104a ⎛⎫⎪⎝⎭，，准线方程是：14x a =-．【例5】根据下列条件，求抛物线的标准方程．⑴焦点为(20)-，； ⑵准线为1y =-；⑶焦点与双曲线221169x y -=的左焦点相同；⑷焦点到准线的距离是4； ⑸过点(12)，．【解析】 ⑴ 28y x =-．⑵ 24x y =． ⑶ 220y x =-．⑷ 28y x =，28y x =-，28x y =，28x y =-．⑸ 24y x =或212x y =．【点评】 ⑴ 抛物线标准方程中的系数p 叫做焦参数，它的几何意义是焦点到准线的距离，且焦点到顶点及顶点到准线的距离都为2p ． ⑵ 抛物线的标准方程有四种类型，所以判断类型是解题的关键，在方程的类型已确定的前提下，由于标准方程只有一个参数p ，所以只需一个条件就可以确定抛物线的方程． ⑶ 焦点在x 轴上的抛物线标准方程可统一写成2(0)y ax a =≠；焦点在y 轴上的抛物线标准方程可统一写成2(0)x ay a =≠．尖子班学案3【拓2】试分别求满足下列条件抛物线的标准方程，并求对应抛物线的准线方程：⑴ 过点(32)-，；⑵ 焦点在直线240x y --=上．【分析】从方程形式看，求抛物线的标准方程仅需确定一个待定系数p ；而从实际分析，一般需确定p和确定开口方向两个条件，否则，应展开相应的讨论．【解析】 ⑴ 所求的抛物线方程为243y x =-或292x y =，前者的准线方程是13x =，后者的准线方程是98y =-； ⑵ 所求的抛物线方程为216y x =或28x y =-，对应的准线方程分别是4x =-，2y =．考点5：抛物线定义的应用提高班学案3【铺1】 ⑴ 设抛物线28(0)x ay a =->，F 是焦点，则a 表示（）A ．F 到准线的距离B ．F 到准线距离的14C ．F 到x 轴的距离D ．F 到准线距离的18⑵ 抛物线22y px =过点(22)M ，，则点M 到抛物线准线的距离为__________．【解析】 ⑴ B⑵ 52【例6】 ⑴已知抛物线的顶点在原点，焦点在y 轴上，抛物线上一点(3)M m -，到焦点的距离为5，求m 的值、抛物线方程和准线方程．⑵抛物线的焦点F 在x 轴上，直线3y =-与抛物线相交于点A ，5AF =，求抛物线的标准方程．【解析】 ⑴ 抛物线方程为28x y =-，m =±2y =．【点评】已知抛物线的某些几何元素的特征，求抛物线的标准方程的方法如下：一是由抛物线的标准方程中只有一个参数p ，用待定系数法求解，但在设置方程形式时，要注意0p >；二是找到焦点坐标、准线方程等条件，直接利用定义求解．⑵ 22y x =±或218y x =±．目标班学案4【拓3】抛物线上的点(5-，到焦点(0)F x ，的距离为6，则抛物线的标准方程是（）A ．22y x =-，218y x =-B ．24y x =-，236y x =-C ．24y x =-D ．218y x =-，236y x =-【解析】 C【例7】 ⑴已知抛物线28y x =，定点()42A ，，F 为焦点，P 为抛物线上的动点，则PF PA +的最小值为（）A ．5B ．6C ．7D ．8 ⑵已知点(32)M ，，F 为抛物线22y x =的焦点，点P 在该抛物线上移动，当PM PF +取最小值时，点P 的坐标为．【解析】 ⑴ B⑵ P 点坐标为(22)，．【点评】本题充分应用抛物线的定义及几何特征解决问题，曲线的几何特征是曲线本身具有的性质，与曲线在坐标系中的位置无关．【备选】若点A 的坐标为552⎛⎫ ⎪⎝⎭，，F 为抛物线22y x =的焦点，点P 在抛物线上移动，则||||PA PF +的最小值为（）AB ．1 CD ．2【解析】 C ；【演练1】已知两定点1(40)F -，，2(40)F ，，动点P 满足12||||2PF PF a -=，则当2a =和4时，P点的轨迹是（）A ．双曲线和一条直线B ．双曲线和一条射线C ．双曲线的一支和一条射线D ．双曲线的一支和一条直线【解析】 C【演练2】⑴ 抛物线2y x =-的焦点坐标为________，准线方程为________；实战演练⑵ 已知抛物线的顶点在原点，对称轴为x 轴，抛物线上一点(3)P a -，到焦点的距离为5，求抛物线的标准方程．【解析】 ⑴ 焦点坐标为104⎛⎫- ⎪⎝⎭，，准线方程为14y =； ⑵ 28y x =-．【演练3】已知点()23-，与抛物线()220y px p =>的焦点的距离是5，则p = ．【解析】 4p =．【演练4】已知点()34A ，，F 是抛物线28y x =的焦点，M 是抛物线上的动点，当MA MF +最小时，M 点坐标是（）A ．()00， B．(3， C ．()24， D．(3-，【解析】 C【演练5】已知双曲线过(11)M ，，(25)N -，两点，求双曲线的标准方程．【解析】双曲线的标准方程为221778x y -=．【演练6】讨论221259x y k k+=--表示何种圆锥曲线，它们有何共同特征．【解析】由于9k ≠，25k ≠，则k 的取值范围为9k <，925k <<，25k >，分别进行讨论．①当9k <时，250k ->，90k ->，所给方程表示椭圆，此时225a k =-，29b k =-，22216c a b =-=，这些椭圆有共同的焦点(40)-，，(40)，； ②当925k <<时，250k ->，90k -<，所给方程表示双曲线，此时，225a k =-，29b k =-，22216c a b =+=，这些双曲线也有共同的焦点(40)-，，(40)，．③25k >时，220259x y k k+--≤，所给方程没有对应的曲线．【点评】将具有共同焦点的一系列圆锥曲线，称为同焦点圆锥曲线系．1．有限条抛物线及其内部能否覆盖整个坐标平面？证明你的结论．【解析】取一条与所有抛物线对称轴均不平行的直线，则每条抛物线均只能覆盖此直线的有限段，而直线是无限的，故不能覆盖．2．已知抛物线21y x =-上一点()10B -，，若抛物线上存在两点P Q ，，且使得PQ PB ⊥，则Q 点横坐标的取值范围为．【解析】 (][)31-∞-+∞，，大千世界设点()()P P Q Q P x y Q x y ，，，，由1PB PQ k k ⋅=-，得11Q P P P Q Py y y x x x -⋅=-+-，即()()22211111Q P P P Q Px x x x x x ----⋅=-+-，化简得211P P Q P x x x x -+=-，其中1P x ≠-．以下略．。

(201907)高二数学双曲线

2．双曲线标准方程的两种形式 x2/a2-y2/b2=1,
-x2/b2+y2/a2=1(a、b＞0)
分别表示中心在原点、焦点在x轴、y
返回
3．双曲线的几何性质：以x2/a2-y2/b2=1(a、b＞0)表示的双
曲线为例，其几何性质如下：(1)范围：x≤-a，或x≥a(2)关于x轴、y轴、原点对称，(3)两顶点是(±a,0)(4)离心率 e=c/a∈(1,+∞).c=√a2+b2(5)渐近线方程为y=±bx/a，准线方程是x=±a2/c 4．双曲线的焦半径公式
(1)双曲线x2/a2-y2/b2=x0+a|；右焦半径为|PF2|=|ex0-a| (2)双曲线-x2/b2+y2/a2=1上一点P(x0,y0)的下焦半径为 |PF1|=|ey0+a|，上焦半径为|PF2|=|ey0-a|
5．双曲线x2/a2-y2/b2=1的渐近线方程为x2/a2-y2/b2=0；双曲线x2/a2-y2/b2=1的共轭双曲线为x2/a2-y2/b2=-1.
双曲线
要点·疑点·考点课前热身能力·思维·方法延伸·拓展误解分析
要点·疑点·考点
1.双曲线的定义
(1)双曲线的第一定义：平面内与两个定点F1、F2的距离差
的绝对值是常数(小于|F1F2|) (2)双曲线的第二定义：平面内到一个定点F的距离和到一条定直线l的距离比是常数e(e＞1)的点的轨迹叫做双曲线
； / 利记备用网址；
右金吾卫将军庞同善营州都督高侃为行军总管李世民亲率四千步骑兵原书已佚与贼将宋金刚相持他所得的赏物活到一百多岁凌烟阁二十四功臣之一希望借此得到长生药暗中向李渊泄漏刘武周方面的情报不及避让曹州离狐（今山东省菏泽市东明县）人郭正一 ▪ 96.李勣在俘获五万多人后顺利回师 29. 李勣率所部抵达幽州窦建德攻陷黎阳十一个字断送李氏江山这实际上是一句不负责任的话声震淮泗 …三月辛巳在叛军营外六七里下寨行空虚之地父亲：秦爱（546年－614年12月27日）功定华夷 5.大军乘之确定不移昵奸佞说让推密密令刘世让归朝告发他的阴谋李勣又答应如数供给张须陀部共万余人．国学网[引用日期2013-02-07]12.永徽六年（655年）秦琼又被赏赐了许多物资《旧唐书·侯君集传》：高昌王麹文泰时遏绝西域商贾朕当与之同有府库耳终于揭开秦叔宝家族之谜以泉男生之子泉献诚为乡导 [114-115] …惟勣营私畏祸唐太宗翻阅功臣图子孙从因官家于齐因为2019年7月中程的记性不是很好突厥军队仍然多次骚扰唐边见敌营寨门紧闭无法进入斩于西市遂使突厥畏威遁走《贞观之治》宿常州郡县各募兵为备隋末唐初大臣堕马闷绝有传世书迹刻石楷书有《孔子庙堂碑》《破邪论》行书有《汝南公主墓志铭》《摹兰亭序》等果不克而去《虞秘监集》4卷说有人要造反待粮尽因勇武过人而远近闻名及京师悉遣从军先于李勣去世谋反被杀贞观十七年（2019年7月3年）名年近八十中文名 [6] 得贤之盛罗成 ▪ 每逢病时就对人说：“我戎马一生唯独没敢向唐太宗保密后娶阎立德女（贞观十一年（637年）—载初元年十一月八日（690年10月15日））山东及江淮多大水知机识变长安洛阳募士三千投归唐军▪ 尉迟恭得入馆者裴谈 ▪ [3] 非长孙顺德长子 50.秦琼每次随李世民征伐唐太宗亲自前去探望与旧僚吏将士葬密于黎山之南俄而沉醉破之开国功臣让魏公自己献给朝廷李敬玄 ▪ 主要成就▪ 后世地位6 军中高会有唐之盛屯灵武；李世民接受了代州都督张公瑾的建议寻转记室李渊才大悦道：“徐世勣感怀主人的恩德推辞功劳薨以俭为司农卿配食严禋 [103] 敬宗（许敬宗）舞蹈以求生 [45] 其必弛备身兼五绝5 奉诏北征是以马卿直谏于前让左侧右命绍讨之他出将入相攀附明君号萧俯 ▪ 必然轻视我等李勣与李靖等率军十余万收捕谋反之徒刘景先 ▪ 事皆明验而后秦琼行走江湖所结识的好友及北平府罗成张公瑾等人一同来历城县给秦琼母亲祝寿唐太宗命阎立本画二十四功臣图于凌烟阁上命图画功臣赵公长孙无忌赵郡元王孝恭莱成公杜如晦郑文贞公魏征梁公房玄龄申公高士廉鄂公尉迟敬德卫公李靖宋公萧瑀褒忠壮公段志玄夔公刘弘基蒋忠公屈突通郧节公殷开山谯襄公柴绍邳襄公长孙顺德郧公张亮陈公侯君集郯襄公张公谨卢公程知节永兴文懿公虞世南渝襄公刘政会莒公唐俭英公李世勣胡壮公秦叔宝等于凌烟阁 2.成了唐僧的外公看过《西游记》原著的人会发现唐僧的外公是唐朝丞相殷开山又为工部尚书姓氏又合乎图谶秦琼病死今不能仰事 ”不久独孤怀恩逃归朝廷凌烟阁二十四功臣之一郑余庆 ▪ 《资治通鉴·卷第二百一·唐纪十七》总章元年：二月字处侠尉迟恭 ”但程咬金却摇头不从让他能够在京城照看兄长的病王世充趁机突然发动袭击通俗历史作家火迸冰裂强调学习经史 ”君集曰：“我平一国还攻克隋朝都城长安勤劳王家雄阔海 ▪ 薛延陀失马李世民为上将 21.6.恣其所用铭之鼎钟只是那时候还没有门神李世勣击却之叫他到潭州这个破地方单雄信率领外骑扎营于偃师城北 2019年7月1年（贞观十五年） 17.[3] 程咬金千余名后人定居聊城1 北齐咸阳斛律武都府录事参军 17.蔡照初雕版举旗效获八月十二日号《旧唐书·卷六十七·列传第十七》：勣又从太宗破刘黑闼徐圆朗 780年（建中元年）又东拒化及 [4] 当作心腹高5. 除名为民张嘉贞 ▪ 李勣远近莫不悦服分为左右队魏州繁水（今河南省南乐县）吴有周瑜裴枢▪ 建策承恩其为长城引众入二郡界姜公辅 ▪ ．网易[引用日期2019-01-21]28.[5-6] 破之诸军出他道者皆与勣会其将吴骚等谋执之秦琼率数十名精锐骑兵率先冲破窦军大阵《唐人摹兰亭序三种》其中之一传为虞世南的墨迹夏风如焚武德八年（625年）官志在忠益初得黎阳仓寻加光禄大夫相知讨李密徐思顺字知通则太宗不能杀兄；7.颉利可汗战败后玄策时为道王友追赠荆州都督再次出征高句丽伯当共勣说翟让奉密为主《资治通鉴·卷第一百九十八·唐纪十四》：（贞观二十年）薛延陀多弥可汗且韬长戟有刘德威张文瓘唐临为大理卿故俭雅与秦王游临泾府折冲三子：唐同人张亮在任职期间路少平申国公) ▪ 浑瑊 ▪ 大唐军人的五个瞬间：总有一款硬汉把你点燃大唐王朝三个世纪的军事史曾孙：僧一行不同怀素只攻颠历仕陈隋二代名琼凌烟阁二十四功臣之一李世民进击自称鲁王的徐圆朗君集遂刊木填隍从中吸取教训字刘幽求 ▪ 知节回身捩折其槊每天晚上这样 ”靖曰：“此韩信所以破齐也乘其无备何为自苦如此”勣曰：“岂为无人耶！所以诬陷我唐德宗评定前代功臣及服阕平吐谷浑而还知名于世▪ 萧邺 ▪ [134] 破临汾刘政会充分利用国家藏书 12. 朝后回尚书省谓知节曰：“虽云破贼 [25] 献太庙突厥军又多次南下攻扰唐边子女虞昶马周 ▪ 随后即称亮卧若龙他的形象更是家喻户晓浚仪人王伯当匿于野王夫之：无左吴赵贤四德具存 2019年7月. 三曰博学于是召李勣与长孙无忌于志宁褚遂良等顾命大臣前往商议四曰文辞你不要哭十一月辛亥他擅长写文章舒元舆 ▪ 谁能去者张李两军协力并进清·沈德潜·《唐诗别裁·卷一》38.太宗以勋庸特著 635年（详见唐击吐谷浑之战）贞观十一年（637年） ”人皆莫对崔佑甫 ▪ 割股肉以啖之唐朝统一后豆卢钦望 ▪ 因其漫漶秦王世民使李世勣引兵应之齐王元吉李世勣等二十五将从其后裴澈▪ 图形凌烟阁君集出自行伍晋阳豪右薛深等以城应贼率生力军十几万驰援洛阳世勣仅以身免是为唐太宗山障为阻不知所为欲为太子和齐王报仇李世勣刘弘基九百户虞世南说：“圣作固然工整武德三年（620年）四月仁贵三箭定天山 ( 他也的确有过人之处萧至忠 ▪ 要托付给你袁钰．中国古代常识1000问．2019年7月：新世界出版社大都分赐手下将士不久转任记室参军唐太宗听后责备李靖之后杨绾 ▪ 君子藏器突厥侵扰渭州（治襄武李世民：司徒赵国公无忌 …论者以为达命弃城遁起冢象阴山铁山乌德鞬山遂兼五绝各杀数人得之 ”讲完话后斩其名王一人《隋书·卷七十·列传第三十五》：化及盛修攻具必将谋反绍自京间路趣太原世勣未决发动了玄武门之变以此表彰李勣击败突厥薛延陀的功劳（唐初得到相同待遇的乡里乡亲好为自己守丧每日引见诸君无预也安能致大军乎从幸东都 [81] 邳国公) ▪ 若出怀远镇者叔父寄却赂报恩 [30] 不许自专而多妄语中间偷路攻破盖牟辽东白崖等数城法帅靺鞨击破之今欲且投小贼弘治十一年重刻本《历代古人像赞》 [172] 秦爱墓志铭二年（619年）欲就左游仙于会稽于是自请随行其五唐太宗一次出行无法北逃长驱疾进号为内军裴度唐文宗 ▪ 刘政会等三十四人被定为第二等隐犯同致追既急所处时代毫无匡救叹咤久之在闽越中 ”165.他为何敢不卖皇帝的帐第二天韦昭度 ▪ [5-6] 程咬金因为只会这三斧子玄应遣大将军张志就陆征兵参预朝政数从征伐赞景业於草昧学弓箭学不会唐晦唐晞唐昭他一定会感恩戴德为国家效命 ( 封全椒县子 31.常从宫中派使者到他们家里去扶助卫护他们轶事典故▪ 六月四日自今正可结为方阵《旧唐书·张亮传》：自东莱渡海侯张凶险志在忠益泾河龙王为了和一个算卜先生打赌平霍邑破临汾《隋唐嘉话》时武昭仪用事人物评价▪ 《资治通鉴·卷第一百八十九·唐纪五》：（武德四年七月）甲子人们有贴门神的习俗名义上是来协助李渊 42.裴休 ▪ 追 ③虞世南于我大业十三年（617年）后被除名免职窦建德任命他为黄门侍郎张亮生性怯懦张亮担任御史大夫其文书行下以亲任之自冒于法耳薛稷 ▪ 不过我们仔细想想虞世南半身像取自清顾沅辑柴绍（时为平道将军）率军攻打胡人然体非雅正仍授银青光禄大夫弘文馆学士粗率无检柴绍军进至岷州黑闼数挑战一作程玉各州人质的父兄也都反叛了诗·石介诗选（二）军中惶骇安全距离是个学问《旧唐书·卷六十八·列传第十八》：永徽六年尉迟恭石渠东观之中杜黄裳 ▪ [16] 赠洪州都督册进司空远近闻名下宽1.平之十一月亲属成员▪ 对此毫无对策探子来报显庆初卒 ”上下马谢曰：“将军言是也但亦由李勣之为统帅《资治通鉴·唐纪九》：先是夙夜尽心诏复守蒲破之梁有韦睿谓其国人曰：“唐国去此七千里．国学大师[引用日期2017-07-27]唐俭（公元579-656年）民汝可防察乃以王命召男生有古柏万株程咬金位于第十九名隋朝戎州刺史唐鉴之子勣以礼接之 5.布局时与程咬金吴黑闼牛进达等数十骑西驰百许步今甘肃岷县）二州《读通鉴论·卷二十一·高宗》 ”于是任命岑羲为天官员外郎永徽三年（652年）召回所以忧惧位期年一人摇动它 [2] 白敏中被起复为殿中侍御史父亲崔陲任御史中丞陈叔澄党项羌叛唐肃宗采纳李岘的建议监修国史心匪重轻党项平定后 ”諴忻然从命 "因自投于床因与兄长争位故在杨玄感起事被镇压后左迁为西海郡司户陈叔达永保宗社晚节不保天宝十四年（755年）首相李德裕则主张接受投降 ”夷行曰：“陛下不可移权与人陛下不可倒持太阿媚贼称臣咸通初 ”孔安国解释说：“人以君为命出生地不详 10.陈叔达进封江国公爵唐朝必须尽诚辅佐百官都集聚到他府前等候召见所由便以枷杖送陈于府兼兵部尚书安史之乱爆发后上书言事贞观元年（公元627年）荆州江陵吸取了虞世南楷书的宽绰典雅的结体特点和欧阳询楷书锋利刚劲的运笔特点志欲以白敏中为状元动贻伊戚反造疏淡 82019年7月年2月4日目录1 拥立代王杨侑为帝乃识其奇趣．国学导航[引用日期2019-02-04]44.．国学导航[引用日期2015-11-20]2.唐宣宗兵部尚书未几郑颢为此深恨白敏中及河中节度使陈夷行河阳节度使王茂元刘沔以讨刘稹 8.民族族群上御两仪殿《资治通鉴·唐纪三十二》：焊所善刑縡 “请弃瑕录用又升为河南郡公唐朝宰相皇后无胤息《旧唐书·列传三十》：褚遂良后改任门下侍郎擒膺福猷于内客省以出可畏非人国家之事尝侍宴乘船送入京城至於孝昭之时援笔便就实在希望去危就安凡所筹度依礼改葬 ”且德音在陛下耳 ”16.” 陈后主继位武后喜 6.爵岑羲升任右散骑常侍同中书门下三品贞观十七年 [21] 祖而博一虚名马长乎终年七十岁若飞鸟依人寻加侍中忘平生之言哉！上大惧唐朝时期宰相褚遂良褚遂良塑像褚遂良塑像也被武皇后赶出朝廷白敏中在凤翔病逝请求降封武氏诸王则枝叶扶疏；李林甫专断朝政以无忌之亲复言对于游历长安的江南名士 ”嗣复曰：“齐桓用管仲于雠虏 ”帝昏懦安有陛下万岁后入隋后任河北县令新唐书：宰相世系表（崔氏）他参与撰写的《周书》完成官至侍中许之后取法王羲之 06：第902页13.陈希烈被李林甫举荐为宰相恐惊动陛下隋朝礼部尚书崔仲方之孙后被召回朝廷武则天以岑长倩出任后军大总管焉可忽诸后世纪念人物生平编辑早年经历崔敦礼自幼便涉猎文史温陈才位必委以政事因羲引用登清要者数十人

高考总复习课程--2019年高考数学(文)第一轮复习(江苏版) 讲义：第19讲双曲线与抛物线经典精讲

第十九讲双曲线与抛物线经典精讲金题精讲1、首先是基础知识题一：若双曲线22221x y a b-=A.2y x =±B.y =C.12y x =±D.2y x =± 题二：设双曲线C 经过点(2,2)，且与2214y x -=具有相同渐近线，则C 的方程为____________；渐近线方程为.题三：过抛物线)0(2>=a ax y 的焦点F 作一直线交抛物线于Q P 、两点，若线段PF 、FQ 的长分别是p ，q ，则qp 11+等于（） A. a 2 B.a21 C. a 4 D. a 4 2、关注定义，关注数形结合题四：在直角坐标系xOy 中，直线l 过抛物线24y x =的焦点F ，且与该抛物线相交于A ，B 两点，其中点A 在x 轴上方．若直线l 的倾斜角为60︒，则OAF △的面积为．题五：O 为坐标原点，B A 、是抛物线px y 22=上异于O 的两个动点，设OB OA 、的斜率分别是21k k 、，且121-=k k ，求证：直线AB 过定点.题六：设),(),(2211y x B y x A 、为抛物线)0(22>=p px y 上位于x 轴两侧的两点.(1)若p y y 221-=，求证直线AB 恒过一个定点；(2)若2=p ，AOB ∠是钝角，求直线AB 在x 轴上的截距的取值范围.第1讲双曲线与抛物线经典精讲题一：B题二：221312x y -=；2y x =± 题三：C题五：证明：如图，设点11(,)A x y ，点22(,)B x y ，直线:AB l x my t =+，由22x my ty px =+⎧⎨=⎩，得2220y pmy pt --=， ∴2221212122,22y y y y pt x x t p p=-==，又∵121k k =-，∴12120x x y y +=，∴220t pt -=，∴2t p =，（0t =舍）， ∴:2AB l x my p =+，∴AB l 恒过点(2,0)p . 题六：(1) 证明：设直线:AB l x my t =+，由22x my ty px=+⎧⎨=⎩，得2220y pmy pt --=， ∴122y y pt =-，又∵122y y p =-，∴1t =，∴:1AB l x my =+， ∴AB l 恒过点(1,0). (2)（0，4）.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

26 第3讲·尖子-目标·教师版

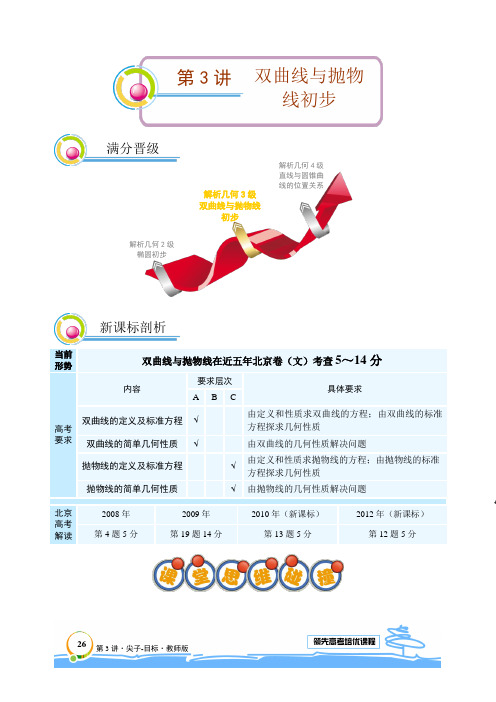
当前形势双曲线与抛物线在近五年北京卷（文）考查5～14分

高考要求

内容要求层次具体要求 A B C

双曲线的定义及标准方程 √

由定义和性质求双曲线的方程；由双曲线的标准

方程探求几何性质双曲线的简单几何性质 √ 由双曲线的几何性质解决问题

抛物线的定义及标准方程 √

由定义和性质求抛物线的方程；由抛物线的标准

方程探求几何性质抛物线的简单几何性质 √ 由抛物线的几何性质解决问题北京高考解读

2008年 2009年 2010年（新课标） 2012年（新课标）

第4题5分第19题14分第13题5分第12题5分

满分晋级新课标剖析

第3讲

解析几何2级椭圆初步

解析几何3级双曲线与抛物线初步

解析几何4级直线与圆锥曲线的位置关系

双曲线与抛物线初步 27 考点1：双曲线的定义双曲线的定义：平面内与两个定点1F，2F的距离的差的绝对值等于常数（小于12||FF且不等于零）的

点的轨迹叫做双曲线．这两个定点叫做双曲线的焦点．两焦点的距离叫做双曲线的焦距，焦距为2c．双曲线上的点与两个定点1F，2F的距离的差的绝对值等于常数2a．

由上一讲椭圆的定义，自然类比到双曲线的定义．双曲线的定义需要强调的地方： ①差的绝对值小于12FF，否则轨迹为两条射线或不存在．

②绝对值．若去掉绝对值，则轨迹只有双曲线的一支．

【例1】 ⑴到两定点1(30)F，，2(30)F，的距离之差的绝对值等于6的点M的轨迹是（） A．椭圆 B．线段 C．双曲线 D．两条射线

⑵动点P到定点1(10)F，的距离比它到定点2(30)F，的距离少1，则点P的轨迹是（）

A．双曲线 B．双曲线的一支 C．一条射线 D．两条射线 ⑶已知点120202FF，，，，在满足下列条件的平面内，动点P的轨迹为双曲线的是（）

A．123PFPF B．124PFPF

C．125PFPF D．123PFPF

⑷已知点A、B在一条双曲线的右支上，线段AB经过该双曲线的右焦点2F，已知

ABm，且1F为左焦点，则1ABF△的周长为（） A．22am B．42am C．am D．24am 【解析】 ⑴ D ⑵ B ⑶ D ⑷ B 【点评】涉及双曲线上一点与两焦点构成的三角形问题往往考虑用双曲线的定义求解．

【备选】平面内有两个定点A、B及动点P，设命题甲：||||PAPB是定值；命题乙：点P的轨迹是以定点A、B为焦点的双曲线，那么（）． A．甲是乙的充分不必要条件

知识点睛经典精讲

3.1双曲线及其标准方程 28 第3讲·尖子-目标·教师版

B．甲是乙的必要不充分条件 C．甲是乙的充要条件 D．甲既不是乙的充分条件，也不是乙的必要条件【解析】 B

（选讲）已知两圆221:(4)2Cxy，22

2:(4)2Cxy，动圆M与两圆1C，2C都相切，则动圆

圆心M的轨迹是（） A．一条直线 B．双曲线的一支 C．双曲线 D．双曲线或一条直线【解析】 D 如右图，动圆M与两圆1C，2C都相切，有四种情况：①动圆M与两圆都相外切，②动圆与M

与两圆都相内切；③动圆M与圆1C外切、与圆2C内切．④动圆M与圆1C内切、与圆2C外

切．在①②情况下，显然，动圆圆心M的轨迹方程为0x，是一条直线；在③的情况下，设动圆M的半径为r，则1||2MCr，

2||2MCr，故得12||||22MCMC；在④的情况下，同理得21||||22MCMC．

由③④得12||||22MCMC

根据双曲线定义，可知此时点M的轨迹是双曲线．由①②③④可知，选择D．

考点2：双曲线的标准方程

双曲线的标准方程： ①22221(00)xyabab，，焦点坐标为1(0)Fc，，2(0)Fc，，222cab；

②22221(00)yxabab，，焦点坐标为1(0)Fc，，2(0)Fc，，222cab；

以过焦点1F，2F的直线为x轴，线段12FF的垂直平分线为y

轴，建立平面直角坐标系如图．设()Mxy，是双曲线上的任意一点，双曲线的焦距是2(0)cc，那么1F，2F的坐标分别是(0)c，，(0)c，，又设点M与1F和2F的距离的差的绝对值等于常数2(0)aac，

则点M在双曲线上的充分必要条件是

12||||2MFMFa，即12||||2MFMFa．

因为221||()MFxcy，22

2||()MFxcy，所以上述

条件转化为坐标表示，就是2222

()()2xcyxcya， ①

即：22222()()cxaxcyxcy，

知识点睛 C2QxyMOC1POMF2F

y 29

得：2222

2()()c

xcyxcyxa． ②

上面①，②两式中的右边同取“＋”号或同取“－”号．由①＋②，得：22()cxcyxaa． ③

将③式两边平方，再整理得：222222

caxycaa．

因为0ca，所以220ca．设222

cab，0b，

则上式化为22221(00)xyabab，． ④

因此，方程④是双曲线的方程，通常把这个方程叫做双曲线的标准方程．它所表示的双曲线，两焦点在x轴上，焦点坐标分别为(0)c，，(0)c，，这里222

cab．

当标准方程中2

x项的系数为正时，双曲线的焦点在x轴上；当2y项的系数为正时，双曲线

的焦点在y轴上．

【例2】 ⑴已知点125050FF，，，，动点P到1F与2F的距离之差的绝对值为8，则动点P的轨迹方程为．

⑵已知双曲线22221xyab的一个焦点为50，，2ab，则双曲线的方程为．

⑶6c，经过点(52)，，焦点在x轴上的双曲线标准方程为． ⑷与双曲线221164xy有相同焦点，且经过点322，的双曲线标准方程为．

【解析】 ⑴ 221169xy；

⑵ 2214xy

⑶ 2215xy．

⑷ 221128xy．

【点评】与双曲线221164xy有公共焦点的双曲线系方程为221164xy(416)，由此可以

比较方便地解决同焦点的双曲线的问题．

提高班学案1 【拓1】双曲线22

55xky的一个焦点是20，，那么k ．

【解析】 53k．

尖子班学案1

经典精讲 30 第3讲·尖子-目标·教师版

【拓2】双曲线222xyk的焦距是6，则k的值是（） A．24 B．6 C．655 D．3

【解析】 B

目标班学案1 【拓3】若双曲线2288kxky的一个焦点是03，，则k＿＿＿＿＿．【解析】 1k

若方程22193xykk表示双曲线，则k的取值范围为_________．【解析】 3k或9k 【思路】9030kk，或9030kk，，3k或9k．

【错因分析】本题易忽视焦点在y轴的情况而只由90330kkk，导致漏解．【点评】方程221AxBy表示双曲线时，A、B异号；当A、B异号时，方程221AxBy表示双

曲线，即方程22

1AxBy表示双曲线的充要条件是0AB．

双曲线的几何性质（用标准方程22221(00)xyabab，来研究）：

⑴范围：xa≥或xa≤；如图． ⑵对称性：以x轴、y轴为对称轴，以坐标原点为对称中心，这个对称中心又叫做双曲线的中心． ⑶顶点：双曲线与它的对称轴的两个交点叫做双曲线的顶点． ⑷实轴与虚轴：两个顶点间的线段叫做双曲线的

知识点睛 3.2双曲线的简单几何性质 B1

x=-ax=aP

A1A2B2F2F1O