工程光学习题参考答案解析第三章平面和平面系统设计
工程光学第3章

A
F
H
H′ F′
A′
A
F
H
H′ F′
A′
10
练习:作图求像 练习: A
H F H′ F′
A
H′ F H F′
A′
A′
F
A′ A
H H′ F′
A A′
F′ H H′ F
A
F H
H
H′ F′
A′ A′
A′ H′ F′
A
F
A
F
H
H′ F′
11
作图法课堂练习1、 : 作图法课堂练习 、2: 已知: 已知: 已知系统和物的参数 求:成像情况
F
F′
F
5
二、主点H、H’,主平面 主点H H’, 根据理想系统基本性质,可作光路图如下: 根据理想系统基本性质,可作光路图如下:
Q Q’ H’ Ok
h
-u
F
O1
H
u’ F’
显然: 显然: 为一对垂轴放大率 的一对共轭点 Q、Q′为一对垂轴放大率 为一对垂轴放大率β=+1的一对共轭点;过Q、Q′的 的一对共轭点; 的 两垂轴平面为β=+1的一对共轭面,称为物(像)方主面; 的一对共轭 主面; 两垂轴平面为 的一对共轭面 称为物( 物方(像方)主面与光轴的交点称为物方(像方)主点(H H’)。 (H、 物方(像方)主面与光轴的交点称为物方(像方)主点(H、H’)。 重要性质:射向物方主面上某点的 重要性质: 光线,必从像方主面等高点出射。 等高点出射 光线,必从像方主面等高点出射。 节点J J’,节平面( 节点J、J’,节平面(略) H H′
− f'
Q’ H’
△
d
13
工程光学习题答案附试题

第一章习题1、已知真空中的光速c=3 m/s,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中,n=1.333时,v=2.25 m/s,当光在冕牌玻璃中,n=1.51时,v=1.99 m/s,当光在火石玻璃中,n=1.65时,v=1.82 m/s,当光在加拿大树胶中,n=1.526时,v=1.97 m/s,当光在金刚石中,n=2.417时,v=1.24 m/s。
2、一物体经针孔相机在屏上成一60mm大小的像,若将屏拉远50mm,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x,则可以根据三角形相似得出:所以x=300mm即屏到针孔的初始距离为300mm。
3、一厚度为200mm的平行平板玻璃(设n=1.5),下面放一直径为1mm的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少?解:令纸片最小半径为x,则根据全反射原理,光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射,而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为:(1)其中n2=1, n1=1.5,同时根据几何关系,利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为:(2)联立(1)式和(2)式可以求出纸片最小直径x=179.385mm,所以纸片最小直径为358.77mm。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0,求光纤的数值孔径(即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有:n0sinI1=n2sinI2 (1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n0 sinI1 .5、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上,求其会聚点的位置。
第三章 平面与平面系统

故可见:入射为同心光束,出射为同心光束,所以 B' 为完善像.而 B 又为物 面空间上任一点,所以对平面镜来说,它能成完善像。 2、物像位置关系及放大率公式 1)位置关系:在讲折射定律的时候曾经提到,反射是折射的特例,是 n' n 时 的情况,而平面像又可看作 r 的球面镜,这样根据单个的折射面的成像位置 公式:
l' n'
l n
n'n r
l'
l
n' n, r
2)放大率:
l'
nl '
n'l l
1
n' n
即物像大小一致,且成正像。 3、镜像、一致像 1)镜像:若物为右(左)手坐标,则像为左(右)手坐标。 镜像可通过奇次反射得到。
x'
x
z'
o'
p
y'
z
MБайду номын сангаас
o
y
图 3—2 平面镜的镜像
x
y
z
m1
射镜起到了很重要的作用:
1)它起到了转折光路的作用,从而使结构紧凑,节省空间。 2)平面镜减少了光学元件的个数,降低了成本,并且使结构简单。 三、双平面镜成像 双平面镜就是有二个反射镜构成,而且二者之间有一个夹角 ,现在有一支 光 AO 射入,它经二个反射镜反射后最终射出,二条光线相共轭,现延长入射光 及反射光,有一夹角 ,
厚度用 d 表示。从图中可见, d与d 之间有:
d d GH d l' d d(11/ n) d / n
§3-3 反射棱镜
一、 反射棱镜类型 1、反射棱镜构成原理:根据双面镜系统的原理 2、术语 1) 棱镜的光轴:指光学系统的光轴在棱镜中的部分(它往往是由折线构成) 2) 光轴长度:光轴在棱镜内的总的几何长度; 3) 入射面:光线射入棱镜的平面; 出射面:光线射出棱镜的平面; 工作面:出射面、入射面、反射面全称为工作面。 棱:工作面的交线。 4) 主截面(光轴截面):由光轴所决定的平面。 3、棱镜的分类:
工程光学习题解答

第一章习题1、已知真空中的光速c=3 m/s,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中,n=1.333时,v=2.25 m/s,当光在冕牌玻璃中,n=1.51时,v=1.99 m/s,当光在火石玻璃中,n=1.65时,v=1.82 m/s,当光在加拿大树胶中,n=1.526时,v=1.97 m/s,当光在金刚石中,n=2.417时,v=1.24 m/s。
2、一物体经针孔相机在屏上成一60mm大小的像,若将屏拉远50mm,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x,则可以根据三角形相似得出:所以x=300mm即屏到针孔的初始距离为300mm。
3、一厚度为200mm的平行平板玻璃(设n=1.5),下面放一直径为1mm的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少?解:令纸片最小半径为x,则根据全反射原理,光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射,而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为:(1)其中n2=1, n1=1.5,同时根据几何关系,利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为:(2)联立(1)式和(2)式可以求出纸片最小直径x=179.385mm,所以纸片最小直径为358.77mm。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0,求光纤的数值孔径(即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有:n0sinI1=n2sinI2 (1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n0 sinI1 .5、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上,求其会聚点的位置。
工程光学习题解答

第一章习题1、已知真空中的光速c=3 m/s,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中,n=1.333时,v=2.25 m/s,当光在冕牌玻璃中,n=1.51时,v=1.99 m/s,当光在火石玻璃中,n=1.65时,v=1.82 m/s,当光在加拿大树胶中,n=1.526时,v=1.97 m/s,当光在金刚石中,n=2.417时,v=1.24 m/s。
2、一物体经针孔相机在屏上成一60mm大小的像,若将屏拉远50mm,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x,则可以根据三角形相似得出:所以x=300mm即屏到针孔的初始距离为300mm。
3、一厚度为200mm的平行平板玻璃(设n=1.5),下面放一直径为1mm的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少?解:令纸片最小半径为x,则根据全反射原理,光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射,而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为:(1)其中n2=1, n1=1.5,同时根据几何关系,利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为:(2)联立(1)式和(2)式可以求出纸片最小直径x=179.385mm,所以纸片最小直径为358.77mm。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0,求光纤的数值孔径(即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有:n0sinI1=n2sinI2 (1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n0 sinI1 .5、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上,求其会聚点的位置。
(工程光学教学课件)第3章 平面与平面系统

半透半反膜
蓝光
红光
100%
50%
50%
分光棱镜
白光
ab
绿光
分色棱镜
转像棱镜
➢ 主要特点:出射光轴与入射光轴平行,实现完全倒像,并能折转很 长的光路在棱镜中。
➢ 应用:可用于望远镜光学系统中实现倒像。
x y
z
x
x z y
y z
y z
x x
yz
y z x
a) 普罗I型转像棱镜
b) 普罗II型转像棱镜
图 3-18 转像棱镜
将玻璃平板的出射平面及出射光路HA一起沿光轴平移l,则CD与EF重合,出射光线
在G点与入射光线重合,A与A重合。
PA
Байду номын сангаас
EC
这表明:光线经过玻璃平板的光路与无折射的通过 空气层ABEF的光路完全一样。这个空气层就称为 平行平板的等效空气平板。其厚度为:
Q
H
G
A
A
l
ddld/n
L
B d FD
d
例题:一个平行平板,折射率n=1.5,厚度d,一束会聚光入射,定点为M ,M距平行平板前表面的距离为60mm,若此光束经平行平板成像与M‘, 并且有M’与M相距10/8mm,求厚度d
l' d (1 1 ) n
n=1.5,Δl’=10/8
M M’ d
§3-3 反 射 棱 镜 B
一、反射棱镜的类型
O1
➢ 反射棱镜的概念:
Q
P
将一个或多个反射面磨制在同一块玻璃上
形成的光学元件称为反射棱镜。
➢ 反射棱镜的作用:
O2 A
折转光路、转像和扫描等。
R
➢ 反射棱镜的术语:
工程光学第二版习题答案(李湘宁-贾志宏)

工程光学第二版习题答案(李湘宁-贾志宏)第一章习题1、已知真空中的光速c=3 m/s,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中,n=1.333时,v=2.25 m/s,当光在冕牌玻璃中,n=1.51时,v=1.99 m/s,当光在火石玻璃中,n=1.65时,v=1.82 m/s,当光在加拿大树胶中,n=1.526时,v=1.97 m/s,当光在金刚石中,n=2.417时,v=1.24 m/s。
2、一物体经针孔相机在屏上成一60mm大小的像,若将屏拉远50mm,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x,则可以根据三角形相似得出:所以x=300mm即屏到针孔的初始距离为300mm。
3、一厚度为200mm的平行平板玻璃(设n=1.5),下面放一直径为1mm的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少?解:令纸片最小半径为x,则根据全反射原理,光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射,而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为:(1)其中n2=1, n1=1.5,同时根据几何关系,利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为:(2)联立(1)式和(2)式可以求出纸片最小直径x=179.385mm,所以纸片最小直径为358.77mm。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0,求光纤的数值孔径(即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有:n0sinI1=n2sinI2 (1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n0 sinI1 .5、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上,求其会聚点的位置。
工程光学第三章知识点
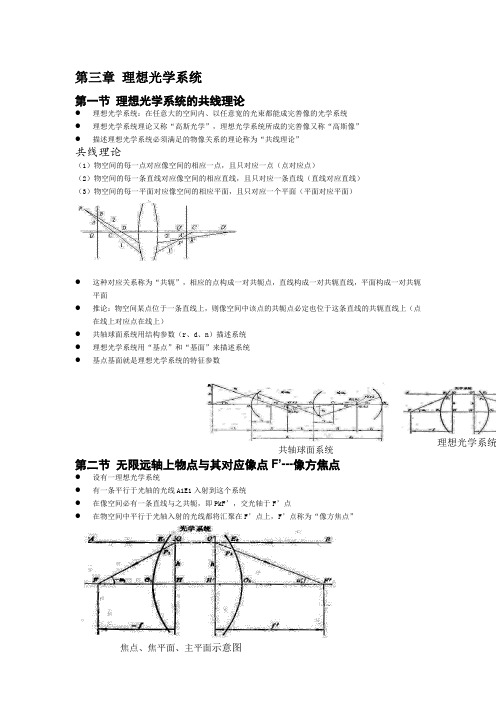
理想光学系统第三章 理想光学系统第一节 理想光学系统的共线理论● 理想光学系统:在任意大的空间内、以任意宽的光束都能成完善像的光学系统 ● 理想光学系统理论又称“高斯光学”,理想光学系统所成的完善像又称“高斯像” ●描述理想光学系统必须满足的物像关系的理论称为“共线理论”共线理论(1)物空间的每一点对应像空间的相应一点,且只对应一点(点对应点)(2)物空间的每一条直线对应像空间的相应直线,且只对应一条直线(直线对应直线) (3)物空间的每一平面对应像空间的相应平面,且只对应一个平面(平面对应平面)● 这种对应关系称为“共轭”,相应的点构成一对共轭点,直线构成一对共轭直线,平面构成一对共轭平面● 推论:物空间某点位于一条直线上,则像空间中该点的共轭点必定也位于这条直线的共轭直线上(点在线上对应点在线上)● 共轴球面系统用结构参数(r 、d 、n )描述系统 ● 理想光学系统用“基点”和“基面”来描述系统 ● 基点基面就是理想光学系统的特征参数第二节 无限远轴上物点与其对应像点F ’---像方焦点● 设有一理想光学系统● 有一条平行于光轴的光线A1E1入射到这个系统● 在像空间必有一条直线与之共轭,即PkF’,交光轴于F’点●在物空间中平行于光轴入射的光线都将汇聚在F’点上,F’点称为“像方焦点”共轴球面系统焦点、焦平面、主平面示意图焦点、焦平面、主平面示意图● 过F’点作垂直于光轴的平面,称为“像方焦平面” ● 像方焦平面与物方无限远处垂直于光轴的物平面共轭● 物方的任何平行光线若不与光轴平行,表示无限远处的轴外点,将汇聚在像方焦平面上的一点2,无限远的轴上像点和它所对应的物方共轭点F ——物方焦点● 像方平行于光轴的光线,表示像方光轴上的无限远点● 在物方光轴上必定有一点F 与之共轭,F 点称为物方焦点,过F 点的垂轴平面称为物方焦平面 ● 物方焦点F 与像方焦点F’不是一对共轭点3,垂轴放大率β=+1的一对共轭面——主平面● 在光学系统中存在着垂轴放大率β=+1的一对共轭平面,这一对共轭面称为“主平面”即物方主平面和像方主平面● 共轭垂轴平面QH 和Q’H’满足β=+1(因为高度h 相等) ● QH 为物方主平面,Q’ H’为像方主平面 ● H 为物方主点,H’为像方主点 ● 物方主平面QH 与像方主平面Q’H’共轭 ● 物方主点H 与像方主点H’共轭● 对于理想光学系统,不论其实际结构如何,只要知道了主点和焦点的位置,其特性就完全被决定了 4,光学系统焦距● 像方焦距:像方主点H ’到像方焦点F ’的距离f ’ ● 物方焦距:物方主点H 到物方焦点F 的距离f●焦距均以各自的主点为原点,与光线传播方向一致为正,相反为负 光学系统的焦距计算式tan tan h f U h f U '='=焦距包含了光学系统主点和焦点的相对位置,是描述光学系统性质的重要参数 像方焦距f ’>0的光组称为正光组,f ’<0的光组称为负光组无限远轴外物点的共轭像点焦点、焦平面、主平面示意图当光学系统的物方与像方处于同一介质中时,物方焦距与像方焦距数值相等,符号相反f = -f ’单折射球面的主平面和焦点共轴球面系统的成像性质可以用一对主平面和两焦点表示,为此目的,先研究单个折射球面的主平面和焦点位置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 平面与平面系统
1. 人照镜子时,要想看到自己的全身,问镜子要多长?人离镜子的距离有没有关系? 解:
镜子的高度为1/2人身高,和前后距离无关。
2有一双面镜系统,光线平行于其中一个平面镜入射,经两次反射后,出射光线与另一平面
镜平行,问两平面镜的夹角为多少? 解:
OA M M //32 3211M M N M ⊥∴1'
'1I I -= 又 2'
'2I I -=∴α
同理:1''1I I -=α 321M M M ∆中 ︒
=-+-+180)()(1''12''2I I I I α
O
︒
=∴60α 答:α角等于60︒。
3. 如图3-4所示,设平行光管物镜L 的焦距'f =1000mm ,顶杆离光轴的距离a =10mm 。
如果推动顶杆使平面镜倾斜,物镜焦点F 的自准直象相对于F 产生了y =2mm 的位移,问平面镜的倾角为多少?顶杆的移动量为多少? 解:
θ'2f y = rad 001.0100022=⨯=
θ α
θx
=
mm a x 01.0001.010=⨯=⨯=∴θ
图3-4
4. 一光学系统由一透镜和平面镜组成,如图3-29所示。
平面镜MM 与透镜光轴垂直交于D
点,透镜前方离平面镜600mm 有一物体AB ,经透镜和平面镜后,所成虚像'
'A ''B 至
平面镜的距离为150mm,且像高为物高的一半,试分析透镜焦距的正负,确定透镜的位置和焦距,并画出光路图。
图3-29 习题4图
解: 由于平面镜性质可得'
'
B A 及其位置在平面镜前150mm 处 '
''
'B A 为虚像,'
'
B A 为实像
则211-=β 2
1
'1-==
L L β 450150600'=-=-L L 解得 300-=L 150'
=L 又
'1L -L 1='
1f mm f 150'=∴ 答:透镜焦距为100mm 。
5.如图3-30所示,焦距为'f =120mm 的透镜后有一厚度为d =60mm 的平行平板,其折射
率n =1.5。
当平行平板绕O 点旋转时,像点在像平面内上下移动,试求移动量△'y 与旋转角φ的关系,并画出关系曲线。
如果像点移动允许有0.02mm 的非线形度,试求φ允许的最大值。
图3-30 习题5图
解: (1)
'1
cos I d DE =
)sin(cos )sin('
11'
1'11'I I I d I I DE d -=-⋅= 由图可知 φ=1I n
n I I φ
sin sin sin 1'
1==
'1cos I
=
2
2sin 1n
φ-=n 1
φ22sin -n
)sin cos cos (sin cos '11'11'
1
'
I I I I I d
d -=
='
1'
111cos sin cos sin I I I d I d -
=)cos cos 1(sin '
1
1
1I n I I d -
=)sin cos 1(sin 2
2
φ
φφ--
n d
(2)
考虑斜平行光入射情况不发生旋转时
'11cos I d OB =
)sin(cos )sin('
1'
1
'11'1I I d I OB d -=-=ωω '
1sin sin I n =ω )sin cos 1(sin 2
2
'
1ω
ωω--
⋅=n d d
当平行板转过φ角时 '
1'11cos )90sin(I d
I d OD =-︒=
A
)sin('11121'
2I I OD D D d -==
φω+=1I '11sin sin I n I = )sin(1
sin '
1φω+=
n
I 2
2'
1)(sin 1cos n
I φω+-==)(sin 12
2φω+-n n )sin sin(cos '11'
1
'
2I I I d
d -=
=
)sin cos cos (sin cos '
11'11'
1
I I I I I d - =))
(sin )
cos(1)(sin()cos cos 1(sin 22'111φωφωφω+-+-+=-
n d I n I I d
ω
ωωωφωφωφωφω2
2
2
2
'
2'1sin cos sin sin )
(sin )sin()cos()[sin(-+
-+-++-
+=-=∆n n d d d d ]
6. 用焦距'f =450mm 的翻拍物镜拍摄文件,文件上压一块折射率n =1.5,厚度d =15mm 的玻璃
平板,若拍摄倍率β=-1⨯
试求物镜主面到平板玻璃第一面的距离。
解:
x
f
-
=β mm x 450-= mm f x L 900450450-=--=+= 又A 和A '
是一对共轭点(关于O 2)
r n
n l n l
n -=-''' ∞→r 0155.11'=--
l mm l 10'
-= mm L 890=∆
答:物镜主面到平板玻璃第一面的距离为890mm 。
Z '
Z '
8.试画出图3-12b 所示030直角棱镜和图e 所示斜方棱镜的展开图。
设300
直交棱镜的口径等于斜边棱镜的一半,斜方棱镜的口径等于直角边,分别求出这两种棱镜的结构参数。
9.试画出图图。
10. 的折射率。
解:
d) c)
Z '
2
sin
2
sin
α
δαn m
=+
2
40760sin 218284540760sin '
''''''''︒︒︒=+n
58998.15009654
.0796527
.0063889.30sin 799725.52sin ===︒
︒
n 答:光学材料的折射率为1.58998。
11. 白光经过顶角α=︒60的色散棱镜,n =1.51的色光处于最小偏向角。
试求其最小偏向
角及n =1.52的色光相对于n =1.51的色光间的夹角。
解:
51.1=n
2
sin
2
sin
α
δαn m
=+
755.030sin 260sin
1
=︒=+︒n m δ 025.492
30=+
︒m
δ
︒=05.381m δ
60︒
52.1=n
sin
︒︒=+30sin 52.12
602
m δ ︒=928.382m δ
'''1242528784.0==-︒
m m δδ
答:所求夹角为'
''4252。
12.如图3-32所示,图a 表示一个单光楔在物镜前移动;图b 表示一个双光楔在物镜前相对转动;图c 表示一块平行平板在物镜前转动。
问无限远物点通过物镜后所成像点在位置上有什么变化?
图3-32 习题12图
13.如图3-33所示,光线以45︒
角入射到平面镜上反射后通过折射率n =1.5163,顶角为︒4的光楔。
若使入射光线与最后的出射光线成︒90,试确定平面镜所应转动的方向和角度值。
a)
b)
c)
图3-33 习题13图
解:rad n 036.0)15163.1(180
)1(=-⨯=-=παδ=2︒06. 在中21NO O ∆ ︒︒=-=∠17618021αNO O
αsin sin 21=∠N O O n
︒︒
==∠∴636787.25163
.14sin arcsin 21N O O ︒=∠∴3632.121O NO
︒=3632.1sin sin n θ
︒=∴067.2θ ︒=∴0336.12θ
答:平面镜顺时针旋转1.0336︒即可使入射光线与出射光线成90︒。
