基于遗传算法的主动轮廓模型
医学图像的分割技术及其新进展
医学图像的分割技术及其新进展3楚存坤,李月卿,王昌元(泰山医学院,山东泰安 271000)关键词:医学图像分割;图像分割评价中图分类号:R319 文献标识码:A 文章编号:100427115(2007)0420315203 近几年,计算机断层成像(Computed T omo2 graphy,CT),核磁共振成像(Magnetic Res onance I m2 age,MR I),超声成像(ultras ound i m age,USI)等医学成像技术已经广泛应用在医疗的诊断、术前计划、术后监测等各个环节中,其目的是全面而精确地获得病人的各种数据,为诊断、治疗计划、手术和术后评估提供正确的数字信息。
只有把感兴趣的目标从图像的复杂景物中提取出来,才有可能进一步对它们进行定量分析或者识别。
目前,医学图像分割主要以各种细胞、组织与器官的图像来作为处理的对象或内容。
图像分割是根据某种均匀性或一致性原则将图像分成若干个有意义的部分,使得每一部分都符合某种一致性的要求[1]。
1 医学图像分割技术的发展111 传统图像处理领域中的医学图像分割技术11111 基于阈值的方法阈值分割法是将灰度图像变为二值图像以达到分割目的的方法,它是一种PR(并行区域)法。
阈值法的过程是决定一个灰度值,用以区分不同的类,这个灰度值就叫做“阈值”。
把灰度值大于阈值的所有像素归为一类,小于阈值的所有像素归为另一类。
阈值法是一种简单但是非常有效的方法,特别是不同物体或结构之间有很大的强度对比时,能够得到很好的效果。
此分割法通常是交互式的。
因为阈值法能够实现实时操作,所以它更能够建立在用户视觉估计的基础上。
阈值法一般可以作为一系列图像处理过程的第一步。
其主要局限是,最简单形式的阈值法只能产生二值图像来区分两个不同的类。
另外,它只考虑像素本身的值[2],一般都不考虑图像的空间特性,这样就对噪声很敏感。
针对它的不足,有许多经典阈值法的更新算法被提了出来[3,4]。
遗传算法与模型预测控制的结合研究综述
遗传算法与模型预测控制的结合研究综述引言在现代科学和工程领域中，模型预测控制（Model Predictive Control, MPC）作为一种强大的控制方法，已经得到了广泛的应用。
然而，MPC的设计和优化过程往往是复杂且耗时的。
为了解决这一问题，研究人员开始探索将遗传算法（Genetic Algorithm, GA）与MPC相结合的方法，以提高控制系统的性能。
本文将对遗传算法与模型预测控制的结合研究进行综述。
遗传算法的基本原理遗传算法是一种模拟自然遗传和进化过程的优化算法。
它通过模拟自然选择、交叉和变异等过程，来搜索问题的最优解。
遗传算法的基本原理包括个体编码、适应度评价、选择、交叉和变异等步骤。
个体编码是将问题的解表示为一个染色体，适应度评价是根据问题的目标函数来评估染色体的优劣，选择是根据适应度值选择优秀的个体，交叉是将两个个体的染色体进行交换，变异是对染色体进行随机改变。
遗传算法在模型预测控制中的应用遗传算法在模型预测控制中的应用主要包括参数优化和约束处理两个方面。
参数优化是指通过遗传算法来寻找最优的控制参数，以使系统的性能指标达到最佳。
约束处理是指通过遗传算法来处理系统约束条件，以确保控制系统的稳定性和安全性。
在参数优化方面，研究人员通常将MPC的控制参数作为染色体的编码，以目标函数的最小化为优化目标，通过遗传算法来搜索最优的控制参数。
例如，某些研究将MPC的预测模型参数和控制权重作为染色体的编码，通过遗传算法来优化这些参数，以使系统的性能指标如稳定性、响应速度等达到最佳。
在约束处理方面，遗传算法可以用于处理MPC中的约束条件，例如状态变量的上下限、输入变量的变化率限制等。
通过将约束条件转化为适应度函数，遗传算法可以搜索满足约束条件的最优解。
一些研究还将遗传算法与其他优化方法相结合，以提高约束处理的效果。
结合研究的案例分析为了更好地理解遗传算法与模型预测控制的结合，我们将对一些相关的案例进行分析。
基于遗传算法的自动化系统参数优化
基于遗传算法的自动化系统参数优化
自动化系统是现代工业化生产和运营的重要手段，系统参数优化可提高其运行效率和稳定性。
随着技术的不断升级，传统的手动参数调整方式已经无法满足复杂系统的需求。
基于遗传算法的自动化系统参数优化成为一种新方案。
遗传算法利用生物进化的原理，通过种群选择、交叉和变异等操作，模拟自然界中基因的遗传和进化过程，从而获得最优解。
将其应用于自动化系统参数优化中，可以自动搜索最优参数，避免了人工试错，提高了效率和精度。
基于遗传算法的自动化系统参数优化的步骤如下：
1. 系统建模：根据实际系统建立数学模型，明确目标函数和参数范围。
2. 初始化种群：随机生成初始种群，种群规模和参数精度要根据实际情况确定。
3. 适应度函数定义：根据目标函数确定适应度函数，将目标函数的取值映射到种群的适应度上。
4. 选择算子：根据适应度函数选择优质的个体，保留其基因信息，淘汰劣质的个体，避免快速陷入局部极小值。
5. 交叉算子：对选出的优质个体进行交叉操作，生成下一代个体。
6. 变异算子：对新生成的个体进行变异操作，增加种群的多样性。
7. 终止条件：根据实际情况，设置优化的迭代次数或误差范围
等终止条件。
基于遗传算法的自动化系统参数优化是一种高效、精确的优化
方式，但适用范围有限。
在实际应用中需要根据具体情况选择不同
的优化方法，综合考虑效果、时间和成本等因素，寻求最佳平衡点。
遗传算法优化模型训练过程及结果预测准确度比较
遗传算法优化模型训练过程及结果预测准确度比较遗传算法是一种模仿自然进化原理的优化算法，广泛应用于解决复杂的优化问题。
在机器学习领域，遗传算法也可以用于优化模型的训练过程，以提高模型的预测准确度。
本文将探讨遗传算法优化模型训练过程及结果预测准确度的比较。
首先，我们需要了解遗传算法的基本原理和步骤。
遗传算法通常包括初始化种群、选择、交叉、变异和替换等步骤。
在初始化种群阶段，通过随机生成一些初始解来构建一个初始的种群。
接下来，通过选择操作，根据某种适应度函数评估每个个体的适应度，并选择一部分适应度较高的个体作为父代。
然后，通过交叉操作，将父代个体的染色体信息进行随机组合生成新的个体。
最后，通过变异操作，在新个体的染色体上引入随机突变来提供种群的多样性。
重复上述步骤，直到达到终止条件。
在模型训练过程中，遗传算法可以用于优化模型的参数。
传统的机器学习算法通常使用梯度下降等优化方法来调整模型的参数，但这些方法对于复杂的模型和优化问题可能面临局部最优和收敛速度慢的困境。
遗传算法因其全局搜索和并行计算的特点，可以在一定程度上避免这些问题。
与传统的优化方法相比，遗传算法对初始解的选择更加灵活。
由于遗传算法具有较好的全局搜索能力，能够通过随机生成初始解的方式来探索更广阔的参数空间。
这对于模型的参数选择来说是非常重要的，因为良好的初始化可以使模型更快地收敛。
此外，遗传算法通过选择、交叉和变异等操作保持种群的多样性，以防止陷入局部最优解。
这种多样性维护使遗传算法更有可能找到更优的模型参数组合，并具有更好的泛化能力。
在优化模型训练过程时，我们可以将遗传算法与其他优化方法进行比较。
一种常用的方法是使用梯度下降法或其他传统的优化算法进行模型的参数调整，然后使用遗传算法对其进行进一步优化。
这种混合的优化策略可以充分利用遗传算法的全局搜索能力，并在较短的时间内获得更好的结果。
另一种方法是直接使用遗传算法进行模型的参数调整。
在这种情况下，我们可以通过比较使用遗传算法与传统优化方法得到的模型参数组合以及模型的预测准确度来评估遗传算法的效果。
基于遗传算法的人工神经网络模型构建与优化研究
基于遗传算法的人工神经网络模型构建与优化研究人工神经网络（Artificial Neural Network，ANN）是一种模仿生物神经网络结构和功能的计算模型，通过模拟神经元之间的连接和信号传递，能够实现机器学习和模式识别任务。
而遗传算法（Genetic Algorithm，GA）是一种基于自然选择和遗传机制的优化算法，通过模拟生物进化过程来寻找最优解。
本文将探讨基于遗传算法的人工神经网络模型的构建与优化研究。
首先，构建人工神经网络模型是研究的首要任务。
人工神经网络由多个神经元和这些神经元之间的连接组成。
每个神经元接收来自其他神经元的输入，并通过激活函数对输入信号进行加权计算，最终输出结果。
遗传算法可以应用于优化神经元的连接权重和调整激活函数的参数，以获得更好的网络性能。
在构建人工神经网络模型时，首先需要确定网络的拓扑结构，包括输入层、隐藏层和输出层的神经元数量，以及它们之间的连接方式。
遗传算法可以通过进化过程搜索最佳的拓扑结构，以提高神经网络的性能。
遗传算法通过定义适应度函数来衡量每个个体的适应度，适应度高的个体将更有可能被选中下一代进化。
通过遗传算法的迭代过程，我们可以找到最佳的拓扑结构。
其次，优化神经元的连接权重是构建人工神经网络模型的关键一步。
连接权重决定了不同神经元之间的信号传递强度。
遗传算法可以通过进化过程调整连接权重，以找到最佳的权重组合。
在遗传算法的优化过程中，通过交叉和变异等操作，通过上一代个体中的优秀基因来生成新的个体，逐步优化连接权重，使神经网络的性能得到提高。
此外，还可以使用遗传算法来优化激活函数的参数。
激活函数决定了神经元输出的非线性特性，常用的激活函数包括Sigmoid、ReLU、Tanh等。
通过调整激活函数的参数，我们可以改变神经元的响应特性，从而使网络更好地拟合训练数据。
遗传算法可以在多个激活函数和参数组合中搜索最佳的选择，以提高神经网络的性能。
此外，在进行人工神经网络的训练和优化时，还可以使用遗传算法来选择最优的训练样本和参数初始化方法。
【计算机应用研究】_能量模型_期刊发文热词逐年推荐_20140724
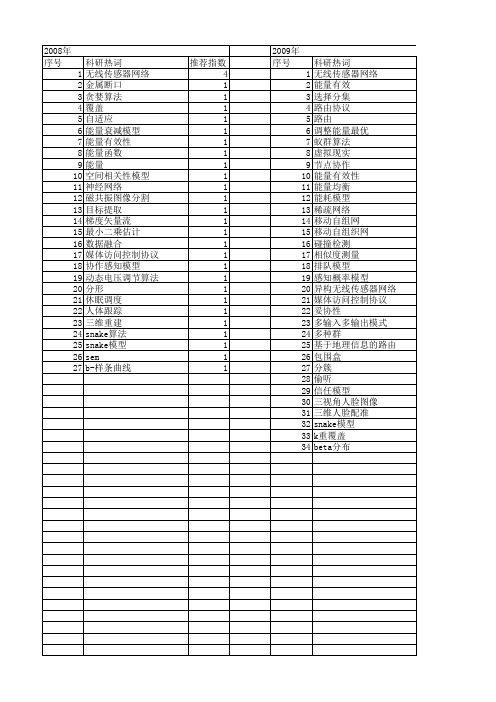
推荐指数 8 3 3 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
时空一致性 故障控制 广义hough变换 媒体访问控制 土壤 图像处理 图像反卷积 图像修复 合成孔径雷达影像 变异 协作分集 协作中继 分割 偷听 偏微分方程 信号源噪声 优先级 二进制 二维hp模型 二次规划 主动轮廓 中断概率 snake模型 ieee 802.15.4 harq graph cut算法 6lowpan无线传感器网络
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
Байду номын сангаас
科研热词 无线传感器网络 金属断口 贪婪算法 覆盖 自适应 能量衰减模型 能量有效性 能量函数 能量 空间相关性模型 神经网络 磁共振图像分割 目标提取 梯度矢量流 最小二乘估计 数据融合 媒体访问控制协议 协作感知模型 动态电压调节算法 分形 休眠调度 人体跟踪 三维重建 snake算法 snake模型 sem b-样条曲线
推荐指数 5 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51
【计算机工程与设计】_轮廓_期刊发文热词逐年推荐_20140726
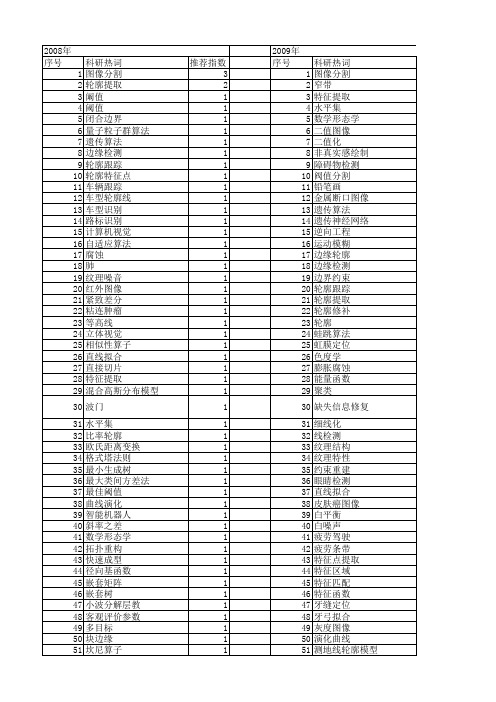
模糊连接 模式匹配 最小二乘法 曲率 方向图 数据挖掘 数字图像处理 排序 指纹识别 折线拟合 抗噪声干扰 感兴趣区域 快速扫描法 形态学 平面曲面化 图像配准 叶缘 可视化 可变形模板 变换扩散投影 参数误差 印鉴提取 单颗牙齿 分裂:收缩变形 分割算法 几何纠正 几何建模 入侵检测 信息安全 人眼轮廓提取 主动轮廓线模型 主动轮廓模型(snake) 三维匹配 三维人脸建模 snake模型 pca投影 mpeg-4 hsv色彩空间 gabor滤波 freeman链码 ct图像 bp算法 ballon模型
科研热词 图像分割 窄带 特征提取 水平集 数学形态学 二值图像 二值化 非真实感绘制 障碍物检测 阀值分割 铅笔画 金属断口图像 遗传算法 遗传神经网络 逆向工程 运动模糊 边缘轮廓 边缘检测 边界约束 轮廓跟踪 轮廓提取 轮廓修补 轮廓 蛙跳算法 虹膜定位 色度学 膨胀腐蚀 能量函数 聚类 缺失信息修复 细线化 线检测 纹理结构 纹理特性 约束重建 眼睛检测 直线拟合 皮肤癌图像 白平衡 白噪声 疲劳驾驶 疲劳条带 特征点提取 特征区域 特征匹配 特征函数 牙缝定位 牙弓拟合 灰度图像 演化曲线 测地线轮廓模型 正交照片
推荐指数 3 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
一种医学图像的轮廓提取方法
方法 ， 用 单 一 的全 局 阈值 难 以正 确 完成 感 兴 趣 区 域 的分 割 。 采 基于直方图法的全 局闻值分割是 图像分割 的常用方法 ，直 ｊ
传算法作为外部约束力 ，控制 曲线在能量最小化的作 用下收
第３ ６卷 第 ５期
Ｖ ３ ｏＬ ６
ＮｏＳ ．
计
算
机
工
程
２ １ 年 ３月 ００
Ｍ ａ ｃ ０１ ｒ ｈ２ ０
Ｃｏ ｍｐｕｔ ｒＥｎｇ ｎ ｅ ｉ ｅ ｉ ｅ ｒｎｇ
・ 图形图像处理 ・
一
文 编 ｌ ｏ ３ ８ ０ ） ＿ ２ — ３ 文 标 码： 章 号： ｏ ＿ ４ （ １０ － １ ０ ０ ＿ ２ ２ ０５ ０ ８ 献 识 Ａ
ｏ ｔ ｒ ｅｓ ｆ ａｇ ｔ．
［ ｅ ｏｄ ｌａｔ ｅ ｏ ｔ ｒ ｏ ｅ ｃ ｎ ｕ ｔ ｃ ｏ ； ｐ ｖ ｄ ｅｅ ｃ ｌ ｒｈ Ｋ ｙ ｒ ｓ ｃ ｖ ｎ ｕ ｍ ｄｌ ｏ ｔ ｒ ｘ ａｔ ｎ ｉ ｒ ｅ ｎ ｔ ｇ ｉ ｍ ｗ ｉ ｃ ｏ ； ｏ ｅ ｒ ｉ ｍ ｏ ｇ ｉａ ｏ ｔ
的过 程 中 。 本文对医学图像的特征进行研究分析后 ，采用改进的遗
出现大幅度的变化。医学图像的几何性状较为模糊 ，在感兴 趣 区域的边界位置、拐角 以及凸出点难 以精确描述 ，边缘无
法 明确确定 ，这在很大程度上影响了图像 的分割。在计算机 视觉系统 中，医学图像分割 的方法主要分为阈值分 割方法、
Ｃｏ ｔ ｕｒＥｘ ｒ ｃ ｉ ｎ Ｍ ｅ ｈｏ ｏ ｅ ｉ ａ ｍ ａ ｅ ｎ ｏ ｔ ａ ｔｏ ｔ ｄ ｆ ｒＭ ｄ ｃ ｌ Ｉ ｇｓ
磁共振颅脑图像的脑组织自动获取方法
ISSN 1000-9825, CODEN RUXUEW E-mail: jos@Journal of Software, Vol.20, No.5, May 2009, pp.1139−1145 doi: 10.3724/SP.J.1001.2009.03577 Tel/Fax: +86-10-62562563© by Institute of Software, the Chinese Academy of Sciences. All rights reserved.∗磁共振颅脑图像的脑组织自动获取方法税午阳1+, 周明全1, 耿国华21(北京师范大学信息科学与技术学院,北京 100875)2(西北大学信息科学与技术学院,陕西西安 710127)Automatic Brain Tissue Extraction Approach of Magnetic Resonance Head ImagesSHUI Wu-Yang1+, ZHOU Ming-Quan1, GENG Guo-Hua21(School of Information Science and Technology, Beijing Normal University, Beijing 100875, China)2(School of Information Science and Technology, North West University, Xi’an 710127, China)+ Corresponding author: E-mail: sissun@Shui WY, Zhou MQ, Geng GH. Automatic brain tissue extraction approach of magnetic resonance headimages. Journal of Software, 2009,20(5):1139−1145. /1000-9825/3577.htmAbstract: This paper presents an effective automatic method of brain extraction through twice segmentationsrespectively. The noise of the image is eliminated through anisotropic diffusion filtering based on Catt model whilethe details of the image are kept. The over-segmentation problem of the watershed algorithm is solved based on themerging of gray-scale similarity regions and the brain tissue is initially segmented. The edges of differentorganizations of every brain image are fuzzy and the MRI data is vulnerable to be affected by noise, therefore thenon-brain region may be mistaken for brain region in the process of merging. In order to solve these problems, theLevel Set method is adopted. The outline of the watershed is taken as the initial curves of level set to realize theautomatic segmentation of brain tissue. The feasibility and practicality of this algorithm is proved by the results inthe experiments.Key words: image filtering; watershed; level set; brain tissue segmentation; regions merging摘要: 提出了一种针对MRI磁共振图像通过两次分割实现颅脑图像脑组织自动获取的方法.通过基于Catt扩散模型的各项异性滤波,实现了在保持图像细节的同时有效地消除图像的噪声.然后通过改进的基于相似性区域合并的分水岭算法解决了过分割问题,实现了脑组织区域的初次分割.由于颅脑图像不同组织之间边缘模糊且自身容易受到噪声的影响,导致区域合并过程中可能会误将非脑组织作为脑组织合并,因此,采用水平集方法将初次分割获得的脑组织轮廓作为初始轮廓曲线,实现了脑组织的自动分割.实验结果验证了算法的可行性和实用性.关键词: 图像滤波;分水岭;水平集;脑组织分割;区域合并中图法分类号: TP391文献标识码: A随着医学影像在临床上的成功应用,医学图像分割在医学影像处理与分析中的地位愈加重要,分割的准确性对该组织重构结果的准确性和完整性、对医生判断疾病的真实情况并作出正确的诊断计划至关重要.图像分∗Supported by the National Natural Science Foundation of China under Grant No.60736008 (国家自然科学基金)Received 2008-09-25; Accepted 2008-12-151140 Journal of Software 软件学报 V ol.20, No.5, May 2009割方法主要分为两类:① 基于区域的方法,通常利用同一区域内的均匀性识别图像中的不同区域,此类方法容易产生过分割;② 边缘分割方法,通常利用各区域的不同性质划出区域之间的分界线,此类方法对于噪声比较敏感.近年来,统计学理论、模糊集理论、神经网络、形态学理论、小波理论、遗传算法、尺度空间等在图像分割中的应用日渐广泛.由于颅脑图像广泛存在着不同组织之间边缘模糊、数据采集过程中产生噪声、磁场的不均匀性以及容积效应等原因会导致图像质量不佳,因此脑组织的分割一直是医学图像处理技术研究的难点和热点.BET(brainextraction tool)[1]算法是当前使用得最广泛的方法,它利用直方图和形变模型的方法实现脑组织的分割.Battaglini 等人[2]指出BET 方法并不能准确分割出脑组织,提出在BET 方法的基础上通过掩码、形态学算子和经验阈值实现脑组织的准确分割.David 等人[3]提出的脑组织分割算法包括图像各向异性滤波、Marr-Hildreth 边界提取、利用数学形态学算子修正3个步骤.SPM 5中的脑组织提取算法就是利用将脑图像空间投射到Talairach [4]图谱的方法确定脑组织区域,该方法将分割看成配准问题,它将已分割好的模板图像一对一地映射到待分割的目标上,映射过程往往是由一系列线性映射和非线性映射构成.宋利伟[5]采用分水岭和聚类方法实现了磁共振脑图像的分割,但是该方法可能会出现误将噪声区域与脑组织区域合并的问题.陈志彬[6]提出了一种基于FCM 和LevelSet 的MRI 医学图像分割方法,将聚类分析得到的模糊隶属度作为图像的全局信息,用于第2阶段的分割. Kass 等人[7]提出以Snake 模型为基础的参数化主动轮廓模型,通过模型能量最小化实现目标轮廓的提取.本文通过基于偏微分方程的去噪方法,在保持边缘的情况下有效消除图像噪声,将改进的分水岭算法的分割结果作为水平集方法的初始曲线,解决了过分割和区域误合并问题,有效实现了脑组织的自动获取.1 颅脑图像滤波虽然扫描技术在空间分辨率、获取速度和信噪比方面有了很大的改进,磁共振图像依然受到信号强度不均一、噪声等因素的影响.这些因素影响了磁共振图像在医学诊断方面的应用效果.传统的去噪方法主要是将图像中的高频成分滤除,中值滤波和均值滤波对噪声和边缘信息不加区分,在去除噪声的同时也使图像边缘变得模糊.高斯滤波是一种被广泛采用的各向同性的扩散去噪方法,它在平滑噪声的同时也使图像中最重要的边缘特征遭到破坏,随着尺度扩散时间的增大,图像变得越来越模糊,最后图像的灰度值变为平均值.然而,采用基于偏微分方程的各向异性扩散去噪方法可以在消除噪声的同时保持图像的特征信息.1.1 P -M 扩散模型Perona 和Malik [8]给出了保持边界异向扩散模型,通过调整扩散系数解决了去噪和保持边缘之间的关系. 0(,,)div[(,,)(,,)](,,0)(,)u x y t c x y t u x y t t u x y u x y ∂⎧=∇⎪∂⎨⎪=⎩(1) 其中,u 0(x ,y )为原始图像,div 为散度算子,∇为梯度算子.传导系数函数c (x ,y ,t )用来保持边缘.c (x ,y ,t )=g (||∇u (x ,y ,t )||).Persona 和Malik 讨论了两种形式的扩散系数函数:(2) 2((||||/))()e I k g I −∇∇= 21()1(||||/)g I I k ∇=+∇ (3) P-M 模型在图像梯度较大时系数较小、扩散较弱,保持边缘;在图像梯度较小时扩散系数大、扩散强度大,图像被模糊,从而实现了各向异性的扩散能力.1.2 Catt 扩散模型对于P-M 扩散方程在强噪声图像中梯度模||∇u ||很难准确计算,同时因为噪声区域也可能会有较大的梯度模,此时噪声也会被当成图像的边界保存下来.另一方面,理论上P-M 模型是病态的,方程解的唯一性和稳定性得税午阳 等:磁共振颅脑图像的脑组织自动获取方法 1141不到保证,即两幅在初始时刻非常相似的图像,经过P-M 方程演化可能变得差别很大.为此,Catté等人提出了Catt模型[9]: 0(,,)div[(||||)(,,)](,,0)(,)u x y t g G u u x y t t u x y u x y σ∂⎧∇⋅∇⎪∂⎨⎪=⎩= (4) 其中,G σ是方差为σ2的高斯函数.该模型对P-M 模型进行了改进,在计算梯度之前先对图像作卷积,有效地消除了噪声,特别是在强噪声情况下,可以更加准确地区分图像边界和噪声.模型中扩散系数g 含阈值k ,它的选择直接影响到各向异性滤波的效果,图像梯度幅值较大的部分作为边缘保留,梯度幅值较小的低对比度边缘将被滤除.因此,把阈值k 改进为基于迭代次数n 的递减函数01()1k n k n ⎛⎞=+⎜⎟⎝⎠可以取得较好的效果.1.3 实验结果颅脑图像滤波的实验结果如图1所示,其中迭代次数为200次,时间增量为0.05,k 0=10.Catt 模型在去除图像噪声的同时充分保存了图像的细节,更适合脑组织的分割.本文选择输入图像和输出图像间均方根误差(rootmean square error)和均方信噪比(signal to noise ratio)作为滤波性能评价的标准,通过给清晰的核磁共振颅脑图像添加噪声再比较去噪结果的方法,定量地比较各种滤波方法的优劣.(a) Original head image(a) 原始颅脑图像 (b) Result of median filtering (b) 中值滤波结果 (c) Result of Catt model filtering (c) Catt 模型滤波结果Fig.1 Results of head image filtering图1 颅脑图像滤波结果2 改进的分水岭算法分割脑组织2.1 分水岭算法分水岭算法(watershed)由Vincent 和Soille [10]应用于图像处理中,它是一种基于数学形态学的非线性分割方法.它将梯度图像看成一幅地图,梯度值对应海拔高度,图像中不同梯度之间的区域对应着山峰和山谷盆地.设想在图像中的局部极小值处形成一个洞,然后将表面侵入湖中,从全局最小值开始,水会逐渐充满各个不同的山谷盆地.当相邻两个盆地的水即将合并时,在两个盆地间建立堤坝拦截.随着这个过程的继续,等到结束时,每个局部极小值会被堤坝完全包围,所建立的堤坝就对应这个图像的分水岭.基于分水岭变换的图像分割方法具有计算负担轻、分割精确度高的优点,但其性能在很大程度上依赖于用来计算待分割图像的梯度算法.Vincent 给出一种利用像素排序的实现方法,具有速度快、结果准确等优点,其步骤分为排序和淹没两个操作:1. 排序:在逐渐淹没的过程中,将图像像素按灰度值以升序排列,得到一个排序后的像素灰度级列表,使得在淹没步骤中可以直接访问任意灰度级的全部像素,加速计算.2. 淹没:利用排序后的图像按灰度值升序访问每一个像素,实现对每一个聚水盆地分配不同的标记.从整个图像的最小像素值开始分配标记,依次淹没利用先进先出的数据结构来扩展标记过的聚水盆地.1142Journal of Software 软件学报 V ol.20, No.5, May 20092.2 改进的分水岭分割算法 假设脑组织图像经分水岭算法被分成k 0个小区域,记为00k i i R R ==∪,R i 表示分割后的每个区域,(num i ,gray i )是区域R i 的两个属性,分别表示该区域像素的个数和灰度均值,11,i j num i j i j gray P num ==⎛⎞=⎜⎟⎟j P ⎜⎝⎠∑表示R i 区域中第j 个像素 的灰度值.分水岭算法会产生过分割问题,需要通过合并相邻区域或者标记控制的方法实现目标图像的分割.通过分析颅脑图像的直方图发现,不同组织之间(白质、灰质、脑脊液、软组织)存在灰度差别,因此,采用本文提出的方法可以实现脑组织的自动分割:(1) 通过定义的判别函数准则实现具有相似性的相邻区域合并.(2) 通过分析脑组织图像的特殊性,将合并后获得的最大连通区域作为种子点,吞并与之相邻的小区域,实现正确分割.区域相似性判别函数是过分割形成的k 0个区域进行合并的基础,直接影响分割的结果.传统的区域合并方法基于颜色特性的判别函数和基于平均灰度差异的判别函数,本文提出了将区域灰度相似性与边界相似性相结合的判别函数作为两个相邻区域R i ,R j 是否合并的准则.定义判别函数e (R i ,R j ):22(,)[]()(,)i j i j i j e R R gray gray I I Range i j −− (5) (6) 1, (,)0, i j i j R R Range i j R R ⎧⎪=⎨⎪⎩和相邻和不相邻 2221, ()()0, ()i j i j i j I I T I I I I T ⎧−⎪−=⎨⎪−>⎩(7) 其中,gray i ,gray j 分别表示R i 和R j 的灰度均值;I i ,I j 分别为R i 和R j 区域边缘轮廓的梯度均值.k 0个区域的图像合并采用邻接图(region adjacency graph)的数据结构描述.RAG 为无向图G =(V ,E ),其中V ={1,2,…,k 0}为各个区域,任意两个相邻区域R i 和R j 之间存在e (R i ,R j )∈E ,如果e (R i ,R j )满足判别函数,则合并两个区域,同时重新标记新区域的范围并计算新区域的判别函数e (R i ,R j ).该判别函数有效地解决了区域合并过程中由于加入相邻区域,造成新产生区域灰度均值发生改变,从而影响最终合并结果的问题.重复上面的过程直至结束,输入脑组织图像被初步分割为脑灰质、脑白质、脑脊液、软组织等几部分区域.此时,将最大连通区域吞并相邻区域,算法完成后,最大连通域即为脑组织.算法的基本流程如下:(1) 根据当前颅脑图像计算其梯度图像.(2) 统计各梯度的频率和累加概率,并将梯度值按从小到大的顺序排列.(3) 根据分水岭算法将颅脑图像划分为不同的区域,记录各区域的位置和总的分区数,建立RAG 图.(4) 计算各区域间的判别函数,每次从所有区域中e (R i ,R j )值最小的区域R i ,R j 开始合并.如果0<e (R i ,R j )<δ,则合并满足条件的区域R i ,R j ,同时更新合并后新区域的信息及RAG 图;如果待判别相邻区域为小区域(面积小于阈值),则直接合并两个区域,但仍以合并前区域的信息作为合并后新区域的信息.(5) 当区域合并停止时,脑组织图像被初步分割为脑灰质、脑白质、脑脊液、软组织等几部分区域,此时将最大连通区域吞并相邻区域,得到的最大连通区域即为脑组织分割结果.采用本文方法的实验结果如图2所示.2.3 非脑组织误合并的问题在相邻区域合并过程中,一方面由于受图像采集设备和图像本身属性的制约,脑组织边缘灰度信息与颅腔中噪声区域的灰度信息差别可能不大,容易将非脑组织误认为脑组织区域而合并;另一方面,由于脑组织本身结构的复杂性,很难设置准确的判别函数阈值区分脑组织与非脑组织,这样也会导致误分割的情况,如图3所示.因税午阳等:磁共振颅脑图像的脑组织自动获取方法1143此,根据上文分水岭算法区域合并后的结果,通过阈值估计将灰度均值较小的区域设置为背景色,然后提取误合并后的脑组织轮廓线,作为水平集方法的初始轮廓线,实现了脑组织的正确分割.该方法解决了水平集方法中需要人工设置初始轮廓线的问题,同时也消除了由于经验阈值不准确而导致的脑组织区域误合并的问题,实现了脑组织的正确分割.(a) Original image(a) 原始图像(b) Catt model filtering(b) Catt模型滤波(c) Gradient image(c) 梯度图像(d) Over-Segmentation(d) 划分区域(e) Region merging(e) 区域合并(f) Segmentation result of brain tissue(f) 脑组织分割结果Fig.2 Segmentation processes of improved watershed algorithm图2 改进的分水岭算法分割过程(a) Original head image(a) 原始颅脑图像(b) Segmentation result of the watershedmethod with the image of medianfiltering as input image(b) 将中值滤波的结果作为本文分水岭算法的输入图像,分割获得的结果(c) Segmentation result of watershedmethod with the image of the Cattmodel filtering as input image(c) 将Catt模型滤波的结果作为本文分水岭算法的输入图像,分割获得的结果Fig.3 Brain tissue segmentation results of the watershed algorithm图3 脑组织分割结果图3 水平集方法Osher和Sethian[11]提出了水平集方法.其最大优势在于其稳定性和拓扑性,特别是在处理具有复杂外形的图像时优点更加明显.水平集方法的提出源于曲线以曲率相关速度演化理论,其基本思想是将平面闭合曲线隐含地表达为二维曲面函数的水平集,即具有相同函数值的点集,通过Level Set函数隐含地求解曲线的运动.将初始曲线嵌入高一维的水平集函数中,这样就将二维的曲线演化问题转化为三维空间中连续曲面的演化问题.嵌入的原始曲线所在平面设定为零水平集,曲线的收缩和扩张就转化为通过水平集函数来移动原始曲线,最终只要确定零水平集即可确定演化的结果.水平集函数是z=F(x,y,t),可以用闭合曲线生成的符号距离函数表示,符号距离函数φ(x,y)=±d,d为平面上的点(x,y)到曲线的距离.曲线将平面划分为内部和外部两部分区域,一般定义曲线内部点的距离符号为负,曲线外部点的距离符号为正.由于曲线随时间的演化,因此距离函数改写为1144Journal of Software 软件学报 V ol.20, No.5, May 2009 φ(x ,y ,t =0)=±d (8)水平集的演化过程满足φt +F |∇φ|=0,|∇φ|表示函数的梯度范数,F 是沿法线方向的速度函数,包含与图像和曲线有关的项,如梯度信息、曲率信息等.速度函数控制曲线的演化,曲线上的点在其能量作用下沿法矢方向扩展.为了求解水平集方程,必须对水平集方程在时间和空间上进行离散化,将图像按像素划分为网格状,将时间划分为若干个时间段Δt ,因此,水平集方程转化为一种差分形式:1||Δn n ij ij n ij ij F t φφφ+−0+∇= (9)即1Δ|n n ij ij ij ij tF |n φφ+=−∇φ (10)文献[12]给出了速度函数: F =k i (F 0+F (k )) (11) 其中,F 0表示常量,k i 表示图像边界信息,F (k )为基于曲率k 的函数.曲率k 定义为22223/22()ii j i j ij jj i i jk φφφφφφφφφ−+=+ (12) 具体形式如下: 0|(,)|e (1)P()G I x y k X tφεφβφ−∇⋅∂0+⋅−∇−⋅∇=∂ (13) Malladi [12]等人提出了窄带算法及自适应窄带算法,该方法将计算区域压缩到零水平曲线周围的一个窄带内,将计算复杂度从O (N 2)降为O (NK ).本文将初始化轮廓曲线设为分水岭方法初次分割获取的脑组织轮廓,然后把水平集方法应用于脑组织的自动分割,具体算法如下:(1) 设置初始轮廓曲线并标记其包含的内部像素为活动点.(2) 在初始轮廓线周围活动点生成宽度为K 的窄带.(3) 计算窄带点到曲线的最短距离,求出窄带内各点到轮廓的有符号距离函数.(4) 用差分方法求出零水平集曲线上每点曲率,计算窄带内各网格点的扩展速度F .窄带点的速度近似等于与其最近的零水平集曲线上的点的速度.(5) 计算窄带内网格点扩展Δt 后新的符号距离值.(6) 计算窄带中的零水平集曲线,由于初始位置与脑组织区域有灰度差可以判断是否演化到脑组织区域,当零水平曲线演化到窄带边界时则重新初始化窄带,依次计算零水平集.(7) 最后根据上面演化得到的轮廓线,采用图像填充的方法获取脑组织区域.实验结果如图4所示.(a) Result of the water shed, containingnon brain regions as a result ofthe wrong merging(a) 分水岭算法的结果,由于误合并,导致包含非脑组织 (b) Contour of the initial segmentation is taken as the initial curve of Level Set algorithm (b) 初次分割结果的轮廓作为 Level set 方法的初始轮廓线 (c) Result of the brain tissue segmentation (c) 脑组织分割结果 Fig.4 Segmentation processes of level set algorithm图4 水平集方法分割过程税午阳等:磁共振颅脑图像的脑组织自动获取方法11454 结论本文通过基于偏微分方程的Catt扩散模型,在保持图像细节的同时实现了磁共振颅脑图像的去噪.提出了基于改进分水岭和水平集方法相结合的脑组织自动分割方法,同时,使用Visual Studio 和matlab7.0开发了脑组织自动分割系统,通过实验结果验证了算法的有效性.本文主要研究了单张颅脑切片的脑组织分割问题,今后将利用脑组织的连通特性在三维数据集中研究脑组织的分割问题,进一步提高复杂脑组织图像分割的准确性.References:[1] Smith SM. Fast robust automated brain extraction. Human Brain Mapping, 2002,17(3):143−155.[2] Battaglini M, Smith SM, Brogi S, Stefano ND. Enhanced brain extraction improves the accuracy of brain atrophy estimation.Neuroimage, 2008,40(2):583−589.[3] Shattuck DW, Sandor-Leahy SR, Schaper KA, Rottenberg DA, Leahy RM. Magnetic resonance image tissue classification using apartial volume model. NeuroImage, 2001,13(5):856−876.[4] Talairach J. Co-Planar Stereotaxic Atlas of the Human Brain. New York: Thieme, 1988.[5] Song LW, Song CY, Zhuang TG. Watershed-Based brain magnetic resonance image automated segmentation. Journal of ShanghaiJiaotong University, 2003,37(11):1754−1756 (in Chinese with English abstract).[6] Chen ZB, Qiu TS, Su R. FCM and level set based segmentation method for brain MR images. Acta Electronica Sinica, 2008,36(9):1733−1736 (in Chinese with English abstract).[7] Kass M, Witkin A, Terzopolos D. Snakes: Active contour models. Int’l Journal of Computer Vision, 1988,1(4):321−331.[8] Perona P, Malik J. Scale-Space and edge detection using anisotropic diffusion. IEEE Trans. on Pattern Analysis and MachinesIntelligence, 1990,12(7):629−639.[9] Catté F, Lions PL, Morel JM, Coll T. Image selective smoothing and edge detection by nonlinear diffusion. SIAM Journal onNumerical Analysis, 1992,29(1):182−193.[10] Vincent L, Soille P. Watersheds in digital space: An efficient algorithm based on immersion simulation. IEEE Trans. on PatterAnalysis and Machine Intelligence, 1991,13(6):583−598.[11] Osher S, Sethian JA. Fronts propagating with curvature dependent speed: Algorithms based on Hamilton-Jacobi formulations.Journal of Computational Physics, 1998,79(1):12−49.[12] Malladi R, Sethian J, Vemuri B. Shape modeling with front propagation: A level set approach. IEEE Trans. on Pattern Analysisand Machine Intelligence, 1995,17(2):158−174.附中文参考文献:[5] 宋利伟,宋朝昀,庄天戈.基于分水岭算法的磁共振脑图像自动分割.上海交通大学学报,2003,37(11):1754−1756.[6] 陈志彬,邱天爽,Su R.一种基于FCM和Level Set的MRI医学图像分割方法.电子学报,2008,36(9):1733−1736.税午阳(1983－),男,陕西西安人,博士生, CCF学生会员,主要研究领域为计算机图形学,医学图像处理.耿国华(1955－),女,博士,教授,博士生导师,CCF高级会员,主要研究领域为图像处理,模式识别,工程数据库.周明全(1954－),男,教授,博士生导师,CCF高级会员,主要研究领域为计算机图形学,数字图像处理,科学计算可视化.。
遗传算法融合回归模型
遗传算法融合回归模型遗传算法是一种基于生物进化原理的优化方法，它模拟了自然界中的生物进化过程，通过对解空间中的候选解进行优胜劣汰、交叉、变异等操作，从而达到寻找最优解的目的。
回归模型则是一种统计学习方法，它通过对数据的拟合来预测未知的数据。
遗传算法和回归模型的结合可以用于优化回归模型的结果。
在使用回归模型预测数据时，常常会遇到模型精度不够高的问题，这时可以使用遗传算法来寻找适合数据的最优参数，从而提高回归模型的预测精度。
1. 确定目标函数在进行优化之前，需要确定回归模型的目标函数。
目标函数是用来评估回归模型预测结果的好坏的，可以根据具体的需求进行调整。
2. 初始化种群根据遗传算法的原理，需要随机生成一定数量的候选解组成种群。
3. 适应度函数的构建适应度函数用来评估每一个种群中的个体的适应性。
在回归问题中，适应度函数可以用目标函数的值来表示。
4. 选择操作选择操作是指根据适应度值选出一定数量的优质个体，使其进入下一轮的进化过程。
常用的选择方法有轮盘赌选择和锦标赛选择。
5. 交叉操作交叉操作是指在选定的个体中随机选取两个个体，交换其基因片段来生成新的个体。
在回归问题中，可以采用单点交叉、多点交叉和均匀交叉等方法。
6. 变异操作变异操作是指在个体基因中随机改变一个或多个基因，以增加种群的多样性。
在回归问题中，可以采用随机变异、非随机变异等方式。
7. 判断终止条件为了避免种群无限制的繁殖下去，需要设置终止条件。
终止条件可以是达到一定的迭代次数或者收敛精度达到一定的要求。
8. 结果评估在遗传算法执行的每一轮中，需要记录当前最优解的适应度值和参数值，以便于最终的结果评估。
通常会比较最优解的预测结果和训练数据之间的误差，来判断遗传算法是否能够提高回归模型的预测精度。
总之，遗传算法融合回归模型可以在一定程度上提高回归模型的预测精度，但其实现过程比较复杂，需要较高的技术水平。
因此，在实际应用中，需要仔细评估遗传算法的适用性和可行性，以确保获得最优的结果。
图像模式识别 5-8章-PPT
区域分裂合并的关键是分裂合并准则的设计，在实际应用中，通常是 将区域生长算法和区域分裂合并算法这两种基本形式结合使用。该类 算法对某些复杂物体定义的复杂场景的分割或对某些自然景物的分割 等类似先验知识不足的图像分割，效果较为理想。
优点：对复杂图像的分割效果较好，不需要预先指定种子点；
缺点：算法较为复杂，计算量大，分裂可能会破坏区域的边界。
11
利用Matlab中的函数qtdecomp、qtsetblk和full能够实现图像的分 裂和合并操作。qtdecomp(I,threshold)函数将输入图像I按允许的 阀值threshold分割子块，返回一个稀疏矩阵，每个子块的左上角给 出子块的大小。qtgetblk(I,s,4,vals)函数可获得四叉树分解后的 子块的像素即位置信息，返回值vals是dim×dim×k矩阵，k是符合 dim×dim大小的子块个数，qtsetblk将四叉树分解得到的子块中符 合条件的部分替换为指定的子块。full(s)函数将稀疏矩阵化为普通 矩阵，显示分裂后的图像。以matlab自带图像rice.png为例，以阀 值为0.2进行四叉树分解，结果如图所示。
区域生长一般步骤为：
选取图像中的1点为种子点(种子点的选取需要具体情况具体分析)。
在种子点处进行8邻域或4邻域扩展，判定准则是：若考虑的像素与种 子像素灰度值差的绝对值小于某个门限T，则将该像素包括进种子像素 所在的区域。
当不再有像素满足加入这个区域的准则时，区域生长停止。
一般来说，在无像素或区域满足加入生长区域的条件时,区域生长就会 停止。 区域生长是串行区域技术，其分割过程后续步骤的处理要根据
前面步骤的结果进行判断而确定。
8
区域分裂、合并
首先，确定一个分裂合并的准则，即区域特征一致性的测度；然后 ，从整个图像出发不断分裂得到各个子区域，然后再把前景区域合 并，实现目标提取。若把一幅图像分裂到像素级，那么就可以判定 该像素是否为前景像素。当所有像素点或子区域完成判断后，把前 景区域或像素合并就可得到前景目标。 当相邻的子区域满足一致性特征时则将它们合成一个大区域，直至 所有区域不再满足分裂合并的条件为止；当分裂到不能再分的情况 时，分裂结束；然后它将查找相邻区域有没有相似的特征，若有就 将相似区域进行合并，最后达到分割的作用。
基于hausdorff距离和遗传算法的物体匹配方法
基于hausdorff距离和遗传算法的物体匹配方法随着计算机技术的发展，计算机视觉（computer vision）技术得到了长足的发展，在智能图像处理中，物体匹配已经成为一个重要的技术。
由于物体外观会随着观察角度、环境、尺度等参数而发生变化，导致物体识别问题非常困难，因此物体匹配也变得更加复杂，而且传统方法在准确度和效率上也存在着一定的局限性。
因此，开发一种新的、能更好地匹配物体外观的方向成为了重要的研究课题。
Hausdorff距离是在模式识别中一种常用的概念，它假设两个物体之间的距离与两者的外观相关。
此外，遗传算法是一种模拟现实生活的自然选择原理。
它根据某一特定任务的优化搜索空间，模拟种群的进化，以解决复杂的组合优化问题。
相较于传统方法，遗传算法具有更优的概率效果和更快的收敛速度，因此在许多应用中被大量使用。
基于Hausdorff距离和遗传算法的物体匹配方法是一种新型的模式匹配方法，它遵循Hausdorff距离的原理，可以计算出两个物体之间的最短距离，从而解决外观变化导致的物体匹配问题，可以准确无误地匹配物体，提高匹配的准确性。
此外，基于遗传算法的优势，这种物体匹配技术还拥有优异的搜索效率，能够有效地搜索出更好的匹配结果，将提高物体识别的准确性和效率。
首先，为了确定两个物体之间的Hausdorff距离，必须先进行特征提取。
基于Hausdorff距离的物体匹配方法从物体的视觉特征（如色彩、边缘等）中提取特征，然后将这些特征用于计算两个物体之间的距离，而不是传统的把物体的形状当做特征来计算距离。
Hausdorff距离的优势是它可以忽略物体形状的变化，从而更加准确地衡量两个物体之间的距离。
之后，基于遗传算法的物体匹配方法可以把Hausdorff距离转换为一个优化问题，使用遗传算法对每一对物体进行搜索，也就是寻找使Hausdorff距离最短的物体匹配结果。
当遗传算法找到最优匹配结果后，就可以通过比较对应特征之间的距离，来得到最终的匹配结果，也就是将物体A和物体B进行最佳匹配。
基于遗传算法B样条曲线优化在机器人轨迹规划中应用
基于遗传算法B样条曲线优化在机器人轨迹规划中应用一、概述随着科技的飞速发展，机器人技术已成为现代工程领域中的研究热点。
在机器人技术中，轨迹规划是机器人运动控制的关键环节，直接影响到机器人的运动性能、工作效率及能量消耗。
传统的机器人轨迹规划方法往往基于预设的路径进行优化，但在复杂环境和动态任务面前，这种方法的灵活性和适应性显得不足。
探索更为智能、高效的轨迹规划方法显得尤为重要。
基于遗传算法的B样条曲线优化在机器人轨迹规划中的应用逐渐受到关注。
遗传算法是一种模拟生物进化过程的智能优化算法，具有强大的全局搜索能力和自适应性，能够处理复杂的非线性、多峰值优化问题。
B样条曲线作为一种灵活的曲线描述工具，能够精确地表示复杂的空间曲线，且在机器人轨迹规划中具有良好的连续性和平滑性。
通过将遗传算法与B样条曲线优化相结合，可以在机器人轨迹规划中实现更为智能的优化过程。
可以利用遗传算法的全局搜索能力，对B样条曲线的控制点进行优化，从而得到更合适的机器人轨迹。
这种方法不仅可以提高机器人的运动性能，还可以适应复杂环境和动态任务的变化，为机器人轨迹规划提供新的解决方案。
基于遗传算法B样条曲线优化在机器人轨迹规划中的应用，是一种具有潜力的新方法。
本文旨在深入探讨这一方法的理论基础、实现过程、优势及其在实际应用中的效果，为机器人轨迹规划的研究提供新的思路和方向。
1. 介绍机器人技术的快速发展和广泛应用。
随着科技的飞速进步，机器人技术已成为当今工业、医疗、军事、服务等多个领域不可或缺的重要技术。
机器人技术的快速发展得益于计算机、电子、传感器、人工智能等多个领域的融合与协同推进。
尤其在轨迹规划方面，随着算法的持续创新和优化，机器人运动的精准性和效率性不断提高。
在此背景下，机器人轨迹规划的重要性愈发凸显，它关乎机器人的工作效率、能源利用率以及人机交互的流畅性。
机器人技术的广泛应用使得其在生产制造、物流运输、医疗手术、家庭服务等领域大放异彩，极大地提高了生产效率和人们的生活质量。
利用遗传算法设计神经网络模型
利用遗传算法设计神经网络模型神经网络是一种模拟人类神经系统功能的数学模型，广泛应用于机器学习和人工智能领域。
设计一个高效准确的神经网络模型是一个复杂而关键的任务。
而遗传算法则是一种基于进化的优化算法，具有全局搜索和自适应优化的特点。
本文将探讨如何利用遗传算法设计神经网络模型。
一、神经网络模型简介神经网络模型由多个神经元和连接它们的权重组成，可以通过训练来学习数据的特征和模式。
它是一种多层结构的模型，一般包括输入层、隐藏层和输出层。
输入层接收输入数据，隐藏层通过一系列非线性变换将输入数据转化为更高级的表示，输出层对隐藏层的输出进行分类或回归预测。
二、遗传算法简介遗传算法是一种模拟达尔文进化论的优化算法，通过模拟生物进化中的自然选择、交叉和变异等过程，来找到问题的最优解。
遗传算法的基本思想是将问题解空间中的每个解编码成染色体，通过基因的交叉和变异来生成新的个体，并利用适应度函数来评估每个个体的适应性。
经过多代进化，逐渐找到最优解。
三、利用遗传算法设计神经网络模型的步骤1. 确定神经网络结构首先，需要确定神经网络的结构，包括输入层的维度、隐藏层的层数和神经元数量，输出层的维度等。
这一步需要根据具体问题和数据情况进行决策。
2. 初始化种群使用遗传算法设计神经网络模型时，首先需要初始化一个种群，即一组初始解。
每个个体代表一个神经网络模型，通过染色体来编码模型的结构和权重。
3. 适应度评估根据适应度函数对种群中的每个个体进行评估，评估个体的适应性。
适应度函数可以根据实际问题来选择，一般可以选择模型在训练集上的准确率或者损失函数的值作为适应度。
4. 选择操作根据适应度函数的评估结果，使用选择操作选择适应度较高的个体作为父代，用于产生下一代。
选择操作可以使用轮盘赌算法、锦标赛选择等方法。
5. 交叉操作从选出的父代中进行交叉操作，生成新的个体。
交叉操作可以采用单点交叉、多点交叉或均匀交叉等方式。
6. 变异操作对新生成的个体进行变异操作，引入新的基因信息，增加种群的多样性。
遗传算法在图像生成与特征提取中的应用技巧
遗传算法在图像生成与特征提取中的应用技巧遗传算法是一种模拟自然界进化过程的优化算法，在图像生成和特征提取领域有着广泛的应用。
本文将探讨遗传算法在这两个领域中的应用技巧，并介绍一些相关的案例。
一、遗传算法在图像生成中的应用技巧1.1 基于遗传算法的图像生成方法遗传算法可以通过对图像的像素值进行编码，通过进化过程来生成新的图像。
首先，将图像转化为一个个像素点，并将每个像素点的像素值编码成遗传算法中的染色体。
然后，通过选择、交叉和变异等操作，对染色体进行进化，生成新的染色体。
最后，将新的染色体解码成图像，即可得到生成的图像。
1.2 遗传算法在图像生成中的优化策略在图像生成过程中，遗传算法可以通过优化策略来提高生成图像的质量。
例如，可以通过适应度函数来评估生成图像的好坏，然后根据适应度值选择优秀的染色体进行繁殖。
此外，还可以通过调整遗传算法的参数，如种群大小、交叉概率和变异概率等，来优化生成图像的效果。
1.3 遗传算法在图像生成中的应用案例遗传算法在图像生成领域有着广泛的应用。
例如，可以利用遗传算法生成艺术风格的图像，通过对染色体进行进化，生成具有特定艺术风格的图像。
此外，还可以利用遗传算法生成逼真的人脸图像，通过对染色体进行进化，生成具有真实感的人脸图像。
二、遗传算法在特征提取中的应用技巧2.1 基于遗传算法的特征选择方法特征选择是特征提取的关键步骤，可以通过遗传算法来进行优化。
遗传算法可以通过选择、交叉和变异等操作，对特征进行进化，选择出对目标任务最有用的特征。
通过遗传算法进行特征选择，可以提高特征的判别能力，减少特征的冗余性。
2.2 遗传算法在特征提取中的优化策略在特征提取过程中，遗传算法可以通过优化策略来提高特征的质量。
例如，可以通过适应度函数来评估特征的好坏，然后根据适应度值选择优秀的特征进行进化。
此外，还可以通过调整遗传算法的参数，如种群大小、交叉概率和变异概率等，来优化特征的效果。
2.3 遗传算法在特征提取中的应用案例遗传算法在特征提取领域也有着广泛的应用。
基于CT图像的肺实质分割技术研究
ａ ｄ ｎ ｔ ｒ ｆｌｎ ａｅ ｃ ｙ ａｓｇ ｅ ｔｔｏ ｎ ａｕ ｅｏ ｇ ｐ ｒ ｎ ｈ ｍ ｅ ｍ ｎ ａｉｎ，ａ ｄ ｉｓｉ ｕ ｎ ｔ ｍｐｏ ｔｎ ｉ ｎｆｃ ｎ ｅ ｉ ｌ ｃ ｌｔｅ ｔ ｅ ｔ ｒａ ｔｓｇ ｉ ａ ｃ ｎ ｃｉ ａ ｒ ａｍ ｎ ．Ａ ａｈ ｒ ｉ ｎｉ ｒｔ ｅ
Ａｂｓ ｒ ｃ ： ｔ ａ ｔ Ｔｈ ｕ ｇ ｐａ ｅ ｃ ｙ ａ ｓ ｇ ｅ ｔ ｔ ｎ ｂ ｓ ｄ ｏ ｅ ｌ ｎ ｒ ｎ ｈ ｍ ｅ ｍ ｎ ａｉ ａ ｅ ｎ ＣＴ ｍ ａ ｅ ｓｎ ｔｏ ｌ ｈｅ ｍ ｏ ｔｂ ｓｃ ａ ｄ ｉ ｏ ｔ ｎ ｏ ｉ ｇ ｓｉ ｏ ｎ ｙ ｔ ｓ ａｉ ｎ ｍｐ ｒａ ｔ ｔ ｃ ｎ ｌ ｇ ｏ ｈ Ｈ ｗｉ ｇ ｐ ｏ ｅ ｓ ｇ ｂ ｔａｓ ｙ ｉａ ｙ ｄ ｆ ｃ ｌ ｐ ｏ ｌ ｍ ． ｅ ａ ｃ ｒ ｔ ｎ ｅ ｅ ｔｔ ｎ ｉ ｅ ｈ ｏ ｏ ｙ ｆ ｒｔ ｅ ｆ ｏ ｎ ｒ ｃ ｓｉ ， ｕ ｌｏ ａ ｔ ｐ ｃ ｌ ｉ ｕ ｔ ｒ ｂ ｅ ｏ ｎ ｌ ｉ Ｔｈ ｃ ｕ ａ ｅ ｌ ｇ ｓ ｍ ｎ ａ ｉ ｓ ｕ ｏ ｔ ｅ ｐ ｅ ｉ ｆｑ ａ ｔ ａ ｉ ｅ ａ ａｙ ｉ， ｏ ｈ ｒ ｍ ｓ ｏ ｕ ｎ ｉ ｔ ｎ ｌ ｓ ｃ ｍｐ ｔ ｒａｄ ｄ ｄ ａ ｎ ｓ ｎ ｒ ａｍ ｅ ｔ Ｔｈ ｓｐ ｐ ｒｉ ｔｏ ｕ ｅ ｈ ｏ ｃ ｐ ｅ ｔ ｖ ｓ ｕ ｅ ｉ ｅ ｉｇ ｏ ｉ ａ ｄ ｔｅ ｔ ｎ ． ｉ ａ ｅ ｎ ｒ ｄ ｃ ｄ ｔ ｅ ｃ ｎ ｅ ｔ ｓ
解决的问题。基于Ｃ 图像的精确的肺实质分割是数学分析 、计算机辅助分析和治疗的前提。本文明确了 Ｔ 肺实质分割的概念及本质，以及肺实质分割在临床治疗中的重大意义。重点介绍了阈值法、区域生长法、
基于机器学习和遗传算法的非局部晶体塑性模型参数识别
基于机器学习和遗传算法的非局部晶体塑性模型参数识别周瑞;熊宇凯;储节磊;阚前华;康国政;张旭【期刊名称】《力学学报》【年(卷),期】2024(56)3【摘要】非局部晶体塑性模型考虑了由非均匀变形引起的位错在空间上的重排,使得其本构模型变得复杂,可调节参数众多,因此采用常规的“试错法”难以准确确定这些参数.虽然遗传算法能够稳健地全局优化解决参数确定问题,但对于非局部晶体塑性模型,其计算成本相对较高.为解决这一问题,提出了一种耦合机器学习模型的遗传算法,以有效降低计算成本.针对含有冷却孔的镍基高温合金的拉伸响应问题,以单拉应力-应变曲线为目标,基于屈服应力和最终应力建立评价公式,使得优化结果与实验尽可能接近.在这一方法中,机器学习模型能够通过非局部晶体塑性模型的参数来预测相应的应力值,从而替代了遗传算法中原本需要的有限元计算过程.为了分析本构模型参数对单拉力学响应的影响,研究采用SHAP框架,并通过有限元结果进行验证.结果表明,通过该方法可以有效获取非局部晶体塑性模型参数,使得参数计算得到的应力-应变响应与实验结果吻合较好.此外, SHAP框架能够提供本构模型参数的重要程度分析,以及对屈服应力和最终应力的影响.【总页数】12页(P751-762)【作者】周瑞;熊宇凯;储节磊;阚前华;康国政;张旭【作者单位】西南交通大学力学与航空航天学院;西南交通大学计算机与人工智能学院【正文语种】中文【中图分类】O344【相关文献】1.基于非局部塑性模型的应变局部化理论分析及数值模拟2.基于非局部位错密度晶体塑性有限元模型的金属晶体薄膜微弯曲变形特点3.基于粘-弹-塑性模型对磁流变胶非线性滞回行为模型参数识别4.晶体塑性本构模型材料参数识别方法研究因版权原因，仅展示原文概要，查看原文内容请购买。
一种医学图像的轮廓提取方法
一种医学图像的轮廓提取方法
罗三定;王建军
【期刊名称】《计算机工程》
【年(卷),期】2010(036)005
【摘要】针对医学图像的模糊性和灰度不均导致目标轮廓难以准确提取的问题,提出使用改进的遗传算法控制主动轮廓模型完成边界提取的方法.采用保优算子保留遗传性状,选择适当的交叉算子,在进化后期可实现由整体寻优到局部寻优的转变.实验结果证明,该方法在提取目标轮廓时抗模糊能力强、鲁棒性好.
【总页数】3页(P218-220)
【作者】罗三定;王建军
【作者单位】中南大学信息科学与工程学院,长沙,410083;中南大学信息科学与工程学院,长沙,410083
【正文语种】中文
【中图分类】TP391
【相关文献】
1.一种改进的医学图像目标轮廓跟踪算法 [J], 王金川;黄雪梅;郝园
2.医学图像中组织轮廓提取方法的改进 [J], 郑丽萍;李光耀;于承敏;李寰
3.一种基于轮廓的医学图像弹性配准方法 [J], 舒小华;沈振康
4.一种辅助轮廓线的断层医学图像三维重建算法 [J], 黎蔚;韩利华;陈家新;冀治航
5.医学图像边界轮廓线的一种提取方法 [J], 张太发;蔡吉花;程东旭
因版权原因，仅展示原文概要，查看原文内容请购买。
基于遗传算法的优化问题求解系统设计
基于遗传算法的优化问题求解系统设计人类一直都在转变自然力量为自己所用，其中一种方式就是借鉴自然进化的原理来解决现实中的优化问题。
而遗传算法正是基于这一原理构建的一类算法。
相信大家对遗传算法并不陌生，那么今天我来为大家介绍关于基于遗传算法的优化问题求解系统的设计。
一、遗传算法的基本原理遗传算法是一种模拟自然进化的搜索算法，主要由遗传、交叉和变异三个操作构成。
整个算法的执行过程模拟了自然界中的生物进化过程，从而达到优化的目的。
具体来说，遗传算法的步骤包括以下几个：1. 初始化种群：随机生成一些初始的解作为种群。
2. 适应度函数：根据问题的不同，设计不同的适应度函数，将每个个体映射到一个实数值上。
3. 选择：根据适应度函数，从种群中选择一些高适应度的个体，保留其基因信息。
4. 对选中的个体进行交叉和变异操作，产生新的解。
5. 判断是否满足结束条件。
如果满足，输出当前最优解；否则，返回第2步。
通过以上几个步骤，遗传算法就可以不断地寻找最优解，适用于那些复杂的优化问题，例如组合优化、约束优化等等。
二、基于遗传算法的优化问题求解系统的设计基于遗传算法的优化问题求解系统视具体问题而定，但一般都是由两个部分组成：遗传算法的求解器和一个相应问题的解析器，前者负责遗传算法的流程实现及优化解的寻找，后者则提供问题定义、问题转换及问题解析等功能。
下面我将从这两个方面来阐述。
1. 遗传算法的求解器遗传算法的本质就是一个搜索算法，其求解器的流程通常包括以下几个步骤：（1）初始化：确定问题的解的范围及初始化种群。
（2）评价：选取适当的适应度函数，对当前种群进行评估。
（3）选择：根据适应度大小，选出一些较好的个体进入下一代。
（4）交叉：对选中的个体进行交叉操作。
（5）变异：对交叉后的个体进行变异操作。
（6）终止条件：到达预设的停止条件时，输出最终结果，否则返回步骤（2）。
特别是在实现过程中要注意以下几个问题：（1）如何设置遗传操作的参数（如种群大小、交叉率、变异率等）？（2）如何选择合适的适应度函数？（3）如何处理解的编码问题？解决上述问题的核心在于需要对具体的问题有清晰的认识，对遗传算法的算法细节进行笼统的概括、简单的拷贝并不会有效果。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第8卷(A 版) 第1期2003年1月中国图象图形学报Jour nal of Image and GraphicsV ol.8(A ),N o.1Jan.2003收稿日期:2001-04-23;改回日期:2002-04-19基于遗传算法的主动轮廓模型刘志俭(国防科技大学自动控制系,长沙 410073)摘 要 由K ass 等人提出的主动轮廓模型,本质上是一条能量最小化的轮廓曲线.它作为一种全新的采用自上而下机制的图象目标提取方法,由于它有效地利用了高级信息,从而提高了目标提取的速度和准确性,已经在数字图象处理和计算机视觉领域得到了广泛的应用.原始的主动轮廓模型算法可以分为构造能量函数、推导欧拉方程、离散化和迭代求解4步.但该算法存在许多问题,为此在分析原始主动轮廓模型算法和一些改进算法的基础上,提出了一种基于遗传算法的主动轮廓模型算法,并给出实验结果.实验结果证明,基于遗传算法的主动轮廓模型不仅成功地解决了原方法收敛易陷入局部最小值的问题,也提高了目标提取的成功率.关键词 主动轮廓模型 遗传算法 目标提取中图法分类号:T P 391.41 文献标识码:A 文章编号:1006-8961(2003)01-0041-06Active Contour Model Based on Genetic AlgorithmLIU Zhi-jian(De p artment of A utomatic Control ,N ational Univ ersity o f De f ence T echnology ,Chang sha 410073)Abstract A ctiv e Co nto ur M odel intr oduced by K ass et al is a ener gy -minim izing cur ve in essentia l .It is a new method o f imag e object ex tr act ion ba sed o n to p-do w n mechanism ,which makes use o f hig h lev el infor mation t o impr ove t he speed a nd v eracity of object ex traction.It has been used mor e and mo re w idely in applicatio ns of imag e analy sis and computer v isio n .T he or ig inal alg or ithm o f activ e co ntour model inv olves fo ur steps :setting up a var iat ional int egr al on the continuo us,deriv ing a pair of Euler equat ions,discr etizing t hem ,a nd so lv ing the discr ete equat ions.T his algo rit hm suffer s a number of pro blems.In this pa per ,w e w ill firstly discuss the o riginal algo rithm and so me impr ov ed alg or it hms of active co nt our model ,then pr opose a alg or it hm based o n the g enetic algo rithm and pr esent the ex periment r esult.T he r esult pr ov es that genetic alg or ithm set tles the pro blem of or ig inal model t hat run into the lo cal least value end enhance the success ra tio of the o bject ext raction.Keywords A ctiv e contour model ,G enetic alg or ithm ,Object extr actio n0 引 言主动轮廓模型[1](又称为蛇)是由Kass 等人提出的一种全新图象目标提取方法.由于其本质上是一条能量最小化的轮廓曲线,因此它的能量函数可以通过一个积分方程来定义,而且它不同于经典的M ar r 视觉计算理论所描述的自下而上的处理过程,而是一种自上而下的充分利用高级信息的处理过程.用该方法进行目标提取时,首先将一个初始化的主动轮廓放置在图象中感兴趣目标的周围,然后在图象作用力、轮廓曲线内部作用力以及外部约束的联合作用下,将该轮廓最终收敛到目标.使用这种模型进行目标提取有诸多好处:¹由于融合了高级信息,即可在提取过程的开始就将注意力放在所希望提取的目标上,因此可大量地减少计算量;º由于使用这种模型可以消除所希望提取的目标上因纹理或噪声而造成的不连续,因此能得到完整的目标轮廓,而不会将目标分为几个小的区域;»与传统的模板方法不同,这种模型不受目标形状的约束,就可以提取任意形状的目标,并且能够及时适应目标形状发生的变化,在目标追踪中有着极大的应用价值.但是由于原始的主动轮廓模型算法(简称原始算法)存在着许多问题,如解的最优性、计算的稳定性、陷入局部最小值以及无法加入外部强约束等,因此在一定程度上限制了模型的应用范围.本文在讨论和分析原始主动轮廓模型及其算法的基础上,结合一些改进算法,提出一种基于遗传算法的主动轮廓模型算法,并且给出了实验结果.1 原始主动轮廓模型及其算法原始的主动轮廓模型为一条在图象空间域内移动的能量最小化的曲线v (s )=(x (s ),y (s )),其中,s 为弧长,其能量函数定义如下E snake =∫sE int(v (s ))+E image (v (s ))+E con (v (s ))d s(1)式中,E int 、E image 和E con 分别代表主动轮廓模型内部作用力产生的能量项,图象作用力产生的能量项和外部约束力产生的能量项.其中,E int 由主动轮廓v (s )关于弧长s 的一阶导数v s (s )和二阶导数v ss (s )构成,即E int (s )=12(A (s )v s (s )2+B (s )v ss (s )2) (2)式中,v s (s )2≡5v /5s 2≈v i -v i -12,v ss (s )2≡52v /5s 22≈v i -1-2v i +v i +12,v i 为离散化后的控制点;A (s )和B (s )为权重参数.该公式说明E int (s )是由一个受A (s )控制的一阶项和一个受B (s )控制的二阶项组成的,其中一阶项表示曲线的斜率,用于控制曲线的连续性;二阶项表示曲线的曲率,用于控制曲线的弯曲程度.通过调整A (s )与B (s )的大小,可以分别改变曲线的斜率和曲率对曲线影响的大小,例如,当设置某点的A (s )=0时,则曲线在该点的斜率可以为无穷大,即允许曲线在该点可以不连续;若设置B (s )=0,则允许曲线在该点可以为一个角.E image 为线能量、边缘能量以及端点能量的线性组合,它们均可由图象信息获得,该能量函数可以表示为E image (s )=X line (s )E line (s )+X edge (s )E edge (s )+X term (s )E term (s )(其中,X line (s ),X edge (s )和X ter m (s )为权重参数,的.综上所述,在实际选取A (s )、B (s )、X line (s )、X edge (s )和X term (s )时,需要根据实际需要提取的目标形状来选取不同的数值.令E ext =E image +E con ,则可以将主动轮廓模型的能量函数重新描述为∫s 12(A (s )v s (s )2+B (s )v ss (s )2)+E ext (v (s ))d s (4)用F (s ,v s ,v ss )表示被积函数,由欧拉-拉格朗日必要条件可知,如果要使方程(4)取极小值,那么它必须满足下面的欧拉方程F v -5F v s 5s +52F v ss5s 2=0(5)将相应的能量函数项代入以上方程,就可以得到一对相互独立的欧拉方程-A x s +B x ss +5E ext5x=0(6)-A y s +B y ss +5E ext5y=0(7)其中,x ,y 代表控制点v 的坐标,为s 的函数,x s 、y s 表示对s 求一阶导,x ss 、y ss 表示对s 求二阶导[1].可将以上两个方程合并为如下一个单独的方程-A v s +B v ss +¨E ext (v )=0(8)取空间步长为h ,对方程(8)进行离散化,可以得到1h (a i (v i -v i -1)-a i +1(v i +1-v i ))+b i -1h 2(v i -2-2v i -1+v i )-2b ih 2(v i -1-2v i +v i +1)+b i +1h2(v i +2-2v i +1+v i )-(E x (v i ),E y (v i ))=0 (9)式中,v i =v (i ×h );a i =A (i ×h )h ;b i =B (i ×h )h 2.方程(9)的矩阵形式为A v +¨E ext (v )=0(10)或Ax +¨E xext (x ,y )=0Ay +¨E y ext (x ,y )=0(11)其中,A 为一个五对角线矩阵.由于一方面考虑到能量函数不是一个凸函数,它可能存在多个局部最小值;另一方面,由于希望在给定的区域内搜索到一个较好的轮廓,所以假定对轮廓曲线已有一个大概的估计,且比较接近实际数A v s +B v s s +¨E ext (v )=0s )=v 0(s ),0)=v 0(0),v (t ,1)=v 0(1)t ,0)=v 0,s (0),v s (t ,1)=v 0,s (1)(12)42中国图象图形学报第8卷(A 版)取时间步长为S和空间步长h,对方程(12)进行离散化得(I+S A)v〈t〉=(v〈t-1〉-S¨E ext(v〈t-1〉))(13)或x〈t〉=(A+K I)-1(K x〈t-1〉-¨E x ext(x〈t-1〉,y〈t-1〉))y〈t〉=(A+K I)-1(K x〈t-1〉-¨E y ext(x〈t-1〉,y〈t-1〉))(14)其中,K=1/S.通过迭代上述方程,就可以求得最终解.2 对原始算法及其改进算法的分析由第1节对原始主动轮廓模型及其算法进行的一般性描述可以发现,由于经典变分方法的使用,导致原始算法中存在着相当多的缺陷:¹由于欧拉-拉格朗日条件仅仅为一个必要条件,而非充要条件,所以并不能保证所求得的解,具有最优性或者相对最优性,在极端情况下,甚至有可能用最大值取代最小值;º基于拉格朗日方法进行求解,对加入方程中的外部强约束有着相当高的要求,即要求外部强约束必须可导,从而极大地增加了计算量,并且导致相当一部分的强约束不能使用;»在使用变分方法进行求解时,必须使用离散的数据来对高阶导数进行估计,但这个过程对噪声相当敏感,有可能导致数值计算的不稳定;¼在寻找最优的数值解时,由于使用了Gauss-Seidel或Jacobi方法,因此必须非常注意解过程的收敛性.由于原始算法存在以上缺陷,Amini等人提出了一种基于动态规划法的改进算法[2],该算法对原始的主动轮廓模型进行了改进,其基本思想为:首先将主动轮廓模型进行离散化,再用一系列的控制点的连线来表示轮廓曲线,这里控制点为实际数字图象中的像素点;然后分别对这些控制点进行能量计算,求和后,就得到了主动轮廓模型的总能量,这样就将原始能量函数的积分形式变为如下求和形式∑n-1i=0(E int(i)+E ext(i))(15)最后在离散的解空间中,利用动态规划法进行全面的搜索,从而求得最优解.这种方法由于从一定程度上解决了原始算法中的一些缺陷,因此不但可以保证算法的收敛性和解的相对最优性,而且可以取消对外部强约束的限制,详细解法可参考文献[2].但是这种算法也存在自身的弱点,由于进行全局解空间的搜索,其计算量和存储量十分巨大,分别为O(n(m+1)3)和n×(m+1)2,其中,n为控制点的个数,m为搜索邻域大小,并且随着控制点的增加和搜索域的增大,计算量和存储量将以几何级数增长,故W illiam s等人针对这个问题,基于Amini等人的思想,又提出了一种改进算法——贪婪算法,对模型算法进行了进一步的改进,他们认为,每一个控制点的能量仅仅与其相邻的控制点有关,而与其他点无关,这样就可以对每一个控制点在其邻域内进行求解,并且认为,其中使控制点能量最小的位置即是当前该控制点的最佳位置,由于其无须像动态规划法那样进行全局的判断,从而也就可大量地节省计算时间,即可以将计算量降低为O(n(m+1)),但是值得注意的一点是,该算法并不保证能够找到最优解,只是找到次优解.详细的算法见参见文献[3].以上两个改进算法都致力于改进原始算法数值计算的稳定性以及外部约束的使用,而对解的最优性考虑则仅仅停留在理想状况下,即图象的信噪比增高,图象质量好的情况.由此不难看到,当在图象中存在一定噪声的情况下,一些控制点将在某些区域陷入能量的局部最小值,并且停留在这些区域不再移动,从而形成连锁反应,最终导致主动轮廓不能收敛到目标轮廓.3 基于遗传算法的主动轮廓模型遗传算法[4～6]是一种模拟自然进化过程,即按照适者生存、优胜劣汰的原则,采用复制、杂交和变异算子来研究线性和非线性问题状态空间的所有区域,并对其中最有希望的区域进行开发,从而获得问题的最优解的计算方法.在算法计算过程得到的每一代种群中,适应值越大的个体被复制,并在下一代中被保留下来的希望越大,从而保证了种群的进化趋势.与传统的优化算法相比,遗传算法有诸多不同之处,首先,遗传算法不是从单个点开始进行搜索,而是从一个种群开始搜索;其次,遗传算法只需利用所定义的适应值函数来计算所得的适应值信息,而无需导数或其他信息;第三,遗传算法只利用概率的和随机的转移规则,而不利用任何确定性的转移规则.遗传算法的优越性主要表现在:搜索最优解的过程中,由于其不易陷入局部最优解,因此即使在所定义的适应函数是不连续的、非规则的情况或存在大量噪声的情况下,它也能以最大的概率搜寻到整体的最优解.这也是本文之所以选用遗传算法来对主43第1期刘志俭:基于遗传算法的主动轮廓模型动轮廓模型进行求解的原因.在本文中,对于主动轮廓模型的描述仍将采用Amini等人的提出的离散化思想,即用一系列的离散的控制点来描述主动轮廓曲线,并将一个连续的能量最小化问题转换为一个离散的组合优化问题,以便于遗传算法的应用,其能量函数的定义参见方程(15),同时该方程也是应用遗传算法时,适应值函数的定义.另外,遗传算法的成功应用,需要解决染色体的表示、遗传算子的定义、初始种群的选择、终止条件的选择以及适应值函数的定义等5个方面的基本问题.下面将针对遗传算法在主动轮廓模型中的应用,对这些问题进行全面的讨论.3.1 染色体的表示对于任何一种遗传算法,染色体的表示(即解的表示)都是一个基础性的问题,它的表述方式不但决定了目标问题在遗传算法中的构造方式,而且决定了选用何种遗传算子,并对以后的计算有着巨大的影响.一般来说,染色体是由一系列基因组合而成,其中基因在一定的范围内取值,例如可以为二进制的0和1,也可以为字母表中的A、B、C、D等.在最初Holland的设计中,是将基因的取值范围限制为二进制的0和1,但是随着应用范围的拓展,已经明显不能有效地表示问题的解.文献[7]已经证明,用自然的方式来表示基因的取值,不但可以提高算法的效率,而且可以搜寻到更好的解.本文算法是将主动轮廓模型的每一个控制点都作为一个基因,再用所有控制点序列构成的基因串来表示染色体,其中不同的控制点位置,即不同的基因取值分别代表不同的解序列.本文算法是将基因的取值与控制点的位置相联系,并且给出一定的连通区域,从而限制了控制点的移动范围,也就限定了基因的取值范围.为了表示方便,可以将该连通区域内的所有像素点进行编号,从1至n,n 为连通区域内像素的总数,这样就可以将基因的取值范围限定为[1,n]区间内的所有正整数.染色体可以用一个1×(m+1)的向量来表示,该向量前m项为用基因表示的控制点序列,m为控制点的总数,最后一项为当前控制点序列的适应值.3.2 遗传算子遗传算子分为复制算子、杂交算子和变异算子3种类型,其中复制算子的主要作用是从目前的种群中选择个体,并复制到下一代种群中.常用的复制算子的选择方案有Roulette w heel法及其扩展、Scaling法、To urnament法、Elitist法和Ranking法等几种.其中Roulette wheel法是最早的一种选择方案,该方案中每一个个体被选择的概率由如下公式定义:P c,i=F i∑kj=1F j(16)其中,F i为个体i的适应值,k为群体中个体的总数,但由于这种选择方案有一个显著的缺点,即适应值不能为负,所以应用不广.在本文的算法中,首先将当前群体中的个体,按适应值大小,由大到小进行个体等级排序,无论正负,最大的个体等级为1,最小的个体等级为k,即个体的总数,然后按以下公式计算被复制的概率:P r,i=q′(1-q)〈r-1〉(17)其中,q为最优个体被选择的概率,r为个体i的等级,q′=q1-(1-q)k,k为个体的总数.杂交算子的作用是在由复制算子得到的新一代种群中,任意选择两个个体进行交配,以便获得新的个体.在本文的算法中,使用的是一种启发式的杂交算子,这是目前为数不多的利用个体适应值的杂交算子之一.它通过利用父代个体X-和Y-的适应值,由下式得到新的个体X-′X-′=X-+r(X--Y-)(18)Y-′=X-(19)再由逻辑判断量(feasibility)L来判断新个体X-′的可行性L=1x′i E a i,x′i F b i0other wise;对于任意的i (20)其中,r∈[0,1],a i和b i分别为基因取值范围的上界和下界,并且个体X-的适应值大于个体Y-的适应值.如果取值为零,则拒绝X-′,并重新产生一个随机数r,再次计算X-′.如果在指定的迭代次数内,其所产生的X-′均被拒绝,则令子代等于父代,并返回.变异算子则是用于在由复制算子得到的新一代种群中任意选取一个个体,并随机地抽取该个体的某些基因进行随机变化,从而得到新的个体.目前应用于变异的遗传算子有很多,如均匀变异算子,非均匀变异算子,边缘变异算子等等,且它们基本上都是基于随机数的变异,没有引入外部信息.通过观察主动轮廓模型的收敛过程发现,其移动有明显的方向性,例如,当初始化的主动轮廓放置在目标轮廓的内部时,模型上所有的控制点均沿它们法线方向向外移动;而当初始化的主动轮廓放置在目标轮廓的外44中国图象图形学报第8卷(A版)部时,模型上所有的控制点则沿它们法线方向向内移动.为本文提出了一种基于方向的变异算子,其用矢量的形式可以表示如下方程x ′i =c (b -x i )+x i r E 0.5x i r <0.5(21)其中,r 和c 为[0,1]之间的随机数,x i 为基因x i 移动的法线方向,b 为在基因x i 的取值范围内,沿x i 的法线方向距离x i 最远的矢量,关于基因x i 可以任意选择,任意选取.在本文算法中,将这种基于方向的变异算子和均匀变异算子联合使用,不仅收到了较好的效果,也明显地降低了进化的代数.3.3 初始种群,终止条件的选择和适应值函数的定义应用遗传算法必须提供一个初始的种群,因为该种群的选择对遗传算法的进化速度有一定的影响,但是目前基本上尚没有一种较为完善的选择方法,即基本上都是采用盲目的随机选择方法.本文算法认为,给定的初始主动轮廓是一个比较好或者近似的解,而且在该初始主动轮廓的邻域内,结合模型移动的方向,就可随机地选择初始种群,而一般种群的规模就是用户给出的控制点的个数.遗传算法何时结束主要由算法的终止条件来决定,一般有3种选择,即适应值落在一定的区域内,进化超过一定的代数或者两者同时使用.但是在主动轮廓模型中,因为对算法结束时的适应值大小根本无法在算法开始前进行估计,所以算法结束的唯一条件是进化超过一定的代数.关于适应值函数,在3.1节已经定义,在此不再重复.3.4 算法流程基于遗传算法的主动轮廓模型搜索算法的大致流程如下:(1)给定初始的主动轮廓Z 1(2)开始循环¹i ←1º以Z i 为初始轮廓,构造一个初始种群»j ←1¼应用复制算子从第j -1代种群S j -1来构造第j 代的初始种群S j½对第j 代的初始种群S j 应用杂交算子和变异算子产生新的第j 代的种群S ′j ¾对种群中所有的个体计算适应值¿j ←j +1À返回到第»步重复执行,直至满足遗传算法的终止条件为止Á从当前种群中的所有个体中寻找适应值最小的个体,并记为Ab ki ←i +1,并令Z i =A ,判断ûZ i -Z i -1û<D 是否成立,D 为一个相当小的正数:若成立,则退出循环,否则返回第¹步,重复执行(3)以Z i 为最优解,算法成功退出4 实验结果由于图象质量的原因,医学图象中的目标提取一直都是一个比较困难的问题.自从主动轮廓模型被提出后,由于其具有各种优良特性,故很快被应用于医学图象中的目标提取,但是由于其能量易陷入局部最小值,从而极大地影响了其实际应用效果.本文采用遗传算法对该模型进行改进后,目标的提取效果得到了明显的改进.图1为实验结果.在计算时间上,原始算法和遗传算法的提取结果没有太大的区别,在赛扬300CPU 、128M 内存的个人计算机上,计算时间分别为2.45s 和2.21s ,两种算法时间相近,是因为计算时间主要与控制点的数目、遗传算法的初始种群的选择以及结束条件的选择有关.在本文的结果中,遗传算法的进化代数为40.(a )原图(b )遗传算法提取过程(c )遗传算法提取结果(d )原始算法提取过程(e )原始算法提取结果图1 医学图象不同算法的提取过程和提取结果(图中央黑色的区域为提取目标,白色圆为初始轮廓)45第1期刘志俭:基于遗传算法的主动轮廓模型 实验结果表明,如果遗传算法的进化代数选择合理,那么在一般情况下,不仅可以得到比原始算法好的提取结果,而且算法具有较好的抗干扰能力,其不足之处在于,遗传算法的进化代数需要人为的选择,下一步的工作是使算法能根据实际的情况自动地选择进化代数,以便为算法实现自主性、缩短计算时间和提高成功率打下基础.参考文献1 Kas s M,W inkin A,Terzopoulos D.Sn akes:Active contour models[A].In:Proceedings of Fir st Intern ational Conference On Computer Vis ion[C],London,1987:259～269.2 Amini A,Tehrani S,W eymouth E.U sing dynamic programming for min imizing the active con tour s in the presen ce of hard cons tr aints[A].In:Proceeding s,S econd Internation al Conference on Comp uter Vision[C],New York,1988:95～99. 3 William D,Sh ah M.A fas t algorith m for active contou r and cur vature estimation[J].C om puter Vis ion Gr aph ics,Image Process,1992,10(55):14～26.4 刘勇,康立山,陈毓屏.非数值并行算法——遗传算法(第二册) [M].北京:科学出版社,1995.5 Bersini H,Renders B.Hybridizin g g enetic algorithms w ith hill-climb ing meth od s for global optimization:T wo pos sible w ays[A].In:IEEE International Symp os ium EvolutionaryCom putation[C].Orlando,FL,US A,1994:312～317.6 J oines J,Houck C.On the us e of n on-stationary penalty functions to solve con strain ed optimiz ation pr ob lem s w ith g enetic algorithm s[A].In:IEEE Intern ational Sympos ium Evolutionary Com putation[C],Orlando,FL,US A,1994:579～584.7 M ichalew icz Z.Genetic algorithms+data structures=evolution pr ogr ams,AI Series[M],New York,S pringer-Verlag,1994. 刘志俭 1975年生,现为国防科技大学自动控制系博士研究生.研究方向为智能控制和模式识别.中国科技期刊引证报告——总被引频次分类排序表(计算技术类)名次期刊名称总被引频次影响因子名次期刊名称总被引频次影响因子1计算机学报6040.63115中文信息学报1270.4942计算机科学5390.65416微型电脑应用1010.1873软件学报4840.56017微型机与应用800.1034计算机研究与发展4840.56018计算机仿真790.2475计算机工程与应用4700.53119物探化探计算技术620.1536计算机辅助设计与图形学学报3640.28420微计算机应用530.1007模式识别与人工智能2920.55321数值计算与计算机应用520.1238小型微型计算机系统2410.57022计算机自动测量与控制450.1959计算机应用2180.32023计算机工程与科学450.13410中国图象图形学报2100.38424计算机应用与软件430.14611计算机应用研究1990.19325计算机工程与设计430.14612计算机集成制造系统-CIM S1840.64926计算机辅助工程140.04213计算机与应用化学1780.44427微处理机140.04214计算机工程1770.16028J C OM PT SCI&T ECH200.021(引自2001年版《中国科技期刊引证报告》) 46中国图象图形学报第8卷(A版)。