2003黑龙江中考数学试卷及答案
2003年哈尔滨中考数学试题(含答案)

哈尔滨市2003年初中升学考试数 学本试卷满分为120分,考试时间为120分钟.第1卷 选择题(30分)一、选择题(每小题分,共30分) 1. 下列式子结果为负数的是( )(A ) (B )-(C ) (D )()03-3-()23-()23--2.点P (3,-4)关于原点对称的点的坐标是( )(A )(3,-4)(B )(-3,-4)(C )(3,4)(D )(-3,4) 3.下列运算正确的是( )(A ) (B ) (C ) (D ) 532a a a =⋅532)(a a =326a a a =÷426a a a =-4.如图1,四边形ABCD 内接于⊙O ,若∠BOD =140°,则∠BCD =()(A )140° (B ) 110° (C )70° (D )20°5.正方形具有而菱形不一定具有的性质是( )(A )四条边相等 (B )对角线互相垂直平分 (C )对角线平分一组对角 (D )对角线相等6.若正比例函数y =(1-2m )x 的图像经过点A (,)和点B (,),当<1x 1y 2x 2y 1x 2x 时>,则m 的取值范围是( )1y 2y (A )m <0(B )m >0(C )m <(D )m > 21217. 如图2,△ABC 中,AB =AC ,点D 在AC 边上,且BD =BC =AD ,则∠A 的度数为.( )(A )30° (B )36° (C )45° (D )70°8.现有下列命题:①的平方根是-5;②近似数3.14有3个有效数字; ③单项式与单项()25-310⨯y x 23式是同类项;④正方形既是轴对称图形,又是中心对称图形 其中真命题的个数23xy -是 ( )(A )1(B )2(C )3(D )49.若一个圆锥的母线长是它底面圆半径的3倍,则它的侧面展开图的圆心角是()(A )180° (B )90° (C )120° (D )135°10.下列各图是在同一直角坐标系内,二次函数与一次函数y =ax +c x c a ax y +++=)(2c 的大致图像,有且只有一个是正确的,正确的是()(A )(B )(C )(D )第2卷 非选择题(90分) 二填空题(每小题3分,共30分)11.据国家统计局公布,去年我国增加就业人数7510000人,将这个数用科学记数法表示为 人.12.若分式的值为零,则x =.392+-x x 13.分解因式:= .ab a bx x +--2214.函数中自变量x 的取值范围是 .12-+=x x y 15.如果长度分别为5,3,x 的三条线段能组成一个三角形,那么x 的范围是 . 16.若在△ABC 中,AB =5cm ,BC =6cm ,BC 边上的中线AD =4cm ,则∠ADC 的度数是 度。
黑龙江省2003年中考试卷

黑龙江省2003年中考试卷一、填空题(每小题3分,满分33分)1.生物学家发现一种病毒的直径约为0.000043米,用科学记数法表示为________米. 2.写出满足方程x +2y =9的一对整数值________.3.如图,△ABC 中,AD ⊥BC ,CE ⊥AB ,垂足分别为D 、E ,AD 、CE 交于点H ,请你添加一个适当的条件:________,使△AEH ≌△CEB .4.函数43--=x x y 中,自变量x 的取值范围是________. 5.矩形一个角的平分线分矩形一边为 1 cm 和 3 cm 两部分,则这个矩形的面积为________2cm .6.已知一次函数y =kx +2,请你补充一个条件:________,使y 随x 的增大而减小. 7.如图,在⊙O 中,AB 、AC 为互相垂直且相等的两条弦,OD ⊥AB ,OE ⊥AC ,垂足分别为D 、E .若AC =2 cm ,则⊙O 的半径为________ cm .8.已知抛物线c x ax y ++=2与x 轴交点的横坐标为-1,则a +c =________. 9.五个正整数从小到大排列,若这组数据的中位数是4,惟一众数是5,则这五个正整数的和为________.10.如图,某同学用一个有60°角的直角三角板估测学校旗杆AB 的高度.他将60°角的直角边水平放在1.5米高的支架CD 上,三角板的斜边与旗杆的顶点在同一直线上,他又量得D 、B 的距离为5米,则旗杆AB 的高度约为________米(精确到1米,3取1.73).11.张大伯从报社以每份0.4元的价格购进了a 份报纸,以每份0.5元的价格售出了b 份报纸,剩余的以每份0.2元的价格退回报社,则张大伯卖报收入________元.二、单项选择题(将正确答案的代号填在题后括号内,每小题3分,满分27分)12.下列计算正确的是( ). A .5322x x x =+ B .632x x x=⋅C .623)(x x =-- D .336x x x =÷13.将一长方形纸片按下图的方式折叠,BC 、BD 为折痕,则∠CBD 的度数为( ). A .60° B .75° C .90° D .95°14.某服装原价为200元,连续两次涨价a %后,售价为242元,则a 的值为( ). A .5 B .10 C .15 D .20 15.若|a -3|-3+a =0,则a 的取值范围是( ).A .a ≤3B .a <3C .a ≥3D .a >316.如图,用8块相同的长方形地砖拼成一个矩形,则每个长方形地砖的面积是( ).A .200 2cm B .300 2cm C .600 2cm D .2400 2cm 17.从哈尔滨开往A 市的特快列车,途中要停靠两个站点.如果任意两站间的票价都不同,那么有( )种不同的票价.A .4B .6C .10D .1218.如图,在等边△ABC 中,P 为BC 上一点,D 为AC 上一点,且∠APD =60°,BP =1,32=CD ,则△ABC 的边长为( ).A .3B .4C .5D .619.平面直角坐标系内,点A (n ,1-n )一定不在( ).A .第一象限B .第二象限C .第三象限D .第四象限20.如图,⊙O 的直径为10 cm ,弦AB 为8 cm ,P 是弦AB 上一点.若OP 的长为整数,则满足条件的点P 有( ).A .2个B .3个C .4个D .5个三、解答题(满分60分) 21.(本题5分) 先化简,再求值: 13)181(+++--x x x x其中23-=x .22.(本题6分)关于x 的方程04)1(2=+++k x k kx 有两个不相等的实数根.(1)求k 的取值范围;(2)是否存在实数k ,使方程的两个实数根的倒数和等于0?若存在,求出k 的值;若不存在,说明理由.23.(本题6分)某中学在一次健康知识测试中,抽取部分学生成绩(分数为整数,满分100分)为样本,绘制成绩统计图如下,请结合统计图回答下列问题:(1)本次测试中抽样的学生有多少人?(2)分数在90.5~100.5这一组的频率是多少? (3)这次测试成绩的众数落在哪个小组内?(4)若这次测试成绩80分以上(含80分)为优秀,则优秀率不低于多少?24.(本题8分) 为美化环境,计划在某小区内用30平方米的草皮铺设一块边长为10米的等腰三角形绿地,请你求出这个等腰三角形绿地的另两边长.25.(本题8分)某空军加油飞机接到命令,立即给另一架正在飞行的运输飞机进行空中加油.在加油过程中,设运输飞机的油箱余油量为1Q 吨,加油飞机的加油油箱余油量为2Q 吨,加油时间为t 分钟,1Q 、2Q 与t 之间的函数图象如图所示,结合图象回答下列问题:(1)加油飞机的加油油箱中装载了多少吨油?将这些油全部加给运输飞机需多少分钟? (2)求加油过程中,运输飞机的余油量1Q (吨)与时间t (分钟)的函数关系式; (3)运输飞机加完油后,以原速继续飞行,需10小时到达目的地,油料是否够用?说明理由.26.(本题9分)已知:如图1,BD 、CE 分别是△ABC 的外角平分线,过点A 作AF ⊥BD ,AG ⊥CE ,垂足分别为F 、G ,连结FG ,延长AF 、AG ,与直线BC 相交,易证)(21AC BC AB FG ++=.图1若(1)BD 、CE 分别是△ABC 的内角平分线(图2);(2)BD 为△ABC 的内角平分线,CE 为△ABC 的外角平分线(图3),则在图2、图3两种情况下,线段FG 与△ABC 三边又有怎样的数量关系?请写出你的猜想,并对其中的一种情况给予证明.图2图327.(本题9分)为了保护环境,某企业决定购买10台污水处理设备.现有A 、B 两种型号的设备,其经预算,该企业购买设备的资金不高于105万元.(1)请你设计该企业有几种购买方案;(2)若企业每月产生的污水量为2040吨,为了节约资金,应选择哪种购买方案; (3)在第(2)问的条件下,若每台设备的使用年限为10年,污水厂处理污水费为每吨10元,请你计算,该企业自己处理污水与将污水排到污水厂处理相比较,10年节约资金多少万元?(注:企业处理污水的费用包括购买设备的资金和消耗费)28.(本题9分)已知:如图,直角坐标系内的梯形AOBC ,AC ∥OB ,AC 、OB 的长分别是关于x 的方程04m mx 6x 22=+-+的两根,并且5:1:=BOC AOC S S ∆∆.(1)求AC 、OB 的长;(2)当BC ⊥OC 时,求OC 的长及OC 所在直线的解析式;(3)在第(2)问的条件下,线段OC 上是否存在一点M ,过M 点作x 轴的平行线,交y 轴于F ,交BC 于D ,过D 点作y 轴的平行线,交x 轴于E ,使A O B C F O E D S S 梯形矩形=21?若存在,请直接写出M 点的坐标;若不存在,说明理由.参考答案一、填空题(每小题3分,满分33分) 1.5103.4-⨯ 2.x =1,y =4等(只要符合要求即可) 3.AH =CB 等(只要符合要求即可) 4.x ≥3且x ≠4 5.4或12 6.K =-3等(写不等式或其他条件,符合要求即可) 7.2 8.1 9.17或18或19 10.10 11.(0.3b -0.2a ) 二、单项选择题(每小题3分,满分27分)12.D 13.C 14.B 15.A 16.B 17.B 18.A 19.C 20.D 三、解答题(满分60分)21.(本题5分)解:原式13)1811(2+++-+-=x x x x x ÷……………………………………………………1分 31192+++-=x x x x ⋅………………………………………………………………1分=x -3.………………………………………………………………………2分 当23-=x 时,原式2323=---=.…………………………………………1分 22.(本题6分) 解:(1)由题意知,K ≠0,且044)1(2>-+=kk k ⋅∆.……………………………………………………2分∴ 21>-k 且K ≠0.………………………………………………………………… 1分 (2)不存在.……………………………………………………………………………1分 设方程的两个根是1x ,2x . ∵ 04121≠=x x ,∴ 011212121=+=+x x x x x x .∴ 021=+x x .∵ kk x x 121+=-+,…………………………………………………………………1分 ∴ k +1=0,211<-=-k .…………………………………………………………1分∴ 满足条件的实数K 不存在. 23.(本题6分) 解:(1)2+3+4+41=50(人).…………………………………………………… 1分 (2)08.0504==总数频数频率=.……………………………………………………1分 (3)众数落在80.5~90.5这一小组内.………………………………………………2分 (4)这次测试成绩的优秀率不低于90%.……………………………………………2分 24.(本题8分)解:分三种情况计算.不妨设AB =10米,过点C 作CD ⊥AB ,垂足为D .CD AB S ABC ⋅∆21=,CD =6(米).……………………………………………………1分 (1)当AB 为底边时,AD =DB =5(米)(如图1),615622=+==BC AC (米).……………………………………………………2分图1(2)当AB 为腰且三角形为锐角三角形时(如图2), AB =AC =10(米),………………………………………………………………………1分 822=-=CD AC AD (米),BD =29(米),………………………………………1分1022622=+=BC (米).…………………………………………………………1分图2(3)当AB 为腰且三角形为钝角三角形时(如图3), AB =BC =10(米),………………………………………………………………………1分 10618622=+=AC (米).………………………………………………………1分图325.(本题8分) 解:(1)由图象知,加油飞机的加油油箱中装载了30吨油,………………………1分 全部加给运输飞机需10分钟.…………………………………………………………1分 (2)设b kt Q +=1,把(0,40)和(10,69)代入,得 ⎩⎨⎧.1069,40b k b +==…………………………………………………………………………… 1分解方程组得⎩⎨⎧.40,9.2==b k ……………………………………………………………………1分∴ 409.21+=t Q (0≤t ≤10).……………………………………………………2分 (3)根据图象可知运输飞机的耗油量为每分钟0.1吨.……………………………1分 ∴ 10小时耗油量为:10×60×0.1=60(吨)<69(吨).∴ 油料够用.…………………………………………………………………………1分26.(本题9分)猜想结果:图中结论)(21BC AC AB FG -+=.……………………………………2分 证明:分别延长AG 、AF 交BC 于H 、K ,……………………………………………1分 易证△BAF ≌△BKF ,AF =KF ,AB =KB .…………………………………………2分 同理可证,AG =HG ,AC =HC ,∴ HK FG 21=.………………………………………………………………………1分 又∵ HK =BK -BH =AB +AC -BC ,…………………………………………………1分 ∴ )(21BC AC AB FG -+=.结论为)(21AB AC BC FG -+=………………………………………………………2分 如果证明图中结论,可参考上面评分标准给分.27.(本题9分) 解:(1)设购买污水处理设备A 型x 台,则B 型(10-x )台.由题意知,12x +10(10-x )≤105.…………………………………………………1分 x ≤2.5.……………………………………………………………………………………1分 ∵ x 取非负整数,∴ x 可取0,1,2.∴ 有三种购买方案:购A 型0台,B 型10台;购A 型1台,B 型9台;购A 型2台,B 型8台.………………………………………………………………………………………1分 (2)由题意得 240x +200(10-x )≥2040.………………………………………1分 x ≥1,∴ x 为1或2.…………………………………………………………………1分 当x =1时,购买资金为: 12×1+10×9=102(万元); 当x =2时,购买资金为: 12×2+10×8=104(万元).∴ 为了节约资金,应选购A 型1台,B 型9台.……………………………………1分 (3)10年企业自己处理污水的总资金为: 102+10×10=202(万元).……………………………………………………………1分 若将污水排到污水厂处理,10年所需费用为:2040×12×10×10=2448000(元)=244.8(万元).………………………………1分 244.8-202=42.8(万元),∴ 能节约资金42.8万元.……………………………………………………………1分 28.(本题9分)解:(1)∵ 5:1:=B O C A O C S S ∆∆,∴ 5:1:=OB AC . 不妨设AC =k ,OB =5k .……………………………………………………………1分由题意得⎩⎨⎧⋅.45,652+==+m k k m k k ……………………………………………………………1分 解得⎩⎨⎧1,1==k m 或⎩⎨⎧--.1,1==k m (不合题意,舍去)∴ AC =1,OB =5.………………………………………………………………1分(2)∵ ∠OAC =∠BCO =90°,∠ACO =∠BOC , ∴ △OBC ∽△COA . ∴ACOC OC OB =,AC OB OC ⋅=2.……………………………………………1分 ∴ 5=OC 或5=-OC (舍去).……………………………………………1分∵ AC =1,∴ AO =2.∴ C (1,2).……………………………………… 1分 ∴ 直线OC 的解析式为y =2x .……………………………………………………1分 (3)存在,1M (21,1),2M (43,23).……………………………………… 2分 说明:如果学生有不同于本参考答案的解题方法,只要正确,可参照本评分标准,酌情给分.。
关于哈市2003年中考数学命题的反思

关于哈市2003年中考数学命题的反思一、考题背景2003年是哈尔滨市中考改革的第一年,考试由原来的两天改为三天,考试科目和往年相比有所变化。
数学是所有学生必考科目之一,而2003年哈市中考的数学考题备受争议。
本文通过对2003年哈市中考数学考题的分析和反思,希望能够找出问题并提出改进建议。
二、考题分析1. 题型设置不合理2003年哈市中考数学试题中,部分题目所占分数过大,而且题型设置不够平衡。
如选择题过多,填空题和解答题的数量相对较少,容易导致时间不够分配,影响考生发挥。
2. 难度不合适试题难度设置不合理,题目涉及的知识点跨度较大,有些题目过于复杂,导致部分学生难以完成,影响了他们的考试成绩。
3. 题目出错有部分试题存在错误,如选项不对称,或者是题目本身存在歧义,导致部分答题人产生困扰,影响了他们的答题心情和答题效果。
三、影响和启示1. 对学生的影响2003年哈市中考数学试题的不合理性直接影响到了学生的心理和发挥,阻碍了他们正常发挥的机会,容易造成学习压力过大、自信心受挫等问题。
2. 对教学改革的启示试题的出题者需要更加贴近教材和教学实际,增强题目的经典性和稳定性,保证考题能够客观公正地考察学生的能力和水平。
四、改进建议1. 试题设置上,应该合理控制题型数量和难度,保持题目平衡,保证学生在考试时间内能够有序完成试卷。
2. 出题者应该更加注重题目的准确性和清晰度,避免错误和歧义的存在,保证试题的客观性和公正性。
五、结语2003年哈市中考数学试题虽然存在一些问题,但正是这些问题的存在,促使我们思考和反思出题的原则和方法,为今后出题提供了宝贵的经验和启示。
希望通过对过去的反思,能够为未来的中考数学命题提供一些建设性的建议。
以上就是对于哈市2003年中考数学命题的反思,希望能够对未来的中考数学出题提供一些借鉴和启示。
2003年哈市中考数学试题的争议引起了社会各界的广泛关注和深入思考。
在教育改革的大背景下,中考数学试题的合理性和公平性成为了备受关注的焦点。
2003年中考数学试卷

2003年中考数学试卷
2003年中考数学试卷指的是在2003年中考中使用的数学科目的试卷。
这份试卷将由当地教育部门或考试机构组织专家进行命题,并按照中考数学科目的要求进行设计。
以下是 2003年中考数学试卷具体的题目示例:
选择题1:若关于 x 的一元二次方程 x^2 + 4x + k - 1 = 0 有两个不相等的实数根,则 k 的取值范围是 ()
A. k < 5
B. k > 5
C. k < -5
D. k > -5
选择题2:下列图形中,是轴对称图形但不是中心对称图形的是 ()
A. 正三角形
B. 正方形
C. 正五边形
D. 正六边形
填空题1:计算:√4 + | -2| - (1/2)^(-1) = ___.
填空题2:若反比例函数 y = (m - 1)/x 的图象在每一个象限中,y随着x 的增大而减小,则m的取值范围是 ___.
计算题1:计算:(π - 3)^0 - 4sin 45° + | -2| + (1/3)^(-1).
计算题2:解方程组:{ 3x + y = 2, 4x - 3y = 15 }.
总结:2003年中考数学试卷指的是在2003年中考中使用的数学科目的试卷。
这份试卷旨在测试学生对数学基础知识的掌握程度和问题解决能力,通过选择题、填空题和计算题等多种题型进行考查。
考生需要通过系统的数学学习和复习,掌握基础知识和应试技巧,以提高自己的数学水平,应对这份试卷的挑战。
黑龙江中考数学试题及答案

黑龙江中考数学试题及答案一、选择题1. 下列各分式中,等式成立的是:A) 1/5 = 2/10 B) 2/3 = 6/9 C) 4/8 = 3/5 D) 5/6 = 4/92. 若ab = 1,且a ≠ 0,则下列各式中,恒成立的是:A) a + b = 2 B) a^2 - b^2 = (a + b)(a - b) C) a^3 + b^3 = (a + b)^3 D) a^4 + b^4 = (a^2 + b^2)^23. 已知函数f(x) = 3x - 5,下列各式中,哪个是正确的?A) f(2) = 1 B) f(3) = 4 C) f(-1) = -8 D) f(0) = 54. 若三角形ABC中,∠B = 90°,且AB = 3,BC = 4,则AC的长度为:A) 5 B) 7 C) 9 D) 125. 已知函数f(x) = 2x^2 + 3x - 1,求f(-1)的值是:A) 0 B) 1 C) 2 D) -1二、填空题1. 二次函数y = ax^2 + bx + c的图像经过点(-1, 4)和(2, -1),则a + b+ c的值为________。
2. 解方程2x - 5 = 3x + 4的解是________。
3. 在△ABC中,∠A = 50°,∠C = 70°,则∠B的大小为________。
4. 若两条直线的斜率分别为3和-1/3,它们的乘积为________。
5. 已知正方体的一个顶点为A,一条棱上的中点为B,则矩形ABCD的面积为________。
三、解答题1. 某商店为促销而将一件商品的价格降低了20%,原价是多少?解:设原价为x元,根据题意,原价减去20%的折扣后的价格为0.8x元。
由此得到方程0.8x = x,解得x = 5。
所以,原价是5元。
2. 若a:b = 3:5,且a + b = 64,则a和b的值分别是多少?解:设a的倍数为3x,b的倍数为5x,根据题意,得到方程3x + 5x = 64。
黑龙江初三初中数学中考真卷带答案解析
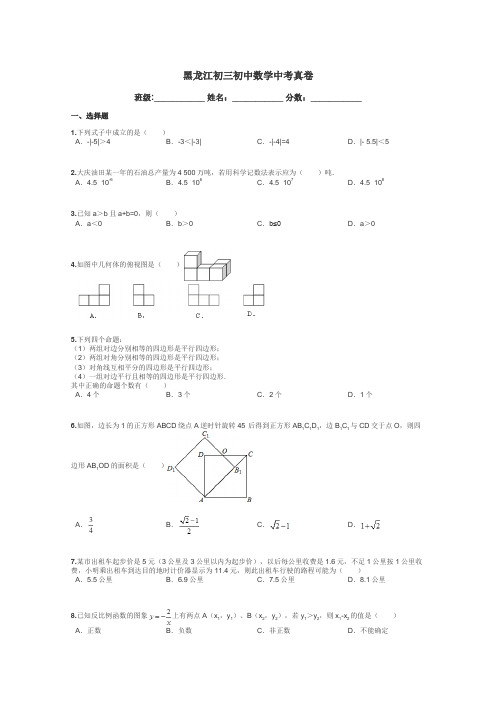
黑龙江初三初中数学中考真卷班级:___________ 姓名:___________ 分数:___________一、选择题1.下列式子中成立的是( )A .-|-5|>4B .-3<|-3|C .-|-4|=4D .|- 5.5|<52.大庆油田某一年的石油总产量为4 500万吨,若用科学记数法表示应为( )吨.A .4.5×10-6B .4.5×106C .4.5×107D .4.5×1083.已知a >b 且a+b=0,则( )A .a <0B .b >0C .b≤0D .a >04.如图中几何体的俯视图是( )5.下列四个命题:(1)两组对边分别相等的四边形是平行四边形;(2)两组对角分别相等的四边形是平行四边形;(3)对角线互相平分的四边形是平行四边形;(4)一组对边平行且相等的四边形是平行四边形.其中正确的命题个数有( )A .4个B .3个C .2个D .1个6.如图,边长为1的正方形ABCD 绕点A 逆时针旋转45°后得到正方形AB 1C 1D 1,边B 1C 1与CD 交于点O ,则四边形AB 1OD 的面积是( )A .B .C .D .7.某市出租车起步价是5元(3公里及3公里以内为起步价),以后每公里收费是1.6元,不足1公里按1公里收费,小明乘出租车到达目的地时计价器显示为11.4元,则此出租车行驶的路程可能为( )A .5.5公里B .6.9公里C .7.5公里D .8.1公里8.已知反比例函数的图象上有两点A (x 1,y 1)、B (x 2,y 2),若y 1>y 2,则x 1-x 2的值是( )A .正数B .负数C .非正数D .不能确定9.如图,一个质地均匀的正四面体的四个面上依次标有数字-2,0,1,2,连续抛掷两次,朝下一面的数字分别是a ,b ,将其作为M 点的横、纵坐标,则点M (a ,b )落在以A (-2,0),B (2,0),C (0,2)为顶点的三角形内(包含边界)的概率是( )A .B .C .D .10.对坐标平面内不同两点A (x 1,y 1)、B (x 2,y 2),用|AB|表示A 、B 两点间的距离(即线段AB 的长度),用‖AB‖表示A 、B 两点间的格距,定义A 、B 两点间的格距为‖AB‖=|x 1-x 2|+|y 1-y 2|,则|AB|与‖AB‖的大小关系为( )A .|AB|≥‖AB‖B .|AB|>‖AB‖C .|AB|≤‖AB‖D .|AB|<‖AB‖二、填空题1.若,则x y-3的值为2.某记者抽样调查了某校一些学生假期用于读书的时间(单位:分钟)后,绘制了频数分布直方图,从左到右的前5个长方形相对应的频率之和为0.9,最后一组的频数是15,则此次抽样调查的人数为 人.(注:横轴上每组数据包含最小值不包含最大值)3.二元一次方程组的解为4.=5.图中直线是由直线l 向上平移1个单位,向左平移2个单位得到的,则直线l 对应的一次函数关系式为 .6.在半径为2的圆中,弦AC 长为1,M 为AC 中点,过M 点最长的弦为BD ,则四边形ABCD 的面积为 .7.如图,矩形ABCD 中,AD=,F 是DA 延长线上一点,G 是CF 上一点,且∠ACG=∠AGC ,∠GAF=∠F=20°,则AB= .8.有一列数如下:1,0,1,0,0,1,0,0,0,1,0,0,0,0,1,…,则第9个1在这列数中是第 个数.三、计算题计算:.四、解答题1.求不等式组的整数解.2.已知非零实数a 满足a 2+1=3a ,求的值. 3.如图,点D 为锐角∠ABC 内一点,点M 在边BA 上,点N 在边BC 上,且DM=DN ,∠BMD+∠BND=180°. 求证:BD 平分∠ABC .4.如图,在平面直角坐标系xOy 中,一次函数y=ax+b 的图象与x 轴相交于点A (-2,0),与y 轴交于点C ,与反比例函数在第一象限内的图象交于点B (m ,n ),连结OB .若S △AOB =6,S △BOC =2.(1)求一次函数的表达式;(2)求反比例函数的表达式.5.甲、乙两名同学进入初四后,某科6次考试成绩如图:(1)请根据下图填写如表: 平均数 方差 中位数 众数 极差(2)请你分别从以下两个不同的方面对甲、乙两名同学6次考试成绩进行分析:①从平均数和方差相结合看;②从折线图上两名同学分数的走势上看,你认为反映出什么问题?6.关于x的函数y=(m2-1)x2-(2m+2)x+2的图象与x轴只有一个公共点,求m的值.7.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,PB与CD交于点F,∠PBC=∠C.(1)求证:CB∥PD;(2)若∠PBC=22.5°,⊙O的半径R=2,求劣弧AC的长度.8.如图,等腰△ABC中,AB=AC,∠BAC=36°,BC=1,点D在边AC上且BD平分∠ABC,设CD=x.(1)求证:△ABC∽△BCD;(2)求x的值;(3)求cos36°-cos72°的值.9.如图①,已知等腰梯形ABCD的周长为48,面积为S,AB∥CD,∠ADC=60°,设AB=3x.(1)用x表示AD和CD;(2)用x表示S,并求S的最大值;(3)如图②,当S取最大值时,等腰梯形ABCD的四个顶点都在⊙O上,点E和点F分别是AB和CD的中点,求⊙O的半径R的值.黑龙江初三初中数学中考真卷答案及解析一、选择题1.下列式子中成立的是()A.-|-5|>4B.-3<|-3|C.-|-4|=4D.|- 5.5|<5【答案】B.【解析】A .-|-5|=-5<4,故A 选项错误;B .|-3|=3>-3, 故B 选项正确;C .-|-4|=-4≠4,故C 选项错误;D .|-5.5|=5.5>5,故D 选项错误;故选B .【考点】有理数的大小比较.2.大庆油田某一年的石油总产量为4 500万吨,若用科学记数法表示应为( )吨.A .4.5×10-6B .4.5×106C .4.5×107D .4.5×108【答案】C .【解析】科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数.确定n 的值是易错点,由于4 500万有8位,所以可以确定n=8-1=7.所以:4 500万="45" 000 000=4.5×107.故选C .【考点】科学记数法—表示较大的数.3.已知a >b 且a+b=0,则( )A .a <0B .b >0C .b≤0D .a >0【答案】D .【解析】∵a >b 且a+b=0,∴a >0,b <0,故选D .【考点】有理数的加法.4.如图中几何体的俯视图是( )【答案】A .【解析】从上面看易得第一层最右边有1个正方形,第二层有3个正方形.故选A .【考点】简单组合体的三视图.5.下列四个命题:(1)两组对边分别相等的四边形是平行四边形;(2)两组对角分别相等的四边形是平行四边形;(3)对角线互相平分的四边形是平行四边形;(4)一组对边平行且相等的四边形是平行四边形.其中正确的命题个数有( )A .4个B .3个C .2个D .1个【答案】A .【解析】(1)两组对边分别相等的四边形是平行四边形,此选项正确;(2)两组对角分别相等的四边形是平行四边形,此选项正确;(3)对角线互相平分的四边形是平行四边形,此选项正确;(4)一组对边平行且相等的四边形是平行四边形,此选项正确.故选A .【考点】1.命题与定理;2.平行四边形的判定.6.如图,边长为1的正方形ABCD 绕点A 逆时针旋转45°后得到正方形AB 1C 1D 1,边B 1C 1与CD 交于点O ,则四边形AB 1OD 的面积是( )A .B .C .D .【答案】C.【解析】连接AC 1,∵四边形AB 1C 1D 1是正方形,∴∠C 1AB 1=×90°=45°=∠AC 1B 1,∵边长为1的正方形ABCD 绕点A 逆时针旋转45°后得到正方形AB 1C 1D 1,∴∠B 1AB=45°,∴∠DAB 1=90°-45°=45°,∴AC 1过D 点,即A 、D 、C 1三点共线,∵正方形ABCD 的边长是1, ∴四边形AB 1C 1D 1的边长是1,在Rt △C 1D 1A 中,由勾股定理得:AC 1=,则DC 1=-1,∵∠AC 1B 1=45°,∠C 1DO=90°,∴∠C 1OD=45°=∠DC 1O ,∴DC 1=OD=-1,∴S △ADO=×OD•AD=,∴四边形AB 1OD 的面积是=2×=. 故选C .【考点】1.旋转的性质;2.正方形的性质.7.某市出租车起步价是5元(3公里及3公里以内为起步价),以后每公里收费是1.6元,不足1公里按1公里收费,小明乘出租车到达目的地时计价器显示为11.4元,则此出租车行驶的路程可能为( )A .5.5公里B .6.9公里C .7.5公里D .8.1公里【答案】B .【解析】设人坐车可行驶的路程最远是xkm ,根据题意得:5+1.6(x-3)=11.4,解得:x=7.观察选项,只有B 选项符合题意.故选B .【考点】一元一次方程的应用.8.已知反比例函数的图象上有两点A (x 1,y 1)、B (x 2,y 2),若y 1>y 2,则x 1-x 2的值是( )A .正数B .负数C .非正数D .不能确定【答案】A .【解析】∵反比例函数的图象的图象在二、四象限,∴当点A (x 1,y 1)、B (x 2,y 2)都在第二象限时,由y 1>y 2,则x 1-x 2>0;当点A (x 1,y 1)、B (x 2,y 2)都在第四象限时,由y 1>y 2,则x 1-x 2>0;当点A (x 1,y 1)在第二象限、B (x 2,y 2)在第四象限时,即y 1>0>y 2,则x 1-x 2>0;故选A .【考点】反比例函数图 象上点的坐标特征.9.如图,一个质地均匀的正四面体的四个面上依次标有数字-2,0,1,2,连续抛掷两次,朝下一面的数字分别是a ,b ,将其作为M 点的横、纵坐标,则点M (a ,b )落在以A (-2,0),B (2,0),C (0,2)为顶点的三角形内(包含边界)的概率是( )A .B .C .D .【答案】C .【解析】解:列举出事件:(-2,1),(-2,0),(-2,2),(0,-2),(0,1),(0,2),(1,2),(1,0),(1,-2),(2,-2),(2,0),(2,1)共有12种结果,而落在以A (-2,0),B (2,0),C (0,2)为顶点的三角形内(包含边界)有:(-2,0),(0,1),(0,2),(1,0),(2,0),(-1,0)共6中可能情况,所以落在以A (-2,0),B (2,0),C (0,2)为顶点的三角形内(包含边界)的概率是=, 故选C .【考点】列表法与树状图法.10.对坐标平面内不同两点A (x 1,y 1)、B (x 2,y 2),用|AB|表示A 、B 两点间的距离(即线段AB 的长度),用‖AB‖表示A 、B 两点间的格距,定义A 、B 两点间的格距为‖AB‖=|x 1-x 2|+|y 1-y 2|,则|AB|与‖AB‖的大小关系为( )A .|AB|≥‖AB‖B .|AB|>‖AB‖C .|AB|≤‖AB‖D .|AB|<‖AB‖【答案】C .【解析】∵|AB|、|x 1-x 2|、|y 1-y 2|的长度是以|AB|为斜边的直角三角形,∴|AB|≤‖AB‖.故选C .【考点】1.线段的性质:两点之间线段最短;2.坐标与图形性质.二、填空题1.若,则x y-3的值为【答案】. 【解析】根据非负数的性质列出方程求出x 、y 的值,代入所求代数式计算即可.试题解析:∵,∴, 解得, ∴x y-3=22-3=.【考点】1.算术平方根;2.绝对值;3.负整数指数幂.2.某记者抽样调查了某校一些学生假期用于读书的时间(单位:分钟)后,绘制了频数分布直方图,从左到右的前5个长方形相对应的频率之和为0.9,最后一组的频数是15,则此次抽样调查的人数为人.(注:横轴上每组数据包含最小值不包含最大值)【答案】150.【解析】根据直方图中各组的频率之和等于1,结合题意可得最后一组的频率,再由频率的计算公式可得总人数,即答案.试题解析:由题意可知:最后一组的频率=1-0.9=0.1,则由频率=频数÷总人数可得:总人数=15÷0.1=150人.【考点】频数(率)分布直方图.3.二元一次方程组的解为【答案】.【解析】利用加减消元法求出解即可.试题解析:①×3-②×2得:11x=33,即x=3,将x=3代入②得:y=2,则方程组的解为.【考点】解二元一次方程组.4.=【答案】.【解析】先把(x+)提,再把4x2-1分解,然后约分即可.试题解析:原式=(2x+1)(2x-1)÷[(2x-1)(2x+1)]=.【考点】整式的混合运算.5.图中直线是由直线l向上平移1个单位,向左平移2个单位得到的,则直线l对应的一次函数关系式为.【答案】y=x-2.【解析】先求得图中直线方程,然后利用平移的性质来求直线l的解析式.试题解析:如图,设该直线的解析式为y=kx+1(k≠0),则0=-k+1,解得 k=1.则该直线的解析式为y=x+1.∵图中直线是由直线l向上平移1个单位,向左平移2个单位得到的,∴由该直线向下平移1个单位,向右移2个单位得到的直线l,∴直线l的解析式为:y=x+1-1-2=x-2.【考点】一次函数图象与几何变换.6.在半径为2的圆中,弦AC长为1,M为AC中点,过M点最长的弦为BD,则四边形ABCD的面积为.【答案】2.【解析】先由直径是圆中最长的弦得出BD=4,再根据垂径定理的推论得出AC⊥BD,则四边形ABCD的面积= AC•BD.试题解析:如图.∵M为AC中点,过M点最长的弦为BD,∴BD是直径,BD=4,且AC⊥BD,∴四边形ABCD的面积=AC•BD=×1×4=2.【考点】1.垂径定理;2.勾股定理.7.如图,矩形ABCD中,AD=,F是DA延长线上一点,G是CF上一点,且∠ACG=∠AGC,∠GAF=∠F=20°,则AB=.【答案】.【解析】根据三角形的一个外角等于与它不相邻的两个内角的和可得∠AGC=∠GAF+∠F=40°,再根据等腰三角形的性质求出∠CAG,然后求出∠CAF=120°,再根据∠BAC=∠CAF-∠BAF求出∠BAC=30°,再根据直角三角形30°角所对的直角边等于斜边的一半可得AC=2BC=2AD,然后利用勾股定理列式计算即可得解.试题解析:由三角形的外角性质得,∠AGC=∠GAF+∠F=20°+20°=40°,∵∠ACG=∠AGC,∴∠CAG=180°-∠ACG-∠AGC=180°-2×40°=100°,∴∠CAF=∠CAG+∠GAF=100°+20°=120°,∴∠BAC=∠CAF-∠BAF=30°,在Rt△ABC中,AC=2BC=2AD=2,由勾股定理,AB=.【考点】1.矩形的性质;2.等腰三角形的判定与性质;3.含30度角的直角三角形;4.直角三角形斜边上的中线;5.勾股定理.8.有一列数如下:1,0,1,0,0,1,0,0,0,1,0,0,0,0,1,…,则第9个1在这列数中是第个数.【答案】45.【解析】根据两个1之间的0的个数分别为1、2、3…个,然后把0的个数相加再加上9,计算即可得解.试题解析:∵两个1之间的0的个数分别为1、2、3…,∴到第9个1,0的个数为:1+2+3+4+5+6+7+8=36,∴第9个1在这列数中是第36+9=45个数.【考点】规律型:数字的变化类.三、计算题计算:.【答案】.【解析】原式第一项利用零指数幂法则计算,第二项利用绝对值的代数意义化简,第三项利用特殊角的三角函数值计算,最后一项利用立方根定义化简计算即可得到结果.试题解析:原式=1+1+-2=.【考点】1.实数的运算;2.零指数幂;3.特殊角的三角函数值.四、解答题1.求不等式组的整数解.【答案】-1,0,1.【解析】此题可先根据一元一次不等式组解出x的取值,根据x是整数解得出x的可能取值.试题解析:,解①得:x<,解②得:x≥-1,则不等式组的解集是:-1≤x<.则整数解是:-1,0,1.【考点】一元一次不等式组的整数解.2.已知非零实数a满足a2+1=3a,求的值.【答案】7.【解析】已知等式两边除以a变形后求出a+的值,两边平方,利用完全平方公式展开即可求出所求式子的值.试题解析:∵a2+1=3a,即a+=3,∴两边平方得:(a+)2=a2++2=9,则a2+=7.【考点】分式的混合运算.3.如图,点D为锐角∠ABC内一点,点M在边BA上,点N在边BC上,且DM=DN,∠BMD+∠BND=180°.求证:BD平分∠ABC.【答案】证明见解析.【解析】在AB上截取ME=BN,证得△BND≌△EMD,进而证得∠DBN=∠MED,BD=DE,从而证得BD平分∠ABC.试题解析:如图所示:在AB上截取ME=BN,∵∠BMD+∠DME=180°,∠BMD+∠BND=180°,∴∠DME=∠BND,在△BND与△EMD中,,∴△BND ≌△EMD (SAS ), ∴∠DBN=∠MED ,BD=DE , ∴∠MBD=∠MED , ∴∠MBD=∠DBN , ∴BD 平分∠ABC .【考点】1.全等三角形的判定与性质;2.角平分线的性质.4.如图,在平面直角坐标系xOy 中,一次函数y=ax+b 的图象与x 轴相交于点A (-2,0),与y 轴交于点C ,与反比例函数在第一象限内的图象交于点B (m ,n ),连结OB .若S △AOB =6,S △BOC =2.(1)求一次函数的表达式;(2)求反比例函数的表达式.【答案】(1)y=2x+4;(2).【解析】(1)由S △AOB =6,S △BOC =2得S △AOC =4,根据三角形面积公式得•2•OC=4,解得OC=4,则C 点坐标为(0,4),然后利用待定系数法求一次函数解析式;(2)由S △BOC =2,根据三角形面积公式得到×4×m=2,解得m=1,则B 点坐标为(1,6),然后利用待定系数法确定反比例函数解析式.试题解析:(1)∵S △AOB =6,S △BOC =2,∴S △AOC =4,∴•2•OC=4,解得OC=4, ∴C 点坐标为(0,4),设一次函数解析式为y=mx+n ,把A (-2,0),C (0,4)代入得,解得, ∴一次函数解析式为y=2x+4;(2)∵S △BOC =2,∴×4×m=2,解得m=1,∴B 点坐标为(1,6),把B (1,6)代入得k=1×6=6, ∴反比例函数解析式为.【考点】反比例函数与一次函数的交点问题.5.甲、乙两名同学进入初四后,某科6次考试成绩如图:(1)请根据下图填写如表: 平均数 方差 中位数 众数 极差(2)请你分别从以下两个不同的方面对甲、乙两名同学6次考试成绩进行分析:①从平均数和方差相结合看;②从折线图上两名同学分数的走势上看,你认为反映出什么问题?【答案】(1)125,75,35;75,72.5,70;(2)①从平均数和方差相结合看,乙同学成绩更稳定;②从折线图上两名同学分数的走势上看,甲同学进步较快,乙同学成绩稳定有小幅度下滑.【解析】(1)分别根据平均数、方差的求解进行计算,中位数的定义,众数的定义以及极差的定义解答;(2)根据方差的意义以及折线统计图的意义解答.试题解析:(1)甲:方差= [(60-75)2+(65-75)2+(75-75)2+(75-75)2+(80-75)2+(95-75)2=(225+100+0+0+25+400)=125,众数:75,极差:95-60=35;乙:平均数=(85+70+70+75+70+80)=75,中位数:(70+75)=72.5,众数:70;(2)①从平均数和方差相结合看,乙同学成绩更稳定;②从折线图上两名同学分数的走势上看,甲同学进步较快,乙同学成绩稳定有小幅度下滑.【考点】1.折线统计图;2.算术平均数;3.中位数;4.极差;5.方差.6.关于x的函数y=(m2-1)x2-(2m+2)x+2的图象与x轴只有一个公共点,求m的值.【答案】1或3.【解析】需要分类讨论:该函数是一次函数和二次函数两种情况.试题解析:①当m2-1=0,且2m+2≠0,即m=1时,该函数是一次函数,则其图象与x轴只有一个公共点;②当m2-1≠0,即m≠±1时,该函数是二次函数,则△=(2m+2)2-8(m2-1)=0,解得 m=3,m=-1(舍去).综上所述,m的值是1或3.【考点】1.抛物线与x轴的交点;2.一次函数图象上点的坐标特征.7.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,PB与CD交于点F,∠PBC=∠C.(1)求证:CB∥PD;(2)若∠PBC=22.5°,⊙O的半径R=2,求劣弧AC的长度.【答案】(1)证明见解析;(2).【解析】(1)先根据同弧所对的圆周角相等得出∠PBC=∠D,再由等量代换得出∠C=∠D,然后根据内错角相等两直线平行即可证明CB∥PD;(2)先由垂径定理及圆周角定理得出∠BOC=2∠PBC=45°,再根据邻补角定义求出∠AOC=135°,然后根据弧长的计算公式即可得出劣弧AC的长度.试题解析:(1)∵∠PBC=∠D,∠PBC=∠C,∴∠C=∠D , ∴CB ∥PD ;(2)∵AB 是⊙O 的直径,弦CD ⊥AB 于点E ,∴,∵∠PBC=∠C=22.5°, ∴∠BOC=∠BOD=2∠C=45°, ∴∠AOC=180°-∠BOC=135°,∴劣弧AC 的长为:.【考点】1.垂径定理;2.圆周角定理;3.弧长的计算.8.如图,等腰△ABC 中,AB=AC ,∠BAC=36°,BC=1,点D 在边AC 上且BD 平分∠ABC ,设CD=x .(1)求证:△ABC ∽△BCD ;(2)求x 的值;(3)求cos36°-cos72°的值.【答案】(1)证明见解析;(2);(3).【解析】(1)由等腰三角形ABC 中,顶角的度数求出两底角度数,再由BD 为角平分线求出∠DBC 的度数,得到∠DBC=∠A ,再由∠C 为公共角,利用两对角相等的三角形相似得到三角形ABC 与三角形BCD 相似;(2)根据(1)结论得到AD=BD=BC ,根据AD+DC 表示出AC ,由(1)两三角形相似得比例求出x 的值即可;(3)过B 作BE 垂直于AC ,交AC 于点E ,在直角三角形ABE 和直角三角形BCE 中,利用锐角三角函数定义求出cos36°与cos72°的值,代入原式计算即可得到结果.试题解析:(1)∵等腰△ABC 中,AB=AC ,∠BAC=36°,∴∠ABC=∠C=72°, ∵BD 平分∠ABC , ∴∠ABD=∠CBD=36°, ∵∠CBD=∠A=36°,∠C=∠C , ∴△ABC ∽△BCD ;(2)∵∠A=∠ABD=36°,∴AD=BD , ∵BD=BC , ∴AD=BD=CD=1,设CD=x ,则有AB=AC=x+1,∵△ABC ∽△BCD ,∴,即,整理得:x 2+x-1=0,解得:x 1=,x 2=(负值,舍去),则x=; (3)过B 作BE ⊥AC ,交AC 于点E ,∵BD=CD ,∴E 为CD 中点,即DE=CE=,在Rt△ABE中,cosA=cos36°=,在Rt△BCE中,cosC=cos72°=,则cos36°-cos72°=-=.【考点】1.相似三角形的判定与性质;2.等腰三角形的性质;3.黄金分割;4.解直角三角形.9.如图①,已知等腰梯形ABCD的周长为48,面积为S,AB∥CD,∠ADC=60°,设AB=3x.(1)用x表示AD和CD;(2)用x表示S,并求S的最大值;(3)如图②,当S取最大值时,等腰梯形ABCD的四个顶点都在⊙O上,点E和点F分别是AB和CD的中点,求⊙O的半径R的值.【答案】(1)AD=18-2x,CD=16+x;(2)S=-2(x-2)2+72,当x=2时,S有最大值72;(3)R=2.【解析】(1)作AH⊥CD于H,BG⊥CD于G,如图①,易得四边形AHGB为矩形,则HG=AB=3x,再根据等腰梯形的性质得AD=BC,DH=CG,在Rt△ADH中,设DH=t,根据含30度的直角三角形三边的关系得AD=2t,AH=t,然后根据等腰梯形ABCD的周长为48得3x+2t+t+3x+t+2t=48,解得t=8-x,于是可得AD=18-2x,CD=16+x;(2)根据梯形的面积公式计算可得到S=-2x2+8x+64,再进行配方得S=-2(x-2)2+72,然后根据二次函数的最值问题求解;(3)连结OA、OD,如图②,由(2)得到x=2时,则AB=6,CD=18,等腰梯形的高为6,所以AE=3,DF=9,由于点E和点F分别是AB和CD的中点,根据等腰梯形的性质得直线EF为等腰梯形ABCD的对称轴,所以EF垂直平分AB和CD,EF为等腰梯形ABCD的高,即EF=6,根据垂径定理的推论得等腰梯形ABCD的外接圆的圆心O在EF上,设OE=a,则OF=6-a,在Rt△AOE中,利用勾股定理得a2+32=R2,在Rt△ODF中,利用勾股定理得(6-a)2+92=R2,然后消去R得到a的方程a2+32=(6-a)2+92,解得a=5,最后利用R2=(5)2+32求解.试题解析:(1)作AH⊥CD于H,BG⊥CD于G,如图①,则四边形AHGB为矩形,∴HG=AB=3x,∵四边形ABCD为等腰梯形,∴AD=BC,DH=CG,在Rt△ADH中,设DH=t,∵∠ADC=60°,∴∠DAH=30°,∴AD=2t,AH=t,∴BC=2t,CG=t,∵等腰梯形ABCD的周长为48,∴3x+2t+t+3x+t+2t=48,解得t=8-x,∴AD=2(8-x)=18-2x,CD=8-x+3x+8-x=16+x;(2)S=(AB+CD)•AH=(3x+16+x)•(8-x)=-2x2+8x+64,∵S=-2(x-2)2+72,∴当x=2时,S有最大值72;(3)连结OA、OD,如图②,当x=2时,AB=6,CD=16+2=18,等腰梯形的高为×(8-2)=6,则AE=3,DF=9,∵点E和点F分别是AB和CD的中点,∴直线EF为等腰梯形ABCD的对称轴,∴EF垂直平分AB和CD,EF为等腰梯形ABCD的高,即EF=6,∴等腰梯形ABCD的外接圆的圆心O在EF上,设OE=a,则OF=6-a,在Rt△AOE中,∵OE2+AE2=OA2,∴a2+32=R2,在Rt△ODF中,∵OF2+DF2=OD2,∴(6-a)2+92=R2,∴a2+32=(6-a)2+92,解得a=5,∴R2=(5)2+32=84,∴R=2.【考点】圆的综合题.。
2003黑龙江中考数学试卷及答案
黑龙江省2003年初中升学统一考试数 学 试 题一、填空题;(每小题3分,共33分)1、生物学家发现一种病毒的直径约为0.000043米,用科学记数法表示为 米。
2、写出满足方程92=+y x 的一对整数值 。
3、如图:△ABC 中,AD ⊥BC ,CE ⊥AB ,垂足分别为D 、E ,AD 、CE 交于点H ,请你添加一个适当的条件: ,使△AEH ≌△CEB 。
4、函数43--=x x y 中,自变量x 的取值范围是 。
第3题图 HEDCBA第7题图OE DCBA第10题图D5、矩形一个角的平分线分矩形一边为1cm 和3cm 两部分,则这个矩形的面积为 cm 2。
6、已知一次函数2+=kx y ,请你补充一个条件: ,使y 随x 的增大而减小。
7、如图:在⊙O 中,AB 、AC 为互相垂直且相等的两条弦,OD ⊥AB ,OE ⊥AC ,垂足分别为D 、E ,若AC =2cm ,则⊙O 的半径为 cm 。
8、已知抛物线c x ax y ++=2与x 轴交点的横坐标为-1,则c a += 。
9、五个正整数从小到大排列,若这组数据的中位数是4,唯一众数是5,则这五个正整数的和为 。
10、如图:某同学用一个有600角的直角三角板估测学校旗杆AB 的高度,他将600角的直角边水平放在1.5米高的支架CD 上,三角板的斜边与旗杆的顶点在同一直线上,他又量得D 、B 的距离为5米,则旗杆AB 的高度约为 米。
(精确到1米,3取1.732)11、张大伯从报社以每份0.4元的价格购进了a 份报纸,以每份0.5元的价格售出了b 份报纸,剩余的以每份0.2元的价格退回报社,则张大伯卖报收入 元。
二、选择题:(每小题3分,共27分) 12、下列计算正确的是( )A 、5322x x x =+B 、632x x x =⋅C 、623)(x x -=-D 、336x x x =÷13、将一张长方形纸片按如图所示的方式折叠,BC 、BD 为折痕,则∠CBD 的度数为( )A 、600B 、750C 、900D 、95014、某服装原价为200元,连续两次涨价a %后,售价为242元,则a 的值为( )A 、5B 、10C 、15D 、20第13题图C E第16题图15、若033=+--a a ,则a 的取值范围是( )A 、a ≤3B 、a <3C 、a ≥3D 、a >316、如图:用8块相同的长方形地砖拼成一个矩形,则每个长方形地砖的面积是( ) A 、200cm 2 B 、300cm 2 C 、600cm 2 D 、2400cm 2 17、从哈尔滨开往A 市的特快列车,途中要停靠两个站点,如果任意两站间的票价都不同,那么有( )种不同的票价。
2003年龙江初中数学中考试题
2003年龙江初中数学中考试题(模拟题)一.填空题:(本题共10小题,每个小题2分,共20分) 1.计算:∣-5∣-3=_______。
2.我国陆地面积约为9600000平方千米,用科学记数法可表示为_____平方千米。
3.函数y =41-x 中自变量x 的取值范围是_____。
4.分解因式:a 2-2ab+b 2-1=__________。
5.计算:._______)11(1=-÷-xx x 6.已知:如图,∠ACB =∠DBC ,要使△ABC ≌△DCB ,只需增加的一个条件是_____(只需填写一个你认为适合的条件)7.如图中,阴影部分表示的四边形是_______。
8.已知梯形的上底长为3cm ,下底长为7cm ,则此梯形中位线长为____cm. 9.在半径为9cm 的圆中,60°的圆心角所对的弧长为______cm.10.下表为杨辉三角系数表,它的作用是指导读者按规律写出形如(a+b )n(n 为正整数)展开式的系数,请你仔细观察下表中的规律,填出(a+b )4展开式中所缺的系数。
(a+b)=a+b(a+b)2=a 2+2ab+b 2(a+b)3=a 3+3a 2b+3ab 2+b 3则(a+b )4=a 4+_______a 3b+6a 2b 2+4ab 3+b 4二.选择题:(本题共10个小题,每个小题3分,满分30分) 11.下列运算正确的是( ) A 、 2a+a=3a 2B 、94)9)(4(-⋅-=--C 、(3a 2)3=9a 6 D 、a 2•a 3=a 512.下列二次根式中,最简二次根式是 ( )A 、22x B 、12+b C 、a 4 D 、x113.下列说法正确的是 ( )A 、 负数和零没有平方根B 、20021的倒数是2002 C 、22是分数 D 、0和1的相反数是它本身 14.二元一次方程组⎩⎨⎧=+-=-1012y x y x 的解是( )A 、 ⎩⎨⎧==37x y B 、 ⎪⎩⎪⎨⎧==311319x y C 、⎩⎨⎧==28x y D 、⎩⎨⎧==73x y15.一元二次方程2x 2-4x+1=0根的情况是 ( ) A 、有两个不相等的实数根 B 、有两个相等的实数根 C 、没有实数根 D 、无法确定 16.下列命题正确的是 ( )A 、对角线相等的四边形是矩形B 、相邻的两个角都互补的四边形是平行四边形C 、平分弦的直径垂直于弦,并且平分弦所对的两条弧D 、三点确定一个圆 17.在同一直角坐标系中,函数y=3x 与y=x1-图象大致是18.两圆的半径分别为3cm 和4cm ,且两圆的圆心距为7cm ,则这两圆听位置关系是( ) A 、相交 B 、外切 C 、内切 D 、相离19.我省为了解决药品价格过高的问题,决定大幅度降低药品价格,其中将原价为a 元的某种常用药降价40%,则降价后此格为 ( ) A 、元4.0a B 、 元6.0a C 、60%a 元 D 、40%a 元则餐厅所有员工工资的众数、中位数是 ( ) A 、340 520 B 、520 340 C 、340 560 D 、560 340三、(本题共4个小题,每小题5分,满分20分) 21.计算:0045sin 2)12(121--++22.解不等式组⎩⎨⎧<-<+-0520)1(2x x x 并解集在数轴上表示出来。
【中考专题】黑龙江省大庆市中考数学历年真题汇总 卷(Ⅲ)(含答案详解)
黑龙江省大庆市中考数学历年真题汇总 卷(Ⅲ) 考试时间:90分钟;命题人:数学教研组 考生注意: 1、本卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I 卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、下列方程变形不正确的是( )A .4332x x -=+变形得:4323x x -=+B .方程110.20.5x x --=变形得:1010212x x --=C .()()23231x x -=+变形得:6433x x -=+D .211332x x -=+变形得:41318x x -=+ 2、一副三角板按如图所示的方式摆放,则∠1补角的度数为( )A .45︒B .135︒C .75︒D .165︒ 3、如图,等腰三角形ABC 的底边BC 长为4,面积是20,腰AC 的垂直平分线EF 分别交AC ,AB 边于E ,F 点,若点D 为BC 边的中点,点M 为线段EF 上一动点,则CDM ∆周长的最小值为( ) ·线○封○密○外A .8B .10C .12D .144、如图,已知点B ,F ,C ,E 在一条直线上,AB DE =,AB DE ∥,那么添加下列一个条件后,仍无法判定ABC DEF ≌△△的是( )A .BF CE =B .A D ∠=∠C .AC DF ∥D .AC DF =5、如图,AB CD ∥,45A ∠=︒,30C ∠=︒,则E ∠的度数是( )A .10°B .15°C .20°D .25°6、如图,有三块菜地△ACD 、△ABD 、△BDE 分别种植三种蔬菜,点D 为AE 与BC 的交点,AD 平分∠BAC ,AD =DE ,AB =3AC ,菜地△BDE 的面积为96,则菜地△ACD 的面积是( )A .24B .27C .32D .367、生活中常见的探照灯、汽车大灯等灯具都与抛物线有关.如图,从光源P 点照射到抛物线上的光线,PA PB 等反射以后沿着与直线PF 平行的方向射出,若CAP α∠=︒,DBP β∠=︒,则APB ∠的度数为( )°A .2αB .2βC .αβ+D .5()4αβ+ 8、如图,一个几何体是由六个大小相同且棱长为1的立方块组成,则这个几何体的表面积是( )A .16B .19C .24D .36 9、如图,在ABC 中,D 是BC 延长线上一点,50B ∠=︒,80A ∠=︒,则ACD ∠的度数为( ) A .140︒ B .130︒ C .120︒ D .110︒ 10、如图,在矩形ABCD 中,6AB =,8AD =,点O 在对角线BD 上,以OB 为半径作O 交BC 于点E ,连接DE ;若DE 是O 的切线,此时O 的半径为( )·线○封○密○外A .716B .2110C .2116D .3516第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、如图,在平面直角坐标系xOy 中,P 为函数)(0m y x x=>图象上一点,过点P 分别作x 轴、y 轴的垂线,垂足分别为M ,N .若矩形PMON 的面积为3,则m 的值为______.2、已知点P 是线段AB 的黄金分割点,AP >PB .若AB =2,则AP =_____.3、如图是正方体的一种展开图,表面上的语句为北京2022年冬奥会和冬残奥会的主题口号“一起向未来!”,那么在正方体的表面与“!”相对的汉字是________.4、如图,将一个边长为3的正方形纸片进行分割,部分①的面积是边长为3的正方形纸片的一半,部分②的面积是部分①的一半,部分③的面积是部分②的一半,以此类推,n 部分的面积是______.(用含n 的式子表示)5、写出n 的一个有理化因式:_______. 三、解答题(5小题,每小题10分,共计50分) 1、先把下列各数在数轴上表示出来,再按照从小到大的顺序用“<”连接起来. ﹣212,-(﹣4),0,+(﹣1),1,﹣|﹣312|2、将两块完全相同的且含60︒角的直角三角板ABC 和AFE 按如图所示位置放置,现将Rt AEF 绕A 点按逆时针方向旋转()090αα︒<<︒.如图,AE 与BC 交于点M ,AC 与EF 交于点N ,BC 与EF 交于点P . ·线○封○密·○外(1)在旋转过程中,连接,AP CE,求证:AP所在的直线是线段CE的垂直平分线.(2)在旋转过程中,CPN是否能成为直角三角形?若能,直接写出旋转角 的度数;若不能,说明理由.3、已知:如图,锐角∠AOB.求作:射线OP,使OP平分∠AOB.作法:①在射线OB上任取一点M;②以点M为圆心,MO的长为半径画圆,分别交射线OA,OB于C,D两点;③分别以点C,D为圆心,大于12CD的长为半径画弧,在∠AOB内部两弧交于点H;④作射线MH,交⊙M于点P;⑤作射线OP.射线OP即为所求.(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)完成下面的证明.证明:连接CD .由作法可知MH 垂直平分弦CD . ∴CP DP =( )(填推理依据). ∴∠COP = . 即射线OP 平分∠AOB . 4、解方程: (1)()8436x x --=; (2)232126x x +--=. 5、完成下面推理填空:如图,已知:AD BC ⊥于D ,EG BC ⊥于G ,1E ∠=∠.求证:AD 平分BAC ∠. 解:∵AD BC ⊥于D ,EG BC ⊥(已知), ∴90ADC EGC ∠=∠=︒(____①_____), ∴EG AD ∥(同位角相等,两直线平行), ∴_____②___(两直线平行,同位角相等) ∠1=∠2(____③_____), 又∵1E ∠=∠(已知), ∴∠2=∠3(_____④______), ∴AD 平分BAC ∠(角平分线的定义). ·线○封○密·○外-参考答案-一、单选题1、D【解析】【分析】根据等式的性质解答.【详解】解:A . 4332x x -=+变形得:4323x x -=+,故该项不符合题意;B . 方程110.20.5x x --=变形得:1010212x x --=,故该项不符合题意; C . ()()23231x x -=+变形得:6433x x -=+,故该项不符合题意;D . 211332x x -=+变形得:46318x x -=+,故该项符合题意;故选:D .【点睛】此题考查了解方程的依据:等式的性质,熟记等式的性质是解题的关键.2、D【解析】【分析】根据题意得出∠1=15°,再求∠1补角即可.【详解】由图形可得1453015∠=︒-︒=︒∴∠1补角的度数为18015165︒-︒=︒故选:D . 【点睛】 本题考查利用三角板求度数和补角的定义,熟记各个三角板的角的度数是解题的关键. 3、C 【解析】 【分析】 连接AD ,由于△ABC 是等腰三角形,点D 是BC 边的中点,故AD ⊥BC ,再根据三角形的面积公式求出AD 的长,再根据EF 是线段AC 的垂直平分线可知,点C 关于直线EF 的对称点为点A ,故AD 的长为CM +MD 的最小值,由此即可得出结论. 【详解】 解:连接AD ,∵△ABC 是等腰三角形,点D 是BC 边的中点, ∴AD ⊥BC , ·线○封○密○外∴11•42022ABC S BC AD AD ==⨯⨯=,解得AD =10, ∵EF 是线段AC 的垂直平分线,∴点C 关于直线EF 的对称点为点A ,∴AD 的长为CM +MD 的最小值,∴△CDM 的周长最短=CM +MD +CD =AD +110410222211BC =+⨯=+=.故选:C .【点睛】本题考查的是轴对称-最短路线问题,熟知等腰三角形三线合一的性质是解答此题的关键.4、D【解析】【分析】结合选项中的条件,是否能够构成,,AAS ASA SAS 的形式,若不满足全等条件即为所求;【详解】解:由AB DE 可得B E ∠=∠,判定两三角形全等已有一边和一角;A 中由BF CE =可得BC EF =,进而可由SAS 证明三角形全等,不符合要求;B 中A D ∠=∠,可由ASA 证明三角形全等,不符合要求;C 中由AC DF 可得ACB DFC ∠=∠,进而可由AAS 证明三角形全等,不符合要求;D 中无法判定,符合要求;故选D .【点睛】本题考查了三角形全等.解题的关键在于找出能判定三角形全等的条件.5、B【解析】【分析】根据平行线的性质求出关于∠DOE ,然后根据外角的性质求解.【详解】解:∵AB ∥CD ,∠A =45°, ∴∠A =∠DOE =45°, ∵∠DOE =∠C +∠E , 又∵30C ∠=︒, ∴∠E =∠DOE -∠C =15°. 故选:B 【点睛】 本题比较简单,考查的是平行线的性质及三角形内角与外角的关系.掌握两直线平行,内错角相等;三角形的一个外角等于和它不相邻的两个内角的和是解题关键. 6、C 【解析】 【分析】 利用三角形的中线平分三角形的面积求得S △ABD =S △BDE =96,利用角平分线的性质得到△ACD 与△ABD 的高相等,进一步求解即可. 【详解】 解:∵AD =DE ,S △BDE =96, ∴S △ABD =S △BDE =96, 过点D 作DG ⊥AC 于点G ,过点D 作DF ⊥AB 于点F , ·线○封○密○外∵AD 平分∠BAC ,∴DG=DF ,∴△ACD 与△ABD 的高相等,又∵AB =3AC ,∴S △ACD =13S △ABD =196323⨯=.故选:C .【点睛】本题考查了角平分线的性质,三角形中线的性质,解题的关键是灵活运用所学知识解决问题.7、C【解析】【分析】根据平行线的性质可得,EPA PAC EPB PBD ∠=∠∠=∠,进而根据APB APE BPE ∠=∠+∠即可求解【详解】 解:,PF AC PF BD ∥∥ ∴,EPA PAC EPB PBD ∠=∠∠=∠∴APB APE BPE ∠=∠+∠αβ=+故选C【点睛】本题考查了平行线的性质,掌握平行线的性质是解题的关键.8、C【解析】【分析】分别求出各视图的面积,故可求出表面积.【详解】 由图可得图形的正视图面积为4,左视图面积为 3,俯视图的面积为5 故表面积为2×(4+3+5)=24 故选C . 【点睛】 此题主要考查三视图的求解与表面积。
2023年黑龙江省哈尔滨市中考数学真题试卷(解析版)
2023年黑龙江省哈尔滨市中考数学真题试卷及答案一、选择题(每小题3分,共计30分)1. 的绝对值是( )A. B. 10 C. D.【答案】A【解析】根据“正数的绝对值是它本身,0的绝对值为0,负数的绝对值是它的相反数”求解即可.解:因为为负数,所以的绝对值为,故选A.【点拨】本题主要考查求绝对值,掌握“正数的绝对值是它本身,0的绝对值为0,负数的绝对值是它的相反数”是解题的关键.2. 下列运算一定正确的是()A. B. C. D.【答案】D【解析】根据积的乘方、同类项的定义、幂的乘方和平方差公式逐一判断即可.A.,故本选项原说法错误;B.,故本选项原说法错误;C.,故本选项原说法错误;D.,故本选项正确.故选D.【点拨】此题考查的是幂的运算性质和整式的运算,掌握积的乘方、合并同类项和幂的乘方是解决此题的关键.3. 下列图形中,既是轴对称图形,又是中心对称图形的是()A. B. C. D.【答案】A【解析】如果一个图形沿着某条直线对折后,直线两旁的部分能够重合,则称这个图形是轴对称图形,这条直线叫做对称轴;中心对称是旋转后与原图重合的图形,根据轴对称图形和中心对称图形的定义进行判断.解:A.既是轴对称图形,又是中心对称图形,故本选项符合题意;B.是轴对称图形,不是中心对称图形,故本选项不符合题意;C.不是轴对称图形,也不是中心对称图形,故本选项不符合题意;D.不是轴对称图形,是中心对称图形,故本选项不符合题意.故选:A.【点拨】本题考查了判断轴对称图形和中心对称图形,熟记定义是解题的关键.4. 七个大小相同的正方体搭成的几间体如图所示,其俯视图是()A. B. C. D.【答案】C【解析】根据从上边看得到的图形是俯视图,可得答案.解:这个组合体的俯视图如下:故选:C.【点拨】本题考查了画小立方块堆砌图形的三视图,掌握从上边看得到的图形是俯视图是解题的关键.5. 如图,是的切线,A为切点,连接﹐点C在上,,连接并延长,交于点D,连接.若,则的度数为()A. B. C. D.【答案】B【解析】利用垂线的性质及切线的性质得到和,再利用四边形的内角和为进而可求得,再利用等边对等角及三角形的内角和即可求解.解:,,又是的切线,,,又,,,又,,,故选B.【点拨】本题考查了圆的切线的性质,四边形内角和是,等腰三角形的性质及三角形的内角和,熟练掌握其基本知识是解题的关键.6. 方程的解为()A. B. C. D.【答案】C【解析】方程两边同时乘以,化为整式方程即可求解.解:程两边同时乘以得,解得:经检验,是原方程的解,故选:C.【点拨】本题考查了解分式方程,熟练掌握解分式方程的步骤是解题的关键.7. 为了改善居民生活环境,云中小区对一块矩形空地进行绿化,这块空地的长比宽多6米,面积为720平方米,设矩形空地的长为x米,根据题意,所列方程正确的是()A. B. C. D.【答案】A【解析】根据矩形面积公式,可得,即可解答.解:根据题意可得矩形空地的宽为米,可列方程,故选:A.【点拨】本题考查了一元二次方程的应用,根据题意得到等量关系,列出方程是解题的关键.8. 将枚黑棋子5枚白棋子装入一个不透明的空盒子里,这些棋子除颜色外无其他差别,从盒子中随机取出一枚棋子,则取出的棋子是黑棋子的概率是()A. B. C. D.【答案】D【解析】取出的棋子是黑棋子的概率:,据此即可求解.解:由题意得:取出的棋子是黑棋子的概率为:故选:D【点拨】本题考查概率的计算.熟记概率公式是解题关键.9. 如图,,相交于点,,是的中点,,交于点.若,则的长为()A. 2B. 4C. 6D. 8【答案】B【解析】根据可得,从而得到,再根据得到,从而得到,最后得到即可求解.解:,,,,,,,,是的中点,,,,,故选:B.【点拨】本题考查相似三角形的性质及判定,掌握相似三角形的性质及判定方法是解决本题的关键.10. 一条小船沿直线从A码头向B码头匀速前进,到达B码头后,停留一段时间,然后原路匀速返回A码头.在整个过程中,这条小船与B码头的距离(单位:)与所用时间(单位:)之间的关系如图所示,则这条小船从A码头到B码头的速度和从B码头返回A码头的速度分别为()A. B. C. D.【答案】D【解析】根据路程除以时间结合函数图象即可求解.解:依题意,小船从A码头到B码头的速度为,从B码头返回A码头的速度为,故选:D.【点拨】本题考查了函数图象,从函数图象获取信息是解题的关键.二、填空题(每小题3分,共计30分)11. 船闸是我国劳动人民智慧的结晶,三峡船闸的“人”字闸门是目前世界上最大的巨型闸门,重867000千克,用科学记数法表示为_______千克.【答案】【解析】把一个数写成的形式,是正整数,这种形式的记数方法叫做科学记数法.根据科学记数法的定义写出答案.科学记数法就是把一个数写成的形式,是整数,,故答案为:.【点拨】本题考查科学记数法,掌握科学记数法的记数方法是解题的关键.12. 在函数中,自变量x的取值范围是_________.【答案】【解析】根据分母不能为求出自变量x的取值范围.分式中分母不能为,,,故答案为:.【点拨】本题考查求函数自变量的取值范围,熟练掌握分式有意义的条件是解题的关键.13. 已知反比例函数的图像经过点,则a的值为_________.【答案】2【解析】将点的坐标代入函数解析式即可.解:将代入得:,解得:,故答案为:2.【点拨】本题考查了反比例函数的定义,根据反比例函数值求自变量是解题的关键.14. 计算的结果是___________.【答案】【解析】利用二次根式的混合运算法则及分母有理数的方法即可求解.解:,故答案:.【点拨】本题考查了二次根式的混合运算及分母有理数,熟练掌握其运算法则是解题的关键.15. 把多项式分解因式的结果是_____.【答案】【解析】先提取公因式m,然后发现还能利用平方差公式继续分解,即可得到结果.解:故答案为:.【点拨】本题考查因式分解,熟练掌握提公因式法及公式法是解题的关键,注意要分解彻底.16. 抛物线与y轴交点坐标是_________.【答案】【解析】与轴的交点的特点为,令,求出的值,即可求出抛物线与轴的交点坐标.令抛物线中,即,解得,故与轴的交点坐标为,故答案为:.【点拨】本题主要考查了抛物线与y轴的交点坐标,解题的关键是令,求出的值.17. 不等式组的解集是_________________.【答案】【解析】根据解一元一次不等式组的步骤即可求解.解:解①得:解②得:故该不等式组的解集为:故答案为:【点拨】本题考查求解一元一次不等式组,掌握求解一元一次不等式组一般步骤是解题的关键.注意计算的准确性.18. 一个扇形的圆心角是,弧长是,则扇形的半径是_________cm.【答案】3【解析】根据弧长公式即可得到关于扇形半径的方程即可求解.解:设扇形的半径是,则解得:.故答案为3.【点拨】题主要考查了扇形的弧长,正确理解公式是解题的关键.19. 矩形的对角线,相交于点,点在矩形边上,连接.若,,则_________.【答案】或【解析】根据题意画出图形,分点在上和上两种情况讨论即可求解.解:∵四边形是矩形,∴,∴,∵,∴∴,如图所示,当点在上时,∵,∴如图所示,当点在上时,∵,∴,故答案为:或.【点拨】本题考查了矩形的性质,等边对等角,三角形的外角的性质,分类讨论是解题的关键.20. 如图在正方形中,点E在上,连接,,F为的中点连接.若,则的长为_________.【答案】【解析】根据正方形的性质得到,,设,根据勾股定理求出的值,再根据勾股定理即可求出的长.解:正方形,F为的中点,设,在中,即解得故,在中解得(负值舍去)故答案为:.【点拨】本题主要考查了正方形的性质,勾股定理,直角三角形斜边上的中线的性质,熟练掌握勾股定理是解题的关键.三、解答题(共60分)21. 先化简,再求代数式的值,其中.【答案】,【解析】先根据分式混合运算法则代简,再将代入代简式计算即可.解:,当时,原式.【点拨】本题考查分式化简求值,特殊角的三角函数值,分母有理化,熟练掌握分式混合运算法则是解题的关键.22. 如图,方格纸中每个小正方形的边长均为1个单位长度,线段和线段的端点均在小正方形的顶点上.(1)在方格纸中画出,且为钝角(点在小正方形的顶点上);(2)在方格纸中将线段向下平移2个单位长度,再向右平移1个单位长度后得到线段(点的对应点是点,点的对应点是点),连接,请直接写出线段的长.【答案】(1)画图见解析(2)画图见解析,【解析】(1)找到的格点的,使得,且,连接,则即为所求;(2)根据平移画出,连接,勾股定理即可求解.(1)解:如图所示,即为所求;(2)解:如图所示,,即为所求;.【点拨】本题考查了平移作图,勾股定理与网格,熟练掌握勾股定理是解题的关键.23. 军乐中学开展以“我最喜欢的劳动实践课”为主题的调查活动,围绕“在园艺课,泥塑课,编织课、烹饪课四门劳动实践课中,你最喜欢哪一门课?(必选且只选一门)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的条形统计图,其中最喜欢泥塑课的学生人数占所调查人数的.请你根据图中提供的信息解答下列问题:(1)在这次调查中,一共抽取了多少名学生?(2)请通过计算补全条形统计图;(3)若军乐中学共有1200名学生,请你估计该中学最喜欢烹饪课的学生共有多少名.【答案】(1)(2)见解析(3)【解析】根据最喜欢泥塑课的学生人数为人,占所调查人数的,用即可求解;(2)根据总人数减去其他类型的人数,即可得出最喜欢编织课的学生人数进而补全统计图;(3)根据最喜欢烹饪课的学生的占比乘以,即可求解.(1)解:最喜欢泥塑课的学生人数为人,占所调查人数的,∴这次调查中,一共抽取了名学生(2)解:最喜欢编织课的学生人数为人,补全统计图如图所示,(3)解:估计该中学最喜欢烹饪课的学生共有名【点拨】本题考查了条形统计图,样本估计总体,从统计图中获取信息是解题的关键.24. 已知四边形是平行四边形,点在对角线上,点在边上,连接,,.(1)如图①,求证;(2)如图②,若,过点作交于点,在不添加任何轴助线的情况下,请直接写出图②中四个角(除外),使写出的每个角都与相等.【答案】(1)见解析;(2),理由见解析.【解析】(1)由平行四边形的性质得,,进而有,从而利用即可证明结论成立;(2)先证四边形是菱形,得,又证,得,由()得得,根据等角的补角相等即可证明.(1)证明:∵四边形是平行四边形,∴,,∴,∵,∴;(2)解:,理由如下:∵四边形是平行四边形,∴四边形是菱形,,∴,,,∴,∵,∴,∴,∴,由()得,∴,∵,∴.【点拨】本题考查了平行四边形的性质、菱形的判定及性质、等边对等角、全等三角形的判定及性质以及等角的补角相等.熟练掌握全等三角形的判定及性质是解题的关键.25. 佳衣服装厂给某中学用同样的布料生产,两种不同款式的服装,每套款服装所用布料的米数相同,每套款服装所用布料的米数相同,若套款服装和套款服装需用布料米,套款服装和套款服装需用布料米.(1)求每套款服装和每套款服装需用布料各多少米;(2)该中学需要,两款服装共套,所用布料不超过米,那么该服装厂最少需要生产多少套款服装?【答案】(1)每套款服装用布料米,每套款服装需用布料米(2)服装厂需要生产套款服装【解析】(1)每套款服装用布料米,每套款服装需用布料米,根据题意列出二元一次方程组,解方程组即可求解;(2)设服装厂需要生产套款服装,则生产套款服装,根据题意列出一元一次不等式,解不等式即可求解.(1)解:每套款服装用布料米,每套款服装需用布料米,根据题意得,,解得:,答:每套款服装用布料米,每套款服装需用布料米;(2)设服装厂需要生产套款服装,则生产套款服装,根据题意得,,解得:,∵为正整数,∴的最小值为,答:服装厂需要生产套款服装.【点拨】本题考查了二元一次方程组的应用,一元一次不等式的应用,根据题意列出不等式以及方程组是解题的关键.26. 已知内接于,为的直径,N为的中点,连接交于点H.(1)如图①,求证;(2)如图②,点D在上,连接,,,交于点E,若,求证;(3)如图③,在(2)的条件下,点F在上,过点F作,交于点G.,过点F作,垂足为R,连接,,,点T在的延长线上,连接,过点T作,交的延长线于点M,若,求的长.【答案】(1)见解析(2)见解析(3)【解析】(1)连接,根据N为的中点,易证,再根据中位线定理得出结论;(2)连接,先证得,再根据得,根据即可得出结论;(3)连接,先证,再证四边形是矩形,过A作垂足为S,先证出,再能够证出从而,得到等腰直角,利用三角函数求出,再根据求出,最后用勾股定理求出答案即可.(1)证明:如图,连接,为的中点,,,,,,是中位线,;(2)证明:如图,连接,设,,,,,,,,,,;(3)解:连接,,,,,,,,,,,,,,,,四边形是平行四边形,是的直径,,四边形矩形,,,过点A作垂足为S,,,,,,,,是的直径,,,,,,,,,,,,,,,,,,,,,,.【点拨】本题是圆的综合题,考查圆的有关知识、全等三角形的判定与性质、垂径定理、三角函数、勾股定理、圆周角定理等知识,构造辅助线解决问题是解题关键.27. 在平面直角坐标系中,为坐标原点,抛物线与轴交于点,,与轴交于点.(1)求,的值;(2)如图①,是第二象限抛物线上的一个动点,连接,,设点的横坐标为,的面积为,求关于的函数解析式(不要求写出自变量的取值范围);(3)如图②,在(2)的条件下,当时,连接交轴于点,点在轴负半轴上,连接,点在上,连接,点在线段上(点不与点重合),过点作的垂线与过点且平行于的直线交于点,为的延长线上一点,连接,,使,是轴上一点,且在点的右侧,,过点作,交的延长线于点,点在上,连接,使,若,求直线的解析式.【答案】(1),(2)(3)【解析】(1)把点,代入抛物线解析式,得方程组,求出,的值即可;(2)过点作轴,垂足为,由(1)知,抛物线的解析式是,得,根据“是第二象限抛物线上的一个动点,点的横坐标为”,得,根据,代入整理即可得到关于的函数解析式;(3)以为一边作,的另一边交的延长线于点;作,垂足为;作,垂足为;作轴,垂足为;根据和,求出,根据“,,,”推理出,,得到,结合,推理出,用证,用证,推理出,根据“,”,得出,,,代入,求出,勾股定理算出,根据“,”,设,则,,代入,算出,运用勾股定理计算,计算,结合点在轴负半轴上,得,设直线的解析式为,把,代入求出完整解析式即可.(1)点,在抛物线上,,解得:,,(2)由(1)知,抛物线的解析式是,是抛物线与轴的交点,时,,,,如下图,过点作轴,垂足为,是第二象限抛物线上一点,点的横坐标为,,(3)如下图,以为一边作,的另一边交的延长线于点;作,垂足为;作,垂足为;作轴,垂足为,,由(2)知,,,,,,,,即,,,,,,,,,又,,,,,,,,,在和中,,,,,,,,,,,,,,,轴,,,,,,,,,,,,,设,则,,,,,,,又点在轴负半轴上,,设直线的解析式为,把,代入,得:,解得:,直线的解析式为【点拨】本题是二次函数综合题,难度大,结合全等三角形、勾股定理、三角函数解直角三角形知识点,综合运用知识、画出辅助线、数形结合、分析与计算是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
黑龙江省2003年中考数学试题一、填空题;(每小题3分,共33分)1、生物学家发现一种病毒的直径约为0.000043米,用科学记数法表示为 米。
2、写出满足方程92=+y x 的一对整数值 。
3、如图:△ABC 中,AD ⊥BC ,CE ⊥AB ,垂足分别为D 、E ,AD 、CE 交于点H ,请你添加一个适当的条件: ,使△AEH ≌△CEB 。
4、函数43--=x x y 中,自变量x 的取值范围是 。
第3题图HEDCBA第7题图OE DCBA第10题图D5、矩形一个角的平分线分矩形一边为1cm 和3cm 两部分,则这个矩形的面积为 cm 2。
6、已知一次函数2+=kx y ,请你补充一个条件: ,使y 随x 的增大而减小。
7、如图:在⊙O 中,AB 、AC 为互相垂直且相等的两条弦,OD ⊥AB ,OE ⊥AC ,垂足分别为D 、E ,若AC =2cm ,则⊙O 的半径为 cm 。
8、已知抛物线c x ax y ++=2与x 轴交点的横坐标为-1,则c a += 。
9、五个正整数从小到大排列,若这组数据的中位数是4,唯一众数是5,则这五个正整数的和为 。
10、如图:某同学用一个有600角的直角三角板估测学校旗杆AB 的高度,他将600角的直角边水平放在1.5米高的支架CD 上,三角板的斜边与旗杆的顶点在同一直线上,他又量得D 、B 的距离为5米,则旗杆AB 的高度约为 米。
(精确到1米,3取1.732)11、张大伯从报社以每份0.4元的价格购进了a 份报纸,以每份0.5元的价格售出了b 份报纸,剩余的以每份0.2元的价格退回报社,则张大伯卖报收入 元。
二、选择题:(每小题3分,共27分) 12、下列计算正确的是( )A 、5322x x x =+B 、632x x x =⋅C 、623)(x x -=- D 、336x x x =÷13、将一张长方形纸片按如图所示的方式折叠,BC 、BD 为折痕,则∠CBD 的度数为( )A 、600B 、750C 、900D 、95014、某服装原价为200元,连续两次涨价a %后,售价为242元,则a 的值为( )A 、5B 、10C 、15D 、20第13题图C第16题图15、若033=+--a a ,则a 的取值范围是( )A 、a ≤3B 、a <3C 、a ≥3D 、a >316、如图:用8块相同的长方形地砖拼成一个矩形,则每个长方形地砖的面积是( ) A 、200cm 2 B 、300cm 2 C 、600cm 2 D 、2400cm 217、从哈尔滨开往A 市的特快列车,途中要停靠两个站点,如果任意两站间的票价都不同,那么有( )种不同的票价。
A 、4B 、6C 、10D 、1218、如图:在等边△ABC 中,P 为BC 上一点,D 为AC 上一点,且∠APD =600,BP =1,CD =32,则△ABC 的边长为( )A 、3B 、4C 、5D 、6600第18题图DPCB A第20题图 19、平面直角坐标系内,点A (n ,n -1)一定不在( )A 、第一象限B 、第二象限C 、第三象限D 、第四象限20、如图:⊙O 的直径为10cm ,弦AB 为8cm ,P 是弦AB 上一点,若OP 的长为整数,则满足条件的点P 有( )A 、2个B 、3个C 、4个D 、5个 三、解答题;(共60分)21、先化简,再求值:13181++÷⎪⎭⎫ ⎝⎛+--x x x x ,其中23-=x 22、关于x 的方程04)1(2=+++kx k kx 有两个不相等的实数根。
(1)求k 的取值范围;(2)是否存在实数k ,使方程的两个实数根的倒数和等于0 ?若存在,求出k 的值;若不存在,请说明理由。
23、某中学在一次健康知识竞赛活动中,抽取了一部分同学测试的成绩为样本,绘制的成绩统计图如下,请结合统计图回答下列问题:(1)本次测试中,抽样的学生有多少人?(2)分数在90.5~100.5这一组的频率是多少?(3)这次测试成绩的众数落在哪个小组内?(4)若这次测试成绩80分以上(含80分)为优秀,则优秀率不低于多少?第23题图分数24、为美化环境,计划在某小区内用30平方米的草皮铺设一个边长为10米的等腰三角形绿地,请你求出这块等腰三角形绿地另两边的长。
25、某空军加油飞机接到命令,立即给另一架正在飞行的运输飞机进行空中加油,在加油过程中,设运输飞机的油箱余油量为1Q 吨,加油飞机的加油油箱....余油量为2Q 吨,加油时间为t 分钟,1Q 、2Q 与t 之间的函数图像如图所示,结合图像回答下列问题:(1)加油飞机的加油油箱中装载了多少吨油?将这些油全部加给运输飞机需多少分钟?(2)求加油过程中,运输飞机的余油量1Q (吨)与时间t (分钟)的函数关系式;(3)运输飞机加完油后,以原速继续飞行,需10小时到达目的地,油料是否够用?说明理由。
分钟)26、(9分)已知:如图,BD 、CE 分别是△ABC 的外角平分线,过点A 作AF ⊥BD ,AG ⊥CE ,垂足分别为F 、G ,连结FG ,延长AF 、AG 与直线BC 相交,易证:)(21AC BC AB FG ++=,若: (1)BD 、CE 分别是△ABC 的内角平分线(如图2); (2)BD 为△ABC 的内角平分线,CE 为△ABC 的外角平分线(如图3),则在图2、图3两种情况下,线段FG 与△ABC 三边又有怎样的数量关系?请写出你的猜测,并对其中的一种情况进行证明。
第26题图1G FEDCBA第26题图2GFE DCBA第26题图3 GFED CBA27、(9分)为了保护环境,某企业决定购买10台污水处理设备,现有A 、B 两种型号的设备,其中经预算,该企业购买设备的资金不高于105万元。
(1)请你设计该企业有几种购买方案;(2)若企业每月产生的污水量为2040吨,为了节约资金,应选择哪种购买方案;(3)在第(2)问的条件下,若每台设备的使用年限为10年,污水厂处理污水费为每吨10元,请你计算,该企业自己处理污水与将污水排到污水厂处理相比较,10年节约资金多少万元?(注:企业处理污水的费用包括购买设备的资金和消耗费)28、(9分)已知,如图,直角坐标系中的梯形AOBC 中,AC ∥OB ,AC 、OB 的长分别是关于x 的方程04622=++-m mx x 的两根,并且AOC S ∆∶BOC S ∆=1∶5(1)求AC 、OB 的长;(2)当BC ⊥OC 时,求OC 的长及OC 所在直线的解析式;(3)在第(2)问的条件下,线段OC 上是否存在一点M ,过M 点作x 轴的平行线交y 轴于F ,交BC 于D ,过D 点作y 轴的平行线交x 轴于E ,使FOED S 矩形=AOBC S 梯形21,若存在,请直接写出M 点的坐标;若不存在,请说明理由。
参考答案一、填空题1、4.3×10-5;2、x =1,y =4等;3、AH =CB 等;4、x ≥3且x ≠4;5、4或12; 6、k =-3等;7、2;8、1;9、17或18或19;10、10;11、)2.03.0(a b - 二、DCBAB ,BACD 三、解答题:21、原式=3-x ;当23-=x 时,原式=2-22、解:(1)由题意知k ≠0,且△=44)1(2kk k ⋅-+>0 ∴k >21-且k ≠0 (2)不存在。
设方程的两个根是1x 、2x ∵21x x ⋅=41≠0 ∴2111x x +=2121x x x x ⋅+=0 ∴1x +2x =0∵1x +2x =k k 1+-∴01=+k ,k =-1<21- ∴满足条件的实数k 不存在。
23、解:(1)2+3+4+41=50(人) (2)总数频数频率==504=0.08 (3)众数落在80.5~90.5这一小组内 (4)这次测试成绩的优秀率不低于90%。
24、解:分三种情况计算,不妨设AB =10米,过点C 作CD ⊥AB 于D ,则: ABC S ∆=CD AB ⋅21,∴CD =6米 (1)当AB 为底边时,AD =DB =5(米)(如图1) AC =BC =2256+=61(米)第24题图1 DCB A第24题图2 D CB A第24题图3DCBA(2)当AB 为腰且三角形为锐角三角形时(如图2) AB =AC =10(米)AD =22CD AC -=8(米),BD =2(米) BC =2226+=102(米) (3)当AB 为腰且三角形为钝角三角形时(如图3)AB =BC =10(米) AC =22186+=106(米)25、解:(1)由图象知,加油飞机的加油油箱中装载了30吨油,全部加给运输飞机需10分钟(2)设1Q =b kt +,把(0,40)和(10,69)代入得: ⎩⎨⎧+==b k b 106940 解这个方程组得⎩⎨⎧==409.2b k ∴1Q =409.2+t (0≤t ≤10)(3)根据图象可知运输飞机的耗油量为每分钟0.1吨∴10小时耗油量为:10×60×0.1=60(吨)<69(吨) ∴油料够用 26、解:猜测结果:图2结论为)(21BC AC AB FG -+=证明:分别延长AG 、AF 交BC 于H 、K ,易证△BAF ≌△BKF 得AF =KF ,AB =KB 同理可证AG =HG ,AC =HC ∴FG =21HK 又∵HK =BK -BH =AB +AC -BC ∴)(21BC AC AB FG -+=图3结论为:)(21AB AC BC FG -+=27、解:(1)设购买污水处理设备A 型x 台,则B 型)10(x -台,由题意知:)10(1012x x -+≤105 ∴x ≤2.5又∵x 是非负整数 ∴x 可取0、1、2∴有三种购买方案:①购A 型0台,B 型10台;②购A 型1台,B 型9台;③购A 型2台,B 型8台; (2)由题意得)10(200240x x -+≥2040,解得x ≥1 ∴x 为1或2当x =1时,购买资金为:12×1+10×9=102(万元)当x =2时,购买资金为:12×2+10×8=104(万元) ∴为了节约资金,应选购A 型1台,B 型9台。
(3)10年企业自己处理污水的总资金为:102+10×10=202(万元)若将污水排到污水厂处理,10年所需费用为:2040×12×10×10=2448000(元)=244.8(万元) ∵244.8-202=42.8(万元) ∴能节约资金42.8万元。
28、解:(1)∵AOC S ∆∶BOC S ∆=1∶5∴AC ∶OB =1∶5不妨设AC =k ,则OB =k 5由题意得⎩⎨⎧+=⋅=+45652m k k m k k 解得⎩⎨⎧==11k m 或⎩⎨⎧-=-=11k m (不符题意;舍去) ∴AC =1,OB =5(2)∵∠OAC =∠BCO =900,∠ACO =∠BOC ∴△OBC ∽△COA∴ACOC OC OB =,即AC OB OC ⋅=2∴OC =5或OC =-5(舍去) ∵AC =1,AO =2 ∴C (1,2) ∴直线OC 的解析式为y =x 2 (3)存在满足条件的点M ,1M (21,1),2M (43,23) 第26题图2K H GFED CB A。
