多期双重差分法,政策实施时间不同的处理方法
双重差分法方法综述

双重差分法方法综述小伙伴们!今天咱们来唠唠双重差分法这个有趣的东西哈。
双重差分法在经济学、社会学等好多领域都挺常用的,用处可不小呢。
一、双重差分法是啥。
简单来说呀,双重差分法就是一种用来评估政策或者项目影响的方法。
比如说,我们想知道某个政策实施后到底有没有效果,效果有多大,这时候双重差分法就可能派上用场啦。
它就像是一个小侦探,能帮我们找出政策带来的真实影响。
举个例子哈,假如有两个地区,一个地区实施了新的教育政策,另一个地区没有实施。
我们先看实施政策前这两个地区的教育水平,比如学生的考试成绩啥的,这是第一个“差”。
然后再看实施政策后这两个地区的教育水平,又得到一个“差”。
最后把这两个“差”再做个减法,就得到了双重差分啦,这个结果就能反映出政策的效果咯。
二、双重差分法的基本假设。
这个方法要想好用,得满足一些假设哈。
一个很重要的假设就是“共同趋势假设”。
啥意思呢?就是说在没有政策干预的情况下,实验组和对照组的变化趋势得是差不多的。
就好比两个人跑步,本来速度都差不多,这时候其中一个人吃了颗神奇的药(相当于政策干预),然后我们才能通过比较他俩后来的速度变化,看出这个药有没有效果。
要是一开始这俩人速度就一个快一个慢,那后面的比较就不太准啦。
还有一个假设是“外生性假设”。
就是说政策的实施不能受到其他因素的干扰,得是一个“纯粹”的干预。
比如说,不能因为某个地区的经济突然变好,然后才实施这个政策,这样就分不清到底是政策的作用还是经济变好的作用啦。
三、双重差分法的应用步骤。
1. 选择实验组和对照组。
这就像是找两个差不多的小伙伴来做对比。
实验组就是接受政策或者项目干预的那一组,对照组就是没有接受干预的那一组。
选择的时候可得小心哦,要尽量保证这两组在其他方面都差不多,除了有没有接受干预这个区别。
比如说研究教育政策对学生成绩的影响,实验组就是实施新政策的学校的学生,对照组就是没有实施新政策的学校的学生,而且这两个学校的学生基础、师资力量啥的都得差不多才行。
互助问答第83问 政策时点不一致DID的问题
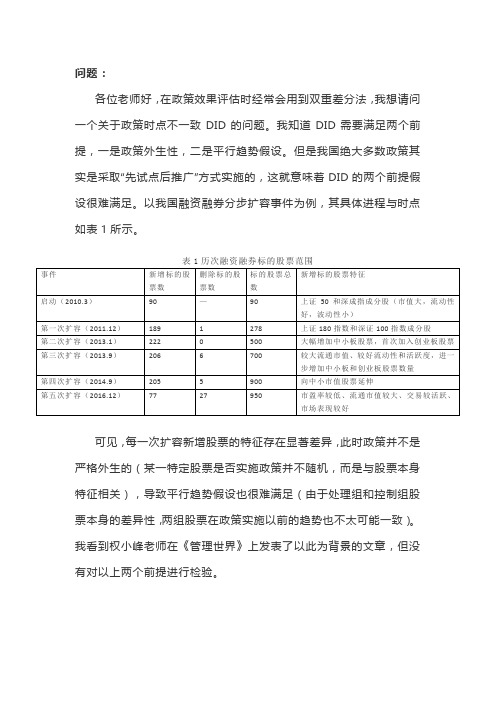
我想请问老师,评估这类“先试点后推广”的政策可以使用DID吗?如果可以,具体实施过程中应如何做外生性和平行趋势假设的检验呢?如果不可以,那么这类政策评估应该用什么方法呢?非常感谢老师!
回答:
DID要求实验组和控制组在没有政策的情况下,结果变量(在线性模型假定下)具有相同的时间趋势,即通常所说的平行趋势假设。
因为反事实状态无法被观察到,该假设是无法通过统计检验进行证实的。
通常的做法是,对政策发生前实验组和控制组结果变量的趋势是否平行进行检验,如果平行,则认为在政策发生时点以后的时期内,如果没有政策冲击,仍然平行,即满足DID识别假设;否则,认为不满足。
这可以看作是一个证伪检验。
对于问题中的例子,也应该进行类似的检验。
需要强调的是,DID估计的识别假设是平行趋势,而不是随机分组。
随机分组的话就不是仅仅是满足共同趋势了,而是意味着实验组和控制组在没有政策的情况下没有统计上显著的差异。
平行趋势允许差异存在,只是假定差异(在线性模型假设下)不随时间变化。
随机分组是DID的识别假设满足的充分不必要条件。
双重差分方法的常见类型

双重差分方法的常见类型一、双重差分方法的概念与作用双重差分方法(Difference-in-Differences,DID)是一种常用的因果推断方法,主要用于评估政策干预或其他处理的因果效应。
它通过比较处理组和对照组在处理前后的平均结果变化来估计处理效应。
双重差分方法的关键假设是,在没有处理的情况下,处理组和对照组的结果变量的变化趋势是相同的,即平行趋势假设。
二、双重差分方法的常见类型1.并行双重差分法:在这种方法中,处理组和对照组在处理前后的结果变量变化趋势是平行的。
这种方法是最常见的双重差分设计,适用于评估政策干预的因果效应。
2.序列双重差分法:在这种方法中,处理组和对照组在处理后的结果变量变化趋势是平行的,但在处理前可能存在差异。
这种方法适用于评估连续性政策干预的因果效应。
3.交叉双重差分法:在这种方法中,处理组和对照组在处理前后的结果变量变化趋势可能不同,但处理组和对照组之间的差异在处理前后保持不变。
这种方法适用于评估跨部门或跨地区的政策干预效应。
4.重复双重差分法:在这种方法中,处理组和对照组在多个处理周期内的结果变量变化趋势是平行的。
这种方法适用于评估重复性政策干预的因果效应。
三、各类型双重差分法的应用场景与优缺点1.并行双重差分法:应用场景广泛,适用于政策干预、产品推广等。
优点是假设较为简单,易于操作;缺点是对于处理效应的估计可能受到平行趋势假设的限制。
2.序列双重差分法:适用于连续性政策干预的评估,可以较好地处理政策实施过程中的时间效应。
优点是能够较好地捕捉政策实施过程中的细节;缺点是对平行趋势假设的要求较高。
3.交叉双重差分法:适用于跨部门或跨地区的政策干预效应评估,可以较好地处理部门或地区间的差异。
优点是具有较强的适用性;缺点是操作复杂,对数据要求较高。
4.重复双重差分法:适用于重复性政策干预的评估,可以较好地处理政策实施过程中的动态效应。
优点是能够较好地捕捉政策实施过程中的动态变化;缺点是对重复处理周期假设的要求较高。
多期双重差分法(DID)的Stata操作

多期双重差分法(DID)的Stata操作如果政策实施时点⼀致的话,那么我们就可以使⽤标准DID愉快地玩耍了。
但是,更多情况下,政策实施时点是不⼀致的,这时候就该多期DID粉墨登场了。
在多期DID模型中,因为不同个体实施政策的时点(period)不同,所以政策分期变量会变成(注意下标)。
与标准DID⼀样,我们需要⽣成地区维度的政策分组变量treat和时间维度的政策分期变量period,交互项treat×period的系数反映的就是经过政策实施前后、处理组和控制组两次差分后所得到的政策效应。
那么,如何在Stata中实现多期DID的操作呢?让我们看⼀个经典的案例!数据说明贾瑞雪⽼师(2014)的论⽂《The Legacies of Forced Freedom: China’s Treaty Ports》是⼀篇经典的计量史学论⽂,《Review of Economics and Statistics》官⽹上公布了这篇论⽂的数据和代码,接下来我就使⽤作者公布的数据和代码跟⼤家分享⼀下多期DID的Stata操作。
Replication Data for: Ruixue Jia . The Legacies of Forced Freedom: China's Treaty Ports[J]. Review ofEconomics and Statistics, 2014, 96(4):596-608.建议⼤家在看下⾯的内容之前,最好先看⼀下“殖民的遗产:通商⼝岸给近现代中国带来了什么?”这篇推⽂,这样可能理解起来更加顺畅。
识别策略清朝末期,清政府与西⽅列强签订了⼀系列不平等条约,开放沿江沿海等城市作为通商⼝岸即是不平等条约的主要内容之⼀。
贾瑞雪⽼师(2014)将近代通商⼝岸的设置作为⼀项准⾃然实验,评估了通商⼝岸对中国近现代⼈⼝和经济发展的长期影响。
从1840年⾄1910年,中国⼀共被迫开放了40多个通商⼝岸。
政策效果评估的双重差分方法

政策效果评估的双重差分方法政策效果评估在政府工作中至关重要,它可以帮助政策制定者了解政策的实际影响,从而做出更为有效的决策。
双重差分方法(Differences-in-Differences,DiD)作为一种常见的政策效果评估方法,具有诸多优点,但也存在一定的局限性。
本文将详细介绍双重差分方法在政策效果评估中的应用,并通过实际案例分析其优势、挑战及改进建议。
双重差分方法是一种广泛应用于政策效果评估、医学、社会科学等诸多领域的方法。
该方法通过比较政策实施组与对照组在政策实施前后的变化差异,来评估政策的实际效果。
近年来,随着大数据技术的发展,双重差分方法在政策效果评估领域的应用日益广泛。
数据来源主要包括政府部门、调查机构和相关研究机构等。
在收集数据时,需要确保数据的准确性、可靠性和时效性。
同时,还需对数据进行必要的处理,如清洗、整理等,以保证数据分析的质量。
因变量即政策效果评估的指标,应根据具体政策的不同进行选择。
例如,教育政策的效果可以通过学生成绩、升学率等指标来评估;环境保护政策的效果可以通过空气质量、水质等指标来评估。
在选择因变量时,应注意选择具有代表性、可操作性和可比较性的指标。
自变量即影响政策效果的因素,包括政策实施前后的时间趋势、地区差异、人群特征等。
在选择自变量时,需要充分了解政策实施的背景和影响因素,并对自变量进行合理控制和分析。
例如,在评估教育政策效果时,需要考虑不同地区的教育资源、师资力量等因素。
双重差分方法的核心是通过比较政策实施组和对照组在政策实施前后的变化差异来评估政策效果。
需要确定实施组和对照组;需要对其在政策实施前后的数据进行比较和分析。
在应用双重差分方法时,应注意选择合适的对照组和处理潜在的混淆因素。
以某城市推行垃圾分类政策为例,采用双重差分方法评估其效果。
收集该城市在推行垃圾分类政策前后的相关数据,包括垃圾产生量、分类投放情况、回收利用率等。
数据来源包括政府部门、研究机构和社会调查等。
DID双重差分法的原理和方法

DID双重差分法的原理和方法双重差分法(DID)是一种在计量经济学中常用的估计因果效应的方法。
它能够在实证研究中有效地处理因果推断中的内生性问题,尤其在面板数据的分析中得到广泛应用。
本文将详细介绍DID方法的原理和应用方法。
一、DID方法的原理DID方法的核心原理是利用面板数据的时间和处理组别维度,通过比较处理组和对照组的差异来估计因果效应。
简而言之,DID方法通过比较处理组在政策干预前后的变化,和同期对照组的变化差异,来估计政策对处理组的因果效应。
为了更好地理解DID方法的原理,我们以一个实际案例为例进行说明。
假设地区实施了一项新的政策措施(如教育),我们想要评估这项政策对学生学习成绩的影响。
我们需要一个对照组和一个处理组,对照组是未接受教育的地区,处理组是接受教育的地区。
在DID方法中,我们同时比较了政策干预前后两个组别的差异。
具体地,我们比较了两个时间点的学生成绩差异:政策实施前的学生成绩差异(处理组与对照组),以及政策实施后的学生成绩差异(处理组与对照组)。
通过比较这两个时间点的差异,我们可以估计政策对学生成绩的因果效应。
二、DID方法的应用方法在实际应用中,DID方法的步骤可以总结如下:1.确定处理组和对照组:根据研究问题和数据可用性,选择合适的处理组和对照组。
处理组是接受政策的群体,对照组是未接受政策的群体。
2.选择合适的时期:确定政策实施的时间点,并选择合适的时间段进行分析。
通常我们需要在政策实施前后收集足够的数据,以便比较两个时期的差异。
3. 建立DID回归模型:为了估计因果效应,我们需要建立DID回归模型。
基本的DID模型可以表示为:Y_it = α + β*T_t + γ*D_i +δ*(T_t * D_i) + ε_i t。
其中,Y_it是观测单位i在时间t的因变量;T_t是时间指标,取1表示政策实施后,取0表示政策实施前;D_i是处理组指标,取1表示处理组,取0表示对照组;α是截距项;β、γ、δ分别是政策效应、处理组效应和DID效应的系数;ε_it是误差项。
双重差分法有效分离时间效应
双重差分法有效分离时间效应
双重差分法是一种有效的统计分析方法,用于分离时间效应。
时间效应是指在不同的时间点,数据之间存在的相关性。
这种相关性可能会导致误差的累积,从而影响数据分析的准确性。
因此,分离时间效应是数据分析中非常重要的一步。
双重差分法的基本思想是对数据进行两次差分。
第一次差分是为了消除数据中的趋势效应,第二次差分是为了消除数据中的季节效应。
通过这样的处理,可以得到一个相对稳定的时间序列,从而更好地进行统计分析。
具体来说,双重差分法的步骤如下:
1. 对原始数据进行一次差分,得到一阶差分序列。
2. 对一阶差分序列进行一次差分,得到二阶差分序列。
3. 对二阶差分序列进行统计分析,得到稳定的时间序列。
需要注意的是,在进行双重差分法之前,需要对原始数据进行一些预处理。
例如,需要检查数据是否存在缺失值或异常值,并进行相应的处理。
双重差分法在实际应用中具有广泛的应用。
例如,在经济学中,双重差分法可以用于消除季节性因素对经济数据的影响,从而更好地研究经济趋势。
在医学研究中,双重差分法可以用于消除季节性因素对疾病发病率的影响,从而更好地研究疾病的传播规律。
总之,双重差分法是一种非常有效的统计分析方法,可以帮助我们更好地理解数据中的时间效应,并消除这些效应对数据分析的影响。
在实际应用中,我们需要根据具体情况选择合适的方法,并进行适当的数据预处理,以确保结果的准确性和可靠性。
双重差分模型介绍及其应用
双重差分模型介绍及其应用
双重差分模型(Double Difference Model)是一种统计分析模型,
用于估计处理效应或政策影响的因果效应。
该模型是在差分法
(Difference-in-Difference)的基础上引入了两个时间点之间的差分,
从而进一步控制了时间固定效应和处理固定效应,更准确地评估了处理效应。
双重差分模型最初在经济学领域中被广泛应用,用于评估各种政策措
施对经济变量的影响。
例如,研究者可以在一些地区实施了项政策(处理组),而另一个地区则没有实施该政策(对照组),通过比较两个地区在
政策实施前后的数据差异,就可以得到该政策的因果效应。
在实际应用中,双重差分模型可以应用于各种领域的研究。
除了经济
学领域,它还在医学、教育、社会科学等领域得到了广泛应用。
例如,在
医学研究中,研究者可以将其中一种新的治疗方法应用于一组患者,而另
一组患者则继续采用传统治疗方法,通过比较两组患者的数据差异,可以
评估新治疗方法的效果。
在教育研究中,研究者可以随机将一些学校或班
级分为处理组和对照组,然后比较两组学生在教育政策实施后的学业成绩,评估政策的效果。
双重差分模型的核心思想是通过数据分析方法消除可能存在的混淆因素,实现对处理效应的准确估计。
然而,该模型也受到一些限制。
首先,
它仍然需要依赖于其中一种原因导致的差异,如果没有合理的随机分组或
自然实验条件,模型的结果可能会受到偏差的影响。
其次,双重差分模型
的应用也需要满足一些基本的假设,如平行趋势假设和稳定性假设,如果
这些假设不能成立,模型的效果可能会受到影响。
双重差分法原理(一)
双重差分法原理(一)双重差分法(Double Difference Method)什么是双重差分法?•双重差分法是一种常用的数据分析方法,用于评估特定事件对观测结果的影响。
•它通过对对照组和实验组之间,以及不同时期的差异进行比较,消除了潜在的混杂因素的影响,得到更准确的因果估计结果。
常见应用领域•双重差分法在经济学、社会学、医学等领域有广泛的应用。
•经济学:用于评估政策变化对经济指标的影响,如最低工资政策对就业率的影响。
•社会学:用于研究特定事件对社会群体的影响,如教育政策对学生成绩的影响。
•医学:用于评估治疗方法的有效性,如新药对患者疾病状况的影响。
双重差分法原理及步骤1.确定观测组和对照组–观测组:受到特定事件/处理影响的群体。
–对照组:没有受到特定事件/处理影响的群体,用于作为比较基准。
2.选择观测期和控制期–观测期:特定事件/处理发生后的时间段。
–控制期:观测期之前的相同时间段,用于作为对照组的基准。
3.计算差分–对观测组和对照组在观测期和控制期的指标进行差分计算。
–差分 = 观测组(观测期) - 观测组(控制期) - 对照组(观测期) + 对照组(控制期)。
4.通过对差分进行回归分析–使用回归模型,将差分作为因变量,并考虑其他可能的解释变量。
–通过回归分析得到差分的系数,用于评估特定事件/处理对观测结果的影响。
5.构建置信区间和假设检验–构建置信区间,评估差分系数的置信度。
–进行假设检验,判断差分系数是否显著不为零。
双重差分法的优势和注意事项•优势:–双重差分法能够消除观测组和对照组之间的固定差异,得到更准确的因果估计结果。
–双重差分法对于潜在的混杂因素具有较强的鲁棒性,可以降低估计结果的偏误。
•注意事项:–双重差分法的有效性依赖于事件的随机性。
如果事件并非随机发生,结果可能受到其他因素的影响。
–双重差分法要求观测组和对照组在除了特定事件/处理之外的其他因素上足够相似,以消除混杂因素的影响。
存款保险制度与银行风险承担——基于风险共担视角的再检验
摘要:完善存款保险制度是深化金融供给侧结构性改革的制度保障,是实施金融安全战略的关键举措。
从风险共担的视角出发研究存款保险制度防范银行风险的作用机制,并利用我国2012年至2021年商业银行面板数据,设计并应用双重差分法检验了存款保险制度防范银行风险的有效性。
研究发现:首先,由“风险共担效应”产生的正面效应会抑制由“道德风险效应”产生的负面效应,存款保险制度的实施会降低银行风险;其次,双重差分法结果说明存款保险制度的实施能够有效降低资本相对丰裕银行的风险承担水平;再次,机制检验说明,我国存款保险制度的建立推动银行从优化股份结构、提高独立董事占比、扩大监事会规模和增强管理层激励等四个维度强化银行内部治理机制和架构,促使“风险共担效应”发挥作用抵消了存款保险制度产生的道德风险等负面效应,使得银行风险显著降低。
关键词:存款保险制度;银行风险承担;双重差分法;风险共担效应文章编号:1003-4625(2023)03-0092-14中图分类号:F832.1文献标识码:A Abstract Abstract::Improving the deposit insurance system is the institutional guarantee for deepening the fi⁃nancial supply-side structural reform,and is a key measure to implement the financial security strat⁃egy.From the perspective of “risk sharing ”,this paper theoretically studies the mechanism of depos⁃it insurance system to prevent bank risks,and uses the panel data of commercial banks in China from 2012to 2021to design and apply the DID method to test the deposit insurance system to pre⁃vent bank risks.The research finds:Firstly,the positive effect produced by the “risk sharing effect ”will suppress the negative effect produced by the “moral hazard effect ”,and the implementation of the deposit insurance system will reduce the bank risk.Secondly,the results of DID method show that the implementation of the deposit insurance system can effectively reduce the risk-taking level of relatively well-capitalized banks.Finally,the mechanism test shows that the establishment of de⁃posit insurance system promotes banks to strengthen the internal governance mechanism and struc⁃ture of the bank from four dimensions:optimizing the share structure,increasing the proportion of in⁃dependent directors,expanding the scale of the board of supervisors,and enhancing management in⁃centives,ultimately promotes the risk-sharing effect.Playing a role not only offsets the negative ef⁃fects of the deposit insurance system,but also significantly reduces bank risks.words Key words::deposit insurance;risk taking;difference in difference;risk-sharing effects刘震1,徐宝亮2,朱衡3(1.西南民族大学经济学院,四川成都610225;2.南昌大学经济管理学院,江西南昌330031;3.西南财经大学金融学院,四川成都611130)存款保险制度与银行风险承担——基于风险共担视角的再检验一、引言完善存款保险制度是深化金融供给侧结构性改革的制度保障,是实施金融安全战略的关键举措。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多期双重差分法,政策实施时间不同的处理方法
今天,计量经济圈主要给圈友引荐一些平时在咱们社群问得比较多的问题——多期双重差分法和一些要点。
我们想检验修建地铁对城市环境污染的影响,那么我们想到的是使用DID方法来得到因果关系。
但是,我们有疑惑的地方是,各个城市修地铁的时间有先有后,而标准的双重差分方法一般要求t为同一时间点,比如20xx年。
对于这个问题,我们可以采用多期DID方法,将所有还没有修建地铁的城市作为控制组,把已经修建地铁的城市作为处理组,即使最终所有城市都修建了地铁,我们也可以把还没有修建地铁之时的城市作为控制组。
简单点讲,就是每个修建地铁的城市的DID交互项在数据中显示的不一样,因为DID交互项是两个虚拟变量的乘积:treated(是不是修建了地铁)和time(修建地铁的时间)。
这个DID的交互项等于1的情况是,这个城市在具体某年修建了地铁,而对于在修建地铁之前的年份,这个城市的DID 交互项等于0。
这就表明,我们在多期DID使用中不再有统一的政策实施年份,而是允许每个城市都有自己的政策实施年份。
这样是不是有助于解决我们遇到的大部分问题。
对于那些压根到目前为止都没有地铁的城市,那他的DID(自然不用说)
就是等于0,因为他的treated始终是为0,属于我们的控制组样本。
注意,现在就是一个普通的xtreg回归,但是这里有些地方需要注意。
第一,我们平时经常看到的
treated+time+treated*time+协变量的标准DID组合已经不见了,现在只剩下了treated*time这个DID交互项和协变量了。
第二,我们尽量控制一下城市的个体效应和时间效应,来消除那些会影响DID交互项估计的不可观测因素和时间效应。
下面这个多期DID模型就是如此的,αt是时间效应,βi
是城市效应,Xit是随着时间变动的协变量,BC*After就属于咱们感兴趣的DID估计量。
第三,这里面的treated(就是BC)虚拟变量当然可以灵活地替换为其他连续变量,比如,我们不仅对是否修建地铁对环境影响感兴趣,更是对修建地铁的里程对环境影响感兴趣。
我们可以把BC替换成地铁的里程(length),然后我们的准DID 交互项就是length*After。
这种DID设置的灵活性让这种方法有很大的适用性。
如果有时候我们不知道处理组具体怎么选择,那该如何设计方法呢?比如我们想要研究一下,美国政府对那些破产的按揭房(金融危机之后的事情)兴起了一个维护修理的政策举动,那这些房子就不至于破败不堪而影响了周围房子的价格。
此时,我们就想看看这个政策举动对周围房子的价格的影响,但我们并不知道到底多远的距离才叫“周围”。
我们可以通过非参数估计方法得出一个大概的cutoff点,然后在这个范围内进一步细分为一些小距离,e.g., 1公里以内,1公里-2公里,2-3公里,然后这三个虚拟变量分别作为三个方程的处理组与time交叉相乘。
若1公里以内这个DID显著,其他不显著就表明政府的政策会对他施加影响的那个地方1公里以内的房价带来正向影响。
