各种封头的卧式容器不同液面高度体积计算
各种形状封头的圆筒形卧式容器在不同液面高度时液体体积计算的统一表达式

各种形状封头的圆筒形卧式容器在不同液面高度时液体体积计
算的统一表达式
蒋心亚;宗光
【期刊名称】《化工设备与管道》
【年(卷),期】2002(39)5
【摘要】本文利用变面积圆缺的线积分来描述各种形状封头的圆筒形卧式容器不同液面高度时的液体体积.推导出了计算液体体积的统一表达式,文中还给出了5种常用封头卧式圆筒形容器不同液面高度时液体体积计算实例,并给出了它们的无量纲化液体体积,即装量系数与无量纲化液面高度的关系曲线,以便工程应用.
【总页数】5页(P30-34)
【作者】蒋心亚;宗光
【作者单位】常州技术师范学院东方学院,常州,213001;上海氯碱化工股份有限公司机械公司,上海,200241
【正文语种】中文
【中图分类】TH49
【相关文献】
1.碟形封头卧式容器不同液面高度的容积计算 [J], 王正秋
2.椭圆形封头卧式容器不同液面高度的容积计算 [J], 陈爱丽
3.椭圆形封头卧式容器容积的计算——根据液面高度计算卧式容器内的物料容积[J], 王宇;陈志军;苏建伟;郭昕
4.PET装置中椭圆形封头卧式容器的液位-体积计算 [J], 张俊宏;许贤文
5.各种封头的卧式容器不同液面高度体积计算 [J], 高炳军;苏秀苹
因版权原因,仅展示原文概要,查看原文内容请购买。
各类储罐不同液位的体积计算
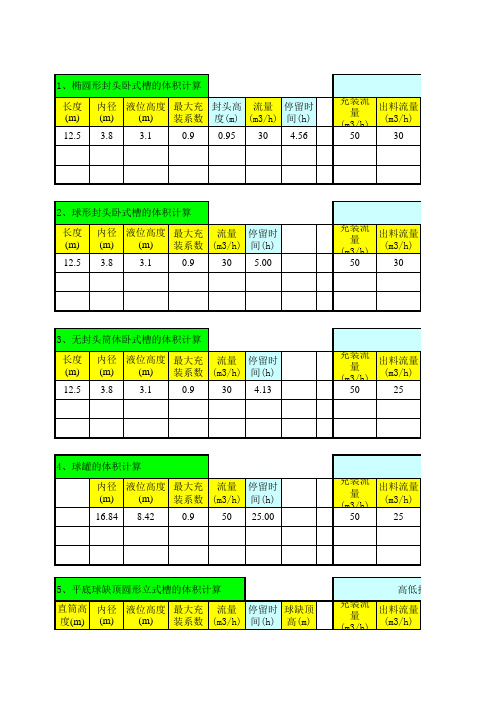
高低报警液位的
4、球罐的体积计算 内径 液位高度 最大充 流量 停留时 (m) (m) 装系数 (m3/h) 间(h) 16.84 8.42 0.9 50 25.00 充装流 出料流量 量 (m3/h) (m3/h) 50 25
计算结果 总体积 充装系 液位 (m3) 数 (%) 11.01 0.325 35.70
高低报警液位的计算(不同时进、出料) 报警时 低报液位 高报液位 低报求 高报求 间(min) (m) (m) 解 解 10 10 10 10 0.66 0.66 0.66 0.66 11.97 11.97 11.97 11.97 -4.77 -3.32 -1.88 -3.32 -12.31 -41.46 -65.23 -41.46 体积 (m3) 0.37 3.50 3.20 5.15
3.76 3.474 2.3
1.4 1 0.8
5 5 5
0.9 0.9 0.9
1.1 0.78 0.62
30 30 30
0.22 0.12 0.08
50 50 50
30 30 30
3.625 2.63 1.82
1.2 0.71 0.51
5 5 5
0.9 0.9 0.9
0.94 0.58 0.43
30 30 30
10 10 10
2.67 2.67 2.67
14.76 14.76 14.76
-2.69 -4.09 -4.51
-20.10 -12.98 -10.91
卧式椭圆封头容器不同液位的体积计算

符号
L(m)R t(m)h(m)hi(m)(E3-D3)/D3Vt(m3)Vf(m3)V(m 3)数值2100.0001000.0001000.000500.0000.0003298672230.000523598766.6673822270996.667卧式椭圆形封头容器不同液位的体积计算
Dt ——筒体内径,m Rt——筒体或球形封头内半径,m h ——液面高度,m V——卧式容器体积,m3hi ——封头曲面深度,m (标准型:hi=1/2Rt ) Vt——筒体部分体积,m3
L ——筒体长度(含封头直边高度),m Vf——封头部分体积,m3
1、 筒体内液体体积计算(如上图):
筒体的截面积方程:X 2+Y 2=Rt 2 故:X=(Rt 2-Y 2)1/2
因此:液面高度为h 时筒体内液体的体积:
2、椭圆封头内液体体积计算(如上图):
椭圆封头的椭球面方程:
]2
arcsin 2)^(1[2^2^2^2π+-+--∙-∙=-=⎰--Rt Rt h Rt Rt h Rt Rt h Rt L dy
y Rt L Vt Rt
h Rt 2^2^2^)/(12
^2^2^2^2^y x Rt Rt hi z hi z Rt y x --=∴=++
因此:当容器内的液面高度为h 时,封头内液体的体积:
]33^233)^()(2^[22^2^2^22^2^0Rt Rt h Rt h Rt Rt hi dx y x Rt dy Rt hi zdxdy
Vf y Rt Rt h Rt
f ----=--==⎰⎰⎰⎰---π。
卧式储罐不同液位下的容积计算

卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图d参数:l :椭圆圭寸头曲面高度(m );l i :椭圆圭寸头直边长度(m);L :卧罐圆柱体部分长度(m);r :卧式储罐半径(d/2, m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);P储液密度(kg/m3)V h:对应h高度卧罐内储液体积(m3);m h:对应h高度卧罐内储液重量(kg);椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下卧式储罐内储液总体积计算公式:若密度为p,则卧式储罐内储液总重量为:m h V h表1卧式储罐不同液位下容积(重量)PrLhV hm h液体密度 (kg/m 3)储罐半径 (m )圆柱体部分长度(m )储液液位高度(m )储液体积 (m 3)储液重量 (kg )2r 3LLr 2arcsi4r*r 2rh-r 2以储罐底部为起点的液咼该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
(1)椭圆球体部分该椭圆球体符合椭圆球体公式:2 2 2 2 2 2务告务 1 其中a=b=r,则有x 2 务 1 a b c a c垂直于y 轴分成无限小微元,任一微元面积为:S yi —(a 2 y 2)a当液面高度为h 时,椭圆球体内液氨容积为h「3 o 3V1=aS yj dya^(a 2 y 2)dy許2h自(2 )直段筒体部分:筒体的纵断面方程为x 2 y 2 a 2任一微元的面积为S yj 2、.、a 2 y 2dy则筒体部分容积为:L 2 a 2 y 2dy La 2(arcsin 」aahV2aSyj.2 _____________a 2八 2)( arcsin -)2a 2(3)卧式储罐储液总体积总容积为V 二V1+V2 ,232c 2- 4h 2a 2(. h h r .2、V= (a h)+ La (arcsin 2 ; a h ) a 3 3 a a2此公式中液位高度h 是以储罐内径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:21 三 Lr 2arcsin^ 3L rr 2-h 2r 21 50 1.3 0.65 8.58 0 1.3 25.078 25.0780.31%1 50 1.3 0.65 8.58 0.975 2.275 46.537 46.5371501.30.658.581.32.650.15550.1550.31%若液位高度h 以卧罐底部为起点,如下图/\ A / __________\rf (1)f\ y丿 1 二;o h \ ............. .... J V7\…一j... J■厶■N K A *则卧式储罐内储液总体积计算公式:若密度为p,则卧式储罐内储液总重量为:m hV hprLhV hm h液体密度 储罐半径 圆柱体部分长度储液液位高度储液体积 储液重量(kg )(kg/m 3)(m )(m )(m )(m 3)11.3 8.580.3253.619 3.6192r3LLr 2 arcsi®rh-r r 2h-r 2其它方法如下:第一种方法| PDF.卧式储罐不同液位 下的容积简化计算公卧式储罐内储液总体积计算公式:(hr ) 2--------------- K r2l (h r )[1」 宀]L[( h r)「2hr h 2 r 2 arcsi n( ---------------------------- )]3 rr若密度为p,则卧式储罐内储液总重量为:Vh V此方式用到参数较多P、V、r、l、L、h。
椭圆封头卧式储罐相应液位体积计算

椭圆封头卧式储罐相应液位体积计算首先,让我们了解一下椭圆封头卧式储罐的结构特点。
椭圆封头卧式储罐由一个圆筒体和两个椭圆形封头组成。
储罐的长轴长度为2a,短轴长度为2b。
液位高度为h,液位高度H在长轴上的位置为x。
储罐的横截面积可以近似看作一个椭圆形。
首先,我们需要计算椭圆封头卧式储罐的横截面积,然后将其乘以液位高度h,即可得到液位对应的体积。
根据椭圆的性质,椭圆的横截面积可以表示为S=πab。
但是由于液位高度H可能在长轴上的任意位置,所以需要对横截面积进行修正。
储罐的长轴上一般会有一条水平导流槽,导流槽的宽度一般为b/8、当液位高度H小于等于b/8时,导流槽会被液体完全淹没,此时椭圆的横截面积可以近似看作是一个圆形,其半径为b/2、当液位高度H大于b/8时,导流槽会露出水面,此时需要计算椭圆截面的面积。
(1)当H>b/8时,椭圆的横截面面积可以通过使用割线法来进行计算。
割线法的基本原理是通过在椭圆上取两个相距一定角度的点来近似表示此两点之间的弧长。
具体的计算公式如下:
L=2a√[1-(x/a)²]
S=πbL/360
其中L表示椭圆截面上两点之间的弧长,S表示椭圆截面的面积。
(2)当H<=b/8时,椭圆的横截面面积近似为一个圆的面积,可以表示为S=π(b/2)²。
通过使用以上的公式,我们可以计算出椭圆封头卧式储罐中液位高度为H的液体体积。
在实际应用中,我们一般将椭圆封头卧式储罐的液位和体积计算与液位计进行配合使用。
液位计可以根据液体的压力、浮力或者声波等原理来实现对液位的准确测量。
各类储罐不同液位的体积计算
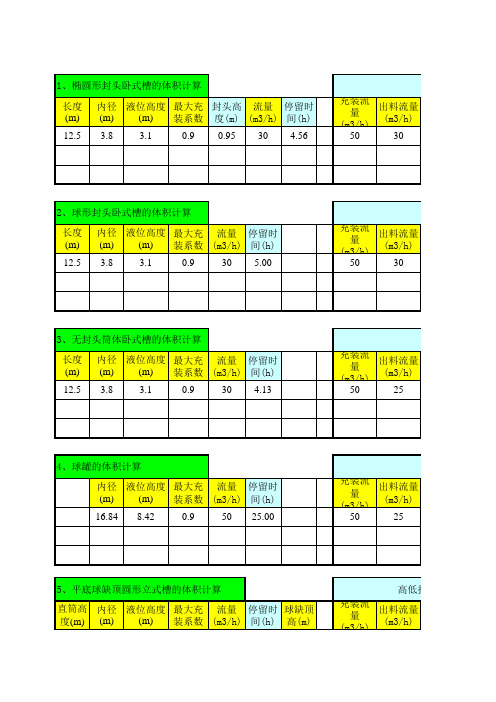
高低报警液位的计算
报警时 低报液位 高报液位
间(min) (m)
(m)
15
0.88 10.15
计算结果
体积 总体积 充装系 液位 (m3) (m3) 数 (%)
56.71 141.76 0.400 40.00
高ቤተ መጻሕፍቲ ባይዱ报警液位的计算
报警时 低报液位 高报液位 低报求 高报求
间(min) (m)
(m)
解
解
10
3.52 3.06 1.149 #####
10
2.67 14.76 -3.86 -14.35
2.31 1.33 1.737 #####
10
2.67 14.76 -2.69 -20.10
4.95 4.68 1.057 #####
10
2.67 14.76 -4.09 -12.98
1.83 1.16 1.568 #####
10
2.67 14.76 -4.51 -10.91
0.96 0.42 2.301 #####
1.01 13.43 -2.72 -43.72
计算结果
体积 总体积 充装系 液位 (m3) (m3) 数 (%)
3.58 11.01 0.325 35.70
高低报警液位的计算(不同时进、出料)
报警时 低报液位 高报液位 低报求 高报求
间(min) (m)
(m)
解
解
10
0.66 11.97 -4.77 -12.31
计算结果
体积 总体积 充装系 液位 (m3) (m3) 数 (%)
123.83 141.76 0.873 81.58
高低报警液位的计算
报警时 低报液位 高报液位 低报求 高报求
各类储罐不同液位的体积计算
出料流量 (m3/h)
40
高低报警液位的
7、球形封头立式槽的体积计算
直筒高 内径 液位高度 最大充 流量 停留时 度(m) (m) (m) 装系数 (m3/h) 间(h)
1.78 2.1 1.385 0.9
30 0.1195
充装流 量
(m3/h) 50
出料流量 (m3/h)
30
高低报警液位的
1.01 13.43 -2.72 -43.72
计算结果
体积 总体积 充装系 液位 (m3) (m3) 数 (%)
3.58 11.01 0.325 35.70
高低报警液位的计算(不同时进、ห้องสมุดไป่ตู้料)
报警时 低报液位 高报液位 低报求 高报求
间(min) (m)
(m)
解
解
10
0.66 11.97 -4.77 -12.31
充装流 量
(m3/h) 50
高低报警液位的计算(不
出料流量 (m3/h)
30
50
30
50
30
50
30
9、下锥上椭圆形封头立式槽的体积计算
直筒高 内径 液位高度 最大充 下锥高 流量 停留时 度(m) (m) (m) 装系数 度(m) (m3/h) 间(h)
充装流 量
(m3/h)
高低报警液位的计算(不
10
2.67 14.76 -4.51 -10.91
0.96 0.42 2.301 #####
1、椭圆形封头卧式槽的体积计算
长度 内径 液位高度 最大充 封头高 流量 停留时 (m) (m) (m) 装系数 度(m) (m3/h) 间(h)
12.5 3.8
椭圆形封头卧式容器不同液面高度的容积计算
椭圆形封头卧式容器不同液面高度的容积计算新疆工学院孟永彪在设计卧式容器时,常常要计算不同液面高度所对应的容积,有时还需列出容积—液位高度对照表或图。
例如,在盛装有毒有害介质的卧式储罐设计中,要根据体积充装系数确定最高液面高度并加以标识。
在一般资料中仅能查到容器的全容积计算公式,而要计算不同液面高度下的容积则需设计者自行推导公式计算。
本文以标准椭圆形封头卧式容器为例介绍不同液面高度下的容积计算方法,并以液化石油气储罐为例编制了QUICK BASIC程序,此法仅供大家参考。
1卧式容器的组成卧式容器是由筒体和两封头组焊而成(如图1),常用的封头为标准椭圆封头。
2卧式容器2.1计算简图及说明计算简图如图2。
L———筒体长度(两封头切线间的距离,含直边段长度)D i———封头及筒体内直径h i———封头曲面深度2.2不同液面高度下封头的容积计算如图2,可假想将卧式容器两端的曲面部分合并,则形成一个完整的椭球面。
2==i ih R c a 122222=++cz a y x )(21222y x a z +-=dxy x a dy h a y a )(2222022+-=⎰⎰--)323(23331a h h a V +-=π其中,a=b=R i因此,椭球面的方程为:推导出: 当容器内的液面高度为h 时(如图3所示)。
封头的容积公式推导:对其积分得从上式可看出,h 变化,V 1也随之变化。
2.3 不同液面高度筒体的容积计算在计算筒体的容积时,忽略尺寸公差及制造误差等因素,可将其断面方程为x 2+y 2=a 2的一圆柱体进行计算,那么如图3所示液面高度的筒体容积为:令:y=acos θ dy=-asin θd θdxdy y x a V s )(2122221+-=⎰⎰dx y x a dy h a y a y a )(2122222222+-=⎰⎰----dy y a L V h a⎰--=2222dy y a L h -=222当 y=-a 时,θ=π;当y=h 时,代入公式积分得:2.4 卧式容器在不同液面高度下的容积通过以上V 1,V 2的计算公式,可计算出卧式容器在不同液面高度下的容积之和V :3 利用QUICK BASIC 语言进行卧式容器的容积计算要计算不同液位高度下的容积以表格、曲线的形式列出是很麻烦的,因此本文利用简便易行的QB 编制程序,当然编程语言可以有多种,本文愿起到抛砖引玉的作用。
各种形状封头的圆筒形卧式容器在不同液面高度时液体体积计算的统一表达式
·30·化工设备与管道第39卷在卧式容器设计中常常需要知道未充满容器液体的体积和重量,而在容器使用时也常常需要确定所谓的装量系数k,即实际液体容量除以容器满载容量,而装量系数k是以液面高度作为标识的。
因此,计算不同液面高度时容器中液体的体积是工程上十分关心的问题。
文[1][2][3]曾讨论过这一问题,有的文献也给出了几种简单封头对未满液体体积的计算公式,而对于较复杂的封头形状,如蝶形封头等,仅给出了双重积分的表达式,通过计算机计算数值积分才可给出近似的结果,实际计算和应用时十分复杂。
本文利用变面积圆缺的线积分给出了各种形状封头的圆筒形卧式容器不同液面高度时液体体积的统一描述方法,并为此推导出了计算液体体积的统一表达式。
这一表达式物理意义清晰,计算公式简练,计算精度极高,实际运算方便。
本文还给出了由统一表达式计算出的五种常用封头卧式圆筒形容器不同液面高度时液体体积的计算公式实例,并给出了它们的无量纲化体积(即装量系数)与无量纲化液面高度的关系曲线,以便工程上应用。
1问题的描述图1给出了任意形状封头圆筒形卧式容器液面高度为h时的纵向剖面图,图中看到容器总长L,圆筒长L0,半径为r,x及y轴均为对称轴,x轴还是容器的旋转轴。
图2为任意x处横向剖面图,从图中可看到任意x处A-A剖面中液体所占面积为一圆缺BCD的面积,而当(L02+x h)≤x≤L2时,此圆缺为一个圆,我们可以在x o y坐标系下统一用A(x)来表示x 处剖面中液体所占的面积,则整个容器液体的体积可表示为:V=2ΘL20A(x)d x(1)式(1)表达式物理意义非常清晰,由于它是一个单积分表达式,计算起来十分方便。
图1容器纵剖面图图2x处A-A横向剖面图图3圆形封头各种形状封头的圆筒形卧式容器在不同液面高度时液体体积计算的统一表达式蒋心亚宗光(常州技术师范学院东方学院,常州213001)(上海氯碱化工股份有限公司机械公司,上海200241)摘要本文利用变面积圆缺的线积分来描述各种形状封头的圆筒形卧式容器不同液面高度时的液体体积。
卧式容器不同液面高度的体积计算
化肥装置卧式容器不同液面高度的体积计算公式及运用(重庆建峰工业集团化肥分公司 乔华勇)摘要: 推导出尿素装置各种卧式容器不同液面高度的体积计算公式 。
并结合EXCEL软件实现便捷运算。
为装置运行过程中物料、蒸汽平衡计算以及即时成本计算 提供方便。
关键词:卧式容器;液面高度;体积;计算公式;EXCEL 。
重庆建峰工业集团化肥分公司于1993年建成投产,日产尿素1750吨。
工艺设备数量众多,包括塔、分解器、储罐等等。
其中,容器、储罐以卧式为主。
卧式容器的体积不像立式容器计算那样便捷,需运用较多数学知识才能实现。
所以每次系统的性能测试、成本计算都会因为容器液位变化问题而导致结果不精确。
因而,一套细致、准确的液面高度对应体积的数据参考,对于系统的各项测试和成本计算能够起到提高计算结果精确度的作用。
本文,笔者借助高等数学积分知识推导出卧式容器体积计算的通用公式,并在化肥尿素装置中加以运用。
1 计算公式容器分为两个部分:筒体、封头 。
公式推导过程中,将其二者分开讨论。
1.1 筒体部分筒体(图1)的横截面方程为:222t r y x =+故2122)(y r x t -=液面高度为h 时的体积:⎥⎥⎦⎤⎢⎢⎣⎡+-+⎥⎦⎤⎢⎣⎡--⨯-=-=⎰--2arcsin12222πt tt t t t t y r h r t r r h r r h r r h Lr d y r LV ttr t :筒体内径,m h i :封头曲面深度,m L :筒体长度(含封头直边高度)V t :筒体体积,3mL图1 筒体1.2 封头部分尿素装置卧式容器的封头均为椭圆形封头(图2)。
所以,封头部分体积公式的推导按照椭圆球体积计算处理。
椭圆球面方程为:122222=++i th z r y x 故21222))(/(y x r r h z t t --=图2 封头当容器内的液面高度为h 时,封头的体积:()()⎥⎦⎤⎢⎣⎡+---=--==⎰⎰⎰⎰---32322332)(02222122t t t t ti r h r y r t s tif r r h r h r r h dx y x r dy r h zdxdy V ttt πh i :封头曲面深度,m V f :封头部分体积, 3m r t :筒体内径,m1.3 卧式容器卧式容器不同液面高度的体积为:ft V V V 2+=V :卧式容器体积, 3m V t :筒体部分体积, 3m V f :封头部分体积, 3m 2 尿素装置卧式容器不同液面高度的体积计算公式 2.1 容器的相关设计参数V05:原料氨储罐 V06:低压系统回收物料储罐 V10:系统蒸汽冷凝回收器设备位号L (m) t r (m)i h (m) 05300V8 1.35 0.868 06300V 12 2.385 1.165 10300V 5.921.50.752.2 容器的计算公式在化肥装置的实际运用 2.2.1 液面高度h 的计算λt r h 2=r t :筒体内径,m λ:容器液位计仪表显示值,1 2.2.2 05300V 不同液面高度对应体积计算公式f t V V V 2+==()()⎥⎥⎦⎤⎢⎢⎣⎡⨯+---⨯⨯⨯+⎥⎥⎦⎤⎢⎢⎣⎡+-+⎥⎦⎤⎢⎣⎡--⨯-⨯⨯335.12335.135.135.135.18689.0235.135.1arcsin 35.135.1135.135.135.183322h h h h h ππ 2.2.3 06300V 不同液面高度对应体积计算公式f t V V V 2+==()⎥⎥⎦⎤⎢⎢⎣⎡⨯+---⨯⨯⨯+⎥⎥⎦⎤⎢⎢⎣⎡+-+⎥⎦⎤⎢⎣⎡--⨯-⨯⨯3385.223385.2)385.2(385.2385.2165.12385.2385.2a r c s i n 385.2385.21385.2385.2385.2123322h h h h h ππ2.2.4 10300V 不同液面高度对应体积计算公式f t V V V 2+==()⎥⎥⎦⎤⎢⎢⎣⎡⨯+---⨯⨯⨯+⎥⎥⎦⎤⎢⎢⎣⎡+-+⎥⎦⎤⎢⎣⎡--⨯-⨯⨯35.1235.1)5.1(5.15.175.025.15.1arcsin 5.15.115.15.15.192.53322h h h h h ππ3 EXCEL 计算从上述推导公式来看,式中使用的都是一些基本函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
文章编号:100027466(1999)0420024203各种封头的卧式容器不同液面高度体积计算Ξ高炳军,苏秀苹(河北工业大学,天津 300130)摘要:推导了各种封头形式的卧式容器不同液面高度的体积计算公式,编制了Q u ick2BA S I C计算程序,可为卧式容器的设计和使用提供方便。
关 键 词:封头;卧式容器;液面高度;体积;计算公式;程序中图分类号:TQ0531202 文献标识码:AVolu m e ca lcula tion of hor izon ta l vessels with var ious for m ed heads a t d ifferen t l iqu id he ightsGAO B ing2jun,SU X iu2p ing(H ebeiU niversity of T echno logy,T ianjin300130,Ch ina)Abstract:V o lum e calculati on fo r m ulae of ho rizontal vessels w ith vari ous fo r m ed heads at different liquid heigh ts are derived,Q uick2BA S I C p rogram is also w o rked out1It w ill p rovide convenience fo r the designing and using of ho rizontal vessels1Key words:head;ho rizontal vessel;liquid heigh t;vo lum e;calculati on fo r m ula;p rogram符 号 说 明 D t——筒体内径,mmF K,F K+1——分别为各层积分区间划分个数为K和 K+1时的体积计算值,m3 h——液面高度,mmh i——封头曲面深度,mmh1,h2——分别为碟形封头球面与圆弧折边过渡 处平行圆的最低和最高高度,mmL——筒体长度(含封头直边高度),mmR——封头球面内半径,mmr——碟形封头折边圆弧半径,mmr t——筒体或球形封头内半径,mmr s——碟形封头球面与圆弧折边过渡处平行圆半径,mmy r——碟形封头折边圆弧圆心与z轴的距离,mm z R——封头球面球心与y轴的距离,mm V——卧式容器体积,m3V t——筒体部分体积,m3V f——封头部分体积,m3 在设计或者使用卧式容器时,常常要计算不同液面高度所对应的体积,有时还需要列出体积高度对照表或图。
在一般资料中仅能查到容器总体积的计算公式,而要计算不同液面高度下的体积,则需要设计者或使用者自行推导公式计算,卧式容器的封头形式不同,则推导计算的难易程度也不同。
球形封头和椭圆封头卧式容器较易推算,而无折边球形封头和碟形封头卧式容器的推算比较难,主要是推导计算中涉及到的积分运算难易不同,前2种比较容易得到解析解,而后2种比较难,只能利用计算机进行数值积分得到数值解。
笔者推导了各种封头形式的卧式容器不同液面高度的体积计算公式,并编制了Q u ick2BA S I C计算程序,可以为卧式容器的设计和使用提供方便。
1 计算公式111 筒体筒体(图1)的横截面方程为:x2+y2=r t2 故 x=(r t2-y2)1 2液面高度为h时的体积为:V t=L∫h-r t-r t2r t2-y2d y=L r t2h-r t r t×第28卷 第4期1999年7月石 油 化 工 设 备PETRO2CH E M I CAL EQU IPM EN TV o l.28 N o.4July1999Ξ收稿日期:1999203230 作者简介:高炳军(19662),男,河北沧县人,讲师,1991年毕业于天津大学化工机械专业,硕士学位。
现任教于河北工业大学化工学院过程装备与控制工程系,从事压力容器强度分析、结构优化及计算机辅助设计的教学与科研。
1-h -r tr t2+arcsin h-r tr t+Π2(1)图1 筒体112 封头(1)球形封头 球形封头(图2)的球面方程为:x 2+y 2+z 2=r t 2故 z =(r t 2-x 2-y 2)12当容器内的液面高度为h 时,封头的体积为:V f =∫∫sz d x d y =2∫h -r t-r td y∫(r t 2-y 2)12r t 2-x 2-y 2d x =Π2r t 2(h -r t )-(h -r t )33+2r t 33 (2)图2 球形封头 (2)椭圆封头[1] 椭圆封头(图3)的椭球面方程为:x 2+y 2r t 2+z2h i2=1故z =(h i r t )r t 2-x 2-y2图3 椭圆封头 当容器内的液面高度为h 时,封头的体积为:V f =∫∫sz d x d y = 2h ir t∫h -r t-r td y ∫(r t 2-y 2)12r t2-x 2-y 2d x =Πh i 2r tr t 2(h -r t )-(h -r t )33+2r t 33 (3) (3)无折边球形封头 无折边球形封头(图4)的球面方程为:x 2+y 2+(z +z R )2=R 2故z =(R 2-x 2-y 2)1 2-z R其中,R =(h i 2+r t 2)(2h i ),z R =(r t 2-h i 2) (2h i )。
当容器内的液面高度为h 时,封头的体积为:V f =∫∫sz d x d y =2∫h -rt-r t d y ×∫(r t 2-y 2)120R 2-x 2-y 2-z R d x (4) 实际上当h i =r t 时,无折边球形封头即为球形封头。
图4 无折边球形封头(4)碟形封头 碟形封头的曲面由半径为R 的球面部分和圆弧半径为r 的折边曲面部分组成,见图5,其球面方程为:x 2+y 2+(z +z R )2=R2故z =(r t 2-x 2-y 2)1 2-z R其中,z R =[(R -r )2-(r t -r )2]1 2。
圆弧半径为r 的折边曲面方程为[2]: [(x 2+y 2)12-y r ]2+z 2=r 2故 z =r 2-[(x 2+y 2)1 2-y r ]2图5 碟形封头其中,y r =r t -r 。
令h 1=r t -r s ,h 2=r t +r s ,其中,r s =R (r t -r )(R -r ),当容器内的液面高度为h ,h ≤h 1时,封头的体积为:V f =∫∫sz d x d y =2∫h -r t-r td y ×∫(r t 2-y 2)120r 2-[(x 2+y 2)1 2-y r ]2d x (5) 当容器内的液面高度为h ,h 1≤h ≤h 2时,封头・52・ 第4期 高炳军,等:各种封头的卧式容器不同液面高度体积计算的体积为:V f =∫∫sz d x d y = 2∫h 1-r t-r td y ∫(r t 2-y 2)120r 2-[(x 2+y 2)1 2-y r ]2d x +2∫h -r th 1-r t d y∫(r t 2-y 2)1 2(r 2s -y 2)1 2r 2-[(x 2+y 2)1 2-y r ]2d x +2∫h -r th 1-r td y ∫(r s 2-y 2)120R 2-x 2-y 2-z R d x (6) 当容器内的液面高度为h ,h >h 2时,封头的体积为:V f =∫∫sz d x d y =2∫h 1-r t—r td y∫(r t 2-y 2)120r 2-[(x 2+y 2)1 2-y r ]2d x +2∫h 2-r th 1-r td y∫(r t 2-y 2)12(r s 2-y2)1 2r 2-[(x 2+y 2)1 2-y r ]2d x +2∫h 2-r th 1-r td y ∫(r s 2-y 2)120R 2-x 2-y 2-z R d x + 2∫h -r th 2-r td y∫(r s 2-y 2)120r 2-[(x 2+y 2)1 2-y r ]2d x (7)113 卧式容器卧式容器不同液面高度的体积为:V =V t +2V f(8)2 电算程序从上面推导的计算公式来看,式(1)~(3)能直接计算,而式(4)~(7)所涉及的积分较为复杂,无法得出解析解,只能进行数值积分,为此笔者利用Q u ick 2BA S I C 语言编制了电算程序,对式(1)~(8)进行计算,其中利用Gau ss 求积公式对式(4)~(7)进行双重积分,得出其近似数值解。
Gau ss 型求积公式是数值积分方法中精度最高的一种,笔者采用8节点Gau ss 2L egendre 求积公式,单层积分可达到17次代数精度,总体积分精度取决于各层积分的区间划分个数K ,计算的终止条件可由控制参数EPS(EPS = (F K +1-F K ) F K +1)决定,Gau ss 型求积公式具体内容及Gau ss 2L egendre 求积公式的节点与节点系数请参阅文献[3]~[4]。
电算程序取名V HVDL H ,程序采用菜单式选择,其操作简便,根据菜单提示,在依次输入封头代号、某种封头形式卧式容器的几何尺寸、计算方式、体积计算所必须的高度及积分精度控制参数EPS 后即可进行计算,计算结果自动保存在“V HVDL H 1OU T ”中,并且在屏幕上显示。
现以D t =1000,L =5000,R =1000,r =125的碟形封头卧式容器为例,进行多点连续计算,起始计算高度0,最大计算高度1000,高度步长100(以上单位均为mm ),EPS =1×10-5,计算结果见表1,体积高度见图6。
表1 碟形封头卧式容器液面高度2体积计算结果h mm V m 3 h mm V m 3 h mm V m 3 010001000000400100115446178001003156449410010001211111500100210736269001003193614120010001582759600100216026361000100411472503001001103892970010031108324— — 图6 碟形封头体积高度3 结语文中不仅推导了各种封头形式卧式容器不同液面高度的体积计算公式,而且编制了专用电算程序,对于积分困难的无折边球形封头和碟形封头卧式容器,采用8节点Gau ss 2L egendre 求积公式,成功地进行了数值积分,计算精度较高,单层积分可达到17次代数精度,可根据实际需要调整总体积分精度控制参数EPS 。
