三角形转动惯量
转动惯量公式表
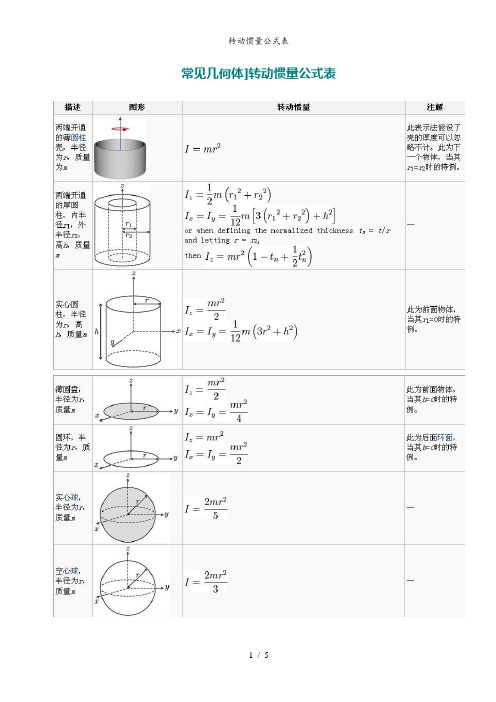
常见几何体]转动惯量公式表对于细杆当回转轴过杆的中点并垂直于杆时;J=m(L^2)/12 其中m是杆的质量,L是杆的长度。
当回转轴过杆的端点并垂直于杆时:J=m(L^2)/3 其中m是杆的质量,L是杆的长度。
对于圆柱体当回转轴是圆柱体轴线时;J=m(r^2)/2其中m是圆柱体的质量,r是圆柱体的半径。
对于细圆环当回转轴通过中心与环面垂直时,J=mR^2;当回转轴通过边缘与环面垂直时,J=2mR^2;R为其半径对于薄圆盘当回转轴通过中心与盘面垂直时,J=﹙1/2﹚mR^2;当回转轴通过边缘与盘面垂直时,J=﹙3/2﹚mR^2;R为其半径对于空心圆柱当回转轴为对称轴时,J=﹙1/2﹚m[(R1)^2+(R2)^2];R1和R2分别为其内外半径。
对于球壳当回转轴为中心轴时,J=﹙2/3﹚mR^2;当回转轴为球壳的切线时,J=﹙5/3﹚mR^2;R为球壳半径。
对于实心球体当回转轴为球体的中心轴时,J=﹙2/5﹚mR^2;当回转轴为球体的切线时,J=﹙7/5﹚mR^2;R为球体半径对于立方体当回转轴为其中心轴时,J=﹙1/6﹚mL^2;当回转轴为其棱边时,J=﹙2/3﹚mL^2;当回转轴为其体对角线时,J=(3/16)mL^2;L为立方体边长。
只知道转动惯量的计算方式而不能使用是没有意义的。
下面给出一些(绕定轴转动时)的刚体动力学公式。
角加速度与合外力矩的关系:角加速度与合外力矩式中M为合外力矩,β为角加速度。
可以看出这个式子与牛顿第二定律是对应的。
角动量:角动量刚体的定轴转动动能:转动动能注意这只是刚体绕定轴的转动动能,其总动能应该再加上质心动能。
只用E=(1/2)mv^2不好分析转动刚体的问题,是因为其中不包含刚体的任何转动信息,里面的速度v 只代表刚体的质心运动情况。
由这一公式,可以从能量的角度分析刚体动力学的问题。
转动惯量(Moment of Inertia)是刚体绕轴转动时惯性(回转物体保持其匀速圆周运动或静止的特性)的量度,用字母I或J表示。
三种计算圆盘类刚体转动惯量的方法探析-力学论文-物理论文

三种计算圆盘类刚体转动惯量的方法探析-力学论文-物理论文——文章均为WORD文档,下载后可直接编辑使用亦可打印——动力学论文第四篇:三种计算圆盘类刚体转动惯量的方法探析摘要:刚体的转动惯量是大学物理刚体力学中的重点。
研究采用了三种方法计算圆盘形状物体绕中心转动对称轴的转动惯量,即微元定义求解法、量纲分析法和等边n角形极限法。
提出了后面两种巧妙的计算方法,引导学生在解决问题的时候开阔思维,激发其学习的积极性及对科研的探索精神。
关键词:圆盘; 转动惯量; 计算方法;Three methods of calculating the moment of inertia of a diskLAN Shan-quanSchool of Physical Science and Technology,Lingnan Normal UniversityAbstract:The moment of inertia of rigid body is the focus of rigid body mechanics in university physics. In this paper,three methods are used to calculate the moment of inertia of a disk-shaped object about a central rotational axis of symmetry,namely,the method of solving the definition of micro element,the method of dimensional analysis and the method of limit of n-angle with equal sides. The last two ingenious calculation methods are put forward to guide students to broaden their thinking when solving problems,stimulate their enthusiasm for learning and explore the spirit of scientific research.1 引言转动惯量度量是刚体在力矩的作用下改变转动角速度的容易程度。
转动惯量

转动惯量在古典力学中,转动惯量(又称质量惯性矩)通常以 I 表示,SI 单位为 kg * m^2。
对于一个质点,I = mr^2,其中 m 是其质量,r 是质点和转轴的垂直距离。
转动惯量在旋转动力学中的角色相当于线性动力学中的质量,可形式地理解为一个物体对于旋转运动的惯性,用于建立角动量、角速度、力矩和角加速度等数个量之间的关系。
转动惯量(Moment of Inertia)是刚体绕轴转动时惯性(回转物体保持其匀速圆周运动或静止的特性)的量度,用字母I或J表示。
其量值取决于物体的形状、质量分布及转轴的位置。
刚体的转动惯量有着重要的物理意义,在科学实验、工程技术、航天、电力、机械、仪表等工业领域也是一个重要参量。
电磁系仪表的指示系统,因线圈的转动惯量不同,可分别用于测量微小电流(检流计)或电量(冲击电流计)。
在发动机叶片、飞轮、陀螺以及人造卫星的外形设计上,精确地测定转动惯量,都是十分必要的。
转动惯量只决定于刚体的形状、质量分布和转轴的位置,而同刚体绕轴的转动状态(如角速度的大小)无关。
形状规则的匀质刚体,其转动惯量可直接用公式计算得到。
而对于不规则刚体或非均质刚体的转动惯量,一般通过实验的方法来进行测定,因而实验方法就显得十分重要。
转动惯量应用于刚体各种运动的动力学计算中。
转动惯量的表达式为若刚体的质量是连续分布的,则转动惯量的计算公式可写成(式中m表示刚体的某个质元的质量,r表示该质元到转轴的垂直距离,ρ表示该处的密度,求和号(或积分号)遍及整个刚体。
)[2]转动惯量的量纲为,在SI单位制中,它的单位是。
此外,计算刚体的转动惯量时常会用到平行轴定理、垂直轴定理(亦称正交轴定理)及伸展定则。
2张量定义刚体绕某一点转动的惯性可由更普遍的惯性张量描述。
惯性张量是二阶对称张量,它完整地刻画出刚体绕通过该点任一轴的转动惯量的大小。
出于简单的角度考虑,这里仅给出绕质心的转动惯量张量的定义及其在力矩方程中的表达.设有一个刚体A,其质心为C,刚体A绕其质心C的转动惯量张量定义为[1]该积分遍及整个刚体A,其中,,是刚体质心C到刚体上任一点B的矢径;表达式是两个矢量的并乘;而为单位张量,标架是一个典型的单位正交曲线标架;是刚体的密度。
工程力学-结构力学课件-12动量矩定理p

12-1、图示三角形薄板,质量为m ,a 、h 已知,求薄板对z 轴的转动惯量z J 。
12-2、如图所示,质量为m 的偏心轮在水平面上作平面运动。
轮子轴心为A ,质心为C ,AC = e ;轮子半径为R ,对轴心A 的转动惯量为A J ;C ,A ,B 三点在同一铅直线上。
1)当轮子只滚不滑时,若A v 已知,求轮子的动量和对地面上B 点的动量矩。
2)当轮子又滚又滑时,若A v ,ω已知,求轮子的动量和对地面上B 点的动量矩。
题12-2图12-3、如图所示,求下列两种情况的动量矩O L :(a) 质量为m ,半径为R 的均质薄圆盘绕水平轴O (垂直纸面)转动的角速度为ω; (b) 质量为m ,长为l 的均质细直杆绕O 轴转动的角速度为ω。
12-4、如图:(a )所示刚体由均质圆环与直秆焊接而成,两者质量均为m ,求绕O 轴的转动惯量;(b )所示均质圆盘质量为1m ,绳子无重且不可伸长.与圆盘之间无相对滑动,物块A 、B 质量均为2m ,求系统对O 轴的动量矩。
(a )(b12-5、某质点对于某定点O 的动量矩矢量表达式为:226(86)(4)t t t =++--O L i j k ,式中为t 时间,i, j, k 分别为x 、y 、z 轴向的单位矢量,求此质点上作用力对O 点的力矩的大小。
12-6、均质杆AB ,长L ;质量m ,在已知力A F ,B F (A B F F ≠)作用下,在铅垂面内作平面运动,若对端点B ,中点C 的转动惯量分别为B J ,C J ,求图示瞬时杆AB 的角加速度。
12-7、两根质量均为8kg的均质细杆固连成T字形,可绕通过O点的水平轴转动,当OAω=。
求该瞬时轴承O处的约束反力。
处于水平位置时,T形杆具有角速度4rad/s12-8、均质圆轮A质量为1m,半径为1r,以角速度ω绕杆OA的A端转动,此时将轮放置在m的另一均质圆轮B上,其半径为2r,如图所示。
轮B原为静止,但可绕其中心轴质量为2自由转动。
矩形惯性矩计算公式

一.矩形惯性矩计算公式
1、矩形:I=b*h^3/12。
2、三角形:I=b*h^3/36。
3、圆形:I=π*d^4/64。
4、环形:I=π*D^4*(1-α^4)/64;α=d/D。
惯性矩通常被用作描述截面抵抗弯曲的性质。
惯性矩的国际单位为(m4)。
即面积二次矩,也称面积惯性矩,而这个概念与质量惯性矩(即转动惯量)是不同概念。
惯性矩应用
结构设计和计算过程中,构件惯性矩Ix为截面各微元面积与各微元至与X 轴线平行或重合的中和轴距离二次方乘积的积分。
主要用来计算弯矩作用下绕X 轴的截面抗弯刚度。
结构设计和计算过程中,构件惯性矩Iy为截面各微元面积与各微元至与Y 轴线平行或重合的中和轴距离二次方乘积的积分。
主要用来计算弯矩作用下绕Y 轴的截面抗弯刚度。
转动惯量

不确定度与相对误差
根据公式
0.3 10 -3 kg m 2
得到圆盘的相对不确定度为:6.2% 根据公式:
4.9
得到圆盘的不确定度为: 10-3 kg m2 0.3
圆盘的转动惯量最终表达式为: 0.3) 10 -3 kg m 2 (4.9
圆环转动惯量的理论值与相对误差
根据公式
下
O
上
H0
R
三线摆示意图
实验原理
1 下盘
(m0 m) gRr 2 (2) T1 2 下盘+圆环 J1 2 4 H gRr J J1 J 0 2 [(m m0 )T12 m0T02 ] (3) 3 圆环 4 H m 2 (4) J 理论 ( R12 R2 ) 2
O' x C
J oo ' J c mx ,这一结论称为转动惯量的平行轴定理。
2
若把质量、半径均为m′和R'的相同
m
平行轴定理
R
x
o
x
圆柱体,对称地放在下盘上,如果圆柱
中心到下盘中心的距离为
O
x(见图),
x
测其周期为Tx.则每个圆柱体绕中心轴OO′转动惯量为:
1 (m0 2m ') gRr 2 Jx Tx J 0 2 2 4 H
(条件:θ≤5°,空气阻力不计,悬线伸长不计 H ,圆环与下盘 H0 中心重合)
m0 gRr 2 J0 T0 2 4 H 0
(1)
因此,通过长度、质量和时间的测量,便可求出刚体绕某 轴的转动惯量。
实验原理
二、验证转动惯量的平行轴定律
若质量为m的物体绕过其质心轴的转动惯量为 J c,当转轴平 行移动距离x时(如图所示),则此物体对新轴的转动惯量为
求转动惯量

yC 7 l 16
此刻质心比B高 1 l
16
7 l 1 相差 16 伸直后质心比B高 l
2
7 l 伸直用 t 16 7 gl 3 gl 12 4
例7(质心系) 线性引力
假设质点间的万有引力是线性的: F G * m1m2 r 其中G*为假想的引力常量,r 为两质点的间距。不考虑碰撞的 可能性,试导出多质点引力系统各质点的运动轨道和周期。 质心系是惯性系,以质心为坐标原点。
2 i 2 i
xi
yi y
I z mi ( xi2 yi2 )
i
i
x
I x I y I z 2 mi ( x y z ) 2mR
2 i 2 i 2 i i
2
Ix I y Iz I
2 I mR 2 3
26
例5(求转动惯量) 求质量为m 半径为R 的匀质球体绕过球 心轴的转动惯量 把球体看作无数个厚度为dr 的同心薄球壳的组合
m
f
r'
M
f'
f' a0 M
f
18
参考点与运动形式
MR mr 0 R m / Mr r' r R r
m绕质心的运动、M绕质心运动、m绕M的运动形式是相同的
m M m 1 其相对偏差为 m M m M
3m 2 dm 4 r dr 3 r dr R
2
4 3 m /( R ) 3
M
R
质量为dm的半径为r的薄球壳转动惯量dI
2 dI dmr 2 3
三角形的函数

三角形中三角函数基本定理【正弦定理】式中R为ABC的外接圆半径(图1.3).【余弦定理】【勾股定理】在直角三角形(C为直角)中,勾方加股方等于弦方(图1.4),即勾股定理也称商高定理,外国书刊中称毕达哥拉斯定理.【正切定理】或【半角与边长的关系公式】式中,r为ABC的内切圆半径,且式中S为ABC的面积.反三角函数基本公式Tag:三角函数点击: 6013 arc sin x + arc sin y = arc sin x – arc sin y =arc cos x + arc cos y = arc cos x – arc cos y =arc tan x + arc tan y = arc tan x – arc tan y =2 arc sin x = 2 arc cos x =2 arc tanx = cos (n arc cos x) =斜三角形解法Tag:三角函数点击:545 已知元素其他元素的求法一边a及两角B, C两边a, b及夹角C三边a, b, c两边a, b及其中一边的对角A b sin A<a时,有两解 b sin A>a时,无解b sin A=a时,有一解特殊角的三角函数值Tag:三角函数点击: 4728度弧度0 0 1 0 11518度弧度22.530 23645 1 15460 267.572>7590 1 0 0 1120135150 2180 0 0表中表示,(即左、右极限).一个锐角的余角的三角函数值等于这个角的余三角函数值,例如,,.立体图形的体积、表面积、侧面积、几何重心与转动惯量Tag:体积表面积侧面积几何重心转动惯量点击: 2210 图形体积V、表面积S、侧面积M、几何重心G与转动惯量*J体积[正方体]表面积a为棱长,d为对角线[长方体]a,b,h 分别为长,宽,高,d为对角线侧面积对角线重心 G在对角线交点上体积表面积侧面积对角线重心 G在对角线交点上转动惯量取长方体中心为坐标原点,坐标轴分别平行三个棱边(当时,即为正方体的情况)表中m为物体的质量,物体都为匀质.一般物体的转动惯量计算公式锥形体积V、表面积S、侧面积M、几何重心G与转动惯量J#e#图形体积V、表面积S、侧面积M、几何重心G与转动惯量J [三棱柱]体积表面积侧面积式中F为底面积a,b,c为边长,h为高[正六棱柱]a为底边长,h为高,d为对角线[正棱锥]n为棱数,a为底边长,h为高,g为斜高重心(P、Q分别为上下底重心)转动惯量对于正三棱柱(a=b=c)取G为坐标原点,z轴与棱平行体积表面积侧面积对角线重心(P、Q分别为上下底重心)转动惯量取G为坐标原点,z轴与棱平行体积表面积侧面积式中F为底面积,为一侧三角形面积重心Q为底面的重心)多面体与棱台体积V、表面积S、侧面积M、几何重心G与转动惯量J#e#图形体积V、表面积S、侧面积M、几何重心G与转动惯量J[四面体]a,b,c,p,q,r为棱长[棱台]h为高[正棱台]a’,a分别为上下底边长,n为棱数,h为高,g为斜高体积重心P为顶点,Q为底面的重心) 体积式中分别为上下底面积重心(P,Q分别为上下底重心)体积表面积侧面积式中分别为上下底面积重心(P、Q分别为上下底重心)方锥体、楔形、球体的体积V、表面积S、侧面积M、几何重心G与转动惯量J#e#图形体积V、表面积S、侧面积M、几何重心G与转动惯量J[截头方锥体] 体积两底为矩形,a’,b’,a,b分别为上下底边长,h为高,为截头棱长[楔形]底为矩形,a,b为其边长,h为高,a’为上棱长[球体]r为半径重心(P,Q分别为上下底重心)体积重心(P为上棱中点,Q为下底面重心)体积表面积重心G与球心O重合转动惯量取球心O为坐标原点半球体、球冠体积V、表面积S、侧面积M、几何重心G与转动惯量J#e#图形体积V、表面积S、侧面积M、几何重心G与转动惯量J[半球体]r为半径,O为球心[球扇形(球状楔)]体积表面积侧面积r为球半径,a为弓形底圆半径,h为拱高,为锥角(弧度)[球冠(球缺)]r为球半径,a为拱底圆半径,h为拱高重心转动惯量取球心O为坐标原点,z轴与GO重合体积表面积侧面积 (锥面部分)重心转动惯量z轴与GO重合体积表面积侧面积(球面部分)重心球台、圆环胎体积V、表面积S、侧面积M、几何重心G与转动惯量J#e#体积V、表面积S、侧面积M、几何重心G与转动图形惯量J[球台]r为球半径,,a分别为上下底圆的半径,h为高[圆环胎]R为中心半径,D为中心直径,r为圆截面半径,d为圆截面直径体积表面积侧面积重心(Q为下底圆心)体积表面积重心 G在圆环的中心上转动惯量取圆环的中心为坐标原点,z轴垂直于圆环所在平面圆柱体体积V、表面积S、侧面积M、几何重心G与转动惯量J#e#图形体积V、表面积S、侧面积M、几何重心G与转动惯量J[圆柱体]体积表面积侧面积r为底面半径,h为高[中空圆柱体(管)]R为外半径,r为内半径,h为高[斜截圆柱体]r为底圆半径,h,H分别为最小,最大高度,为截角,D为截头椭圆轴重心(P,Q分别为上下底圆心)转动惯量取重心G为坐标原点,z轴垂直底面体积表面积侧面积式中t为管壁厚,为平均半径重心转动惯量取z轴与GQ重合体积表面积侧面积截头椭圆轴重心(GQ为重心到底面距离,GK 为重心到轴线的距离)椭圆体体积V、表面积S、侧面积M、几何重心G与转动惯量J#e#图形体积V、表面积S、侧面积M、几何重心G与转动惯量J[圆柱截段]h为截段最大高度,b为底面拱高,2a为底面弦长,r为底面半径,为弧所对圆心角(弧度)[椭球体]a,b,c为半轴体积侧面积(柱面部分)体积重心G在椭球中心O上转动惯量取椭球中心为坐标原点,z轴与c轴重合拟锥台体积V、表面积S、侧面积M、几何重心G与转动惯量J#e#图形体积V、表面积S、侧面积M、几何重心G与转动惯量J[圆锥体]r为底圆半径,h为高,l为母线[圆台]r,R分别为上,下底圆半径,h为高,l为母线[拟棱台]上下底平行,,分别为上,下底面积,为中截面面积,h为高体积表面积侧面积母线重心(Q为底圆中心,O为圆锥顶点)转动惯量取圆锥顶点为坐标原点,z轴与GQ重合体积表面积侧面积母线圆锥高(母线交点到底圆的距离)重心(P,Q分别为上下底圆心)体积[注] 棱台、圆台、球台、圆锥、棱柱、圆柱等都是拟棱台的特例桶形体体积V、表面积S、侧面积M、几何重心G与转动惯量J#e#图形体积V、表面积S、侧面积M、几何重心G与转动惯量J [桶形体]d为上,下底圆直径,D为中截面直径,h为高母线为圆弧时:体积母线为抛物线时:体积重心(P,Q分别为上下底圆心)三角函数的相互关系表Tag:点击: 1294例如,若,则反三角函数的定义域与主值范围Tag:三角函数点击: 1851 函数主值记号定义域主值范围反正弦若,则反余弦若,则反正切若,则反余切若,则反正割若,则反余割若,则一般反三角函数与主值的关系为式中n为任意整数.反三角函数的相互关系Tag:三角函数点击: 1596 arc sin x = arc cos x = arc tan x = arc cot x =带有*号者只当x为正值时适用.反三角函数的图形与特征Tag:三角函数点击: 4704 反正弦曲线反余弦曲线拐点(同曲线对称中心):,该点切线斜率为1拐点(同曲线对称中心):,该点切线斜率为-1反正切曲线反余切曲线拐点(同曲线对称中心):,该点切线斜率为1 拐点:,该点切线斜率为-1渐近线:渐近线:名称反正割曲线反余割曲线方程图像顶点渐近线诱导公式表Tag:三角函数点击: 1299函数角sin cos tan cot seccsc表中n为整数.【基本关系】与圆有关的各量计算公式Tag:点击: 1221 与圆有关的各量计算公式[圆的切线与弦的夹角]式中表示AMB弧所对应的圆心角∠AOB的角度(下同),C为ANB弧上的任意点.[两割线及其夹角][两弦及其夹角]AE*BE= CE*DE=r2-OE2式中r为圆的半径.AE*BE= CE*DE=ET2[两切线的夹角][圆内接四边形面积S]式中a,b,c,d为四边角的度量与换算Tag:三角函数点击: 1217 【角度制与弧度制】1o 整个圆周的的弧称为含有1度的弧,而1度的弧所对的圆心角称为1度的角.1度等于60分(记作),1分等于60秒(记作).这种用度来度量角的方法称为角度制.2o 把等于半径长的弧称为含有1弧度的弧,而1弧度的弧所对的圆心角称为1弧度的角,这种用弧度来度量角的方法称为弧度制.【度与弧度的换算】弧度与度的关系是式中θ与α分别表示同一角的度数与弧度数.度与弧度换算表Ⅰ弧度 ( r ) 度(°) 分( ′) 秒 (" )1 57.29577951 3437.746771 206264.80630.017453293 1 60 36000.0002908882 0.016666667 1600.0000048481 0.000277778 0.016666667 1.表中黑体数字为精确值.度与弧度换算表Ⅱ度360 180 90 60 45 30弧度【祖率(圆周率)π】圆的周长与直径的比值称为圆周率,用π 表示.由于我国古代南朝的数学家祖冲之在计算圆周率方面取得辉煌成就,因而圆周率也常称为祖率.祖冲之算出π的值为3.1415926<π<3.1415927.球面三角形基本定理与公式Tag:球面三角点击: 1238 【正弦定理】【余弦定理】边:角:【余切定理】边:角:【正切定理】【五元素公式】边:角:【半角公式】式中. 【半边公式】【德兰布-高斯公式】【耐普尔公式】三角函数的定义Tag:三角函数点击: 1097 【三角函数的定义和符号变化】名称正弦余弦正切余切正割余割定义符号与增减变化Ⅰ +↑ +↓ +↑ +↓ +↑ +↓Ⅱ +↓ -↓ -↑ -↓ -↑ +↑Ⅲ -↓ -↑ +↑ +↓ -↓ -↑Ⅳ -↑ +↑ -↑ -↓ +↓ -↓【三角函数的图形与特征】标准正弦曲线周期:与x轴交点(同拐点):极值点(极大点或极小点):余弦曲线周期:与x轴交点(同拐点):极值点:一般正弦曲线周期:式中A>0为振幅,为角频率,为初相与x轴交点(同拐点):极值点:同时,也属于一般正弦曲线(设,可化为) 它是将标准正弦曲线在y轴方向上伸长A倍,在x轴方向上压缩倍,并向左平移一段距离而得到. 正切曲线周期:与x轴交点(同拐点):,该点切线斜率为1. 渐近线:余切曲线周期:与x轴交点(同拐点):,该点切线斜率为-1. 渐近线:正割曲线周期:极大点:极小点:渐近线:余割曲线周期:极大点:极小点:渐近线:斜三角形解法Tag:三角函数点击: 546 已知元素其他元素的求法一边a及两角B, C两边a, b及夹角C三边a, b, c两边a, b及其中一边的对角Ab sin A<a时,有两解 b sin A>a时,无解 b sin A=a时,有一解三角函数加法公式Tag:三角函数点击: 765弧放样法Tag:几何作图点击: 395在土木建筑工程中,由于受各种施工条件的限制,不能用圆规一转就画出圆弧,可采用下面方法在施工现场直接放大样.这种方法可在有限平面内放出任意大半径的圆弧实样,又便于工人同志掌握.[已知弦长和拱高作圆弧]方法作AB等于弦长,作CO垂直平分AB,并使CO等于拱高,连接BC,作BC的中垂线DE.作的平分线交DE于E,在ED延长线上取DF=DE,则F为的分点.由对称性,F的对称点也是的分点.重复上述步骤,可得的各分点,将各分点以光滑曲线顺次连接,即为所求圆弧(图2.17).此方法概念明确,步骤较少,占地最少.方法作AB等于弦长,作CO垂直平分AB,并使CO等于拱高.作BC的中垂线DF,截OE=CD.过E 作AB的垂线交DF于F,则F为的分点.由对称性,F的对称点也是的分点.重复上述步骤,可得的各分点,将各分点以光滑曲线顺次连接,即为所求圆弧(图2.18).此方法步骤最少.[已知弦长和圆弧上任一点作圆弧] 已知AB为弦长,C为已知圆弧上一点.以BC为边作角.再以AC为边按相同方向作角.上的点.当取a为一系列值时,便得到圆弧上一系列点,将各点以光滑曲线顺次连接,即为所求圆弧(图2.19).此方法最适于采用经纬仪、罗盘仪来测放半径很大的圆弧.几何作图问题Tag:几何作图点击: 646 所谓初等几何作图问题,是指使用无刻度的直尺和圆规来作图.若使用尺规有限次能作出几何图形,则称为作图可能,或者说欧几里得作图法是可能的,否则称为作图不可能.很多平面图形可以用直尺和圆规作出,例如上面列举的正五边形、正六边形、正八边形、正十边形等.而另一些就不能作出,例如正七边形、正九边形、正十一边形等,这些多边形只能用近似作图法.如何判断哪些作图可能,哪些作图不可能呢?直到百余年前,用代数的方法彻底地解决了这个问题,即给出一个关于尺规作图可能性的准则:作图可能的充分必要条件是,这个作图问题中必需求出的未知量能够由若干已知量经过有限次有理运算及开平方运算而算出.几千年来许多数学家耗费了不少的精力,企图解决所谓“几何三大问题”:立方倍积问题,即作一个立方体,使它的体积二倍于一已知立方体的体积.三等分角问题,即三等分一已知角.化圆为方问题,即作一正方形,使它的面积等于一已知圆的面积.后来已严格证明了这三个问题不能用尺规作图.什么是数学Tag:什么是数学点击: 391在数学创立的初期,数学的定义应该是数数的学问。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形转动惯量
转动惯量是指刚体绕轴转动时惯性的一种量度。而三角形转动惯
量是指一个三角形绕其一边旋转时所需要的力矩,与其质量和该边长
度平方的乘积成正比。
根据平行轴定理,一个三角形绕过其质心且与某一边垂直的轴的
转动惯量,等于该三角形绕其任意一边的转动惯量减去其质量与三角
形质心到该边的垂直距离的平方的乘积。
如果一个三角形可以分成四个全等的、相似的三角形,那么这个
三角形绕其质心轴的转动惯量就是四个小三角形转动惯量的总和。例
如,一个等边三角形的转动惯量可以表示为:I=(4/3)ml²,其中m是
三角形的质量,l是三角形的边长。
以上信息仅供参考,如有需要,建议您查阅物理学书籍或咨询物
理学专家。
