4-2灰色预测模型及其应用
灰色理论预测模型
灰⾊理论预测模型灰⾊理论通过对原始数据的处理挖掘系统变动规律,建⽴相应微分⽅程,从⽽预测事物未来发展状况。
优点:对于不确定因素的复杂系统预测效果较好,且所需样本数据较⼩;缺点:基于指数率的预测没有考虑系统的随机性,中长期预测精度较差。
灰⾊预测模型在多种因素共同影响且内部因素难以全部划定,因素间关系复杂隐蔽,可利⽤的数据情况少下可⽤,⼀般会加上修正因⼦使结果更准确。
灰⾊系统是指“部分信息已知,部分信息未知“的”⼩样本“,”贫信息“的不确定系统,以灰⾊模型(G,M)为核⼼的模型体系。
灰⾊预测模型建模机理灰⾊系统理论是基于关联空间、光滑离散函数等概念,定义灰导数与会微分⽅程,进⽽⽤离散数据列建⽴微分⽅程形式的动态模型。
灰⾊预测模型实验以sin(pi*x/20)函数为例,以单调性为区间检验灰⾊模型预测的精度通过实验可以明显地看出,灰⾊预测对于单调变化的序列预测精度较⾼,但是对波动变化明显的序列⽽⾔,灰⾊预测的误差相对⽐较⼤。
究其原因,灰⾊预测模型通过AGO累加⽣成序列,在这个过程中会将不规则变动视为⼲扰,在累加运算中会过滤掉⼀部分变动,⽽且由累加⽣成灰指数律定理可知,当序列⾜够⼤时,存在级⽐为0.5的指数律,这就决定了灰⾊预测对单调变化预测具有很强的惯性,使得波动变化趋势不敏感。
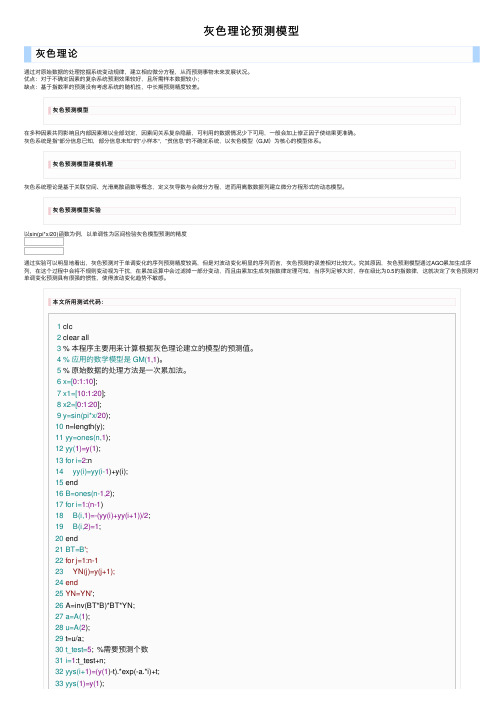
本⽂所⽤测试代码:1 clc2 clear all3 % 本程序主要⽤来计算根据灰⾊理论建⽴的模型的预测值。
4 % 应⽤的数学模型是 GM(1,1)。
5 % 原始数据的处理⽅法是⼀次累加法。
6 x=[0:1:10];7 x1=[10:1:20];8 x2=[0:1:20];9 y=sin(pi*x/20);10 n=length(y);11 yy=ones(n,1);12 yy(1)=y(1);13 for i=2:n14 yy(i)=yy(i-1)+y(i);15 end16 B=ones(n-1,2);17 for i=1:(n-1)18 B(i,1)=-(yy(i)+yy(i+1))/2;19 B(i,2)=1;20 end21 BT=B';22 for j=1:n-123 YN(j)=y(j+1);24 end25 YN=YN';26 A=inv(BT*B)*BT*YN;27 a=A(1);28 u=A(2);29 t=u/a;30 t_test=5; %需要预测个数31 i=1:t_test+n;32 yys(i+1)=(y(1)-t).*exp(-a.*i)+t;33 yys(1)=y(1);34 for j=n+t_test:-1:235 ys(j)=yys(j)-yys(j-1);36 end37 x=1:n;38 xs=2:n+t_test;39 yn=ys(2:n+t_test);40 det=0;41 for i=2:n42 det=det+abs(yn(i)-y(i));43 end44 det=det/(n-1);4546 subplot(2,2,1),plot(x,y,'^r-',xs,yn,'b-o'),title('单调递增' ),legend('实测值','预测值');47 disp(['百分绝对误差为:',num2str(det),'%']);48 disp(['预测值为: ',num2str(ys(n+1:n+t_test))]);495051 %递减52 y1=sin(pi*x1/20);53 n1=length(y1);54 yy1=ones(n1,1);55 yy1(1)=y1(1);56 for i=2:n157 yy1(i)=yy1(i-1)+y1(i);58 end59 B1=ones(n1-1,2);60 for i=1:(n1-1)61 B1(i,1)=-(yy1(i)+yy1(i+1))/2;62 B1(i,2)=1;63 end64 BT1=B1';65 for j=1:n1-166 YN1(j)=y1(j+1);67 end68 YN1=YN1';69 A1=inv(BT1*B1)*BT1*YN1;70 a1=A1(1);71 u1=A1(2);72 t1=u1/a1;73 t_test1=5; %需要预测个数74 i=1:t_test1+n1;75 yys1(i+1)=(y1(1)-t1).*exp(-a1.*i)+t1;76 yys1(1)=y1(1);77 for j=n1+t_test1:-1:278 ys1(j)=yys1(j)-yys1(j-1);79 end80 x21=1:n1;81 xs1=2:n1+t_test1;82 yn1=ys1(2:n1+t_test1);83 det1=0;84 for i=2:n185 det1=det1+abs(yn1(i)-y1(i));86 end87 det1=det1/(n1-1);8889 subplot(2,2,2),plot(x1,y1,'^r-',xs1,yn1,'b-o'),title('单调递增' ),legend('实测值','预测值');90 disp(['百分绝对误差为:',num2str(det1),'%']);91 disp(['预测值为: ',num2str(ys1(n1+1:n1+t_test1))]);9293 %整个区间93 %整个区间94 y2=sin(pi*x2/20);95 n2=length(y2);96 yy2=ones(n2,1);97 yy2(1)=y2(1);98 for i=2:n299 yy2(i)=yy2(i-1)+y2(i);100 end101 B2=ones(n2-1,2);102 for i=1:(n2-1)103 B2(i,1)=-(yy2(i)+yy2(i+1))/2;104 B2(i,2)=1;105 end106 BT2=B2';107 for j=1:n2-1108 YN2(j)=y2(j+1);109 end110 YN2=YN2';111 A2=inv(BT2*B2)*BT2*YN2;112 a2=A2(1);113 u2=A2(2);114 t2=u2/a2;115 t_test2=5; %需要预测个数116 i=1:t_test2+n2;117 yys2(i+1)=(y2(1)-t2).*exp(-a2.*i)+t2;118 yys2(1)=y2(1);119 for j=n2+t_test2:-1:2120 ys2(j)=yys2(j)-yys2(j-1);121 end122 x22=1:n2;123 xs2=2:n2+t_test2;124 yn2=ys2(2:n2+t_test2);125 det2=0;126 for i=2:n2127 det2=det2+abs(yn2(i)-y2(i));128 end129 det2=det2/(n2-1);130131 subplot(2,1,2),plot(x2,y2,'^r-',xs2,yn2,'b-o'),title('全区间' ),legend('实测值','预测值'); 132 disp(['百分绝对误差为:',num2str(det2),'%']);133 disp(['预测值为: ',num2str(ys2(n2+1:n2+t_test2))]);。
灰色预测模型及其应用

x(0) {x(0) (1), x(0) (2), , x(0) (N ) } {6, 3, 8, 10, 7}
4.2 灰色系统的模型
对数据累加
x(1) (1) x(0) (1) 6, x(1) (2) x(0) (1) x(0) (2) 6 3 9, x(1) (3) x(0) (1) x(0) (2) x(0) (3) 6 3+8 17, x(1) (4) x(0) (1) x(0) (2) x(0) (3) x(0) (4) 6 3+8+10 27, x(1) (5) x(0) (1) x(0) (2) x(0) (3) x(0) (4) x(0) (5)
第四章 灰色预测模型及其应用
灰色预测模型(Gray Forecast Model)是通过少量 的、不完全的信息,建立数学模型并做出预测的 一种预测方法.当我们应用运筹学的思想方法解决 实际问题,制定发展战略和政策、进行重大问题 的决策时,都必须对未来进行科学的预测. 预测是 根据客观事物的过去和现在的发展规律,借助于 科学的方法对其未来的发展趋势和状况进行描述 和分析,并形成科学的假设和判断.
(5)系统预测. 通过对系统行为特征指标建立一组相互关联的灰 色预测模型,预测系统中众多变量间的相互协调关系的变化。
灰色预测理论及其应用

灰色预测理论及其应用作者:谢威廖飞来源:《时代金融》2013年第36期【摘要】本文运用灰色系统理论中的灰色预测模型,利用我国2005—2011年的国内生产总值对我国2012—2015年的国内生产总值进行预测。
【关键词】灰色预测模型国内生产总值国内生产总值(Gross Domestic Product,简称GDP)是指在一定时期内(一个季度或一年),一个国家或地区的经济中所生产出的全部最终产品和劳务的价值,常被公认为衡量国家经济状况的最佳指标。
它不但可反映一个国家的经济表现,还可以反映一国的国力与财富。
本文利用灰色预测理论对我国的国内生产总值进行预测,可以为经济部门的经济决策提供相关的依据。
灰色预测通过鉴别系统因素之间发展趋势的相异程度,并对原始数据进行生成处理来寻找系统变动的规律,生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测事物的未来发展趋势。
在诸多的灰色模型中,以灰色系统中单序列一阶线性微分方程模型模型最为常用。
一、模型设有原始数据列,为数据个数。
如果根据数据列建立来实现预测功能,则基本步骤如下:1.对原始序列做累加得序列,累加使序列减少随机性,使生成序列呈一定规律,由此得到。
2.设满足单变量常微分方程,其中为待定系数,分别称为发展系数和灰色作用量。
只要求出,就能求出,进而求出的未来预测值。
3.灰色建模途径是已经过一次累加后的序列值通过最小二乘法来估计常数。
则得到4.将参数代入,并对进行求解,得5.对函数表达式及进行离散,并将二者做差以便还原原序列,得到近似数据序列如下:二、利用模型对我国GDP进行预测选用2004-2011年我国GDP的数据进行分析,原始序列为:利用MATLAB软件估计出参数列如下:三、结论我国的GDP正在快速增长阶段,通过灰色预测模型分析,今后我国的GDP还将持续快速的增长。
针对我国GDP发展的趋势,有关部门应该分析利弊,合理调控我国GDP的增长速度。
参考文献[1]刘思峰,党耀国,方志耕.灰色系统理论及其应用[M].北京:科学出版社,2004.[2]李志强,张丽,陈茂周.山东省国民生产总值预测的灰色模型[J].山东农业大学学报,2008(02).[3]杨树玲.股票价格的灰色预测[J].江西财经大学学报,2006(05).基金项目:牡丹江市科学技术计划项目(20121107106);黑龙江省教育厅教改工程立项指导项目(《高等数学》教学内容与课程体系优化的研究与实践);牡丹江师范学院科学技术研究项目青年指导项目(QZ201214)。
灰色模型及其在经济预测中的应用

G一 一一 一一一 一一 一一 一 , ∥ 色 ( ry 《】 G e ) , 、
对 x 。做 1一A O, ‘ ’ G 得
M一 一一 一一一 一 一一一表示 模 型 ( d1 Mo e)
X ’ = ( ( ) ‘ ( ) ( ) ‘ 4 , ‘ 1 , 2 ,‘ 3 , ( ) ’
出预测 。
近 年来 , 灰色 预 测理 论 在 许 多 领 域 得 到 了 广泛 关注, 它能 够有 效 处理 不 确 定性 显 著 和 数 据样 本 较
少 的系统 , 因此得 到 了越来 越广泛 地应用 。
3 灰色系统理论能处理贫信息系统。 .
灰色 预测模 型 只要 求较 短 的观 测 资料 即可 , 这
中 ,‘ ( )≥0 k=1 2 … , , ’为 ‘ 的一次累 。 k , , , 凡 ‘ 。
灰色系统理论 以“ 部分信 息已知, 部分信息未 知” 小样本” “ 的“ 、 贫信息” 不确定性 系统作为研究 对象 , 主要通过对“ 部分” 已知信息 的生成和开发提
取有 c筑 的信息 , f r 实现对 系统 运行 行 为 、 化 规律 的 演
灰 色模 型及其 在 经 济 预测 中 的应用
侯 丽 敏
( 州铁路 职业技 术 学院 河南郑州 4 0 5 ) 郑 50 2
灰 色 系统及 其特点
一
、
量 或灰色过 程 , 过 累 加 生成 或 累减 生 成 逐步 使 灰 通 色量 白化 , 而建 立 相 应 于微 分 方 程解 的模 型并 做 从
第2 O卷
:= = = 一 = == : == == :
第 3期
郑州铁路职业技术学院学报
J un f h n z o a w yV c t n l T c nc o ee o ra o Z e gh uR i a o a o a & e h i C l g l l i l a l
灰色预测模型理论及其应用

灰色预测模型理论及其应用灰色系统理论认为对既含有已知信息又含有未知或非确定信息的系统进行预测,就是对在一定方位内变化的、与时间有关的灰色过程的预测. 尽管过程中所显示的现象是随机的、杂乱无章的,但毕竟是有序的、有界的,因此这一数据集合具备潜在的规律,灰色预测就是利用这种规律建立灰色模型对灰色系统进行预测.灰色预测模型只需要较少的观测数据即可,这和时间序列分析,多元回归分析等需要较多数据的统计模型不一样. 因此,对于只有少量观测数据的项目来说,灰色预测是一种有用的工具.本文主要围绕灰色预测GM(1,1)模型及其应用进行展开。
一、灰色系统及灰色预测的概念1.1灰色系统灰色系统产生于控制理论的研究中。
若一个系统的内部特征是完全已知的,即系统的信息是充足完全的,我们称之为白色系统。
若一个系统的内部信息是一无所知,一团漆黑,只能从它同外部的联系来观测研究,这种系统便是黑色系统。
灰色系统介于二者之间,灰色系统的一部分信息是已知的,一部分是未知的。
区别白色和灰色系统的重要标志是系统各因素间是否有确定的关系。
特点:灰色系统理论以“部分信息已知、部分信息未知”的“小样本”、“贫信息”不确定型系统的研究对象。
1.2灰色预测灰色系统分析方法是通过鉴别系统因素之间发展趋势的相似或相异程度,即进行关联度分析,并通过对原始数据的生成处理来寻求系统变动的规律。
生成数据序列有较强的规律性,可以用它来建立相应的微分方程模型,从而预测事物未来的发展趋势和未来状态。
灰色预测是用灰色模型GM(1,1)来进行定量分析的,通常分为以下几类:(1) 灰色时间序列预测。
用等时距观测到的反映预测对象特征的一系列数量(如产量、销量、人口数量、存款数量、利率等)构造灰色预测模型,预测未来某一时刻的特征量,或者达到某特征量的时间。
(2) 畸变预测(灾变预测)。
通过模型预测异常值出现的时刻,预测异常值什么时候出现在特定时区内。
(3) 波形预测,或称为拓扑预测,它是通过灰色模型预测事物未来变动的轨迹。
灰色预测模型原理

灰色预测模型原理灰色预测模型(Grey Prediction Model)是一种基于灰色系统理论和数学建模方法的预测模型。
灰色系统理论是我国学者黄金云教授于1982年提出的一种系统理论,它是研究非确定性和不完备信息系统的一种新方法,可用于研究多变量、小样本和非线性系统。
灰色预测模型主要基于灰色数学建模方法,通过对已知的部分序列数据进行建模和预测,来推测未知的序列数据趋势。
它适用于研究数据量小、信息不完备、非线性关系复杂的系统。
下面将简要介绍灰色预测模型的原理、模型建立过程以及一些应用案例。
1. 灰色预测模型的原理灰色预测模型的核心思想是通过对已知数据进行灰色关联度的度量,从而建立出合适的数学模型,进行未来数据的预测。
其基本原理可以概括为以下五个步骤:(1)建立灰色微分方程:根据原始数据的特点,确定合适的灰色微分方程,通常使用一阶或高阶灰色微分方程。
(2)求解灰色微分方程:根据所选择的灰色微分方程,求解其参数,得到模型的特征参数。
(3)模型检验:检验所建立的灰色预测模型的拟合程度和误差是否符合要求。
(4)进行灰色关联度分析:根据已知数据的变化规律,计算各个因素的灰色关联度,确定相关因素的重要性。
(5)进行预测:利用建立好的灰色预测模型,对未来的数据进行预测和分析,得出预测值。
2. 模型建立过程灰色预测模型的建立过程中,通常包括以下几个步骤:(1)数据的建立与处理:对原始数据进行筛选、预处理和归一化处理,以满足模型的要求。
(2)建立灰色微分方程:从已知数据中提取主要特征,并根据数据的特点选择合适的灰色微分方程。
(3)求解灰色微分方程:根据所选的灰色微分方程,通过累加生成序列、求解参数等方法,得到模型的特征参数。
(4)模型的检验:根据已知数据的拟合程度和误差范围,评估所建立的灰色预测模型的准确性和可靠性。
(5)模型的应用与预测:利用已建立的模型进行未来数据的预测和分析,得出预测结果。
3. 应用案例灰色预测模型在实际应用中具有广泛的应用范围,以下是一些常见的应用案例:(1)经济领域:用于对经济指标、市场需求、价格变动等进行预测,为经济决策提供参考。
灰色预测模型及其在沉降预测中的应用
维普资讯
灰 色 预 测 模 型 及 其 在 沉 降 预 测 中 的 应 用 : 显 富 郭 淳 赵
( (
31
; O
/L
O
/
O
/
据 列
’ 下 式 构 成 由
一
2 ( ) 般 n一1> N, 43式 为 超 定 线 性 方 程 组 , 据 线 性 空 根
建 筑 物 、 市 、 区对 各 种 不 良地 质 地 段 沉 降 观 测 城 矿
展 变 化 进 行 全 局 观 察 、 析 和 长 期 预 测 。根 据 预 测 因 分 子 的 数 目可 分 为 一 阶 多 元 预 测 模 型 G 1 M( ,N)和 一 阶
一
的 目的不 仅 仅 是 观 测 其 在 工 程 时 刻 的 沉 降 值 , 为 重 更 要 的 是 根 据 已观 测 的 量 , 过 建 立 一 定 的 模 型 来 预 测 通、 、 源自0 /L0
/【
、 J
f ‘()= ∑ 。 k ’ ‘( ) ’
间 正 交 分 解 理 论 ,4 式 得 最 小 二 乘解 为 ()
据列 :
() 0 = () 1 ( ), 0 () 0 ( )’ 2 () 0 () … 3 ’ … , () 0 () ^
作 者 简 介 : 显 富 ( 92 ) 男 , 教 授 , 程 测 量 硕 士 。 赵 16 一 , 副 工
灰色预测模型及其在工程中的应用
2 .浙江 东洲 建设监 理 咨询 有 限公 司 ,浙 江
摘
杭州
300 ) 102
要 :采 用灰 色预 测法 对某 工程 试验 堤 的实 测沉 降进 行沉 降 预测 ,并 经模 型 精度 检验 和 与双 曲线法 、
,
按照灰色系统的建模方法 , 可以得到 1 个一阶非线性 动
态微分方程式 , 也就是 vrus模 型 : e lt h
= 叩 ()一 £ () £ () 1
s增篆 达 最 , 变 率 突 ,值 到 大但 化 较 其
。
z J , x曲线接 近直线 ; c 在 d段 , s增 加值趋 于 O a趋 于 O , d
取 、初始条件 、边 界 条 件 等 方 面 ,都存 在 许 多 不 确定 性 , 用传统的沉降计算 方法很 难获 得较 准确 的计算 结果 。因此
把 系数 o b代入式 ()解微 分方 程( ) : 、 1, 1得
() 2
通过实际沉降观测 数据进 行反 分析确 定模 型参 数 ,再对 后 期沉降进行预测 的方 法是 目前在 实 际工程 应用较 多 的 1 种
表 1 沉 降预 测 结 果 表 c n l
( 小 差 率 格 检验 设 ∑ : = 2 误 概 合 模型 。 = 1 {, ) ;
{∑( 一)分 为 的 值 方 。 = I 别 均 和 差若P PI 。
e I .64 C} ()一 <0075 称为小误差 概率 , 对于给定 的 P , 0 当
的最终沉 降相 比 ,用 灰色 模型 预测 的最终 沉 降要 小 ,一般
认为用双曲线法 所求 的结果 偏大 ,因 此 ,上述结 果还 是可 信的。
灰色预测模型及应用论文设计
灰色系统理论的研究GM(1,1)预测与关联度的拓展摘要:科学地预测尚未发生的事物是预测的根本目的和任务。
无论个体还是组织,在制定和规划面向未来的策略过程中,预测都是必不可少的重要环节,它是科学决策的重要前提。
在众多的预测方法中,灰色预测模型自开创以来一直深受许多学者的重视,它建模不需要太多的样本,不要求样本有较好的分布规律,计算量少而且有较强的适应性,灰色模型广泛运用于各种领域并取得了辉煌的成就。
本文详细推导GM(1,1)模型,另外对灰关联度进行了进一步的改进,让改进的计算式具有唯一性和规范性[]4。
通过给出的实例高校传染病发病率情况,建立了GM(1,1)预测模型,并预测了1993年的传染病发病率。
另外对传染病发病率较高的痢疾、肝炎、疟疾三种疾病做了关联度分析,发现痢疾与整个传染病关系最密切,而肝炎、疟疾与整个传染病的密切程度依次差些。
关键词:灰色预测模型;灰关联度;灰色系统理论The Research of Grey System TheoryGM(1,1) prediction and the expansion of correlationxueshenping Instructor: tangshaofangAbstract:Science has not yet occurred to predict the fundamental thing is to predict the purpose and mission. Whether individuals or organizations, in developing future-oriented strategy and planning process, the forecasts are essential and important aspect, which is an important prerequisite for scientific decision-making. Among the many prediction methods, the gray prediction model has been well received since its inception attention of many scholars, it does not require much sample modeling, does not require a better distribution of the sample was calculated, and has strong adaptability less , gray model widely used in various fields and has made brilliant achievements. This paper is derived GM (1,1) model, the other on the gray correlation was further improved, so that the improved formula is unique and normative. University by giving examples of the incidence of infectious diseases, establishing the GM (1,1) prediction model and predict the incidence of infectious diseases in 1993. In addition to the high incidence of infectious diseases, dysentery, hepatitis, malaria, made the three diseases, correlation analysis, found that dysentery is most closely with the infectious disease, and hepatitis, malaria and infectious diseases, the closeness of the order of hearing.Key words:Grey prediction model ; Grey relational grade;Grey system theory目录1、引言 (1)1.1、研究背景 (1)1.1.1、国内研究现状 (1)1.1.2、国外研究现状 (1)1.2、研究意义 (1)2、灰色系统及灰色预测的概念 (2)2.1、灰色系统理论发展概况 (2)2.1.1、灰色系统理论的提出 (2)2.1.2、灰色系统理论的研究对象 (2)2.1.3、灰色系统理论的应用范围 (2)2.1.4、三种不确定性系统研究方法的比较分析 (3)2.2、灰色系统的特点 (3)2.3、常见灰色系统模型 (4)2.4、灰色预测 (4)2.5、基本概念 (4)2.5.1、灰数的概念 (4)2.5.2、灰色生成数列 (5)2.5.3、累加生成 (5)2.5.4、累减生成 (5)2.5.5、加权邻值生成 (5)2.5.6、关联度 (5)3、简单的灰色预测——GM(1,1)预测 (6)3.1、GM(1,1)预测模型的基本原理 (6)3.2、GM(1,1)模型检验 (9)3.2.1、残差检验 (9)3.2.2、关联度检验 (9)3.2.3、后验差检验 (9)3.3、GM(1,1)残差模型 (10)3.4、GM(1,N)模型 (11)3.5、灰色系统建模的基本思路 (12)4、灰色关联度分析 (12)4.1、灰色关联分析理论及方法 (12)4.2、灰色关联技术的应用 (13)4.3、灰色关联度计算式及改进 (13)5、传染病的问题 (15)5.1、传染病发病率的的预测 (15)5.2、三种传染病的关联分析 (17)6、小结 (18)参考文献: (19)附录 (20)灰色系统理论的研究GM(1,1)预测与关联度的拓展1、引言模型按照对研究对象的了解程度可分为:黑箱模型、白箱模型、灰箱模型。
灰色预测模型在人口增长预测中的运用
灰色预测模型在人口增长预测中的运用摘要:本文依照灰色理论建立相应灰色预测模型,对榆林市城市人口未来人口总量进行了分析和预测。
笔者首先是对初始数据榆林市近年来城市人口数量进行预处理,进行合理的假设;其次,建立GM(1,1)模型,结合数据,推算出榆林市未来人口增长趋势;然后是对模型进行合理的检验,并对此模型进行评价。
关键词:人口增长;灰色预测;GM(1,1)模型一、灰色预测模型1、灰色预测模型灰色模型理论是由我国学者邓聚龙教授在1982年创立的。
灰色模型理论以“部分信息已知,部分信息未知”的“小样本”、“贫信息”不确定性系统为研究对象,主要通过对“部分”已知信息的生成、开发,提取有价值的信息,实现对系统运行规律的正确认识和有效控制。
灰色预测模型属于全因素的非线性拟合外推类方法,在形式上是单数列预测,只运用研究对象自身的时间序列建立模型,与其相关联的因素没有参与建模,这正是灰色系统“灰”的体现。
因为任何一个系统究竟包含多少因素,难以说清。
比如人口系统的再生产是由生育、死亡、疾病、灾害、环境、社会、经济等诸多因素影响、制约的共同结果,如此众多的因素不可能通过几个指标就能表达清楚,它们对人口增长的潜在而复杂的影响更是无法精确计算。
这反映人口系统具有明显的灰色性,适宜采用灰色模型去发掘和认识其原始时间序列综合灰色量所包涵的内在规律。
灰色预测的基本思路事将已知的数据序列按照某种规则构成动态或非动态的白色模块,再按照某种变化、解法来求解未来的灰色模型。
它的主要特点是模型使用的不是原始数据序列,而是生成的数据序列。
其核心体系是灰色模型GM(1,1),即对原始数据作累加生成得到近似的指数规律再进行建模的方法。
优点是不需要很多数据,一般只需要四个数据就够,能解决历史数据少、序列的完整性及可靠性低的问题;能利用微分方程来充分挖掘系统的本质,精度较高;能将无规律的原始数据进行生成得到规律性较强的生成数列,运算简便,易于检验,具有不考虑分布规律,不考虑变化趋势的特点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.2 灰色系统的模型
4.GM(1,1)的建模步骤
综上所述,GM(1,1)的建模步骤如下:
4.3 销售额预测
4.3 销售额预测
随着生产的发展、消费的扩大,市场需求通常总是 增加的,一个商店、一个地区的销售额常常呈增长趋 势. 因此,这些数据符合建立灰色预测模型的要求。 【例4.2】 表4.2列出了某公司1999—2003年逐年的销 售额.试用建立预测模型,预测2004年的销售额,要求 作精度检验。
类似地有
x(1) (3) x(1) ( N ) (0) x (3),..., x(0) ( N ). t t
于是,由式(4.3)有
ì x (0) (2) + ax (1) (2) = u, ï ï ï ï (0) ï x (3) + ax (1) (3) = u, ï ï í ï .............................. ï ï ï (0) ï x (N ) + ax (1) (N ) = u . ï ï î
(4.8)
当k
x (1) (k 1) 是拟合值; 由(4.8)式算得的 ˆ 1, 2,, N 1时,
ˆ 当k N时,x (1) (k 1) 为预报值.这是相对于一次累加序列
x (1) 的拟合值,用后减运算还原, k 1, 2,, N 1时, 当
就可得原始序列 x
(0)
当 ˆ 的拟合值 x(0) (k 1); k N时,
(1) (1) (1)
x (1) (3) x (1) (3) x (1) (2) 17 9 8, x (1) (2) x (1) (2) x (1) (1) 9 6 3, x (1) (1) x (1) (1) x (1) (0) 6 0 6. 归纳上面的式子得到如下结果:一次后减
4.2 灰色系统的模型
图4.1
图4.2
为了把累加数据列还原为原始数列,需进行后减运算 或称相减生成,它是指后前两个数据之差,如上例中
4.2 灰色系统的模型
x (1) (5) x (1) (5) x (1) (4) 34 27 7, x (4) x (4) x (3) 27 17 10,
4.1灰色系统的定义和特点
1. 灰色系统的定义
灰色系统是黑箱概念的一种推广。我们把既含有已知信 息又含有未知信息的系统称为灰色系统。作为两个极端, 我们将称信息完全未确定的系统为黑色系统;称信息完全 确定的系统为白色系统。区别白色系统与黑色系系统的定义和特点
x (1) (i) x(1) (i) x (1) (i 1) x (0) (i)
其中
i 1, 2,..., N,x (0) 0.
(0)
4.2 灰色系统的模型
2. 建模原理 给定观测数据列
x (0) {x (0) (1), x (0) (2), , x (0) ( N ) }
则(4.6)式的矩阵形式为
y BU
(4.6)’
方程组(4.6)’的最小二乘估计为
ˆ a T 1 T ˆ U ( B B) B y ˆ u
(4.7)
4.2 灰色系统的模型
ˆ ˆ 把估计值 a与u 代入(4.4)式得时间响应方程
ˆ ˆ u ˆ u ˆ (1) (k 1) x(1) (1) e ak x ˆ ˆ a a
4.1 灰色系统的定义和特点
4.2 灰色系统的模型
4.3 销售额预测 4.4 城市道路交通事故次数的灰色预测 4.5 城市火灾发生次数的灰色预测 4.6 灾变与异常值预测
4.1 灰色系统的定义和特点
4.1灰色系统的定义和特点
灰色系统理论是由华中理工大学邓聚龙教授于 1982年提出并加以发展的。二十几年来,引起了不 少国内外学者的关注,得到了长足的发展。目前, 在我国已经成为社会、经济、科学技术在等诸多领 域进行预测、决策、评估、规划控制、系统分析与 建模的重要方法之一。特别是它对时间序列短、统 计数据少、信息不完全系统的分析与建模,具有独 特的功效,因此得到了广泛的应用.在这里我们将简 要地介绍灰色建模与预测的方法.
第四章 灰色预测模型及其应用
灰色预测模型(Gray Forecast Model)是通过少量 的、不完全的信息,建立数学模型并做出预测的 一种预测方法.当我们应用运筹学的思想方法解决
实际问题,制定发展战略和政策、进行重大问题
的决策时,都必须对未来进行科学的预测. 预测 是根据客观事物的过去和现在的发展规律,借助 于科学的方法对其未来的发展趋势和状况进行描 述和分析,并形成科学的假设和判断.
4.2 灰色系统的模型
4.2 灰色系统的模型
通过下面的数据分析、处理过程,我们将了解到,有 了一个时间数据序列后,如何建立一个基于模型的灰色 预测。 1. 数据的预处理 首先我们从一个简单例子来考察问题. 【例4.1】 设原始数据序列
x(0) {x(0) (1), x(0) (2), , x(0) ( N ) } {6, 3, 8, 10, 7}
经一次累加得
(4.1)
x
(1)
{x (1), x (2), , x ( N ) }
(1) (1) (1)
(4.2)
设 x (1) 满足一阶常微分方程
dx (1) + ax = u dt
(1)
(4.3)
4.2 灰色系统的模型
其中a是常数,称为发展灰数;u称为内生控制灰数(或内 生变量),是对系统的常定输入.此方程满足初始条件 (4.3)’ 当t t0时x(1) x(1) (t0 ) 的解为
2. 灰色系统的特点
(1)用灰色数学处理不确定量,使之量化。 (2)充分利用已知信息寻求系统的运动规律。 (3)灰色系统理论能处理贫信息系统。
4.1灰色系统的定义和特点
常用的灰色预测有五种:
(1)数列预测,即用观察到的反映预测对象特征的时间序列来 构造灰色预测模型,预测未来某一时刻的特征量,或达到某一特征 量的时间。 (2)灾变与异常值预测,即通过灰色模型预测异常值出现的时 刻,预测异常值什么时候出现在特定时区内。 (3)季节灾变与异常值预测,即通过灰色模型预测灾变值发生 在一年内某个特定的时区或季节的灾变预测。 (4)拓扑预测,将原始数据作曲线,在曲线上按定值寻找该定 值发生的所有时点,并以该定值为框架构成时点数列,然后建立模 型预测该定值所发生的时点。 (5)系统预测. 通过对系统行为特征指标建立一组相互关联的灰 色预测模型,预测系统中众多变量间的相互协调关系的变化。
将(4.5)写为矩阵表达式
x (0) (2) 1 [ x (1) (2) x (1) (1)] 2 (0) 1 (1) x (3) 2 [ x (3) x (1) (2)] (0) 1 (1) x ( N ) 2 [ x ( N ) x (1) ( N 1)] 1 1 a u . 1 1
4.2 灰色系统的模型
对数据累加
x (1) (1) x (0) (1) 6, x (1) (2) x (0) (1) x (0) (2) 6 3 9, x (1) (3) x (0) (1) x (0) (2) x (0) (3) 6 3+8 17, x (1) (4) x (0) (1) x (0) (2) x (0) (3) x (0) (4) 6 3+8+10 27, x (1) (5) x (0) (1) x (0) (2) x (0) (3) x (0) (4) x (0) (5) 6 3+8+10+7 34.
可得原始序列 x ( 0 ) 预报值.
4.2 灰色系统的模型
3.精度检验
(1)残差检验:分别计算
4.2 灰色系统的模型
(3)预测精度等级对照表,见表4.1.
表4-1 等 级 对 照 表
4.2 灰色系统的模型
由于模型是基于一阶常微分方程(4.3)建立的,故称为 一阶一元灰色模型,记为GM(1,1).须指出的是, 建模时 先要作一次累加,因此要求原始数据均为非负数.否则, 累加时会正负抵消,达不到使数据序列随时间递增的目的. 如果实际问题的原始数据列出现负数,可对原始数据列进 行“数据整体提升”处理. 注意到一阶常微分方程是导出GM(1,1)模型的桥梁,在我 们应用GM(1,1)模型于实际问题预测时,不必求解一阶常 微分方程(4.3).
灰色系统理论是研究解决灰色系统分析、建模、
预测、决策和控制的理论.灰色预测是对灰色系统
所做的预测.目前常用的一些预测方法(如回归分
析等),需要较大的样本.若样本较小,常造成较
大误差,使预测目标失效.灰色预测模型所需建模 信息少,运算方便,建模精度高,在各种预测领 域都有着广泛的应用,是处理小样本预测问题的 有效工具.
(4.6)
令
y ( x(0) (2), x(0) (3), , x(0) ( N ))T .
这里,T表示转置.令
4.2 灰色系统的模型
B=
1 [ x (1) (2) x (1) (1)] 1 2 1 (1) (1) 1 a 2 [ x (3) x (2)] , U , u 1 (1) (1) 2 [ x ( N ) x ( N 1)] 1
4.2 灰色系统的模型
因 x (1) (1) 留作初值用,故将 x(1) (2), x(1) (3),..., x(1) ( N ) 分别代入方程(4.3),
用差分代替微分,又因等间隔取样, t (t 1) t 1, 故得
x(1) (2) x(1) (2) x(1) (2) x (1) (1) x (0) (2), t
