2015春北师大七年级下册数学《2.2 探索直线平行的条件》习题3

合集下载

(word完整版)北师大七年级下2.2《探索直线平行的条件》习题含详细答案

《探究直线平行的条件》习题一、选择题1．如图，直线AB ，CD 被直线EF 所截，以下判断中不正确的选项是( )A.∠3=∠6B.∠2=∠6C.∠1 和∠4 是内错角D.∠3 和∠5 是同位角2．如图，以下四组角中是同位角的是( )A.∠1 与∠7B.∠3 与∠5C.∠4 与∠5D.∠2 与∠63．如图，此中内错角的对数是( )A.5B.2C.3D.44．∠1 和∠2 是直线AB ，CD 被直线EF 所截而形成的内错角，那么∠1 和∠2 的大小关系是( )A.∠1=∠2B.∠1＞∠2C.∠1＜∠2D.没法确立5．如图，在以下条件中，能判断AD ∥BC 的是( )A.∠DAC= ∠BCAB.∠DCB+ ∠ABC=180°C.∠ABD= ∠BDCD.∠BAC= ∠ACD6．如图，在平移三角尺画平行线的过程中，原因是( )A.两直线平行，同位角相等B.两直线平行，内错角相等C.同位角相等，两直线平行D.内错角相等，两直线平行二、填空题7．如图，按角的地点关系填空：∠A 与∠2 是_____．8．如图，∠B 的同位角是_____．9．如图，以下条件中：①∠B+∠BCD=18°0 ；②∠1=∠2；③∠3=∠4；④∠B=∠5；则必定能判断AB ∥CD 的条件有_____(填写全部正确的序号)．10．如图：已知：∠1=105°，∠2=105°，则_____∥_____．三、解答题11．如图，∠1和∠2是哪两条直线被哪一条直线所截形成的？它们是什么角？∠1和∠3是哪两条直线被哪一条直线所截形成的？它们是什么角？12．如图，直线AB，CD订交于点O．写出∠1，∠2，∠3，∠4中每两个角之间的地点关系．13．如图，直线AB，CD订交于O，∠AOD+∠C=180°，直线AB与CE必定平行吗？试着说明你的原因．14．如图：已知∠1和∠D互余，CF⊥DF，试证明AB∥CD．15．如图，△ABC中，∠ACB=90°，CD⊥AB，点D为垂足，点E，F分别在AC．AB边上，且∠AEF=∠B．求证：EF∥CD．参照答案一、选择题1．答案：B分析：【解答】A、依据对顶角相等可得∠3=∠6，故此选项不合题意；B、∠2 和∠6 是同位角，不必定相等，故此选项切合题意；C、∠1 和∠4 是内错角，故此选项不合题意；D、∠3 和∠5 是同位角，故此选项不合题意；应选：B．【剖析】依据对顶角相等，三线八角同位角、内错角或同旁内角定义进行剖析．2．答案：D分析：【解答】依据同位角、邻补角、对顶角的定义进行判断，A、∠1 与∠7 不是同位角，故A 错误；B、∠3 与∠5 是内错角，故B 错误；C、∠4 与∠5 是同旁内角，故C 错误；D、∠2 与∠6 是同位角，故D 正确．应选：D．【剖析】同位角就是：两个角都在截线的同旁，又分别处在被截的两条直线同侧的地点的角．3．答案：D分析：【解答】以下图，是内错角的有：∠ 2 与∠3；∠1 与∠3；∠ 2 与∠4；∠ 1 与∠4．应选D．【剖析】内错角就是：两个角都在截线的异侧，又分别处在被截的两条直线之间的角．4．答案：D分析：【解答】由于两直线的地点关系不确立，因此∠ 1 和∠2 的大小关系也没法确立．应选D．【剖析】从两直线能否平行的角度考虑．5．答案：A分析：【解答】A、∵∠DAC= ∠BCA ，∴AD ∥BC（内错角相等，两直线平行）．故本选项正确；B、依据“∠DCB+ ∠ABC=180°”只好判断“DC∥AB”，而非AD ∥BC．故本选项错误；C、依据“∠ABD= ∠BDC”只好判断“DC∥AB”，而非AD ∥BC．故本选项错误；D、依据“∠BAC= ∠ACD”只好判断“DC∥AB”，而非AD ∥BC．故本选项错误；应选 A ．【剖析】依据各选项中各角的关系及利用平行线的判断定理，分别剖析判断AD、BC 能否平行即可．6．答案：C分析：【解答】∵∠DPF=∠BMF∴AB ∥CD（同位角相等，两直线平行）．应选C．【剖析】由题意联合图形可知∠DPF=∠BMF ，从而得出同位角相等，两直线平行．二、填空题7．答案：同旁内角分析：【解答】依据图形，∠ A 与∠2 是同旁内角．【剖析】依据两直线被第三条直线所截，在截线的同一侧，被截线的同一方向的两个角是同位角；在截线的双侧，被截线的内部的两个角是内错角；在截线的同一侧，被截线的内部的两个角是同旁内角，联合图形找出即可．8．答案：∠ECD，∠ACD分析：【解答】∠ B 的同位角是∠ECD ，∠ACD ，【剖析】依据同位角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，而且在第三条直线（截线）的同旁，进行剖析可得答案．9．答案：①③④分析：【解答】①∵∠B+∠BCD=18°0 ，∴AB ∥CD；②∵∠1=∠2，∴AD ∥CB；③∵∠3=∠4，④∵∠B=∠5，【剖析】依据平行线的判断方法：同旁内角互补，两直线平行可得①能判断AB ∥CD；依据内错角相等，两直线平行可得③能判断AB ∥CD；依据同位角相等，两直线平行可得④能判断AB ∥CD．10．答案：a b分析：【解答】∵∠1=105°，∠2=105°，∴∠1=∠2，∴a∥b．【剖析】依据角度相等获得∠1=∠2，再依据同位角相等，两直线平行解答．三、解答题11．答案：∠1 和∠2 是直线EF、DC 被直线AB 所截形成的同位角，∠1 和∠3 是直线AB 、CD 被直线EF 所截形成的同位角．分析：【解答】∠ 1 和∠2 是直线EF、DC 被直线AB 所截形成的同位角，∠ 1 和∠3 是直线AB 、CD 被直线EF 所截形成的同位角．【剖析】依据同位角的观点作答．正确辨别同位角、内错角、同旁内角的重点，是弄清哪两条直线被哪一条线所截．也就是说，在鉴别这些角以前，要弄清哪一条直线是截线，哪两条直线是被截线．12．答案：∠1 和∠3 是对顶角；∠1 和∠2 是邻补角，∠2 与∠3 是邻补角；∠1 和∠ 4 是同位角，∠ 2 与∠4 是同旁内角，∠ 3 与∠ 4 是内错角．分析：【解答】∠ 1 和∠ 3 是对顶角；∠ 1 和∠ 2 是邻补角，∠ 2 与∠3 是邻补角；∠1 和∠ 4 是同位角，∠ 2 与∠4 是同旁内角，∠ 3 与∠ 4 是内错角．【剖析】联合图形，依据同位角、内错角、同旁内角和对顶角、邻补角的定义求解．正确识别同位角、内错角、同旁内角的重点，是弄清哪两条直线被哪一条线所截．也就是说，在辨别这些角以前，要弄清哪一条直线是截线，哪两条直线是被截线．13．答案：看法答过程．分析：【解答】直线AB 与CE 必定平行．原因以下：∵∠AOD+ ∠C=180°，而∠AOD= ∠BOC，∴∠BOC+ ∠C=180°，∴AB ∥CE．(word完整版)北师大七年级下2.2《探索直线平行的条件》习题含详细答案【剖析】依据对顶角相等获得∠AOD= ∠BOC，又∠AOD+ ∠C=180°，则有∠BOC+ ∠C=180°，依据同旁内角互补，两直线平行即可获得AB ∥CE.14．答案：看法答过程．分析：【解答】∵CF⊥DF ，∴∠C+∠D=90°，又∠1 和∠D 互余，即∠1+∠D=90°，∴∠1=∠C，∴AB ∥CD．【剖析】经过∠ D 中间量的转变，获得∠1=∠C，从而可得出平行．15．答案：看法答过程．分析：【解答】证明：∵∠ACB=90°，∴∠B+∠A=90°，∵CD⊥AB ，∴∠ADC=9°0 ，∴∠A+∠ACD=9°0 ，∴∠B=∠ACD ，∵∠AEF= ∠B，∴∠AEF= ∠ACD ，∴EF∥CD．【剖析】第一依据直角三角形的性质可得∠B+ ∠A=90°，再依据CD⊥AB 可得∠A+ ∠ACD=90°，从而获得∠B=∠ACD ，而后在证明∠AEF= ∠ACD ，可证明EF∥CD．1 / 11。

数学北师大版七年级下册《探索直线平行的条件》同步练习

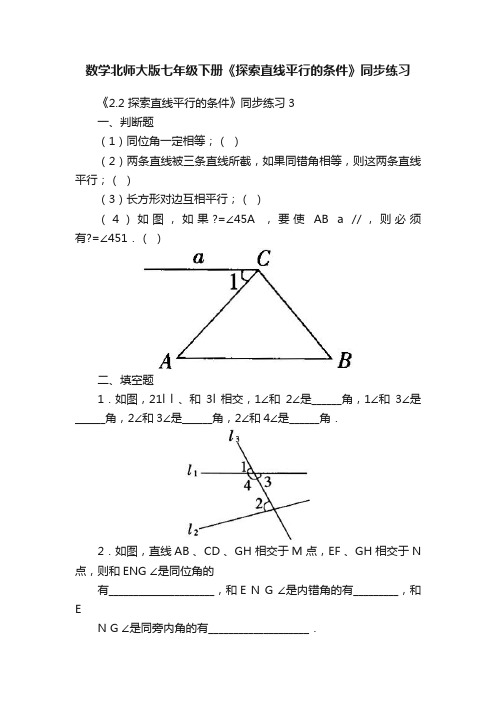
数学北师大版七年级下册《探索直线平行的条件》同步练习《2.2 探索直线平行的条件》同步练习3一、判断题（1）同位角一定相等；（）（2）两条直线被三条直线所截，如果同错角相等，则这两条直线平行；（）（3）长方形对边互相平行；（）（4）如图，如果?=∠45A ，要使AB a //，则必须有?=∠451．（）二、填空题1．如图，21l l 、和3l 相交，1∠和2∠是______角，1∠和3∠是______角，2∠和3∠是______角，2∠和4∠是______角．2．如图，直线AB 、CD 、GH 相交于M 点，EF 、GH 相交于N 点，则和ENG ∠是同位角的有_____________________，和E N G ∠是内错角的有_________，和EN G ∠是同旁内角的有____________________．3．如果两条直线被第三条直线所截，要使这两条直线平行，角的条件必须有________或__________或________．4．如图：C ∠的同位角是______，B ∠的内错角是______，EAC ∠的同旁内角是______．三、解答题1．如图：?=∠+∠∠=∠∠=∠18031,42,41，找出其中互相平行的直线，并说明理由．2．如图，已知DE 平分AF BDF ,∠平分BAC ∠，且21∠=∠，试说明AC DF //．3．在同一平面内，垂直于同一直线的两条直线平行吗？如果平行请说明理由．参考答案一、判断题（1）× （2）√ （3）√ （4）√二、填空题1．（1）同位，对顶，内错，同旁内2．GMC ∠和BMN AMG ∠∠,和CMN DMN ∠∠,和AMN ∠3．内错角相等、同位角相等、同旁内角互补4．C ∠∠∠,2,1三、解答题1．b a n m l // //// 理由（略）2．说明：因为22,12∠=∠∠=∠BAC BDF ，又因为21∠=∠，所以BAC BDF ∠=∠，所以AC DF //，根据是同位角相等，两直线平行．3．平行，根据是同位角都是直线，或内错角都是直角，即相等，两直线平行，或根据同旁内角都是直角所以互补，故两直线平行．。

北师大版七年级数学下册2.2《探索直线平行的条件》同步测试

北师大版七年级数学下册 2.2《探索直线平行的条件》同步测试北师大版七年级数学下册2.2探索直线平行的条件同步测试一、单选题1．如图，用两个相同的三角板按照如图所示的方式作平行线，能解释其中道理的是( ) A. 同位角相等，两直线平行 B. 内错角相等，两直线平行C. 同旁内角互补，两直线平行D. 以上都不对第1题图第3题图第4题图第5题图2．若直线a∥b，b∥c，则a∥c的依据是( )A. 平行公理B. 等量代换C. 等式的性质D. 平行于同一条直线的两条直线互相平行3．如图，下列能判定AB∥EF的条件有（）①∠B+∠BFE=180°②∠1=∠2③∠3=∠4④∠B=∠5．A. 1个B. 2个C. 3个D. 4个4．如图，直线AB，CD被直线EF所截，∠1=55°，下列条件中能判定AB∥CD的是（）A. ∠2=35° B. ∠2=45° C. ∠2=55° D. ∠2=125°5．如图所示，点E在AC的延长线上，下列条件中能判断AB∥CD的是（）A. ∠3=∠AB. ∠1=∠2C. ∠D=∠DCED. ∠D+∠ACD=180°6．已知如图直线a，b被直线c所截，下列条件能判断a∥b的是（）A. ∠1=∠2B. ∠2=∠3C. ∠1=∠4D. ∠2+∠5=180°第6题图第7题图第8题图第9题图7．如下图，在下列条件中，能判定AB//CD的是（）A. ∠1=∠3B. ∠2=∠3C. ∠1=∠4D. ∠3=∠48．如图所示，“过点P画直线a的平行线b”的作法的依据是（）A. 内错角相等，两直线平行B. 同位角相等，两直线平行C. 两直线平行，内错角相等D. 两直线平行，同位角相等9．如图所示,若∠1与∠2互补,∠2与∠4互补,则()A. l3∥l4l2∥l5 C. l1∥l5 D. l1∥l210．如图所示，下列说法正确的是（）A. 若∠3＝∠5，则CD∥EFB. 若∠2＝∠6，则CD∥EFC. 若∠4＝∠3，则CD∥EFD. 若∠1＝∠6，则GH∥AB第10题图第11题图第12题图11．如图所示，要得到DE∥BC，则需要条件（）A. CD⊥AB，GF⊥ABB. ∠4＋∠5＝180°C. ∠1＝∠3D. ∠2＝∠312．在下列条件中，不能判定AB DF的是（）A. 2180A∠+∠=︒ B. 3A∠=∠ C. 14∠=∠ D. 1A∠=∠二、填空题13．如图，已知∠B＝40°，要使AB∥CD，需要添加一个条件，这个条件可以是___．第13题图第14题图第15题图第16题图14．如图，若AB⊥BC，BC⊥CD，则直线AB与CD的位置关系是______．15．如图，PC∥AB，QC∥AB，则点P，C，Q在一条直线上．理由是____________________ 16．如图，两直线a．b被第三条直线c所截，若∠1=50°，∠2=130°，则直线a．b的位置关系是____________ ．17．如图，下列条件中：①∠B+∠BCD=180°；②∠1=∠2；③∠3=∠4；④∠B=∠5；则一定能判定AB∥CD的条件有_____(填写所有正确的序号)．第17题图第18题图18.已知：如图，∠EAD=∠DCF，要得到AB∥CD，则需要的条件________．（填一个你认为正确的条件即可）三、解答题19．如图所示，EF⊥BD，垂足为E，∠1＝50°，∠2＝40°，试判断AB与CD是否平行，并说明理由．20．如图，一条直线分别与直线BE、直线CE、直线CF、直线BF相交于点A，G，D，H且∠1=∠2，∠B=∠C（1）找出图中相互平行的线，说说它们之间为什么是平行的；（2）证明：∠A=∠D．21．将一副三角板拼成如图所示的图形，过点C作CF平分∠DCE交DE于点F．求证：CF//AB22．如图，在ΔABC中，CD是高，点E、F、G分别在BC、AB、AC上且EF⊥AB，∠1=∠2，试判断DG与BC的位置关系，并说明理由.23．如图，已知∠ADE=∠B，∠1=∠2，那么CD与FG平行吗？说明理由．24．如图，已知∠1=50°，∠2=50°，∠3=130°，找出图中的平行线，并说明理由；25．已知：如图：∠1=∠2，∠3+∠4= 180°；确定直线a，c的位置关系，并说明理由；解：a c；理由：∵∠1=∠2（）,∴ a // ( )；∵∠3+∠4= 180°（）,∴ c // ( )；∵ a // ,c // ,∴// ( )参考答案及解析1．B【解析】如图：∵∠ABD=∠BAC=30°,根据内错角相等两直线平行，可得AC∥BD.故选：B. 点睛：本题主要考查平行线的判定，解题的关键是：对顶角相等两直线平行这一判定定理的理解和掌握.2．D【解析】因为直线a∥b,b∥c,所以a∥c的依据是平行于同一条直线的两条直线互相平行,故选D.3．C【解析】①∠B+∠BFE=180°，根据同旁内角互补，两直线平行得出AB∥EF；②∠1=∠2，根据内错角相等，两直线平行，得出//DE BF；③∠3=∠4,根据内错角相等，两直线平行，得出AB∥EF；④∠B=∠5，根据同位角相等，两直线平行，得出AB∥EF；故选C.4．C【解析】试题分析：A、由∠3＝∠2＝35°，∠1＝55°推知∠1≠∠3，故不能判定AB∥CD，故本选项错误；B、由∠3＝∠2＝45°，∠1＝55°推知∠1≠∠3，故不能判定AB∥CD，故本选项错误；C、由∠3＝∠2＝55°，∠1＝55°推知∠1＝∠3，故能判定AB∥CD，故本选项正确；D、由∠3＝∠2＝125°，∠1＝55°推知∠1≠∠3，故不能判定AB∥CD，故本选项错误；故选：C．点睛：本题考查了平行线的判定定理，正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键，不能遇到相等或互补关系的角就误认为具有平行关系，只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行．5．B【解析】试题解析：B, 12,∠=∠AB∴∥.CD(内错角相等，两直线平行).故选B.6．A【解析】试题解析：∵∠1=∠2，∴a∥b；故选A．7．C【解析】根据平行线的判定，可由∠2=∠3，根据内错角相等，两直线平行，得到AD∥BC，由∠1=∠4，得到AB∥CD.故选：C.8．A 【解析】如图所示，根据图中直线a、b被c所截形成的内错角相等，可得依据为内错角相等，两直线平行．故选：A.点睛：本题考查的是平行线的判定定理，即内错角相等，两直线平行．比较简单．9．D【解析】因为∠1与∠2互补，∠2与∠4互补，可知∠1+∠2=180°，∠2+∠4=180°，所以∠1=∠4，根据内错角相等，两直线平行可得l1∥l2，故选D.10．C【解析】解：∠4和∠3是直线EF和CD被直线GB所截形成的内错角，所以∠4＝∠3时，CD∥EF．故选C．11．C【解析】解：∠1和∠3是直线DE和BC被直线CD所截形成的内错角，所以要得到DE∥BC，需∠1＝∠3．故选C．12．D【解析】∵∠A+∠2=180°，∴AB∥FD，故A选项能判定；∵∠A=∠3，∴AB∥FD，故B选项能判定；∵∠1=∠4，∴AB∥FD，故C选项能判定；∵∠1=∠A，∴ED∥FC，故D选项不能判定.故选D.点睛：掌握平行线的判定定理.13．∠BED＝40°【解析】当∠B=∠BED时,AB∥CD，所以添加∠BED=40°时,可得到AB∥CD.故答案为∠BED=40°.14．AB∥CD【解析】∵AB⊥BC，BC⊥CD，∴∠ABC=∠BCD=90°，∴AB∥CD，故答案为AB∥CD.15．经过直线外一点，有且只有一条直线与这条直线平行【解析】∵PC∥AB,QC∥AB,∵PC和CQ都过点C,∴P,C,Q在一条直线上（过直线外一点有且只有一条直线和已知直线平行）,故答案为:过直线外一点有且只有一条直线平和已知直线平行．16．a∥b．【解析】因为∠2=130°，所以∠3=50°，∠1=50°,所以a∥b．故答案为a∥b．17．①③④【解析】试题解析：①∵∠B+∠BCD=180°，∴AB∥CD；②∵∠1=∠2，∴AD∥CB；③∵∠3=∠4，∴AB∥CD；④∵∠B=∠5，∴AB∥CD考点：平行线的判定．18．答案不唯一，如∠EAD=∠B【解析】如图，∵∠EAD=∠DCF，即∠1=∠3，而想要AB//CD，则需∠2=∠3，∴只要添加条件∠1=∠2即可，即∠EAD=∠B.故答案为∠EAD=∠B（答案不唯一）19．AB与CD平行，理由见解析.【解析】试题分析：首先根据垂直的定义求出∠D的度数，再根据同位角相等，证明两直线平行．试题解析：AB与CD平行．理由：∵EF⊥BD，∴∠FED＝90°，∴∠D＝90°－∠1＝40°，∴∠2＝∠D，∴AB∥CD.20．（1）CE∥BF，AB∥CD．理由见解析.（2）证明见解析.【解析】试题分析：（1）根据同位角相等，两直线平行可得CE∥FB，进而可得∠C=∠BFD，再由条件∠B=∠C可得∠B=∠BFD，从而可根据内错角相等，两直线平行得AB∥CD；（2）根据（1）可得AB∥CD，再根据两直线平行，内错角相等可得∠A=∠D．试题解析：（1）CE∥BF，AB∥CD．理由：∵∠1=∠2，∴CE∥FB，∴∠C=∠BFD，∵∠B=∠C，∴∠B=∠BFD，∴AB∥CD；（2）由（1）可得AB∥CD，∴∠A=∠D．21．详见解析.【解析】试题分析：利用三角板角的大小关系证明∠1=∠3=45°，所以内错角相等，两直线平行.试题解析：∵CF平分∠DCE，∴∠1=∠2=12∠DCE，∵∠DCE=90°，∴∠1=45°，∵∠3=45°，∴∠1=∠3，∴AB∥CF（内错角相等，两直线平行）；22．见解析【解析】试题分析：DG∥BC，由EF⊥AB，CD⊥AB，可得EF∥CD，所以∠2=∠DCB，因为∠1=∠2，所以∠DCB=∠1，所以DG∥BC.试题解析：DG∥BC，理由如下：∵EF⊥AB，CD⊥AB，∴EF∥CD，∴∠2=∠DCB，∵∠1=∠2，∴∠DCB=∠1，∴DG∥BC.点睛：掌握平行线的性质及判定方法.23．CD∥FG，理由见解析.【解析】试题分析：先由∠ADE=∠B可得DE∥BC，进而得出∠1=∠DCB，又因为∠1=∠2，所以∠2=∠DCB，即可证明CD∥FG.试题解析：CD∥FG；证明：∵∠ADE=∠B，∴DE∥BC，∴∠1=∠DCB，∵∠1=∠2，∴∠2=∠DCB，∴CD∥FG.点睛：掌握平行线的性质定理和判定定理.24．AC//OB，OA//BC【解析】试题分析：证明如下：如图所示，因为∠1=∠2，由“同位角相等，两直线平行”，可得AC//O B。

七年级数学下册2.2.1探索直线平行的条件同步练习3北师大版

C。AB，CD被A D所截构成
D.AB，CD被BC所截构成
4．如图，直线AB,CD与直线EF，GH分别相交,图中的同旁内角共有（ )．
A。4对B.8对
C.12对D.16对
二、填空题
5．如图所示，
(1)∠B和∠ECD可看成是直线AB、CE被直线______所截得的_______角；
（2)∠A和∠ACE可看成是直线_______、______被直线_______所截得的______角．
10.解：同位角有∠1和∠3，∠5和∠6，内错角有∠2和∠4,∠1和∠6，
同旁内角有∠1和∠5，∠2和∠6,∠3和∠4，∠3和∠5。
尊敬的读者：
本文由我和我的同事在百忙中收集整编出来，本文稿在发布之前我们对内容进行仔细校对，但是难免会有不尽如人意之处，如有疏漏之处请指正，希望本文能为您解开疑惑,引发思考。文中部分文字受到网友的关怀和支持，在此表示感谢！在往后的日子希望与大家共同进步，成长。
7.如图所示，在∠1、∠2、∠3、∠4中，
（1）同位角有____对,它们是____;
（2)内错角有____对,它们是____；
(3）同旁内角有____对，它们是____．
8。探究题：
(1)如图①，两条水平的直线被一条竖直的直线所截，同位角有____对，内错角有____对,同旁内角有____对；
（2)如图②,三条水平的直线被一条竖直的直线所截，同位角有____对，内错角有_ ___对，同旁内角有____对；
This article is collected and compiled by my colleagues and I in our busy schedule. We proofread the content carefully before the release of this article, but it is inevitable that there will be some unsatisfactory points. If there are omissions, please correct them. I hope this article can solve your doubts and arouse your thinking. Part of the text by the user's care and support, thank you here! I hope to make progress and grow with you in the future.

北师大版数学七年级下册2.2《探索直线平行的条件》精选练习(含答案)

北师大版数学七年级下册2.2《探索直线平行的条件》精选练习一、选择题1.如图，其中内错角的对数是( )A.5B.2C.3D.42.如图，直线AB，CD被直线EF所截，下列判断中不正确的是( )A.∠3=∠6B.∠2=∠6C.∠1和∠4是内错角D.∠3和∠5是同位角3.如图，下列说法不正确的是（）A.∠1和∠3是对顶角B.∠1和∠4是内错角C.∠3和∠4是同位角D.∠1和∠2是同旁内角4.如图，在所标识的角中，互为对顶角的两个角是（）A.∠2和∠3B.∠1和∠3C.∠1和∠4D.∠1和∠25.如图，下列说法错误的是( )A.∠1和∠3是同位角B.∠A和∠C是同旁内角C.∠2和∠3是内错角D.∠3和∠B是同旁内角6.如图所示，∠1与∠2不是同位角的是( )7.如图，在下列条件中，能判断AD∥BC的是( )A.∠DAC=∠BCAB.∠DCB+∠ABC=180°C.∠ABD=∠BDCD.∠BAC=∠ACD8.下列说法正确的是( ).A.不相交的两条直线即平行B.过一点有且只有一条直线与已知直线平行C.与同一条直线相交的两直线相交D.若a∥b，b∥c，则a∥b∥c.9.过直线l外一点P作直线l的平行线，下列尺规作图中错误的是（）A. B. C. D.10.如图，AB∥CD，EF∥GH，且∠1=50°，下列结论错误的是( )A.∠2=130°B.∠3=50°C.∠4=130°D.∠5=50°11.下列图形中，已知∠1=∠2,则可得到AB∥CD的是 ( )12.设a,b,c是三条不同的直线，则在下面四个命题中，正确的有( )①如果a与b相交，b与c相交，那么a与c相交；②如果a与b平行，b与c平行，那么a与c平行；③如果a与b垂直，b与c垂直，那么a与c垂直；④如果a与b平行，b与c相交，那么a与c相交.A.4个B.3个C.2个D.1个二、填空题13.如图，按角的位置关系填空：∠A与∠2是_____.14.如图，写出图中的一对内错角 .15.如图，用给定的∠1至∠5完成填空：∠1与是同位角，∠2与是内错角.16.如图，∠ABC与是同位角；∠ADB与是内错角；∠ABC与是同旁内角.17.如图，下列条件中：①∠B+∠BCD=180°；②∠1=∠2；③∠3=∠4；④∠B=∠5；则一定能判定AB∥CD的条件有_____(填写所有正确的序号).18.看图填理由：∵直线AB，CD相交于O,（已知）∴∠1与∠2是对顶角∴∠1=∠2（___________________）∵∠3+∠4=180°（已知）∠1+∠4=180°（__________________）∴∠1=∠3（__________________）∴CD//AB（__________________）三、解答题19.如图，∠1和∠2是哪两条直线被哪一条直线所截形成的？它们是什么角？∠1和∠3是哪两条直线被哪一条直线所截形成的？它们是什么角？20.如图，BE是AB的延长线，指出下面各组中的两个角是由哪两条直线被哪一条直线所截形成的？它们是什么角？（1）∠A和∠D；（2）∠A和∠CBA；（3）∠C和∠CBE.21.如图：已知∠1和∠D互余，CF⊥DF，试证明AB∥CD.22.如图所示,CB⊥AB,CE平分∠BCD,DE平分∠CDA,∠1+∠2=90°,试说明DA⊥AB.23.如图,已知CD⊥DA，DA⊥AB,∠1=∠2,问直线DE与AF是否平行？为什么？24.如图,已知∠1＋∠2=180°,∠DEF=∠A,试判断∠ACB与∠DEB的大小关系，并证明.参考答案25.答案为：D26.答案为：B27.答案为：D28.答案为：A29.答案为：A；30.答案为：B；31.答案为：A32.答案为：D；33.答案为：D.34.答案为：C；35.B36.C37.答案为：同旁内角38.答案为：∠FAC与∠DBA39.答案为：∠4，∠140.答案为：∠EAD，∠DBC，∠EAD，∠DAB，∠BCD.41.答案为：①③④42. 答案为：对顶角相等；平角定义；同角的补角相等；同位角相等，两直线平行．43.解：∠1和∠2是直线EF、DC被直线AB所截形成的同位角，∠1和∠3是直线AB、CD被直线EF所截形成的同位角.44.解：（1）∠A和∠D是由直线AE、CD被直线AD所截形成的，它们是同旁内角；（2）∠A和∠CBA是由直线AD、BC被直线AE所截形成的，它们是同旁内角；（3）∠C和∠CBE是由直线CD、AE被直线BC所截形成的，它们是内错角. 45.解：∵CF⊥DF，∴∠C+∠D=90°，又∠1和∠D互余，即∠1+∠D=90°，∴∠1=∠C，∴AB∥CD.46.证明：∵DE平分∠ADC,CE平分∠BCD,∴∠1=∠ADC,∠2=∠BCD.∵∠1+∠2=90°,∴∠ADC+∠BCD=180°,∴AD∥BC,∴∠A+∠B=180°.∵CB⊥AB,∴∠B=90°,∴∠A=90°,∴DA⊥AB.47.【解答】解：DE∥AF，理由如下：∵CD⊥DA，DA⊥AB，∴∠CDA=∠DAB=90°，∴CD∥AB，∵∠1=∠2，∴∠CDA﹣∠1=∠DAB﹣∠2，∴∠3=∠4，∴DE∥AF．48.解：∠ACB与∠DEB相等，理由如下：证明：∵∠1+∠2=180°（已知），∠1+∠DFE=180°（邻补角定义），∴∠2=∠DFE（同角的补角相等），∴AB∥EF（内错角相等两直线平行），∴∠BDE=∠DEF（两直线平行，内错角相等），∵∠DEF=∠A（已知），∴∠BDE=∠A（等量代换），∴DE∥AC（同位角相等两直线平行），∴∠ACB=∠DEB（两直线平行，同位角相等）．。

七年级下册数学北师大版同步课时作业 2.2探索直线平行的条件(有答案)

2.2探索直线平行的条件一、单选题1.已知直线AB 及一点P ，要过点P 作一直线与AB 平行，那么这样的直线( ) A.有且只有一条 B.有两条C.不存在D.不存在或者只有一条2.有下列语句：①不相交的两条直线叫平行线；②在同一平面内，两条直线的位置关系只有两种：相交和平行； ③如果线段AB 和线段CD 不相交，那么直线AB 和直线CD 平行； ④如果两条直线都和第三条直线平行，那么这两条直线平行； ⑤过一点有且只有一条直线与已知直线平行. 正确的个数是( ) A.1B.2C.3D.43.如图所示，以下几种说法，其中正确的个数是( ) ①3∠和4∠是同位角；②6∠和7∠是同位角； ③4∠和5∠是内错角；④2∠和5∠是同旁内角 ⑤2∠和7∠是同位角；⑥1∠和2∠是同位角A.3B.4C.5D.6 4.如图，下列条件能判定直线12//l l 的是( )A.12∠=∠B.15∠=∠C.13180∠+∠=︒D.35∠=∠5.如图，下列选项中，不可以得到12//l l 的是( )A.12∠=∠B.23∠=∠C.35∠=∠D.34180∠+∠=︒6.如图，直线,a b 被直线c 所截，下列条件中，不能判定//a b 的是( )A.24∠=∠B.14180∠+∠=︒C.54∠=∠D.13∠=∠7.如图，下列条件不能判定//AB CD 的是( )A.B DCE ∠=∠B.A ACD ∠=∠C.180B BCD ∠+∠=︒D.A DCE ∠=∠8.如图，分别将木条,a b 与木条c 钉在一起，若150280∠=︒∠=︒，，要使木条a 与b 平行，则木条a 需要顺时针转动的最小度数为( )A.30°B.50°C.80°D.130°9.如图，下列条件不能判定直线12//l l 的是( )A.13∠=∠B.14∠=∠C.23180∠+∠=︒D.35∠=∠二、填空题10.如图，2∠的内错角是，3∠与B ∠是角，B ∠的同旁内角是 .11.小友把一副三角板摆放在桌面上，如图所示，其中边,BC DF 在同一条直线上，可以得到_______//______，依据是___________.12.如图，已知//175a b ∠=︒，，则2∠=________．三、解答题13.如图，直线AB 和CD 被直线MN 所截.（1）如图①，EG 平分,BEF F ∠平分DFE ∠（平分的是一对同旁内角），则1∠与2∠满足时，//AB CD ；（2）如图②，EG 平分,MEB FH ∠平分DFE ∠（平分的是一对同位角），则1∠与2∠满足时，//AB CD ；（3）如图③，EG 平分,AEF F ∠平分DFE ∠（平分的是一对内错角），则1∠与2∠满足什么条件时，//AB CD ？为什么？参考答案1.答案：D解析：当点P 在直线AB 上时，这样的直线不存在；当点P 在直线AB 外时，这样的直线只有一条. 2.答案：A解析：①不相交的两条直线叫平行线，必须是在同一平面内，故错误；②在同一平面内，不重合的两条直线的位置关系只有两种：相交和平行，故错误； ③线段AB 和线段CD 不相交，直线AB 和直线CD 不一定平行，故错误；④在同一平面内，如果两条直线都和第三条直线平行，那么这两条直线平行，故正确； ⑤过直线外一点有且只有一条直线与已知直线平行，故错误，故选A. 3.答案：B解析：根据同位角、内错角、同旁内角的特征可知，3∠和4∠是同位角，1∠和2∠是同位角，4∠和5∠是内错角，2∠和5∠是同旁内角，6∠和7∠不是同位角，2∠和7∠不是同位角则正确的为③④①，共4个，故选B4.答案：C解析：1∠与3∠是直线12l l ，被3l 所截而成的同旁内角，当13180∠+∠=︒时，12//l l 5.答案：C解析：A 项，12∠∠=，12//l l ∴（同位角相等，两直线平行）； B 项1223l l ∠=∠∴，，（内错角相等，两直线平行）； C 项，由35∠=∠不能判定12l l ； D 项，1234180l l ∠+∠=∴，（同旁内角互补，两直线平行）6.答案：D解析：选项A 符合同位角相等，两直线平行；选项B 符合同旁内角互补，两直线平行；选项C 符合内错角相等，两直线平行；只有选项D 不能判定直线a 与b 平行. 7.答案：D解析：由B DCE ∠=∠，根据同位角相等，两直线平行，即可判定//AB CD . 由A ACD ∠=∠，根据内错角相等，两直线平行，即可判定//AB CD . 由180B BCD ∠+∠=︒，根据同旁内角互补，两直线平行，即可判定//AB CD . 故A,B,C 不符合题意，故选D. 8.答案：A 解析：如图.当150AOB ∠=∠=︒时，//OA b ，∴要使木条a 与b 平行，木条a 需要顺时针转动的最小度数为805030︒-︒=︒.故选A. 9.答案：A解析：A 项，13∠=∠，不能判定直线12//l l ，故此选项符合题意；B 项，14∠=∠，根据内错角相等，两直线平行，可判定直线12//l l ，故此选项不合题意；C 项，23180∠+∠=︒，根据同旁内角互补，两直线平行，可判定直线12//l l ，故此选项不合题意；D 项，35∠=∠，根据同位角相等，两直线平行，可判定直线12//l l ，故此选项不合题意.故选A. 10.答案：C ∠ 内错 1∠或DAB ∠或C ∠解析：2∠和C ∠在被截线AD 和BC 的内部，截线AC 的两侧，故2∠的内错角是C ∠；3∠与B ∠在被截线AE 和BC 的内部，截线AB 的两侧，故3∠与B ∠是内错角；B ∠的同旁内角是1∠或DAB ∠或C ∠11.答案：AC DE ；；内错角相等，两直线平行解析：由90ACB EDF ∠=∠=︒可以得到//AC DE ，依据是内错角相等，两直线平行. 12.答案：105°解析：18075105︒-︒=︒ 13.答案：（1）1290∠+∠=︒. （2）12∠=∠.（3）12∠=∠.理由：EG 平分,AEF FH ∠平分DFE ∠， 21,22,12,,//.AEF DFE AEF DFE AB CD ∴∠=∠∠=∠∠=∠∴∠=∠∴。

七年级数学下册2.2探索直线平行的条件三课后作业新版北师大版.doc

探索平行的条件（三）课后作业一、选择题1、如图，下列条件中能判定直线ll 〃12的是（）A. Z1 = Z2B. Z1 = Z5C. Z l + Z3 = 180°D. Z3=Z52、如图，点E 在AC 的延长线上，下列条件屮能判断AB 〃CD 的是（）A. Z3=Z4B. ZD=ZDCEC. Z 1 = Z2D.ZD+ZACD 二 180° A. Z1 = Z2B. Z2 = Z4C. Z3 = Z4D. Z1 + Z4 二180。

3、对于图中标记的各角, 下列条件能够推理得到3〃b 的是（DA. Z1 = Z3B. Z2 二Z4C. Z1 = Z4D. AB/7CD5、系是（A. 平行B. 垂直C. 相交但不垂直D. 无法确定二、填空题6、如图，己知C、E三点在同一直线上，Zl = 105° , ZA=75° •求证：AB/7CD.证明一：TC、D、E三点在同一直线上,••• Z 1+ Z2 二180。

（平角定义）,一个弯形管道ABCD的弯角ZABC二130。

, ZBCD二50。

,则管道AB与CD的位置关••• Z 2=75 °(又V ZA=75° ,••• Z2=ZA,••• AB // CD ____________________________ .证明二：VC. D、E三点在同一直线上，・・・Z1和ZA是直线AB和直线CD被直线AD所截得到的同旁内角（同旁内角定义）,又••• ZA=75° , Zl = 105° ,・・・ ZA+Z 1 = 75° +105° =180° ,A AB//CD _____________________________________7、如图，两直线a, b被第三条直线c所截，若Zl=50° , Z2 = 130°,则直线a, b的位置关系是________________ .8、如图所示，已知Z1二Z2,则再添上条件_____________________ 可使AB〃CD・9、如图所示，若Z1二ZC二60° , ZD二120。

北师大版七年级下册 2.2 探索直线平行的条件练习题

2.2探索直线平行的条件练习题一、选择题1．如图，下列说法中不正确的是（）A．∠1和∠3是同旁内角B．∠2和∠3是内错角C．∠2和∠4是同位角D．∠3和∠5是对顶角2．如图，下列四个条件中，能判断DE∥AC的是（）A．∠3＝∠4 B．∠1＝∠2 C．∠EDC＝∠EFC D．∠ACD＝∠AFE 3．如图，下列条件：①∠1＝∠3；②∠2+∠4＝180°；③∠4＝∠5；④∠2＝∠3；⑤∠6＝∠2+∠3，其中能判断直线l1∥l2的有（）A．5 个B．4 个C．3 个D．2 个4．如图，能判断AB∥CE的条件是（）A．∠A＝∠ACE B．∠A＝∠ECD C．∠B＝∠BCA D．∠B＝∠ACE 5．如图，下列条件中，一定能判断AB∥CD的是（）A．∠2＝∠3 B．∠1＝∠2 C．∠4＝∠5 D．∠3＝∠4 6．如图，在下列给出的条件中，不能判定AC∥DE的是（）A．∠1＝∠A B．∠A＝∠3 C．∠3＝∠4 D．∠2+∠4＝180°7．如图，有以下四个条件：①∠B+∠BCD＝180°，②∠1＝∠2，③∠3＝∠4，④∠B＝∠5，其中能判定AB∥CD的条件的个数有（）A．1 B．2 C．3 D．48．如图所示，直线a，b与直线c相交，给出下列条件：①∠1＝∠2；②∠3＝∠6；③∠4+∠7＝180°；④∠5+∠3＝180°．其中能判断a∥b的是（）A．①②③④B．①③④C．①③D．②④二、填空题9．如图，按角的位置关系填空：∠A与∠1是；∠A与∠3是；∠2与∠3是．10．如图，∠A＝70°，O是AB上一点，直线OD与AB所夹角∠BOD＝82°，要使OD∥AC，直线OD绕点O按逆时针方向至少旋转度．11．如图，点E在AC的延长线上，对于给出的四个条件：（1）∠3＝∠4；（2）∠1＝∠2；（3）∠A＝∠DCE；（4）∠D+∠ABD＝180°．能判断AB∥CD的有个．12．如图，给出了过直线外一点作已知直线的平行线的方法，其依据是．三、解答题13．如图，AE与CD交于点O，∠A＝50°，OC＝OE，∠C＝25°，求证：AB∥CD．14．如图，点B、E分别在AC、DF上，AF分别交BD、CE于点M、N，∠1＝∠2，∠C＝∠D．求证：AC∥DF．15．填空并完成以下证明：已知，如图，∠1＝∠ACB，∠2＝∠3，FH⊥AB于H，求证：CD⊥AB．证明：FH⊥AB（已知）∴∠BHF＝．∵∠1＝∠ACB（已知）∴DE∥BC（）∴∠2＝．（）∵∠2＝∠3（已知）∴∠3＝．（）∴CD∥FH（）∴∠BDC＝∠BHF＝．°（）∴CD⊥AB．16．如图，已知AF平分∠BAC，DE平分∠BDF，且∠1＝∠2，能判定DF∥AC吗？请说明理由？17．如图，若AB∥CD，∠1＝∠2，∠3＝∠4，AD与BC平行吗？并请说明理由．。

北师大版七年级数学下册同步要点总结(含答案)2.2-探索直线平行的条件.docx

2.2探索直线平行的条件第1课时同位角及平行公理要点感知1.同位角的判定：如图，具有4与这样位置关系的角称为同位角，图中的同位角还有Z3与, Z5 与, Z7 与.2.平行线的判定：两条直线被第三条直线所截，如果同位角,那么这两条直线平行，简称为；同位角,两直线平行.【答案】相等3.平行公理：(1)过直线外一点_________ 直线与这条直线平行.(2)平行于同一条直线的两条直线.【答案】(1)有且只有一条(2)互相平行A./1 = /2B. Z2 = Z6C. Z1 = Z4D. Z3 = Z5 【答案】AA基础训练达标区1.如图，直线AB、被直线EF所截，则ZAMN的同位角是( ).FA. ZCNMB. ZCNFC. ZDNFD. ZDNM【答案】B【答案】D3.如图，下列说法不正确的是（）.A.4与/2是同位角B.N2与Z3是同位角C.Z1与匕3是同位角D.4与Z3不是同位角【答案】C4.如图，可以推理得到AB//CD的条件是（）.A./2,= /RB. Z1 = ZAC. Z3 = ZBD. Z3 = ZA 【答案】C5.下列说法中正确的个数是（）.①过一点一定有一条直线与已知直线平行；②一条直线的平行线有无数条；③两条不相交的直线叫做平行线；④与一条直线平行的直线只有一条A. 0个B. 1个C. 2个D. 3个【答案】B6.如图所示，将一张长方形纸对折两次，则产生的折痕与折痕间的位置关系是（【答案】A 7. 直线/同侧有A 、B 、C 三点，若A 、B 两点确定的直线〈与3、C 两点确定的直线A 都与/平行, 则A 、B 、C 三点,其理论依据是.【答案】共线，过直线处一点有且只有一条直线与这条直线平行.8. 如图，三角形ABC 中，已知ZC = 45° , ZADB = 9Q° ,庞为匕4DB 的平分线，与CA 平行吗？说明你的理由.【答案】解：DE//CA.因为ZADB = 90° , QE 平分匕所以ZBDE = -ZADB = 45。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

《2.2 探索直线平行的条件》习题（三）
1．如图所示，CE与CD相交于点C，AB平分∠EAD，∠C=∠D，∠EAD=∠C+∠D，试说明AB∥CD的理由．
2．如图所示，BE是∠ABD的平分线，DE是∠BDC的平分线，且∠1+∠2=90°，那么直线AB，CD的位置关系如何？并说明理由．
3．物理实验发现：光线从空气射入玻璃中，会发生折射现象，光线从玻璃射入空气中，同样也会发生折射现象．如图所示的是光线从空气射入玻璃中，再从玻璃射入空气中的示意图，已知∠1=∠2，∠3=∠4，那么光线AB与CD是否平行？并说明理由．
4．工人师傅做了一个如图所示的零件，形状近似“V”形，他先把材料弯成一个40°的锐角，然后准备在A处第二次加工拐弯，请你帮他计算一下，他应该怎样弯，才能保证弯过来的部分AD与BC保持平行．
5．如图所示，点E在AD的延长线上，下列条件中能判断BC∥AD的是（）
A．∠3=∠4 B．∠A+∠ADC=180°C．∠1=∠2 D．∠A=∠5
6．如图所示，请填写一个你认为恰当的条件：_________，使AD∥BC．
7．如图所示，已知∠B=40°，∠BCD=71°，∠D=31°，试探究AB与DE的位置关系．
8．如图所示，已知∠1=∠2，•请你添上一个适当的条件，使AB∥CD．。