初二一次函数动点经典题型(全部题型)
一次函数之动点问题 (习题及答案).

一次函数之动点问题(习题)1.如图,在平面直角坐标系中,四边形AOBC 是正方形,已知点A 的坐标为(0,2),点D 在x 轴正半轴上,B 是线段OD 的中点,连接CD.动点P 从点O 出发,以每秒1 个单位长度的速度沿O→A→C→B 的路线向终点B 运动,动点Q 从点O 同时出发,以相同的速度沿O→B→D→B 的路线向终点B 运动.设△OPQ 的面积为S,点P 运动的时间为t 秒(0<t<6).求S 与t 之间的函数关系式,并写出自变量t 的取值范围.2 2. 如图,直线 y =x +4 与 x 轴、y 轴分别交于点 A ,B ,直线 y =-x +b过点 B ,且与 x 轴交于点 C .动点 P 从点 C 出发,沿 CA 方向以每秒 1 个单位长度的速度向终点 A 运动,动点 Q 从点 A 同 时出发,沿折线 AB -BC 以每秒 个单位长度的速度向终点 C 运动.设点 P 运动的时间为 t 秒.(1) 设△CPQ 的面积为 S ,求 S 与 t 之间的函数关系式,并写出自变量 t 的取值范围;(2) 当 t = 时,PQ ∥AB ;(3) 当 0<t ≤4 时,若△APQ 是等腰三角形,求 t 的值.⎨ 【参考答案】⎧ 1 t 2(0 < t ≤2) 2 1. S = ⎪ 2 < t ≤ 4) . ⎨t ( ⎪ 1 2⎪ t - 7t + 24(4 < t < 6) ⎩ 2⎧ 1 t 2(0 < t ≤ 4) 2. (1) S = ⎪ 2 ⎪- 1 ⎩ 2(2) 16 ;3; t 2 + 4t (4 < t < 8) (3)t 的值为8 - 8 , 8 或 4. 32 ⎪。
初二数学期末复习一次函数的应用—动点问题附练习及答案

课 题一次函数的应用——动点问题教学目标1.学会结合几何图形的性质,在平面直角坐标系中列函数关系式。
2.通过对几何图形的探究活动和对例题的分析,感悟探究动点问题列函数关系式的方法,提高解决问题的能力。
重点、难点理解在平面直角坐标系中,动点问题列函数关系式的方法。
小结:1用函数知识求解动点问题,需要将问题给合几何图形的性质,建立函数模型求解,解要符合题意,要注意数与形结合。
2.以一次函数为背景的问题,要充分运用方程、转化、函数以及数形结合等思想来研究解决,注意自变量的取值围例题1:如图,直线1l 的解析表达式为33y x =-+,且1l 与x 轴交于点D ,直线2l 经过点A B ,,直线1l ,2l 交于点C .〔1〕求点D 的坐标;〔2〕求直线2l 的解析表达式;〔3〕求ADC △的面积;〔4〕在直线2l 上存在异于点C 的另一点P ,使得ADP △与ADC △的面积相等,请直接..写出点P 的坐标. 例题2:如图,在平面直角坐标系,点A 〔0,6〕、点B 〔8,0〕,动点P 从点A 开场在线段AO 上以每秒1个单位长度的速度向点O 移动,同时动点Q 从点B 开场在线段BA 上以每秒2个单位长度的速度向点A 移动,设点P 、Q 移动的时间为t 秒.(1) 求直线AB 的解析式;(2) 当t 为何值时,△APQ 的面积为524个平方单位.当堂稳固:如图,直线6y kx =+与*轴、y 轴分别交于点E 、F ,点E 的坐标为〔-8,0〕,点A 的坐标为〔-6,0〕。
〔1〕求k 的值;〔2〕假设点P 〔x ,y 〕是第二象限的直线上的一个动点,在点P 的运动过程中,试写出△OPA 的面积S 与*的函数关系式,并写出自变量*的取值围;〔3〕探究:当点P 运动到什么位置时,△OPA 的面积为278,并说明理由。
课后检测:1、如果一次函数y=-*+1的图象与*轴、y 轴分别交于点A 点、B 点,点M 在*轴上,并且使以点A 、B 、M 为顶点的三角形是等腰三角形,则这样的点M 有〔〕。
(完整版)一次函数动点问题

一次函数动点问题1.模型介绍:古希腊有一个著名的“将军饮马问题”,大致内容如下:古希腊一位将军,每天都要巡查河岸侧的两个军营A、B,他总是先去 A 营,再到河边饮马,之后再去 B 营,如图①,他时常想,怎么走才能使每天的路程之和最短呢?大数学家海伦曾用轴对称的方法巧妙的解决了这问题如图②,作B关于直线l的对称点B′,连接AB′与直线l交于点C,点C就是所求的位置.请你在下列的阅读、应用的过程中,完成解答.(1)理由:如图③,在直线L 上另取任一点C′,连接AC′,BC′,B′C,′ ∵直线l 是点B,B′的对称轴,点C,C′在l 上∴ CB= ,C′B=∴ AC+CB=AC+CB′=.在△ AC′B中′,∵ AB′<AC′+C′B,′∴AC+CB<AC′+C′B即′AC+CB 最小归纳小结:本问题实际是利用轴对称变换的思想,把A、B 在直线的同侧问题转化为在直线的两侧,从而可利用“两点之间线段最短”,即转化为“三角形两边之和大于第三边”的问题加以解决(其中C为AB′与l的交点,即A、C、B′三点共线).本问题可拓展为“求定直线上一动点与直线外两定点的距离和的最小值”问题的数学模型.(2)模型应用如图④,正方形ABCD的边长为2,E为AB的中点,F是AC上一动点.求EF+FB 的最小值分析:解决这个问题,可以借助上面的模型,由正方形的对称性可知,B与 D 关于直线AC对称,连结ED 交AC于F,则EF+FB的最小值就是线段的长度,EF+FB的最小值是如图⑥,一次函数y=﹣2x+4 的图象与x,y 轴分别交于A,B两点,点O 为坐标原点,点C与点D分别为线段OA,AB的中点,点P为OB上一动点,求:PC+PD 的最小值,并写出取得最小值时P 点坐标.2.已知一次函数图象经过点A(3,5)和点B(﹣4,﹣9)两点,①求此一次函数的解析式;②若点(a,2)在该函数的图象上,试求 a 的值.③若此一次函数的图象与x轴交点C,点P(m,n)是图象上一个动点(不与点C重合),设△ POC的面积是S,试求S关于m 的函数关系式.3.已知函数y=kx+b 的图象经过点A(4,3)且与一次函数y=x+1 的图象平行,点B(2,m)在一次函数y=kx+b 的图象上(1)求此一次函数的表达式和m 的值?(2)若在x 轴上有一动点P(x,0),到定点A(4,3)、B(2,m)的距离分别为PA和PB,当点P 的横坐标为多少时,PA+PB的值最小.4.已知:一次函数图象如图:(1)求一次函数的解析式;(2)若点P为该一次函数图象上一动点,且点A为该函数图象与x 轴的交点,若S△OAP=2,求点P 的坐标.5.阅读下面的材料:在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线给出它们平行的定义:设一次函数y=k1x+b1(k1≠ 0)的图象为直线l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2,若k1=k2,且b1≠b2,我们就称直线l1 与直线l2互相平行.解答下面的问题:(1)已知正比例函数y=﹣x 的图象为直线l1,求过点P(1,3)且与已知直线l1 平行的直线l2 的函数表达式;(2)设直线l2分别与y轴、x轴交于点A、B,求l1和l2两平行线之间的距离;(3)若Q为OA上一动点,求QP+QB的最小值时Q点的坐标为.(4)在x轴上找一点M,使△ BMP为等腰三角形,求M 的坐标.(直接写出答案)6.阅读下面的材料:在平面几何中,我们学过两条直线互相垂直的定义,下面就两个一次函数的图象所确定的两条直线,给出它们相互垂直的定义:设一次函数y=k1x+b1(k1≠ 0)的直线为l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2.若k1?k2=﹣1,我们就称直线l1 与直线l2 相互垂直,现请解答下面的问题:已知直线l 与直线y=﹣x﹣1 互相垂直,且直线l的图象过点P(﹣1,4),且直线l分别与y轴、x轴交于A、B两点.(1)求直线l 的函数表达式;(2)若点 C 是线段AB 上一动点,求线段OC长度的最小值;(3)若点Q是AO上的一动点,求△ BPQ周长的最小值,并求出此时点Q的坐标;(4)在(3)的条件下,若点P关于BQ的对称点为P′,请求出四边形ABOP′的面积.一次函数动点问题参考答案与试题解析一.解答题(共 6 小题)1.模型介绍:古希腊有一个著名的“将军饮马问题”,大致内容如下:古希腊一位将军,每天都要巡查河岸侧的两个军营A、B,他总是先去 A 营,再到河边饮马,之后再去 B 营,如图①,他时常想,怎么走才能使每天的路程之和最短呢?大数学家海伦曾用轴对称的方法巧妙的解决了这问题如图②,作B关于直线l的对称点B′,连接AB′与直线l交于点C,点C就是所求的位置.请你在下列的阅读、应用的过程中,完成解答.(1)理由:如图③,在直线L 上另取任一点C′,连接AC′,BC′,B′C,′ ∵直线l 是点B,B′的对称轴,点C,C′在l 上∴CB= CB' ,C′B= C'B'∴ AC+CB=AC+CB′=AB' .在△ AC′B中′,∵ AB′<AC′+C′B,′∴AC+CB<AC′+C′B即′AC+CB 最小归纳小结:本问题实际是利用轴对称变换的思想,把A、B 在直线的同侧问题转化为在直线的两侧,从而可利用“两点之间线段最短”,即转化为“三角形两边之和大于第三边”的问题加以解决(其中C为AB′与l的交点,即A、C、B′三点共线).本问题可拓展为“求定直线上一动点与直线外两定点的距离和的最小值”问题的数学模型.(2)模型应用如图④,正方形ABCD的边长为2,E为AB的中点,F是AC上一动点.求EF+FB 的最小值分析:解决这个问题,可以借助上面的模型,由正方形的对称性可知,B与 D 关于直线AC 对称,连结ED交AC于F,则EF+FB 的最小值就是线段DE 的长度,EF+FB的最小值是.如图⑤,已知⊙ O的直径CD为4,∠ AOD的度数为60°,点B是的中点,在直径CD 上找一点P,使BP+AP 的值最小,则BP+AP 的最小值是 2 ;如图⑥,一次函数y=﹣2x+4 的图象与x,y 轴分别交于A,B两点,点O 为坐标原点,点C与点D分别为线段OA,AB的中点,点P为OB上一动点,求:PC+PD 的最小值,并写出取得最小值时P 点坐标.【解答】解:(1)理由:如图③,在直线L 上另取任一点C′,连接AC′,BC′,B′C,′ ∵直线l 是点B,B′的对称轴,点C,C′在l 上∴ CB=CB,' C′B=C'B'∴AC+CB=AC+CB′=A.B'在△ AC′B中′,∵ AB′<AC′+C′B,′∴AC+CB<AC′+C′B即′AC+CB 最小故答案为:CB',C'B',AB';(2)模型应用①解决这个问题,可以借助上面的模型,由正方形的对称性可知,B与D 关于直线AC对称,连结ED交AC于F则EF+FB的最小值就是线段DE的长度,EF+FB的最小值是.在正方形ABCD中,AB=AD=2,∠BAD=9°0 ∵点E是AB 中点,∴AE=1,根据勾股定理得,DE= ,即:EF+FB的最小值,故答案为:DE,;②如图⑤,由圆的对称性可知,A与A'关于直径CD对称,连结A'B交CD于F,则AE+EB 的最小值就是线A'BE的长度,∴∠ AOD=∠A'OD=60°∵点 B 是的中点,∴∠ AOB=∠BOD= ∠AOD=3°0,∴∠ A'OB=90°∵⊙ O的直径为4,∴OA=OA'=OB=2,在Rt△A'OB中,A'B=2 ,∴ BP+AP的最小值是 2 .故答案为 2 ,③如图⑥,由平面坐标系中的对称性可知,C与C'关于直径y轴对称,连结C'D交y轴于P,则PC+PD的最小值就是线C'D 的长度,∵一次函数y=﹣2x+4的图象与x,y 轴分别交于A,B两点,∴A(2,0),B (0,4),∴C(1,0),D(1,2),∵C与C'关于直径y 轴对称,∴C'(﹣1,0),∴ C'D= =2 ,∴ PC+PD的最小值为 2 ,∵C'(﹣1,0),D(1,2),∴直线C'D 的解析式为y=x+1,∴P(0,1).2.已知一次函数图象经过点A(3,5)和点B(﹣4,﹣9)两点,①求此一次函数的解析式;②若点(a,2)在该函数的图象上,试求 a 的值.③若此一次函数的图象与x轴交点C,点P(m,n)是图象上一个动点(不与点C重合),设△ POC的面积是S,试求S关于m 的函数关系式.解答】解:①设一次函数解析式为y=kx+b,依题意,得解得,次函数解析式为y=2x﹣1;②将点(a,2)代入y=2x﹣1 中,得2a﹣1=2,③由 y=2x ﹣1,令 y=0得 x= , ∴C ( 又∵点 P(m ,n )在直线 y=2x ﹣1 上, ∴ n=2m ﹣1,3.已知函数 y=kx+b 的图象经过点A 43 y=x+1 的图象平行,点 B ( 2, m )在一次函数 y=kx+b 的图象上1)求此一次函数的表达式和 m 的值?2)若在 x 轴上有一动点 P (x ,0),到定点 A (4,3)、B (2,m )的距离分别 为 PA 和 PB ,当点 P 的横坐标为多少时, PA+PB 的值最小.解答】 解:(1)∵函数 y=kx+b 的图象经过点 A (4,3)且与一次函数 y=x+1 的图象平行,,解得:∴一次函数的表达式为 y=x ﹣1. 当 x=2 时, m=x ﹣1=2﹣ 1=1, ∴m 的值为1.(2)作点 B 关于x 轴的对称点 B ′,连接 AB ′交x 轴于点 P ,此时PA+PB 取最小值, 如图所示. ∵点 B 的坐标为( 2,1), ∴点 B ′的坐标为( 2,﹣ 1). 设直线 AB ′的表达式为 y=ax+c , 将( 2,﹣1)、(4,3)代入 y=ax+c ,,解得:∴直线 AB ′的表达式为 y=2x ﹣5. 当 y=0 时, 2x ﹣ 5=0,,0),∴S= × ×|n|= | (2m ﹣1)|=|m﹣4.已知:一次函数图象如图: 1)求一次函数的解析式;2)若点 P 为该一次函数图象上一动点,且点 A 为该函数图象与 x 轴的交点,若 S △OAP =2,求点 P 的坐标.解答】 解:(1)设一次函数解析式为 y=kx+b ,所以一次函数解析式为 y=﹣x+1;(2)当 y=0时,﹣ x+1=0,解得 x=1,则 A ( 1, 0), 设 P (t ,﹣ t+1), 因为 S △OAP =2,所以 ×1×|﹣t+1|=2,解得 t=﹣3或t=5, 所以 P 点坐标为(﹣ 3,4)或( 5,﹣ 4).5.阅读下面的材料:在平面几何中, 我们学过两条直线平行的定义. 下面就两个一次函数的图象所确 定的两条直线给出它们平行的定义:设一次函数 y=k 1x+b 1(k 1≠ 0)的图象为把(﹣ 2,3)、(2, 分别代入得,解得PA+PB 的值最小.P 的横坐标为 ﹣1)直线l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2,若k1=k2,且b1≠b2,我们就称直线l1 与直线l2互相平行.解答下面的问题:(1)已知正比例函数y=﹣x 的图象为直线l1,求过点P(1,3)且与已知直线l1 平行的直线l2 的函数表达式;(2)设直线l2分别与y轴、x轴交于点A、B,求l1和l2两平行线之间的距离;(3)若Q为OA上一动点,求QP+QB的最小值时Q点的坐标为Q(0,).(4)在x轴上找一点M,使△ BMP为等腰三角形,求M 的坐标.(直接写出答案)【解答】解:(1)根据正比例函数y=﹣x的图象为直线l1,设直线l2的函数表达式为y=﹣x+b,把P(1,3)代入得:3=﹣1+b,即b=4,则过点P(1,3)且与已知直线l1 平行的直线l2的函数表达式为y=﹣x+4;(2)过O作ON⊥AB,如图1所示,ON为l1和l2两平行线之间的距离,对于直线y=﹣x+4,令x=0,得到y=4;令y=0,得到x=4,∴ A(0,4),B(4,0),即OA=OB=4,∵△ ABC为等腰直角三角形,∴AB= =4 ,且ON 为斜边上的中线,∴ ON= AB=2 ,则l1 和l2 两平行线之间的距离为 2 ;(3)找出B关于y轴的对称点B′(﹣4,0),连接PB′,与y轴交于点Q,连接PQ,此时QP+QB 最小,设直线B′P的解析式为y=mx+n,把B′和P 坐标代入得:,解得:m= ,n= ,∴直线B′P的解析式为y= x+ ,令x=0,得到y= ,即Q(0,);故答案为:Q(0,);(4)如图 2 所示,分三种情况考虑:当PM1=PB时,由对称性得到M1(﹣2,0);当PM2=BM2时,M2 为线段PB垂直平分线与x轴的交点,∵直线PB的解析式为y=﹣x+4,且线段PB中点坐标为( 2.5, 1.5),∴线段PB垂直平分线解析式为y﹣1.5=x﹣2.5,即y=x﹣1,令y=0,得到x=1,即M 2(1,0);当PB=M3B= =3 时,OM3=OB+BM3=4+3 ,此时M 3(4﹣3 ,0),M 3(4+3 ,0).综上,M的坐标为(﹣2,0)或(1,0)或(4﹣ 3 ,0)或(4+3 ,0).6.阅读下面的材料:在平面几何中,我们学过两条直线互相垂直的定义,下面就两个一次函数的图象所确定的两条直线,给出它们相互垂直的定义:设一次函数y=k1x+b1(k1≠ 0)的直线为l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2.若k1?k2=﹣1,我们就称直线l1 与直线l2 相互垂直,现请解答下面的问题:已知直线l 与直线y=﹣x﹣1 互相垂直,且直线l的图象过点P(﹣1,4),且直线l分别与y轴、x轴交于A、B两点.(1)求直线l 的函数表达式;(2)若点 C 是线段AB 上一动点,求线段OC长度的最小值;(3)若点Q是AO上的一动点,求△ BPQ周长的最小值,并求出此时点Q的坐标;(4)在(3)的条件下,若点P关于BQ的对称点为P′,请求出四边形ABOP′的面积.【解答】解:(1)设直线l 的解析式为y=kx+b,∵直线l 与直线y=﹣x﹣1 互相垂直,∴﹣k=﹣1,解得k=2,∵直线l 的图象过点P(﹣1,4),∴﹣k+b=4,即﹣2+b=4,解得b=6,∴直线l 的解析式为y=2x+6;(2)如图1,过O作OC⊥AB 于点C,在y=2x+6 中,令x=0 可得y=6,令y=0 可求得x=﹣3,∴A(0,6),B(﹣3,0),∴OA=6,OB=3∴ AB= =3 ,∵ AB?OC= OA?OB,∴ 3 OC=3×6,∴ OC= ,即线段OC长度的最小值为;(3)如图2,作点P关于y轴的对称点P″,连接BP″交y轴于点Q,过P″作P″G⊥x 轴于点G,则PQ=P″Q,∴PQ+BQ=BQ+QP″,∵点B、Q、P″三点在一条线上,∴ BQ+PQ最小,∵P(﹣1,4),∴P″(1,4),∴ P″G=,4 OG=1,∴BG=BO+OG=4=″P G,∴∠ OBQ=4°5,BP″=4 ,∴ OQ=BO=3,∴ Q点坐标为(0,3),又BP= =2 ,此时△ BPQ的周长=BP+BP″=4 +2 ;(4)由(3)可知∠ OBQ=∠OQB=4°5,∴∠PQA=∠P″QA=45°,∴PQ⊥BQ,如图3,延长PQ到点P′,使PQ=P′Q,则P′即为点P 关于BQ的对称点,过P′作由(3)可知PQ=Q′P = ,∴QH=H′P =1,∴OH=OQ﹣QH=3﹣1=2,∴ S四边形ABO′P=S△AOB+S△AOP′= ×6×3+ × 6× 1=12,四边形△ △即四边形ABOP′的面积为12.。
一次函数动点综合题(含解析)

一次函数综合题(含解析)一.解答题(共12小题)1.求出将直线y=﹣x+绕点A(2,1)顺时针旋转45度得到的直线表达式.2.如图1,一次函数y=﹣2x+2的图象与y轴交于点A,与x轴交于点B,过点B 作线段BC⊥AB且BC=AB,直线AC交x轴于点D.(1)求A,B两点的坐标;(2)求点C的坐标,并直接写出直线AC的函数关系式;(3)若点P是图1中直线AC上的一点,连接OP,得到图2.请在下面的A,B两题中任选一题解答,我选择.A.当点P的纵坐标为3时,求△AOP的面积;B.当点P在第二象限,且到x轴,y轴的距离相等时,求△AOP的面积;(4)若点Q是图1中坐标平面内不同于点B、点C的一点.请在下面的A,B两题中任选一题解答,我选择A.当以点B,D,Q为顶点的三角形与△BCD全等时,直接写出点Q的坐标;B.当以点C,D,Q为顶点的三角形与△BCD全等时,直接写出点Q的坐标.3.如图,直线OB是一次函数y=2x的图象,点A的坐标是(0,2),点C在直线OB上且△ACO为等腰三角形,求C点坐标.4.如图,直线y=4﹣x与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于点D.(1)当点M在AB上运动时,则四边形OCMD的周长=.(2)当四边形OCMD为正方形时,将正方形OCMD沿着x轴的正方向移动,设平移的距离为a(0<a≤4),在平移过程中,当平移距离a为多少时,正方形OCMD的面积被直线AB分成1:3两个部分?5.如图,在平面直角坐标系中,直线AB交x轴于点A(﹣4,0),交y轴于点B (0,2),P为线段OA上一个动点,Q为第二象限的一个动点,且满足PQ=PA,OQ=OB.(1)求直线AB的函数关系式;(2)若△OPQ为直角三角形,试求点P的坐标,并判断点Q是否在直线AB上.6.矩形ABCD在如图所示的直角坐标系中,点A的坐标为(0,3),BC=2AB、直线l经过点B,交AD边于点P1,此时直线l的函数表达式是y=2x+1.(1)求BC、AP1的长;(2)沿y轴负方向平移直线l,分别交AD、BC边于点P、E.①当四边形BEPP1,是菱形时,求平移的距离;②设AP=m,当直线l把矩形ABCD分成两部分的面积之比为3:5时,求m的值.7.如图,平面直角坐标系中,直线AB:y=﹣x+b交y轴于点A(0,4),交x轴于点B.(1)求直线AB的表达式和点B的坐标;(2)直线l垂直平分OB交AB于点D,交x轴于点E,点P是直线l上一动点,且在点D的上方,设点P的纵坐标为n.①用含n的代数式表示△ABP的面积;②当S=8时,求点P的坐标;△ABP③在②的条件下,以PB为斜边在第一象限作等腰直角△PBC,求点C的坐标.8.如图,点A的坐标是(﹣2,0),点B的坐标是(6,0),点C在第一象限内且△OBC为等边三角形,直线BC交y轴于点D,过点A作直线AE⊥BD,垂足为E,交OC于点F.(1)求直线BD的函数表达式;(2)求线段OF的长;(3)连接BF,OE,试判断线段BF和OE的数量关系,并说明理由.9.在直角坐标系xOy中,点A、点B、点C坐标分别为(4,0)、(8,0)、(0,﹣4).(1)求过B、C两点的一次函数解析式;(2)若直线BC上有一动点P(x,y),以点O、A、P为顶点的三角形面积和以点O、C、P为顶点的三角形面积相等,求P点坐标;(3)若y轴上有一动点Q,使以点Q、A、C为顶点的三角形为等腰三角形,求Q点坐标.10.已知:如图,平面直角坐标系xOy中,点A、B的坐标分别为A(4,0),B (0,﹣4),P为y轴上B点下方一点,PB=m(m>0),以AP为边作等腰直角三角形APM,其中PM=PA,点M落在第四象限.(1)求直线AB的解析式;(2)用m的代数式表示点M的坐标;(3)若直线MB与x轴交于点Q,判断点Q的坐标是否随m的变化而变化,写出你的结论并说明理由.。
一次函数(压轴专练)(十大题型)(原卷版)—2024-2025学年八年级数学上册(北师大版)

一次函数(压轴专练)(十大题型)(1)求直线AB 的解析式;(2)作直线OC ,当点C 运动到什么位置时,AOB V 的面积被直线OC 分成1:2的两部分;(3)过点C 的另一直线CD 与y 轴相交于D 点,是否存在点C 使BCD △与AOB V 全等?若存在,求出点坐标;若不存在,说明理由.(1)求直线2l的函数表达式;(2)求四边形ABCD的面积;(3)在直线2l上是否存在点不存在,请说明理由.题型2:最值问题3.如图,直线392y x =-+交y 轴于点A ,交x 轴于点B ,点()4,C t 在第四象限,点(,0)P m 在线段OB 上.连接OC ,BC ,过点P 作x 轴的垂线,交边AB 于点E ,交折线段OCB 于点F .(1)求点A ,B 的坐标;(2)设点E ,F 的纵坐标分别为1y ,2y ,当04m ££时,12y y -为定值,求t 的值;(3)在(2)的条件下,分别过点E ,F 作EG ,FH 垂直于y 轴,垂足分别为点G ,H ,当06m ££时,求长方形EGHF 周长的最大值.(1)B 的坐标为_________,线段OA 的长为_________.(2)求直线CD 的解析式和点D 的坐标.(3)如图(2),点M 是线段CE 上一动点(不与点C ,E 重合),ON ①在点M 移动过程中,线段OM 与ON 数量关系是否不变,并证明;②连结MN ,当DMN V 面积最大时,求OM 的长度和DMN V 的面积.(1)求直线CD 解析式;(2)如图2,点M 是线段CE 上一动点(不与点C 、E 重合),ON ①点M 移动过程中,线段OM 与ON 数量关系是否不变,并证明;②当OMN V 面积最小时,求点M 的坐标和OMN V 面积.(1)若点E 坐标为2,3n æöç÷èø.ⅰ)求m 的值;ⅱ)点P 在直线2l 上,若3AEP BDE S S =V V ,求点P 的坐标;(2)点F 是线段CE 的中点,点G 为y 轴上一动点,是否存在点形.若存在,求出m 的值,若不存在,请说明理由.(1)经过点A 且与直线33y x =-平行的直线交x 轴于点B ,试求B (2)如图1,若()4,0B ,过()1,0M 的直线与直线AB 所夹锐角为45(3)如图2,在(1)的条件下,现有点(),C m n 在线段AB 上运动,点的中点.直接写出当C 从点A 开始运动,到点B 停止运动,M 点的运动路径长为(1)如图1,求A 、C 两点坐标.(2)点P 是AOC V 内一点,点P 的坐标为(,25)m m -+,点Q 在第二象限,连接PC ,QC ,PCQ Ð请用含m 的式子表示点Q 的坐标.(3)在(2)的条件下,点B 在x 轴上与点A 关于y 轴对称,过Q 做QE OC ⊥于点E ,延长延长MP 交x 轴于点N ,连接BM ,取BM 的中点G ,连接QG 并延长交x 轴于点H ,当QM 点P 的坐标.(1)求点A ,C 的坐标.(2)现有一动点P 沿折线O C B O ®®®以2个单位长度/秒的速度运动,运动时间为①当OAP △为等腰三角形时,求出所有满足条件的t 的值.②如图2,已知x 轴正半轴上有一动点Q ,当点P 在线段OB 上运动时,连接线CQ 的对称图形CQA ¢V ,作CPB △关于直线CP 的对称图形CPB ¢V ,射线10.在平面直角坐标系中,点O 为坐标原点,直线()40y kx k k =-¹交x 轴的正半轴于点A ,交y 轴的正半轴于点,B AB =.(1)求OB 的长;(2)如图1,点C 在x 轴的负半轴上,点D 在AB 上,连接CD 交y 轴于点E ,点E 为CD 的中点,设点C 的横坐标为,t ACD △的面积为S ,求S 与t 的函数解析式;(3)如图2,在(2)的条件下,将射线EC 绕点E 顺时针旋转45°,交x 轴的负半轴于点F ,连接BF ,若2BFE BED OEF Ð+Ð=Ð,求S 的值.11.如图,平面直角坐标系中,直线4y x =-+分别交x 、y 轴于A 、B 两点,点P 为线段AB 的中点.(1)直接写出点P的坐标;⊥交y轴正半轴于点(2)如图1,点C是x轴负半轴上的一动点,过点P作PD PCÐ的度数;分别是CD、OB的中点,连接MN,求MNO(3)如图2,点Q是x轴上的一个动点,连接PQ.把线段PQ绕点Q顺时针旋转+的值最小时,求此时点T的坐标.OT.当PT OT(1)则a = ,b = ,c = ;(2)如图1,在x 轴上是否存在点D ,使ACD 的面积等于V ABC 的面积?若存在,请求出点存在,请说明理由;(3)如图2,连接OC 交AB 于点M ,是否存在一点()0,N n 在y 轴上,使得积,若有,请求出n 的取值范围;若没有,请说明理由.(1)求点A的坐标;V(2)若点C在第二象限,ACD①求点C的坐标;x+>②直接写出不等式组4V沿x轴平移,点③将CAD(1)若33k =-,点P 是直角NOM △的“近N 点”,则OP 的长度可能是①1 ;②2 ;③3 ;④23(2)若线段MN 上的所有点(不含M 和)N 都是直角NOM △的“(3)当1k >时,若一次函数y x k =+与2y kx =+的交点恰好是直角值范围是______ .(1)当OA OB =时,求点A 坐标及直线l 的解析式;(2)在(1)的条件下,如图2所示,设Q 为AB 延长线上的一点,作直线OQ ,过AB 、两点分别作于M ,BN OQ ⊥于N ,若8AM =,求BN 的长.(3)当m 取不同值时,点B 在y 轴正半轴上运动,分别以OB AB 、为边,点B 为直角顶点在第一、二象限内作等腰直角OBF V 和等腰直角ABE V ,连接EF 交y 轴于点P ,如图3,问:当点B 在y 轴正半轴上运动时,试猜想PB 的长度是否为定值?若是,请求出其值;若不是,说明理由.17.定义:在平面直角坐标系中,我们称直线(y ax b a =+,b 为常数)是点(,)P a b 的关联直线,点(,)P a b 是直线y ax b =+的关联点;特别地,当0a =时,直线y b =的关联点为(0,)P b .如图,直线:24AB y x =-+与x 轴交于点A ,与y 轴交于点B .【定义辨析】(1)直线AB 的关联点的坐标是( )A .(0,0)B .(0,4)C .(2,0)D .(2,4)-【定义延伸】(2)点A 的关联直线与直线AB 交于点C ,求点C 的坐标;;【定义应用】(3)点(1,)K m 的关联直线与x 轴交于点E ,=45ABE а,求m 的值.18.在平面直角坐标系xOy 中,对于任意两点()111P x y ,与()222P x y ,的“非常距离”,给出如下定义:若1212x x y y -³-,则点1P 与点2P 的“非常距离”为12x x -;若1212x x y y -<-,则点1P 与点2P 的“非常距离”为12y y -.例如:点()112P ,,点()235P ,,因为1325-<-,所以点1P 与点2P 的“非常距离”为253-=,也就是图1中线段1PQ 与线段2P Q 长度的较大值(点Q 为垂直于y 轴的直线1PQ 与垂直于x 轴的直线2P Q 的交点).(1)已知点102A æö-ç÷èø,B 为y 轴上的一个动点.①若点A 与点B 的“非常距离”为2,直接写出点B 的坐标;②直接写出点A 与点B 的“非常距离”的最小值;(2)已知点3,34C x x æö+ç÷èø是直线m 上的一个动点.①如图2,点D 的坐标是()01,,求点C 与点D 的“非常距离”的最小值及相应的点C 的坐标;②如图3,正方形FGMN 的边长为1,边FG 在x 轴上,点E 是正方形FGMN 边上的一个动点,记d 为点C 与点E 的“非常距离”的最小值,当正方形FGMN 沿x 轴平移,在平移过程中点G 的横坐标大于等于0,且小于等于9时,直接写出d 的最大值.20.“一方有难、八方支援”,在某地发生自然灾害后,某公司响应“助力乡情献爱心”活动,捐出了九月份的全部利润.已知该公司九月份只售出了A、B、C三种型号的产品若干件,每种型号产品不少于4件,九月份支出包括这批产品进货款20万元和其他各项支出1.9万元(含人员工资和杂项开支).这三种产品的售价和进价如下表,人员工资1y(万元)和杂项支出2y(万元)分别与销售总量x(件)成一次函数关系(如图).型号A B C进价(万元/件)0.50.80.7售价(万元/件)0.8 1.20.9(1)写出1y与x的函数关系式为______;九月份A、B、C三种型号产品的销售的总件数为_____件.(2)设公司九月份售出A种产品n件,九月份总销售利润为W(万元),求W与n的函数关系式并直接写出n的取值范围;(3)请求出该公司这次爱心捐款金额的最大值.21.一队学生从学校出发去劳动基地,行进的路程与时间的函数图象如图所示,队伍走了0.8小时后,队伍中的通讯员按原路加快速度返回学校取材料.通讯员经过一段时间回到学校,取到材料后立即按返校时加快的速度追赶队伍,并比学生队伍早18分钟到达基地.如图,线段OD表示学生队伍距学校的路程y(千米)与时间x(小时)之间的函数关系,折线OABC表示通讯员距学校的路程y(千米)与时间x(小时)之间的函数关系,请你根据图象信息,解答下列问题:(1)学校与劳动基地之间的距离为________千米;(2)a=________,B点的坐标是________.(3)若通讯员与学生队伍的距离不超过3千米时能用无线对讲机保持联系,请你直接写出通讯员离开队伍后他们能用对讲机保持联系的时间的取值范围.。
一次函数之动点问题综合测试(北师版)(含答案)
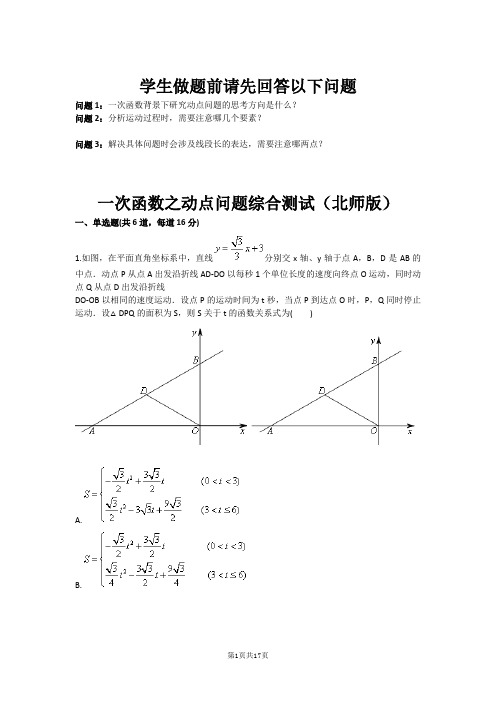
学生做题前请先回答以下问题问题1:一次函数背景下研究动点问题的思考方向是什么?问题2:分析运动过程时,需要注意哪几个要素?问题3:解决具体问题时会涉及线段长的表达,需要注意哪两点?一次函数之动点问题综合测试(北师版)一、单选题(共6道,每道16分)1.如图,在平面直角坐标系中,直线分别交x轴、y轴于点A,B,D是AB的中点.动点P从点A出发沿折线AD-DO以每秒1个单位长度的速度向终点O运动,同时动点Q从点D出发沿折线DO-OB以相同的速度运动.设点P的运动时间为t秒,当点P到达点O时,P,Q同时停止运动.设△DPQ的面积为S,则S关于t的函数关系式为( )A.B.C.D.答案:D解题思路:试题难度:三颗星知识点:一次函数之动点问题2.如图,直线y=-x+4与x轴交于点B,与y=x交于点A,点P是线段OA上一动点,从点O 开始沿OA方向以每秒个单位长度的速度向点A运动(点P不与点O,A重合),作PQ∥x轴交直线y=-x+4于点Q,以PQ为边,向下作正方形PQMN.当点P从点O运动到点A的过程中,设运动时间为t秒,记正方形PQMN与△OAB重叠部分的面积为S,则S与t之间的函数关系式为( )A.B.C.D.答案:D解题思路:试题难度:三颗星知识点:一次函数之动点问题3.如图,过A(8,0),B两点的直线与直线交于点C,动点P从原点O出发,以每秒1个单位长度的速度沿x轴向右平移,过点P作x轴的垂线,分别交线段BC,OC于点D,E,以DE为边向左侧作等边△DEF,当直线到达点C时,停止运动.设△DEF与△BCO重叠部分的面积为S,点P的运动时间为t.(1)C点坐标是( ),根据S表达的不同,t的分段是( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:一次函数之动点问题4.(上接第3题)(2)S与t的函数关系式是( )A.B.C.D.答案:C解题思路:试题难度:三颗星知识点:一次函数动点问题5.如图,在平面直角坐标系中,,BC⊥y轴于点C,点A在x轴正半轴上,且∠OAB=45°.动点P从点C出发,以每秒2个单位长度的速度,沿折线CB—BA运动;动点Q 从点A出发,以每秒1个单位长度的速度,向终点O运动,当一点停止运动时,另一点也停止运动.设点Q运动的时间为t秒.(1)设△OPQ的面积为S,则S与t的关系式为( )A.B.C.D.答案:D解题思路:试题难度:三颗星知识点:一次函数之动点问题6.(上接第5题)(2)当点P在线段BA上时,存在某个时刻使得△APQ为等腰三角形,则此时t的值为( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:一次函数之动点问题。
初二数学期末复习《一次函数的应用—动点问题》(附练习及答案)
课题一次函数的应用——动点问题教学目标1.学会结合几何图形的性质,在平面直角坐标系中列函数关系式。
2.通过对几何图形的探究活动和对例题的分析,感悟探究动点问题列函数关系式的方法,提高解决问题的能力。
重点、难点理解在平面直角坐标系中,动点问题列函数关系式的方法。
小结:1用函数知识求解动点问题,需要将问题给合几何图形的性质,建立函数模型求解,解要符合题意,要注意数与形结合。
2.以一次函数为背景的问题,要充分运用方程、转化、函数以及数形结合等思想来研究解决,注意自变量的取值范围例题1:如图,直线的解析表达式为,且与轴交于点,直线经过点,直线,交于点.(1)求点的坐标;(2)求直线的解析表达式;(3)求的面积;(4)在直线上存在异于点的另一点,使得与的面积相等,请直接写出点的坐标.例题2:如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q 从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.(1) 求直线AB的解析式;(2) 当t为何值时,△APQ的面积为个平方单位?[来源:学。
科。
网]当堂巩固:如图,直线与x轴、y轴分别交于点E、F,点E的坐标为(-8,0),点A的坐标为(-6,0)。
(1)求的值;(2)若点P(,)是第二象限内的直线上的一个动点,在点P的运动过程中,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;(3)探究:当点P运动到什么位置时,△OPA的面积为,并说明理由。
课后检测:1、如果一次函数y=-x+1的图象与x轴、y轴分别交于点A点、B点,点M在x轴上,并且使以点A、B、M为顶点的三角形是等腰三角形,那么这样的点M有()。
A.3个 B.4个 C.5个 D.7个2、直线与y=x-1与两坐标轴分别交于A、B两点,点C在坐标轴上,若△ABC 为等腰三角形,则满足条件的点C最多有().A.4个 B.5个 C.6个 D.7个4、如图,在平面直角坐标系中,直线与交于点,分别交轴于点和点,点是直线上的一个动点.(1)求点的坐标.(2)当为等腰三角形时,求点的坐标.5、如图:直线与x轴、y轴分别交于A、B两点,,点C(x,y)是直线y=kx+3上与A、B不重合的动点。
初二数学期末复习一次函数的应用动点问题附练习及答案
课题一次函数的应用——动点问题教学目的1.学会结合几何图形的性质,在平面直角坐标系中列函数关系式。
2.通过对几何图形的探究活动和对例题的分析,感悟探究动点问题列函数关系式的方法,进步解决问题的实力。
重点、难点理解在平面直角坐标系中,动点问题列函数关系式的方法。
小结:1用函数学问求解动点问题,须要将问题给合几何图形的性质,建立函数模型求解,解要符合题意,要留意数及形结合。
2.以一次函数为背景的问题,要充分运用方程、转化、函数以及数形结合等思想来探讨解决,留意自变量的取值范围例题1:如图,直线1l的解析表达式为33y x=-+,且1l及x轴交于点D,直线2l经过点A B,,直线1l,2l交于点C.〔1〕求点D的坐标;〔2〕求直线2l的解析表达式;〔3〕求ADC△的面积;〔4〕在直线2l上存在异于点C的另一点P,使得ADP△及ADC△的面积相等,请干脆..写出点P的坐标.例题2:如图,在平面直角坐标系内,点A〔0,6〕、点B〔8,0〕,动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O挪动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A挪动,设点P、Q挪动的时间为t秒.(1) 求直线AB的解析式;(2) 当t为何值时,△APQ的面积为524个平方单位?当堂稳固:如图,直线6y kx=+及x轴、y轴分别交于点E、F,点E的坐标为〔-8,0〕,点A的坐标为〔-6,0〕。
〔1〕求k 的值;〔2〕假设点P 〔x ,y 〕是第二象限内的直线上的一个动点,在点P 的运动过程中,试写出△OPA 的面积S 及x 的函数关系式,并写出自变量x 的取值范围;〔3〕探究:当点P 运动到什么位置时,△OPA 的面积为278,并说明理由。
课后检测:1、假如一次函数y=-x+1的图象及x 轴、y 轴分别交于点A 点、B 点,点M 在x 轴上,并且使以点A 、B 、M 为顶点的三角形是等腰三角形,那么这样的点M 有〔 〕。
人教版八年级下册数学一次函数与动点最值问题
一次函数与动点最值问题知识导航1.关于x 的一次函数y =k (x -m )+n 或y =kx -km +n 一定过定点(m ,n ).2.直线外一点与直线上各点的连线中,垂线段最短.3.利用三角形两边之和大于第三边,两边之差小于第三边求最值.4.利用平方数,绝对值,算术平方根的非负性求最值.【板块一】过定点的直线题型一 定点动直线【例1】(1)一次函数y =kx 一定经过点_________;若一次函数的图象经过原点,那么该一次函数的解析式可设为_________.(2)一次函数y =kx +2一定经过点_________;若一次函数的图象经过点(0,-4),那么该一次函数的解析式可设为_________;(3)一次函数y =kx -2k +1一定经过点_________;若一次函数的图象经过点(-2,4),该一次函数的解析式可设为_________. 题型二 动点定直线【例2】利用坐标判断点在定直线上. (1)点P (m ,m +2)一定在直线_________上; (2)点P (m +1,2m -3)一定在直线_________上.针对练习11.过定点的动直线的应用: 已知一次函数y =2kx -k +2. (1)其图象过定点_________;(2)直线y =2kx -k +2和直线y =4x 的交点是_________; (3)若0<k <2,不等式2kx -k +2≤4x 的解集是_________; (4)当x =1时,y <0,则k 的取值范围是_________;(5)若A (32,3),B (4,-3),该一次函数的图象与线段AB 有交点,则k 的取值范围是_________.2.动点在定直线上的应用:直线AB:y=2x+4交x轴于点A,交y轴于点B,C(1,0),点P为直线AB上一点,将线段PC绕点C 顺时针旋转90°,得CQ.(1)若点P横坐标为-1时,求点Q坐标;(2)若点P横坐标为m,试用含m的式子表示点Q的坐标;(3)当点P在直线AB上运动时,则点Q总在直线l上运动,求直线l的解析式.【板块二】直线型动点最值问题题型三点到直线的距离最短方法技巧利用垂线段最短,可求定点到直线型动点的最小值问题.【例1】点P是x轴上一点,A(0,4),将线段P A绕点A逆时针旋转90°得到线段AQ,求OQ的最小值.【例2】如图,A(4,0),△OAB为等边三角形,点C为x轴上一动点,以BC为边在直线BC的右侧作等边△BCD,连接OD.(1)点D在某一确定的函数图象上运动,其解析式为_________;(2)OD的最小值为_________.题型四两线段或多线段的和差最值问题方法技巧利用两边之和大于第三边,两边之差小于第三边,求两线段或多线段的和差最大值或最小值;在平面直角坐标系中,常作一个定点的对称点,然后连接这一对称点与另一定点,求最值.这一方法也叫化折为直.【例3】如图,A(-4,2),B(-1,1),在x轴上找一点P,使△P AB的周长最小,求这个最小值及点P的坐标.【例4】如图,A(-4,2),B(-1,1),在x轴上找一点P,使|P A-PB|的值最大,并求此时点P的坐标.针对练习21.一次函数y=k(x-1)+3k-4的图象与x轴交于点A,与y轴交于点B,则点O到该直线的距离的最大值是_________;2.如图,B(0,3),点A为x轴上一动点,将线段AB绕点A顺时针旋转90°得线段AC,连接OC.(1)设A(a,0),用含a的式子表示点C坐标_________;(2)点C在某一确定的函数图象上运动,其解析式为_________;(3)OC长度的最小值为_________.3.如图,A(0,23),点B为x轴上一动点,将线段AB绕点A逆时针旋转60°,得线段AC,线段OC的最小值是_________.第2题第3题第4题第5题4.如图,在△ABC中,∠ACB=90°,AC=BC=4,点M为AB的中点,点D是射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接ME,点D在运动的过程中,ME的最小值为()A.2B.2 2C.4D.4 25.如图,在△ABC中,∠C=90°,BC=3,AC=5,点D为线段AC上一动点,将线段BD绕点D逆时针旋转90°,点B的对应点为E,连接AE,则AE的最小值为_________.6.如图,直线y=x+4与坐标轴交于点A,B,点C(-3,m)在直线AB上,在y轴上找一点P,使P A+PC的值最小,求这个最小值及点P的坐标.【板块三】动点的运动路径(轨迹)问题方法技巧动点的运动路径问题解题方法:1.选取三个或多个特殊点探索三个或多个特殊位置,一般选取起点,终点,和另外的特殊点探索;2.根据这些特殊点的位置猜想运动路径,然后验证.现阶段多用全等转换求值.【例1】如图,直线AB:y=2x+4交x轴于点A,交y轴于点B,C(1,0),点P为直线AB上一点,将线段PC绕点C顺时针旋转90°得CQ.(1)当点P从点A运动到点B时,点Q的运动路径长为_________;(2)线段OQ的最小值为_________.【例2】如图,A(4,0),B(0,4),点P在线段AB上运动,PQ⊥PO且PQ=PO.(1)试说明点Q在某一确定的直线上;(2)点M是OQ的中点,当点P从点A运动到点B时,求点M运动的路径长.针对练习31.在平面直角坐标系中,A(0,4),点B沿着某条路径运动,以点B为旋转中心,将点A逆时针旋转60°到点C(m,2).若-5≤m≤5,则点B运动的路径长为_________.2.在平面直角坐标系中,已知点A(a,0),C(0,b),且a,b满足(a+1)2+b+3=0.(1)直接写出:a=_________,b=_________;(2)如图1,点B为x轴正半轴上的一点,BE⊥AC于点E,交y轴于点D,连接OE.若OE平分∠AEB,求直线BE的解析式;(3)如图2,在(2)的条件下,点M为直线BE上的一动点,连接OM,将线段OM绕点M逆时针旋转90°,点O的对应点为N,当点M运动时,判断点N的运动路线是什么图形,并说明理由.图1图23.如图1,直线y=-3x+33分别与y轴、x轴交于点A,B,点C的坐标为(-3,0),点D为直线AB 上的一动点,连接CD交y轴于点E.(1)点B的坐标为_________,不等式-3x+33>0的解集为_________;(2)若S△COE=S△ADE,求点D的坐标;(3)如图2,以CD为边作菱形CDFG,且∠CDF=60°,当点D运动时,点G在一条定直线上运动,请求出这条定直线的解析式.图1图2一次函数大综合——数形结合1.已知点A(a,3),点B(b,6),点C(5,c),AC⊥x轴,CB⊥y轴,点B在第二象限且到两坐标轴的距离相等.(1)写出A,B,C三点的坐标;(2)求△ABC的面积;(3)若点P为线段OB上的动点,当△BCP面积大于12小于16时,求点P的横坐标的取值范围.2. 在平面直角坐标系中,A(a,b),B(c,d),且a-c+4+|b-d-6|=0.(1)直接写出a与c,b与d的关系式;(2)如果b=c=0,点P(m,32m+6),且m>0,S△P AB=4S△AOB,求点P的坐标;(3)如果b=3,连接AB交x轴于点Q.①直接写出点Q的坐标(用含a的式子表示);②若S△AOB≤24,求a的取值范围.3. (2019黄陂区期末)如图,在平面直角坐标系中,点A在第一象限,AB⊥x轴于点B.AC⊥y轴于点C,点A(4a,3a),且四边形ABOC的面积为48.(1)如图1,直接写出点A的坐标为_________;(2)如图2,点D从点O出发以每秒1个单位长度的速度沿y轴正半轴运动,同时,点E从点A出发,以每秒2个单位长度的速度沿射线BA运动,DE交线段AC于点F,设运动的时间为t秒,当S△AEF<S△CDF 时,求t的取值范围;(3)如图3,将线段BC平移,使点B的对应点M恰好落在y轴负半轴上,点C的对应点为N,连接BN交y轴轴于点P,当OM=3OP时,求点M的坐标.4. 在平面直角坐标系中,已知点A(a,0),B(a,6),C(a-2,2).(1)若a=2,则△ABC的面积为_________;(2)将线段BC向右平移m个单位,若△ABC的面积小于4,求m的取值范围;(3)若点D(a+8,8),连结AD,将线段BC向右平移n个单位,若线段BC与线段AD有公共点,请直接写出n的取值范围_________.5.在平面直角坐标系中,点A(a,b),B(c,d),且a-c+3+|b-d-4|=0.(1)如果a=-1,b=-3,求A,B两点的坐标;(2)如果a=-1,b=-3,求直线AB与x轴的交点M以及与y轴的交点N的坐标;(3)如果点A在x轴上方平行于x轴,且在到x轴距离等于2的直线上运动,若△ABO的面积不超过21,求a的取值范围.6.如图,在平面直角坐标系中,直线l交x轴于点A,交y轴于点B,下表列举的是直线l上的点P(x,y)的取值情况:(1)直线l上的点P(x,y)的横、纵坐标之间的数量关系是_________(直接写出结果);(2)若点P(-2,2),点Q(q,0),若以P,Q,O,B为顶点的四边形的面积大于5,求q的取值范围;(3)已知坐标平面内第一象限的点M(m,n),N(m+4,n+4),若△PMN的面积是12,求m,n的数量关系.。
(完整版)八年级数学一次函数动点问题
(2)试求点Q与点M相遇前S与t的函数关系式,并写出相应的t的取值范围。
(3)试求题(2)中当t为何值时,S的值最大,并求出S的最大值。
(4)随着P、Q两点的运动,当点M在线段CB上运动时,设PM的延长线与直线 相交于点N。试探究:当t为何值时,△QMN为等腰三角形?请直接写出t的值.
(3)在坐标平面内存在这样的点M,使得△MAC为等腰三角形且底角为30°,写出所有符合要求的点M的坐标。
6、如图,在平面直角坐标系中.四边形OABC是平行四边形.直线 经过O、C两点.点A的坐标为(8,o),点B的坐标为(11.4),动点P在线段OA上从点O出发以每秒1个单位的速度向点A运动,同时动点Q从点A出发以每秒2 个单位的速度沿A→B→C的方向向点C运动,过点P作PM垂直于x轴,与折线O一C—B相交于点M。当P、Q两点中有一点到达终点时,另一点也随之停止运动,设点P、Q运动的时间为t秒( ).△MPQ的面积为S.
为(-6,0)。(1)求 的值;(2)若点P( , )是第二象限内的直线上的一个动点,在点P的运动过程中,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)探究:当点P运动到什么位置时,△OPA的面积为 ,并说明理由。
5、己知如图在直角坐标系中,矩形OABC的对角线AC所在直线的解析式为 。
(2)当 为等腰三角形时,求点 的坐标.
(3)在直线 上是否存在点 ,使得以点 为顶点的四边形是平行四边形?
9、如图:直线 与x轴、y轴分别交于A、B两点, ,点C(x,y)是直线y=kx+3上与A、B不重合的动点。(1)求直线 的解析式;(2)当点C运动到什么位置时△AOC的面积是6;(3)过点C的另一直线CD与y轴相交于D点,是否存在点C使△BCD与△AOB全等?若存在,请求出点C的坐标;若不存在,请说明理由。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一次函数动点问题例题如图,直线1l 的解析表达式为33y x =-+,且1l 与x 轴交于点D ,直线2l 经过点A B ,,直线1l ,2l 交于点C .(1)求点D 的坐标; (2)求直线2l 的解析表达式; (3)求ADC △的面积;(4)在直线2l 上存在异于点C 的另一点P ,使得ADP △与ADC △的面积相等,请直接..写出点P 的坐标.练习题 如图,以等边△OAB 的边OB 所在直线为x 轴,点O 为坐标原点,使点A 在第一象限建立平面直角坐标系,其中△OAB 边长为6个单位,点P 从O 点出发沿折线OAB 向B 点以3单位/秒的速度向B 点运动,点Q 从O 点出发以2单位/秒的速度沿折线OBA 向A 点运动,两点同时出发,运动时间为t (单位:秒),当两点相遇时运动停止.① 点A 坐标为_____________,P 、Q 两点相遇时交点的坐标为________________; ② 当t =2时,S =△OPQ ____________;当t =3时,OPQ S =△____________;③ 设△OPQ 的面积为S ,试求S 关于t 的函数关系式;④ 当△OPQ 的面积最大时,试求在y 轴上能否找一点M ,使得以M 、P 、Q 为顶点的三角形是Rt △,若能找到请求出M 点的坐标,若不能找到请简单说明理由。
x yOAB xyOAB xyOAB例题如图,在Rt △AOB 中,∠AOB=90°,OA=3cm ,OB=4cm ,以点O 为坐标原点建立坐标系,设P 、Q 分别为AB 、OB 边上的动点它们同时分别从点A 、O 向B 点匀速运动,速度均为1cm/秒,设P 、Q 移动时间为t (0≤t ≤4)(1)过点P 做PM ⊥OA 于M ,求证:AM :AO=PM :BO=AP :AB ,并求出P 点的坐标(用t 表示)(2)求△OPQ 面积S (cm 2),与运动时间t (秒)之间的函数关系式,当t 为何值时,S 有最大值?最大是多少?(3)当t 为何值时,△OPQ 为直角三角形?(4)证明无论t 为何值时,△OPQ 都不可能为正三角形。
若点P 运动速度不变改变Q 的运动速度,使△OPQ 为正三角形,求Q 点运动的速度和此时t 的值。
练习题己知如图在直角坐标系中,矩形OABC 的对角线AC 所在直线的解析式为313y x 。
(1)求线段AC 的长和ACO 的度数。
(2)动点P 从点C 开始在线段CO 3个 单位长度的速度向点O 移动,动点Q 从点O 开始 在线段OA 上以每秒1个单位长度的速度向点A 移动, (P 、Q 两点同时开始移动)设P 、Q 移动的时间为t 秒。
①设BPQ 的面积为S ,求S 与t 之间的函数关系式,并求出当t 为何值时,S 有最小值。
(3)在坐标平面内存在这样的点M ,使得MAC 为等腰三角形且底角为30°,写出所有符合要求的点M的坐标。
yO第33题图QPCBA例题如图,在平面直角坐标系内,已知点A (0,6)、点B (8,0),动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动,同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动,设点P 、Q 移动的时间为t 秒.(1) 求直线AB 的解析式;(3) 当t 为何值时,△APQ 的面积为524个平方单位?练习题如图,在平面直角坐标系中.四边形OABC 是平行四边形.直线l 经过O 、C 两点.点A 的坐标为(8,o),点B 的坐标为(11.4),动点P 在线段OA 上从点O 出发以每秒1个单位的速度向点A 运动,同时动点Q 从点A 出发以每秒2个单位的速度沿A →B →C 的方向向点C 运动,过点P 作PM 垂直于x 轴,与折线O 一C —B 相交于点M 。
当P 、Q 两点中有一点到达终点时,另一点也随之停止运动,设点P 、Q 运动的时间为t 秒(0t ).△MPQ 的面积为S .(1)点C 的坐标为___________,直线l 的解析式为___________.(每空l 分,共2分) (2)试求点Q 与点M 相遇前S 与t 的函数关系式,并写出相应的t 的取值范围。
(3)试求题(2)中当t 为何值时,S 的值最大,并求出S 的最大值。
(4)随着P 、Q 两点的运动,当点M 在线段CB 上运动时,设PM 的延长线与直线l 相交于点N 。
试探究:当t 为何值时,△QMN 为等腰三角形?请直接写出t 的值.例题如图(1),在矩形ABCD 中,AB=10cm,BC=8cm,点P 从A 出发, 沿A →B →C →D 路线运动,到D 停止;点Q 从D 出发,沿D →C →B →A 路线运动,到A 停止. 若点P 、点Q 同时出发,点P 的速度为1cm/s,点Q 的速度为2cm/s,as 时点P 、点Q 同时改变速度,点P 的速度变为bcm/s,点Q 的速度变为dcm/s .图(2)是点P 出发x秒后△APD 的面积S1(cm 2)与x(s)的函数关系图象;图(3)是点Q 出发x 秒后△AQD 的面积S 2(cm 2)与x(s)的函数关系图象.(1)参照图(2),求a 、b 及图(2)中c 的值; (2)求d 的值;(3)设点P 离开点A 的路程为y 1(cm),点Q 到A 还需走的路程为y 2(cm), 请分别写出动点P 、Q 改变速度后y 1、y 2与出发后的运动时间x(s)的函数关系式,并求出P 、Q 相遇时x 的值; (4)当点Q 出发_______s 时,点P 、点Q 在运动路线上相距的路程为25cm.(1)PQCBA D x(秒)(2)20840caOS 1(cm 2)x(秒)(3)2240OS 2(cm 2)练习题、如图,正方形ABCD 的边长为5,P 为CD 边上一动点,设DP 的长为x ,ADP 的面积为y ,y 与x 之间的函数关系式,及自变量x 的取值范围12.如图1,在直角梯形ABCD 中,动点P 从点B 出发,沿BC ,CD 运动至点D 停止.设点P 运动的路程为x ,△ ABP 的面积为y ,如果y 关于x 的函数图象如图2所示,则△BCD 的面积是( ) A .3 B .4 C .5 D .613.如图,△ABC 和的△DEF 是等腰直角三角形,∠C=∠F=90°,AB=2.DE=4.点B 与点D 重合,点A,B(D),E 在同一条直线上,将△ABC 沿D E 方向平移,至点A 与点 E 重合时停止.设点B,D 之间的距离为x ,△ABC 与△DEF 重叠 部分的面积为y ,则准确反映y 与x 之间对应关系的图象是( ) 图12 O5 x D 图240.如图,点G 、D 、C 在直线a 上,点E 、F 、A 、B 在直线b 上,若a b Rt GEF ∥,△从如图所示的位置出发,沿直线b 向右匀速运动,直到EG 与BC 重合.运动过程中GEF △与矩形ABCD 重合部分....的面积(S )随时间(t )变化的图象大致是( )45.(2009年牡丹江)如图,平面直角坐标系中,在边长为1的正方形ABCD 的边上有一动点P 沿A B C D A →→→→运动一周,则P 的纵坐标y 与点P 走过的路程s 之间的函数关系用图象表示大致是( )G D C E F A B b a (第11题s t O A s t O B C s t O Ds tO 1 2 3 4 1 2 y sO 1 2 3 41 2 y s O s 1 2 3 412 y sO 1 2 3 412 y O A .B .C .D .46.如图,动点P 从点A 出发,沿线段AB 运动至点B 后,立即按原路返回,点P 在运动过程中速度大小不变,则以点A 为圆心,线段AP 长为半径的圆的面积S 与点P 的运动时间t 之间的函数图象大致为( )8.如图,正方形ABCD 的边长为10,点E 在CB 的延长线上,10EB =,点P 在边CD 上运动(C 、D 两点除外),EP 与AB 相交于点F ,若CP x =,四边形FBCP 的面积为y ,则y 关于x 的函数关系式是 .2、如图,直线6y kx =+与x 轴、y 轴分别交于点E 、F ,点E 的坐标为(-8,0),点A 的坐标为(-6,0)。
(1)求k 的值;(2)若点P (x ,y )是第二象限内的直线上的一个动点,在点P 的运动过程中,试写出△OPA 的面积S 与x 的函数关系式,并写出自变量x 的取值范围;(3)探究:当点P 运动到什么位置时,△OPA 的面积为278,并说明理由。
A .B .C .D .(第8题)PDCBFAE八年级数学《一次函数动点问题》练习题1、如果一次函数y=-x+1的图象与x 轴、y 轴分别交于点A 点、B 点,点M 在x 轴上,并且使以点A 、B 、M 为顶点的三角形是等腰三角形,那么这样的点M 有( )。
A .3个B .4个C .5个D .7个2、直线与y=x-1与两坐标轴分别交于A 、B 两点,点C 在坐标轴上,若△ABC 为等腰三角形,则满足条件的点C 最多有( ).A .4个B .5个C .6个D .7个3、直线643+-=x y 与坐标轴分别交于A 、B 两点,动点P 、Q 同时从O 点出发,同时到达A 点,运动停止.点Q 沿线段OA 运动,速度为每秒1个单位长度,点P 沿路线O ⇒B ⇒A 运动. (1)直接写出A 、B 两点的坐标; (2)设点Q 的运动时间为t (秒),△OPQ 的面积为S ,求出S 与t 之间的函数关系式; (3)当548=S 时,求出点P 的坐标,并直接写出以点O 、P 、Q 为顶点的平行四边形的第四个顶点M 的坐标.4、如图,在平面直角坐标系xOy 中,直线1y x =+与334y x =-+交于点A ,分别交x 轴于点B 和点C ,点D 是直线AC 上的一个动点. (1)求点A B C ,,的坐标.(2)当CBD △为等腰三角形时,求点D 的坐标. (3)在直线AB 上是否存在点E ,使得以点E D O A ,,,为顶点的四边形是平行四边形?A y xDCOBxy OBA5、如图:直线3+=kx y 与x 轴、y 轴分别交于A 、B 两点,43=OA OB ,点C(x ,y)是直线y =kx +3上与A 、B 不重合的动点。
(1)求直线3+=kx y 的解析式;(2)当点C 运动到什么位置时△AOC 的面积是6; (3)过点C 的另一直线CD 与y 轴相交于D 点,是否存 在点C 使△BCD 与△AOB 全等?若存在,请求出点C 的坐标;若不存在,请说明理由。
二、经典例题:1、已知,如图在边长为2的等边△ABC 中,E 是AB 边上不同于点A 、点B 的一动点,过点E 作ED ⊥BC 于点D ,过点D 作DH ⊥AC 于点H ,过点H 作HF ⊥AB 于点F ,设BE 的长为x ,AF 的长为y ;⑴求y 与x 的函数关系式,并写出自变量的范围;⑵当x 为何值时,点E 与点F 重合,判断这时△EDH 为什么三角形(判断形状,不需证明).2、如图,点A 、B 、C 的坐标分别是(0,4),(2,4),(6,0).点M 是折线ABC 上一个动点,MN ⊥x 轴于N ,设ON 的长为x ,MN 左侧部分多边形的面积为S. ⑴写出S 与x 的函数关系式; ⑵当x =3时,求S 的值.3、如图,已知在平面直角坐标系中,直线l :y =-21x +2分别交两坐标轴于A 、B 两点,M 是线段AB 上一个动点,设M 的横坐标为x ,△OMB 的面积为S ; ⑴写出S 与x 的函数关系式;⑵若△OMB 的面积为3,求点M 的坐标;⑶当△OMB 是以OB 为底的等腰三角形时,求它的面积; ⑷画出函数s 图象.lM y xO BA四、自我检测:如图,直线OC 、BC 的函数关系式分别为y =x 和y =-2x +6,动点P(x ,0)在OB 上移动(0<x <3), ⑴求点C 的坐标;⑵若A 点坐标为(0,1),当点P 运动到什么位置时(它的坐标是什么),AP+CP 最小; ⑶设△OBC 中位于直线PC 左侧部分的面积为S ,求S 与x 之间的函数关系式。
