2012年郊尾、枫江、东宅教研小片区九年级(上)第一次月考数学试卷
2012-2013学年度第一学期九年级数学第一次月考试卷1111111
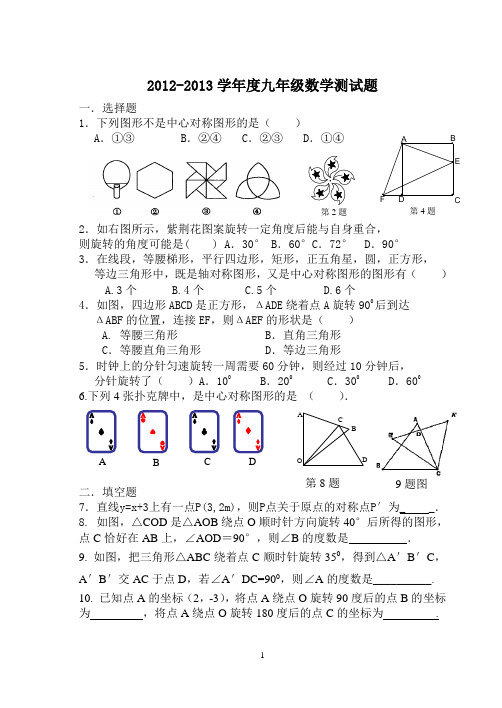
2012-2013学年度九年级数学测试题一.选择题1.下列图形不是中心对称图形的是( )A .①③B .②④C .②③D .①④2.如右图所示,紫荆花图案旋转一定角度后能与自身重合, 则旋转的角度可能是( ) A .30° B .60°C .72° D .90°3.在线段,等腰梯形,平行四边形,矩形,正五角星,圆,正方形, 等边三角形中,既是轴对称图形,又是中心对称图形的图形有( )A.3个B.4个C.5个D.6个4.如图,四边形ABCD 是正方形,ΔADE 绕着点A 旋转900后到达 ΔABF 的位置,连接EF ,则ΔAEF 的形状是( )A. 等腰三角形 B .直角三角形C .等腰直角三角形D .等边三角形5.时钟上的分针匀速旋转一周需要60分钟,则经过10分钟后, 分针旋转了( )A .100 B .200 C .300 D .6006.下列4张扑克牌中,是中心对称图形的是 ( ).二.填空题7.直线y=x+3上有一点P(3,2m),则P 点关于原点的对称点P ′为_ _.8. 如图,△COD 是△AOB 绕点O 顺时针方向旋转40°后所得的图形,点C 恰好在AB 上,∠AOD =90°,则∠B 的度数是 .9. 如图,把三角形△ABC 绕着点C 顺时针旋转350,得到△A 'B 'C ,A 'B '交AC 于点D ,若∠A 'DC=900,则∠A 的度数是__________.10. 已知点A 的坐标(2,-3),将点A 绕点O 旋转90度后的点B 的坐标为 ,将点A 绕点O 旋转180度后的点C 的坐标为 .第2题 第4题 O DC BA 第8题 ABCD 9题图三.解答题11.如图所示的正方形网格中,△ABC 的顶点均在格点上,在所给直角坐标系中解答下列问题:(1)分别写出点A 、B 两点的坐标;(2)作出△ABC 关于坐标原点成中心对称的△A 1B 1C 1;12.已知PA=5,PB=4,PC=3,点P 是等边三角形ABC 内一点,则∠BPC 是多少度?13. 正方形ABCD 和正方形AEFG 有一公共点A ,点G .E 分别在线段AD 、AB 上(如图(1)所示),连接DF 、BF .(1)求证:DF=BF ,(2)若将正方形AEFG 绕点A 按顺时针方向旋转,连接DG 、BE (如图(2)所示),在旋转过程中,请猜想线段DG 、BE 始终有什么数量关系和位置关系并证明你的猜想.图9。
2012年九年级上册数学月考试卷

2012年九年级上册数学月考试卷重庆市大足区宝兴中学初2013级12—13学年度上期统一考试数学试卷(全卷共五个大题,满分150分,考试时间120分钟)抛物线的顶点坐标为一、选择题(本大题10个小题,每小题4分,共40分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请将正确答案的代号填在答题卷中相应的位置上.1.计算的结果是()A.B.C.2xD.3x2.下列图形中,既是轴对称图形又是中心对称图形的是()A.B.C.D.3、已知⊙O的半径为5,点P⊙O在内,则的长度可能为()A、3B、5C、7D、84、下列调查中,适合用普查方式的是()A、了解美制“毒刺”导弹的杀伤半径B、了解我国民众对“中日钓鱼岛争端”的看法C、了解嘉陵江的水质情况D、了解某班学生对“鸟叔”的知晓率5.在函数的图象上有三个点的坐标分别为、、,函数值、、的大小关系是().A.B.C.D.6.如图,点A、B、C在⊙O上,∠ABC=30°,则∠OAC等于()A.60°B.45°C.35°D.30°7.当取一切实数时,函数的最小值为()A.—2B.2C.—1D.18.用若干张大小相同的黑白两种颜色的正方形纸片,按下列拼图的规律拼成一列图案,则第6个图案中黑色正方形纸片的张数是()A.22B.21C.20D.199.如图,某天早晨王老师沿⊙M的半圆形M→A→B→M路径匀速散步,此时王老师离出发点M的距离y与时间x之间的函数关系的大致图象是()10.已知二次函数的图象与x轴交于点(-2,0)、(x1,0),且1A.2B.3C.4D.5二、填空题(本大题6个小题,每小题4分,共24分)在每小题中,请将答案填在答题卷相应位置的横线上.11.分解因式:.12、目前,我国每年死于吸烟相关疾病的人数高达120万,比艾滋病、肝炎、结核等传染病的死亡人数总和还要多,数据120万用科学记数法表示为。
2012–2013学年度上期九年级第-次月考数学题

上期九年级第-次月考数学题本试卷满分120分,。
班别------ 座号----------- 姓名------- 评分-------温馨提示: 亲爱的同学,请你沉着冷静,充满自信,认真审题,仔细答卷,祝你考出好成绩!一、精心选一选(本大题共10小题,每小题3分,共30分. 1、一元二次方程. x 2 _ 4=0的解是 ( )A 、 2=xB 、2-=xC 、21=x ,22-=xD 、21=x ,22-=x2、已知一个等腰三角形有一个角为50o,则顶角是( ) A 、50o B 、80o C 、50o 或80o D 、不能确定3、方程2650x x +-=的左边配成完全平方后所得方程为 ( ) A. 14)3(2=+x ;B 14)3(2=-x ; C 21)6(2=+x ; D 以上答案都不对.4、下列两个三角形中,一定全等的是( )(A )有一个角是40°,腰相等的两个等腰三角形 (B )两个等边三角形 (C )有一个角是100°,底边相等的两个等腰三角形 (D )有一条边相等,有一个内角相等的两个等腰三角形5、如图,三角形纸片ABC ,10cm 7cm 6cm AB BC AC ===,,, 沿过点B 的直线折叠这个三角形,使顶点C 落在A B 边上的点E 处, 折痕为B D ,则AED △的周长为( )A 、9 cmB 、1 3 cmC 、16 cmD 、10 cm6、三角形两边的长分别是4和6,第三边的长是一元二次方程060162=+-x x的一个实数根,则该三角形的周长是 ( )A 、 20B 、 20或16 C.16 D 、18或217、△ABC 中,∠A ∶∠B ∶∠C=1∶2∶3,CD ⊥AB 于点D 若BC=a ,则AD 等于( ) A.21a B.23a C.23a D.3a8、已知关于x 的一元二次方程x 2-kx -4=0的一个根为2,则另一根是( )A 、4B 、1C 、2D 、-29、如图,OP 平分∠BOA ,∠BOA=45°, PC ∥OA ,PD ⊥OA , 若PC=4,则PD 等于( )A.4B.22C.32D.2二、耐心填一填:(本大题5小题,每小题3分,计1112、如图,已知AB =AC ,∠A =440,AB 则∠DBC = 。
九年级数学上册第一次月考试卷 试题

九年级数学上册第一次月考试卷温馨提示:本套试卷一共120分,须在90分钟内完成。
希望你认真审题,仔细答题,遇到困难时也不要轻易放弃。
相信你只要努力考虑,不断探求。
慎密作解,一定有个好成绩。
要有信心哟!一、选择题 (此题一共5小题,每一小题3分,满分是15分) 1.方程x(x+3)=x+3的解是 ( ) A. x=1B. x 1=0, x 2=-3C. x 1=1, x 2=3D. x 1=1, x 2=-32. 到△ABC 的三个顶点间隔 相等的点是△ABC 的〔 〕3. 如图〔1〕,在△ABC中,D,E分别是AB,AC的中点,将△ADE沿线段DE向下折叠,得到图〔2〕,以下关于图〔2〕的四个结论中,不一定成立.....的是〔 〕 A.点A落在边BC的中点 B.∠1+∠B+∠C=180° C.△DBA是等腰三角形 D.DE ∥ BC4. 李教师出示了小黑板上的题目〔如图2〕后,小明答复:“方程有一根为1”,小颖答复:“方程有一根为2”。
那么你认为〔 〕图2已知方程x 2-3x+k+1=0,试添加一个条件,使它的两根之积为2图3AP图4AC.小明、小颖答复都正确D.小明、小颖答复都不正确5.如图3::AC 平分∠PAQ ,点B 、B ′分别在AP 、AQ 上,假如添加一个条件,即可推出 AB=AB ′,那么这个条件不可以...是〔 〕 ′⊥AC B.∠ABC=∠AB ′C C.∠ACB=∠ACB ′ D.BC=B ′C二、填空题(此题一共5小题,每一小题4分,满分是20分)6. 写出两个一元二次方程,使每个方程都有一个根为0,并且二次项系数都为1: 。
7.22____)(2129____21-=+-x x x 8. 如图4是2021年8月在召开的第24届国际数学家大会的会标,它是由4个一样的直角三角形拼和而成。
假设图中大小正方形的面积分别为52cm 2和4cm 2,那么直角三角形的两条直角边的和是 cm.9. 假如42-x 的值是5,那么241621x x -+的值是 .10. 正方形ABCD 的边长为12cm ,和它面积相等的矩形的一边长为18cm ,那么矩形的另一边长为 .三、解答题 (此题一共5小题,每一小题6分,一共30分)11.用配方法解解方程:01522=--x x 12.用公式法解解方程:02852=+-x x13. 如图5,在△ABC中,点D在AB上,点E在BC上,BD=BE。
2012学年九年级上数学第一次月考试卷(浙江版)

2012学年 九年级数学上第一月考数学试卷 (100分) 成绩____________一. 选择题 (每小题4分, 共40分)1、B (x 2,y 2)、C (x 3,y 3)都在反比例函数y =- 3x的图象上,且x 1<x 2<0<x 3,则y 1、y 2、y 3的大小关系是-------------------------------------------( ) A .y 3<y 1<y 2 B .y 1<y 2<y 3 C .y 3<y 2<y 1 D .y 2<y 1<y 32、坐标平面上有一函数y=24x 2-48的图形,其顶点坐标为 --------------------( ) (A) (0,-2) (B) (1,-24) (C) (0,-48) (D) (2,48) 。
3、已知二次函数y=2(x ﹣3)2+1.下列说法:①其图象的开口向下;②其图象的对称轴为直线x=﹣3;③其图象顶点坐标为(3,﹣1);④当x <3时,y 随x 的增大而减小.则其中说法正确的有--------------------------------------------------------------------------------( ) A .1个 B .2个 C .3个 D .4个4、已知抛物线2y ax bx c =++(a <0)过A (2-,0)、O (0,0)、B (3-,1y )、C (3,2y )四点, 则1y 与2y 的大小关系是------------------( ) A .1y >2y B .1y 2y = C .1y <2yD .不能确定5、下列图形中,阴影部分的面积相等的是-----------------------------------( )(A)、①②(B)、②③ (C)、③④ (D)、①④6.已知二次函数2y ax bx c =++的图像如图所示,那么一次函数y bx c =+和反比例函数ay x=在同一平面直角坐标系中的图像大致是 ---------------------------- ( )7、抛物线2ax y =与直线1=x ,2=x ,1=y ,2=y 围成的正方形有公共点,则实数a 的取值范是 ------------------------------------------------------------( ) A 、241≤≤a B 、221≤≤a C 、121≤≤a D 、141≤≤a 8、学校大门如图8所示是一抛物线形水泥建筑物,大门的地面宽度为8米,两侧距 地4米高处各有一挂校名横匾用的铁环,两铁环的水平距离为6米,则该校门的高度(精确到0.1米)为 -------------------------------------------------------------------(A 、8.9米B 、9.1米C 、9.2 米D 、9.3米9.小英同时掷甲、乙两枚质地均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6).记甲立方体朝上一面上的数字为x 、乙立方体朝上一面朝上的数字为y ,这样就确定点P 的一个坐标(x y ,),那么点P 落在双曲线x y 6=上的概率为---------( )A .118B .112 C .19D .16yx O2y x =-+①yx O ②yx O③yx O3y x =21y x =-2y x=1④6m8m 图8 4m xy O x y O x y O xy O x y O A B C D 校 姓名 ……………………装……………………………………………………………………订……………………………………………………………线…………………10.如图,函数y=x 2-2x +m (m 为常数)的图象如图,如果x a =时,0y <; 那么x=a -2时,函数值----------------------------------( )A .0y <B .0y m <<C .y m =D .y m >二、填空题 (共30分,请你绝对要认真思考,细心计算)1、抛物线242my x x =-+与x 轴的一个交点的坐标为(l,0), 则此抛物线与x 轴的另一个交点的坐标是___________(4分)2、上抛出一小球,小球的高度h (米)与小球运动时间t (秒)的函数关系式是29.8 4.9h t t =-,那么小球运动中的最大高度为___________米.(4分)3、已知二次函数的图象开口向下,且顶点在x 轴的负半轴上,请你写出一个满足条件的二次函数的表达式_______________________________(4分)4、设a 、b 是常数,且b >0,抛物线y=ax 2+bx+a 2-5a-6为下图中四个图象之一, 则a 的值为__________(4分)5、将抛物线221210y x x =-+绕它的顶点旋转180°,所得 抛物线的解析式是_________________ (4分) 6、如图,双曲线xy 2=(x >0)与矩形OABC 的边CB , BA 分别 交于点E ,F ,且AF=BF ,连接EF ,则△OEF 的面积为 (2分) 7.已知二次函数221y x bx =++(b 为常数),当b 取不同的值时, 对应得到一系列二次函数的图象,它们的顶点都在一条抛物线上,则 这条抛物线的解析式是_________________;若二次函数221y x bx =++ 的顶点只在x 轴上方移动,那么b 的取值范围是______________ .(2分) 8、已知抛物线1C :221y x mx =-++(m 为常数,且0m ≠)的顶点为A , 与y 轴交于点C ;抛物线2C 与抛物线1C 关于y 轴对称,其顶点为B .若点P 是抛物线1C 上的点,使得以A 、B 、C 、P 为顶点的四边形为菱形,则m 的值为______________(2分) 9、(共4分)(1)将抛物线y 1=2x 2向右平移2个单位,得到抛物线y 2的图象, 则y 2=_________________;(2)如图,P 是抛物线y 2对称轴上的一个动点,直线x =t 平行于y 轴, 分别与直线y =x 、抛物线y 2交于点A 、B .若△ABP 是以点A 或点B 为 直角顶点的等腰直角三角形,求满足条件的t 的值, 则t =_________________________ 三、解答题(32分)yxO yxO yxO1 -1 yxO1 -1 第10题图xy O x 1x 2P yxy x = 2yO·第(5)题1、(10分)王强在一次高尔夫球的练习中,在某处击球,其飞行路线 满足抛物线21855y x x =-+,其中y (m )是球的飞行高度,x (m )是球飞出的水平距离,结果球离球洞的水平距离还有2m .(1)请写出抛物线的开口方向、顶点坐标、对称轴.(3分)(2)请求出球飞行的最大水平距离.(3分)(3)若王强再一次从原处击球,要想让球飞行的最大高度不变且球刚好进洞,则球飞行路线应满足怎样的抛物线,求出其解析式.(4分)2.(10分)公司准备投资开发A 、B 两种新产品,通过市场调研发现:如果单独投资A 种产品,则所获利润(万元)与投资金额x (万元)之间满足正比例函数关系:A y kx =;如果单独投资B 种产品,则所获利润(万元)与投资金额x (万元)之间满足二次函数关系:2B y ax bx =+.根据公司信息部的报告,,A B y y (万元)与投资金额x (万元)的部分对应值(如下表)(1)填空:A y =______________________; B y =_______________________;(4分)(2)如果公司准备投资20万元同时开发A,B 两种新产品,请你设计一个能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少万元?(4分)(3)如果公司采用以下投资策略:相同的投资金额哪种方式获利大就选哪种,且财务部给出的投资金额为10至15万元.请你帮助保障部预测(直接写出结果):公司按这种投资策略最少可获利多少万元?(2分)答: 最少获利为________________ 3、(12分) 如图,已知抛物线与x 轴交于点(20)A -,,(40)B ,,与y 轴交于点(08)C ,. (1)求抛物线的解析式及其顶点D 的坐标;(4分)x 1 5 A y 0.6 3 B y 2.8 10(2)设直线CD 交x 轴于点E .在线段OB 的垂直平分线上是否存在点P ,使得点P 到直线CD 的距离等于点P 到原点O 的距离?如果存在,求出点P 的坐标;如果不存在,请说 明理由;(4分)(3)过点B 作x 轴的垂线,交直线CD 于点F ,将抛物线沿其对称轴平移,使抛物线与线段EF 总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?(4分)部分参考答案三、解答题 1.解:(1)21855y x x =-+2116(4)55x =--+ ························································································· 1分 ∴抛物线21855y x x =-+开口向下,顶点为1645⎛⎫⎪⎝⎭,,对称轴为直线4x = ················ 3分(2)令0y =,得:218055x x -+= ····························································································· 4分 解得:10x =,28x = ···················································································· 5分∴球飞行的最大水平距离是8m . ······································································ 6分(3)要让球刚好进洞而飞行最大高度不变,则球飞行的最大水平距离为10m∴抛物线的对称轴为5x =,顶点为1655⎛⎫ ⎪⎝⎭, ························································ 7分设此时对应的抛物线解析式为216(5)5y a x =-+ ·················································· 8分 又点(00),在此抛物线上,162505a ∴+= 16125a =-···································································································· 9分 21616(5)1255y x ∴=--+ 2163212525y x x =-+ ·················································10分 2. (1)x y A 6.0=, x x y B 32.02+-= (4分)(2) 设投资开发B产品的金额为x万元,总利润为y万元.则220.6(20)(0.23)0.2 2.412y x x x x x =-+-+=-++ (3分)2.19,6==∴最大时当y x 即投资开发A 、B 产品的金额分别为14万元和6万元时,能获得最大的总利润19.2万元 (2分)(3) 7.2万元(2分)20.230.6y x x y x ⎧=-+⎨=⎩⇒ 127.2x y =⎧⎨=⎩借助直线和抛物线的示意图可以得出答案。
九年级上第一次月考数学试题含答案

第1页 共4页 t/小时S/千米a440560
54321D
C
B
A
O
九年级数学试卷 一、选择题(每小题3分,共计30分) 1. 点M(-1,2)关于x轴对称的点的坐标为( ) (A)(-1,-2) (B)(-1,2) (C)(1,-2) (D)(2,-1) 2. 下列计算正确的是( )
(A)235aaa+= (B)()326aa= (C)326aaa (D)aaa632 3. 下列图案中,既是轴对称图形又是中心对称图形的是( ) 4. 抛物线()2345yx=-+的顶点坐标是( ) (A)(4,5) (B)(-4,5) C、(4,-5) (D)(-4,5) 5. 等腰三角形的一边长为4 cm,另一边长为9 cm,则它的周长为( ) (A)13 cm (B)17 cm (C)22 cm (D)17 cm或22 cm
6. 已知反比例函数kyx=的图象经过点P(-l,2),则这个函数的图象位于( ) (A)第二、三象限 (B)第一、三象限 (C)第三、四象限 (D)第二、四象限 7. 某电动自行车厂三月份的产量为1 000辆,由于市场需求量不断增大,五月份的产量提高到 l 210辆,则该厂四、五月份的月平均增长率为( ) (A)12.1% (B)20% (C)21% (D)10% 8. 如图,在Rt△ABC中,∠BAC=90°,∠B=60°,△ADE可以由△ABC绕点 A顺时针旋转900得 到,点D 与点B是对应点,点E与点C是对应点),连接CE,则∠CED的度数是( ) (A)45° (B)30° (C)25° (D)15° 9. 如图,矩形ABCD中,对角线AC、BD相交于点O,∠AOB=600,AB=5,则AD的长是( )
(A)53 (B)52 (C)5 (D)10 10. 甲乙两车分别从M、N两地相向而行,甲车出发1小时后,乙车出发,并以各自的速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是甲乙两车之间的路程S(千米)与甲车所用时间t(小时)之间的函数图象,其中D点表示甲车到达N地停止运行,下列说法中正确的是( ) (A)M、N两地的路程是1000千米; (B)甲到N地的时间为4.6小时; (C)甲车的速度是120千米/小时; (D)甲乙两车相遇时乙车行驶了440千米.
九年级数学上学期【第一次月考卷】(原卷版)
九年级数学上学期【第一次月考卷】(人教版)(满分120分,完卷时间100分钟)考生注意:1.本试卷含三个大题,共26题.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效.2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出解题的主要步骤.一.选择题(共10小题)1.若关于x的一元二次方程(m﹣3)x2+5x+m2﹣3m+2=0的常数项为0,则m的值等于()A.1B.2C.1或2D.02.方程(x﹣1)(x+3)=12化为ax2+bx+c=0的形式后,a、b、c的值为()A.1、2、﹣15B.1、﹣2、﹣15C.﹣1、﹣2、﹣15D.﹣1、2、﹣153.某果园2012年水果产量为100吨,2014年水果产量为144吨,求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率为x,则根据题意可列方程为()A.144(1﹣x)2=100B.100(1﹣x)2=144C.144(1+x)2=100D.100(1+x)2=1444.下列一元二次方程中,两实数根之和为3的是()A.x2﹣3x+3=0B.x2+3x﹣3=0C.x2﹣3x﹣3=0D.x2+3x+3=05.二次函数y=2x2﹣x﹣1的顶点坐标是()A.(0,﹣1)B.(2,﹣1)C.(,﹣)D.(﹣,)6.方程x(x−2)=x−1化成一元二次方程的一般形式是()A.x2﹣2x+2=0B.x2﹣2x=0C.x2﹣3x﹣1=0D.x2﹣3x+1=07.如图,△ABC的边BC=y,BC边上的高AD=x,△ABC的面积为3,则y与x的函数图象大致是()A.B.C.D.8.已知三角形的一边长是3,三角形的另两条边长分别是关于x的方程x2﹣4x+2=0的两个根,则此三角形的周长为()A.10B.8C.7D.59.如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m2.若设道路的宽为xm,则下面所列方程正确的是()A.(32﹣2x)(20﹣x)=570B.32x+2×20x=32×20﹣570C.(32﹣x)(20﹣x)=32×20﹣570D.32x+2×20x﹣2x2=57010.已知四个二次函数的图象如图所示,那么a1,a2,a3,a4的大小关系是()A.a1>a2>a3>a4B.a2>a1>a4>a3C.a2>a1>a3>a4D.a1>a2>a4>a3二.填空题(共8小题)11.当方程(m﹣1)x﹣(m+1)x﹣2=0是一元二次方程时,m的值为.12.如果关于x的方程x2﹣2x+m=0(m为常数)有两个相等实数根,那么m=.13.已知二次函数y=2x2﹣3x+m(m为常数)的图象与x轴的一个交点为(1,0),则m =.14.如图是一张长9cm、宽5cm的矩形纸板,将纸板四个角各剪去一个同样的正方形,可制成底面积是12cm2的一个无盖长方体纸盒,设剪去的正方形边长为xcm,则可列出关于x的方程为.15.参加一次聚会的每两人都握了一次手,所有人共握手66次,则有人参加聚会.16.若抛物线y=ax2+bx+c过点A(﹣1,2),B(3,2),则此抛物线的对称轴是直线.17.对于实数a,b,定义运算“⊗”:,例如:5⊗3,因为5>3,所以5⊗3=5×3﹣32=6.若x1,x2是一元二次方程x2﹣6x+8=0的两个根,则x1⊗x2=.18.已知抛物线y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②b2>4ac;③4a+2b+c>0;④(a+b)2<b2,其中正确的有.三.解答题(共8小题)19.解下列方程:5x2﹣3x=x+1.20.求二次函数y=x2﹣2x﹣1的顶点坐标及它与x轴的交点坐标.21.已知等腰三角形底边长为8,腰长是方程x2﹣9x+20=0的一个根,求这个三角形的面积.22.某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖户第1年的可变成本为2.6万元,设可变成本平均每年增长的百分率为x.(1)用含x的代数式表示第3年的可变成本为万元;(2)如果该养殖户第3年的养殖成本为7.146万元,求可变成本平均每年增长的百分率x.23.已知关于x的方程x2﹣(k+1)x+k2+1=0.(1)当k取何值方程有两个实数根.(2)是否存在k值使方程的两根为一个矩形的两邻边长,且矩形的对角线长为.24.如图,抛物线y=ax2+4ax+2的顶点A在x轴上,经过点A的直线交该抛物线于点C,交y轴于点B,且点B是线段AC的中点,(1)求该抛物线的解析式;(2)求直线AC的解析式.25.在Rt△ABC中,∠C=90°,点O是AB的中点,M、N分别在边AC、BC上,OM⊥ON,连MN,AC=4,BC=8.设AM=a,BN=b,MN=c.(1)求证:a2+b2=c2;(2)①若a=1,求b;②探究a与b之间的函数关系式;(3)△CMN的面积等于△ABC的面积的时,求b.26.如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点(A在B的左侧),与y轴交于点N,过A点的直线l:y=kx+n与y轴交于点C,与抛物线y=﹣x2+bx+c的另一个交点为D,已知A(﹣1,0),D(5,﹣6),P点为抛物线y=﹣x2+bx+c上一动点(不与A、D重合).(1)求抛物线和直线l的解析式;(2)当点P在直线l上方的抛物线上时,过P点作PE∥x轴交直线l于点E,作PF∥y轴交直线l于点F,求PE+PF的最大值;(3)设M为直线l上的点,探究是否存在点M,使得以点N、C,M、P为顶点的四边形为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.。
九上数学第一次月考试卷及答案.doc
绝密★启用前2016-2017学年九年级9月月考卷考试范围:1. 用配方法解方程a 2-4a- 1=0,下列配方正确的是()A. (a-2) 2-4=0B. (a+2) 2 - 5=0C. (a+2) 2 - 3=0D. (a-2) 2 - 5=02. 下列命题中正确的是()A. 有一组邻边相等的四边形是菱形B. 有一个角是直角的平行四边形是矩形C. 对角线垂直的平行四边形是正方形D. 一组对边平行的四边形是平行四边形3. 已知x 二・1是一元二次方程x'+mx ・5二0的一个解,则m 的值是()A.・ 4B.・ 5C. 5D. 44. 如图:在菱形ABCD 屮,AC 二6, BD 二8,则菱形的边长为()A. 5B. 10C. 6D. 85. 某种品牌运动服经过两次降价,每件零售价由560元降为315元,己知两次降价的 百分率相同,求每次降价的百分率.设每次降价的百分率为x,下面所列的方程屮正确 的是()A. 560 (1+x)冬315B. 560 (1 - x) 2=315C. 560 (1 - 2x) 2二315 0. 560 (1 - x 2) =3156. 一个平行四边形的两条对角线的长分别为8和10,则这个平行四边形边长不可能是 () A. 2B. 5C. 8D. 107. 关于x 的一元二次方稈3x+m 二0有两个不相等的实数根,则实数m 的取值范围为 ()A. ID >-YB. m<C-7C.D. 4 4 4 48. 如图,点0 (0, 0), A (0, 1)是正方形0AA t B 的两个顶点,以OAi 对角线为边作正 方形0AAB”再以正方形的对角线0A2作正方形OA 1A 2B l ,…,依此规律,则点A&的坐标 是() A. ( - 8, 0) B. (0, 8) C. (0, 8^2)D. (0, 16) 评卷人 得分题号—- 二总分得分评卷人 得分一、选择题(每题3分,共24分)北师大九上一二章;考试时间:100分钟;满分120分;二、填空题(每题3分,共21分)9.若一元二次方程x2・3x+l二0的两根为Xi和X2,则X1+X2二__ .10.已矢口m是关于x的方程X2-2X-3=0的一个根,则2m2-4m= __________ .11.如图,口ABCD中,ZC=110° , BE平分ZABC,则ZAEB的度数等于______ .12.学校课外生物小组的试验园地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道(如图),要使种植面积为600平方米,求小道的宽.若11题图 12题图13. 如果x J - x - 1= (x+1) °,那么x 的值为 __________ .14. 如图,己知:正方形EFGH 的顶点E 、F 、G 、H 分别在正方形ABCD 的边DA 、AB 、BC 、CD 上.若正方形ABCD 的面积为16, AE=1,则正方形EFGII 的面积为 ____________ .15. 如图,把矩形ABCD 沿EF 折耗,使点C 落在点A 处,点D 落在点G 处,若ZCFE 二60° , 且DE 二1,则边BC 的长为 ____三、解答题(16-19题每题8分,20题9分,21题10分, 22题、23题各12分,共75分)16. 解下列方程:(1) (x+3) 2=5 (x+3); (2) x'+4x - 2二0.17. 如图,在平行四边形ABCD 屮,点E, F 分别为边BC, AD 的屮点.求证:四边形AECF18. 如图,用长为22米的篱笆,一面利用墙(墙的最大可用长度为14米),围成中间 隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在BC 上用其他材料 做了宽为1米的两扇小门.(1) 设花圃的一边AB 长为x 米,请你用含x 的代数式表示另一边AD 的长为 ______ 米;(2) 若此时花圃的面积刚好为45m 2,求此时花圃的长与宽.l§14mA—m\—— —D —19. 如图,在AABC 中,AB 二BC, D 、E 、F 分别是BC 、AC 、AB 边上的中点.试卷第2页,总2页(1) 求证:四边形BDEF 是菱形;(2) 若AB 二12cm,求菱形BDEF 的周长.20. 如图,在AABC 中,ZBAC=90° , AD 是中线,E 是AD 的中点,过点A 作AF 〃BC 交 BE 评卷人得分15题图 14题图的延长线于F,连接CF.(1)求证:AD=AF;(2)如果AB二AC,试判断四边形ADCF的形状,并证明你的结论.21・买树一学校为了绿化校园环境,向某园林公司购买了一批树苗,园林公司规定:如果购苗不超过60棵,每棵售价120元;如果购买树苗超过60棵,每增加1棵,所出售的这批树苗每棵售价均降低0.5元,但每棵树苗最低售价不得少于100元,该校最终向园林公司支付树苗款8800元,请问该校共购买了多少棵树苗?22.已知关于x的方程x1 2 3- (k+1) x+4 k2+l=0的两根是一个矩形两邻边的长,且矩形的对角线长为、仮,求k的值.23.如图,在厶ABC44, D是BC边上的一点,E是AD的屮点,过A点作BC的平行线交CE 的延长线于点F,且AF二BD,连接BF.1BD与CD有什么数量关系,并说明理由;2①当AABC满足什么条件时,四边形AFBD是矩形?并说明理由.②当AABC满足什么条件时,四边形AFBD是菱形?并说明理由.参考答案1. D2. B3. A4. A5. B6. D7. B8. D9. 310. 6.11.35°12.(35 - 2x) (20 - x) =60013. 214.1015. 316.(1) xi= - 3, X2二2; (2) xi= - 2+V6> x2= - 2 - V6-17.详见解析18.(1) (24 - 3x); (2)花圃的长为9米,宽为5米.19.(1)见解析(2) 24cm20.(1)见解析;(2)四边形ADCF是正方形.21.该校共购买了80棵树苗.22. 2.23.(1) BD二DC (2)①当AB二AC时,四边形AFBD是矩形.②当ZBAC二90°时,四边形AFBD 是菱形.。
2012年九年级上册数学第一次月考试卷
2012年九年级上册数学第一次月考试卷湖北省宜昌市土门初中2012-2013学年九年级上学期第一次月考数学试题(限时120分钟满分120分)一、选择题(本题满分45分)1、已知△ABC的三边长分别为6,10,8,则△ABC的面积为()A、24B、48C、30D、不能确定2、下列四句话中,正确的是()A、任何一个命题都有逆命题B、任何一个定理都有逆定理C、若原命题是真命题,则其逆命题也是真命题D、若原命题是假命题,则其逆命题也是假命题3、在联欢晚会上,有A、B、C三名同学站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在△ABC的()A、三边中线的交点B、三条角平分线的交点C、三边上高的交点D、三边中垂线的交点4、.如图,加条件能满足AAS来判断⊿ACD≌⊿ABE的条件是()A.∠AEB = ∠ADC ∠C = ∠D B.∠AEB = ∠ADC CD = BEC.AC = AB AD = AE D.AC = AB∠AEB = ∠BDC5、用配方法解方程,经过配方,得到()A.B.C.D.6、用反证法证明“三角形中必有一个内角不小于60°”,先应当假设这个三角形中()A.有一个内角小于60°B.每一个内角都小于60°C.有一个内角大于60°D.每一个内角都大于60°7、方程的根的情况是()A.方程有两个不相等的实数根B.方程有两个相等的实数根C.方程没有实数根D.方程的根的情况与的取值有关8、如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论①AC=AF.②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是()A.1个B.2个C.3个D.4个9、一元二次方程. x 2 _ 4=0的解是()A、B、C、,D、,10、如图,三角形纸片,,沿过点的直线折叠这个三角形,使顶点落在边上的点处,折痕为,则的周长为()A、9 cmB、1 3 cmC、16 cmD、10 cm11、如图,梯形ABCD中,AD∥BC,点M是AD的中点,且MB=MC,若AD=4,AB=6,BC=8,则梯形ABCD 的周长为()A.22 B.24 C.26 D.2812、.若a,b是一元二次方程x2+2x-1=0的两个根,则的值是()A.1B.-1C.2D.-213、如果关于x的一元二次方程x2+4x+a=0的两个不相等实数根x1,x2满足x1x2﹣2x1﹣2x2﹣5=0,那么a的值为()A.3B.-3C.13D.-1314、如图,△ABC是等边三角形,P是∠ABC的平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC 于点F,垂足为点Q.若BF=2,则PE的长为()A.2B.2C.D.315、如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为()A.B.C.5D.二、解答题(共75分)16、(6分)解方程:x2-6x=1(用配方法)17、(6分)解方程:(x-3)2=(2x+1)2(用适当的方法)18、(7分)已知:如图,△ABC中,AB=AC,∠A=120°.(1)用直尺和圆规作AB的垂直平分线,分别交BC、AB 于点M、N(保留作图痕迹,不写作法).(2)猜想CM与BM之间有何数量关系,并证明你的猜想。
初三上册第一次月考数学 试卷
初三上册第一次月考数学试卷(一)(同学们,本学期的第一次月考开始了,希望你仔细审题,认真作答,给自己交上一 份满意的答卷。
选择题、填空题的答案请填写到道题卡的对应位置。
本试卷只交卷二。
) 一、选择题(每小题3分,共54分)1、下列方程中,关于x 的一元二次方程是( )A .(x+1)2=2(x+1) B .+﹣2=0 C .ax 2+bx+c=0D .x 2+2x=x 2﹣12、抛物线y=-(x-8) 2+2的顶点坐标是 ( )A. (2,8)B. (8,2)C. (-8,2)D. (-8,-2)3、已知m 是方程x 2﹣x ﹣1=0的一个根,则代数式m 2﹣m 的值等于( ) A . 1 B . 0 C . ﹣1 D . 24、 4、若函数是二次函数,则m 的值是( )A 、3或6B 、6C 、3D 、-35、下列方程中,有两个不相等的实数根的是( )A . x 2+1=0B . x 2﹣2x+1=0C . x 2+x+2=0D . x 2+2x ﹣1=06、关于x 的一元二次方程(m ﹣1)x 2+5x+m 2﹣3m+2=0,常数项为0,则m 值等于( ) A . 1 B . 0 C . 1或2 D . 27、抛物线y=-6x 2可以看作是由抛物线y=-6x 2+5按下列何种变换得到( )。
A: 向上平移5个单位 B: 向下平移5个单位 C: 向左平移5个单位 D: 向右平移5个单位8、关于x 的一元二次方程(a-1)x 2+x+a 2-1=0的一个根是0,则a 的值为( )A.1B.-1C.1或-1D.0.59、将方程x 2-6x-5=0化为(x+m)2=n 的形式,则m,n 的值分别是( )A. 3和5B. -3和5C. -3和14D. 3和1410、下列函数中,当x >0时,y 随x 的增大而增大的是( )A .y =-x +1B .y =x 2-1C .y = x1D .y =-x 2+111、已知三角形两边长分别为2和9,第三边的长为二次方程x 2-14x+48=0的根,则这个三角形的周长为( )A. 11B. 17C. 17或19D. 1912、对于抛物线y=﹣(x ﹣5)2+3,下列说法正确的是( ) A . 开口向下,顶点坐标(5,3) B . 开口向上,顶点坐标(5,3)C . 开口向下,顶点坐标(﹣5,3)D . 开口向上,顶点坐标(﹣5,3)13、某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1035张照片,如果全班有x 名同学,根据题意,列出方程为( )A . x (x+1)=1035B . x (x ﹣1)=1035×2C . x (x ﹣1)=1035D . 2x (x+1)=103514、一个两位数等于它的个位数的平方,且个位数字比十位数字大3,则这个两位数为( ) A. 25 B. 36 C. 25或36 D. -25或-3615、某车的刹车距离y(m)与开始刹车时的速度x(m/s)之间满足二次函数,若该车某次的刹车距离为5m,则开始刹车时的速度为( ) A.B.C.D.16、已知a ≠0,在同一直角坐标系中函数y =a x 与y =a x 2的图象有可能是( )17、已知A(-4,y 1),B(-3,y 2),C(3,y 3)三点都在二次函数y=-2(x+2)2的图像上,则y 1,y 2,y 3的大小关系为( ).A 、y 2>y 1>y 3B 、y 1>y 2>y 3C 、y 2>y 3 >y 1D 、y 3>y 1>y 218、某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干,支干和小分支的总数是73,则每个支干长出的小分支数是( ) A.7个 B.8个 C.9个 D.10个二、填空题(每小题3分,共18分)19、方程x (x ﹣2)=x 的根是 .20、已知二次函数y=(m-2)x 2的图象开口向下,则m 的取值范围是 .21、已知m 和n 是方程2x 2-5x-3=0的两根,则=________22、已知x=-2是方程x 2+mx-6=0的一个根,则方程的另一个根是_____23、某机械厂七月份生产零件50万个,第三季度生产零件196万个。
