2008年中考数学第一轮复习专题训练十五相似图形
《相似三角形》2008年中考试题汇编一 20095

《相似三角形》2008年中考试题汇编一 2009.5班级__________ 姓名______________ 得分__________一 选择题:1. (2008湘潭)如图,已知D 、E 分别是ABC ∆的AB 、 AC 边上的点,,DE BC //且1ADE DBCE S S :=:8,四边形 那么:AE AC 等于( ) A .1 : 9 B .1 : 3 C .1 : 8 D .1 : 2 2.(2008年常德)如图,已知等边三角形ABC 的边长为2,DE 是它的中位线,则下面四个结论: (1)DE=1,(2)AB 边上的高为3,(3)△CDE ∽△CAB , (4)△CDE 的面积与△CAB 面积之比为1:4. 其中正确的有 ( )A .1个B .2个C .3个D .4个3. (2008福建永春)如图,□ABCD 中,E 为AD 的中点.已知△DEF 的面积为S , 则△DCF 的面积为( ) A .SB .2SC .3SD .4S .4.( 2008茂名市)如图,△ABC 是等边三角形,被一平行于 BC 的矩形所截,AB 被截成三等分,则图中阴影部分的面积 是△ABC 的面积的 ( )A.91 B.92 C.31 D.945.如图,在□ABCD 中,E 是BC 的中点,且∠AEC =∠DCE , 则下列结论不正确...的是( ) A .12BF DF =B . 2AFD EFB S S =△△C .四边形AECD 是等腰梯形 D .AEB ADC ∠=∠6.(黄石市2008)如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与左图中ABC △相似的是( )7.(2008贵阳)在一个晴朗的上午,小丽拿着一块矩形木板在阳光下做投影实验,矩形木板在地面上形成的投影不可能...是()A .B .C .D .ABC((第10题图)BA DEBB第9题图8.右图中的两个三角形是位似图形,它们的位似中心是( ) A .点P B .点O C .点M D .点N9.如下图,DEF △是由ABC △经过位似变换得到的,点O 是 位似中心,D E F ,,分别是OA OB OC ,,的中点,则DEF △ 与ABC △的面积比是( ) A .1:6 B .1:5 C .1:4 D .1:2 10.(荆州市2008)如图,五边形ABCDE 与五边形A ′B ′C ′D ′E ′是位似图形,O 为位似中心,OD=12OD ′,则A ′B ′:AB 为( )A.2:3B.3:2C.1:2D.2:111.(荆州市2008)如图,直角梯形ABCD 中,∠BCD =90°,A D ∥BC ,BC =CD ,E 为梯形内一点,且∠BEC =90°,将△BEC 绕C 点旋转90°使BC 与DC 重合,得到△DCF ,连EF 交CD 于M .已知BC =5,CF =3,则DM :MC 的值为 ( )A.5:3B.3:5C.4:3D.3:4 12.(2008株洲市)在方格纸(每个小方格都是边长为1个单位长度的正方形) 中,我们把每个小正方形的顶点称为格点,以格点为顶点的图形称为格点图 形.如上图中的△ABC 称为格点△ABC . 现将图中△ABC 绕点A 顺时针旋转 180 ,并将其边长扩大为原来的2倍,则变形后点B 的对应点所在的位置是 A .甲 B .乙 C .丙 D .丁A .B .C .D .8题 F(第11题图)(第14题图)13、(2008金华)如中图,是小明设计用手电来测量某古城墙高度的示意图,点P 处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是()A、6米B、8米C、18米D、24米14.(2008浙江绍兴)兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为1米的竹竿的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.4米,则树高为()A.11.5米B.11.75米C.11.8米D.12.25米15.(2008年河南)如图,已知□ABCD中,AB=4,AD=2,E是AB边上的一动点(动点E与点A不重合,可与点B重合),设AE=x,DE的延长线交CB的延长线于点F,设CF=y,则下列图象能正确反映y与x的函数关系的是()。
08~10年中考数学相似难题压轴题汇编
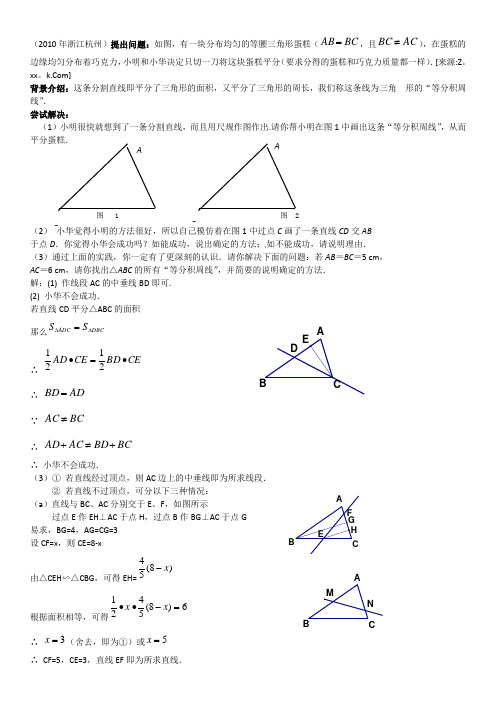
(2010年浙江杭州)提出问题:如图,有一块分布均匀的等腰三角形蛋糕(BC AB =,且AC BC ≠),在蛋糕的边缘均匀分布着巧克力,小明和小华决定只切一刀将这块蛋糕平分(要求分得的蛋糕和巧克力质量都一样).[来源:Z 。
xx 。
]背景介绍:这条分割直线即平分了三角形的面积,又平分了三角形的周长,我们称这条线为三角 形的“等分积周线”.尝试解决:(1)小明很快就想到了一条分割直线,而且用尺规作图作出.请你帮小明在图1中画出这条“等分积周线”,从而平分蛋糕.(2) 小华觉得小明的方法很好,所以自己模仿着在图1中过点C 画了一条直线CD 交AB 于点D .你觉得小华会成功吗?如能成功,说出确定的方法;如不能成功,请说明理由.(3)通过上面的实践,你一定有了更深刻的认识.请你解决下面的问题:若AB =BC =5 cm , AC =6 cm ,请你找出△ABC 的所有“等分积周线”,并简要的说明确定的方法. 解:(1) 作线段AC 的中垂线BD 即可. (2) 小华不会成功.若直线CD 平分△ABC 的面积 那么DBC ADC S S ∆∆=∴ CEBD CE AD ∙=∙2121∴ AD BD = ∵ BC AC ≠∴ BC BD AC AD +≠+∴ 小华不会成功.(3)① 若直线经过顶点,则AC 边上的中垂线即为所求线段.② 若直线不过顶点,可分以下三种情况: (a )直线与BC 、AC 分别交于E 、F ,如图所示过点E 作EH ⊥AC 于点H ,过点B 作BG ⊥AC 于点G 易求,BG=4,AG=CG=3 设CF=x ,则CE=8-x由△CEH ∽△CBG ,可得EH=)8(54x - 根据面积相等,可得6)8(5421=-∙∙x x∴ 3=x (舍去,即为①)或5=x ∴ CF=5,CE=3,直线EF 即为所求直线.A B AB 图 1 图 2(b )直线与AB 、AC 分别交于M 、N, 如图所示由 (a)可得,AM=3,AN=5,直线MN 即为所求直线. (仿照上面给分)(c) 直线与AB 、BC 分别交于P 、Q ,如图所示过点A 作AY ⊥BC 于点Y ,过点P 作PX ⊥BC 于点X由面积法可得, AY=524设BP=x ,则BQ=8-x由相似,可得PX=x2524根据面积相等,可得6)8(252421=-∙∙x x∴52148>+=x (舍去)或2148-=x 而当BP2148-=时,BQ=52148>+,舍去.∴ 此种情况不存在.综上所述,符合条件的直线共有三条.(2010年教育联合体)如图,点P 是菱形ABCD 的对角线BD 上一点,连结CP 并延长,交AD 于E ,交BA 的延长线点F .问:(1) 图中△APD 与哪个三角形全等?并说明理由.[来源:学|科|网] (2) 求证:△APE ∽△FPA .(3) 猜想:线段PC 、PE 、PF 之间存在什么关系?并说明理由. (1) △APD ≌△CPD理由: ∵四边形ABCD 菱形∴AD=CD, ∠ADP=∠CDP又∵PD=PD[来源:学科网ZXXK] ∴△APD ≌△CPD(2) 证明:∵△APD ≌△CPD ∴∠DAP=∠DCP ∵CD ∥BF ∴∠DCP=∠F ∴∠DAP= ∠F 又∵∠APE=∠FPA ∴△APE ∽△FPA(3) 猜想:PF PE PC ∙=2理由: ∵△APE ∽△FPA∴PA PEFPAP =∴ PF PE PA ∙=2 ∵△APD ≌△CPD∴PA=PC ∴PF PE PC ∙=2(2009年湖州)如图,在正三角形ABC 中,D ,E ,F 分别是BC ,AC ,AB 上的点,DE AC ⊥,EF AB ⊥,FD BC ⊥,则DEF △的面积与ABC △的面积之比等于( )A .1∶3B .2∶3C2D3【关键词】等边三角形的性质,相似的性质 【答案】A(2009年山西省)如图,在Rt ABC △中,90ACB ∠=°,3BC =,4AC =,AB 的垂直平分线DE 交BC 的延长线于点E ,则CE 的长为( )A .32B .76C .256D .2【关键词】相似三角形判定和性质;勾股定理;线段和角的概念、性质 【答案】B(2009武汉)如图1,在Rt ABC △中,90BAC ∠=°,AD BC ⊥于点D ,点O 是AC 边上一点,连接BO 交AD 于F ,OE OB ⊥交BC 边于点E . (1)求证:ABF COE △∽△;(2)当O 为AC 边中点,2AC AB =时,如图2,求OFOE 的值; (3)当O 为AC 边中点,AC nAB =时,请直接写出OFOE 的值.【关键词】相似三角形的判定和性质【答案】解:(1)AD BC ⊥,90DAC C ∴∠+∠=°.90BAC BAF C ∠=∴∠=∠ °,. 90OE OB BOA COE ∴∠+∠= ⊥,°, 90BOA ABF ∠+∠= °,ABF COE ∴∠=∠.ABF COE ∴△∽△;(2)解法一:作OG AC ⊥,交AD 的延长线于G .2AC AB = ,O 是AC 边的中点,AB OC OA ∴==.BBAACE D DECF图1图2F BAD E COFG由(1)有ABF COE △∽△,ABF COE ∴△≌△,BF OE ∴=.90BAD DAC ∠+∠= °,90DAB ABD DAC ABD ∠+∠=∴∠=∠°,,又90BAC AOG ∠=∠=°,AB OA =.ABC OAG ∴△≌△,2OG AC AB ∴==. OG OA ⊥,AB OG ∴∥,ABF GOF ∴△∽△, OF OG BF AB ∴=,2OF OF OGOE BF AB ===.解法二:902BAC AC AB AD BC ∠== °,,⊥于D , Rt Rt BAD BCA ∴△∽△.2AD ACBD AB ∴==.设1AB =,则2AC BC BO ==,12AD BD AD ∴===.90BDF BOE BDF BOE ∠=∠=∴ °,△∽△, BD BO DF OE ∴=.由(1)知BF OE =,设OE BF x ==,5DF=,x ∴=. 在DFB △中2211510x x =+,x ∴=.OF OB BF ∴=-=32OF OE ∴==.(3)OFn OE =.BADE COF(2009年上海市)已知∠ABC=90°,AB=2,BC=3,AD ∥BC ,P 为线段BD 上的动点,点Q 在射线AB 上,且满足AB ADPCPQ =(如图1所示).(1)当AD=2,且点Q 与点B 重合时(如图2所示),求线段PC 的长;(2)在图中,联结AP .当32AD =,且点Q 在线段AB 上时,设点B Q 、之间的距离为x ,APQPBC S y S =△△,其中APQS △表示△APQ 的面积,PBC S △表示PBC △的面积,求y 关于x 的函数解析式,并写出函数定义域;(3)当AD AB <,且点Q 在线段AB 的延长线上时(如图3所示),求QPC ∠的大小.【关键词】等腰直角三角形 相似三角形 共高三角形的面积 直角三角形相似的判定【答案】(1)∵Rt △ABD 中,AB=2,AD=2,∴AB ADPC PQ ==1,∠D=45° ∴PQ=PC 即PB=PC ,过点P 作PE ⊥BC ,则BE=2321=BC 。
2008中考数学分类汇编(相似)
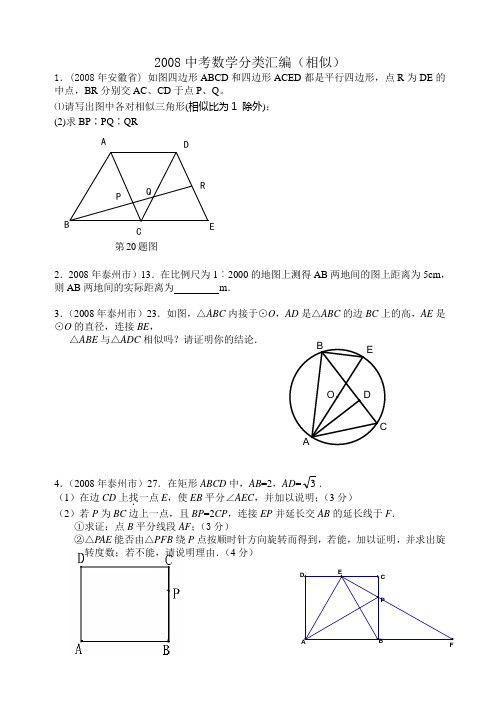
F2008中考数学分类汇编(相似)1.(2008年安徽省) 如图四边形ABCD 和四边形ACED 都是平行四边形,点R 为DE 的中点,BR 分别交AC 、CD 于点P 、Q 。
⑴请写出图中各对相似三角形(相似比为1 除外); (2)求BP ∶PQ ∶QR2.2008年泰州市)13.在比例尺为1︰2000的地图上测得AB 两地间的图上距离为5cm ,则AB 两地间的实际距离为 m . 3.(2008年泰州市)23.如图,△ABC 内接于⊙O ,AD 是△ABC 的边BC 上的高,AE 是⊙O 的直径,连接BE ,△ABE 与△ADC 相似吗?请证明你的结论.4.(2008年泰州市)27.在矩形ABCD 中,AB =2,AD =3. (1)在边CD 上找.一点E ,使EB 平分∠AEC ,并加以说明;(3分) (2)若P 为BC 边上一点,且BP =2CP ,连接EP 并延长交AB 的延长线于F .①求证:点B 平分线段AF ;(3分)②△P AE 能否由△PFB 绕P 点按顺时针方向旋转而得到,若能,加以证明,并求出旋转度数;若不能,请说明理由.(4分)第20题图QPADBCER5.(2008年南京市)7.小刚身高1.7m ,测得他站立在阳光下的影子长为0.85m ,紧接着他把手臂竖直举起,测得影子长为1.1m ,那么小刚举起的手臂超出头顶( ) A .0.5m B .0.55m C .0.6m D .2.2m6.(2008年南京市)如图,已知O 的半径为1,AB 与O 相切于点A ,OB 与O 交于点C ,OD OA ⊥,垂足为D ,则cos AOB ∠的值等于( )A .ODB .OAC .CD D .AB7.(2008年巴中市)若0234x y z ==≠,则23x yz+= .8.(2008福建福州)如图,在ABC △中,D E ,分别是AB AC ,的中点,若5DE =,则BC 的长是 .9.(2008年贵阳市)6.如果两个相似三角形的相似比是1:2,那么它们的面积比是( ) A .1:2B .1:4C.D .2:110。
2008年学业考试冲刺第一模之全等三角形与相似三角形(浙江省台州市)

2008年学业考试冲刺第一模之全等三角形与相似三角形◆考点分析三角形的全等与相似是解决数学中图形问题的两个重要的工具,也是初中数学的重点内容,因此也是中考的重要考查内容。
主要考查以下几方面的内容:1.会运用三角形全等、相似的性质与判定进行有关的计算和推理。
2.能运用三角形全等与相似的知识解决相关的实际问题。
3.能探索解决一些与三角形全等、相似有关的综合性题型。
◆典型例题例1(2006·金华市)如图,△ABC 与△ABD 中, AD 与BC 相交于O 点,∠1=∠2,请你添加一个条件(不再添加其它线段,不再标注或使用其他字母),使AC =BD ,并给出证明.你添加的条件是: . 证明:【解题分析】可以添加的条件有:AD =BC ; OC =OD ;∠C =∠D ;∠CAO =∠DBC 等. 以添加条件AD =BC 为例证明: ∵ AB=AB ,∠1=∠2,BC =AD , ∴ △ABC ≌△BAD . ∴ AC=BD .【每题一得】条件或结论的探究性题型或者是组合命题型题型越来越多地出现在各地的中考题中,这样的题型体现了较高的灵活性和开放性,比较全面地考察了全等相关的知识。
【同类变式】(2006·贺州市)如图,AB CD ,相交于E ,现给出如下三个论断: ①A C ∠=∠;②AD CB =;③AE CE =.请你选择其中两个论断为条件,另外一个论断为结论,构造一个命题. (1)在构成的所有命题中,真命题有 个. (2)在构成的真命题中,请你选择一个加以证明. 你选择的真命题是:__⎫⇒⎬⎭____(用序号表示).ADCEB例 2 (2007南京)如图,在梯形A B C D 中,AD BC ∥,6AB DC AD ===,60ABC ∠= ,点E F ,分别在线段AD DC ,上(点E 与点A D ,不重合),且120BEF ∠=,设AE x =,DF y =.⑴ 求y 与x 的函数表达式;⑵ 当x 为何值时,y 有最大值,最大值是多少?【解题分析】⑴ 由18012060AEB ABE ∴+=-= ∠∠和18012060AEB DEF ∴+=-= ∠∠得ABE DEF ∴=∠∠. 从而可得ABE DEF ∴△∽△∴y 与x 的函数表达式是216y x x =-+ 【每题一得】抓住运动变化过程中的不变量是解决运动变化问题的关键.【同类变式】(2007长沙)如图,□ABCD中,4AB =,3BC =,120BAD =∠,E 为BC 上一动点(不与B 重合),作EF AB ⊥于F ,FE ,DC 的延长线交于点G ,设BE x =,DEF △的面积为S .(1)求证:BEF CEG △∽△;(2)求用x 表示S 的函数表达式,并写出x 的取值范围; (3)当E 运动到何处时,S 有最大值,最大值为多少?例3(2007浙江义鸟).如图1,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),量得他们的斜边长为10cm ,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,但点B 、C 、F 、D 在同一条直线上,且点C 与点F 重合(在图3至图6中统一用F 表示) 小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决。
人教版初中数学图形的相似技巧及练习题附答案解析

人教版初中数学图形的相像技巧及练习题附答案分析一、选择题DG1.如图,四边形ABCD 和四边形AEFG均为正方形,连结CF, DG,则()CFA.2B.2C.3D.3 3232【答案】 B 【分析】【剖析】连结 AC 和 AF,证明△DAG∽△ CAF可得DG的值.CF【详解】连结 AC 和 AF,则 AD AG 2 ,AC AF2∵∠ DAG=45°-∠ GAC,∠ CAF=45°-GAC,∴∠ DAG=∠ CAF.∴△ DAG∽△ CAF.∴ DG AD 2 .CF AC2故答案为: B.【点睛】本题主要考察了正方形的性质、相像三角形的判断和性质,解题的重点是结构相像三角形.2.如图,正方形().1A.3【答案】 D【分析】【剖析】AO ABCD中, E、F 分别为 AB、BC 的中点, AF 与 DE 订交于点O,则DO B.2 5C.2D.1532由已知条件易证△ADE≌△ BAF,从而进一步得△AOD∽△ EAD.运用相像三角形的性质即可求解.【详解】∵四边形ABCD是正方形∴A E=BF, AD=AB,∠ EAD=∠B=90∴△ ADE≌△ BAF∴∠ ADE=∠ BAF,∠ AED=∠ BFA∵∠ DAO+∠ FAB=90,∠ FAB+∠ BFA=90,∴∠ DAO=∠ BFA,∴∠ DAO=∠ AED∴△ AOD∽△ EAD∴AO AE1DO AD2应选: D【点睛】本题考察了正方形的性质,全等三角形的判断与性质,相像三角形的判断与性质.3.如图,在Rt△ABC中,∠ C= 90°, AC= 3,BC= 4,点 D 是 AB 的中点,点P 是直线 BC 上一点,将△BDP沿 DP 所在的直线翻折后,点 B 落在 B1处,若 B1D⊥ BC,则点 P 与点 B之间的距离为()A .1B .5C .1或3D .5或54 4【答案】 D 【分析】 【剖析】分点 B 1 在 BC 左边,点 B 1 在 BC 右边两种状况议论,由勾股定理可 AB=5,由平行线分线段成比率可得 BDBE DE 1 ,可求 BE , DE 的长,由勾股定理可求 PB 的长. ABBCAC 2【详解】解:如图,若点B 1 在 BC 左边,∵∠ C=90°,AC=3,BC=4,∴AB= AC 2 BC 2 5 ∵点 D 是 AB 的中点,∴ B D= 1BA= 522∵B 1D ⊥ BC ,∠ C=90°∴B 1D ∥ AC∴BDBEDE1AB BCAC 2∴ B E=EC=1BC=2, DE=1 AC=322 2∵折叠∴B 1D=BD= 5, B 1P=BP2∴B 1E=B 1D-DE=1∴在 Rt △B 1PE 中, B 1 P 2=B 1E 2+PE 2, ∴BP 2=1+( 2-BP ) 2,∴ B P= 54如图,若点 B 1 在 BC 右边,∵B1E=DE+B1D= 3+5,22∴B1E=4在 Rt△EB1P 中, B1P2=B1E2+EP2,∴BP2=16+( BP-2)2,∴BP=5应选: D.【点睛】本题考察了折叠的性质、直角三角形的性质以及勾股定理.本题难度适中,注意数形联合思想的应用,注意折叠中的对应关系.4.在 Rt△ABC中,∠ BAC= 90°, AD 是△ABC的中线,∠ ADC=45°,把△ADC沿 AD 对折,使点 C 落在 C′的地点, C′D 交 AB 于点 Q,则BQ)的值为(AQA.2B.32D.3 C.2 2【答案】 A【分析】【剖析】依据折叠获得对应线段相等,对应角相等,依据直角三角形的斜边中线等于斜边一半,可得出 AD= DC=BD, AC= AC′,∠ ADC=∠ ADC′= 45°, CD= C′D,从而求出∠ C、∠ B 的度数,求出其余角的度数,可得AQ= AC,将BQ转变为BQ,再由相像三角形和等腰直角AQ AC三角形的边角关系得出答案.【详解】解:如图,过点 A 作 AE⊥BC,垂足为 E,∵∠ ADC= 45°,∴△ ADE 是等腰直角三角形,即AE= DE=2AD,2在 Rt△ABC中,∵∠ BAC= 90°, AD 是△ABC的中线,∴AD= CD= BD,由折叠得: AC= AC′,∠ ADC=∠ ADC′= 45°, CD= C′D,∴∠ CDC′=45°+45°= 90°,∴∠ DAC=∠ DCA=( 180°﹣ 45°)÷2=67.5 °=∠ C′AD,∴∠ B=90°﹣∠ C=∠ CAE= 22.5 °,∠ BQD= 90°﹣∠ B=∠ C′QA= 67.5 °,∴AC′= AQ= AC,由△AEC∽△ BDQ 得:BQ=BD,AC AEBQ=BQ=AD=2AE=2.∴AQ AC AE AE应选: A.【点睛】考察直角三角形的性质,折叠轴对称的性质,以及等腰三角形与相像三角形的性质和判断等知识,合理的转变是解决问题的重点.5.如图,已知点A( 4,0), O 为坐标原点,P 是线段 OA 上随意一点(不含端点O,A),过 P、 O 两点的二次函数极点分别为 B、 C,射线 OB 与之和等于()y1和过 P、 A 两点的二次函数 y2的图象张口均向下,它们的AC 订交于点 D.当 OD=AD=3 时,这两个二次函数的最大值A.5B.45C. 3D. 4 3【答案】 A【分析】【剖析】【详解】过 B 作 BF⊥OA 于 F,过 D 作 DE⊥OA于 E,过 C作 CM⊥OA 于 M,∵ B F ⊥ OA , DE ⊥ OA ,CM ⊥ OA ,∴BF ∥ DE ∥ CM .∵ O D=AD=3, DE ⊥ OA ,∴ O E=EA=1OA=2.2由勾股定理得: DE=5 .设 P ( 2x , 0),依据二次函数的对称性得出OF=PF=x ,∵BF ∥ DE ∥ CM ,∴△ OBF ∽△ ODE ,△ACM ∽△ ADE .BF OF CMAM BF x CM2 x ∴OE ,,即5 2,,解得:DEDE AE52BF5?x , CM5 2 x .22∴BF+CM= 5 .应选 A .6.矩形 ABCO 如图摆放,点B 在 y 轴上,点C 在反比率函数 yk (x > 0)上, OA = 2,ABx=4,则 k 的值为()32 42 A .4B . 6C .D .55【答案】 C【分析】【剖析】依据矩形的性质获得∠A=∠ AOC=90°,OC=AB ,依据勾股定理获得OBOA 2 AB 2 2 5 ,过 C 作 CD ⊥ x 轴于 D ,依据相像三角形的性质获得8 5 4 58 5 4 5CD, OD5,求得C(, )于是获得结论.555【详解】解:∵四边形 ABCO 是矩形,∴∠ A =∠ AOC = 90°, OC =AB ,∵OA =2, AB = 4,∴过 C 作 CD ⊥ x 轴于 D ,∴∠ CDO =∠ A = 90°,∠ COD+∠ COB =∠ COB+∠AOB = 90°,∴∠ COD =∠ AOB ,∴△ AOB ∽△ DOC ,∴OB AB OA , OCCD OD∴ 2 542 , 4CD OD∴CD8 5,OD4 5 ,55∴ C (4 5,8 5),5 532 ∴k,5应选: C .【点睛】本题考察了反比率函数图象上点的坐标特色,反比率函数的性质,矩形的性质,相像三角形的判断和性质,正确的作出协助线是解题的重点.7.如图,在正方形ABCD 中,AB3 ,点M在 CD的边上,且DM1, AEM与ADM对于AMADMA90°获得ABF接 EF,则cosEFC的值是 ()A.1713B.613C.715D.6 65652517【答案】 A【分析】【剖析】过点 E 作HG//AD,交 AB 于 H,交 CD 于 G,作 EN BC 于 N,第一证明VAEH : VEMGEH AE1x ,则 EH 3x ,,则有EM,设 MGMG3DG AH1x ,在 RtVAEH 中利用勾股定理求出x 的值,从而可求EH , BN , CG , EN 的长度,从而可求FN,再利用勾股定理求出EF 的长度,最后利用cos EFC FN即可求解.EF【详解】过点 E 作HG//AD,交 AB 于 H,交 CD 于 G,作 EN BC 于 N,则AHG MGE 90 ,∵四边形ABCD是正方形,∴AD AB3, ABC C D90 ,∴四边形 AHGD,BHEN,ENCG都是矩形.由折叠可得,AEM D90 ,AE AD3,DMEM 1,AEH MEG EMG MEG90,AEH EMG ,VAEH : VEMG ,EH AE1.MG EM3设 MG x ,则 EH 3x , DG AH 1 x在 RtVAEH 中,Q AH2EH 2AE 2,(1 x)2 (3x)232,解得 x 41 (舍去),或 x5EH BN 12,CG CD DG EN65.5Q BF DM1FN BF BN 175.在 Rt△ EFN 中,由勾股定理得,EF EN2FN 213 ,FN17.cos EFC13EF65应选: A.【点睛】本题主要考察正方形,矩形的性质,相像三角形的判断及性质,勾股定理,锐角三角函数,能够作出协助线是解题的重点.8.如图,在平面直角坐标系中,已知点A ( ―3, 6)、B ( ―9,一 3),以原点 O 为位似中心,相像比为,把 △ABO 减小,则点 A 的对应点 A ′的坐标是( )A .( ―1,2)B .( ―9, 18)C .( ―9,18)或( 9,― 18)D .( ―1, 2)或( 1, ―2) 【答案】 D【分析】【剖析】【详解】试题剖析:方法一:∵△ABO 和 △A ′B ′O 对于原点位似,∴△ ABO ∽△ A ′B ′O 且OA'=1.OA3∴ AE =0E= 1.∴ A ′E = 1 AD = 2, OE = 1 OD = 1.∴ A ′(- 1,2) .同理可得 A ′′(1, ―2) .AD 0D333方法二:∵点 A ( ―3, 6)且相像比为 1,∴点 A 的对应点 A ′的坐标是( ―3×1,331 6× ),∴ A ′(- 1,2) .3∵点 A ′′和点 A ′(- 1,2)对于原点 O 对称,∴ A ′′(1, ―2) .故答案选 D.考点:位似变换.9.如图,□ ABCD的对角线 AC, BD 交于点 O, CE均分∠ BCD 交 AB 于点 E,交 BD 于点 F,且∠ ABC= 60°, AB=2BC,连结 OE.以下结论:① EO⊥ AC;②S△AOD=4S△OCF;③ AC:BD =21: 7;④ FB2= OF?DF.此中正确的选项是()A.①②④【答案】 B【分析】【剖析】① 正确.只需证明② 错误.想方法证明B.①③④C.②③④D.①③EC=EA=BC,推出∠ ACB=90°,再利用三角形中位线定理即可判断.BF=2OF,推出 S△BOC=3S△OCF即可判断.③正确.设BC=BE=EC=a,求出 AC, BD 即可判断.④正确.求出BF, OF, DF(用 a 表示),经过计算证明即可.【详解】解:∵四边形ABCD是平行四边形,∴CD∥AB, OD=OB, OA=OC,∴∠ DCB+∠ABC=180°,∵∠ ABC=60°,∴∠ DCB=120°,∵EC均分∠ DCB,1∴∠ ECB=∠ DCB=60°,2∴∠ EBC=∠BCE=∠ CEB=60°,∴△ ECB是等边三角形,∴E B=BC,∵ AB=2BC ,∴EA=EB=EC ,∴∠ ACB=90°,∵ O A=OC , EA=EB ,∴OE ∥BC ,∴∠ AOE=∠ ACB=90°,∴EO ⊥ AC ,故 ① 正确,∵OE ∥BC ,∴△ OEF ∽△ BCF ,∴OE OF 1,BCFB2∴ O F= 1OB ,3∴S △AOD =S △BOC =3S △OCF ,故 ② 错误,设 BC=BE=EC=a ,则 AB=2a , AC= 3 a ,OD=OB= a2( 3 a)27a ,22∴BD= 7 a ,∴AC :BD= 3 a : 7 a= 21 : 7,故 ③ 正确,∵OF= 1 O B=7a ,36∴ B F= 7a ,327 2 , OF?DF= 77 7 72∴BF = 9aa?aaa ,6269∴ B F 2=OF?DF ,故 ④ 正确,应选: B . 【点睛】本题考察相像三角形的判断和性质,平行四边形的性质,角均分线的定义,解直角三角形,解题的重点是灵巧运用所学知识解决问题,学会利用参数解决问题.10. 如图,将图形用放大镜放大,应当属于 ( ).A .平移变换B .相像变换C .旋转变换D .对称变换【答案】 B【分析】【剖析】依据放大镜成像的特色,联合各变换的特色即可得出答案.【详解】解:依据相像图形的定义知,用放大镜将图形放大,属于图形的形状同样,大小不同样,因此属于相像变换.应选: B .【点睛】本题考察的是相像形的辨别,重点要联系图形,依据相像图形的定义得出.11. 如图,在 ABC 中, D , E 分别是边 AB, AC 的中点,ADE 和四边形 BCED 的面积分别记为S 1, S 2 S 1的值为( ),那么 S 2A .1 1 1 2B .4C .D .233【答案】 C【分析】【剖析】依据已知可获得 △ADE ∽△ ABC ,从而可求得其面积比,则不难求得S 1的值.S 2【详解】∵ D , E 分别是边 AB, AC 的中点,∴DE ∥BC ,∴△ ADE ∽△ ABC ,∴DE :BC=1: 2,因此它们的面积比是 1: 4,因此S1=11,S2 4 13应选 C.【点睛】本题考察了三角形的中位线定理和相像三角形的性质:(1)相像三角形周长的比等于相像比;( 2)相像三角形面积的比等于相像比的平方;(3)相像三角形对应高的比、对应中线的比、对应角均分线的比都等于相像比.12.( 2016 山西省)宽与长的比是5 1(约0.618)的矩形叫做黄金矩形,黄金矩形蕴2藏着丰富的美学价值,给我们以协调解均匀的美感.我们能够用这样的方法画出黄金矩形:作正方形 ABCD,分别取 AD、 BC 的中点 E、 F,连结 EF:以点 F 为圆心,以 FD 为半径画弧,交 BC 的延伸线于点 G;作 GH⊥ AD,交 AD 的延伸线于点 H,则图中以下矩形是黄金矩形的是()A.矩形ABFE B.矩形EFCD C.矩形EFGH D.矩形DCGH【答案】D【分析】【剖析】先依据正方形的性质以及勾股定理,求得DF 的长,再依据DF=GF求得 CG 的长,最后依据CG与 CD 的比值为黄金比,判断矩形DCGH为黄金矩形.【详解】解:设正方形的边长为2,则 CD=2, CF=1在直角三角形 DCF 中,DF12225FG5CG51CG51CD2∴矩形 DCGH为黄金矩形应选: D.【点睛】本题主要考察了黄金切割,解决问题的重点是掌握黄金矩形的观点.解题时注意,宽与长的比是51的矩形叫做黄金矩形,图中的矩形 ABGH 也为黄金矩形.213. 如图, △AOB 是直角三角形,∠ AOB = 90°, △AOB 的两边分别与函数y 1, y 2 的xx图象交于 B 、 A 两点,则等于( )2 1 13 A .B .C .D .2243【答案】 A【分析】【剖析】过点 A,B 作 AC ⊥ x 轴 ,BD ⊥x 轴 ,垂足分别为 C,D.依据条件获得 △ACO ∽△ ODB.依据反比率函S OBD( OB1 1利用相像三角形面积比等于相像比 数比率系数 k 的几何意义得出 )2= 2 =S AOC OA12的平方得出OB2OA2【详解】∵∠ AOB =90°,∴∠ AOC+∠ BOD =∠ AOC+∠CAO =90°,∠CAO =∠ BOD ,∴△ ACO ∽△ BDO ,∴S OBD (OB ) 2 , S AOC OA∵S △1 △1 1 ,AOC =2×2=1, S BOD =2×1=2∴ (OB )2= 1 2=OA1∴ OB 2 ,OA 2应选 A .1 ,2【点睛】本题考察了反比率函数图象上点的坐标特色和相像三角形的判断与性质,解题重点在于做协助线,而后获得相像三角形再进行求解14.已知线段 MN = 4cm,P 是线段 MN 的黄金切割点,MP>NP,那么线段MP 的长度等于()A.( 2 5 +2)cm B.( 2 5 ﹣2)cm C.( 5 +1)cm D.( 5 ﹣1)cm 【答案】 B【分析】【剖析】依据黄金切割的定义进行作答.【详解】由黄金切割的定义知,MP 5 1,又 MN=4 ,因此, MP=2 5 2. 因此答案选 B.MN2【点睛】本题考察了黄金切割的定义,娴熟掌握黄金切割的定义是本题解题重点.15.如图,Rt ABO中,AOB290 , AO 3BO ,点B在反比率函数y的图象x上, OA 交反比率函数y k0的图象于点 C ,且 OC2CA ,则 k 的值为(k)xA.2B.4C.6D.8【答案】 D【分析】【剖析】过点 A 作 AD ⊥x 轴,过点 C 作 CE ⊥x 轴,过点B 作 BF ⊥ x 轴,利用 AA 定理和平行证得△COE ∽△ OBF ∽△ AOD ,而后依据相像三角形的性质求得SVBOF (OB )2 1 ,S VOAD OA9 SVCOE(OC 24SVBOF2 1 ,从而求得SV AOD),依据反比率函数比率系数的几何意义求得2OA9S VCOE 4 ,从而求得 k 的值.【详解】解:过点 A 作 AD ⊥ x 轴,过点 C 作 CE ⊥ x 轴,过点 B 作 BF ⊥ x 轴 ∴CE ∥ AD ,∠ CEO=∠BFO=90° ∵AOB 90∴∠ COE+∠ FOB=90°,∠ ECO+∠ COE=90°∴∠ ECO=∠ FOB∴△ COE ∽△ OBF ∽△ AOD又∵ AO 3BO , OC2CA∴ OB1 , OC 2OA3 OA3∴ SV BOF (OB )21 , SVCOE (OC )2 4SVOADOA9SVAODOA 9S VCOE4∴SV BOF∵点 B 在反比率函数y2的图象上x∴SV BOF 212∴ S V COE 4∴ k4 ,解得 k= ±82又∵反比率函数位于第二象限, ∴ k =-8应选: D .【点睛】本题考察反比率函数的性质和相像三角形的判断和性质,正确增添协助线证明三角形相像,利用数形联合思想解题是重点.16.如图,已知△ABC, D、 E 分别在边AB、 AC 上,以下条件中,不可以确立△ADE∽△ ACB 的是()A.∠ AED=∠ B B.∠ BDE+∠ C= 180 °C. AD?BC= AC?DE D. AD?AB= AE?AC【答案】C【分析】【剖析】A、依占有两组角对应相等的两个三角形相像,进行判断即可;B:依据题意可获得∠ ADE=∠ C,依占有两组角对应相等的两个三角形相像,进行判断即可;C、依据两组对应边的比相等且夹角对应相等的两个三角形相像,进行判断即可;D、依据两组对应边的比相等且夹角对应相等的两个三角形相像,进行判断即可.【详解】解: A、由∠ AED=∠ B,∠ A=∠A,则可判断△ADE∽△ ACB;B、由∠ BDE+∠ C=180°,∠ ADE+∠ BDE=180°,得∠ ADE=∠ C,∠ A=∠ A,则可判断△ADE∽△ ACB;C、由AD?BC=AC?DE,得不可以判断△ADE∽△ ACB,一定两组对应边的比相等且夹角对应相等的两个三角形相像.D、由AD?AB=AE?AC得,∠ A=∠ A,故能确立△ADE∽△ ACB,应选:C.本题考察了相像三角形的判断:两组对应边的比相等且夹角对应相等的两个三角形相像(注意,必定是夹角);有两组角对应相等的两个三角形相像.17. 如图,在 □A BCD 中, E 、F 分别是边 BC 、CD 的中点, AE 、 AF 分别交 BD 于点 G 、 H ,则图中暗影部分图形的面积与 □ABCD 的面积之比为( )A .7 : 12B .7 : 24C .13 : 36D .13 : 72【答案】 B 【分析】 【剖析】依据已知条件想方法证明【详解】解:∵四边形 ABCD 是平行四边形,∴AB ∥ CD , AD ∥ BC , AB=CD , AD=BC , ∵ D F=CF , BE=CE ,∴ DHDF1 , BG BE 1 , HBAB2 DG AD2∴ DHBG 1 , BDBD3∴BG=GH=DH ,∴S △ABG =S △AGH =S △ADH , ∴S 平行四边形 ABCD =6 S △AGH ,∴S △AGH : S 平行四边形 ABCD =1: 6, ∵E 、 F 分别是边 BC 、 CD 的中点 ,∴EF 1, BD 2S VEFC1∴S V BCDD 4,SVEFC1∴8 ,S 四边形 ABCDSV AGHSVEFC1 1 7∴6 824 =7∶24,S四边形ABCDBG=GH=DH ,即可解决问题;【点睛】本题考察了平行四边形的性质、平行线分线段成比率定理、等底同高的三角形面积性质,题目的综合性很强,难度中等.18.如图, AB∥ GH∥CD,点 H 在 BC 上, AC 与 BD 交于点 G, AB=2, CD=3,则 GH 长为()A.1B. 1.2C. 2D. 2.5【答案】 B【分析】【剖析】由 AB∥ GH∥ CD可得:△CGH∽△ CAB、△BGH∽△ BDC,从而得:GHCH 、AB BCGH BH CD ,而后两式相加即可.BC 【详解】解:∵ AB∥GH,∴△ CGH∽△ CAB,∴GHCH ,即 GH CH① ,AB BC2BC∵CD∥ GH,∴△ BGH∽△ BDC,∴GHBH,即GHBH② ,CD BC3BCGH GH CH BH1,解得: GH 61.2 .① +②,得:3BC BC52应选: B.【点睛】本题考察了相像三角形的判断和性质,属于基本题型,娴熟掌握相像三角形的判断和性质是解题的重点.19.两个相像三角形的对应边分别是15cm和23cm,它们的周长相差40cm,则这两个三角形的周长分别是()A.45cm ,85cm【答案】 CB. 60cm, 100cm C. 75cm, 115cm D. 85cm, 125cm 【分析】【剖析】依据相像三角形的周长的比等于相像比列出方程,解方程即可.【详解】设小三角形的周长为xcm,则大三角形的周长为(x+40) cm,人教版初中数学图形的相似技巧及练习题附答案解析由题意得,x15,40 x 23解得, x=75,则 x+40=115,应选 C.20.在平面直角坐标系中,已知点E(﹣ 4, 2), F(﹣ 2,﹣ 2),以原点 O 为位似中心,相像比为,把△EFO减小,则点 E 的对应点 E′的坐标是A.(﹣ 2, 1)B.(﹣ 8, 4)C.(﹣ 8,4)或( 8,﹣ 4)D.(﹣ 2,1)或( 2,﹣ 1)【答案】 D【分析】试题剖析:依据位似的性质,减小后的点在原点的同侧,为(-2,1),而后求在另一侧为(2, -1).应选 D考点:位似变换。
2008年中考数学试题分类解析(九)——相似和解直角三角形

2008年中考数学试题分类解析(九)——相似和解直角三角形刘金英
【期刊名称】《中国数学教育(初中版)》
【年(卷),期】2009(000)001
【摘要】@@ "相似和解直角三角形"的内容主要涉及图形的相似、锐角三角函数的知识.一方面,它是解决三角形之间以及直角三角形内部角与角、边与边、角与边之间数量关系的有力工具;另一方面,由于它在实际问题中有着广泛的应用,其相关知识在解决实际问题中具有重要的作用.
【总页数】8页(P80-87)
【作者】刘金英
【作者单位】天津市教育教学研究室
【正文语种】中文
【相关文献】
1.2009年中考数学试题分类解析(九)——相似和解直角三角形 [J], 薛红霞
2.2008年中考数学试题分类解析(七)——圆的认识与证明 [J], 薛红霞
3.2008年中考数学试题分类解析(三)——函数 [J], 孟祥静;朱航
4.2008年中考数学试题分类解析(八)——图形与变换 [J], 韩际清;陈玉华;刘文
5.2008年中考数学试题分类解析(五)——三角形的认识与证明 [J], 游建平;陈元章因版权原因,仅展示原文概要,查看原文内容请购买。
2008年中考数学分类汇编-相似三角形(含答案)
2008年中考数学分类汇编-相似三角形(含答案)D15、(2008山东潍坊)如图,Rt △ABAC 中,AB ⊥AC ,AB =3,AC =4,P 是BC 边上一点,作PE ⊥AB 于E,PD ⊥AC 于D ,设BP =x ,则PD+PE =( )A.35x +B.45x -C.72D.21212525x x-16、 (2008山东烟台)如图,在Rt △ABC 内有边长分别为,,a b c 的三个正方形,则,,a b c 满足的关系式是( )A 、b a c =+ B 、b ac = C 、222b ac =+ D 、22b a c ==17、(2008年广东茂名市)如图,△ABC 是等边三角形,一平行于BC 的矩形所截,AB 被截成三等分,则图中阴影部分的面积是△ABC 的积的 ( )A.91 B.92 C.31 .9419、(2008 江西南昌)下列四个三角形,与左图中的三角形相似的是( )(第7A . B . C .D . ABC D EP((第10题22、(2008江苏南京)小刚身高1.7m ,测得他站立在阳关下的影子长为0.85m 。
紧接着他把手臂竖直举起,测得影子长为1.1m ,那么小刚举起手臂超出头顶 A.0.5m B.0.55m C.0.6mD.2.2m33、(2008湖北黄石)如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与左图中ABC △相似的是( )二、填空题7、(08浙江温州)如图,点1234A A A A ,,,在射线OA 上,点123B B B ,,在射线OB 上,且112233A B A B A B ∥∥,213243A B A B A B ∥∥.若212A B B △,323A B B △的面积分别为1,4,则图中三个阴影三角形面积之和为 . 三、解答题4、 (2008年杭州市)(本小题满分10分)如图:在等腰△ABC 中,CH 是底边上的高线,点P 是线段CH 上不与A .B .C .D . AB C FC B P EH(第16O 1 2 3 4BB 1B 2 B 31 4端点重合的任意一点,连接AP 交BC 于点E,连接BP 交AC 于点F.(1) 证明:∠CAE=∠CBF; (2) 证明:AE=BF;(3) 以线段AE ,BF 和AB 为边构成一个新的三角形ABG (点E 与点F 重合于点G ),记△ABC 和△ABG 的面积分别为S △ABC 和S △ABG ,如果存在点P,能使得S △ABC =S △ABG ,求∠C 的取之范围。
《相似三角形》中考试题选编(含答案)
图3图8相似三角形中考真题试题汇编二、填空题 6、(2008年江苏省南通市)已知∠A =40°,则∠A 的余角等于=________度. 8、(2008年荆州)两个相似三角形周长的比为2:3,则其对应的面积比为___________.9、(2008年庆阳市) 两个相似三角形的面积比S 1:S 2与它们对应高之比h 1:h 2之间的关系为 . 10、(2008年庆阳市) 如图8,D 、E 分别是ABC △的边AB 、AC上的点,则使AED △∽ABC △的条件是 .11、(2008年•南宁市)如图4,已知AB ⊥BD ,ED ⊥BD ,C 是线段BD 的中点,且AC ⊥CE ,ED=1,BD=4,那么AB=13、(2008年广东梅州市)如图3,要测量A 、B 两点间距离,在O 点打桩,取OA 的中点C ,OB 的中点D ,测得CD =30米,则AB =______米.14、(2008新疆建设兵团)如图,一束光线从y 轴上点A (0,1)发出,经过x 轴上点C 反射后,经过点B (6,2),则光线从A 点到B 点经过的路线的长度为 .(精确到0.01)15、如图,ABC △中,AB AC ,D E ,两点分别在边AC AB ,上,且DE 与BC 不平行.请填上一个..你认为合适的条件: ,使ADE ABC △∽△. (不再添加其他的字母和线段;只填一个条件,多填不给分!) 17、(2008上海市)如果两个相似三角形的相似比是1:3,那么这两个三角形面积的比是 .18、 (2008上海市)如图,平行四边形ABCD 中,E 是边BC上的点,AE交B第18题图AB CDEFBD于点F,如果23BEBC=,那么BFFD=.一、选择题1、(2008湖北襄樊)如图1,已知AD与VC相交于点O,AB//CD,如果∠B=40°,∠D=30°,则∠AOC的大小为()A.60°B.70°C.80°D.120°2、(2008湘潭市)如图,已知D、E分别是ABC∆的AB、AC边上的点,,DE BC//且1ADE DBCES S:=:8,四边形那么:AE AC等于()A.1 : 9 B.1 : 3C.1 : 8 D.1 : 23、(2008 台湾)如图G是❒ABC的重心,直线L过A点与BC平行。
08年中考数学第一轮复习相似三角形2
16.相似三角形(二)知识考点:本节知识主要包括相似三角形、相似多边形的性质及应用精典例题:【例1】如图,在△ABC 中,AB =14cm ,95=BD AD ,DE ∥BC ,CD ⊥AB ,CD =12cm ,求△ADE 的面积和周长。
分析:由AB =14cm ,CD =12cm 得ABC S ∆=84,再由DE ∥BC 可得△ABC ∽△ADE ,有2⎪⎭⎫ ⎝⎛=∆∆AB AD S S ABC ADE 可求得ADE S ∆,利用勾股定理求出BC 、AC ,再用相似三角形的性质可得△ADE 的周长。
答案:△ADE 的面积为775cm 2,周长为15 cm 。
例1图EDCBA例2图Q PM F ED C B A变式1图P N MCB A【例2】如图,正方形DEMF 内接于△ABC ,若1=∆A D E S ,4=D EFM S 正方形,求ABC S ∆ 分析:首先利用正方形的面积求出其边长,过A 点作AQ ⊥BC 于Q ,交DE 于P ,利用ADE S ∆可得AP 及AQ 的长,再由△ADE ∽△ABC 求出BC ,从而求得ABC S ∆。
解:∵正方形的面积为4,∴DE =MF =2。
过A 点作AQ ⊥BC 于Q ,交DE 于P∵1=∆ADE S ,∴AP =1∵DE ∥BC ,∴△ADE ∽△ABC ,∴BCDEAQ AP =,即BC 231=∴BC =6,故ABC S ∆=9变式1:如图,已知菱形AMNP 内接于△ABC ,M 、N 、P 分别在AB 、BC 、AC 上,如果AB =21 cm ,CA =15 cm ,求菱形AMNP 的周长。
答案:35 cm变式2:如图,在△ABC 中,有矩形DEFG ,G 、F 在BC 上,D 、E 分别在AB 、AC 上,AH ⊥BC 交DE 于M ,DG ∶DE =1∶2,BC =12 cm ,AH =8 cm ,求矩形的各边长。
变式2图MD E F CA例3图问题一图PNMD CB A答案:724 cm ,748 cm 【例3】如图,已知P 为△ABC 内一点,过P 点分别作直线平行于△ABC 的各边,形成小三角形的面积1S 、2S 、3S ,分别为4、9、49,求△ABC 的面积。
中考数学一轮复习专题解析—相似三角形
中考数学一轮复习专题解析—相似三角形复习目标1.了解相似图形和相似三角形的概念。
2.掌握三角形相似的判定方法和性质并学会运用。
考点梳理一、相似图形1.形状相同的图形叫相似图形,在相似多边形中,最简单的是相似三角形.2.比例线段的相关概念如果选用同一单位量得两条线段b a ,的长度分别为n m ,,那么就说这两条线段的比是nm b a =,或写成n m b a ::=. 注意:在求线段比时,线段单位要统一,单位不统一应先化成同一单位. 在四条线段d c b a ,,,中,如果b a 和的比等于d c 和的比,那么这四条线段d c b a ,,,叫做成比例线段,简称比例线段.注意:(1)当两个比例式的每一项都对应相同,两个比例式才是同一比例式.(2)比例线段是有顺序的,如果说a 是d c b ,,的第四比例项,那么应得比例式为:ad c b =. 3. 比例的性质基本性质:(1)bc ad d c b a =⇔=::;(2)b a c b c c a ⋅=⇔=2::.注意:由一个比例式只可化成一个等积式,而一个等积式共可化成八个比例式,如bc ad =,除了可化为d c b a ::=,还可化为d b c a ::=,b a d c ::=,c a d b ::=,c d a b ::=,b d a c ::=,a b c d ::=,a c b d ::=.更比性质(交换比例的内项或外项):()()()a b c d a c d c b d b ad b c a ⎧=⎪⎪⎪=⇒=⎨⎪⎪=⎪⎩,交换内项,交换外项.同时交换内外项 反比性质(把比的前项、后项交换):cd a b d c b a =⇒=. 合比性质:dd c b b a d c b a ±=±⇒=. 注意:实际上,比例的合比性质可扩展为:比例式中等号左右两个比的前项,后项之间 发生同样和差变化比例仍成立.如:⎪⎪⎩⎪⎪⎨⎧+-=+--=-⇒=d c d c b a b a c c d a a b d c b a 等等. 等比性质: 如果)0(≠++++====n f d b n m f e d c b a ,那么b a n f d b m e c a =++++++++ . 注意:(1)此性质的证明运用了“设k 法” ,这种方法是有关比例计算,变形中一种常用方法.(2)应用等比性质时,要考虑到分母是否为零.(3)可利用分式性质将连等式的每一个比的前项与后项同时乘以一个数,再利用等比性质也成立.4.比例线段的有关定理平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.推论:(1)平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例.(2)平行于三角形一边并且和其它两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例.定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形第三边.5.黄金分割把线段AB 分成两条线段)(,BC AC BC AC >,且使AC 是BC AB 和的比例中项,叫做把线段AB 黄金分割,点C 叫做线段AB 的黄金分割点,其中AB AC 215-=≈0.618AB 例1.如果0ab cd =≠,则下列正确的是( )A .::a c b d =B .::a d c b =C .::a b c d =D .::d c b a = 【答案】B【分析】根据比例的基本性质,列出比例式即可.【详解】解:∵0ab cd =≠,∵::a d c b =,故选:B .例2.两个相似多边形的一组对应边的长分别为6cm ,9cm ,那么它们的相似比为( )A .23B C .49 D .94【答案】A【分析】根据相似多边形的性质求解即可;【详解】两个相似多边形一组对应边的长分别为6cm ,9cm ,∵它们的相似比为:6293=.故选A .二、相似三角形的概念对应角相等,对应边成比例的三角形,叫做相似三角形.相似用符号“∵”表示,读作“相似于” .相似三角形对应边的比叫做相似比(或相似系数).相似三角形对应角相等,对应边成比例.注意:∵对应性:即两个三角形相似时,通常把表示对应顶点的字母写在对应位置上,这样写比较容易找到相似三角形的对应角和对应边.∵顺序性:相似三角形的相似比是有顺序的.∵两个三角形形状一样,但大小不一定一样.∵全等三角形是相似比为1的相似三角形.二者的区别在于全等要求对应边相等,而相似要求对应边成比例.三、相似三角形的等价关系(1)反身性:对于任一ABC ∆有ABC ∆∵ABC ∆.(2)对称性:若ABC ∆∵'''C B A ∆,则'''C B A ∆∵ABC ∆.(3)传递性:若ABC ∆∵C B A '∆'',且C B A '∆''∵C B A ''''''∆,则ABC ∆∵C B A ''''''∆.四、相似三角形的基本定理定理:平行于三角形一边的直线和其它两边(或两边延长线)相交,所构成的三角形与原三角形相似.定理的基本图形:五、三角形相似的判定方法1、定义法:对应角相等,对应边成比例的两个三角形相似.2、平行法:平行于三角形一边的直线和其它两边(或两边的延长线)相交,所构成的三角形与原三角形相似.3、判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.简述为:两角对应相等,两三角形相似.4、判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.简述为:两边对应成比例且夹角相等,两三角形相似.5、判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似.简述为:三边对应成比例,两三角形相似.6、判定直角三角形相似的方法:(1)以上各种判定均适用.(2)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.(3)直角三角形被斜边上的高分成的两个直角三角形与原三角形相似.直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(相似图形)
一、填空题:(每题3分,共36分)
1、若3a=5b,则
a
b
=_____。
2、若线段a、b、c、d成比例且a=3cm,b=6cm,c=5cm,则d=____cm。
3、已知,线段AB=15,点C在AB上,且AC∶BC=3∶2,则BC=_____。
4、甲、乙两地的实际距离20千米,则在比例尺为1∶1000000 的地图上两地间的距离应为____厘米。
5、已知△ABC∽△A'B'C',AB=21cm,A'B'=18cm,则△ABC与△A'B'C'的相似比k=_
___。
6、如图,△ABC中,∠ACB=90°,CD⊥AB于D,则图中有____对相似三角形。
7、如图,△ABC中,DE∥BC,已知
DE
BC
=
2
5
,则
AE
AC
=____。
8、两个相似三角形对应高的比为2∶3,且已知较小的三角形的面积为4,
则较大的三角形的面积为____。
9、如图,已知:∠BAC=∠DAE,当______时,△ABC∽△ADE。
10、如图,□ABCD中,E为DC边的中点,AE交BD于O,若DO=4cm,BO=__cm。
第6题第7题第9题第10题第12题
11、在同一时刻物高与影长成比例,小华量得综合楼的影长为6米,同一时刻她量得身高1.6
米的同学的影长为0.6 米,则可知综合楼高为____。
12、在长8cm,宽4cm 的矩形中截去一个矩形(图中阴影部分)使留下的矩形与矩形相似,
那么留下的矩形的面积为____cm2。
二、选择题:(每题 4 分,共24 分)
1、以下列长度(同一单位)为长的四条线段中,不成比例的是()
A、2,5,10,25
B、4,7,4,7
C、2,
1
2
,
1
2
,4D、2,5,25,52
2、两地的距离是500 米,而地图上的距离为10 厘米,则这张地图的比例尺为()
A、1∶50
B、1∶500
C、1∶5000
D、1∶50000
3、下列各组图形不一定相似的是()
A、两个等边三角形
B、各有一个角是100°的两个等腰三角形
C、两个正方形
D、各有一个角是45°的两个等腰三角形
4、△ABC 的三边之比为3∶4∶5,若△ABC∽△A'B'C' ,且△A'B'C' 的最短边长为6,则△A'B'C'的周长为()
A、36
B、24
C、18
D、12
5、如图,D是BC上的点,∠ADC=∠BAC,则下列结论正确的是()
A、△ABC∽△DAC
B、△ABC∽△DAB
C、△ABD∽△ACD
D、以上都不对6、如图,△ABC中,AB、AC边上的高C
E、BD相交于P点,图中
所有的相似三角形共有()
A、2 个
B、3 个
C、4 个
D、5 个
三、解答题:(每题9 分,共54 分)
1、在△ABC和△A'B'C'中,已知AB=3cm,BC=4cm,AC=5cm,
A D
E
C
B
O
九年级数学15-1(共4页)
九年级数学15-2(共4页)
A'B'=18cm ,B'C'=24cm ,A'C'=30cm ,试说明△ABC ∽△A'B'C'。
2、如图,DE ∥AB ,AD ∥BC ,求证:△EAD ∽△ACB 。
3、如图,∠1=∠2,AE =12,AD =15,AC =20,AB =25。
证明:△ADE ∽△ABC 。
4、如图,以O 点为位似中心,把四边形ABCD 放大到原来的 2 倍(不写画法)。
5、利用方格将三角形放大两倍。
6、已知:AB AE =AC
AD
,AD =3,BD =5,AC =6,求CE 的长。
五、(12分)如图,AB 是斜靠在墙上的长梯,梯脚B 距墙脚 60cm ,梯上点D 距离50cm ,BD 长55cm ,求出梯子的长。
六、(12分)如图,在边长为 1的正方形网格上有P 、A 、B 、C 四点。
(1)求证:△PAB ∽△PCA (2)求证:∠APB +∠PBA =45°
四、(12分)为了测量水塘边A 、B 两点之间的距离,在可以看到A 、B 的E 处,取AE 、BE 延长线上的C 、D 两点,使CD ∥AB ,如果测量得CD =5米,AD =15米,ED =3米,你能求出AB 两点之间的距离吗?
A B
C D A
E C
B A
E
C B D
┌
┌
答案:
(十五)
一、1、5
3
2、10
3、6
4、2
5、
7
6
6、3
7、
2
5
8、99、∠ADE=∠B10、8
11、16米12、8
二、1、C2、C3、D4、B5、A6、C
三、1、∵AB
AB
=
1
6
,
BC
B'C'
=
1
6
,
AC
A'C'
=
1
6
∴
AB
A'B'
=
BC
B'C'
=
AC
A'C'
∴△ABC∽△A'B'C'
2、∵DE∥AB∴∠DEA=∠CAB又∵AD∥BC∴∠DAE=∠BCA∴△EAD∽△ACB
3、∵∠1=∠2∴∠DAE=∠BAC又∵AD
AB
=
AE
AC
∴△ADE∽△ABC
4-5、略6、∵AB
AE
=
AC
AD
∴
3+5
6-x
=
6
3
∴x=2
四、∵AB
CD
=
AE
ED
∴
AB
5
=
12
3
∴AB=20米五、∵
AD
AB
=
DE
BC
∴
x-55
x
=
50
60
x=330cm
六、①PC=1PA=5PB=5∴PA
PC
=
BP
PA
又∵∠APC=∠BPA∴△PAB∽△PCA
②∵∠B=∠PAC∴∠APB+∠PBA=∠APB+∠PAC=∠ACB=45°
A
P B
C
九年级数学15-3(共4页)。
