数学文卷·2019届四川省德阳市高三二诊考试

合集下载

2019届四川省德阳市高三一诊考试数学(文)试题(word版)

2019届四川省德阳市高三一诊考试数学试卷（文史类）第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合，则（）A. B. C. D.【答案】C2.设是虚数单位，复数为纯虚数，则实数的值为（）A. B. C. D.【答案】A3.将甲、乙两个篮球队10场比赛的得分数据整理成如图所示的茎叶图，由图可知：A. 甲队得分的众数是3B. 甲、乙两队得分在分数段频率相等C. 甲、乙两队得分的极差相等D. 乙队得分的中位数是38.5【答案】D4.一个三棱锥的三视图是三个直角三角形，如图所示，则三棱锥的外接球的表面积为A. B. C. D. 13【答案】A5.如图所示的程序框图输出的结果是A. 34B. 55C. 78D. 89【答案】B6.已知等差数列中，，是函数的两个零点，则的前项和等于（）A. B. C. D.【答案】C7.若函数在上是增函数，那么的最大值为A. B. C. D.【答案】B8.我国古代著名的数学家刘徽著有《海岛算经》.内有一篇：“今有望海岛，立两表齐、高三丈，前后相去千步，今后表与前表相直，从前表却行百二十三步，人目著地望岛峰，与表末参合.从后表却行百二十七步，人目著地取望岛峰，亦与表末参合.问岛高及去表各几何？”（参考译文．．．．：假设测量海岛，立两根标杆，高均为5步，前后相距1000步，令前后两根标杆的底部和岛的底部在同一水平直线上，从前标杆退行123步，人的视线从地面（人的高度忽略不计）过标杆顶恰好观测到岛峰，从后标杆退行127步，人的视线从地面过标杆顶恰好观测到岛峰，问岛高多少？岛与前标杆相距多远？）（丈、步为古时计量单位，三丈=5步）.则海岛高度为A. 1055步B. 1255步C. 1550步D. 2255步【答案】B9.在边长为4的菱形中，，为的中点，为平面内一点，若，则A. 16B. 14C. 12D. 8【答案】B10.已知实数、满足，若恒成立，那么的取值范围是A. B. C. D.【答案】D11.已知点在动直线上的投影为点，若点，那么的最小值为A. 2B.C. 1D.【答案】D12.已知点是函数的图像上的一个最高点，点、是函数图像上相邻两个对称中心，且三角形的面积为1.若，使得，则函数的解析式为A. B.C. D.【答案】A第Ⅱ卷（共90分）本卷包括必考题和选考题两部分，第13～21题为必考题，每个试题考生都必须作答，第22、23题为选考题，考生根据要求作答.二、填空题（每题5分，满分20分，将答案填在答题纸上）13.若函数，，则__________．【答案】14.已知正数、的等差中项为1，则的最小值为__________．【答案】15.已知有相同焦点、的椭圆和双曲线交于点，，椭圆和双曲线的离心率分别是、，那么__________（点为坐标原点）．【答案】16.已知函数，若存在唯一的整数，使得成立，则实数的取值范围为__________．【答案】三、解答题（解答应写出文字说明、证明过程或演算步骤.）17.已知等比数列的各项均为正数，，公比为；等差数列中，，且的前项和为，，.（1）求与的通项公式；（2）设数列满足，求的前项和.【答案】（1），，（2）【解析】试题分析：（1）利用基本元的思想，将已知条件转化为，联立方程组求得，由此求得通项公式；（2）化简的表达式得到，利用裂项求和法求其前项和.试题解析：（1）设数列的公差为，∵，，∴，，，，，，（2）由题意得：，，.18.在中，角、、对应的边分别为、、，若.（1）求角；（2）若且时，求的面积.【答案】（1）；（2）.【解析】【分析】（1）利用正弦定理和三角恒等变换化简即得C的值.(2)先根据及得到，，再利用正弦定理求出b最后利用三角形的面积公式求面积.【详解】（1）在中，由正弦定理得：即所以（不合题意舍去）或且得：.（2）由（1）知及得：得：即整理得：∵∴所以即，在中由正弦定理得：即所以.【点睛】本题主要考查正弦定理解三角形，考查三角恒等变换和三角形的面积的求法，意在考查学生对这些知识的掌握水平和分析推理计算能力.19.某市工业部门计划对所辖中小型企业推行节能降耗技术改造，下面是对所辖企业是否支持技术改造进行的问卷调查的结果：已知从这560家企业中随机抽取1家，抽到支持技术改造的企业的概率为.（1）能否在犯错误的概率不超过0.025的前提下认为“是否支持节能降耗技术改造”与“企业规模”有关？（2）从支持节能降耗的中小企业中按分层抽样的方法抽出8家企业，然后从这8家企业选出2家进行奖励，分别奖励中型企业20万元，小型企业10万元.求奖励总金额为20万元的概率.附：【答案】（1）能；（2）.【解析】【分析】(1)先完成列联表，再利用独立性检验求，所以能在犯错误的概率不超过0.025的前提下认为“是否支持节能降耗技术改造”与“企业规模”有关.（2）利用古典概型求奖励总金额为20万元的概率.【详解】（1）由从这560家企业中随机抽取1家，抽到支持技术改造的企业的概率为.可知：支持技术改造的企业共有320家，故列联表为所以故能在犯错误的概率不超过0.025的前提下认为“是否支持节能降耗技术改造”与“企业规模”有关. （2）由（1）可知支持技术改造的企业中，中小企业比为.所以按分层抽样的方法抽出8家企业中2家中型企业，分别用、表示，6家小型企业，分别用1、2、3、4、5、6表示.则从中选取2家的所有可能为、、、、、、、、、、、、、12、13、14、15、16、23、24、25、26、34、35、36、45、46、56，共28种.其中总奖金为20万的有12、13、14、15、16、23、24、25、26、34、35、36、45、46、56，共15种.所以奖励总金额为20万元的概率为.【点睛】本题主要考查独立性检验和古典概型，意在考查学生对这些知识的掌握水平和分析推理能力.20.已知函数和函数.（1）求函数的单调区间；（2）已知，且函数有三个零点、、，若成立，求实数的取值范围.【答案】（1）单调增区间为，；（2）.【解析】【分析】(1)先分别求出x＞2和x≤2的单调区间，再综合得到函数的单调区间.(2)先讨论x＞2的零点情况，再讨论x≤2的零点情况. 当时，先求出，再解不等式得解.【详解】（1）显然时，单增.当时，令得：.或时，；时，.故函数的单调增区间为，；单调减区间为.（2）当时，令得：当时，令即：即：得，（舍去）所以.由得：即且，故只要解得：综上，实数的取值范围为.【点睛】本题主要考查利用导数求函数的单调区间，考查函数的零点和解不等式，意在考查学生对这些知识的掌握水平和分析推理能力.21.已知函数在处的切线斜率为.（1）若函数在上单调，求实数的最大值；（2）当时，若存在不等的使得，求实数的取值范围.【答案】（1）；（2）.【解析】【分析】(1)先根据切线的斜率求出，再根据函数单调，得到恒成立，求出b的最大值.(2)转化为存在不等的，且使得，得函数在上单调递增.结合（1）进而得到k＞0.【详解】（1）函数在处的切线斜率为解得.所以，故因为函数在上单调故或在上恒成立.显然即在上不恒成立.所以恒成立即可.因为可知在上单减，单增故，所以实数的最大值为1.（2）当时，由（1）知函数在上单调递增不妨设，使得即为存在不等的，且使得.其否定为：任意，都有即：函数在上单调递增.由（1）知：即所以若存在不等的使得实数的取值范围为.【点睛】本题主要考查利用导数研究函数的单调性问题和最值，考查利用导数研究不等式的存在性问题，意在考查学生对这些知识的掌握水平和分析推理能力.请考生在22、23两题中任选一题作答.注意：只能做所选定的题目，如果多做，则按所做的第一题记分.作答时，请用2B铅笔在答题卡上将所选题号后的方框涂黑.22.已知圆和圆的极坐标方程分别为和，曲线分别交圆和圆于、两点，以极点为原点，极轴为轴正半轴建立直角坐标系.（1）将圆和圆的极坐标方程化为直角坐标方程；（2）已知点在圆上，求三角形面积取最大值时，点的直角坐标.【答案】（1）圆的直角坐标方程为,圆的直角坐标方程为；（2）. 【解析】【分析】(1)利用极坐标的公式得到圆和圆的直角坐标方程.(2)先求出|AB|=2,分析得到点C到直线的距离最大时，三角形面积取最大值.【详解】（1）由题得圆的直角坐标方程为，圆的直角坐标方程为.（2）将代入圆和圆的极坐标方程得、所以，要使三角形面积取最大值，只要圆上的点到直线的距离最大,与直线AB垂直过点（0,2）的直线方程为，解得点的直角坐标为.【点睛】本题主要考查极坐标与直角坐标的互化，考查直线和圆的位置关系和三角形面积的最值的求法，意在考查学生对这些知识的掌握水平和分析推理能力.23.已知函数，.（1）解不等式；（2）若存在、，使得成立，求实数的取值范围.【答案】（1）；（2）.【解析】【分析】(1)利用零点讨论法解不等式得解.(2) 由（1）可知的值域为，显然的值域为,所以，所以实数的取值范围为.【详解】（1）因为故由得：或或解得原不等式解集为：.（2）由（1）可知的值域为，显然的值域为.依题意得：所以实数的取值范围为.【点睛】本题主要考查零点讨论法解绝对值不等式，考查函数的值域问题，意在考查学生对这些知识的掌握水平和分析推理能力.。

2019年四川省南充市高2019届高2016级文科数学二诊试题及详细解析

2019年四川省南充市高2016级文科数学试题二诊试卷文科数学试题及详细解析一、选择题：本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合{|2P x x k ==,}k Z ∈,{|21Q x x k ==+,}k Z ∈,则( ) A.P Q = B.P Q ÜC.P Q ÝD.P Q =∅I2.(5分)复数21i-等于( ) A.1i +B.1i -C.1i -+D.1i --3.(5分)如图是2012年在某大学自主招生考试的面试中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )A.84,4.84B.84,1.6C.85,1.6D.85,44.(5分)已知()f x 是定义在R 上的奇函数,当0x …时,()(1)f x x x =+,则(1)(f -= ) A.2-B.1-C.0D.25.(5分)在等比数列{}n a 中,2623a a π=g ,则24sin()(3a π-= ) A.12-B.123D.3 6.(5分)P 是双曲线22134x y -=的右支上一点1F ,2F 分别为双曲线的左右焦点,则△12PF F 的内切圆的圆心横坐标为( ) 3 B.27D.37.(5分)已知函数()sin()(0f x A x A ωϕ=+>,0)ω>在6x π=处取得最小值,则( )A.()6f x π+一定是奇函数B.()6f x π+一定是偶函数C.()6f x π-一定是奇函数D.()6f x π-一定是偶函数8.(5分)阅读程序框图,如果输出的函数值在区间11[,]42内,则输入的实数x 的取值范围是()A.(-∞,2]-B.[2-,1]-C.[1-,2]D.[2,)+∞9.(5分)已知m ,n 为异面直线,m ⊥平面α,n ⊥平面β.直线l 满足l m ⊥,l n ⊥,l α⊂/,l β⊂/,则( ) A.//αβ且//l αB.αβ⊥且l β⊥C.α与β相交,且交线垂直于lD.α与β相交,且交线平行于l10.(5分)椭圆的焦点为1F ,2F ,过1F 的最短弦PQ 的长为10,△2PF Q 的周长为36,则此椭圆的离心率为( )A.3B.13C.23D.6 11.(5分)如图,原点O 是ABC ∆内一点,顶点A 在x 上,150AOB ∠=︒,90BOC ∠=︒,||2OA =u u u r,||1OB =u u u r ,||3OC =u u u r ,若OC OA uOB λ=+u u u r u u u r u u u r ,则(uλ= )A.C.12.(5分)定义在R 上的函数()f x 满足(4)()f x f x +=,21,11()|2|1,13x x f x x x ⎧-+-=⎨--+<⎩剟….若关于x的方程()0f x ax -=有5个不同实根,则正实数a 的取值范围是( )A.11(,)43B.11(,)64C.1(16)6-D.1(,86-二、填空题：本大题共4小题,每小题5分,共20分.13.(5分)已知变量x ,y 满足202300x y x y x -⎧⎪-+⎨⎪⎩………,则5z x y =++的最大值为 . 14.(5分)设等差数列{}n a 满足：127a a +=,136a a -=-.则5a = . 15.(5分)直线12y x b =+是曲线y lnx =的一条切线,则实数b 的值为 . 16.(5分)设点P是函数y =,点(2Q a ,3)()a a R -∈,则||PQ 的最小值为 .三、解答题；共70分.解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题：共60分 17.(12分)ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c .已知45B =︒,b =cos C =. (1)求a ；(2)设D 为AB 边的中点,求CD 的长.18.(12分)某地区为了调查高粱的高度、粒的颜色与产量的关系,对700棵高粱进行抽样调查,得到高度频数分布表如下：表1：红粒高粱频数分布表表2：白粒高粱频数分布表(1)估计这700棵高粱中红粒高粱的棵数；(2)画出这700棵高粱中红粒高粱的频率分布直方图；(3)估计这700棵高粱中高粱高()cm 在[165,180)的概率.19.(12分)如图,在六面体ABCDEFG 中,平面//ABC 平面DEFG ,AD ⊥平面DEFC ,ED DG ⊥,//EF DG ,且22AB AD DE DG AC BF =====.(1)求证：//BF 平面ACGD ；(2)若1AC =,求点D 到平面GFBC 的距离20.(12分)已知抛物线2:2(0)C y px P =>的焦点到直线:22l y x =+45. (1)求抛物线C 的方程；(2)若O 为坐标原点,(1,2)A -,是否存在平行于OA 的直线l ',使得直线l '与抛物线C 有公共点,且直线OA 与l '5？若存在,求出直线的方程；若不存在说明理由. 21.(12分)已知函数()()f x x ln x =---,[x e ∈-,0),其中e 为自然对数的底数. (1)求()f x 的单调区间和极值； (2)求证：()1()2ln x f x x -+>. (二)选考题：共10分.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分.[选修4-4：坐标系与参数方程]22.(10分)在直角坐标系xOy 中,曲线21:(21x C y ααα⎧=+⎪⎨=+⎪⎩为参数),在以O 为极点,x 轴的非负半轴为极轴的极坐标系中,直线:sin cos l m ρθρθ+= (1)若0m =,判断直线l 与曲线C 的位置关系； (2)若曲线C 上存在点P 到直线l 2,求实数m 的取值范围. [选修4-5：不等式选讲]23.已知函数()|4|||()f x x x a a R =-+-∈的最小值为a (1)求实数a 的值； (2)解不等式()5f x ….2019年四川省南充市高2016级文科数学试题二诊试卷(文科)参考答案与试题解析一、选择题：本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.【解答】解：P 表示偶数集,Q 表示奇数集； P Q ∴=∅I .故选：D .【解答】解：原式2(1)1(1)(1)i i i i +==+-+.故选：A .【解答】解：去掉一个最高分93和一个最低分79后的数据为84,84,86,84,87,共5个数据.所以平均数为1(8438687)855⨯++=.方差为22218[3(8485)(8685)(8785)] 1.655⨯-+-+-==.故选：C .【解答】解：()f x Q 是定义在R 上的奇函数, (1)f f ∴-=-(1)2=-,故选：A .【解答】解：在等比数列{}n a 中,2623a a π=g , 可得242623a a a π==g ,则24sin()sin 33a ππ-==,故选：C .【解答】解：如图所示：1(F 0)、2F 0),设内切圆与x 轴的切点是点H ,1PF 、2PF 与内切圆的切点分别为M 、N ,Q 由双曲线的定义可得12||||2PF PF a -==由圆的切线长定理知,||||PM PN =,故12||||MF NF -=即12||||23HF HF -=,设内切圆的圆心横坐标为x ,则点H 的横坐标为x , 故(7)(7)23x x +--=,3x ∴=. 故选：A .【解答】解：函数()sin()(0f x A x A ωϕ=+>,0)ω>在6x π=处取得最小值,即函数()f x 关于直线6x π=对称,将函数()f x 的图象向左平移6π个单位后其图象关于直线0x =对称, 即将函数()f x 的图象向左平移6π个单位后其图象对应的函数()6f x π+为偶函数,故选项B 正确, 故选：B .【解答】解：分析程序中各变量、各语句的作用再根据流程图所示的顺序,可知：该程序的作用是计算分段函数2,[2,2]()2,(,2)(2,)xx f x x ⎧∈-⎪=⎨∈-∞-+∞⎪⎩U 的函数值.又Q 输出的函数值在区间11[,]42内,[2x ∴∈-,1]-故选：B .【解答】解：由m ⊥平面α,直线l 满足l m ⊥,且l α⊂/,所以//l α,又n ⊥平面β,l n ⊥,l β⊂/,所以//l β.由直线m ,n 为异面直线,且m ⊥平面α,n ⊥平面β,则α与β相交,否则,若//αβ则推出//m n ,与m ,n 异面矛盾.故α与β相交,且交线平行于l . 故选：D .【解答】解：设椭圆方程为22221x y a b +=,Q △2PF Q 的周长为36,22364PF QF PQ a ∴++==,解得9a =,Q 过1F 的最短弦PQ 的长为10221(3610)132PF QF ∴==-=,在直角三角形12QF F 中,根据勾股定理得,212C ==, 6c ∴=,∴6293c e a === 故选：C .【解答】解：建立如图所示的直角坐标系,则(2,0)A,(B ,1)2, 1(2C -,,因为OC OA OB λμ=+u u u r u u u r u u u r ,由向量相等的坐标表示可得：1222λμ⎧=-⎪⎪⎨⎪=⎪⎩,解得：1λμ=-⎧⎪⎨=⎪⎩即3μλ=,故选：D.【解答】解：由题意可得函数()f x是以4为周期的周期函数,做出函数()y f x=与函数y ax=的图象,由图象可得方程2(4)1y x ax=--+=即2(8)150x a x+-+=在(3,5)上有2个实数根,由2(8)60093(8)150255(8)1508352aaaa⎧=-->⎪+-+>⎪⎪⎨+-+>⎪-⎪<<⎪⎩V解得08215a<<-.再由方程()f x ax=在(5,6)内无解可得61a>,16a>.综上可得182156a<<-,故选：D.二、填空题：本大题共4小题,每小题5分,共20分.【解答】解：由约束条件20230x yx yx-⎧⎪-+⎨⎪⎩………作出可行域如图,联立20230x y x y -=⎧⎨-+=⎩,解得(1,2)A ,化目标函数5z x y =++为5y x z =-+-,由图可知,当直线5y x z =-+-过点(1,2)A 时,直线在y 轴上的截距最大,z 有最大值为8. 故答案为：8.【解答】解：Q 等差数列{}n a 满足：127a a +=,136a a -=-.∴1111726a a d a a d ++=⎧⎨--=-⎩,解得12a =,3d =,51424314a a d ∴=+=+⨯=.故答案为：14.【解答】解：设切点为(,)P m n ,则n lnm =,12n m b =+,y lnx =的导数为1y x'=, 即有112m =, 解得2m =,2n ln =,21b ln =-. 故答案为：21ln -.【解答】解：由函数24(1)y x =---,得22(1)4x y -+=,(0)y …, 对应的曲线为圆心在(1,0)C ,半径为2的圆的下部分, Q 点(2,3)Q a a -,2x a ∴=,3y a =-,消去a 得260x y --=,即(2,3)Q a a -在直线260x y --=上,过圆心C 作直线的垂线,垂足为A , 则||||225214min PQ CA =-=-=-+.故答案为：52-.三、解答题；共70分.解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题：共60分【解答】解：(1)由题意得：25cos C =,22sin cos 1C C +=,0C π<<, ∴2255sin 1()5C =- 45B =︒Q ,A B C π++=,∴310sin sin()sin cos cos sin A B C B C B C =+=+=, ∴由正弦定理sin sin a bA B=,得：32a =. (2)解法一：Q 在ABC ∆中,由余弦定理得2222cos 4c b a ab C =+-=,2AB c ∴==,1BD AD ∴==,Q 在DBC ∆中,2222cos 13CD BD BC BD BC B =+-⨯⨯=,13CD ∴=.解法二：延长CD 到E 点,使CD DE =,连接AE ,BE , 则四边形ACBE 为平行四边形.222(2)2cos()52CD BE BC BE BC ACB π=+-⨯-∠=Q ,∴13CD =【解答】解：(1)样本中红粒高粱为40棵,白粒高粱30棵,由抽样比例可得这亩地中红粒高粱棵数为400.(2)频率分布直方图如图所示：由表1、表2可知,样本中高在[165,180)的棵数为5141363142+++++=,样本容量为70, ∴样本中高在[165,180)的频率423705f ==. 【解答】解：(1)证明：已知如右图：Q 平面//ABC 平面DEFG ,平面ABC ⋂平面ADEB AB =, 平面DEFG ⋂平面//ADEB DE AB DE =∴.AB DE AB DE ==Q Q ,ADEB ∴为平行四边形,//BE AD .(2分)AD ∴⊥平面DEFG ,BE ⊂Q 平面BEF ,∴平面BEF ⊥平面DEFG .(3分)取DG 的中点为M ,连接AM 、FM ,则由已知条件易证四边形DEFM 是平行四边形,//DE FM ∴,又//AB DE Q ,//AB FM ∴(4分)∴四边形ABFM 是平行四边形,即//BF AM ,又BF ⊂/平面ACGD 故//BF 平面ACGD .(6分)(2)由(1)得//BF 平面ACGD ,所以//BF CG ,根据几何关系得：5BF FG ==以DG 、DE 、DA 为方向建立空间直角坐标系,则(2B ,0,2),(2F ,1,0),(0G ,2,0),所以(0,1,2)FB =-u u u r ,(2,1,0)FG =-u u u r设平面BGF 法向量为(,,)n x y z =r ,则2020nFB y z nFGx y ⎧=-=⎪⎨=-+=⎪⎩r r 取1y =得11(,1,)22n =r 所以点D 到平面BGF (即平面)BFGC 的距离||23||n DG d n ==⋯u u u r r g r (12分)【解答】解：(1)抛物线的焦点为(,0)2P ,455d ==,得2p =,6p =-(舍去)； ∴抛物线C 的方程为24y x =⋯(4分) (2)假设存在符合题意的直线l '其方程为2y x t =-+由224y x t y x=-+⎧⎨=⎩得2220y y t +-= Q 直线l '与抛物线C 有公共点,∴△480t =+…解得12t -… 此外,由直线OA 与l '的距离15d 55解得12t =± 因为11[,)2-∉+∞,11[,)2∈-+∞ 所以符合题意的直线l '存在,其方程为210x y +-=⋯(12分)【解答】解：(1)()()f x x ln x =--- 1()1f x x'=--；令()0f x '=,得1x =- 1e x -<-…时,()0f x '<,()f x 单调递减10x -<<时,()0f x '>,()f x 单调递增()f x ∴单调递减区间是[e -,1)-,单调递增区间是(1,0)-()f x 有极小值,极小值是(1)1f -=,(2)由(1)知,()f x 的最小值为(1)1f -=.令1()()2ln x g x x -=- 所以21()()ln x g x x --'=,当[x e ∈-,0)时,()0g x '<, 所以()g x 在[e -,0)上单调递减；()g x ∴的最大值为11()2g e e -=+, ()()min max f x g x ∴>当1a =-时,()1()2ln x f x x -+>恒成立. (二)选考题：共10分.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分.[选修4-4：坐标系与参数方程]【解答】解：(1)曲线1:(1x C y ααα⎧=+⎪⎨=+⎪⎩为参数),曲线C 的直角坐标方程为：22(1)(1)2x y -+-=,是一个圆；圆心(1,1),. 直线:sin cos 0l ρθρθ+=,可得直线l 的直角坐标方程为：0x y +=圆心C 到直线l 的距离d r ==,所以直线l 与圆C 相切 ⋯(5分)(2)由已知曲线C 上存在点P 到直线l 的距离为2,可得：圆心C 到直线:l x y m +=的距离；所以：d 解得15m -⋯剟(10分) [选修4-5：不等式选讲]【解答】解：(1)()|4||||4|f x x x a a a =-+--=…, 从而解得2a =⋯(5分)(2)由(1)知,26,2()|4||2|2,2426,4x x f x x x x x x -+⎧⎪=-+-=-<<⎨⎪-⎩……,2x …时,265x -+…,解得：12x …, 24x <<时,25-<,符合题意, 4x …时,265x -…,解得：112x …, 故不等式的解集为11122x x ⎧⎫⋯⎨⎬⎩⎭剟(10分)。

2020届四川省德阳市高三“二诊”考试数学（文）试题（解析版）

2020届四川省德阳市高三“二诊”考试数学（文）试题一、单选题 1．已知复数21z i =+　，其中i 为虚数单位，则z =（）A ．BC ．2D【答案】D【解析】把已知等式变形，然后利用数代数形式的乘除运算化简，再由复数模的公式计算得答案. 【详解】解：()()()2121111i z i i i i -===-++- ，则z =. 故选：D. 【点睛】本题考查了复数代数形式的乘除运算，考查了复数模的求法，是基础题.2．函数y =A ，集合(){}2log 11B x x =+>，则A B =（）A ．{}12x x <≤ B ．{}22x x -≤≤C ．{}23x x -<<D ．{}13x x <<【答案】A【解析】根据函数定义域得集合A ，解对数不等式得到集合B ，然后直接利用交集运算求解. 【详解】解：由函数y =240x -≥，解得22x -≤≤，即{}22A x x =-≤≤；又()22log 11og 2l x +>=，解得1x >，即{}1B x x =>，则{}12A B x x ⋂=<≤. 故选：A. 【点睛】本题考查了交集及其运算，考查了函数定义域的求法，是基础题.3．执行如图所示的程序框图，若输出的结果为3，则可输入的实数x 值的个数为（）A ．1B ．2C ．3D ．4【答案】C【解析】试题分析：根据题意，当2x ≤时，令213x -=，得2x =±；当2x >时，令2log 3x =，得9x =，故输入的实数值的个数为3．【考点】程序框图． 4．函数()()cos ln x x x xf x e e -=+在[],ππ-的图象大致为（）A ．B ．C ．D ．【答案】A【解析】根据函数的奇偶性，在x π=时函数范围的判断进行排除，即可得答案. 【详解】解：由已知()()()()()cos cos ln ln x x x xx x x xf x f x e e e e -----==-=-++，则函数()()cos ln x x x xf x e e -=+在[],ππ-上是奇函数，故排除B ；又()()()()cos 0,1ln ln ln ln f e e e e e e e πππππππππππππ---==-<->-=-+++，故排除CD ；故选：A. 【点睛】本题考查函数图像的识别，利用函数的性质，如奇偶性，单调性，特殊点的函数值等进行排除是常用的方法，是基础题. 5．要得到函数sin 23y x π⎛⎫=+ ⎪⎝⎭的图象，只需将函数sin 2y x =的图象（） A ．向右平移6π个单位 B ．向右平移3π个单位 C ．向左平移3π个单位 D ．向左平移6π个单位【答案】D【解析】直接根据三角函数的图象平移规则得出正确的结论即可；【详解】解：函数sin 2sin 236y x x ππ⎡⎤⎛⎫⎛⎫=+=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦， ∴要得到函数sin 23y x π⎛⎫=+ ⎪⎝⎭的图象，只需将函数sin 2y x =的图象向左平移6π个单位．故选：D ．【点睛】本题考查三角函数图象平移的应用问题，属于基础题．6．二项式52x ⎫-⎪⎭的展开式中，常数项为（）A ．80-B ．80C ．160-D ．160【答案】A【解析】求出二项式52x ⎫⎪⎭的展开式的通式，再令x 的次数为零，可得结果.【详解】解：二项式52x ⎫⎪⎭展开式的通式为()()55225215512rrr rrr r rr T C x C x---+-+=-=-，令5202rr --+=，解得1r =，则常数项为()11451280C -=-.故选：A. 【点睛】本题考查二项式定理指定项的求解，关键是熟练应用二项展开式的通式，是基础题. 7．已知122a -=，1313b ⎛⎫= ⎪⎝⎭，121log 5c =，则（） A ．b a c << B ．a b c <<C ．c b a <<D ．b c a <<【答案】A【解析】先分析,,a b c 与1的大小关系,可得0,1a b c <<<,再分析66,a b 的大小即可.【详解】因为102221a -=<=,10311133b <⎛⎫⎛⎫= ⎪ ⎪⎝⎝⎭=⎭,12221log log 5log 215c ==>=.故c 最大. 又166321228a -⨯-===,16236111339b ⨯⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭,故66a b >,又,0a b >故a b >. 故b a c <<. 故选：A 【点睛】本题主要考查了根据指对幂函数的单调性与计算分析函数值大小的问题.属于基础题. 8．已知l 为抛物线24x y =的准线，抛物线上的点M 到l 的距离为d ，点P 的坐标为()4,1，则MP d +的最小值是（）A．B ．4C ．2D．1【答案】B【解析】设抛物线焦点为F ，由题意利用抛物线的定义可得，当,,P M F 共线时，MP d +取得最小值，由此求得答案.【详解】解：抛物线焦点()0,1F ，准线1y =-，过M 作MN l ⊥交l 于点N ，连接FM由抛物线定义MN MF d ==，244MP d MP MF PF ∴+=+≥==，当且仅当,,P M F 三点共线时，取“＝”号， ∴MP d +的最小值为4. 故选：B. 【点睛】本题主要考查抛物线的定义、标准方程，以及简单性质的应用，体现了数形结合的数学思想，属于中档题.9．不等式组201230x y y x x y -≥⎧⎪⎪≥⎨⎪+-≤⎪⎩表示的平面区域为Ω，则（）A ．(),x y ∀∈Ω，23x y +>B ．(),x y ∃∈Ω，25x y +>C ．(),x y ∀∈Ω，231y x +>- D ．(),x y ∃∈Ω，251y x +>- 【答案】D【解析】根据题意，分析不等式组的几何意义，可得其表示的平面区域，设1222,1y z x y z x +=+=-，分析12,z z 的几何意义，可得12,z z 的最小值，据此分析选项即可得答案. 【详解】解：根据题意，不等式组201230x y y x x y -≥⎧⎪⎪≥⎨⎪+-≤⎪⎩其表示的平面区域如图所示，其中()2,1A ，()1,2B ，设12z x y =+，则122z x y =-+，1z 的几何意义为直线122zx y =-+在y 轴上的截距的2倍，由图可得：当122z x y =-+过点()1,2B 时，直线12z x y =+在y 轴上的截距最大，即25x y +≤，当122z x y =-+过点原点时，直线12z x y =+在y 轴上的截距最小，即20x y +≥，故AB 错误；设221y z x +=-，则2z 的几何意义为点(),x y 与点()1,2-连线的斜率，由图可得2z 最大可到无穷大，最小可到无穷小，故C 错误，D 正确；故选：D. 【点睛】本题考查本题考查二元一次不等式的性质以及应用，关键是对目标函数几何意义的认识，属于基础题.10．平行四边形ABCD 中，已知4AB =，3AD =，点E 、F 分别满足2AE ED =，DF FC =，且6AF BE ⋅=-，则向量AD 在AB 上的投影为（）A ．2B ．2-C ．32D ．32-【答案】C【解析】将,AF BE 用向量AD 和AB 表示，代入6AF BE ⋅=-可求出6AD AB ⋅=，再利用投影公式AD AB AB⋅可得答案.【详解】解：()()AF BE AD DF BA AE ⋅=+⋅+21123223AD AB AD AD AB AB AB AD =⋅+⋅-⋅+⋅22421346332AD AB =⋅+⨯-⨯=，得6AD AB ⋅=，则向量AD 在AB 上的投影为6342AD AB AB⋅==. 故选：C. 【点睛】本题考查向量的几何意义，考查向量的线性运算，将,AF BE 用向量AD 和AB 表示是关键，是基础题.11．已知ABC 的内角A 、B 、C 的对边分别为a 、b 、c ，且60A =︒，3b =，AD 为BC 边上的中线，若72AD =，则ABC 的面积为（）A ．BC ．154D 【答案】B【解析】延长AD 到E ，使AD DE =，连接,BE CE ，则四边形ABEC 为平行四边形，根据余弦定理可求出5AB =，进而可得ABC 的面积. 【详解】解：延长AD 到E ，使AD DE =，连接,BE CE ，则四边形ABEC 为平行四边形，则3BE AC ==，18060120ABE ∠=-=，27AE AD ==，在ABE △中，2222cos AE AB BE AB BE ABE =+-⋅∠ 则2227323cos120AB AB =+-⨯⨯⨯，得5AB =，11sin 60532224ABCSAB AC =⋅⋅=⨯⨯⨯=. 故选：B.【点睛】本题考查余弦定理的应用，考查三角形面积公式的应用，其中根据中线作出平行四边形是关键，是中档题.12．已知实数0a >，1a ≠，函数()2,14ln ,1x a x f x x a x x x ⎧<⎪=⎨++≥⎪⎩在R 上单调递增，则实数a 的取值范围是（） A ．12a <≤ B ．5a < C ．35a << D ．25a ≤≤【答案】D【解析】根据题意，对于函数分2段分析：当1,()xx f x a <=，由指数函数的性质分析可得1a >①，当241,()ln x f x x a x x≥=++，由导数与函数单调性的关系可得24()20af x x x x'=-+≥，在[1,)+∞上恒成立，变形可得2a ≥②，再结合函数的单调性，分析可得14a ≤+③，联立三个式子，分析可得答案. 【详解】解：根据题意，函数()2,14ln ,1x a x f x x a x x x ⎧<⎪=⎨++≥⎪⎩在R 上单调递增，当1,()xx f x a <=，若()f x 为增函数，则1a >①，当241,()ln x f x x a x x≥=++，若()f x 为增函数，必有24()20af x x x x'=-+≥在[1,)+∞上恒成立，变形可得：242a x x≥-，又由1x ≥，可得()242g x x x =-在[1,)+∞上单调递减，则2442212x x -≤-=，若242a x x≥-在[1,)+∞上恒成立，则有2a ≥②，若函数()f x 在R 上单调递增，左边一段函数的最大值不能大于右边一段函数的最小值，则需有145a ≤+=，③ 联立①②③可得：25a ≤≤. 故选：D. 【点睛】本题考查函数单调性的性质以及应用，注意分段函数单调性的性质.13．ABC 是边长为23的等边三角形，E 、F 分别为AB 、AC 的中点，//EF BC ，沿EF 把AEF 折起，使点A 翻折到点P 的位置，连接PB 、PC ，当四棱锥P BCFE -的外接球的表面积最小时，四棱锥P BCFE -的体积为（） A ．53B ．33C ．6 D ．36【答案】D【解析】由题意知当四棱锥P BCFE -的外接球的表面积最小时球半径最小.且球心O 到四棱锥P BCFE -各顶点的距离相等,再计算此时P 到平面BCFE 的距离求解即可. 【详解】由题,取BC 中点O ,连接,,EF EO FO ,因为ABC 是边长为23的等边三角形,故,,,AEF EBO EOC EFO 均为边长为3的等边三角形.连接AO 交EF 于G .易得G 为EF 中点,且,AO EF AO BC ⊥⊥.32AG OG ==.又四棱锥P BCFE -的外接球的表面积最小时球半径最小,且球心到,,,E F B C 的距离相等.故球心在过O 且与平面BCFE 垂直的直线上.故当球心为O 时,球半径取得最小值3.此时有33,2OP OG PG ===. 在POG 中由余弦定理可得2222333122cos 3322OGP ⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭∠==⎛⎫⋅ ⎪⎝⎭. 因为,GO EF GP EF ⊥⊥,故EF ⊥平面OPG .故P 到平面BCFE 的距离231sin 1223d PG OGP ⎛⎫=⋅∠=-= ⎪⎝⎭又底面(113362332322BCFE S =⨯⨯=故选：D 【点睛】本题主要考查了几何体外接球的问题,需要根据题意分析球心的位置,并根据解三角形求解相关的线段长度进而求得体积等.需要一定的空间想象能力与计算能力.属于难题. 14．ABC 是边长为23E 、F 分别在AB 、AC 上滑动，EF BC ∥，沿EF 把AEF 折起，使点A 翻折到点P 的位置，连接PB 、PC ，则四棱锥P BCFE -的体积的最大值（）为 A ．2 B 3C ．3D ．2【答案】D【解析】以四边形BCFE 为底面,易得当平面PBC 与平面BCFE 垂直时四棱锥P BCFE -的体积取最大值.再求得底面积与高即可.【详解】以四边形BCFE 为底面,则当P 与平面BCFE 距离最远时四棱锥P BCFE -的体积取最大值.易得此时平面PBC 与平面BCFE 垂直. 作AM BC ⊥于M ,交EF 于N .则易得AN EF ⊥,sin 3AM AC C =⋅=.又因为ABC 是边长为23的等边三角形, 设NF x =,则2EF x =,3AN x =.则33NM x =-.此时底面(())2122333332BCFE S x x x =+⨯=-. 故四棱锥P BCFE -的体积为)()22133333V x x x x =-=-.其中(3x ∈.设()()23f x x x =-,故()()()22'3233f x x x x x=-+⋅-=-,令()'0f x =有1x =.故()()23f x x x=-在()0,1上单调递增,在()1,3上单调递减.故()f x 的最大值为()()211312f =-=.故选：D 【点睛】本题主要考查了利用导数求解立体几何中体积的最值问题,需要根据题意分析取最值时的垂直情况,再设对应的自变量,列出关于体积的表达式,求导分析最值求解即可.属于中档题.二、填空题15．已知函数()2f x x ax =+的图象在点()()1,1A f 处的切线与直线l ：320x y -+=垂直，则实数a 的值为__________．【答案】5-【解析】根据导数的几何意义求解()2f x x ax =+的图象在点()()1,1A f 处的切线斜率,再根据直线垂直列式求解即可. 【详解】由题, ()'2f x x a =+,故函数在点()()1,1A f 处的切线斜率为()'12f a =+. 又320x y -+=斜率为13,故()12153a a +=-⇒=-. 故答案为：5- 【点睛】本题主要考查了导数的几何意义,属于基础题.16．在一个袋子中装有分别标注1、2、3、4、5的5个小球，这些小球除标注的数字外完全相同，现从中随机取出2个小球，则取出的小球标注的数字之差的绝对值为2或4的概率是__________．【答案】25【解析】利用枚举法将所有可能的情况列出再分析即可. 【详解】易得所有可能的情况有()()()()()()()()()()1,2,1,3,1,4,1,5,2,3,2,4,2,5,3,4,3,5,4,5共10种情况.其中满足取出的小球标注的数字之差的绝对值为2或4的有()()()()1,3,1,5,2,4,3,5 共4种情况.故概率取出的小球标注的数字之差的绝对值为2或4的概率是42105=. 故答案为：25【点睛】本题主要考查了枚举法求解古典概型的方法,属于基础题.17．已知a 、b 为正实数，直线10x y ++=截圆()()224x a y b -+-=所得的弦长为ab 的最大值为__________．【答案】14【解析】根据垂径定理求得,a b 的关系,【详解】因为直线10x y ++=截圆()()224x a y b -+-=所得的弦长为且圆的半径为2.故圆心(),a b 到直线的距离d ===,因为a 、b 为正实数,故1a b +=,所以2124a b ab +⎛⎫≤= ⎪⎝⎭.当且仅当12a b ==时取等号. 故答案为：14【点睛】本题主要考查了垂径定理的运用以及基本不等式求最值的问题,属于中档题.18．在ABC 中，B 、C 的坐标分别为()-，()，且满足sin sin 2B C A -=，O 为坐标原点，若点P 的坐标为()4,0，则AO AP ⋅的取值范围为__________. 【答案】()12,+∞【解析】由正弦定理可得点A 在曲线221,244x y x -=<-上，设(),A x y ，则224AO AP x x y ⋅=-+，将224y x =-代入可得()2216AO x AP ⋅-=-，利用二次函数的性质可得范围. 【详解】解：由正弦定理得422AC AB BC -===< 则点A 在曲线221,244x y x -=<-上，设(),A x y ，则221,244x y x -=<-，()()224.4,AO AP x y x y y x x --⋅=⋅--=-+，又224y x =-，()22242641AO x AP x x x ∴⋅=--=--+，因为2x <-，则()2221612AO AP ⋅>⨯---=，即AO AP ⋅的取值范围为()12,+∞. 故答案为：()12,+∞. 【点睛】本题考查双曲线的定义，考查向量数量积的坐标运算，考查学生计算能力，有一定的综合性，但难度不大.三、解答题19．已知数列{}n a 满足：()12311232222122nn n a a a a n +⋅+⋅+⋅+⋅⋅⋅+⋅=-⋅+对一切n *∈N 成立.（1）求数列{}n a 的通项公式；（2）求数列21n n a a +⎧⋅⎫⎨⎬⎩⎭的前n 项和n S .【答案】（1）n a n =；（2）()()()35412n n n S n n +=++【解析】（1）先通过1n =求得11a =，再由2n ≥得()123112312222222n n n a a a a n --⋅+⋅+⋅+⋅⋅⋅+⋅=-⋅+，和条件中的式子作差可得答案；（2）变形可得2111122n n a a n n +⎛⎫=- ⎪⋅+⎝⎭，通过裂项求和法可得答案.【详解】（1）()12311232222122n n n a a a a n +⋅+⋅+⋅+⋅⋅⋅+⋅=-⋅+①，∴当1n =时，1122a ⋅=，11a ∴=，当2n ≥时，()123112312222222n n n a a a a n --⋅+⋅+⋅+⋅⋅⋅+⋅=-⋅+②，①-②得：22n nn a n ⋅=⋅，n a n ∴=，适合11a =，故n a n =；（2）()211111222n na a n n n n +⎛⎫==- ⎪⋅++⎝⎭，11111111121324352n S n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫∴=-+-+-+⋅⋅⋅+- ⎪ ⎪ ⎪ ⎪⎢⎥+⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ 111112212n n ⎛⎫=+-- ⎪++⎝⎭()()()35412n n n n +=++.【点睛】本题考查n S 法求数列的通项公式，考查裂项求和，是基础题.20．如图，四棱锥P ABCD -的底面ABCD 中，ABD △为等边三角形，BCD 是等腰三角形，且顶角120BCD ∠=︒，PC BD ⊥，平面PBD ⊥平面ABCD ，M 为PA 中点．（1）求证：DM //平面PBC ；（2）若23AB =PD PB ⊥，求三棱锥P BDM -的体积．【答案】（1）证明见解析（2）32【解析】(1)设AB 中点为N ,连接MN 、DN ,再证明平面//DMN 平面PBC ,进而得到DM //平面PBC 即可.(2) 设BD 中点为O ,连接AO 、CO ,根据12P BDM P ABD V V --=,再计算底面ABD △的面积,并证明三棱锥P ABD -的高为PO 计算即可. 【详解】（1）证明：设AB 中点为N ,连接MN 、DNABD 为等边三角形DN AB ∴⊥DC CB =,120DCB ∠=︒30CBD ∴∠=︒603090ABC ∴∠=︒+︒=︒即CB AB ⊥ DN AB ⊥ //DN BC ∴BC ⊂平面PBC ,DN ⊄平面PBC //DN ∴平面PBCMN 为PAB △的中位线//MN PB ∴PB ⊂平面PBC ,MN ⊄平面PBC//MN ∴平面PBCMN 、DN 为平面DMN 内二相交直线∴平面//DMN 平面PBCDM ⊂平面DMN//DM ∴平面PBC ．（2）解：设BD 中点为O ,连接AO 、CO 与POABD 为等边三角形,BCD 是等腰三角形,且顶角120BCD ∠=︒ AO BD ∴⊥,CO BD ⊥A ∴、C 、O 共线PC BD ⊥,BD CO ⊥,PC CO C =,PC ,CO ⊂平面PCOBD ∴⊥平面PCO ．PO ⊂平面PCO BD PO ∴⊥平面PBD ⊥平面ABCD ,交线为BD ,PO ⊂平面PBDPO ∴⊥平面ABCD ．设23AB =3AO ∴=PD PB ⊥,O 为BD 中点132PO BD ∴==111113223622P BDM P ABD ABD V V S PO AO BD PO --∴==⋅⋅⋅=⨯⨯⨯⨯=△．【点睛】本题主要考查了根据面面平行证明线面平行的方法与三棱锥体积的求法,需要根据题意证明线面垂直得到三棱锥的高,再根据平面几何的关系求解面积等.属于中档题. 21．贫困人口全面脱贫是全面建成小康社会的标志性指标．党的十九届四中全会提出“坚决打赢脱贫攻坚战，建立解决相对贫困的长效机制”对当前和下一个阶段的扶贫工作进行了前瞻性的部署，即2020年要通过精准扶贫全面消除绝对贫困，实现全面建成小康社会的奋斗目标．为了响应党的号召，某市对口某贫困乡镇开展扶贫工作．对某种农产品加工生产销售进行指导，经调查知，在一个销售季度内，每售出一吨该产品获利5万元，未售出的商品，每吨亏损2万元．根据往年的销售经验，得到一个销售季度内市场需求量的频率分布直方图如图所示．设该厂在下个销售周期内生产210吨该产品，以x （单位：吨，180230x ≤≤）表示下一个销售周期市场的需求量，Y （单位：万元）表示下一个销售周期市场的销售总利润，视x 分布在各区间内的频率为相应的概率．（1）求实数a 的值；（2）将Y 表示成x 的函数，并求出解析式；（3）估计销售利润不少于910万元的概率．【答案】（1）0035a =．（2）7420,1802101050,210230x x Y x -≤<⎧=⎨≤≤⎩（3）0.9【解析】(1)根据频率分布直方图的面积之和为1列式求解即可.(2)根据题意,当210x ≥时生产的210吨该产品能全卖完,当210x <时,再利用总收入减去亏损计算即可.(3)根据(2)中的解析式求解910Y ≥时x 的取值范围,再结合频率分布直方图求解概率即可. 【详解】解：（1）由()0.010015003001101a ++++⨯=．．．得：0035a =．．(2)当210x ≥时,21051050Y =⨯=当210x <时,()521027420Y x x x =--⨯=-所以7420,1802101050,210230x x Y x -≤<⎧=⎨≤≤⎩（3）当210230x ≤≤时,1050910Y => 由7420910x -≥得：190x ≥1901001)9(100P x ≥=-⨯=．．∴估计销售利润不少于910万元的概率为0.9．【点睛】本题主要考查了频率分布直方图的理解以及根据分段函数求利润的问题,属于中档题.22．已知椭圆C ：()222210x y a b a b+=>>，右焦点为抛物线24y x =的焦点F .（1）求椭圆C 的标准方程；（2）O 为坐标原点，过O 作两条射线，分别交椭圆于M 、N 两点，若OM 、ON 斜率之积为45-，求证：MON △的面积为定值. 【答案】（1）22154x y +=；（2）见解析【解析】（1）由条件可得1c =，再根据离心率可求得,a b ，则可得椭圆方程；（2）当MN 与x 轴垂直时，设直线MN 的方程为：()0x t t t =<<≠，与椭圆联立求得,M N 的坐标，通过OM 、ON 斜率之积为45-列方程可得t 的值，进而可得MON △的面积；当MN 与x 轴不垂直时，设()11,M x y ，()22,N x y ，MN 的方程为y kx m =+，与椭圆方程联立，利用韦达定理和OM 、ON 斜率之积为45-可得22254m k =+，再利用弦长公式求出MN ，以及O 到MN 的距离，通过三角形的面积公式求解. 【详解】（1）抛物线24y x =的焦点为()1,0F ，1c ∴=， 55e =，5c a ∴=， 5a ∴=，2b =，∴椭圆方程为22154x y +=；（2）（ⅰ）当MN 与x 轴垂直时，设直线MN的方程为：()0x t t t =<<≠代入22154x y +=得：,M t ⎛ ⎝，,N t ⎛- ⎝，2122455t k k t-∴⋅==-⋅ 2245455t t -∴-⋅=-，解得：252t =，12MONS t ∴=⋅⋅=△ （ⅱ）当MN 与x 轴不垂直时，设()11,M x y ，()22,N x y ，MN 的方程为y kx m =+由()2222245105200154y kx mk x kmx m x y =+⎧⎪⇒+++-=⎨+=⎪⎩，由22054k m ∆>⇒+>①1221045km x x k +=-+，212252045m x x k-⋅=+ 4·5OM ON k k =-，121245y y x x ∴⋅=-，1212540y y x x ∴+= 即()()22121254550k x x mk x x m +⋅+++=()2222252010545504545m kmk mk m k k-⎛⎫∴+⋅+⋅-+= ⎪++⎝⎭整理得：22254m k =+ 代入①得：0m ≠MN ===O 到MN的距离d =12MON S MN d ∴=△===综上：MON S =△. 【点睛】本题考查椭圆方程的求解，考查直线和椭圆的位置关系，考查韦达定理的应用，考查了学生的计算能力，是中档题.23．已知函数()axf x e x =-（a R ∈，e 为自然对数的底数）．（1）若()f x 有两个零点，求实数a 的取值范围；（2）当()f x 有两个零点1x ，2x ，且12x x <，求证：212x x e ⋅>．【答案】（1）10,e ⎛⎫ ⎪⎝⎭（2）证明见解析【解析】(1)参变分离可知ln xa x =有两个相异实根,再构造函数()ln x G x x=,分析函数的单调性与最值,进而求得函数的取值范围数形结合求解即可.(2) 由题意得1212ax ax e x e x ⎧=⎨=⎩,再运算求得2121ln ln x x a x x -=-,又要证：212x x e ⋅>,只需证12ln ln 2x x +>,代入2121ln ln x x a x x -=-化简可得212122111ln ln ln 1x x x x x x x x ⎛⎫+ ⎪ ⎪+=⋅ ⎪- ⎪⎝⎭,再令21x t x =,构造函数分析单调性与最值证明1ln 21t t t +⎛⎫⋅> ⎪-⎝⎭即可. 【详解】解：（1）()f x 有两个零点⇔关于x 的方程ax e x =有两个相异实根由0>ax e ,知0x >()f x ∴有两个零点ln x a x ⇔=有两个相异实根．令()ln x G x x =,则()21ln x G x x -'= 由()0G x '>得：0x e <<,由()0G x '<得：x e >()G x ∴在()0,e 单调递增,在(),e +∞单调递减()()max 1G x G e e∴== 又()10G =∴当01x <<时,()0G x <,当1x >时,()0G x >当x →+∞时,()0G x →()f x ∴有两个零点时,实数a 的取值范围为10,e ⎛⎫ ⎪⎝⎭．（2）由题意得1212ax ax e x e x ⎧=⎨=⎩10x ∴>,20x >1122ln ln ax x ax x =⎧∴⎨=⎩ ()1212ln ln a x x x x ∴+=+ ①()2121ln ln a x x x x -=-12x x <2121ln ln x x a x x -∴=- 要证：212x x e ⋅>,只需证12ln ln 2x x +>由①知：()()22112121212221111ln ln ln ln =ln 1x x x x x x x a x x x x x x x x x ⎛⎫+ ⎪- ⎪+=+=⋅+⋅- ⎪- ⎪⎝⎭ 120x x <<211x x ∴> 令21x t x =,1t > ∴只需证1ln 21t t t +⎛⎫⋅> ⎪-⎝⎭1t >101t t +∴>- ∴只需证：()()21ln 1t t t ->+ 令()()()()21F ln 11t t t t t -=->+ ()()()()222114011t F t t t t t -'∴=-=>++ ()F t ∴在()1,+∞递增()()0F t F t ∴>=()()21ln 1t t t -∴>+ 即12ln ln 2x x +>,即212x x e ⋅>．【点睛】本题主要考查了利用导数分析函数的单调性以及求解零点有关的问题,同时也考查了双变量构造函数证明单调性的方法,需要根据题意将参数a 用零点表达,再构造函数分析单调性证明不等式.属于难题.24．已知点A 为圆C ：()2211x y -+=上的动点，O 为坐标原点，过()0,4P 作直线OA 的垂线（当A 、O 重合时，直线OA 约定为y 轴），垂足为M ，以O 为极点，x 轴的正半轴为极轴建立极坐标系.（1）求点M 的轨迹的极坐标方程；（2）直线l 的极坐标方程为sin 43πρθ⎛⎫+= ⎪⎝⎭，连接OA 并延长交l 于B ，求OA OB 的最大值.【答案】（1）4sin ρθ=；（2【解析】（1）设M 的极坐标为(),ρθ，在OPM 中，有4sin ρθ=，即可得结果；（2）设射线OA ：θα=，,22ππα⎛⎫∈- ⎪⎝⎭，圆C 的极坐标方程为2cos ρθ=，联立两个方程，可求出OA ，联立sin 43πρθθα⎧⎛⎫+=⎪ ⎪⎝⎭⎨⎪=⎩可得OB，则计算可得1sin 243OAOB πα⎛⎫=++ ⎪⎝⎭. 【详解】（1）设M 的极坐标为(),ρθ，在OPM 中，有4sin ρθ=， ∴点M 的轨迹的极坐标方程为4sin ρθ=；（2）设射线OA ：θα=，,22ππα⎛⎫∈- ⎪⎝⎭，圆C 的极坐标方程为2cos ρθ=，由2cos ρθθα=⎧⎨=⎩得：12cos OA ρα==，由sin 43πρθθα⎧⎛⎫+=⎪ ⎪⎝⎭⎨⎪=⎩得：24sin 3OB ρα==π⎛⎫+ ⎪⎝⎭， 2cos 4sin 3OA OB αα∴=π⎛⎫+ ⎪⎝⎭ 1cos sin 23ααπ⎛⎫=⋅+ ⎪⎝⎭1cos sin sin cos cos sin 233αααππ⎛⎫=+ ⎪⎝⎭21sin cos 4ααα=)1sin 2cos 218αα=++1sin 243πα⎛⎫=+ ⎪⎝⎭， ,22ππα⎛⎫∈- ⎪⎝⎭242333απππ∴-<+<， ∴当232ππα+=，即12πα=时，max OA OB ⎛⎫= ⎪ ⎪⎝⎭，OAOB ∴. 【点睛】本题考查极坐标方程的应用，考查三角函数性质的应用，是中档题.25．已知函数()1f x x =+.（1）求不等式()423f x x ≤--的解集；（2）若正数m 、n 满足2m n mn +=，求证：()()28f m f n +-≥.【答案】（1）{}02x x ≤≤；（2）见解析【解析】（1）()423f x x ≤--等价于（Ⅰ）()()11234x x x <-⎧⎨-+--≤⎩或（Ⅱ）()()3121234x x x ⎧-≤≤⎪⎨⎪+--≤⎩或（Ⅲ）()()321234x x x ⎧>⎪⎨⎪++-≤⎩，分别解出，再求并集即可；（2）利用基本不等式及2m n mn +=可得28m n +≥，代入()()21212f m f n m n m n +-=++-+≥+可得最值.【详解】（1）()423f x x ≤--等价于（Ⅰ）()()11234x x x <-⎧⎨-+--≤⎩或（Ⅱ）()()3121234x x x ⎧-≤≤⎪⎨⎪+--≤⎩或（Ⅲ）()()321234x x x ⎧>⎪⎨⎪++-≤⎩由（Ⅰ）得：123x x x <-⎧⎪⇒∈∅⎨≥-⎪⎩由（Ⅱ）得：3130220x x x ⎧-≤≤⎪⇒≤≤⎨⎪≥⎩由（Ⅲ）得：332222x x x ⎧>⎪⇒<≤⎨⎪≤⎩. ∴原不等式的解集为{}02x x ≤≤；（2）0m >，0n >，2m n mn +=，()()221122224m n m n m n +∴+=⋅≤⨯， 28m n ∴+≥，当且仅当22m n m n mn =⎧⎨+=⎩，即42m n =⎧⎨=⎩时取等号， ()()212128f m f n m n m n ∴+-=++-+≥+≥，当且仅当210n -+≤即12n ≥时取等号， ()()28f m f n ∴+-≥.【点睛】本题考查分类讨论解绝对值不等式，考查三角不等式的应用及基本不等式的应用，是一道中档题.。

2019届四川省成都市第七中学高三二诊模拟考试数学(文)试题(解析版)

，
据此可得： c2 a b2 c2 1 ，
b2
22
整理可得： 9 4 2 c4 4 2 18 a2c2 9a2 0 ，则：
9 4 2 e4 4 2 18 e2 9 0 ，
分解因式有：

94
2
e2 9
3
A．
2
B． 3
【答案】B
C． 2 3
D． 2
【解析】试题分析：由题意得，因为 ABC 的面积为 3 ，所以 2
SABC

1 2
bcsinA

1 2b 2
3 2
3 ，解得 b 1，在 ABC 中，由余弦定理可得 2
BC 2 b2 c2 2bccosA 1 4 2 1 2cos600 3 ，所以 BC 3 ，故选 B.
【考点】正弦定理；余弦定理.
【方法点晴】本题主要考查了解三角形的综合问题，其中解答中涉及到三角形的正弦定
理、余弦定理的应用，以及三角形的面积公式等知识点的综合考查，着重考查了学生分
析问题和解答问题的能力，以及推理与运算能力，本题的解答中根据三角形的面积公式，
求得 b 1，再利用正、余弦定理是解得关键.
时，y 的值，计算通经，即可。
焦点坐标为【点睛】
，故当
时，
，故通经长为 8.
考查了抛物线的性质，考查了通经的概念，难度中等。
14．某人次上班途中所花的时间（单位：分钟）分别为，，，， .已知这组数据的平均数为，方差为，则的值为__________. 【答案】【解析】结合平均数和方差的计算方法，建立方程，计算结果，即可。【详解】结合题意，建立方程，得到

2019年四川省广元市高考数学二诊试卷(文科)-普通用卷

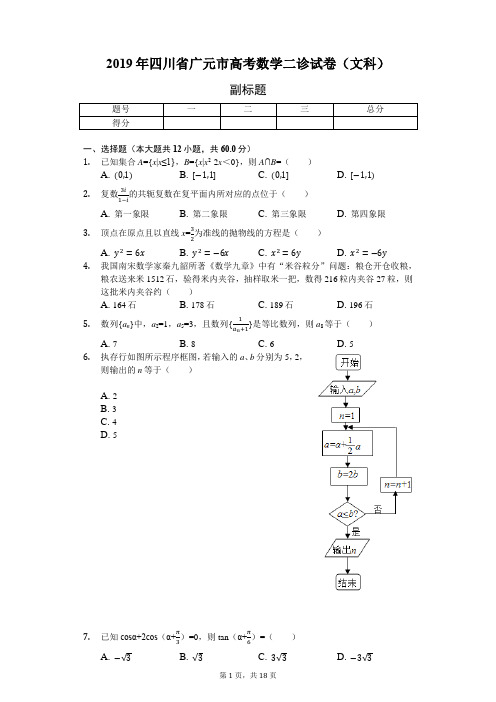
2019年四川省广元市高考数学二诊试卷（文科）副标题一、选择题（本大题共12小题，共60.0分）1.已知集合A={x|x≤1}，B={x|x2-2x＜0}，则A∩B=（）A. B. C. D.2.复数的共轭复数在复平面内所对应的点位于（）A. 第一象限B. 第二象限C. 第三象限D. 第四象限3.顶点在原点且以直线x=为准线的抛物线的方程是（）A. B. C. D.4.我国南宋数学家秦九韶所著《数学九章》中有“米谷粒分”问题：粮仓开仓收粮，粮农送来米1512石，验得米内夹谷，抽样取米一把，数得216粒内夹谷27粒，则这批米内夹谷约（）A. 164石B. 178石C. 189石D. 196石5.数列{a n}中，a2=1，a5=3，且数列{}是等比数列，则a8等于（）A. 7B. 8C. 6D. 56.执存行如图所示程序框图，若输入的a、b分别为5，2，则输出的n等于（）A. 2B. 3C. 4D. 58.一个几何体的三视图如图所示，则该几何体的体积是（）A.B.C.D.9.在等差数列{a n}中，a1=-2018，其前n项和为S n，若=5，则S2019的值等于（）A. 0B.C.D.10.已知双曲线C：=1（a＞0，b＞0）的左、右顶点分别为A1，A2，且以线段A1A2为直径的圆与直线ax-by+2ab=0相切，则双曲线C的离心率等于（）A. B. C. D.11.直三棱柱ABC-A1B1C1中，∠BCA=90°，M，N分别是A1B1，A1C1的中点，BC=CA=CC1，则BM与AN所成角的余弦值为（）A. B. C. D.12.已知函数f（x）满足x＜1时，f（x）=sin x；x≥1时f（x）=x3-9x2+25x+m，若函数f（x）的图象与直线y=x有四个不同的公共点，则实数m的取值范围是（）A. B.C. D.二、填空题（本大题共4小题，共20.0分）13.已知实数x，y满足，则z=的最大值是______．14.曲线y=x3-3x2+1在点（1，-1）处的切线方程为______．15.已知f（x）=2|x|+cos x，x∈R，若f（t-1）-f（1-2t）≥0成立，则实数t的取值范围是______．16.在等腰梯形ABCD中，已知AB∥DC，AB=2，BC=1，∠ABC=60°，动点E和F分别在线段BC和DC上，且=，=，则的最小值为______．三、解答题（本大题共7小题，共82.0分）17.在△ABC中，角A、B、C所对的边分别为a、b、c，且满足cos2C-cos2A=2sin（+C）•sin（-C）．（1）求角A的值；（2）若a=且b≥a，求2b-c的取值范围．18.随着共享单车的成功运营，更多的共享产品逐步走人大家的世界，共享汽车、共享篮球、共享充电宝等各种共享产品层出不穷．广元某景点设有共享电动车租车点，共享电动车的收费标准是每小时2元（不足1小时的部分按1小时计算）．甲、乙两人各租一辆电动车，若甲、乙不超过一小时还车的概率分别为，；一小时以上且不超过两小时还车的概率分别为，；两人租车时间都不会超过三小时．（Ⅰ）求甲、乙两人所付租车费用相同的概率；（Ⅱ）求甲、乙两人所付的租车费用之和大于或等于8的概率．19.如图，在斜三棱柱ABC-A1B1C1中，已知∠B1C1A1=90°，AB1⊥A1C，且AA1=AC．（1）求证：平面ACC1A1⊥平面A1B1C1；（2）若AA1=AC1=B1C1=2，求四棱锥A1-BB1C1C的体积．20.椭圆=1（a＞b＞0）的上、下焦点分别为F1（0，c），F2（0，-c），右顶点为B，且满足=0．（Ⅰ）求椭圆的离心率e；（Ⅱ）设P为椭圆上异于顶点的点，以线段PB为直径的圆经过点F2，求证该圆与直线x+2y-c=0恒相切．21.已知函数f（x）=x3+x2-4ax+1（a∈R）．（Ⅰ）若函数f（x）有两个极值点，且都小于0．求a的取值范围；（Ⅱ）若函数h（x）=a（a-1）ln x-x3+3x+f（x），求函数h（x）的单调区间．22.在直角坐标系xOy中，以原点O为极点，x轴的正半轴为极轴建立极坐标系，已知直线l的参数方程为：，（t为参数）．P点的极坐标为（2，π），曲线C的极坐标方程为ρcos2θ=sinθ．（Ⅰ）试将曲线C的极坐标方程化为直角坐标方程，并求曲线C的焦点在直角坐标系下的坐标；（Ⅱ）设直线l与曲线C相交于两点A，B，点M为AB的中点，求|PM|的值．23.设函数f（x）=|2x+l|-|x-4|．（1）解不等式f（x）＞0；（2）若f（x）+3|x-4|≥m对一切实数x均成立，求m的取值范围．答案和解析1.【答案】C【解析】解：集合A={x|x≤1}，B={x|x2-2x＜0}={x|0＜x＜2}，则A∩B={x|x≤1}∩{x|0＜x ＜2}=（0，1]，故选：C．由题意求出集合B，然后直接求出交集即可．本题是基础题，考查不等式的求法，集合的基本运算，送分题．2.【答案】C【解析】解：复数z===-+i；则z的共轭复数=--i，它在复平面内所对应的点位于第三象限．故选：C．化简复数z=，求出它的共轭复数，写出在复平面内所对应的点位于第几象限．本题考查了复数的定义与运算问题，是基础题．3.【答案】B【解析】解：依题意，设抛物线的方程为：y2=-2px（p＞0），∵准线方程为x=，∴=，∴p=3，∴抛物线的方程是y2=-6x．故选：B．利用抛物线的性质可知该抛物线的形式为：y2=-2px（p＞0），依题意可求p的值，从而可得答案．本题考查抛物线的简单几何性质，设出方程y2=-2px（p＞0）是关键，属于中档题4.【答案】C【解析】解：由已知，抽得样本中含谷27粒，占样本的比例为=，则由此估计总体中谷的含量约为1512×=189石．故选：C．根据216粒内夹谷27粒，可得比例，即可得出结论．本题考查利用数学知识解决实际问题，考查学生的计算能力，比较基础．5.【答案】A【解析】解：∵数列{}是等比数列，其公比为q设b n=∴b2==，b5==，∴q3==，∴b8=b5q3=×=，∴=，∴a8=7，故选：A．根据数列{}是等比数列，其公比为q，设b n=，求出公比，即可得到=，解得即可本题考查了等比数列的通项公式，考查额运算能力，属于基础题6.【答案】C【解析】解：当n=1时，；当n=2时，；当n=4时，．故选：C．由已知中的程序框图可知：该程序的功能是利用循环结构计算并输出变量n 的值，模拟程序的运行过程，可得答案．本题考查的知识点是程序框图，当循环的次数不多，或有规律时，常采用模拟循环的方法解答．7.【答案】C【解析】解：由cosα+2cos（α+）=0，得cosα+2（cos-sin）=0，∴2cosα-=0，则tanα=．∴tan（α+）=．故选：C．由已知求得tanα，然后展开两角和的正切求tan（α+）的值．本题考查三角函数的恒等变换及化简求值，考查同角三角函数基本关系式及两角和的正切，是基础题．8.【答案】B【解析】解：根据几何体的三视图转换为几何体，该几何体由和个底面半径为2，高为3的圆锥构成．故：=故选：B．首先把三视图转换为几何体，进一步利用几何体的体积公式求出结果．本题考查的知识要点，三视图和几何体的转换，几何体的体积和表面积公式9.【答案】A【解析】解：设等差数列{a n}的公差为d，由等差数列的性质可得：=a1+d为等差数列，{}的公差为．∵=5，∴=5，解得d=2．则S2019=2019×（-2018）+=0．故选：A．设等差数列{a n}的公差为d，由等差数列的性质可得：=a1+d为等差数列，{}的公差为．再利用=5，即可得出d，再利用求和公式即可得出．本题考查了等差数列的通项公式及其求和公式、转化法，考查了推理能力与计算能力，属于中档题．10.【答案】C【解析】解：双曲线（a＞0，b＞0）的实轴的两端点分别为A，B，且以线段AB为直径的圆的圆心（0，0），以线段AB为直径的圆与直线ax-by+2ab=0相切，圆心到直线的距离为d则，则a2=3b2又c2=b2+a2则，．故选：C．求出圆心坐标，利用点到直线的距离公式列出方程推出a，b关系，然后求解双曲线的离心率即可．本题考查双曲线的简单性质以及直线与圆的位置关系的应用，考查计算能力．11.【答案】C解：直三棱柱ABC-A1B1C1中，∠BCA=90°，M，N分别是A1B1，A1C1的中点，如图：BC 的中点为O，连结ON，，则MN0B是平行四边形，BM与AN所成角就是∠ANO，∵BC=CA=CC1，设BC=CA=CC1=2，∴CO=1，AO=，AN=，MB===，在△ANO中，由余弦定理可得：cos∠ANO===．故选：C．画出图形，找出BM与AN所成角的平面角，利用解三角形求出BM与AN所成角的余弦值．本题考查异面直线对称角的求法，作出异面直线所成角的平面角是解题的关键，同时考查余弦定理的应用．12.【答案】B【解析】解：由函数f（x）的图象与直线y=x有四个不同的公共点等价于g（x）=f（x）-x有四个零点，①当x＜1时，g（x）=sinx-x，则g′（x）=cosx-1≤0，即g（x）在（-∞，1）为减函数，又g（0）=0，即y=g（x）在（-∞，1）上有一个零点，②当x≥1时，g（x）=x3-9x2+24x+m，则g′（x）=3x2-18x+24=3（x-2）（x-4），当1≤x＜2或x＞4时，g′（x）＞0，当2＜x＜4时，g′（x）＜0，又g（1）=16+m，g（2）=20+m，g（4）=16+m，由已知有g（x）=x3-9x2+24x+m在[1，+∞）有3个零点，则，解得：-20＜m＜-16，综合①②得：函数f（x）的图象与直线y=x有四个不同的公共点，则实数m的取值范围为：-20＜m＜-16，故选：B．由函数图象的交点与函数的零点的相互转化得：函数f（x）的图象与直线y=x 有四个不同的公共点等价于g（x）=f（x）-x有四个零点，由利用导数研究函数的图象与最值得：①当x＜1时，g（x）=sinx-x，y=g（x）在（-∞，1）上有一个零点，②当x≥1时，g（x）=x3-9x2+24x+m，则g′（x）=3x2-18x+24=3（x-2）（x-4），即函数在[1，2），（4，+∞）为增函数，在（2，4）为减函数，由已知有g（x）=x3-9x2+24x+m在[1，+∞）有3个零点，则，解得：-20＜m＜-16，得解本题考查了函数图象的交点与函数的零点的相互转化及利用导数研究函数的图象与最值，属中档题13.【答案】2【解析】解：由实数x，y满足作出可行域如图，z=的几何意义为可行域内的动点与定点D（-1，-2）连线的斜率，∵k DO==2，∴z=的最大值是：2．故答案为：2．由约束条件作出可行域，由z=的几何意义可知，z为可行域内的动点与定点D（-1，-2）连线的斜率，求出DO的斜率得答案．本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．14.【答案】y=-3x+2【解析】解：由曲线y=x3-3x2+1，所以y′=3x2-6x，曲线y=x3-3x2+1在点（1，-1）处的切线的斜率为：y′|x=1=3（1）2-6=-3．此处的切线方程为：y+1=-3（x-1），即y=-3x+2．故答案为：y=-3x+2．求出函数y=x3-3x2+1在x=1处的导数值，这个导数值即函数图象在该点处的切线的斜率，然后根据直线的点斜式方程求解即可．本题考查导数的几何意义、关键是求出直线的斜率，正确利用直线的点斜式方程，考查计算能力．15.【答案】[0，]【解析】解：根据题意，f（x）=2|x|+cosx，则f（-x）=2|-x|+cos（-x）=2|x|+cosx=f（x），则函数f（x）为偶函数，当x≥0时，f（x）=2x+cosx，其导数f′（x）=2-sinx＞0，则函数f（x）在[0，+∞）为增函数，则f（t-1）-f（1-2t）≥0⇒f（t-1）≥f（1-2t）⇒f（|t-1|）≥f（|1-2t|）⇒|1-t|≥|1-2t|，解可得：0≤t≤，即t的取值范围为[0，]；故答案为：[0，]．根据题意，由函数的解析式可得f（-x）=f（x），即函数f（x）为偶函数，当x≥0时，f（x）=2x+cosx，求出函数的导数，分析可得f（x）在[0，+∞）为增函数，据此分析可得f（t-1）-f（1-2t）≥0⇒f（t-1）≥f（1-2t）⇒f（|t-1|）≥f（|1-2t|）⇒|1-t|≥|1-2t|，解可得t的取值范围，即可得答案．本题考查函数的奇偶性与单调性的综合应用，关键是分析函数f（x）的奇偶性与单调性，属于基础题．16.【答案】【解析】解：等腰梯形ABCD中，已知AB∥DC，AB=2，BC=1，∠ABC=60°，∴DC==1，∵=2×=1，∵=，==，∴===，∵==，===，则=（）•（）==+λ×（-1）=当且仅当即λ=1时有最小值故答案为：由梯形性质可求DC==1，结合已知及向量加法的三角形法则可表示，，然后由向量数量积的性质及基本不等式即可求解．本题主要考查了平面向量的基本运算及向量数量积的性质的应用，还考查了基本不等式在求解最值中的应用，试题具有一定的综合性．17.【答案】解：（1）∵cos2C-cos2A=2sin（+C）•sin（-C）=2（cos C+sin C）（cos C-sin C）=cos2C-sin2C=•-•=+cos2C，∴-cos2A=，解得：cos2A=-．∵A∈（0，π），2A∈（0，2π），∴当2A=时，解得：A=，当2A=时，解得：A=．（2）∵b≥a，∴A为锐角，由（1）可得：A=，又∵a=，∴由正弦定理可得：==2，∴2b-c=2（2sin B-sin C）=4sin B-2sin（-B）=4sin B-（cos B+sin B）=3sin B-cos B=2sin （B-），∵B∈[，），B-∈[，），可得sin（B-）∈[，1），∴2b-c=2sin（B-）∈[，2）．【解析】（1）利用三角函数恒等变换的应用化简已知可解得：cos2A=-，结合2A∈（0，2π），可得A的值．（2）由b≥a，由（1）可得：A=，又a=，由正弦定理可得：=2，从而利用三角函数恒等变换的应用可得2b-c=2sin（B-），结合范围B-∈[，），可得2b-c取值范围．本题主要考查了三角函数恒等变换的应用，考查了正弦定理，正弦函数的图象和性质在解三角形中的应用，属于中档题．18.【答案】解：（Ⅰ）甲、乙两人所付费用相同即同为2，4，6元，都付2元的概率P1==，都付4元的概率P2==，都付6元的概率P3=，∴所付费用相同的概率为P=P1+P2+P3==．（Ⅱ）设两人费用之和8、10、12的事件分别为A、B、C，P（A）==，P（B）==，P（C）=，设两人费用之和大于或等于8的事件为W，则W=A+B+C，∴两人费用之和大于或等于8的概率：P（W）=P（A）+P（B）+P（C）==．【解析】（Ⅰ）甲、乙两人所付费用相同即同为2，4，6元，都付2元的概率P1==，都付4元的概率P2==，都付6元的概率P3=，由此利用互斥事件概率加法公式能求出所付费用相同的概率．（Ⅱ）设两人费用之和8、10、12的事件分别为A、B、C，P（A）==，P（B）==，P（C）=，设两人费用之和大于或等于8的事件为W，则W=A+B+C，由此能求出两人费用之和大于或等于8的概率．本题考查概率的求法，考查互斥事件概率加法公式、相互独立事件概率乘法公式等基础知识，考查运算求解能力，是基础题．19.【答案】（1）证明：如图，连接AC1，∵AA1=AC，∴四边形AA1C1C为菱形，则AC1⊥A1C，又AB1⊥A1C，且AB1∩AC1=A，∴A1C⊥平面AB1C1，则A1C⊥B1C1，又∠B1C1A1=90°，即A1C1⊥B1C1，且A1C∩A1C1=A1，∴B1C1⊥平面ACC1A1，而B1C1⊂平面A1B1C1，∴平面ACC1A1⊥平面A1B1C1；（本小题满分12分）（2）∵=+=+V=××4×2×2=故四棱锥A1-BB1C1C的体积为．【解析】（1）连接AC1，由AA1=AC，可得AC1⊥A1C，又AB1⊥A1C，可得A1C⊥平面AB1C1，则A1C⊥B1C1，再由∠B1C1A1=90°，得A1C1⊥B1C1，利用线面垂直的判定可得B1C1⊥平面ACC1A1，则平面ACC1A1⊥平面A1B1C1；（2）=+=+V，即可求出答案本题考查面面垂直的证明，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，训练了体积的求法，是中档题．20.【答案】解：（Ⅰ）F1（0，c），F2（0，-c），B（b，0），∵=0．∴b2-c2=0，即b=c．∴椭圆的离心率e==．（Ⅱ）由（Ⅰ）可得b=c，故可设椭圆的方程为，P（x0，y0）．∵F1（0，c），F2（0，-c），∴，，，．∵，∴x0+y0+c=0…①又因为点P在椭圆上，∴…②由①②可得=0．（y0≠0）．可得，．故P（，-）．设圆心为（x1，y1），则，y1=-．圆的半径r=．则圆心到直线直线x+2y-c=0的距离为d=．∴圆与直线x+2y-c=0恒相切．【解析】（Ⅰ）由=0可得b=c，即可得椭圆的离心率e==．（Ⅱ）由，可得x0+y0+c=0，从而可得=0．（y0≠0）．P（，-）．求得圆心到直线直线x+2y-c=0的距离为d=，即可证明．本题考查了椭圆的方程、直线与圆的位置关系，属于中档题．21.【答案】解：（Ⅰ）由f（x）有2个极值点且都小于0，得f′（x）=3x2+3x-4a=0有2个不相等的负实根，故△ ＞＜＞，解得：-＜a＜0，故a的范围是（-，0）；（Ⅱ）∵h（x）=a（a-1）ln x+x2-（4a-3）x+1，x＞0，h′（x）=+3x-（4a-3）=（3x-a）[x-（a-1）]，令（3x-a）[x-（a-1）]=0，得x=或x=a-1，令=0，得a=0，令a-1=0，得：a=1，令=a-1，得：a=，①当a≤0时，h′（x）＞0恒成立，h（x）在（0，+∞）递增；②当0＜a≤1时，（3x-a）[x-（a-1）]＞0⇔x＜a-1或x＞，h′（x）＞0⇔x＞，h′（x）＜0⇔x＜，故h（x）在（0，）递减，在（，+∞）递增；③当1＜a＜时，＞a-1＞0，h′（x）＞0⇔0＜x＜a-1或x＞，h′（x）＜0⇔a-1＜x＜，故h（x）在（0，a-1）递增，在（a-1，）递减，在（，+∞）递增；④当a=时，h′（x）≥0恒成立，函数在（0，+∞）递增；⑤当a＞时，0＜＜a-1，h′（x）＞0⇔0＜x＜或x＞a-1，h′（x）＜0⇔＜x＜a-1，函数在（0，）递增，在（，a-1）递减，在（a-1，+∞）递增．【解析】（Ⅰ）求出函数的导数，结合二次函数的性质得到关于a的不等式组，解出即可；（Ⅱ）求出函数的导数，通过讨论a的范围，求出函数的单调区间即可．本题考查了函数的单调性，极值，最值问题，考查导数的应用以及分类讨论思想，转化思想，是一道综合题．22.【答案】解：（Ⅰ）把x=ρcosθ，y=ρsinθ代入ρcos2θ=sinθ，可得曲线C的直角坐标方程为x2=y，它是开口向上的抛物线，焦点坐标为，．（Ⅱ）点P的直角坐标为（-2，0），它在直线l上，在直线l的参数方程中，设点A，B，M对应的参数为t1，t2，t0，由题意可知．把直线l的参数方程代入抛物线的直角坐标方程，得．因为△ ＞，所以，则．【解析】（Ⅰ）把x=ρcosθ，y=ρsinθ代入曲线C的方程ρcos2θ=sinθ，可得曲线C的直角坐标方程．（Ⅱ）设点A，B，M对应的参数为t1，t2，t0，由题意可知．把直线l的参数方程代入抛物线的直角坐标方程，利用韦达定理求得t1+t2的值，可得|PM|=|t0|的值．本题主要考查参数方程和极坐标的应用，参数的几何意义，属于基础题．23.【答案】解：（1）当x≥4时，f（x）=2x+1-（x-4）=x+5＞0，得x＞-5，所以x≥4成立；当-≤x＜4时，f（x）=2x+1+x-4=3x-3＞0，得x＞1，所以1＜x＜4成立；当x＜-时，f（x）=-x-5＞0，得x＜-5，所以x＜-5成立．综上，原不等式的解集为{x|x＞1或x＜-5}；（2）令F（x）=f（x）+3|x-4|=|2x+1|+2|x-4|≥|2x+1-（2x-8）|=9，当-时等号成立．即有F（x）的最小值为9，所以m≤9．即m的取值范围为（-∞，9]．【解析】（1）对x讨论，分当x≥4时，当-≤x＜4时，当x＜-时，分别解一次不等式，再求并集即可；（2）运用绝对值不等式的性质，求得F（x）=f（x）+3|x-4|的最小值，即可得到m 的范围．本题考查绝对值不等式的解法，以及不等式恒成立思想转化为求函数的最值问题，运用分类讨论的思想方法和绝对值不等式的性质是解题的关键．。

四川2019届成都高三理数二诊理科数学(含答题卡及答案)

ʑ有９９％的把握认为满意程度与年龄有关． ( 据题意 , 该８名员工的贡献积分及按甲 , 乙两种方案所获补贴情况为 : Ⅱ) 积分方案甲方案乙２４００３０００２３１００３０００３５２００５６００６５９００５６００７５９００５６００７８７００９０００１１９４００９０００１２
��４分
��２分
( 解: 根据列联表可以求得 K 的观测值 : １８． Ⅰ)
２
n ) ( ２１－２ n＋１ n＋１＝－ nˑ２＝( １－ n) －２．２１－２ n＋１ ) n－１２＋２． ʑTn ＝ (
８０ (２５ˑ３０－１０ˑ１５) ２８０ k＝＝ ʈ１１．４２９．３５ˑ４５ˑ４０ˑ４０７ ȵ１１．４２９＞６．６３５,
２ [ , ] ; １３．－１; ㊀㊀㊀１４．３ π;㊀㊀㊀１５．１㊀㊀㊀１６．６．２ ( 三．解答题 : 共７０分)
( 二㊁填空题 : 每小题５分 , 共２０分)
第Ⅱ卷
( 非选择题 , 共９０分)
( ) ( 解: 由题意 , 得２又 S３＝１７． a２＋１ a１＋ a３． a１＋ a２＋ a３＝１＝４, Ⅰ) ( ) ʑ２ a２＋１ a２ , a２＝４, ＝１４－ ʑ １４ ȵS３＝＋４＋４４, ʑ q＝１ q＝２或q＝ , ２ q , ȵ q＞１ ʑ q＝２．
＋ nˑ２．
n
��７分 ��１０分 ��１１分 ��１２分 ��３分

四川省成都市外国语学校2019届高三二诊模拟考试数学(文)试题 Word版含解析

成都实外高三二诊模拟考试文科数学一、选择题.在每小题给出的四个选项中，只有一个是符合题目要求的.1.设集合则( )A. B. C. D.【答案】A【解析】【分析】根据两集合中元素的特征判断出两集合间的关系．【详解】由题意得，集合为奇数集合，集合为整数集合，所以．故选A．【点睛】判断两集合间的关系时，关键是分清两集合元素的特征，根据元素的特征作出判断，考查集合的元素和集合间的包含关系，属于基础题．2.在复平面内，复数对应的点位于( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限【答案】D【解析】【分析】通过复数的运算求出复数的代数形式，然后再进行判断即可．【详解】由题意得，所以复数在复平面内对应的点为，在第四象限．故选D．【点睛】解题的关键是将复数化为代数形式，然后再根据复数的几何意义进行判断，属于基础题．3.已知位学生得某次数学测试成绩得茎叶图如图，则下列说法正确的是( )A. 众数为7B. 极差为19C. 中位数为64.5D. 平均数为64【答案】C【解析】【分析】根据茎叶图中的数据求得这组数据的众数、极差、中位数和平均数．【详解】根据茎叶图中的数据知，这组数据的众数为67，A错误；极差是75﹣57＝18，B错误；中位数是64.5，C正确；平均数为60（﹣3﹣1+1+2+7+7+12+15）＝65，D错误．故选：C．【点睛】本题考查了利用茎叶图求众数、极差、中位数和平均数的应用问题，是基础题．4.函数的图像大致为( )A. B.C. D.【答案】D【解析】【分析】先根据奇偶性淘汰A,C，再根据函数最值确定选项.【详解】因为，所以为奇函数，不选A,C，又因为，所以选D.【点睛】由解析式确定函数图象的判断技巧：（1）由函数的定义域，判断图象左右的位置，由函数的值域，判断图象的上下位置；②由函数的单调性，判断图象的变化趋势；③由函数的奇偶性，判断图象的对称性；④由函数的周期性，判断图象的循环往复5.等比数列各项均为正数，若则的前6项和为( )A. B. C. D.【答案】B【解析】【分析】利用等比数列的性质及，可得q的值，计算即可.【详解】解：等比数列各项均为正数，且，，，可得q=2或q=-4(舍去)，=63，故选B.【点睛】本题考查了等比数列的性质及前n项和的公式，考查了推理能力与计算能力，属于中档题.6.已知向量与的夹角为，=2，=5，则在方向上的投影为( )A. B. C. D.【答案】B【解析】【分析】先求出，再根据投影的定义可得所求结果．【详解】∵=2，=5，向量与的夹角为，∴，∴在方向上的投影为．故选B．【点睛】解答本题的关键利用投影的定义求解，其中先求出两个向量的数量积是必须的步骤，考查数量积的定义和数量积的运算，属于基础题．7.设是两条直线，是两个平面，则的一个充分条件是( )A. B.C. D.【答案】C【解析】试题分析：A．可能垂直也可能不垂直，平行都有可能；B．；D．可能垂直，不垂直，或是平行都有可能；C．，，那么，，那么，故C正确．考点：线线，线面，面面位置关系8.已知双曲线:的一条渐近线与直线的夹角为，若以双曲线的实轴和虚轴为对角线的四边形面积为，则双曲线的标准方程为( )A. B. C. D.【答案】A【解析】因为双曲线的一条渐近线与直线的夹角为，所以双曲线的渐近线方程为，所以．因为以双曲线的实轴和虚轴为对角线的四边形的面积为，所以，即．由，解得，所以双曲线的标准方程为．故选A．9.若执行如图所示的程序框图，则输出S的值为( )A. B. C. D.【答案】C【解析】【分析】首先确定流程图的功能为计数的值，然后利用裂项求和的方法即可求得最终结果.【详解】由题意结合流程图可知流程图输出结果为，，.本题选择C选项.【点睛】识别、运行程序框图和完善程序框图的思路：(1)要明确程序框图的顺序结构、条件结构和循环结构．(2)要识别、运行程序框图，理解框图所解决的实际问题．(3)按照题目的要求完成解答并验证．10.已知则( )A. B.C. D.【答案】C【解析】【分析】由题意可得，=，由的性质可得a＜c，同理可得，=，由可得c＜b，可得答案.【详解】解：由题意得：，=，在为单调递增函数，a＜c，同理可得：，=，在R上为单调递增函数，c＜b，综上，故选C.【点睛】本题主要考查利用指数函数、幂函数比较函数值的大小，需熟练掌握指数函数、幂函数的性质.11.在中，角的对边分别是若，则的最小值为( )A. B. C. D.【答案】D【解析】【分析】由题意利用正弦定理化简已知等式，利用同角三角函数间基本关系可求tan A＝3tan B，进而利用正弦定理，基本不等式化简所求即可求解．【详解】解：∵a cos B﹣b cos A，∴由正弦定理化简得：sin A cos B﹣sin B cos A sin C sin（A+B）sin A cos B cos A sin B，整理得：sin A cos B＝3cos A sin B，∴cos A cos B＞0，∴tan A＝3tan B；∴则222．∴可得的最小值为．故选：D．【点睛】本题主要考查了正弦定理，同角三角函数间基本关系，基本不等式在解三角形中的综合应用，考查了转化思想，属于中档题．12.一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱.这个四棱锥的底面为正方形，且底面边长与各侧棱长相等，这个三棱锥的底面边长与各侧棱长也都相等. 设四棱锥、三棱锥、三棱柱的高分别为h1、h2、h，则h1﹕h2﹕h=A. ﹕1﹕1B. ﹕2﹕2C. ﹕2﹕D. ﹕2﹕【答案】B【解析】解：如图，设正三棱锥P-ABE的各棱长为a，则四棱锥P-ABCD的各棱长也为a，于是故选B二、填空题。

精品解析：【全国百强校】四川省成都市第七中学2019届高三二诊模拟考试数学(文)(解析版)

成都七中高2019届高三二诊模拟考试数学（文科）试卷注意：1．考生答题前，务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸上。

2．选择题的答案须用2B铅笔将答题纸上对应题目的答案标号涂黑，如要改动，须将原填涂处用橡皮擦净。

3．非选择题的答案须用黑色字迹的签字笔或钢笔写在答题纸上相应区域内，答案写在本试题卷上无效。

一、选择题：（共12个小题，每小题5分，共60分.）1.命题“，”的否定形式是（）.A. ，B. ，C. ，D. ，【答案】D【解析】【分析】结合命题的否定改写,即可.【详解】命题的否定为:改为,改为,故否定形式为，,故选D.【点睛】考查了命题的否定改写,关键抓住改为,改为,即可,难度较容易.2.已知复数满足，则为A. B. C. 2 D. 1【答案】A【解析】【分析】首先利用复数的运算法则，求出复数z，再应用复数的模的运算公式，求得结果.【详解】由，得，所以，故选A.【点睛】该题考查的是有关复数的问题，涉及到的知识点有复数的乘法运算法则和除法运算法则，还有复数的模，属于简单题目.3.设全集，集合，，则A. B.C. D.【答案】B【解析】【分析】由集合或，先求解，再由集合能够求出答案. 【详解】因为全集,集合或，所以，所以，故选B.【点睛】本题主要考查了集合的混合运算，属于基础题，其中解答中准确计算集合和集合的交集、补集的运算是解答的关键，着重考查了推理与运算能力.4.函数在处的切线方程为（）A. B.C. D.【答案】C【解析】【分析】计算导函数,计算切线斜率和切点坐标,结合点斜式方程计算方法,计算切线方程,即可.【详解】,故在处切线斜率为,在该点坐标为故切线方程为,得到,故选C.【点睛】考查了利用导函数计算曲线某一点的切线方程,难度中等.5.在△中，,,且的面积为，则的长为（）A. B. C. D.【答案】B【解析】试题分析：由题意得，因为的面积为，所以，解得，在中，由余弦定理可得，所以，故选B.考点：正弦定理；余弦定理.【方法点晴】本题主要考查了解三角形的综合问题，其中解答中涉及到三角形的正弦定理、余弦定理的应用，以及三角形的面积公式等知识点的综合考查，着重考查了学生分析问题和解答问题的能力，以及推理与运算能力，本题的解答中根据三角形的面积公式，求得，再利用正、余弦定理是解得关键.6.已知函数为上的偶函数，当时，单调递减，若，则的取值范围是（）A. B. C. D.【答案】C【解析】【分析】结合题意,大致绘制函数图像,利用数形结合思想,建立不等式,计算范围,即可.【详解】结合题意,为偶函数,则该函数关于y轴对称，当时，单调递减，根据大致绘制函数图像,要满足,则要求,解得,故选C.【点睛】考查了偶函数的性质,考查了函数单调性,考查了数形结合思想,难度中等.7.在区间内随机取两个数分别记为，则使得函数有零点的概率为（）A. B. C. D.【答案】B【解析】试题分析：先判断概率的类型，由题意知本题是一个几何概型，由a，b使得函数f（x）=x2+2ax-b2+π有零点，得到关于a、b的关系式，写出试验发生时包含的所有事件和满足条件的事件，做出对应的面积，求比值得到结果．解：由题意知本题是一个几何概型，∵a，b使得函数f（x）=x2+2ax-b2+π有零点，∴△≥0∴a2+b2≥π试验发生时包含的所有事件是Ω={（a，b）|-πaπ，-πbπ}∴S=（2π）2=4π2，而满足条件的事件是{（a，b）|a2+b2≥π}，∴s=4π2-π2=3π2，由几何概型公式得到P=，故选B．考点：几何概型点评：高中必修中学习了几何概型和古典概型两种概率问题，先要判断该概率模型是不是古典概型，再要找出随机事件A包含的基本事件的个数和试验中基本事件的总数．再看是不是几何概型，它的结果要通过长度、面积或体积之比来得到8. 如果执行如图所示的程序框图，输出的S＝110，则判断框内应填入的条件是( )．A. k＜10?B. k≥11?C. k≤10?D. k＞11?【答案】C【解析】试题分析：因为，所以时结束循环，因此选C.考点：循环结构流程图【方法点睛】研究循环结构表示算法，第一要确定是当型循环结构，还是直到型循环结构；第二要注意根据条件，确定计数变量、累加变量等，特别要注意正确理解循环结构中条件的表述，以免出现多一次循环或少一次循环的情况．9.已知函数，将的图像上的所有点的横坐标缩短到原来的，纵坐标保持不变；再把所得图像向上平移个单位长度，得到函数的图像，若，则的值可能为（）A. B. C. D.【答案】D【解析】【分析】结合三角函数平移原理，得到的解析式，计算结果，即可。

四川省德阳市普通高中2019级2022届高三毕业班第二次高考诊断性考试(德阳二诊)理科综合试题

绝密★启用前四川省德阳市普通高中2019级2022届高三毕业班第二次高考诊断性考试(德阳二诊)理科综合试题说明：1．本试卷分为选择题和非选择题两部分，第1卷（选择题）和第II卷（非选择题）。

考生作答时，须将答案答在答题卡上，在本试卷、草稿纸上答题无效。

考试结束后，将答题卡交回。

2．本试卷满分300分，150分钟完卷。

可能用到的相对原子质量：H 1 C 12O 16 S 32 Cr 52 Cu 64第I卷（选择题共126分）一、选择题（本题包括13小题，每小题6分，共78分。

每个小题只有一个选项符合题意）1．根据《中小学生膳食指南》建议，某同学的一份午餐搭配如下：二两米饭、一份红烧肉、一份蔬菜、一个煮鸡蛋。

下列叙述正确的是A.生鸡蛋比熟鸡蛋的蛋白质更易消化B.该午餐仅含有的脂质为脂肪和固醇C.该同学午餐后的血液中含有纤维素D.该份午餐包含肌糖原、淀粉等多糖2．细胞内的生物膜把细胞分隔成一个个小的“区室”，使得细胞内能够同时进行多种化学反应，而不会相互干扰，保证了细胞的生命活动高效、有序地进行。

下列所示化学反应不在这些“区室”内完成的是合成三碳化合物A．叶肉细胞中利用CO2B.动物细胞中损伤、衰老细胞器的分解C.酵母菌利用葡萄糖生成丙酮酸的过程D.细胞核中DNA的复制以及转录过程3．当肿瘤细胞的呼吸作用受到抑制时，细胞内的S物质可以通过激活信号来增加嘌呤和嘧啶的合成，进而促进细胞的增殖。

这一过程说明S物质可以A.提供细胞增殖时所需的能量B.降低化学反应所需的活化能C.增加DNA复制时所需的原料D.提高遗传物质突变时的频率4．控制果蝇眼色（红眼、白眼）的基因位于X染色体上，某果蝇种群足够大、个体间自由交配、自然选择对果蝇眼色没有影响、不发生基因突变、没有迁入和迁出，其中白眼雄果蝇（X＇Y）占5％。

在上述条件保持不变的情况下，下列有关分析错误的是A．该种群中白眼雌果蝇占2.5％B．该种群X的基因频率为10％C.该种群在眼色这一性状上不会发生进化D.该种群眼色基因频率和基因型频率都不改变5．科研人员配制了含有0、0.1、1.0、10.0、100.0μmol／L茉莉酸（JA）的培养基，将一定条件下培养的水稻植株转移至含有不同浓度的JA培养基表面生长48h，侧根的生长情况如下表所示。

四川省成都市实验外国语学校2019届高三二诊模拟考试数学(文科)试卷及解析

第1页，总18页………○…………装……………订…学校:___________姓名：_______________考号………○…………装……………订四川省成都市实验外国语学校2019届高三二诊模拟考试数学（文科）试卷注意事项：1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上第I 卷（选择题）一、选择题1.设集合M ={x |x =2k −1,k ∈Z }, N ={x |x =k +2,k ∈Z },则( )A. M⊂≠NB. M=N C. N ⊂≠MD. M ∩N =∅2.已知8位学生得某次数学测试成绩得茎叶图如图，则下列说法正确的是( )A. 众数为7B. 极差为19C. 中位数为64.5D. 平均数为643.函数f(x)=xsin 2x (−3π2≤x ≤3π2)的图像大致为( )A. B.C. D.4.等比数列{a n }各项均为正数，若a 1=1,a n+2+2a n+1=8a n,则{a n }的前6项和为( )A. 1365B. 63C. 6332D. 136510245.已知向量a ⃑⃑ 与b ⃑⃑ 的夹角为60°，|a ⃑⃑ |=2，|b ⃑⃑ |=5，则2a −b⃑ 在a ⃑⃑ 方向上的投影为( ) A. −√32B. 32C. 2D. 526.设a,b 是两条直线，α,β是两个平面，则a ⊥b 的一个充分条件是( )答案第2页，总18页…………订…………○…※订※※线※※内※※答※※题※※…………订…………○…A. a ⊥α,b//β,α⊥β B. a ⊥α,b ⊥β,α//β C. a⊂α,b ⊥β,α//βD. a⊂α,b//β,α⊥β7.已知双曲线C:x 2a 2−y 2b 2=1(a >0,b >0)的一条渐近线与直线x =0的夹角为30°，若以双曲线C的实轴和虚轴为对角线的四边形的面积为8√3，则双曲线C 的标准方程为（） A. x 24−y 212=1B. x 24−y 28=1 C. x 212−y 24=1D. x 28−y 24=1 8.若执行如图所示的程序框图，则输出S 的值为( )A.10072015B.10082017C.10092019D.101020219.已知a =3615,b =343,c =925,则( )A. b <a <cB. a <b <cC. a<c <bD. c<a <b10.在△ABC 中，角A,B,C 的对边分别是a,b,c,若acosB −bcosA =c2，则acosA−bcosBacosB 的最小值为( )A. √3B.4√33C.√33D.2√3311.一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱.这个四棱锥的底面为正方形，且底面边长与各侧棱长相等，这个三棱锥的底面边长与各侧棱长也都相等. 设四棱锥、三棱锥、三棱柱的高分别为h 1、h 2、h ，则h 1﹕h 2﹕h = A. √3﹕1﹕1 B. √3﹕2﹕2 C. √3﹕2﹕√2 D. √3﹕2﹕√3第II 卷（非选择题）请点击修改第II 卷的文字说明二、填空题（题型注释）第3页，总18页……外…………○…学校……内…………○…12.设x,y 满足条件{2x −y ≥0x +y ≥1y ≥0，则2x +3y 的最小值为_______．13.某单位有职工200人，其年龄分布如下表：为了解该单位职工的身体健康状况，用分层抽样的方法抽取一个容量为40的样本进行调查，则年龄在[30,40)内的职工应抽取的人数为______14.已知函数f(x)={log 2x,x ≥1x 2+m 2,x <1，若f(f (−1))=2，则实数m =____15.已知A (3,0)，若点P 是抛物线y 2=8x 上的任意一点，点Q 是圆(x −2)2+y 2=1上任意一点，则|PA |2|PQ |最小值是_____三、解答题（题型注释）16.某商场举行购物抽奖活动，抽奖箱中放有编号分别为1，2，3，4，5的五个小球.小球除编号不同外，其余均相同.活动规则如下：从抽奖箱中随机抽取一球，若抽到的小球编号为3，则获得奖金100元；若抽到的小球编号为偶数，则获得奖金50元；若抽到其余编号的小球，则不中奖.现某顾客依次有放回的抽奖两次.（1）求该顾客两次抽奖后都没有中奖的概率；（2）求该顾客两次抽奖后获得奖金之和为100元的概率. 17.如图，在四棱锥P−ABCD 中，PA ⊥平面ABCD , AB ⊥AD ，AD//BC ，AD =2BC =4，PB =4√2,M 是线段AP 的中点.（1）证明：BM//平面PCD ; （2）当PA 为何值时，四棱锥P −ABCD 的体积最大？并求此最大值18.已知函数f (x )=2cosωx(sinωx +√3cosωx)−√3−1(ω>0)， f (x 1)=答案第4页，总18页…………○…※答※※题※※…………○…1，f(x 2)=−3，且|x 1−x 2|min =π2. （1）求f (x )的单调递减区间；（2）若α,β∈(π3,2π3),f (β2−π3)=35,sin (α+β)=−725，求f (α2)的值.19.已知椭圆C :x 2a 2+y 2b2=1(a >b >0)的左右焦点分别是F 1,F 2，抛物线y 2=4x 与椭圆C 有相同的焦点，点P 为抛物线与椭圆C 在第一象限的交点，且满足|PF 2|=53.（1）求椭圆C 的方程；（2）过点F 1作直线l 与椭圆C 交于A,B 两点，设AF 1⃑⃑⃑⃑⃑⃑⃑⃑⃑ =λF 1B ⃑⃑⃑⃑⃑⃑⃑⃑⃑ .若λ∈[1,2]，求ΔABF 2面积的取值范围.20.已知函数f(x)=cos2x,g (x )=sinx(1)是否存在x 0∈(π6,π4)，使得f (x 0),g (x 0),f (x 0)·g (x 0)，按照某种顺序成等差数列？若存在，请确定x 0的个数；若不存在，请说明理由； (2)求实数a 与正整数n ，使得F(x)=f (x )+ag (x )在(0,nπ)内恰有2019个零点.21.在平面坐标系xoy 中，曲线C 1的参数方程为{x =2t 2y =2t（t 为参数）.以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系并取相同的单位长度，曲线C 2的极坐标方程为ρsin (θ−π4)=−√22.（1）把曲线C 1的方程化为普通方程，C 2的方程化为直角坐标方程（2）若曲线C 1,C 2相交于A ，B 两点，AB 的中点为P ，过P 点作曲线C 2的垂线交曲线C 1于E ，F 两点，求|EF ||PE |⋅|PF |.22.已知函数ℎ(x )=|x −m |,g (x )=|x +n |，其中m >0，n >0.（1）若函数ℎ(x )的图像关于直线x =1对称，且f (x )=ℎ(x )+|2x −3|，求不等式f(x)>2的解集.（2）若函数φ(x)=ℎ(x)+g(x)的最小值为2，求1m +1n的最小值及相应的m 和n 的值.第5页，总18页参数答案1.A【解析】1.根据两集合中元素的特征判断出两集合间的关系．由题意得，集合M 为奇数集合，集合N 为整数集合，所以M⊂≠N ．故选A ． 2.C【解析】2.根据茎叶图中的数据求得这组数据的众数、极差、中位数和平均数．根据茎叶图中的数据知，这组数据的众数为67，A 错误；极差是75﹣57＝18，B 错误；中位数是62+672=64.5，C 正确；平均数为60+18（﹣3﹣1+1+2+7+7+12+15）＝65，D 错误．故选：C ． 3.D【解析】3.先根据奇偶性淘汰A,C ，再根据函数最值确定选项. 因为−3π2≤x ≤3π2，f (−x )=−xsin 2x =−f (x )，所以f (x )为奇函数，不选A,C ，又因为−3π2≤x ≤3π2时f(x)≤f(3π2)，所以选D.4.B【解析】4.利用等比数列的性质及a n+2+2a n+1=8a n ，可得q 的值，计算S 6即可.解：∵等比数列{a n }各项均为正数，且a n+2+2a n+1=8a n ，答案第6页，总18页装…………※要※※在※※装装…………∴ a n q 2+2a n q =8a n ，q 2+2q =8，可得q=2或q=-4(舍去)， ∴ S 6=a 1(1−q 6)(1−q)=63，故选B. 5.B【解析】5. 先求出(2a−b ⃑ )⋅a ，再根据投影的定义可得所求结果．∵|a ⃑⃑ |=2，|b ⃑⃑ |=5，向量a ⃑⃑ 与b ⃑⃑ 的夹角为60°， ∴(2a −b ⃑ )⋅a =2a 2−b ⃑ ⋅a =2×22−5×2×cos60°=3，∴2a−b ⃑ 在a ⃑⃑ 方向上的投影为(2a ⃑⃑ −b ⃑ )⋅a ⃑⃑|a ⃑⃑ |=32．故选B ． 6.C【解析】6. 试题分析：A ．可能垂直也可能不垂直，平行都有可能；B ．；D ．可能垂直，不垂直，或是平行都有可能；C ．，，那么，，那么，故C 正确．7.A【解析】7. 因为双曲线C:x 2a 2−y 2b 2=1(a >0,b >0)的一条渐近线与直线x =0的夹角为30°，所以双曲线C 的渐近线方程为y =±√3x ，所以ba =√3．因为以双曲线C 的实轴和虚轴为对角线的四边形的面积为8√3所以4×12ab =8√3，即ab =4√3．由{ba=√3ab =4√3，解得{a =2b =2√3，所以双曲线C 的标准方程为x 24−y 212=1．故选A ．8.C【解析】8.第7页，总18页首先确定流程图的功能为计数S =11×3+13×5+15×7+⋯+12017×2019的值，然后利用裂项求和的方法即可求得最终结果.由题意结合流程图可知流程图输出结果为S =11×3+13×5+15×7+⋯+12017×2019，∵1n(n+2)=12×(n+2)−n n(n+2)=12(1n−1n+2)，∴S =11×3+13×5+15×7+⋯+12017×2019=1[(1−1)+(1−1)+(1−1)+⋯+(1−1)] =12(1−12019)=10092019.本题选择C 选项. 9.C【解析】9. 由题意可得a=3615，c =925=8115，由y =x15的性质可得a ＜c ，同理可得b =343，c =925=345，由y =3x 可得c ＜b ，可得答案.解：由题意得：a=3615，c =925=8115，∵ y =x15在[0,+∞)为单调递增函数，∴a ＜c ，同理可得：b =343，c =925=345，∵ y =3x 在R 上为单调递增函数，∴c ＜b ，综上a<c <b ，故选C. 10.D【解析】10.由题意利用正弦定理化简已知等式，利用同角三角函数间基本关系可求tan A ．3tan B ，进而利用正弦定理，基本不等式化简所求即可求解．解：∵a cos B ．b cos A =c2．∴由正弦定理化简得：sin A cos B ．sin B cos A =12sin C =12sin．A +B ．=12sin A cos B +12cos A sin B ．答案第8页，总18页…装…………○不※※要※※在※※装※※…装…………○整理得：sin A cos B ．3cos A sin B ．．cos A cos B ．0．．tan A ．3tan B ． ∴则acosA+bcosBacosB=cosA cosB +b a =cosA cosB +sinB sinA ≥2√cosA cosB ⋅sinB sinA =2√tanB tanA =2√13=2√33． ∴可得acosA+bcosB acosB 的最小值为2√33．故选：D ． 11.B【解析】11.略 12.2【解析】12.根据已知条件画出可行域，平移目标函数，得到最优解，可得答案. 解：由题意，根据已知条件作出如下可行域：设z=2x+3y ，即:y =−23x +23z ，由图可知，当目标函数过点C 时，z=2x+3y 最小，由{x +y =1y =0，可得C(1,0),故(2x +3y)min =2故答案：2 13.18【解析】13.先确定每层的抽样比，然后根据此比例进行抽取即可得到所求结果．由题意得该抽样的抽样比例为4070+90+40=15，第9页，总18页所以由分层抽样的步骤可得，在在[30,40)内的职工应抽取的人数为90×15=18人．故答案为18． 14.±√3【解析】14. 先求出f (−1)=m 2+1，然后再根据log 2(m 2+1)=2求出m =±√3．由题意得f (−1)=m 2+1≥1，所以f(f (−1))=f (m 2+1)=log 2(m 2+1)=2，故m 2+1=4，解得m =±√3．故答案为±√3． 15.4√3−4【解析】15. 抛物线y 2=8x 的焦点为F (2,0)，准线方程为x =−2．由题意得|PQ|max =|PF|+1，所以|PA|2|PQ|≥|PA|2|PF|+1，即|PA|2|PQ|的最小值为|PA|2|PF|+1．令t =|PF|+1，则点P 的横坐标为x P =|PF|−2=t −3，由此得|PA|2 =(x P −3)2+y P 2=(x P −3)2+8x P =(t −6)2+8(t −3)，然后再根据基本不等式求解可得结果．由题意得抛物线y 2=8x 的焦点为F (2,0)，准线方程为x =−2．又点P 是抛物线上一点，点Q 是圆(x −2)2+y 2=1上任意一点，∴|PQ|max=|PF|+1，∴|PA|2|PQ|≥|PA|2|PF|+1．令t=|PF|+1，点P 的坐标为(x P ,y P )，则x P=|PF|−2=t −3，∴|PA|2 =(x P −3)2+y P 2=(x P −3)2+8x P =(t −3−3)2+8(t −3)=t 2−4t +12，∴|PA|2|PF|+1=t2−4t+12t=t +12t −4≥2√t ⋅12t−4=4√3−4，当且仅当t =12t，即t =2√3时等号成立．答案第10页，总18页∴|PA|2|PQ|的最小值为4√3−4．故答案为4√3−4． 16.（1）P =425（2）825【解析】16.（1）用列举法得到所有的基本事件数，然后根据古典概型概率公式可得事件发生的概率；（2）根据互斥事件的概率加法公式求解可得结果．（1）由题意得，该顾客有放回的抽奖两次的所有可能结果为：(1,1),(1,2),(1,3),(1,4),(1,5),(2,1),(2,2),(2,3),(2,4),(2,5), (3,1),(3,2),(3,3),(3,4),(3,5), (4,1),(4,2),(4,3),(4,4),(4,5), (5,1),(5,2),(5,3),(5,4),(5,5).共有25种情况．设“该顾客两次抽奖后都没有中奖”为事件A ，则事件A 包含的结果为(1,1),(1,5),(5,1),(5,5)，共4种，所以P(A)=425．即该顾客两次抽奖后都没有中奖的概率为425．（2）两次抽奖奖金之和为100元包括三种情况：①第一次奖金为100元，第二次没有获奖，其包含的情况为(3,1),(3,5)，概率为P 1=225；②第一次没中奖，第二次奖金为100元，其包含的情况为(1,3),(5,3)，概率为P 2=225；③两次各获奖金50元，包含的情况有(2,2),(2,4),(4,2),(4,4)，概率为P 3=425．由互斥事件有一个发生的概率公式可得所求概率为P=P 1+P 2+P 3=825，即该顾客两次抽奖后获得奖金之和为100元的概率为825． 17.（1）见解析（2）当PA ＝4时，体积最大值为16．【解析】17.（1）取PD中点N，易证MNCB为平行四边形，进而得BM，CN平行，得证；（2）设PA＝x（0＜x＜4√2），把体积表示为关于x的函数，借助不等式求得最大值．（1）取PD中点N，连接MN，CN，∵M是AP的中点，∴MN∥AD且MN=12 AD，∵AD∥BC，AD＝2BC，∴MN∥BC，MN＝BC，∴四边形MNCB是平行四边形，∴MB∥CN，又BM⊄平面PCD，CN⊂平面PCD，∴BM∥平面PCD；（2）设PA＝x（0＜x＜4√2），∵PA⊥平面ABCD，∴PA⊥AB，∵PB=4√2，∴AB=2−AB2=√32−x2，又∵AB⊥AD，AD＝2BC＝4，∴V P﹣ABCD=13S ABCD×PA=13×12(AD+BC)×AB×PA=x√32−x2≤x2+32−x22＝16，当且仅当x=√32−x2，即x＝4时取等号，故当PA＝4时，四棱锥P﹣ABCD的体积最大，最大值为16．答案第12页，总18页○…………线…………○○…………线…………○18.(1) 单调递减区间为[kπ+π12,kπ+7π12],k ∈Z ； (2) 15.【解析】18.（1）根据题意求出函数f (x )的解析式，然后可求出它的单调递减区间．（2）结合条件求出sin (β−π3)=45,cos (α+β)=−2425，然后由f(α2)=2sin (α+π3)−1=2sin [(α+β)−(β−π3)]−1可得结果．（1）f (x )=2cosωx(sinωx +√3cosωx)−√3−1=2sinωxcosωx +2√3cos 2ωx −√3−1=sin2ωx +√3(2cos 2ωx −1)−1=sin2ωx +√3cos2ωx −1=2sin(2ωx +π3)−1．∵−1≤sin(2ωx +π3)≤1，∴−3≤2sin(2ωx +π3)−1≤1，∴f (x )的最大值为1，最小值为−3．又f (x 1)=1,f(x 2)=−3，且|x 1−x 2|min =π2，∴函数f (x )的最小正周期为2×π2=π，∴ω=1，∴f(x)=2sin(2x +π3)−1．由2kπ+π2≤2x+π3≤2kπ+3π2,k∈Z，得kπ+π12≤x≤kπ+7π12,k∈Z，∴f(x)的单调递减区间为[kπ+π12,kπ+7π12],k∈Z．（2）由（1）得f(β2−π3)=2sin(β−π3)−1=35，∴sin(β−π3)=45．∵β∈(π3,2π3)，∴β−π3∈(0,π3)，∴cos(β−π3)=√1−sin2(β−π3)=35．∵sin(α+β)=−725且α,β∈(π3,2π3)，∴α+β∈(2π3,4π3)，∴cos(α+β)=−√1−sin2(α+β)=−2425．∴f(α2)=2sin(α+π3)−1=2sin[(α+β)−(β−π3)]−1=2[sin(α+β)cos(β−π)−cos(α+β)sin(β−π)]−1=2×[−725×35−(−2425)×45]−1=15．19.(1) x 24+y23=1 (2) [9√58,3]【解析】19.（1）由题意可得点P的坐标为(23,2√63)，然后求出|PF1|=73，根据椭圆的定义可得a=2，进而得到b2=3，于是可得椭圆的方程．（2）由题意直线l的斜率不为0，设其方程为x=my−1，代入椭圆方程后结合根与系数的关系得到S△ABF2=12|F1F2||y1−y2|=12√m2+13m2+4，然后通过换元法求出12√m2+13m2+4的范围即可．（1）由题意得抛物线y2=4x的焦点坐标为F2(1,0)，准线方程为x=−1．答案第14页，总18页∵|PF 2|=53， ∴点P 到直线x=−1的距离为53，从而点P 的横坐标为53−1=23，又点P 在第一象限内， ∴点P 的坐标为(23,2√63)．∴|PF 1|=√(23+1)2+(2√63)2=73， ∴2a =|PF 1|+|PF 2|=53+73=4，∴a =2．∴b2=a 2−c 2=3，∴椭圆C 的方程为x 24+y 23=1．（2）根据题意得直线l 的斜率不为0，设其方程为x =my −1，由{x =my −1x 24+y 23=1消去x 整理得(3m 2+4)y 2−6my −9=0，显然Δ=36m 2+36(3m 2+4)=144(m 2+1)>0．设Α(x 1，y 1),Β(x 2,y 2)，则{y 1+y 2=63m 2+4y 1y 2=−93m 2+4①∵AF 1⃑⃑⃑⃑⃑⃑⃑⃑⃑ =λF 1B ⃑⃑⃑⃑⃑⃑⃑⃑⃑ ，即AF 1⃑⃑⃑⃑⃑⃑⃑⃑⃑ (−1−x 1,−y 1)=λ(x 2+1,y 2)， ∴−y 1=λy 2，代入①消去y 1,y 2得4m 23m 2+4=(λ−1)2λ．∵λ∈[1,2]，∴(λ−1)2λ=λ+1λ−2∈[0,12]，∴0≤4m 23m +4≤12，解得0≤m 2≤45．由题意得S △ABF 2=12|F 1F 2||y 1−y 2|=|y 1−y 2|=√(y 1+y 2)2−4y 1y 2=12√m 2+13m 2+4．令√1+m 2=t ∈[1,3√55]，则m 2=t 2−1，∴S ΔABF 2=12t3t 2+1=123t+1t，设f(t)=3t +1t,t ∈[1,3√55]，则f(t)在[1,3√55]上单调递增，∴f(1)≤f(t)≤f(3√55)，即4≤3t +1t≤32√515，∴9√58≤123t+1t≤3．即ΔABF 2面积的取值范围为[9√58,3]．20.(1)见解析；(2)见解析【解析】20.（1）根据题意可得sinx>cosx >sinxcos2x ，所以可将问题转化为判断方程2cos2x =sinx +sinxcos2x 在区间[π6,π4]内是否有解处理，设G (x )=sinx +sinxcos2x −2cos2x,x ∈[π6,π4]，判断出函数G (x )的单调性，再根据零点存在性定理求解．（2）结合题意可将问题转化为研究当x ∈(0,π)∪(π,2π)时，方程a =−cos2x sinx的解的情况．然后利用导数和函数的周期性进行分析、求解后可得结论．（1）∵x ∈(π6,π4)，∴12<sinx <√22,√22<cosx <√32,0<cos2x <12，所以sinx >cosx >sinxcos2x ．所以问题转化为方程2cos2x =sinx +sinxcos2x 在区间[π6,π4]内是否有解．设G (x )=sinx +sinxcos2x −2cos2x,x ∈[π6,π4]，则G ′(x )=cosx +sinxcos2x +2sin2x (2−sinx )，因为x∈[π6,π4]，所以G ′(x )>0 ,G (x )在区间[π6,π4]上单调递增，又G(π6)=−14<0,G(π4)=√22>0，所以G (x )在区间[π6,π4]内存在唯一零点x 0，即存在唯一的x 0 ∈[π6,π4]满足题意．（2）由题意得F (x )=asinx +cos2x ．令F (x )=asinx +cos2x =0，答案第16页，总18页当sinx=0，即x =kπ(k ∈Z )时，cos2x =1，从而x =kπ(k ∈Z )不是方程F (x )=0的解．所以方程F (x )=0等价于关于x 的方程a =−cos2x sinx,x ≠kπ(k ∈Z )，下面研究当x ∈(0,π)∪(π,2π)时，方程a =−cos2x sinx的解的情况．令ℎ(x )=−cos2x sinx，x ∈(0,π)∪(π,2π)，则问题等价于直线y =a 与曲线y =ℎ(x ),x ∈(0,π)∪(π,2π)的交点情况．又ℎ′(x )=cosx(2sin 2x+1)sin 2x，令ℎ′(x )=0得x =π2或x =3π2．当x 变化时，ℎ′(x ),ℎ(x )的变化情况如下表：当x >0且x 趋近于0时，ℎ(x )趋向于−∞，当x <π且x 趋近于π时，ℎ(x )趋向于−∞，当x >π且x 趋近于π时，ℎ(x )趋向于+∞，当x<2π且x 趋近于2π时，ℎ(x )趋向于+∞，故当a >1时，直线y =a 与曲线y =ℎ(x )在(0,π)内无交点，在(π,2π)内有2个交点；当a<−1时，直线y =a 与曲线y =ℎ(x )在(0,π)内有2个交点，在(π,2π)内无交点；当−1<a <1时，直线y =a 与曲线y =ℎ(x )在(0,π)内有2个交点，在(π,2π)内有2个交点.由ℎ(x )的周期性可知当a ≠±1时，直线y =a 与y =ℎ(x )在(0,nπ)内总有偶数个交点，从而不存在正整数n ，使y =a 与y =ℎ(x )在(0,nπ)内有2019个交点．又当a=1或a =−1时，直线y =a 与y =ℎ(x )在(0,π)∪(π,2π)内有三个交点，由周期性知2019=3×673，所以n=673×2=1346．21.（1）C 1：y 2=2x ，C 2：x −y −1=0；（2）√143【解析】21.(1)利用代入法消去参数可得到曲线C 1的普通方程，利用{x =ρcosθy =ρsinθ可得C 2的直角坐标方程；(2)利用(1)的结论，利用一元二次方程根和系数关系求得线段AB 的中垂线参数方程为{x =2−√22ty =1+√22t(t 为参数)，代入y 2=2x ，利用直线参数方程的几何意义可得结果．(1)曲线C 1的参数方程为{y =2t x =2t2(其中t 为参数)，转换为直角坐标方程为：y 2=2x ．曲线C 2的极坐标方程为ρsin (θ−π4)=−√22．转换为直角坐标方程为：x −y −1=0．(2)设A (x 1,y 1)，B (x 2,y 2)，且中点P (x 0,y 0)，联立方程为：{y 2=2xx −y −1=0，整理得：x 2−4x +1=0所以：x 1+x 2=4，x 1x 2=1，由于：x 0=x 1+x 22=2，y 0=1．所以线段AB 的中垂线参数方程为{x =2−√22t y =1+√22t(t 为参数)，代入y 2=2x ，得到：t 2+4√2t −6=0，故：t 1+t 2=−4√2，t 1⋅t 2=−6，所以：EF=|t 1−t 2|=√(t 1+t 2)2−4t 1t 2=2√14，|PE ||PF |=|t 1⋅t 2|=6故：|EF ||PE |⋅|PF |=2√146=√143． 22.（1）(−∞,23)∪(2,+∞)；（2）1m +1n的最小值为2，相应的m =n =1【解析】22.(1)先根据对称性求出m =1，对x 分三种情况讨论，分别去掉绝对值符号，然后求解不等式组，再求并集即可得结果；(2)根据绝对值三角不等式即可求出m +n =2，可得1m +1n =12(1m +1n)(m +n )，再根据基本不等式即可求出. (1)函数h (x )的图象关于直线x=1对称，∴m =1，∴f (x )=h (x )+|2x −3|=|x −1|+|2x −3|，①当x ≤1时，(x )=3−2x +1−x =4−3x >2，解得x <23，②当1<x <32时，f (x )=3−2x +x −1=2−x >2，此时不等式无解，②当x ≥32时，f (x )=2x −3+x −1=3x −4>2，解得x >2，综上所述不等式f (x )>2的解集为(−∞,23)∪(2,+∞)． (2)∵φ(x )=ℎ(x )+g (x )=|x −m |+|x +n |≥|x −m −(x +n )|=|m +n |=m +n ，答案第18页，总18页又φ(x )=ℎ(x )+g (x )的最小值为2，∴m +n =2，∴1m+1n=12(1m+1n)(m +n )=12(2+n m+m n)≥12(2+2√m n⋅nm)=2，当且仅当m =n =1时取等号，故1m +1n 的最小值为2，其相应的m=n =1．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

德阳市高中2015级“二诊”考试数学试卷（文史类）第Ⅰ卷（选择题共60分）一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1.已知i为虚数单位，实数x，y满足(2)xiiyi，则xyi（）

A．1 B．2 C．3 D．5 2.已知集合2{|40}AxNxx，集合2{|20}Bxxxa，若{1,2,3,3}AB，则AB（）

A．{1} B．{2} C．{3} D． 3.函数()sin(2)fxx的图象向右平移6个单位后所得的图象关于原点对称，则可以是（） A．6 B．3 C．4 D．23 4.实验测得四组数对(,)xy的值为(1,2)，(2,5)，(4,7)，(5,10)，则y与x之间的回归直线方程是（） A．1.80.6yx B．1.80.6yx C．1.52.5yx D．0.57.5yx

参考公式：121()()()niiiniixxyybxx，aybx. 5.如图所示的三视图表示的几何体的体积为323，则该几何体的外接球的表面积为（）

A．12 B．24 C．36 D．48 6.《九章算术》是我国古代一部数学名著，某数学爱好者阅读完其相关章节后编制了如图的程序框图，其中(,)MODmn表示m除以n的余数，例如(7,3)1MOD.若输入m的值为8时，则输出i的值为（）

A．2 B．3 C．4 D．5 7.已知235logloglog0xyz，则2x、3y、5z的大小排序为（）

A．235xyz B．325yxz C．523zxy D．532zyx 8.以等腰直角三角形ABC的斜边BC上的中线AD为折痕，将ABD与ACD折成互相垂直的两个平面，得到以下四个结论：①BD平面ACD；②ABC为等边三角形；③平面ADC平面ABC；④点D在平面ABC内的射影为ABC的外接圆圆心.其中正确的有（） A．①②③ B．②③④ C．①②④ D．①③④

9. 已知双曲线22221(0,0)xyabab的离心率为2，其一条渐近线被圆22()4(0)xmym截得的线段长为22，则实数m的值为（）

A．3 B．1 C．2 D．2 10.已知函数()sinfxxx，若[2,1]x，使得2()()0fxxfxk成立，则实数k的取值范围是（） A．[1,3] B．[0,3] C．(,3] D．[0,) 11. 如图，过抛物线24yx的焦点F作倾斜角为的直线l，l与抛物线及其准线从上到下依次交于A、B、C点，令1AFBF，2BCBF，则当3时，12的值为（）

A．3 B．4 C．5 D．6 12. 已知A、B是函数2,()()(2),()xaexafxfaxxa（其中常数0a）图象上的两个动点，点(,0)Pa，若PAPB的最小值为0，则函数()fx的最大值为（） A．21e B．1e C．2ee D．ee 第Ⅱ卷（非选择题共90分）二、填空题：共4小题，每小题5分，共20分.将答案填在答题卡上.

13.已知实数x，y满足条件2300xyxyxy，则3xy的最大值为． 14.为弘扬我国优秀的传统文化，某小学六年级从甲、乙两个班各选出7名学生参加成语知识竞赛，他们取得的成绩（满分100分）的茎叶图如图，其中甲班学生的平均分是85，乙班学生成绩的中位数是83，则yx的值为． 15.如图，在三角形OPQ中，M、N分别是边OP、OQ的中点，点R在直线MN上，且ORxOPyOQ(,)xyR，则代数式22xy的最小值为． 16.已知ABC中，角A、B、C所对的边分别是a、b、c且6a，4sin5sinBC，2AC，若O为ABC的内心，则ABO的面积为．

三、解答题：解答应写出文字说明、证明过程或演算步骤.

17.已知数列{}na满足11a，121nnaa. （1）求证：数列{1}na为等比数列；

（2）求数列12nnnaa的前n项和nT. 18.省环保厅对A、B、C三个城市同时进行了多天的空气质量监测，测得三个城市空气质量为优或良的数据共有180个，三城市各自空气质量为优或良的数据个数如下表所示： A城 B城 C城

优（个） 28 x y

良（个） 32 30 z 已知在这180个数据中随机抽取一个，恰好抽到记录B城市空气质量为优的数据的概率为0.2. （1）现按城市用分层抽样的方法，从上述180个数据中抽取30个进行后续分析，求在C城中应抽取的数据的个数；（2）已知23y，24z，求在C城中空气质量为优的天数大于空气质量为良的天数的概率. 19.如图，在四棱锥PABCD中，底面ABCD为菱形，60DAB，PD平面ABCD，2PDAD，点E、F分别为AB和PD的中点.

（1）求证：直线//AF平面PEC；（2）求点A到平面PEC的距离.

20.已知椭圆C：22221(0)xyabab的两个焦点与短轴的一个端点构成的三角形的面积

为23，且椭圆C的离心率为32. （1）求椭圆C的方程；（2）过点(4,0)且斜率不为零的直线l与椭圆C交于两点M、N，点(22,0)T，试探究：直线MT与NT的斜率之积是否为常数.

21.已知函数2()lnfxxmxx. （1）若12x是()fx的一个极值点，求()fx的最大值；

（2）若121,,xxee，12xx，都有2112()()xfxxfx1221()xxxx，求实数m的取值范围. 请考生在22、23两题中任选一题作答.注意：只能做所选定的题目.如果多做，则按所做的第一题记分，做答时，请用2B铅笔在答题卡上将所选题号后的方框涂黑.

22.在平面直角坐标系xOy中，直线l：22xtyt（t为参数），以坐标原点为极点，x轴正半轴为极轴，建立极坐标系，曲线C：2sin. （1）求直线l的极坐标方程及曲线C的直角坐标方程；

（2）记射线0,02与直线l和曲线C的交点分别为点M和点N（异

于点O），求ONOM的最大值.

23.已知函数()1fxx. （1）解关于x的不等式2()1fxx；（2）若关于x的不等式2()1fxaxx的解集非空，求实数a的取值范围. 德阳市高中2015级“二诊”试题数学参考答案（文史类）一、选择题 1-5: DABAC 6-10: BACDA 11、12：CB 二、填空题

13. 8 14. 35 15. 24 16. 7 三、解答题 17.解：（1）∵121nnaa，∴112(1)nnaa. 又11a，∴1120a，10na. ∴{1}na是以2为首项，2为公比的等比数列. （2）由（1）知21nna，

∴1122(21)(21)nnnnnnaa1112121nn, ∴22111212121nT31111212121nn 11121n.

18.解：（1）由题意得0.2180x，即36x. ∴1802832363054yz， ∴在C城中应抽取的数据个数为30549180. （2）由（1）知54yz，,yzN且23y，24z， ∴满足条件的数对(,)yz可能的结果有(23,31)，(24,30)，(25,29)，(26,28)，(27,27)，(28,26)，(29,25)，(30,24)共8种.

其中“空气质量为优的天数大于空气质量为良的天数”对应的结果有(28,26)，(29,25)，(30,24)共3种. ∴在C城中空气质量为优的天数大于空气质量为良的天数的概率为38. 19.解：（1）取PC的中点Q，连结EQ、FQ，由题意，//FQDC且12FQCD，//AECD且12AECD，故//AEFQ且AEFQ，所以，四边形AEQF为平行四边形，所以，//AFEQ，又EQ平面PEC，AF平面PEC，所以，//AF平面PEC. （2）设点A到平面PEC的距离为d. 由题意知在EBC中，

222cosECEBBCEBBCEBC

11421272，

在PDE中227PEPDDE，在PDC中2222PCPDCD，故EQPC，5EQAF， 1225102PECS，

131322AECS，

所以由APECPAECVV得：113102332d，解得3010d. 20.解：（1）由题意得2332bcca（其中c椭圆的半焦距），解得2282ab. 所以椭圆C的方程为：22182xy. （2）由题意设直线l的方程为：4xmy，11(,)Mxy，22(,)Nxy，

由224182xmyxy得：22(4)880mymy，

所以1221222284846432(4)0myymyymmm，故1212()8xxmyy2324m， 21212124()xxmyymyy

2648164mm



，

MTNTkk1212(22)(22)yyxx

12121222()8yyxxxx

3224（常数）.

21.解：（1）1'()21(0)fxmxxx，由题意得1'02f，即210m，所以1m，所以1'()21fxxx(21)(1)xxx，