2020年广州市初中数学竞赛专项练习:塞瓦定理(含答案)
初中数学重点梳理:塞瓦定理

塞瓦定理知识定位使用塞瓦定理可以进行线段长度的计算,其定理还可以用来解决三点共线、三线共点等问题的判定方法,是平面几何学以及射影几何学中的一项基本定理,具有重要的作用.本讲将通过例题来说明这些方法的运用。
知识梳理1、 塞瓦定理设A ',B ',C '分别是△ABC 的三边BC ,CA ,AB 或其延长线上的点,若AA ',BB ',CC '三线平行或共点,则1BA CB AC A C B A C B'''⋅⋅='''.①证明 如图2-1(b )、(c ),若AA ',BB ',CC '交于一点P ,则过A 作BC 的平行线,分别交BB ',CC '的延长线于D ,E ,得,CB BC AC EAB A ADC B BC''==''. A′B'C 'ABPPCBAA′B'C 'D ECBAA′B'C 'D E (c)(b)(a)图2-1又由BA A P A C AD PA EA '''==,有BA ADA C EA '='. 从而1BA CB AC AD BC EA A C B A C B EA AD BC'''⋅⋅=⋅⋅='''.若AA ',BB ',CC '三线平行,可类似证明(略). 注 (1)对于图2-1(b )、(c )也有如下面积证法:由:1PAB PBC PCAPCA PAB PBCS S S BA CB AC A C B A C B S S S '''⋅⋅=⋅⋅='''△△△△△△,即证.(2)点P 常称为塞瓦点.(3)共点情形的塞瓦定理与梅涅劳斯定理可以互相推证.首先,由梅涅劳斯定理推证共点情形的塞瓦定理. 如图2-1(b )、(c ),分别对△ABA '及截线C PC ',对△AA C '及截线B PB '应用梅涅劳斯定理有1BC A P AC CA PA C B ''⋅⋅='',1A B CB APBC B A PA''⋅⋅=''. 上述两式相乘,得1BA CB AC A C B A C B'''⋅⋅='''.其次,由共点情形的塞瓦定理推证梅涅劳斯定理.如图2-2,设A ',B ',C '分别为△ABC 的三边BC ,CA ,AB 所在直线上的点,且A ',B ',C '三点共线.令直线BB '与CC '交于点X ,直线C C '与AA '交于点Y ,直线AA '与BB '交于点Z .CBAA′B'C 'XY ZXYZ CBAA′B'C '图2-2分别视点C ',A ',B ',C ,A ,B 为塞瓦点,应用塞瓦定理,即对△BCB '及点C '(直线BA ,CX ,B A ''的交点),有1BA CA B XA C AB XB ''⋅⋅=''.对△CAC '及点A '(直线CB ,AY ,C B ''的交点),有1CB AB C YB C BC YC ''⋅⋅=''.对△ABA '及点B '(直线AC ,BZ ,A C ''的交点),有1AC BC A ZC B CA ZA ''⋅⋅=''.对△BBC '及点C (直线BA ',B A ',C X '的交点),有1BX B A C AXB A C AB '''⋅⋅='''.对△CC A ''及点A (直线CB ',C B ',A Y '的交点),有1CY C B A BYC B A BC '''⋅⋅='''.对△AA B ''及点B (直线AC ',A C ',B Z '的交点),有1AZ A C B CZA C B CA '''⋅⋅='''.上述六式相乘,有21BA CB AC A C B A C B '''⎛⎫⋅⋅= ⎪'''⎝⎭. 故1BA CB AC A C B A C B'''⋅⋅='''. 2、 塞瓦定理的逆定理设A ',B ',C '分别是△ABC 的三边BC ,CA ,AB 或其延长线上的点,若 1BA CB AC A C B A C B'''⋅⋅=''', ② 则AA ',BB ',CC '三直线共点或三直线互相平行.证明:若AA '与BB '交于点P ,设CP 与AB 的交点为1C ,则由塞瓦定理,有111AC BA CB A C B A C B''⋅⋅='', 又已知有111AC BA CB A C B A C B ''⋅⋅='',由此得11AC AC C B C B '=',即1AC AC AB AB'=, 亦即1AC AC '=,故1C 与C '重合,从而AA ',BB ',CC '三线共点. 若AA BB ''∥, 则CB CB B A BA '=''.代入已知条件, 有AC A CC B CB''=', 由此知CC AA ''∥, 故AA BB CC '''∥∥. 上述两定理可合写为:设A ',B ',C '分别是△ABC 的BC ,CA ,AB 所在直线上的点,则三直线AA ',BB ',CC '平行或共点的充要条件是1BA CB AC A C B A C B'''⋅⋅='''.③3、 第一角元形式的塞瓦定理设A ',B ',C '分别是△ABC 的三边BC ,CA ,AB 所在直线上的点,则三直线AA ',BB ',CC '平行或共点的充要条件是: sin sin sin 1sin sin sin BAA ACC CBB A AC C CB B BA'''⋅⋅='''∠∠∠∠∠∠.④ 证明 由sin sin ABA AA C S BA AB BAA A C S AC A AC''''⋅==''⋅△△∠∠, sin sin CB BC CBB B A AB B BA ''⋅=''⋅∠∠, sin sin AC AC ACC C B BC C CB''⋅=''⋅∠∠,三式相乘,再运用塞瓦定理及其逆定理, 知结论成立.4、 第二角元形的塞瓦定理设A ',B ',C '分别△ABC 的三边BC ,CA ,AB 所在直线上的点,O 是不在△ABC 的三边所在直线上的点,则AA ',BB ',CC '平行或共点的充要条件是 sin sin sin 1sin sin sin BOA AOC COB A OC C OB B OA'''⋅⋅='''∠∠∠∠∠∠.⑤ 证明 注意到塞瓦定理及其逆定理,有1BOA COB AOC A OC B OA C OB S S S BA CB AC A C B A C B S S S '''''''''=⋅⋅=⋅⋅'''△△△△△△ sin sin sin sin sin sin BO BOA CO COB AO AOC CO A OC AO B OA BO C OB'''⋅⋅⋅=⋅⋅'''⋅⋅⋅∠∠∠∠∠∠.由此即证得结论.注: 在上述各定理中,若采用有向线段或有向角,则①、②、③、④、⑤式的右端仍为1. 特别要注意的是三边所在直线上的点或者两点在边的延长线上,或者没有点在边的延长线上.④、⑤式中的角也可按①式的对应线段记忆.推论 设1A ,1B ,1C ,分别是△ABC 的外接圆三段弧BC ,CA ,AB 上的点,则1AA ,1BB ,1CC 共点的充要条件是1111111BA CB AC AC B A C B ⋅⋅=. 证明 如图2-3,设△ABC 的外接圆半径为R ,1AA 交BC 于A ',1BB 交CA 于B ',1CC 交AB 于C '.由A ,1C ,B ,1A ,C ,1B 六点共圆及正弦定理, 有11112sin sin 2sin sin BA R BAA BAA AC R A AC A AC '⋅=='⋅∠∠∠∠. A 1B1C 1CBAA′B'C '图2-3同理,11sin sin CB CBB B A B BA'='∠∠,11sin sin AC ACC C B C CB '='∠∠. 三式相乘,并应用第一角元形式的塞瓦定理即证.为了使读者熟练地应用塞瓦定理,针对图2-4中的点A 、B 、C 、D 、E 、F ,将其作为塞瓦点,我们写出如下式子:HG FEDC BA图2-4对△ACE 及点D 有 1AB CG EFBC GE FA ⋅⋅=, 对△CDE 及点A 有1CF DB EGFD BE GC⋅⋅=,对△ADE 及点C 有 1DG AF EBGA FE BD ⋅⋅=, 对△ABD 及点F 有 1AC BE DHCB ED HA ⋅⋅=, 对△ACD 及点E 有 1AG DF CBGD FC BA ⋅⋅=, 对△ADF 及点B 有 1AH DC FEHD CF EA ⋅⋅=, 对△ABF 及点D 有1BC AE FHCA EF HB ⋅⋅=, 对△BDF 及点A 有 1BE DC FHED CF HB⋅⋅=例题精讲【试题来源】【题目】图1-12,E 、F 分别为ABC ∆的AC 、AB 边上的点,且3AE EC =,3BF FA =,BE 、CF 交于P ,AP 的延长线交BC 于D .求:AP PD 的值.【答案】103AP PD = 【解析】 解: ∵P 为ABC ∆的塞瓦点.∴11133AF BD CE BD FB DC EA DC ⋅⋅=⋅⋅= ∴91BD DC =,∴910BD BC =. ∵EPB 为ACD ∆的梅氏线, ∴911103AP DB CE AP PD BC EA PD ⋅⋅=⋅⋅= 图1-12P FE DCBA∴103AP PD =【知识点】塞瓦定理 【适用场合】当堂例题 【难度系数】3【试题来源】【题目】在梯形ABCD 中,AB ∥CD ,AC 、BD 交于E ,AD 、BC 的延长线交于H ,过E 作FG ∥AB 交AD 于F ,交BC 于G ,求证:AG 、BF 、EH 三线共点.【答案】如下解析【解析】 证明:设直线HE 交AB 于Q ,由已知可得,HF HE BG EQFA EQ GH HE==, ∴1HF BGFA GH⋅= 由E 为HAB ∆的塞瓦点可得:1HD AQ BCDA QB CH⋅⋅= 同理可得:1HD BCDA CH⋅=, ∴1AQQB=, ∴1HF AQ BGFA QB GH⋅⋅= ∴AG 、BF 、EH 三线共点【知识点】塞瓦定理 【适用场合】当堂练习 【难度系数】3Q F图1-13HGED C BA图1-14-1PFED CBA【试题来源】【题目】已知:AD 、BE 、CF 为ABC ∆的高。
塞瓦定理

塞瓦定理:1:=⋅⋅∆RBAR QA CQ PCBP CR BQ AP AB CA BC ABC R Q P 的充要条件是三线共点、、边上的点,则、、的分别是、、设,111BCM ABP BMP ABM ACP CMP ACM ABM AP BQ CR M S S S S BP CQ AR PC S S S QA S RB BP CQ AR PC QA RBBP CQ AR AP BQ PC QA RBBP CQ AR AR PC QA R B ∆∆∆∆∆∆∆∆=====⋅⋅⋅⋅=⋅⋅=拻‘证:先证必要性:设、、相交于点,则:同理:以上三式相乘,得:=再证充分性:若,设与相交于由塞瓦定理有:,于是:AR R B RB AB R R AP BQ CR ‘’=段上,所以必与重合,故、、交于一点;:证明:三角形的中线例1111111111111111111,,1ABC AA BB CC C B AC B A AC BA CB AC C B BA AC CB B A ABC ∆⋅⋅====⋅⋅=∴∆证明:记的中线,,,我们只须证明而显然有:即成立,交于一点;】证明:三角形的角平【练习1】证明:锐角三角形的【练习22ABC C AB L L AC BC M N AN BM P CP AB∆∠⊥例:在锐角中,角的平分线交于于,从作边和的垂线,垂足分别是和,设和的交点是,证明: 111CK AB CK BM AN P CK BM AN AM CN BKMC CNMC NB AKAM BK AM ALAML AKC AK NB AK ACBK BC AL BCBNL BKC NB BL AC BL⊥⋅⋅==⋅=∆≅∆⇒=∴∆≅∆⇒=⋅= 证:作下证、、三线共点,且为点,要证、、三线共点,依塞瓦定理即要证:又即要证明:即要证1AL BC AC BLCK BM AN P CP AB⋅=∴∴⊥依三角形的角平分线定理可知:、、三线共点,且为点3.AD ABC D BC P AD BP CP AC AB E F EDA FDA∆∠∠例设是的高,且在边上,若是上任一点,、分别与、交于和,则=A AD DE DF M N EDA FDA ∠=∠证:过作的垂线,与、的延长线分别交于、。
8年级竞赛:梅涅劳斯定理塞瓦定理教师版.doc
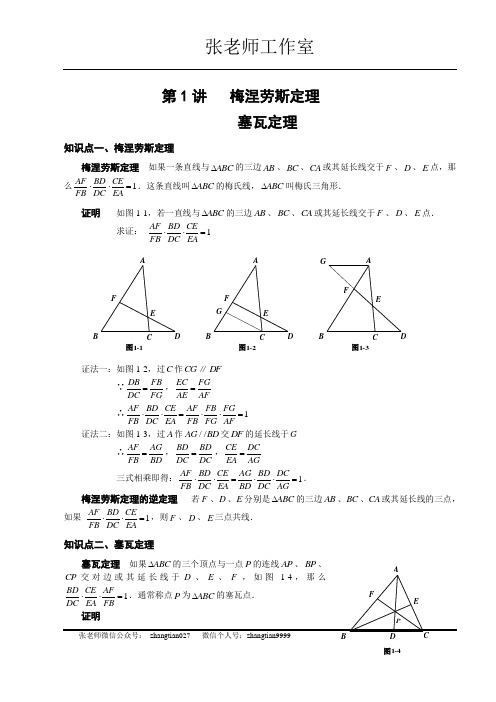
第1讲 梅涅劳斯定理塞瓦定理知识点一、梅涅劳斯定理梅涅劳斯定理 如果一条直线与ABC ∆的三边AB 、BC 、CA 或其延长线交于F 、D 、E 点,那么1AF BD CEFB DC EA⋅⋅=.这条直线叫ABC ∆的梅氏线,ABC ∆叫梅氏三角形. 证明如图1-1,若一直线与ABC ∆的三边AB 、BC 、CA 或其延长线交于F 、D 、E 点.求证: 1AF BD CEFB DC EA⋅⋅=图1-1FECDBA图1-2GF E CD BA图1-3GFECDB A证法一:如图1-2,过C 作CG ∥DF∵DB FB DC FG =,EC FGAE AF=∴1AF BD CE AF FB FGFB DC EA FB FG AF⋅⋅=⋅⋅= 证法二:如图1-3,过A 作//AG BD 交DF 的延长线于G∴AF AG FB BD =,BD BD DC DC =,CE DCEA AG=三式相乘即得:1AF BD CE AG BD DCFB DC EA BD DC AG⋅⋅=⋅⋅=. 梅涅劳斯定理的逆定理 若F 、D 、E 分别是ABC ∆的三边AB 、BC 、CA 或其延长线的三点,如果1AF BD CEFB DC EA⋅⋅=,则F 、D 、E 三点共线. 知识点二、塞瓦定理塞瓦定理 如果ABC ∆的三个顶点与一点P 的连线AP 、BP 、F 'P图1-5FECDBAAB DCEF图1-6∵直线FPC 、EPB 分别是ABD ∆、ACD ∆的梅氏线, ∴1BC DP AF CD PA FB ⋅⋅=,1DB CE APBC EA PD⋅⋅= 两式相乘即可得:1BD CE AFDC EA FB⋅⋅= 塞瓦定理的逆定理 如果点D 、E 、F 分别在ABC ∆的边BC 、CA 、AB 上或其延长线上,并且1BD CE AFDC EA FB⋅⋅=,那么AD 、BE 、CF 相交于一点(或平行). 证明⑴ 若AD 与BE 相交于一点P 时,如图1-5,作直线CP 交AB 于'F .由塞瓦定理得:F 1BD CE A DC EA F B'⋅⋅=', 又已知1BD CE AF DC EA FB ⋅⋅=,∴AF AFFB F B'=', ∴AB ABFB F B=',∴FB F B '=. ∴'F 与F 重合 ∴'CF 与CF 重合∴AD 、BE 、CF 相交于一点.⑵ 若AD 与BE 所在直线不相交,则AD ∥BE ,如图1-6.∴BD EA DC AC =,又已知1BD CE AF DC EA FB⋅⋅=, ∴1EA CE AF AC EA FB ⋅⋅=,即CE FBAC AF =. ∴//BE FC ,∴////AD BE FC .【例 1】 已知ABC ∆中,AD 为中线,过C 点任作一直线交AB 于F ,交AD 于E ,如图1-7,求证::2:AE ED AF FB =.【分析】∵直线FEC 是ABD ∆的梅氏线, ∴1AE DC BF ED BC FA ⋅⋅=. 而12DC BC =, ∴112AE BF ED FA ⋅⋅=,即2AE AFED BF=.【例 2】 (2003年深圳市中考题)如图1-8,直线1l ∥2l ,:2:3AF FB =,:2:1BC CD =,则:AE EC是 ( )A .5:2B .4:1C .2:1D .3:2图1-7FECD BA图1-8l 2l 1GF EDC BA【分析】∵DG 截ABC ∆的三边AB 、AC 、BC 或其延长线于F 、E 、D 三点, ∴1AF BD ECFB CD AE ⋅⋅=. ∵23AF FB =,21BC CD = ∴31BD CD =,∴23131ECAE ⨯⨯= ∴12EC AE =,即21AE EC =【例 3】 如图1-9,ABC ∆中,D 为AC 中点,BE EF FC ==,求证:::5:3:2BM MN ND =.【分析】∵直线AE 是BCD ∆的梅氏线, ∴1BM DA CEMD AC EB⋅⋅=. ∴12121BM MD ⋅⋅=,∴11BM MD = ∵直线AF 是BCD ∆的梅氏线, ∴1BN DA CFND AC FB⋅⋅=, ∴11122BN ND ⋅⋅=,41BN ND = ∴::5:3:2BM MN ND =.【例 4】 如图1-10-1,ABC ∆中,5AB =,8BC =,BD BE =,2AF FC =,BF 交DE 于P .求:DP PE .FPE DCBA 图1-10-1O P GFEDCBA图1-10-2【分析】过A 作AG ∥DE 交BC 于G ,交BF 于Q ,如图1-10-2.N M FE CDBA图1-9可得:5AB BG ==,且DP AQPE QG=∵直线BF 是ACG ∆的梅氏线, ∴51182AQ GB CF AQ QG BC FA QG ⋅⋅=⋅⋅= ∴165DP AQ PE QG ==.【例 5】如图1-11,平行四边形ABCD 的对角线相交于点O ,在AB 的延长线上任取一点E ,连接OE 交BC 于点F . 若AB a =,AD c =,BE b =,求BF 的长.图1-11OFE DCBA【分析】∵OE 截ABC ∆的三边AB 、AC 、BC 或其延长线于E 、O 、F 三点.∴1CO AE BFAO BE FC⋅⋅=. 在平行四边形ABCD 中, ∵OA OC =,∴1OAOC= ∵AE AB BE a b =+=+,∴AE a bBE b+=∴BF b FC a b =+,即FC a bBF b+=∴2FC BF a b BF b ++=,即2BC a bBF b+=. ∵BC AD =,∴2c a b BF b +=,∴2bcBF a b=+.【例 6】 如图1-12,E 、F 分别为ABC ∆的AC 、AB 边上的点,且3AE EC =,3BF FA =,BE 、CF交于P ,AP 的延长线交BC 于D .求:AP PD 的值.【分析】图1-14-1PFED CB A ∵EPB 为ACD ∆的梅氏线, ∴911103AP DB CE AP PD BC EA PD ⋅⋅=⋅⋅= ∴103AP PD =.【例 7】 在梯形ABCD 中,AB ∥CD ,AC 、BD 交于E ,AD 、BC 的延长线交于H ,过E 作FG ∥AB交AD 于F ,交BC 于G ,求证:AG 、BF 、EH 三线共点.【分析】设直线HE 交AB 于Q , 由已知可得,HF HE BG EQ FA EQ GH HE ==,∴1HF BGFA GH⋅=由E 为HAB ∆的塞瓦点可得:1HD AQ BCDA QB CH⋅⋅= 同理可得:1HD BCDA CH⋅=,∴1AQ QB =,∴1HF AQ BG FA QB GH ⋅⋅= ∴AG 、BF 、EH 三线共点.【例 8】 已知:AD 、BE 、CF 为ABC ∆的高。
36-初中数学竞赛中常用重要定理 (1)

数学竞赛中几个重要定理1、 梅涅劳斯定理:如果在△ABC 的三边BC 、CA 、AB 或其延长线上有点D 、 E 、F 且D 、E 、F 三点共线,则FBAFEA CE DC BD ••=12、 梅涅劳斯定理的逆定理:如果在△ABC 的三边BC 、CA 、AB 或其延长线上有点D 、E 、F ,且满足FBAFEA CE DC BD ••=1,则D 、E 、F 三点共线。
3、 塞瓦定理:设O 是△ABC 内任意一点,AO 、BO 、CO 分别交对边于N 、P 、M ,则1=••PACPNC BN MB AM4、 塞瓦定理的逆定理:设M 、N 、P 分别在△ABC 的 边AB 、BC 、CA 上,且满足1=••PACPNC BN MB AM ,则AN 、BP 、CM 相交于一点。
5、 广勾股定理的两个推论:推论1:平行四边形对角线的平方和等于四边平方和。
推论2:设△ABC 三边长分别为a 、b 、c ,对应边上中线长分别为m a 、m b、m c则:m a =2222221a c b -+;m b =2222221b c a -+;m c =2222221c b a -+ 6、 三角形内、外角平分线定理:内角平分线定理:如图:如果∠1=∠2,则有ACABDC BD =外角平分线定理:如图,AD 是△ABC 中∠A 的外角平分线交BC 的延长线与D , 则有ACABDC BD =7、 托勒密定理:四边形ABCD 是圆内接四边形,则有AB ·CD+AD ·BC=AC ·BD8、 三角形位似心定理:如图,若△ABC 与△DEF 位似,则通过对应点的三直线AD 、BE 、CF 共点于P 9、 正弦定理、在△ABC 中有R CcB b A a 2sin sin sin ===(R 为△ABC 外接圆半径) 余弦定理:a 、b 、c 为△ABC 的边,则有:a 2=b 2+c 2-2bc ·cosA; b 2=a 2+c 2-2ac ·cosB; c 2=a 2+b 2-2ab ·cosC;10、西姆松定理:点P 是△ABC 外接圆周上任意一点,PD ⊥BC ,PE ⊥AC , PF ⊥AB ,D 、E 、F 为垂足,则D 、E 、F 三点共线,此直线称为西姆松线。
中学数学竞赛中常用的几个重要定理
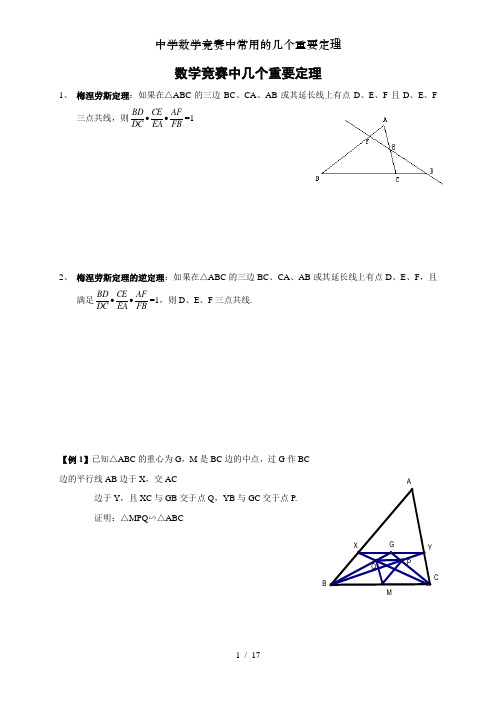
数学竞赛中几个重要定理1、 梅涅劳斯定理:如果在△ABC 的三边BC 、CA 、AB 或其延长线上有点D 、E 、F 且D 、E 、F三点共线,则FBAFEA CE DC BD ••=12、 梅涅劳斯定理的逆定理:如果在△ABC 的三边BC 、CA 、AB 或其延长线上有点D 、E 、F ,且满足FBAFEA CE DC BD ••=1,则D 、E 、F 三点共线.【例1】已知△ABC 的重心为G ,M 是BC 边的中点,过G 作BC 边的平行线AB 边于X ,交AC边于Y ,且XC 与GB 交于点Q ,YB 与GC 交于点P. 证明:△MPQ ∽△ABCj MQGAC BXY P【例2】以△ABC的底边BC为直径作半圆,分别与边AB,AC交于点D和E,分别过点D,E作BC的垂线,垂足依次为F,G,线段DG和EF交于点M.求证:AM⊥BC【例3】四边形ABCD内接于圆,其边AB,DC的延长线交于点P,AD和BC的延长线交于点Q,过Q作该圆的两条切线,切点分别为E,F.求证:P,E,F三点共线.【练习1】设凸四边形ABCD 的对角线AC 和BD 交于点M ,过M 作AD 的平行线分别交AB ,CD于点E ,F ,交BC 的延长线于点O ,P 是以O 为圆心,以OM 为半径的圆上一点. 求证:∠OPF=∠OEP【练习2】 在△ABC 中,∠A=900,点D 在AC 上,点E 在BD 上,AE 的延长线交BC 于F. 若BE :ED=2AC :DC ,则∠ADB=∠FDCD塞瓦定理:设O是△ABC内任意一点,AO、BO、CO分别交对边于N、P、M,则1=••PACPNCBNMBAM塞瓦定理的逆定理:设M、N、P分别在△ABC的边AB、BC、CA上,且满足1=••PACPNCBNMBAM,则AN、BP、CM相交于一点.【例1】B E是△ABC的中线,G在BE上,分别延长AG,CG交BC,AB于点D,F,过D作DN∥CG交BG于N,△DGL及△FGM是正三角形.求证:△LMN为正三角形.GCLMEDFN【例2】在△ABC 中,D 是BC 上的点DC BD =31,E 是AC 中点.AD 与BE 交于O ,CO 交AB 于F 求四边形BDOF 的面积与△ABC 的面积的比【练习1】设P 为△ABC 内一点,使∠BPA=∠CPA ,G 是线段AP 上的一点,直线BG ,CG 分别交边AC ,AB 于E ,F.求证:∠BPF=∠CPE【练习2】 在△ABC 中,∠ABC 和∠ACB 均为锐角.D 是BC 边BC 上的内点,且AD 平分∠BAC ,过点D 作垂线DP ⊥AB 于P ,DQ ⊥AC 于Q ,CP 于BQ 相交于K. 求证:AK ⊥BCCCC托勒密定理:四边形ABCD 是圆内接四边形,则有AB ·CD+AD ·BC=AC ·BD【例1】 已知在△ABC 中,AB >AC ,∠A 的一个外角的平分线交△ABC 的外接圆于点E ,过E 作EF ⊥AB ,垂足为F.求证:2AF=AB -AC【例2】经过∠XOY 的平分线上的一点A ,任作一直线与OX 及OY 分别相交于P ,Q.求证:OP 1+OQ1为定值HABCEFAXYPOQ【例3】 解方程42-x+12-x=x 7【练习1】 设AF 为⊙O1与⊙O2的公共弦,点B ,C 分别在⊙O1,⊙O2上,且AB=AC ,∠BAF ,∠CAF 的平分线交⊙O1,⊙O2于点D ,E. 求证:DE ⊥AF【练习2】⊙O 为正△ABC 的外接圆,AD 是⊙O 的直径,在弧BC 上任取一点P (与B ,C不重合).设E ,F 分别为△PAB ,△PAC 的内心.证明:PD=∣PE-PF ∣西姆松定理:点P 是△ABC 外接圆周上任意一点,PD ⊥BC ,PE ⊥AC ,PF ⊥AB ,D 、E 、F 为垂足,则D 、E 、F 三点共线,此直线称为西姆松线.【例1】过正△ABC 外接圆的弧AC 上点P 作P D ⊥直线AB 于D,作PE ⊥AC 于E,作PF ⊥BC 于F.求证:PF 1+PD 1=PE1【练习1】设P 为△ABC 外接圆周上任一点,P 点关于边BC ,AC 所在的直线的对称点分别为P 1,P 2.求证:直线P 1P 2经过△ABC 的垂心.CABPEFD HABP1P2CP三角形的五心内心【例1】设点M 是△ABC 的BC 边的中点,I 是其内心,AH 是BC 边上的高,E 为直线IM 与AH 的交点.求证:AE 等于内切圆半径r【例2】在△ABC 中,AB=4,AC=6,BC=5,∠A 的平分线AD 交△ABC的外接圆于K.O ,I 分别为△ABC 的外心,内心.求证:OI ⊥AK【练习】 在△ABC 中,∠BAC=300,∠ABC=700,M 为形内一点,∠MAB=∠MCA=200求∠MBA 的度数.B外心【例1】锐角△ABC的外心为O,线段OA,BC的中点为M,N,∠ABC=4∠OMN,∠ACB=6∠OMN.求∠OMN【例2】在等腰△ABC中,AB=BC,CD是它的角平分线,O是它的外心,过O作CD的垂线交BC于E,再过E作CD的平行线交AB于F,证明:BE=FD.【练习】1、⊙O 1与⊙O 2相交于P ,Q ,⊙O 1的弦PA 与⊙O 2相切,⊙O 2的弦PB 与⊙O 1相切.设△PAB 的外心为O ,求证:OQ ⊥PQ重心【例1】在△ABC 中,G 为重心,P 是形内一点,直线PG 交直线BC ,CA ,AB 于F ,E ,D.求证:FG FP +EG EP +DGDP=3【例2】已知△ABC 的重心G 和内心I 的连线GI ∥BC ,求证:AB+AC=2BCC【练习】1、设M 为△ABC 的重心,且AM=3,BM=4,CM=5,求△ABC 的面积.2、设O 是△ABC 的外心,AB=AC ,D 是AB 的中点,G 是△ACD 的重心,求证:OG ⊥CD垂心三角形任一顶点到垂心的距离,等于外心到对边的距离的2倍.BCB【例1】△ABC 的外接圆为⊙O ,∠C=600,M 是弧AB 的中点,H 是△ABC 的垂心.求证:OM ⊥OH【例2】已知AD ,BE ,CF 是锐角△ABC 的三条高,过D 作EF 的平行线RQ ,RQ 分别交AB 和AC 于R ,Q ,P 为EF 与CB 的延长线的交点.证明:△PQR 的外接圆通过BC 的中点M.旁心【例1】在锐角∠XAY 内部取一点,使得∠ABC=∠XBD ,∠ACB=∠YCD.证明:△ABC 的外心在线段AD 上.CD【例2】AD是直角△ABC斜边BC上的高(AB<AC),I1,I2分别是△ABD,△ACD的内心,△A I1 I2的外接圆⊙O分别交AB,AC于E,F,直线FE与CB的延长线交于点M.证明:I1,I2分别是△ODM的内心与旁心.相交两圆的性质与应用【例1】证明:若凸五边形ABCDE中,∠ABC=∠ADE,∠AEC=∠ADB. 证明:∠BAC=∠DAEE【例2】已知⊙O1与⊙O2相交于A,B,直线MN垂直于AB且分别与⊙O1与⊙O2交于M,N,P 是线段MN的中点,Q1,Q2分别是⊙O1与⊙O2上的点,∠AO1Q1=∠AO2Q2求证:PQ1=PQ2【练习】梯形ABCD中,AB∥CD,AB>CD,K,M分别是腰AD,CB上的点,∠DAM=∠CBK,求证:∠DMA=∠CKBA其他的一些数学竞赛定理1、 广勾股定理的两个推论:推论1:平行四边形对角线的平方和等于四边平方和.推论2:设△ABC 三边长分别为a 、b 、c ,对应边上中线长分别为m a 、m b 、m c 则:m a =2222221a c b -+;m b =2222221b c a -+;m c =2222221c b a -+2、 三角形内、外角平分线定理:内角平分线定理:如图:如果∠1=∠2,则有ACABDC BD =外角平分线定理:如图,AD 是△ABC 中∠A 的外角平分线交BC 的延长线与D ,则有ACABDC BD =3、 三角形位似心定理:如图,若△ABC 与△DEF 位似,则通过对应点的三直线AD 、BE 、CF 共点于P4、 正弦定理、在△ABC 中有R CcB b A a 2sin sin sin ===(R 为△ABC 外接圆半径) 余弦定理: a 、b 、c 为△ABC 的边,则有: a 2=b 2+c 2-2bc ·cosA;b 2=a 2+c 2-2ac ·cosB; c 2=a 2+b 2-2ab ·cosC;5、欧拉定理:△ABC 的外接圆圆心为O ,半径为R ,内切圆圆心为I ,半径为r,记OI=d,则有:d 2=R 2-2Rr.6、巴斯加线定理:圆内接六边形ABCDEF (不论其六顶点排列次序如何),其三组对边AB 与DE 、BC 与EF 、CD 与FA 的交点P 、Q 、R 共线.。
初中数学竞赛专题.梅涅劳斯定理与塞瓦定理.(有答案)

初中数学竞赛专题.梅涅劳斯定理与塞瓦定理.(有答案)第 1 页板块一梅涅劳斯定理及其逆定理梅涅劳斯定理:如果一条直线与ABC △的三边AB 、BC 、CA 或其延长线交于F 、D 、E 点,那么1AF BD CE FB DC EA=.这条直线叫ABC △的梅氏线,ABC △叫梅氏三角形.证法一:如左图,过C 作CG ∥DF证法二:如中图,过A 作AG BD ∥交DF 的延长线于G三式相乘即得:1AF BD CE AG BD DCFB DC EA BD DC AG=??=.证法三:如右图,分别过A B C 、、作DE 的垂线,分别交于123H H H 、、.则有123AH BH CH ∥∥,所以3122311CH AH BH AF BD CE FB DC EA BH CH AH ??=??=.梅涅劳斯定理的逆定理:若F 、D 、E 分别是ABC △的三边AB 、BC 、CA 或其延长线的三点,如果1AF BD CE FB DC EA=,则F 、D 、E 三点共线.【例1】如图,在ABC △中,AD 为中线,过点C 任作一直线交AB 于点F ,交AD 于点E ,求证::2:AE ED AF FB =.【解析】∵直线FEC 是ABD △的梅氏线,∴1AE DC BF ED BC FA ??=.而12DC BC =,∴112AE BF ED FA ??=,即2AE AF ED BF=.习题1. 在△ABC 中,D 是BC 的中点,经过点D 的直线交AB于点E ,交CA 的延长线于点F .求证:FA EAFC EB=.【解析】直线截ABC △三边于D 、E 、F 三点,应用梅氏定理,知1CD BE AFDB EA FC=,又因为BD BC =,所以1BE AF EA FC ?=,即FA EAFC EB=.习题2. 如图,在△ABC 中,90ACB ∠=?,AC BC =.AM 为BC 边上的中线,CD AM ⊥于点D ,CD 的延长线交AB 于点E .求AEEB.【解析】由题设,在Rt AMC △中,CD AM ⊥,2AC CM =,由射影定理224AD AD AM AC DM DM AM CM===?.对ABM △和截线EDC ,由梅涅劳斯定理,1AE BC MD EB CM DA ??=,即21114AE EB ??=.所以2AE EB=.知识导航夯实基础梅涅劳斯定理与塞瓦定理【例2】如图,在ABC △中,D 为AC 中点,BE EF FC ==,求证:::5:3:2BM MN ND =.【解析】∵直线AE 是BCD △的梅氏线,∵直线AF 是BCD △的梅氏线,习题3. 如图,在ABC △中,D 为BC 的中点,::4:3:1AE EF FD =.求::AG GH AB .【解析】∵HFC 是ABD △的梅氏线,∵D 为BC 的中点,::4:3:1AE EF FD =,∵GEC 是ABD △的梅氏线,【例3】过ABC △的重心G 的直线分别交AB 、AC 于点E 、F ,交CB 的延长线于点D .求证:1BE CFEA FA+=.【解析】作直线AG 交BC 于M ,同理,2CF DCFA DM=,而2BD DC BD BD BM +=++2()2BD BM DM =+=【例4】如图,点D 、E 分别在ABC △的边AC 、AB 上, AE EB =,23AD DC =,BD 与CE 交于点F ,40ABC S =△.求AEFD S .【解析】对ECA △和截线BFD ,由梅氏定理得:1EF CD AB FC DA BE ??=,即32121EF FC ??=,所以13EF FC =.所以1148BFE BEC ABC S S S ==△△△,进而211140115840AEFD ABD BEF ABC S S S S ??=-=-==△△△.习题4. 如图,在ABC △中,三个三角形面积分别为5,8,10.四边形AEFD 的面积为x ,求x的值.【解析】对ECA △和截线BFD ,由梅氏定理得:1CD AB EF DA BE FC ??=,即1823115152x x +??=+,解得22x =.【备选】如图,ABC △被通过它的三个顶点与一个内点O 的三条直线分为6个小三角形,其中三个小三角形的面积如图所示,求ABC △的面积.【解析】对ABD △和截线COF ,由梅氏定理得:1AF BC DO FB CD OA ??=,即41132BC CD ??=,所以32BC CD =,所以3BCBD=.所以33105315ABC ABD S S ==?=△△.【例5】如图,在ABC △中,A ∠的外角平分线与边BC 的延长线交于点P ,B ∠的平分线与边CA 交于点Q ,C ∠的平分线与边AB 交于点R ,求证:P 、Q 、R 三点共线.【解析】 AP 是BAC ∠的外角平分线,则BQ 是ABC ∠的平分线,则 CR 是ACB ∠的平分线,则??①②③得非常挑战探索提升第 3 页因R 在AB 上,Q 在CA 上,P 在BC 的延长线上,则根据梅涅劳斯定理的逆定理得:P 、Q 、R 三点共线.习题5. 证明:不等边三角形的三个角的外角平分线与对边的交点是共线的三个点.【解析】如图,CD BE AF 、、分别为三角形ABC 的三个外角平分线,分别交AB AC BC 、、于D E F 、、.过C 作BE 的平行线,则BCP CBE EBD CPB ∠=∠=∠=∠,所以BPC △是等腰三角形.则PB CB =.则有:CE PB CBEA BA BA ==.同理AD AC DB CB =;BF BA FC AC=.所以1CE AD BF CB AC BA EA DB FC BA CB AC ??=??=.所以D E F 、、共线.板块二塞瓦定理及其逆定理塞瓦定理:如果ABC △的三个顶点与一点P 的连线AP 、BP 、CP 交对边或其延长线于点D 、E 、F ,如图,那么1BD CE AFDC EA FB=.通常称点P 为ABC △的塞瓦点.证明:∵直线FPC 、EPB 分别是ABD △、ACD △的梅氏线,两式相乘即可得:1BD CE AFDC EA FB=.塞瓦定理的逆定理:如果点D 、E 、F 分别在ABC △的边BC 、CA 、AB 上或其延长线上,并且1BD CE AF DC EA FB=,那么AD 、BE 、CF 相交于一点(或平行).证明:⑴ 若AD 与BE 相交于一点P 时,如图,作直线CP 交AB 于'F .由塞瓦定理得:'1BD CE AF DC EA F B=',又已知1BD CE AF DC EA FB ??=,∴AF AF FB F B'=',∴'F 与F 重合∴'CF 与CF 重合∴AD 、BE 、CF 相交于一点.⑵ 若AD 与BE 所在直线不相交,则AD ∥BE ,如图.∴BD EA DC AC=,又已知1BD CE AF DC EA FB ??=,∴1EA CE AF AC EA FB ??=,即CE FB AC AF=.说明:三线平行的情况在实际题目中很少见.【例6】(1)设AX BY CZ ,,是ABC △的三条中线,求证:AX BY CZ ,,三线共点.探索提升知识导航(2)若AX BY CZ ,,为ABC △的三条内角平分线.求证:AX BY CZ ,,三线共点.【解析】(1)由条件知,BX XC YC YA ZA ZB ===,,.∴1BX CY AZXC YA ZB=,根据塞瓦定理的逆定理可得三条中线AX BY CZ ,,共点.这个点称为这个三角形的重心.(2)由三角形内角平分线定理得:BX AB CY BC AZ ACXC AC YA BA ZB BC===,,.三式分别相乘,得:1BX CY AZ AB BC ACXC YA ZB AC AB BC=??=.根据塞瓦定理的逆定理可得三角形三内角平分线AX BY CZ ,,共点,这个点称为这个三角形的内心.习题6. 若AX BY CZ ,,分别为锐角ABC △的三条高线,求证:AX BY CZ ,,三线共点.【解析】由ABX CBZ △∽△得:BX AB BZ BC =;由BYA CZA △∽△得:AZ ACAY AB =;由AXC BYC △∽△可得:YC BC CX AC =.所以1BX AZ YC AB AC BCBZ AY CX BC AB AC=??=.根据塞瓦定理的逆定理可得三条高线AX BY CZ ,,共点.对直角三角形、钝角三角形,同样也可以证得三条高线共点.我们把一个三角形三条高线所在直线的交点叫做这个三角形的垂心.【例7】如图,M 为ABC △内的一点,BM 与AC 交于点E ,CM 与AB 交于点F ,若AM 通过BC 的中点D ,求证:EF BC ∥.【解析】对ABC △和点M 应用塞瓦定理可得:1AF BD CEFB DC EA=.又因为BD DC =,所以1AF CE FB EA ?=.进而AF AEFB EC=,所以EF BC ∥.习题7. 如果梯形ABCD 的两腰AD 、BC 的延长线交于M ,两条对角线交于N .求证:直线MN必平分梯形的两底.∵1MD AQ BC DA QB CM=(由塞瓦定理得)板块三梅涅劳斯定理、塞瓦定理综合【备选】如图,E 、F 分别为ABC △的AC 、AB 边上的点,且3AE EC =,3BF FA =,BE 、CF 交于点P ,AP 的延长线交BC 于点D .求:AP PD 的值.【解析】∵P 为ABC △的塞瓦点.∵EPB 为ACD △的梅氏线,【备选】如图,四边形ABCD 的对边AB 和DC ,DA 和CB 分别相交于点L K ,,对角线AC 与BD 交于点M .直线KL 与BD 、AC 分别交于点F G 、.求证:KF KGLF LG=.【解析】对DKL △与点B 应用塞瓦定理得:1DA KF LCAK FL CD=.对DKL △和截线ACG 应用梅涅劳斯定理可得:1DA KG LCAK GL CD=.非常挑战进而可得KF KGLF LG.第 5 页。
初中数学竞赛中常用重要定理
3、三角形的三条中线交于一点,并且,各中线被这个点分成2:1的两部分4、四边形两边中心的连线的两条对角线中心的连线交于一点5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。
6、三角形各边的垂直一平分线交于一点。
7、从三角形的各顶点向其对边所作的三条垂线交于一点8、设三角形ABC的外心为O,垂心为H,从O向BC边引垂线,设垂足不L,则AH=2OL9、三角形的外心,垂心,重心在同一条直线上。
10、(九点圆或欧拉圆或费尔巴赫圆)三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上,11、欧拉定理:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线(欧拉线)上12、库立奇*大上定理:(圆内接四边形的九点圆) 圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。
13、(内心)三角形的三条内角平分线交于一点,内切圆的半径公式:r=(s-a)(s-b)(s-c)ss为三角形周长的一半14、(旁心)三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点15、中线定理:(巴布斯定理)设三角形ABC的边BC的中点为P,则有AB2+AC2=2(AP2+BP2)16、斯图尔特定理:P将三角形ABC的边BC内分成m:n,则有n×AB2+m×AC2=(m+n)AP2+mnm+nBC217、波罗摩及多定理:圆内接四边形ABCD的对角线互相垂直时,连接AB中点M和对角线交点E的直线垂直于CD18、阿波罗尼斯定理:到两定点A、B的距离之比为定比m:n(值不为1)的点P,位于将线段AB分成m:n的内分点C和外分点D为直径两端点的定圆周上19、托勒密定理:设四边形ABCD内接于圆,则有AB×CD+AD×BC=AC20、以任意三角形ABC的边BC、CA、AB为底边,分别向外作底角都是30度的等腰△BDC、△CEA、△AFB,则△DEF是正三角形,21、爱尔可斯定理1:若△ABC和三角形△都是正三角形,则由线段AD、BE、CF的重心构成的三角形也是正三角形。
奥数-第3讲三角形中与比例线段有关的定理竞赛班学生版
第三讲 三角形中与比例线段有关的几个定理梅涅劳斯(Menelaus )是约公元一世纪时的希腊数学家兼天文学家,著有几何学及三角学书籍.下面以他名字命名的定理是他首先发现的,发表在球面几何学的教科书《球论》里,有着广泛的应用,不仅可以证明点共线,对其他几何问题也非常有用.塞瓦(Ceva )是17世纪意大利数学家兼水力工程师,1678年塞瓦自己发现了后来以他名字命名的定理,同时他重新发现梅涅劳斯定理,当时他一并刊登发表,两个定理齐名流传至今. 一、 基础知识1. 梅涅劳斯定理(Menelaus theorem )在⊿ABC 的三边BC 、CA 、AB 或其延长线上有点D 、E 、F ,若D 、E 、F 共线,则:1AF BD CEFB DC EA⋅⋅=;2. 梅涅劳斯定理的逆定理在⊿ABC 的三边BC 、CA 、AB 或其延长线上有点D 、E 、F ,若1AF BD CEFB DC EA⋅⋅=,则D 、E 、F 共线.3. 塞瓦定理(Ceva theorem )设O 是⊿ABC 内任意一点,AO 、BO 、CO 分别交对边于D 、E 、F ,则1AE BD CF EB DC FA⋅⋅=4. 塞瓦定理的逆定理设点D 、E 、F 分别在⊿ABC 的边BC 、AB 、CA 上,若1AE BD CF EB DC FA⋅⋅=,则AD 、CE 、BF 交于一点.二、 例题部分-梅氏定理及逆定理的应用例1.(★)设AD 为⊿ABC 的一条中线,作任一直线CF 交AD 于E ,交AB 于F ,求证:2AE AFED FB=例2.(★,97年湖北荆州竞赛题)如图,D 为⊿ABC 的BC 边的中点,E 为AC 边上的点,且AC =3CE ,BE 和AD 交于F 点,求AFFD的值;例3.(★)图中AD 是⊿ABC 的中线,E 是AD 上的点,且AE =2DE ,连结BE 并延长交AC 于F .(1)求证:AF=FC;(2)求BFEF的值;例4.(★,90年全国部分省市初中通讯赛)设D、E分别在⊿ABC的边AC与AB上,BD与CE交于F,AE=EB,23ADDC=,ABCS=40,求AEFDS四边形例5.(★★,第七届“祖冲之杯”数学邀请赛)图中,⊿ABC的∠B的平分线BE与BC边的中线AD垂直且相等,已知BE=AD=4,求⊿ABC的三边.例6.(★★,93年第19届全俄中学生竞赛)在梯形ABCD的对角线AC的延长线上任意取一点P,过P 点及梯形两底中点的直线分别交腰AB及CD于M、N点,求证:线段MN与梯形的底平行;例7.(★★)如图,已知1111PA PD PC PB+=+,求证:∠BPQ=∠DPQ.例8.(★★)如图⊿ABC的∠A的外角平分线与边BC的延长线交于P点,∠B的平分线与边CA交于Q点,∠C的平分线与边AB交于R点,求证:P、Q、R三点共线.例9.(★★★,笛沙格(Desargues)定理)若⊿ABC与⊿A’B’C’的对应顶点连线AA’,BB’,CC’相交于一点O,则对应边BC与B’C’,CA与C’A’,AB与A’B’的交点D、E、F共线.三、例题部分-塞瓦定理及逆定理的应用例10.(★)求证:(1)三角形的三条中线共点(重心);(2)三角形的三条内角平分线共点(内心);(3)锐角三角形的三条高所在的直线共点(垂心);例11.(★★,78年全国高中竞赛)在⊿ABC中,D、E分别在边AB、AC上,且DE∥BC,设BE与CD交于S,求证:AS通过BC边的中点M.例12.(★★)⊿ABC中,M是BC的中点,AD平分∠A,BE⊥AD于E,BE交AM于N,求证:DN∥AB.例13.(★★)试证:过三角形三顶点且平分三角形周长的三条直线共点.例14.(★★★,99年全国联赛)四边形ABCD中,对角线AC平分∠BAD,在CD上取一点E,连BE 交AC于F,延长DF交BC于G,求证:∠GAC=∠EAC;四、练习题1.(★)在⊿ABC的两边AB、AC上分别取点Q、R,满足AQ:QB=2:1,AR:RC=1:2,连结QR交CB延长线于P,那么PC:PB等于()A.4:1 B.2:1 C.1:4 D.1:22.(★)ABCD为平行四边形,BC=12,DC=10,对角线AC与BD交于O,E是BC延长线上一点,且CE=4,OE交DC于F,那么CF的长是()A.1 B.2 C.0.5 D.33.(★)已知M、N分别在⊿ABC的边AC、AB上,且MN∥BC,BM、CN交于O点,连结AO并延长交BC于D,那么BD:DC()A.大于1 B.小于1 C.等于1 D.以上都可能4.(★)在⊿ABC中,如果AD交BC于D,BE交AC于E,CF交BA于F,AD、BE、CF相交于一点,2BDEA=,3CEFB=,那么AFDC等于________;5.(★)在⊿ABC的BC边上任取一点D,设∠ADB、∠ADC的平分线与AB、AC分别相交于F、E,求证AD、BE、CF交于一点;6.(★)在⊿ABC中,D、E分别是BC、CA上的点,且BD:DC=m:1,CE:EA=n:1,AD与BE 相交于F,那么:ABF ABCS S=___________;7.(★★)在⊿ABC中,D是BC上的点,13BDDC=,E是AC中点,AD、BE相交于点O,CO交AB 于F,求四边形BDOF的面积与⊿ABC的面积之比.8.(★★)在面积为1的⊿ABC的三边上分别取D、E、F,使1BD CE AFkDC EA FB===>,连结AD、BE、CF交出⊿MNP,试求MNPS9.(★★★,2005年全国初中数学联赛)锐角三角形ABC中,AB>AC,CD、BE分别是AB、AC边上的高,DE与BC的延长线交于T,过D作BC的垂线交BE于F,过E作BC的垂线交CD于G,求证:F、G、T三点共线.。
初中数学竞赛专题.梅涅劳斯定理与塞瓦定理.(有答案)
初中数学竞赛专题.梅涅劳斯定理与塞瓦定理.(有答案)板块一 梅涅劳斯定理及其逆定理梅涅劳斯定理:如果一条直线与ABC △的三边AB 、BC 、CA 或其延长线交于F 、D 、E 点,那么1AF BD CE FB DC EA⋅⋅=.这条直线叫ABC △的梅氏线,ABC △叫梅氏三角形.GF EDCBAGFE DCBAH3H 2H 1F E DCBA证法一:如左图,过C 作CG ∥DF∵DB FB DC FG =,EC FG AE AF= ∴1AF BD CE AF FB FG FB DC EA FB FG AF⋅⋅=⋅⋅=. 证法二:如中图,过A 作AG BD ∥交DF 的延长线于G∴AF AG FB BD =,BD BD DC DC =,CE DC EA AG= 三式相乘即得:1AF BD CE AG BD DCFB DC EA BD DC AG⋅⋅=⋅⋅=.证法三:如右图,分别过A B C 、、作DE 的垂线,分别交于123H H H 、、. 则有123AH BH CH ∥∥,所以3122311CH AH BH AF BD CE FB DC EA BH CH AH ⋅⋅=⋅⋅=.梅涅劳斯定理的逆定理:若F 、D 、E 分别是ABC △的三边AB 、BC 、CA 或其延长线的三点,如果1AF BD CE FB DC EA⋅⋅=,则F 、D 、E 三点共线.知识导航梅涅劳斯定理与塞瓦定理【例1】 如图,在ABC △中,AD 为中线,过点C 任作一直线交AB 于点F ,交AD 于点E ,求证::2:AE ED AF FB =.EC D B FA【解析】 ∵直线FEC 是ABD △的梅氏线,∴1AE DC BF ED BC FA ⋅⋅=. 而12DC BC =,∴112AE BF ED FA ⋅⋅=,即2AE AF ED BF=.习题1. 在△ABC 中,D 是BC 的中点,经过点D 的直线交AB 于点E ,交CA 的延长线于点F .求证:FA EAFC EB=. EFBDCA【解析】 直线截ABC △三边于D 、E 、F 三点,应用梅氏定理,知1CD BE AFDB EA FC⋅⋅=,又因为BD BC =,所以1BE AF EA FC ⋅=,即FA EAFC EB=.习题2. 如图,在△ABC 中, 90ACB ∠=︒,AC BC =.AM 为BC 边上的中线,CD AM ⊥于点D ,CD 的延长线交AB 于点E .求AEEB. DEBMCA夯实基础初中数学竞赛专题.梅涅劳斯定理与塞瓦定理.(有答案)【解析】 由题设,在Rt AMC △中,CD AM ⊥,2AC CM =,由射影定理224AD AD AM AC DM DM AM CM ⋅===⋅.对ABM △和截线EDC ,由梅涅劳斯定理,1AE BC MD EB CM DA ⋅⋅=,即21114AE EB ⋅⋅=.所以2AE EB=.【例2】 如图,在ABC △中,D 为AC 中点,BE EF FC ==,求证:::5:3:2BM MN ND =.NMDCF EBA【解析】 ∵直线AE 是BCD △的梅氏线,∴1BM DA CE MD AC EB ⋅⋅=. ∴12121BM MD ⋅⋅=,∴11BM MD = ∵直线AF 是BCD △的梅氏线, ∴1BN DA CF ND AC FB ⋅⋅=, ∴11122BN ND ⋅⋅=,41BN ND =. ∴::5:3:2BM MN ND =.习题3. 如图,在ABC △中,D 为BC 的中点,::4:3:1AE EF FD =.求::AG GH AB .CEF DBH GA【解析】 ∵HFC 是ABD △的梅氏线,探索提升∴1AH BC DFHB DC FA⋅⋅=. ∵D 为BC 的中点,::4:3:1AE EF FD =, ∴21BC DC =,17DF FA =. ∴21117AH HB ⋅⋅=,∴72AH HB =. ∵GEC 是ABD △的梅氏线, ∴1AG BC DE GB DC EA ⋅⋅=, ∴21111AG GB ⋅⋅=,∴12AG GB =. ∴::3:4:2AG GH HB =. ∴::3:4:9AG GH AB =.【例3】 过ABC △的重心G 的直线分别交AB 、AC 于点E 、F ,交CB 的延长线于点D .求证:1BE CFEA FA+=.M DGFECB A【解析】 作直线AG 交BC 于M ,∵:1:2MG GA =,BM MC =. ∴AE BD MG EB DM GA ⋅⋅112AE BD EB DM =⋅⋅=. ∴2EB BD AE DM=. 同理,2CF DCFA DM=, 而2BD DC BD BD BM +=++2()2BD BM DM =+= ∴21222BE CF BD DC DM EA FA DM DM DM+=+==.【例4】 如图,点D 、E 分别在ABC △的边AC 、AB 上, AE EB =,23AD DC =,BD 与CE 交于点F ,40ABC S =△.求AEFD S .初中数学竞赛专题.梅涅劳斯定理与塞瓦定理.(有答案)FDECBA【解析】 对ECA △和截线BFD ,由梅氏定理得:1EF CD AB FC DA BE ⋅⋅=,即32121EF FC ⋅⋅=, 所以13EF FC =.所以1148BFE BEC ABC S S S ==△△△, 进而211140115840AEFD ABD BEF ABC S S S S ⎛⎫=-=-=⋅= ⎪⎝⎭△△△.习题4. 如图,在ABC △中,三个三角形面积分别为5,8,10.四边形AEFD 的面积为x ,求x的值.x 1085F DE CBA【解析】 对ECA △和截线BFD ,由梅氏定理得:1CD AB EF DA BE FC ⋅⋅=,即1823115152x x +⋅⋅=+,解得22x =.【备选】如图,ABC △被通过它的三个顶点与一个内点O 的三条直线分为6个小三角形,其中三个小三角形的面积如图所示,求ABC △的面积.354030O F ECDBA【解析】 对ABD △和截线COF ,由梅氏定理得:1AF BC DO FB CD OA ⋅⋅=,即41132BC CD ⋅⋅=,所以32BC CD =,所以3BCBD=.所以33105315ABC ABD S S ==⨯=△△.【例5】 如图, 在ABC △中,A ∠的外角平分线与边BC 的延长线交于点P ,B ∠的平分线与非常挑战边CA 交于点Q ,C ∠的平分线与边AB 交于点R ,求证:P 、Q 、R 三点共线.P C B QRA【解析】 AP 是BAC ∠的外角平分线,则BP ABPC CA=① BQ 是ABC ∠的平分线,则 CQ BCQA AB=② CR 是ACB ∠的平分线,则 AR CARB BC=③ ⨯⨯①②③得1BP CQ AR AB BC CAPC QA RB CA AB BC⋅⋅=⋅⋅= 因R 在AB 上,Q 在CA 上,P 在BC 的延长线上,则根据梅涅劳斯定理的逆定理得:P 、Q 、R 三点共线.习题5. 证明:不等边三角形的三个角的外角平分线与对边的交点是共线的三个点.F EDCBAP F E D CBA【解析】 如图,CD BE AF 、、分别为三角形ABC 的三个外角平分线,分别交AB AC BC 、、于D E F 、、.过C 作BE 的平行线,则BCP CBE EBD CPB ∠=∠=∠=∠, 所以BPC △是等腰三角形.则PB CB =.则有:CE PB CBEA BA BA==.初中数学竞赛专题.梅涅劳斯定理与塞瓦定理.(有答案)同理AD AC DB CB =;BF BAFC AC=. 所以1CE AD BF CB AC BA EA DB FC BA CB AC ⋅⋅=⋅⋅=.所以D E F 、、共线.板块二 塞瓦定理及其逆定理塞瓦定理:如果ABC △的三个顶点与一点P 的连线AP 、BP 、CP 交对边或其延长线于点D 、E 、F ,如图,那么1BD CE AFDC EA FB⋅⋅=.通常称点P 为ABC △的塞瓦点. PFED CB A证明: ∵直线FPC 、EPB 分别是ABD △、ACD △的梅氏线,∴1BC DP AF CD PA FB ⋅⋅=,1DB CE AP BC EA PD⋅⋅=. 两式相乘即可得:1BD CE AFDC EA FB⋅⋅=.塞瓦定理的逆定理:如果点D 、E 、F 分别在ABC △的边BC 、CA 、AB 上或其延长线上,并且1BD CE AF DC EA FB⋅⋅=,那么AD 、BE 、CF 相交于一点(或平行). F PF'ED C BAFED CB A证明: ⑴ 若AD 与BE 相交于一点P 时,如图,作直线CP 交AB 于'F .由塞瓦定理得:'1BD CE AF DC EA F B⋅⋅=',知识导航又已知1BD CE AF DC EA FB ⋅⋅=,∴AF AF FB F B '=', ∴AB AB FB F B =',∴FB F B '=. ∴'F 与F 重合 ∴'CF 与CF 重合∴AD 、BE 、CF 相交于一点.⑵ 若AD 与BE 所在直线不相交,则AD ∥BE ,如图. ∴BD EA DC AC=,又已知1BD CE AF DC EA FB ⋅⋅=, ∴1EA CE AF AC EA FB ⋅⋅=,即CE FB AC AF =. ∴//BE FC ,∴AD BE FC ∥∥.说明:三线平行的情况在实际题目中很少见.【例6】 (1)设AX BY CZ ,,是ABC △的三条中线,求证:AX BY CZ ,,三线共点.ZYXCBA(2)若AX BY CZ ,,为ABC △的三条内角平分线.求证:AX BY CZ ,,三线共点.ZYXCBA【解析】 (1)由条件知,BX XC YC YA ZA ZB ===,,.∴1BX CY AZXC YA ZB⋅⋅=, 根据塞瓦定理的逆定理可得三条中线AX BY CZ ,,共点. 这个点称为这个三角形的重心.(2)由三角形内角平分线定理得:BX AB CY BC AZ ACXC AC YA BA ZB BC===,,. 三式分别相乘,得:1BX CY AZ AB BC ACXC YA ZB AC AB BC⋅⋅=⋅⋅=.根据塞瓦定理的逆定理可得三角形三内角平分线AX BY CZ ,,共点, 这个点称为这个三角形的内心.习题6. 若AX BY CZ ,,分别为锐角ABC △的三条高线,求证:AX BY CZ ,,三线共点.探索提升初中数学竞赛专题.梅涅劳斯定理与塞瓦定理.(有答案)ZYX CBA【解析】 由ABX CBZ △∽△得:BX AB BZ BC =;由BYA CZA △∽△得:AZ ACAY AB =; 由AXC BYC △∽△可得:YC BC CX AC =.所以1BX AZ YC AB AC BCBZ AY CX BC AB AC⋅⋅=⋅⋅=.根据塞瓦定理的逆定理可得三条高线AX BY CZ ,,共点.对直角三角形、钝角三角形,同样也可以证得三条高线共点.我们把一个三角形三条高线所在直线的交点叫做这个三角形的垂心.【例7】 如图, M 为ABC △内的一点,BM 与AC 交于点E ,CM 与AB 交于点F ,若AM 通过BC 的中点D ,求证:EF BC ∥.FDEMBA【解析】 对ABC △和点M 应用塞瓦定理可得:1AF BD CEFB DC EA⋅⋅=.又因为BD DC =,所以1AF CE FB EA ⋅=.进而AF AEFB EC=,所以EF BC ∥.习题7. 如果梯形ABCD 的两腰AD 、BC 的延长线交于M ,两条对角线交于N .求证:直线MN必平分梯形的两底.BQ A NCP DM【解析】 ∵AB CD ∥∴MD CM DA BC = ∴1MD BC DA CM⋅= ∵1MD AQ BC DA QB CM⋅⋅=(由塞瓦定理得)∴1AQQB=,∴AQ QB = ∵DP PC AQ QB =,∴DP PC =.板块三 梅涅劳斯定理、塞瓦定理综合【备选】如图,E 、F 分别为ABC △的AC 、AB 边上的点,且3AE EC =,3BF FA =,BE 、CF 交于点P ,AP 的延长线交BC 于点D .求:AP PD 的值.ABCD EFP【解析】 ∵P 为ABC △的塞瓦点.∴11133AF BD CE BD FB DC EA DC ⋅⋅=⋅⋅= ∴91BD DC =,∴910BD BC =. ∵EPB 为ACD △的梅氏线, ∴911103AP DB CE AP PD BC EA PD ⋅⋅=⋅⋅= ∴103AP PD =【备选】如图,四边形ABCD 的对边AB 和DC ,DA 和CB 分别相交于点L K ,,对角线AC 与BD 交于点M .直线KL 与BD 、AC 分别交于点F G 、.求证:KF KGLF LG=. 非常挑战初中数学竞赛专题.梅涅劳斯定理与塞瓦定理.(有答案)11 / 11 F L K M DC BA【解析】 对DKL △与点B 应用塞瓦定理得:1DA KF LC AK FL CD⋅⋅=. 对DKL △和截线ACG 应用梅涅劳斯定理可得:1DA KG LC AK GL CD⋅⋅=. 进而可得KF KG LF LG=.。
2020版初三数学竞赛试卷含答案
2020版初三数学竞赛试卷含答案2020版初三数学竞赛试卷一、选择题(共5小题,每小题6分,共30分)1.已知a≠0,14(a2b2c2)=(a2b3c)2,那么a:b:c=()A、2:3:6B、1:2:3C、1:3:4D、1:2:42.抛物线y=kx2-7x-7的图象和x轴有交点,则k的取值范围是()A、B、且k≠0;C、D、且k≠03.如图,已知P是正方形ABCD内一点,△PBC是等边三角形,若△PAD的外接圆半径为a,则正方形ABCD边长为()A、B、C、D、4.一个等腰三角形被过一个顶点的一条直线分割成两个较小的等腰三角形,那么这个等腰三角形的顶的角度数的值可能有()A、2种B、3种C、4种D、5种5.如图所示,二次函数y=ax 2+bx+c 的图象经过点(-1,2),且与x 轴交点的横坐标分别为x 1,x 2,其中-2<x 1<-1,0<x 2<1,下列结论:①4a-2bc<0;②2a-b<0;③a<-1;④b 28a>4ac。
其中正确的有()(A)1个(B)2个(C)3个(D)4个二、填空题(共5小题,每小题6分,共30分)6.已知x 2xy y=14①,y 2xy x=28②,则x y 的值为.7.已知a,b 均为质数,且满足a 2b a =13,则a b b 2=.8.设整数a 使得关于x 的一元二次方程的两个根都是整数,则整数a的值=.9.如图是一个数的转换器,每次输入3个不为零的数,经转换器转换后输出3个新数,规律如下:当输入数分别为x,y,z时,对应输出的新数依次为,,.例如,输入1,2,3,则输出,,.那么当输出的新数为,,时,输入的3个数依次为.10.若实数a、b满足a2ab b2=1,且t=ab-a2-b2,则t的取值范围是。
三、解答题(共4题,满分60分)11、规定符号[x]表示不超过x的最大整数,例[3.1]=3,[-73]=-3,[6]=6。
求:满足方程2-x2=[x]且大于-3的x的解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年广州市初中数学竞赛专项练习:塞瓦定理(含答案)1. 设1A 、1B 分别是ABC △的边BC 和AC 上的点,D 、E 分别是1AA 与1BB 、11A B 与CD 的交点.证明:若190A EC ∠=︒,点A 、B 、1A 、E 共圆,则11AA BA =.【解析】 如图,延长AE 交BC 于F ,为证11AA BA =,只需证明11ABA A AB ∠=∠.而A 、B 、1A 、E 共圆,故11A EF ABA ∠=∠,11A AB BEA ∠=∠,于是只需证明1EA 为BEF ∠的平分线.ABCDB 1A 1E F对1AA C △的割线1BDB 及其内一点E 分别利用梅涅劳斯定理和塞瓦定理,得 11111CB A BAD B A DA BC ⋅⋅=, 11111CB A FAD B A DA FC⋅⋅=. 所以,11A F CFA B CB=. ①在射线CB 上取一点B ',使得11B EA A EF '∠=∠,则由190A EC ∠=︒,可知EC 为B EF '∠的外角平分线,于是,利用内、外角平分线定理,可知 11B A B E CB A F EF CF'''==. 从而,11A F A B CF CB'='. 对比式①得11A B A BCB CB'=',故B 与B '重合,因此,1A E 为BEF ∠的角平分线.2. 给定ABC △,点M 为BAC △内一点,使得MAB MCA ∠=∠,MAC MBA ∠=∠;N 为ABC △内一点,使得NBA NCB ∠=∠,NBC NAB ∠=∠;P 为ACB △内一点,使得PCA PBC ∠=∠,PCB PAC ∠=∠.证明:AM 、BN 和CP 三线共点,且该公共点在MNP △的外接圆上.A M1【解析】 延长AM 交BC 于点1A ,则11BMA MAB MBA MAC MCA CMA BAC ∠=∠+∠=∠+∠=∠=∠,即1MA为BMC ∠的平分线,于是,11BA BM A C MC =.而由条件,易知ABM △∽CAM △,故BM AM ABAM MC AC===cb(这里a 、b 、c 为ABC △的三边长),从而2BM BM AM c MC AM MC b ⎛⎫=⋅= ⎪⎝⎭,故 211BA c A C b ⎛⎫= ⎪⎝⎭. 同理可证:211CB a A B c ⎛⎫= ⎪⎝⎭,211AC b B C a ⎛⎫= ⎪⎝⎭,其中1B 为BN 与AC 的交点,1C 为CP 与AB 的交点(图中N 、P未画出).从而1111111BA CB AC AC B A C B ⋅⋅=. 于是,由塞瓦定理的逆定理可知AM 、BN 、CP 三线共点.设上述公共点为K ,O 为ABC △的外心,则2BMC BAC BOC ∠=∠=∠,故B 、M 、O 、C 四点共圆.于是设1MA 交这个圆于另一点2A ,则2A 为»BC 的中点.结合OB OC =,可知2OA 为B 、M 、O 、C 所共圆的直径.因此,290OMA OMK ∠=∠=︒,类似可证,90ONK ∠=︒,90OPK ∠=︒.所以,M 、N 、P 在以OK 为直径的圆上.3. 已知ABC △,向外外作长方形ABDE 、ACFG 、BCHK ,又设直线DE 与直线GF 交于P ,直线DE 与直线KH 交于Q ,直线KH 与直线GF 交于R ,则AP 、BQ 、CR 共点.【解析】 如图,设PA 延长后交BC 于A ',同理定义B '、C '(图中未画出).P E GAD QKHR C F B A'连结PB 、PC ,则ABDEPAB PAC ACFGS S BA A C S S '=='矩形△△矩形, 同理BCHK ABDE S CB B A S '='矩形矩形,ACFG BCHK S AC C B S '='矩形矩形,故1BA CB AC A C B A C B'''⋅⋅=''',AP 、BQ 、CR 共点或平行,由于A 、B 、C 均在PQR △内,故平行不可能.4. 已知ABC △内有一点P ,今过点A 作一直线1l 与AP 关于A ∠的角平分线对称,同样,过点B 、C 分别作直线2l 、3l ,求证:1l 、2l 、3l 交于一点.【解析】 如图,设1l 与直线BC 交于A ',则22sin sin AA B CAP AA C PAB S S BA AB BAA AB CA S AC PAB AC S ''''∠===⋅'∠△△△△,同理,CB B A '='22BAP CBP S CB BA S ⋅△△,22CBPCAPS AC AC C B CB S '=⋅'△△. AB A'CP于是1BA CB AC A C B A C B'''⋅⋅=''',由塞瓦逆定理,即知1l 、2l 、3l 共点.这个公共点P ',称为P 的等角共轭点.5. 已知ABC △,向外作相似的等腰三角形BCD △、ACE △及ABF △,其中D ∠、E ∠、F ∠是顶角.求证:AD 、BE 、CF 交于一点.【解析】 如图,不妨设AD 与BC 交于A ',同理定义B '、C '.设FAB FBA ACE θ∠=∠==∠=L ,则BA A C'⋅'AFEBC D A'B'C'sin()sin()sin()1sin()sin()sin()ABD BCE AFC ACD ABE BFC S S S CB AC AB B BC C AC A B A C B S S S AC C AB A BC B θθθθθθ''+++⋅=⋅⋅=⋅⋅=''+++△△△△△△,由塞瓦逆定理,便得结论.6. 已知:ABC △中,AD 、BE 、CF 是角平分线,则120BAC ∠=︒当且仅当DE DF ⊥.K AGHFBD E【解析】 当120BAC ∠=︒,延长CA 至任一点K ,则60KAB BAD ∠=︒=∠,于是F 至AK 距离等于F 至AD 距离;又CF 平分ACB ∠,故F 至AK 距离等于F 至BC 距离,因此可知DF 平分ADB ∠,同理DE 平分ADC ∠,故DE DF ⊥.反之,若DE DF ⊥,过A 作GH BC ∥,与DF 、DE 延长线分别交于G 、H ,则由塞瓦定理知AG BD =⋅AF AECD AH FB EC=⋅=,于是DA AG AH ==,故FDB G ADG ∠=∠=∠,即DF 平分ADB ∠,于是过F 作AK 、AD 、BC 的垂线,不难得出AF 平分KAD ∠,于是120BAC ∠=︒.7. 已知ABC △中,D 、E 分别在AB 、AC 上,DE BC ∥,BE 、CD 交于F ,AF 延长后交BC 于S ,SD 与BE 交于G ,SE 与CD 交于H ,AG 、AH 延长后分别交BC 于M 、P ,求BM ∶ MP ∶PC .P S MBHF GED A【解析】 由塞瓦定理易知BS CS =,又由梅氏定理,1BC PH ADCP HA BD ⋅⋅=, 1SC PH AE SP HA EC⋅⋅=, 两式相除,注意AD AE BD EC =,2BC SC =,得2CP SP =.易得13CP BC =,同理13BM BC =,故 BM ∶MP ∶1PC =∶1∶1.8. 如图,AM 是锐角ABC △的角平分线,ME AB ⊥于点E ,MF AC ⊥于点F ,CE 与BF 交于点P ,求证:AP BC ⊥.AD EGF HBMS P C【解析】 作AD BC ⊥,易知BEM △∽BDA △,MCF △∽ACD △,故而有BE BM ED AB =,CD ACCF MC=,于是1BE CD AC BMBD CF AB MC⋅=⋅=.9. 锐角ABC △,向外作ABE △和ACF △, 使得AB BE ⊥,AC CF ⊥,EAB CAF ∠=∠,若BF 、CE 交于点P ,求证:AP BC ⊥.AEB DCFN P M【解析】 为证明结论,我们干脆作ABC △的高AD ,设法证明AD 、BF 与CE 共点. 由EAC FAB ∠=∠及AE AFAB AC=知AEC ABF S S =△△. 设CE 与AB 交于点M ,BF 与AC 交于点N ,则有AM BD CNBM CD NA⋅⋅cos cos ACE BCFEBC ABFS S AB B S AC C S ⋅=⋅⋅⋅△△△△ cos sin(90)cos sin(90)AB B BC C CF AC C BC B BE ⋅⋅︒+⋅=⋅⋅⋅︒+⋅1AB CFAC BE=⋅=.于是由塞瓦逆定理,结论成立,最后一步用到的仍是ABE △∽ACF △.10. ABC △中,D 、E 、F 分别在边BC 、CA 、AB 上,且AD 、BE 、CF 共点于P .D '也在BC 上,且DD '与BC 的中点重合,同理定义E '、F '.求证:AD '、BE '、CF '也共点.【解析】 由塞瓦定理和逆定理,注意到BD DCD C BD'='等,立得结果. 评注 新共点与点P 互为等边共轭点.11. 设ABC △的边AB 、BC 、CA 上分别有点F 、D 、E ,且AD 、BE 、CF 共点,又DEF △的边DE 、EF 、FD 上分别有点Z 、X 、Y ,DX 、EY 、FZ 也共点,求证:AX 、BY 、CZ 共点. 【解析】 如图,又设AX 延长后与BC 交于X '(为简洁起见,图中未图出),同理定义Y '、Z '.于是AFXAXBAXCAEX ABS S BX AB AE FX AF AC X C S AC AF EX S AE'===⋅⋅'△△△△,同理CY BC BF YD AY AB BD FY '=⋅⋅',AZ AC CD EZ BZ BC CE DZ '=⋅⋅',由条件及塞瓦定理,得1BX CY AZ X C AY BZ '''⋅⋅=''',于是AX 、BY 、CZ 共点. AF XEYZ BDC12. 一个三角形的一边上的高、第二边上的中线与第三边上的角平分线交于一点,这个三角形一定是正三角形吗?【解析】 不一定.不妨设ABC △中,AD 、BE 、CF 分别为高、中线与角平分线,于是AE CE =,若三线交于一点,则由塞瓦定理(此处设AB c =,BC a =,CA b =),知有BD BF BC aCD FA AC b===. 而由BD CD a +=,222222BD CD AB AC c b -=-=-,知222222BD a c b CD a b c +-=+-,于是有222222a c b aa b c b +-=+-,c =例如令15a =,12b =,则13c =.13. 如图,AB 、AC 是两条切线,APQ 与AMN 是任意两条割线,求证:PN 、MQ 与BC 交于一点.AB CQNMP【解析】 本题无疑是要运用塞瓦逆定理,比如在PQC △中,知只需证1PQN QMCBPC BQC PCN QMPS S S S S S ⋅⋅=△△△△△△. 由圆内接四边形对角互补知,上式等价于1BP PC PQ QN QC MC BQ QC PC CN PQ PM ⋅⋅⋅⋅⋅=⋅⋅⋅,化简,得1BP QN MCBQ CN PM⋅⋅=⋅⋅.由ABP △∽AQB △、APM △∽ANQ △及AMC △∽ACN △,得BP AP BQ AB =,QN AN PM AP =,MC ACCN AN=,于是1BP QN MC ACBQ CN PM AB⋅⋅==.14. 设ABC △的内切圆分别与BC 、CA 、AB 切于点D 、E 、F ,DM EF ⊥于点M ,BM 与FD 交于点P ,CM与DE 交于点Q ,求证:MD 、FQ 与PE 共点.AF M EPQBD【解析】 易知 FP DQPD QE⋅FMB MCDBDM MECS S S S =⋅△△△△ sin sin sin sin BF FM AFE CD MD MDC FMBD MD MDB CE ME AEF ME⋅⋅∠⋅⋅∠=⋅=⋅⋅∠⋅⋅∠,由塞瓦逆定理,知三线共点. 评注 此处MD EF ⊥这个条件多余,但可用来证明MD 平分BMC ∠.证明如下:设ABC △中内角为A ∠、B ∠、C ∠,于是易知12FDM C ∠=∠,12EDM B ∠=∠,故sin2sin 2CFD FM BF B ME CE ED ==,又由BFM ∠= 1902A CEM ︒+∠=∠,故FMB △∽EMC △,于是命题得证.15. 已知凸四边形ABCD ,BAC DAC ∠=∠,P 是AC 上任一点,延长BP 、DP ,分别交CD 、CB 于Q 、R ,求证:QAC RAC ∠=∠.【解析】 如图,分别作CM AB ∥,CN AD ∥,且M 、R 、A 共线,N 、Q 、A 共线,设BD 与AC 交于J .由塞瓦定理及角平分线性质定理,有1AD BR CQAB RC QD⋅⋅=.但CRCM AB BR=⋅,CQ CN AD DQ =⋅,于是CM CN =. 又180180ACM BAC DAC ACN ∠=︒-∠=︒-∠=∠,AC AC =,故ACM △≌ACN △,于是QAC RAC ∠=∠.BARMJ PC QND。
