3近年考点分布与真题练习讲解3
第三章陆地与海洋(重难讲解思维导图真题训练)-七年级地理上学期期末考点大串讲(人教版2024)

② 位于南半球的大洲:大
洋洲、非洲南部、南极洲和
东半球
南美洲大部。 ③ 位于东半球的大洲:亚
洲、欧洲、大洋洲和南极洲
大部。
④ 位于西半球的大洲:北
类地行星
巨行星 美洲、南美洲和南极洲小部。
南半球
重难点解析
重难点1:七大洲的位置
⑤ 南极洲纬度最高、跨经度最广,绝大部分位于南极圈内,四周被大洋环绕。这里终年
C.不变
D.不确定
真题检测
(2024·山东菏泽·中考真题)2023年11月1日,
中国第40次南极科考队(“雪龙”号和“雪龙2”号极地科考船)
从上海出发踏上科考征程。按照计划,相关作业队员将于12月中旬
抵达秦岭站建设区域,并在60天内完成建设任务。下图示意中国第
40次赴南极科考航线。据此完成下面小题。
冰雪覆盖,是唯一没有人类定居的大洲。
⑥ 全部位于北半球的大洲是:欧洲和北美洲。 ⑦ 全部位于南美洲的大洲是:南极洲。
⑧ 赤道穿过的大洲是:非洲、亚洲、大洋洲和南美洲。 ⑨ 跨纬度最广的大洲是:亚洲。
北美洲
20°W
欧洲 亚 洲
非洲
赤道
南美洲
西半球
南极洲
南极洲
东半球
重难点解析
重难点2:七大洲分界线
① 亚洲与欧洲:乌拉尔山—乌拉
海洋具有互联互通的特点
考点梳理 考点7:陆地主要地形区
阿尔卑斯山脉
伊朗高原
青藏高原
刚果盆地
埃塞俄比亚高原
落基山脉
安第斯山脉
亚马孙平原 巴西高原
考点梳理 考点8:七大洲的地形特征
欧洲:地形以平原为主, 地势南北高,中间低。 平均海拔最低的大洲。
2024年高考真题完全解读课件:2024年高考地理真题完全解读(广东卷)
02 命题思路
三、优化教考衔接,引导地理教学 试题设计既注重考察学生对新课标中必备知识的掌握,考察学生迁
移和运用这些必备知识解决实际问题的能力,为中学地理教学回归、注 重地理过程和成因机制发挥了积极的导向作用。如第17题考察学生对于 产业转移与布局和城乡协调等内容的理解,具体涉及市域,村域等不同 时空人的关系。
02 命题思路
二、注重核心素养考察,服务人才选拔
2.体现地理学综合性和交叉性的学科,体现学科融合
试题内容充分体现了地理学综合性和交叉性的学科特点,对标课程 标准,加强学科融合,考察学生对一日内不同时段气温和相对湿度的变 化如何影响硫酸钠可逆反应的理解,体现了学科融合,表现特征的异同 性及其对其驱动机制的正确理解。如第9~10题在理解北半球,温带气候 ,峡湾和极地气候峡湾形成的气候条件基础上,通过在极地地区出现温 带气候峡湾这一反常现象,考察了学生对自然环境整体性特征的理解以 及洋流对自然地理环境整体性的影响,有助于引导学生树立对地理问题 认知的正确时空尺度观。
三、在试题结构上 全卷分为选择题和非选择题两个部分,由16道选择题、3道综合题、
8小问(3+2+3)。选择题仍然为一带二的形式,共8个题组。仍旧是图文 材料结合的形式。
四、选择题答案分布
4A+5B+3C+4D
选项 1
2
3
4
5
6
7
8
答案 A
D
B
D
B
A
C
C
选项 9 答案 B
10
11
12
13
14
15
16
A
对应“葡萄酒 生产集群规模 不断扩大且重 心向东南方向 移动” 该地区:贺兰 山东麓地区
考点36 超几何分布与二项分布——2021年高考数学专题复习真题练习
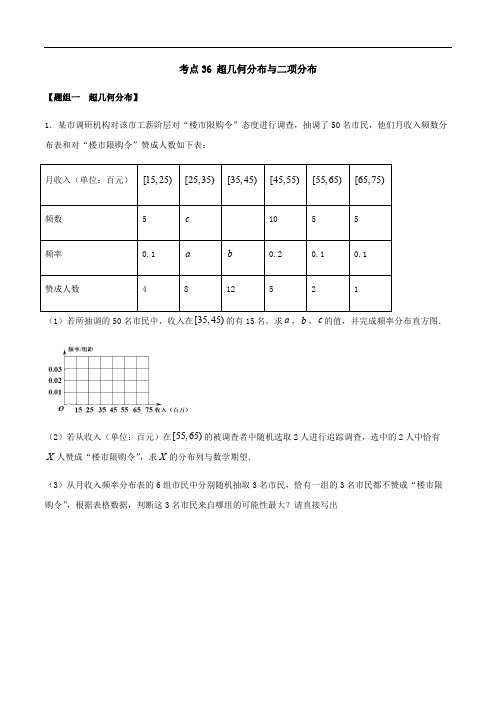
考点36 超几何分布与二项分布【题组一超几何分布】1.某市调硏机构对该市工薪阶层对“楼市限购令”态度进行调查,抽调了50名市民,他们月收入频数分布表和对“楼市限购令”赞成人数如下表:月收入(单位:百元)[15,25)[25,35)[35,45)[45,55)[55,65)[65,75)频数 5 c10 5 5频率0.1 a b0.2 0.1 0.1赞成人数 4 8 12 5 2 1[35,45)a b c(1)若所抽调的50名市民中,收入在的有15名,求,,的值,并完成频率分布直方图.[55,65)(2)若从收入(单位:百元)在的被调查者中随机选取2人进行追踪调查,选中的2人中恰有X X人赞成“楼市限购令”,求的分布列与数学期望.(3)从月收入频率分布表的6组市民中分别随机抽取3名市民,恰有一组的3名市民都不赞成“楼市限购令”,根据表格数据,判断这3名市民来自哪组的可能性最大?请直接写出2.某大学数学学院拟从往年的智慧队和理想队中选拔4名大学生组成志愿者招募宣传队.往年的智慧对和理想队的构成数据如下表所示,现要求选出的4名大学生中两队中的大学生都要有.(1)求选出的4名大学生仅有1名女生的概率;X X(2)记选出的4名大学生中女生的人数为,求随机变量的分布列和数学期望.3.某电视台举行一个比赛类型的娱乐节目,两队各有六名选手参赛,将他们首轮的比赛成绩作为样A B 、本数据,绘制成茎叶图如图所示,为了增加节目的趣味性,主持人故意将队第六位选手的成绩没有给A 出,并且告知大家队的平均分比队的平均分多4分,同时规定如果某位选手的成绩不少于21分,则B A 获得“晋级”.(1)根据茎叶图中的数据,求出队第六位选手的成绩;A (2)主持人从队所有选手成绩中随机抽2个,求至少有一个为“晋级”的概率;A (3)主持人从两队所有选手成绩分别随机抽取2个,记抽取到“晋级”选手的总人数为,求的A B 、ξξ分布列.【题组二二项分布】1.某学校实行自主招生,参加自主招生的学生从8个试题中随机挑选出4个进行作答,至少答对3个才能通过初试已知甲、乙两人参加初试,在这8个试题中甲能答对6个,乙能答对每个试题的概率为,且34甲、乙两人是否答对每个试题互不影响.(1)试通过概率计算,分析甲、乙两人谁通过自主招生初试的可能性更大;(2)若答对一题得5分,答错或不答得0分,记乙答题的得分为,求的分布列及数学期望和方差. Y Y2.2020年1月10日,引发新冠肺炎疫情的病毒基因序列公布后,科学家们便开始了病毒疫9COVID 苗的研究过程.但是类似这种病毒疫苗的研制需要科学的流程,不是一朝一夕能完成的,其中有一步就是做动物试验.已知一个科研团队用小白鼠做接种试验,检测接种疫苗后是否出现抗体.试验设计是:每天接种一次,3天为一个接种周期.已知小白鼠接种后当天出现抗体的概率为,假设每次接种后当天是否出12现抗体与上次接种无关.(1)求一个接种周期内出现抗体次数的分布列;K (2)已知每天接种一次花费100元,现有以下两种试验方案:①若在一个接种周期内连续2次出现抗体即终止本周期试验,进行下一接种周期,试验持续三个接种周期,设此种试验方式的花费为元;X ②若在一个接种周期内出现2次或3次抗体,该周期结束后终止试验,已知试验至多持续三个接种周期,设此种试验方式的花费为元.本着节约成本的原则,选择哪种实验方案. Y3.某校高三男生体育课上做投篮球游戏,两人一组,每轮游戏中,每小组两人每人投篮两次,投篮投进的次数之和不少于次称为“优秀小组”.小明与小亮同一小组,小明、小亮投篮投进的概率分别为312,p p .(1)若,,则在第一轮游戏他们获“优秀小组”的概率;123p =212p =(2)若则游戏中小明小亮小组要想获得“优秀小组”次数为次,则理论上至少要进行多少1243p p +=16轮游戏才行?并求此时的值. 12,p p4.2020年1月10日,引发新冠肺炎疫情的COVID-9病毒基因序列公布后,科学家们便开始了病毒疫苗的研究过程.但是类似这种病毒疫苗的研制需要科学的流程,不是一朝一夕能完成的,其中有一步就是做动物试验.已知一个科研团队用小白鼠做接种试验,检测接种疫苗后是否出现抗体.试验设计是:每天接种一次,3天为一个接种周期.已知小白鼠接种后当天出现抗体的概率为,假设每次接种后当天是否出现抗12体与上次接种无关.(1)求一个接种周期内出现抗体次数的分布列;k (2)已知每天接种一次花费100元,现有以下两种试验方案:①若在一个接种周期内连续2次出现抗体即终止本周期试验,进行下一接种周期,试验持续三个接种周期,设此种试验方式的花费为元;X ②若在一个接种周期内出现2次或3次抗体,该周期结束后终止试验,已知试验至多持续三个接种周期,设此种试验方式的花费为元.Y 比较随机变量和的数学期望的大小. X Y【题组三超几何分布与二项分布综合运用】1.全国中小学生的体质健康调研最新数据表明我国小学生近视眼发病率为22.78%,初中生为55.22%,高中生为70.34%.影响青少年近视形成的因素有遗传因素和环境因素,主要原因是环境因素.学生长时期近距离的用眼状态,加上不注意用眼卫生、不合理的作息时间很容易引起近视.除了学习,学生平时爱看电视、上网玩电子游戏、不喜欢参加户外体育活动,都是造成近视情况日益严重的原因.为了解情况,现从某地区随机抽取16名学生,调查人员用对数视力表检查得到这16名学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶),如图:(1)写出这组数据的众数和中位数;(2)若视力测试结果不低于5.0,则称为“好视力”.①从这16名学生中随机选取3名,求至少有2名学生是“好视力”的概率;②以这16名学生中是“好视力”的频率代替该地区学生中是“好视力”的概率.若从该地区学生(人数X X较多)中任选3名,记表示抽到“好视力”学生的人数,求的分布列及数学期望.如何学好数学1.圆锥曲线中最后题往往联立起来很复杂导致k算不出,这时你可以取特殊值法强行算出k过程就是先联立,后算代尔塔,用下伟达定理,列出题目要求解的表达式,就ok了2.选择题中如果有算锥体体积和表面积的话,直接看选项面积找到差2倍的小的就是答案,体积找到差3倍的小的就是答案,屡试不爽!3.三角函数第二题,如求a(cosB+cosC)/(b+c)coA之类的先边化角然后把第一题算的比如角A等于60度直接假设B和C都等于60°带入求解。
2023年高考地理真题完全解读01(山东卷)

我国地级市一般由市辖区和其他县级行政区组成。图示意我国某地级市2010年和2020年的常住 人口数量。该市的常住人口变化状况在全国具有一定的代表性。完成下面小题。 3.图示意四种人口流动情况,与该市2010~2020年情况相符的是( )
A.①ห้องสมุดไป่ตู้
B.② C.③
D.④
4.与该市的其他县级行政区相比,市辖区( )
19
土壤
情境材料 亚寒带针叶林生态系统简单碳储量高
我国某地级市常住人口数量变化
墨西哥湾沿岸的马德雷湖 广东佛山的工业设计城 辽宁省抚顺市的城市发展 某文化广场的十二生肖石像 滇池流域人类活动与聚落发展
某地焚风的发展变化和锋面的形成与移 动 西南山区M乡的地形,带动作用与发展 白浆化棕壤的影响及其改良
试卷评析
三、深化关键能力考查,突出创新思维 2023年高考试题充分利用图文信息载体及巧妙的问题设计,深化对获取解读地理
信息,描述阐释地理事物、论证探讨地理问题等关键能力的考查,有效鉴别学生的思 维品质和发展潜能。 四、优化必备知识考查,引领同向同行
必备知识是形成核心价值、关键能力和学科素养的基础。高考地理试题强调基础性、 综合性和应用性的考查要求,以此引领中学教学遵循教育规律,与高考改革同频共振。 五、重视试题情境设计,构建考查载体
2.分值分布
0.7 0.6 0.5 0.4 0.3 0.2 0.1
0 2020年
图表标题
2021年 自然地理
2022年 人文地理
2023年
从分值分布看,每年的 试题中自然地理和人文 地理考察比较均衡。 近三年自然地理比重波 动下降,人文地理比重 波动上升。
3.情境类型
近三年试卷
生活实践情境
专题31新定义与阅读理解创新型问题-中考数学必刷真题考点分类专练【解析版】

加油!考生!专题31新定义与阅读理解创新型问题一.选择题(共3小题)1.(2022•娄底)若10x=N,则称x是以10为底N的对数.记作:x=lgN.例如:102=100,则2=lg100;100=1,则0=lg1.对数运算满足:当M>0,N>0时,lgM+lgN=lg(MN).例如:lg3+lg5=lg15,则(lg5)2+lg5×lg2+lg2的值为()A.5B.2C.1D.0【分析】首先根据定义运算提取公因式,然后利用定义运算计算即可求解.【解析】原式=lg5(lg5+lg2)+lg2=lg5×lg(5×2)+lg2=lg5lg10+lg2=lg5+lg2=lg10=1.故选:C.2.(2022•重庆)在多项式x﹣y﹣z﹣m﹣n中任意加括号,加括号后仍只有减法运算,然后按给出的运算顺序重新运算,称此为“加算操作”.例如:(x﹣y)﹣(z﹣m﹣n)=x﹣y ﹣z+m+n,x﹣y﹣(z﹣m)﹣n=x﹣y﹣z+m﹣n,….下列说法:①至少存在一种“加算操作”,使其运算结果与原多项式相等;②不存在任何“加算操作”,使其运算结果与原多项式之和为0;③所有可能的“加算操作”共有8种不同运算结果.其中正确的个数是()A.0B.1C.2D.3【分析】根据“加算操作”的定义可知,当只给x﹣y加括号时,和原式相等;因为不改变x,y的运算符号,故不存在任何“加算操作”,使其运算结果与原多项式之和为0在多项式x﹣y﹣z﹣m﹣n中,可通过加括号改变z,m,n的符号,因为z,m,n中只有加减两种运算,求出即可.【解析】①(x﹣y)﹣z﹣m﹣n=x﹣y﹣z﹣m﹣n,与原式相等,故①正确;②∵在多项式x﹣y﹣z﹣m﹣n中,可通过加括号改变z,m,n的符号,无法改变x,y的符号,故不存在任何“加算操作”,使其运算结果与原多项式之和为0;故②正确;③在多项式x﹣y﹣z﹣m﹣n中,可通过加括号改变z,m,n的符号,加括号后只有加减两种运算,∴2×2×2=8种,所有可能的加括号的方法最多能得到8种不同的结果.故选:D.3.(2022•常德)我们发现:=3,=3,=3,…,=3,一般地,对于正整数a,b,如果满足=a时,称(a,b)为一组完美方根数对.如上面(3,6)是一组完美方根数对,则下面4个结论:①(4,12)是完美方根数对;②(9,91)是完美方根数对;③若(a,380)是完美方根数对,则a=20;④若(x,y)是完美方根数对,则点P(x,y)在抛物线y=x2﹣x上,其中正确的结论有()A.1个B.2个C.3个D.4个【分析】将(4,12),(9,91)代入验证即可判断①②;将(a,380)代入公式,建立方程可得出结论;若(x,y)是完美方根数对,则满足给出公式,化简可得出结论.【解析】将(4,12)代入=4,=4,=4,…,∴(4,12)是完美方根数对;故①正确;将(9,91)代入=10≠9,=,∴(9,91)不是完美方根数对,故②错误;③∵(a,380)是完美方根数对,∴将(a,380)代入公式,=a,=a,解得a=20或a=﹣19(舍去),故③正确;④若(x,y)是完美方根数对,则=x,=x,整理得y=x2﹣x,∴点P(x,y)在抛物线y=x2﹣x上,故④正确;故选:C.二.填空题(共1小题)4.(2022•内江)对于非零实数a,b,规定a⊕b=﹣.若(2x﹣1)⊕2=1,则x的值为.【分析】利用新规定对计算的式子变形,解分式方程即可求得结论.【解析】由题意得:=1,解得:x=.经检验,x=是原方程的根,∴x=.故答案为:.三.解答题(共23小题)5.(2022•遵义)新定义:我们把抛物线y=ax2+bx+c(其中ab≠0)与抛物线y=bx2+ax+c 称为“关联抛物线”.例如:抛物线y=2x2+3x+1的“关联抛物线”为:y=3x2+2x+1.已知抛物线C1:y=4ax2+ax+4a﹣3(a≠0)的“关联抛物线”为C2.(1)写出C2的解析式(用含a的式子表示)及顶点坐标;(2)若a>0,过x轴上一点P,作x轴的垂线分别交抛物线C1,C2于点M,N.①当MN=6a时,求点P的坐标;②当a﹣4≤x≤a﹣2时,C2的最大值与最小值的差为2a,求a的值.【分析】(1)根据“关联抛物线”的定义可直接得出C2的解析式,再将该解析式化成顶点式,可得出C2的顶点坐标;(2)①设点P的横坐标为m,则可表达点M和点N的坐标,根据两点间距离公式可表达MN的长,列出方程,可求出点P的坐标;②分情况讨论,当a﹣4≤﹣2≤a﹣2时,当﹣2≤a﹣4≤a﹣2时,当a﹣4≤a﹣2≤﹣2时,分别得出C2的最大值和最小值,进而列出方程,可求出a的值.【解析】(1)根据“关联抛物线”的定义可得C2的解析式为:y=ax2+4ax+4a﹣3,∵y=ax2+4ax+4a﹣3=a(x+2)2﹣3,∴C2的顶点坐标为(﹣2,﹣3);(2)①设点P的横坐标为m,∵过点P作x轴的垂线分别交抛物线C1,C2于点M,N,∴M(m,4am2+am+4a﹣3),N(m,am2+4am+4a﹣3),∴MN=|4am2+am+4a﹣3﹣(am2+4am+4a﹣3)|=|3am2﹣3am|,∵MN=6a,∴|3am2﹣3am|=6a,解得m=﹣1或m=2,∴P(﹣1,0)或(2,0).②∵C2的解析式为:y=a(x+2)2﹣3,∴当x=﹣2时,y=﹣3,当x=a﹣4时,y=a(a﹣4+2)2﹣3=a(a﹣2)2﹣3,当x=a﹣2时,y=a(a﹣2+2)2﹣3=a3﹣3,根据题意可知,需要分三种情况讨论,Ⅰ、当a﹣4≤﹣2≤a﹣2时,0<a≤2,且当0<a≤1时,函数的最大值为a(a﹣2)2﹣3;函数的最小值为﹣3,∴a(a﹣2)2﹣3﹣(﹣3)=2a,解得a=2﹣或a=2+(舍);当1≤a≤2时,函数的最大值为a3﹣3;函数的最小值为﹣3,∴a3﹣3﹣(﹣3)=2a,解得a=或a=﹣(舍);Ⅱ、当﹣2≤a﹣4≤a﹣2时,a≥2,函数的最大值为a3﹣3,函数的最小值为a(a﹣2)2﹣3;∴a3﹣3﹣[a(a﹣2)2﹣3]=2a,解得a=(舍);Ⅲ、当a﹣4≤a﹣2≤﹣2时,a≤0,不符合题意,舍去;综上,a的值为2﹣或.6.(2022•长沙)若关于x的函数y,当t﹣≤x≤t+时,函数y的最大值为M,最小值为N,令函数h=,我们不妨把函数h称之为函数y的“共同体函数”.(1)①若函数y=4044x,当t=1时,求函数y的“共同体函数”h的值;②若函数y=kx+b(k≠0,k,b为常数),求函数y的“共同体函数”h的解析式;(2)若函数y=(x≥1),求函数y的“共同体函数”h的最大值;(3)若函数y=﹣x2+4x+k,是否存在实数k,使得函数y的最大值等于函数y的“共同体函数“h的最小值.若存在,求出k的值;若不存在,请说明理由.【分析】(1)①由题意求出M=6066,N=2022,再由定义可求h的值;②分两种情况讨论:②当k>0时,M=kt+k+b,N=kt﹣k+b,h=k;当k<0时,M=kt﹣k+b,有N=kt+k+b,h=﹣k;(2)由题意t﹣≥1,M=,N=,则h=,所以h有最大值;(3)分四种情况讨论:①当2≤t﹣时,M=﹣(t﹣﹣2)2+4+k,N=﹣(t+﹣2)2+4+k,h=t﹣2;②当t+≤2时,N=﹣(t﹣﹣2)2+4+k,M=﹣(t+﹣2)2+4+k,h=2﹣t,;③当t﹣≤2≤t,即2≤t≤,N=﹣(t+﹣2)2+4+k,M=4+k,h=(t ﹣)2;④当t<2≤t+,N=﹣(t﹣﹣2)2+4+k,M=4+k,h=(t﹣)2,画出h的函数图象,结合图象可得=4+k,解得k=﹣.【解析】(1)①∵t=1,∴≤x≤,∵函数y=4044x,∴函数的最大值M=6066,函数的最小值N=2022,∴h=2022;②当k>0时,函数y=kx+b在t﹣≤x≤t+有最大值M=kt+k+b,有最小值N=kt ﹣k+b,∴h=k;当k<0时,函数y=kx+b在t﹣≤x≤t+有最大值M=kt﹣k+b,有最小值N=kt+k+b,∴h=﹣k;综上所述:h=|k|;(2)t﹣≥1,即t≥,函数y=(x≥1)最大值M=,最小值N=,∴h=,当t=时,h有最大值;(3)存在实数k,使得函数y的最大值等于函数y的“共同体函数“h的最小值,理由如下:∵y=﹣x2+4x+k=﹣(x﹣2)2+4+k,∴函数的对称轴为直线x=2,y的最大值为4+k,①当2≤t﹣时,即t≥,此时M=﹣(t﹣﹣2)2+4+k,N=﹣(t+﹣2)2+4+k,∴h=t﹣2,此时h的最小值为;②当t+≤2时,即t≤,此时N=﹣(t﹣﹣2)2+4+k,M=﹣(t+﹣2)2+4+k,∴h=2﹣t,此时h的最小值为;③当t﹣≤2≤t,即2≤t≤,此时N=﹣(t+﹣2)2+4+k,M=4+k,∴h=(t﹣)2,④当t<2≤t+,即≤t<2,此时N=﹣(t﹣﹣2)2+4+k,M=4+k,∴h=(t﹣)2,h的函数图象如图所示:h的最小值为,由题意可得=4+k,解得k=﹣;综上所述:k的值为﹣.7.(2022•重庆)对于一个各数位上的数字均不为0的三位自然数N,若N能被它的各数位上的数字之和m整除,则称N是m的“和倍数”.例如:∵247÷(2+4+7)=247÷13=19,∴247是13的“和倍数”.又如:∵214÷(2+1+4)=214÷7=30……4,∴214不是“和倍数”.(1)判断357,441是否是“和倍数”?说明理由;(2)三位数A是12的“和倍数”,a,b,c分别是数A其中一个数位上的数字,且a>b >c.在a,b,c中任选两个组成两位数,其中最大的两位数记为F(A),最小的两位数记为G(A),若为整数,求出满足条件的所有数A.【分析】(1)根据“和倍数”的定义依次判断即可;(2)设A=(a+b+c=12,a>b>c),根据“和倍数”的定义表示F(A)和G(A),代入中,根据为整数可解答.【解析】(1)∵357÷(3+5+7)=357÷15=23……12,∴357不是“和倍数”;∵441÷(4+4+1)=441÷9=49,∴441是9的“和倍数”;(2)设A=(a+b+c=12,a>b>c),由题意得:F(A)=,G(A)=,∴===,∵a+c=12﹣b,为整数,∴====7+(1﹣b),∵1<b<9,∴b=3,5,7,∴a+c=9,7,5,①当b=3,a+c=9时,(舍),,则A=732或372;②当b=5,a+c=7时,,则A=156或516;③当b=7,a+c=5时,此种情况没有符合的值;综上,满足条件的所有数A为:732或372或156或516.8.(2022•常州)第十四届国际数学教育大会(ICME﹣14)会徽的主题图案有着丰富的数学元素,展现了我国古代数学的文化魅力,其右下方的“卦”是用我国古代的计数符号写出的八进制数3745.八进制是以8作为进位基数的数字系统,有0~7共8个基本数字.八进制数3745换算成十进制数是3×83+7×82+4×81+5×80=2021,表示ICME﹣14的举办年份.(1)八进制数3746换算成十进制数是2022;(2)小华设计了一个n进制数143,换算成十进制数是120,求n的值.【分析】(1)根据已知,从个位数字起,将八进制的每一位数分别乘以80,81,82,83,再把所得结果相加即可得解;(2)根据n进制数和十进制数的计算方法得到关于n的方程,解方程即可求解.【解析】(1)3746=3×83+7×82+4×81+6×80=1536+448+32+6=2022.故八进制数字3746换算成十进制是2022.故答案为:2022;(2)依题意有:n2+4×n1+3×n0=120,解得n1=9,n2=﹣13(舍去).故n的值是9.9.(2022•盐城)【发现问题】小明在练习簿的横线上取点O为圆心,相邻横线的间距为半径画圆,然后半径依次增加一个间距画同心圆,描出了同心圆与横线的一些交点,如图1所示,他发现这些点的位置有一定的规律.【提出问题】小明通过观察,提出猜想:按此步骤继续画圆描点,所描的点都在某二次函数图象上.【分析问题】小明利用已学知识和经验,以圆心O为原点,过点O的横线所在直线为x轴,过点O且垂直于横线的直线为y轴,相邻横线的间距为一个单位长度,建立平面直角坐标系,如图2所示.当所描的点在半径为5的同心圆上时,其坐标为(﹣3,4)或(3,4).【解决问题】请帮助小明验证他的猜想是否成立.【深度思考】小明继续思考:设点P(0,m),m为正整数,以OP为直径画⊙M,是否存在所描的点在⊙M上.若存在,求m的值;若不存在,说明理由.【分析】【分析问题】根据题意可知:该点的纵坐标为4,利用勾股定理,即可求出该点的横坐标,进而可得出点的坐标;【解决问题】设所描的点在半径为n(n为正整数)的同心圆上,则该点的纵坐标为(n ﹣1),利用勾股定理可得出该点的坐标为(﹣,n﹣1)或(,n﹣1),结合点横、纵坐标间的关系,可得出该点在二次函数y=x2﹣的图象上,进而可证出小明的猜想正确;【深度思考】设该点的坐标为(±,n﹣1),结合⊙M的圆心坐标,利用勾股定理,即可用含n的代数式表示出m的值,再结合m,n均为正整数,即可得出m,n的值.【解答】【分析问题】解:根据题意,可知:所描的点在半径为5的同心圆上时,其纵坐标y=5﹣1=4,∵横坐标x=±=±3,∴点的坐标为(﹣3,4)或(3,4).【解决问题】证明:设所描的点在半径为n(n为正整数)的同心圆上,则该点的纵坐标为(n﹣1),∴该点的横坐标为±=±,∴该点的坐标为(﹣,n﹣1)或(,n﹣1).∵(±)2=2n﹣1,n﹣1=,∴该点在二次函数y=(x2﹣1)=x2﹣的图象上,∴小明的猜想正确.【深度思考】解:设该点的坐标为(±,n﹣1),⊙M的圆心坐标为(0,m),∴=m,∴m====n﹣1+2+.又∵m,n均为正整数,∴n﹣1=1,∴m=1+2+1=4,∴存在所描的点在⊙M上,m的值为4.10.(2022•遂宁)在平面直角坐标系中,如果一个点的横坐标与纵坐标互为相反数,则称该点为“黎点”.例如(﹣1,1),(2022,﹣2022)都是“黎点”.(1)求双曲线y=上的“黎点”;(2)若抛物线y=ax2﹣7x+c(a、c为常数)上有且只有一个“黎点”,当a>1时,求c的取值范围.【分析】(1)设双曲线y=上的“黎点”为(m,﹣m),构建方程求解即可;(2)抛物线y=ax2﹣7x+c(a、c为常数)上有且只有一个“黎点”,推出方程ax2﹣7x+c =﹣x有且只有一个解,即ax2﹣6x+c=0,Δ=36﹣4ac=0,可得结论.【解析】(1)设双曲线y=上的“黎点”为(m,﹣m),则有﹣m=,∴m=±3,经检验,m=±3的分式方程的解,∴双曲线y=上的“黎点”为(3,﹣3)或(﹣3,3);(2)∵抛物线y=ax2﹣7x+c(a、c为常数)上有且只有一个“黎点”,∴方程ax2﹣7x+c=﹣x有且只有一个解,即ax2﹣6x+c=0,Δ=36﹣4ac=0,∴ac=9,∴a=,∵a>1,∴0<c<9.11.(2022•兰州)在平面直角坐标系中,P(a,b)是第一象限内一点,给出如下定义:k1=和k2=两个值中的最大值叫做点P的“倾斜系数”k.(1)求点P(6,2)的“倾斜系数”k的值;(2)①若点P(a,b)的“倾斜系数”k=2,请写出a和b的数量关系,并说明理由;②若点P(a,b)的“倾斜系数”k=2,且a+b=3,求OP的长;(3)如图,边长为2的正方形ABCD沿直线AC:y=x运动,P(a,b)是正方形ABCD 上任意一点,且点P的“倾斜系数”k<,请直接写出a的取值范围.【分析】(1)根据“倾斜系数”k的定义直接计算即可;(2)①根据“倾斜系数”k的的定义分情况得出结论即可;②根据“倾斜系数”k的的定义求出P点坐标,进而求出OP的值即可;(3)根据k的取值,分情况求出a的取值范围即可.【解析】(1)由题意知,k==3,即点P(6,2)的“倾斜系数”k的值为3;(2)①∵点P(a,b)的“倾斜系数”k=2,∴=2或=2,即a=2b或b=2a,∴a和b的数量关系为a=2b或b=2a;②由①知,a=2b或b=2a∵a+b=3,∴或,∴OP==;(3)由题意知,当P点与D点重合时,且k=时,a有最小临界值,如下图:连接OD,延长DA交x轴于E,此时=,则,解得a=;当P点与B点重合时,且k=时,a有最大临界值,如下图:连接OB,延长CB交x轴于F,此时=,则=,解得a=3+,综上所述,若点P的“倾斜系数”k<,则+1<a<3+.12.(2022•北京)在平面直角坐标系xOy中,已知点M(a,b),N.对于点P给出如下定义:将点P向右(a≥0)或向左(a<0)平移|a|个单位长度,再向上(b≥0)或向下(b<0)平移|b|个单位长度,得到点P′,点P′关于点N的对称点为Q,称点Q为点P的“对应点”.(1)如图,点M(1,1),点N在线段OM的延长线上.若点P(﹣2,0),点Q为点P的“对应点”.①在图中画出点Q;②连接PQ,交线段ON于点T,求证:NT=OM;(2)⊙O的半径为1,M是⊙O上一点,点N在线段OM上,且ON=t(<t<1),若P为⊙O外一点,点Q为点P的“对应点”,连接PQ.当点M在⊙O上运动时,直接写出PQ长的最大值与最小值的差(用含t的式子表示).【分析】(1)①根据定义,先求出P'的坐标,从而得出Q的位置;②连接PP',利用三角形中位线定理得NT=PP',从而证明结论;(2)连接PO,并延长至S,使OP=OS,延长SQ到T,使ST=OM,由题意知,PP1∥OM,PP1=OM,P1N=NQ,利用三角形中位线定理得QT的长,从而求出SQ的长,在△PQS中,PS﹣QS<PS+QS,则PS的最小值为PS﹣QS,PS的最大值为PS+QS,从而解决问题.【解析】(1)①由题意知,P'(﹣2+1,0+1),∴P'(﹣1,1),如图,点Q即为所求;②连接PP',∵∠P'PO=∠MOx=45°,∴PP'∥ON,∵P'N=QN,∴PT=QT,∴NT=PP',∵PP'=OM,∴NT=OM;(2)如图,连接PO,并延长至S,使OP=OS,延长SQ到T,使ST=OM,由题意知,PP1∥OM,PP1=OM,P1N=NQ,∴TQ=2MN,∵MN=OM﹣ON=1﹣t,∴TQ=2﹣2t,∴SQ=ST﹣TQ=1﹣(2﹣2t)=2t﹣1,在△PQS中,PS﹣QS<PS+QS,∴PS的最小值为PS﹣QS,PS的最大值为PS+QS,∴PQ长的最大值与最小值的差为(PS+QS)﹣(PS﹣QS)=2QS=4t﹣2.13.(2022•青岛)【图形定义】有一条高线相等的两个三角形称为等高三角形、例如:如图①,在△ABC和△A'B'C'中,AD,A'D'分别是BC和B'C'边上的高线,且AD =A'D'、则△ABC和△A'B'C'是等高三角形.【性质探究】,S△A'B'C′分别表示△ABC和△A′B′C′的面积,如图①,用S△ABC=BC•AD,S△A'B'C′=B′C′•A′D′,则S△ABC∵AD=A′D′:S△A'B'C′=BC:B'C'.∴S△ABC【性质应用】:S△ADC=(1)如图②,D是△ABC的边BC上的一点.若BD=3,DC=4,则S△ABD3:4;(2)如图③,在△ABC中,D,E分别是BC和AB边上的点.若BE:AB=1:2,CD:BC=1:3,S△ABC=1,则S△BEC=,S△CDE=;(3)如图③,在△ABC中,D,E分别是BC和AB边上的点.若BE:AB=1:m,CD:BC=1:n,S△ABC=a,则S△CDE=.【分析】(1)根据等高的两三角形面积的比等于底的比,直接求出答案;(2)同(1)的方法即可求出答案;(3)同(1)的方法即可求出答案.【解析】(1)∵BD=3,DC=4,:S△ADC=BD:DC=3:4,∴S△ABD故答案为:3:4;(2)∵BE:AB=1:2,:S△ABC=BE:AB=1:2,∴S△BEC=1,∵S△ABC=;∴S△BEC∵CD:BC=1:3,:S△BEC=CD:BC=1:3,∴S△CDE=S△BEC=×=;∴S△CDE故答案为:,;(3)∵BE:AB=1:m,:S△ABC=BE:AB=1:m,∴S△BEC=a,∵S△ABC=S△ABC=;∴S△BEC∵CD:BC=1:n,:S△BEC=CD:BC=1:n,∴S△CDE=S△BEC=•=,∴S△CDE故答案为:.14.(2022•常州)在四边形ABCD中,O是边BC上的一点.若△OAB≌△OCD,则点O 叫做该四边形的“等形点”.(1)正方形不存在“等形点”(填“存在”或“不存在”);(2)如图,在四边形ABCD中,边BC上的点O是四边形ABCD的“等形点”.已知CD =4,OA=5,BC=12,连接AC,求AC的长;(3)在四边形EFGH中,EH∥FG.若边FG上的点O是四边形EFGH的“等形点”,求的值.【分析】(1)根据“等形点”的定义可知△OAB≌△OCD,则∠OAB=∠C=90°,而O 是边BC上的一点.从而得出正方形不存在“等形点”;(2)作AH⊥BO于H,由△OAB≌△OCD,得AB=CD=4,OA=OC=5,设OH=x,则BH=7﹣x,由勾股定理得,(4)2﹣(7﹣x)2=52﹣x2,求出x的值,再利用勾股定理求出AC的长即可;(3)根据“等形点”的定义可得△OEF≌△OGH,则∠EOF=∠HOG,OE=OG,∠OGH =∠OEF,再由平行线性质得OE=OH,从而推出OE=OH=OG,从而解决问题.【解析】(1)∵四边形ABCD是正方形,∴∠C=90°,∵△OAB≌△OCD,∴∠OAB=∠C=90°,∵O是边BC上的一点.∴正方形不存在“等形点”,故答案为:不存在;(2)作AH⊥BO于H,∵边BC上的点O是四边形ABCD的“等形点”,∴△OAB≌△OCD,∴AB=CD=4,OA=OC=5,∵BC=12,∴BO=7,设OH=x,则BH=7﹣x,由勾股定理得,(4)2﹣(7﹣x)2=52﹣x2,解得,x=3,∴OH=3,∴AH=4,∴CH=8,在Rt△CHA中,AC===4;(3)如图,∵边FG上的点O是四边形EFGH的“等形点”,∴△OEF≌△OGH,∴∠EOF=∠HOG,OE=OG,∠OGH=∠OEF,∵EH∥FG,∴∠HEO=∠EOF,∠EHO=∠HOG,∴∠HEO=∠EHO,∴OE=OH,∴OH=OG,∴OE=OF,∴=1.15.(2022•青海)两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,把具有这个规律的图形称为“手拉手”图形.(1)问题发现:如图1,若△ABC和△ADE是顶角相等的等腰三角形,BC,DE分别是底边.求证:BD =CE;(2)解决问题:如图2,若△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一条直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系并说明理由.【分析】(1)根据△ABC和△ADE是顶角相等的等腰三角形,证明△ABD≌△ACE(SAS),即可得BD=CE;(2)根据△ACB和△DCE均为等腰直角三角形,可得△ACD≌△BCE(SAS),即有AD =BE,∠ADC=∠BEC,从而可得∠BEC=∠ADC=135°,即知∠AEB=∠BEC﹣∠CED =90°,由CD=CE,CM⊥DE,∠DCE=90°,可得DM=ME=CM,故AE=AD+DE =BE+2CM.【解答】(1)证明:∵△ABC和△ADE是顶角相等的等腰三角形,∴AB=AC,AD=AE,∠BAC=∠DAE,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,∴△ABD≌△ACE(SAS),∴BD=CE;(2)解:∠AEB=90°,AE=BE+2CM,理由如下:如图:∵△ACB和△DCE均为等腰直角三角形,∴AC=BC,DC=EC,∠ACB=90°=∠DCE,∴∠ACD=∠BCE,∴△ACD≌△BCE(SAS),∴AD=BE,∠ADC=∠BEC,∵△CDE是等腰直角三角形,∴∠CDE=∠CED=45°,∴∠ADC=180°﹣∠CDE=135°,∴∠BEC=∠ADC=135°,∴∠AEB=∠BEC﹣∠CED=135°﹣45°=90°,∵CD=CE,CM⊥DE,∴DM=ME,∵∠DCE=90°,∴DM=ME=CM,∴DE=2CM,∴AE=AD+DE=BE+2CM.16.(2022•嘉兴)小东在做九上课本123页习题:“1:也是一个很有趣的比.已知线段AB(如图1),用直尺和圆规作AB上的一点P,使AP:AB=1:.”小东的作法是:如图2,以AB为斜边作等腰直角三角形ABC,再以点A为圆心,AC长为半径作弧,交线段AB于点P,点P即为所求作的点.小东称点P为线段AB的“趣点”.(1)你赞同他的作法吗?请说明理由.(2)小东在此基础上进行了如下操作和探究:连结CP,点D为线段AC上的动点,点E在AB的上方,构造△DPE,使得△DPE∽△CPB.①如图3,当点D运动到点A时,求∠CPE的度数.②如图4,DE分别交CP,CB于点M,N,当点D为线段AC的“趣点”时(CD<AD),猜想:点N是否为线段ME的“趣点”?并说明理由.【分析】(1)利用等腰三角形的性质证明,再利用AC=AP,即可得出结论;(2)①由题意可得:∠CAB=∠B=45°,∠ACB=90°,AC=AP=BC,再求解∠ACP =∠APC=67.5°,∠CPB=112.5°,证明∠DPE=∠CPB=112.5°,从而可得答案;②先证明△ADP∽△ACB,可得∠APD=45°,DP∥CB,再证明MP=MD=MC=MN,∠EMP=45°,∠MPE=90°,从而可得出结论.【解析】(1)赞同,理由如下:∵△ABC是等腰直角三角形,∴AC=BC,∠A=∠B=45°,∴cos45°=,∵AC=AP,∴,∴点P为线段AB的“趣点”.(2)①由题意得:∠CAB=∠B=45°,∠ACB=90°,AC=AP=BC,∴=67.5°,∴∠BCP=90°﹣67.5°=22.5°,∴∠CPB=180°﹣45°﹣22.5°=112.5°,∵△DPE∽△CPB,D,A重合,∴∠DPE=∠CPB=112.5°,∴∠CPE=∠DPE+∠CPB﹣180°=45°;②点N是线段ME的趣点,理由如下:当点D为线段AC的趣点时(CD<AD),∴,∵AC=AP,∴,∵,∠A=∠A,∴△ADP∽△ACB,∴∠ADP=∠ACB=90°,∴∠APD=45°,DP∥CB,∴∠DPC=∠PCB=22.5°=∠PDE,∴DM=PM,∴∠MDC=∠MCD=90°﹣22.5°=67.5°,∴MD=MC,同理可得MC=MN,∴MP=MD=MC=MN,∵∠MDP=∠MPD=22.5°,∠E=∠B=45°,∴∠EMP=45°,∠MPE=90°,∴=,∴点N是线段ME的“趣点”.17.(2022•兰州)如图,在Rt△ABC中,∠ACB=90°,AC=3cm,BC=4cm,M为AB边上一动点,BN⊥CM,垂足为N.设A,M两点间的距离为xcm(0≤x≤5),B,N两点间的距离为ycm(当点M和B点重合时,B,N两点间的距离为0).小明根据学习函数的经验,对因变量y随自变量x的变化而变化的规律进行了探究.下面是小明的探究过程,请补充完整.(1)列表:下表的已知数据是根据A,M两点间的距离x进行取点、画图、测量,分别得到了y与x的几组对应值:x/cm00.51 1.5 1.82 2.53 3.54 4.55 y/cm4 3.96 3.79 3.47a 2.99 2.40 1.79 1.230.740.330请你通过计算,补全表格:a= 3.2;(2)描点、连线:在平面直角坐标系中,描出表中各组数值所对应的点(x,y),并画出函数y关于x的图象;(3)探究性质:随着自变量x的不断增大,函数y的变化趋势:y随x的增大而减小;(4)解决问题:当BN=2AM时,AM的长度大约是 1.67cm.(结果保留两位小数)【分析】(1)先求出AB边上的高,进而求出AM',判断出点M与M'重合,即可得出答案;(2)先描点,再连线,即可画出图象;(3)根据图象直接得出结论;(4)利用表格和图象估算出AM的长度.【解析】(1)如图,在Rt△ABC中,AC=3,BC=4,根据勾股定理得,AC=5,过点C作CM'⊥AB于M,=AC•BC=AB•CM',∴S△ABC∴CM'=,在Rt△ACM'中,根据勾股定理得,AM'==1.8,当x=1.8时,点M与点M'重合,∴CM⊥AB,∵BN⊥CM,∴点M,N重合,∴a=BN=BM=AB﹣AM=3.2,故答案为:3.2;(2)如图所示,(3)由图象知,y随x的增大而减小,故答案为:y随x的增大而减小;(3)借助表格和图象得,当BN=2AM时,AM的长度大约是1.67cm,故答案为:1.67.18.(2022•深圳)二次函数y=2x2,先向上平移6个单位,再向右平移3个单位,用光滑的曲线画在平面直角坐标系上.y=2x2y=2(x﹣3)2+6(0,0)(3,m)(1,2)(4,8)(2,8)(5,14)(﹣1,2)(2,8)(﹣2,8)(1,14)(1)m的值为6;(2)在坐标系中画出平移后的图象并写出y=﹣x2+5与y=x2的交点坐标;(3)点P(x1,y1),Q(x2,y2)在新的函数图象上,且P,Q两点均在对称轴同一侧,若y1>y2,则x1<或>x2.(填不等号)【分析】(1)根据平移的性质分析对应点的坐标;(2)利用描点法画函数图象,联立方程组求得两函数的交点坐标;(3)结合二次函数图象的性质分析求解.【解析】(1)将(0,0)先向上平移6个单位,再向右平移3个单位后对应点的坐标为(3,6),∴m=6,故答案为:6;(2)平移后的函数图象如图:联立方程组,解得,∴y=﹣x2+5与y=x2的交点坐标为(,),(﹣,);(3)∵点P(x1,y1),Q(x2,y2)在新的函数图象上,且P,Q两点均在对称轴同一侧,当P,Q两点同在对称轴左侧时,若y1>y2,则x1<x2,当P,Q两点同在对称轴右侧时,若y1>y2,则x1>x2,故答案为:<或>.19.(2022•潍坊)某市在盐碱地种植海水稻获得突破性进展,小亮和小莹到海水稻种植基地调研.小莹根据水稻年产量数据,分别在直角坐标系中描出表示2017﹣2021年①号田和②号田年产量情况的点(记2017年为第1年度,横轴表示年度,纵轴表示年产量),如图.小亮认为,可以从y=kx+b(k>0),y=(m>0),y=﹣0.1x2+ax+c中选择适当的函数模型,模拟①号田和②号田的年产量变化趋势.(1)小莹认为不能选y=(m>0).你认同吗?请说明理由;(2)请从小亮提供的函数模型中,选择适当的模型分别模拟①号田和②号田的年产量变化趋势,并求出函数表达式;(3)根据(2)中你选择的函数模型,请预测①号田和②号田总年产量在哪一年最大?最大是多少?【分析】(1)由当m>0时,y=的性质可得答案;(2)观察①号田和②号田的年产量变化趋势可知,①号田为y=kx+b(k>0),②号田为y=﹣0.1x2+ax+c,用待定系数法可得模拟①号田的函数表达式为y=0.5x+1,模拟①号田的函数表达式为y=﹣0.1x2+x+1;(3)设①号田和②号田总年产量为w吨,w=0.5x+1+(﹣0.1x2+x+1)=﹣0.1x2+1.5x+2=﹣0.1(x﹣7.5)2+7.625,根据二次函数性质可得答案.【解析】(1)认同,理由是:当m>0时,y=中,y随x的增大而减小,而从图中描点可知,x增大y随之增大,故不能选y=(m>0);(2)观察①号田和②号田的年产量变化趋势可知,①号田为y=kx+b(k>0),②号田为y=﹣0.1x2+ax+c,把(1,1.5),(2,2.0)代入y=kx+b得:,解得,∴y=0.5x+1;把(1,1.9),(2,2.6)代入y=﹣0.1x2+ax+c得:,解得,∴y=﹣0.1x2+x+1,答:模拟①号田的函数表达式为y=0.5x+1,模拟②号田的函数表达式为y=﹣0.1x2+x+1;(3)设①号田和②号田总年产量为w吨,由(2)知,w=0.5x+1+(﹣0.1x2+x+1)=﹣0.1x2+1.5x+2=﹣0.1(x﹣7.5)2+7.625,∵﹣0.1<0,抛物线对称轴为直线x=7.5,而x为整数,∴当x=7或8时,w取最大值,最大值为7.6,答:①号田和②号田总年产量在2023年或2024年最大,最大是7.6吨.20.(2022•潍坊)为落实“双减”,老师布置了一项这样的课后作业:二次函数的图象经过点(﹣1,﹣1),且不经过第一象限,写出满足这些条件的一个函数表达式.【观察发现】请完成作业,并在直角坐标系中画出大致图象.【思考交流】小亮说:“满足条件的函数图象的对称轴一定在y轴的左侧.”小莹说:“满足条件的函数图象一定在x轴的下方.”你认同他们的说法吗?若不认同,请举例说明.【概括表达】小博士认为这个作业的答案太多,老师不方便批阅,于是探究了二次函数y=ax2+bx+c 的图象与系数a,b,c的关系,得出了提高老师作业批阅效率的方法.请你探究这个方法,写出探究过程.【分析】由题意写出一个符合条件的函数解析式即可;【观察发现】画出一个符合条件的函数图象即可;【思考交流】由题意可知抛物线的对称轴可以在y轴的左侧,也可以在y轴的右侧,或者是y轴,抛物线的图象一定在x轴的下方;【概括表达】设经过点(﹣1,﹣1)的函数解析式为y=a(x+1)2+m(x+1)﹣1,则b =2a+m,c=a+m﹣1,由a<0,c≤0,a﹣b+c=﹣1,可得b<1.【解析】y=﹣x2(答案不为唯一);【观察发现】如图:【思考交流】∵抛物线的对称轴为x=﹣,a<0,∴抛物线的对称轴可以在y轴的左侧,也可以在y轴的右侧,或者是y轴,例如:y=﹣x2;∴小亮的说法不正确;∵抛物线不经过第一象限,∴抛物线的图象一定在x轴的下方,∴小莹的说法不正确;【概括表达】设经过点(﹣1,﹣1)的函数解析式为y=a(x+1)2+m(x+1)﹣1,∴y=ax2+(2a+m)x+a+m﹣1,∵y=ax2+bx+c,∴b=2a+m,c=a+m﹣1,∵二次函数的图象不经过第一象限,∴a<0,c≤0,∵经过点(﹣1,﹣1),∴a﹣b+c=﹣1,∴a+m﹣1≤0,∴a+m≤1,∴b=2a+m=a+a+m≤a+1,∴b<1,综上所述:a<0,b<1,c≤0且a﹣b+c=﹣1.21.(2022•临沂)杠杆原理在生活中被广泛应用(杠杆原理:阻力×阻力臂=动力×动力臂),小明利用这一原理制作了一个称量物体质量的简易“秤”(如图1).制作方法如下:第一步:在一根匀质细木杆上标上均匀的刻度(单位长度1cm),确定支点O,并用细麻绳固定,在支点O左侧2cm的A处固定一个金属吊钩,作为秤钩;第二步:取一个质量为0.5kg的金属物体作为秤砣.(1)图1中,把重物挂在秤钩上,秤砣挂在支点O右侧的B处,秤杆平衡,就能称得重物的质量.当重物的质量变化时,OB的长度随之变化.设重物的质量为xkg,OB的长为ycm.写出y关于x的函数解析式;若0<y<48,求x的取值范围.(2)调换秤砣与重物的位置,把秤砣挂在秤钩上,重物挂在支点O右侧的B处,使秤杆平衡,如图2.设重物的质量为xkg,OB的长为ycm,写出y关于x的函数解析式,完成下表,画出该函数的图象.x/kg……0.250.5124……y/cm……421……【分析】(1)根据阻力×阻力臂=动力×动力臂解答即可;(2)根据阻力×阻力臂=动力×动力臂求出解析式,然后根据列表、描点、连线的步骤解答.【解析】(1)∵阻力×阻力臂=动力×动力臂,∴重物×OA=秤砣×OB,∵OA=2cm,重物的质量为xkg,OB的长为ycm,秤砣为0.5kg,∴2x=0.5y,∴y=4x,∵4>0,∴y随x的增大而增大,∵当y=0时,x=0;当y=48时,x=12,∴0<x<12;(2)∵阻力×阻力臂=动力×动力臂,∴秤砣×OA=重物×OB,∵OA=2cm,重物的质量为xkg,OB的长为ycm,秤砣为0.5kg,∴2×0.5=xy,∴y=,当x=0.25时,y==4;当x=0.5时,y==2;当x=1时,y=1;当x=2时,y=;当x=4时,y=;故答案为:4;2;1;;;作函数图象如图:22.(2022•赤峰)阅读下列材料定义运算:min|a,b|,当a≥b时,min|a,b|=b;当a<b时,min|a,b|=a.例如:min|﹣1,3|=﹣1;min|﹣1,﹣2|=﹣2.完成下列任务(1)①min|(﹣3)0,2|=1;②min|﹣,﹣4|=﹣4.(2)如图,已知反比例函数y1=和一次函数y2=﹣2x+b的图象交于A、B两点.当﹣2<x<0时,min|,﹣2x+b|=(x+1)(x﹣3)﹣x2,求这两个函数的解析式.【分析】(1)根据定义运算的法则解答即可;(2)根据反比例函数和一次函数图象的性质解答即可.【解析】(1)由题意可知:①min|(﹣3)0,2|=1,②min|﹣,﹣4|=﹣4;故答案为:1,﹣4.(2)当﹣2<x<0时,min|,﹣2x+b|=(x+1)(x﹣3)﹣x2=﹣2x﹣3,∵一次函数y2=﹣2x+b,∴b=﹣3,∴y2=﹣2x﹣3,当x=﹣2时,y=1,∴A(﹣2,1)将A点代入y1=中,得k=﹣2,∴y1=﹣.23.(2022•赤峰)【生活情境】为美化校园环境,某学校根据地形情况,要对景观带中一个长AD=4m,宽AB=1m的长方形水池ABCD进行加长改造(如图①,改造后的水池ABNM仍为长方形,以下简称水池1).同时,再建造一个周长为12m的矩形水池EFGH(如图②,以下简称水池2).【建立模型】如果设水池ABCD的边AD加长长度DM为x(m)(x>0),加长后水池1的总面积为y1(m2),则y1关于x的函数解析式为:y1=x+4(x>0);设水池2的边EF的长为x(m)(0<x<6),面积为y2(m2),则y2关于x的函数解析式为:y2=﹣x2+6x(0<x<6),上述两个函数在同一平面直角坐标系中的图象如图③.【问题解决】(1)若水池2的面积随EF长度的增加而减小,则EF长度的取值范围是3≤x<6(可省略单位),水池2面积的最大值是9m2;(2)在图③字母标注的点中,表示两个水池面积相等的点是C,E,此时的x(m)值是1或4;(3)当水池1的面积大于水池2的面积时,x(m)的取值范围是0<x<1或4<x<6;(4)在1<x<4范围内,求两个水池面积差的最大值和此时x的值;(5)假设水池ABCD的边AD的长度为b(m),其他条件不变(这个加长改造后的新水池简称水池3),则水池3的总面积y3(m2)关于x(m)(x>0)的函数解析式为:y3=x+b(x>0).若水池3与水池2的面积相等时,x(m)有唯一值,求b的值.【分析】(1)依据函数图象和函数解析式,利用二次函数的性质解答即可;(2)利用图象交点的数学意义解答即可;(3)依据图象,利用数形结合法解答即可;。
2024年6月高考地理真题完全解读(浙江省)

【答案】5、C
04全面试解题密详解
2024年6月浙江省高考地理真题完全解读
02全面命解题密思路
2024年6月浙江省高考地理真题完全解读
二、素养立意,引导学科教学 学科核心素养是学科育人价值的集中体现,是学科评价的重要指标。 试题选取时代性、生活化的真实情景,设置梯度性、创新性问题,考查地 理原理、地理规律的运用能力。如第11、12题以生活化、时代性的情景 切入,从产业布局变化特征到原因分析,体现了从现象到本质,从浅层认 知到深度思考,考查了进阶思维,同时引导教师将生活中的地理事象融入 课堂教学;第26题通过创设主题情景,设问多角度、有层次的问题链,考 查认识区域的思维方式,形成解决问题的思维链,从而引导课堂教学走进 生活、走向深度。
04全面试解题密详解
2024年6月浙江省高考地理真题完全解读
下图为世界局部海域8月份表层海水盐度 和洋流分布图。完成下面小题。
1. 从河口到阿拉伯海,表层海水盐度( ) A. 持续升高 B. 持续降低 C. 先升后降 D. 先降后升
据图可知,河口处出现37‰的盐度数值 ,阿拉伯海也出现37‰的盐度数值,而 两者之间的海域盐度最大处是39‰,所 以,从河口到阿拉伯海,表层海水盐度先 升后降,C正确
03全面试解题密评析
2024年6月浙江省高考地理真题完全解读
三、深化教改衔接,引导教学回归本源
本试卷在问题设计上,充分体现了情境设置的重要性、迁移应用的必要性以及思维 创新的鼓励性。这不仅使试卷成为服务人才选拔的精准标尺,更成为导向教学、引领中 学地理教育发展的有力指针。如第16-17题,通过比较陕西省粮食和耕地重心的变迁, 引导学生关注我国耕地安全与粮食安全;第22-23题,通过分析锂应用行业市场份额的 变化,引导学生从全球视角,关注我国战略性矿产资源的安全。又如第27题,情境材料 新、问题切口小、思维含量高,都是要求学生在理解地理原理、规律的基础上,对地理 事象进行深度思考和变式迁移。
2025年新高考物理-圆周运动(解析版)
圆周运动1.高考真题考点分布题型考点考查考题统计选择题描述圆周运动的基本物理量2024年辽宁卷计算题圆锥摆模型2024年江西卷实验题水平圆盘模型2024年海南卷2.命题规律及备考策略【命题规律】高考对圆周运动基本规律的考查较为频繁,大多联系实际生活。
圆周运动的临界问题的单独考查不是太常见,大多在综合性的计算题中出现的比较频繁,并且会结合有关的功能关系。
【备考策略】1.掌握圆周运动各个物理量之间的关系。
2.能够分析圆周运动的向心力的来源,并会处理有关锥摆模型、转弯模型、圆盘模型的动力学问题。
3.掌握水平面内圆盘模型的动力学分析及临界条件。
4.掌握竖直面内圆周运动的基本规律,并能够联系实际问题做出相应问题的分析。
【命题预测】重点关注竖直面内圆周运动规律在综合性问题中的应用。
一、匀速圆周运动及其描述1.匀速圆周运动(1)定义:做圆周运动的物体,若在相等的时间内通过的圆弧长相等,就是匀速圆周运动。
(2)特点:加速度大小不变,方向始终指向圆心,是变加速运动。
(3)条件:合外力大小不变、方向始终与速度方向垂直且指向圆心。
2.描述匀速圆周运动的物理量及其关系(1)线速度:v=ΔsΔt =2πrT,描述物体圆周运动快慢的物理量。
(2)角速度:ω=ΔθΔt =2πT,描述物体绕圆心转动快慢的物理量。
(3)周期和频率:T=2πrv,T=1f,描述物体绕圆心转动快慢的物理量。
(4)向心加速度:a n=rω2=v2r =ωv=4π2T2r,描述速度方向变化快慢的物理量。
二、匀速圆周运动的向心力1.向心力的来源向心力是按力的作用效果命名的,可以是重力、弹力、摩擦力等各种力,也可以是几个力的合力或某个力的分力,因此在受力分析中要避免再另外添加一个向心力。
2.向心力的确定(1)确定圆周运动的轨道所在的平面,确定圆心的位置。
(2)分析物体的受力情况,所有的力沿半径方向指向圆心的合力,就是向心力。
3.向心力的公式:F n=ma n=m v2r =mω2r=m4π2T2r。
2021年新课标新高考地理复习练习讲义:专题三第二讲 大气环流与气候
第二讲大气环流与气候备考篇提纲挈领【考情探究】课标解读考情分析备考指导内容解读全球性大气环流全球气压带、风带的分布、移动规律及其对气候的影响近5年本讲内容一直是高考考查的重点,是高频考点。
试题多以区域图附加气候要素信息的方式呈现,考查学生获取信息、运用知识分析问题及运用地理原理阐释自然现象的能力。
突出考查区域认知、综合思维和地理实践力的学科素养本讲内容为自然地理的核心知识,是高考知识点中的重点和难点。
备考复习时要突出对基础知识的理解,理顺知识点之间的关系。
多联系生活和生产实际,分析和解决现实生活中的问题是备考的关键气温与降水气候类型全球气候变化全球气候变化对人类活动的影响【真题探秘】基础篇固本夯基【基础集训】知识1全球性大气环流读全球近地面气压带和风带局部示意图,回答下面两题。
1.图中的M气压带为()A.赤道低气压带B.北半球副热带高气压带C.南半球副热带高气压带D.副极地低气压带答案B2.下列关于图中M、N两气压带所反映的时间与季节的叙述,正确的是()A.M表示3月份、春季B.N表示7月份、夏季C.M表示12月份、夏季D.N表示1月份、冬季答案B知识2 气温与降水下图示意某地区年均温的分布。
读下图,完成下面两题。
1.影响该地区年均温分布特征的主要因素是()A.台风B.海陆分布C.地形D.大气环流答案C2.图示①②③④四地中,年降水量最低的是()A.①地B.②地C.③地D.④地答案A知识3气候类型读四城市资料图,完成下面两题。
1.关于四城市气候的分析,正确的是()A.乙地气候海洋性最强B.甲地年降水量最大C.丁地气候一年分干湿两季D.丙地气候类型南北半球都有分布答案D2.关于四城市气候成因的判断,正确的是()A.丁地主要受赤道低气压带的控制B.甲地受气压带和风带的交替控制C.乙地受海陆热力性质差异影响D.丙地终年受西风带的影响答案C知识4全球气候变化2016年上海沿海海平面比常年高102毫米,比2015年高45毫米,预计未来30年,上海沿海海平面将上升65~150毫米,读下图,完成下面两题。
第03讲 二项式定理(学生版)-2025版高中数学一轮复习考点帮
第03讲二项式定理(13类核心考点精讲精练)1.5年真题考点分布2.命题规律及备考策略【命题规律】本节内容是新高考卷的常考内容,设题稳定,难度较低或中等,分值为5分【备考策略】1.理解、掌握二项式定理的通项公式,会相关基本量的求解2.能分清二项式系数与系数的定义,并会相关求解3.能清晰计算二项式系数和与系数和及其大(小)项计算4.会三项式、乘积式的相关计算【命题预测】本节内容是新高考卷的常考内容,一般考查二项式系数和、系数和、求给定项的二项式系数或系数及相关最大(小)项计算,需重点强化复习1.二项式定理(1)二项式定理:(a +b )n =C 0n a n +C 1n a n -1b +…+C k n a n -k b k +…+C n n b n (n ∈N *);(2)通项公式:T k +1=C k n an -k b k ,它表示第k +1项;(3)二项式系数:二项展开式中各项的系数为C 0n ,C 1n ,…,C n n .若二项展开式的通项为T r +1=g (r )·x h (r )(r =0,1,2,…,n ),g (r )≠0,则有以下常见结论:(1)h (r )=0⇔T r +1是常数项.(2)h (r )是非负整数⇔T r +1是整式项.(3)h (r )是负整数⇔T r +1是分式项.(4)h (r )是整数⇔T r +1是有理项.注1.二项式的通项易误认为是第k 项,实质上是第k +1项.注2.易混淆二项式中的“项”“项的系数”“项的二项式系数”等概念,注意项的系数是指非字母因数所有部分,包含符号,二项式系数仅指C k n (k =0,1,…,n ).2.二项式系数的性质性质内容对称性与首末两端等距离的两个二项式系数相等,即mn nmn C C -=(a +b )n 的展开式的各个二项式系数的和等于2n ,即C 0n +C 1n +C 2n +…+C k n +…+C n n =2n.二项展开式中,偶数项的二项式系数的和等于奇数项的二项式系数的和,即C 1n +C 3n +C 5n +…=C 0n +C 2n +C 4n+…=12-n.1.(2024·浙江绍兴·二模)612x x ⎛⎫- ⎪⎝⎭的展开式的第四项为.1.(2024·陕西宝鸡·一模)622x x ⎛⎫- ⎪⎝⎭展开式中的第四项为()A .3160xB .3160x -C .240D .240-1.(2024·辽宁·模拟预测)二项式812x ⎛⎫+ ⎪⎝⎭展开式的第3项的二项式系数是.2.(2024·上海·三模)若1nx x ⎛⎫+ ⎪⎝⎭的二项展开式中第3项与第5项的系数相等,则该展开式中41x 的系数为.1.(2024·全国·模拟预测)21nx x ⎛⎫- ⎪⎝⎭的展开式中第2项的二项式系数为6,则其展开式中的常数项为.2.(2024·江苏无锡·模拟预测)在()n a b +的展开式中,若第4项与第5项的二项式系数之和等于第10项与第11项的二项式系数之和,则n =()A .16B .15C .14D .131.(2024·浙江·三模)若2nx⎛⎝展开式的二项式系数之和为128,则展开式中x 的系数为.2.(2024·四川攀枝花·三模)若*(12)(N )n x n -∈的展开式中3x 的系数为80-,则展开式中所有项的二项式系数之和为.(以数字作答)1.(2024·广东东莞·模拟预测)已知2n x x ⎛⎫- ⎪⎝⎭的展开式中所有项的二项式系数之和为32,则2nx x ⎛⎫- ⎪⎝⎭的展开式中3x 的系数为()A .10-B .20-C .10D .202.(24-25高三上·贵州贵阳·阶段练习)若nax ⎫⎪⎭的展开式的二项式系数和为32,且2x -的系数为80,则实数a 的值为.1.(23-24高二下·广东深圳·期中)6212x x ⎛⎫- ⎪⎝⎭的展开式中二项式系数最大的项为()A .第二项B .第三项C .第四项D .第五项2.(2024·江西南昌·三模)(多选)已知412x x ⎛⎫- ⎪⎝⎭的展开式中二项式系数的最大值与3+a x x ⎛⎫⎪⎝⎭的展开式中1x 的系数相等,则实数a 的值可能为()A .2B .2-C .22D .22-1.(23-24高二下·四川南充·阶段练习)()12nx -的展开式中只有第6项的二项式系数最大,则n =()A .9B .10C .11D .122.(2024·贵州·模拟预测)42x x ⎛⎫- ⎪⎝⎭的展开式中,二项式系数最大的项的系数是.(用数字作答)考点五、求指定项的系数1.(2024·湖北武汉·模拟预测)7212x x ⎛⎫- ⎪⎝⎭展开式中含21x 项的系数为()A .420B .420-C .560D .560-2.(2024·黑龙江哈尔滨·模拟预测)已知二项式()5nx x的展开式中第3项与第7项的二项式系数相等,则其展开式中5x 的系数为.1.(2024·浙江绍兴·三模)()61x -的展开式中3x 的系数为.(用数字作答)2.(2024·黑龙江大庆·三模)在4312x x ⎛⎫+ ⎪⎝⎭的展开式中,含4x 项的系数是.考点六、由项的系数确定参数1.(2024·黑龙江·模拟预测)若9a x x ⎛⎫+ ⎪⎝⎭的展开式中5x 的系数为144,则a =.2.(2024·福建宁德·模拟预测)已知()6x ay +的展开式中含33x y 项的系数为160,则实数a 的值为.1.(2024·安徽芜湖·模拟预测)(1)n x +的展开式中2x 的系数为15,则n =.2.(2024·山东·模拟预测)二项式5a x x ⎛⎫+ ⎪⎝⎭的展开式中,3x 的系数为10,则a =.1.(2024·江西鹰潭·模拟预测)10的展开式中,常数项的值为.2.(浙江·高考真题)在二项式9)x 的展开式中,常数项是;系数为有理数的项的个数是.1.(2024·湖北武汉·模拟预测)6131⎛⎫⎪⎝⎭展开式的7项中,系数为有理数的项共有()项A .1B .2C .3D .42.(2024·河南·模拟预测)已知2nx ⎛⎝(其中0a >)的展开式中的第7项为7,则展开式中的有理项共有()A .6项B .5项C .4项D .3项3.(2024·辽宁·模拟预测)(多选)若()26nn x ⎫≥⎪⎭的展开式中第4项的二项式系数最大,则二项展开式中的有理项(x α项中α是整数)可以是()A .第2项B .第3项C .第4项D .第5项1.(2024·上海·高考真题)在(1)n x +的二项展开式中,若各项系数和为32,则2x 项的系数为.2.(2024·福建泉州·一模)(多选)已知()*nx n ⎛+∈ ⎝N 展开式中共有8项.则该展开式结论正确的是()A .所有项的二项式系数和为128B .所有项的系数和为832⎛⎫⎪⎝⎭C .系数最大项为第2项D .有理项共有4项3.(2024·河南驻马店·二模)(多选)已知()7270127(43)13(13)(13)x a a x a x a x -=+-+-++- ,则()A .4945a =B .77141i i a ==-∑C .136024622a a a a +++=+D .613135722a a a a +++=-4.(2024·四川乐山·三模)设2023220240122024(2024)(21)x x a a x a x a x +-=++++ ,则32024122320242222a a a a ++++= ()A .1B .1-C .2024D .2024-1.(2024·辽宁·三模)(多选)关于二项式5(31)x -的展开式,下列说法正确的是()A .第三项系数为270B .2x 的系数为90C .二项式系数和为52D .系数和为522.(2024·福建福州·模拟预测)(多选)已知9290129(12)x a a x a x a x -=++++ ,则()A .01a =B .118a =C .1291a a a +++=- D .913579132a a a a a +++++=-3.(2024·湖北武汉·模拟预测)(多选)已知()26012661a a x a x a x x =+++-+ ,则下列结论正确的是()A .215a =B .12360a a a a ++++= C .024664+++=a a a a D .12362360a a a a ++++= 考点九、三项展开式的系数问题1.(2024·湖南衡阳·一模)621()x xy -+的展开式中xy 的系数为()A .30B .30-C .60D .60-2.(2024·江苏南京·模拟预测)621x y ⎛⎫+- ⎪⎝⎭的展开式中,42x y 的系数为()A .60B .60-C .120D .120-1.(2024·云南昆明·模拟预测)()522x x y +-的展开式中,52x y 项的系数为()A .10B .30-C .60D .60-2.(2024·安徽·三模)52x y ⎛⎫-+ ⎪⎝⎭的展开式中2y x 的系数为.1.(2024·山西长治·模拟预测)()()52x y x y +-的展开式中33x y 的系数是()A .﹣10B .0C .10D .302.(2024·江苏南京·模拟预测)26(23)(21)x x x +++的展开式中,2x 的系数是.1.(2024·江西·一模)72323(1)x x x+-的展开式中的常数项为()A .147B .147-C .63D .63-2.(2024·江西宜春·模拟预测)在()()6212a b a b -+-的展开式中,34a b 项的系数是.1.(23-24高二下·河北邢台·阶段练习)24(1)x +的展开式中,系数最大的项是()A .第11项B .第12项C .第13项D .第14项2.(2024·安徽·二模)已知2nx x ⎛⎫- ⎪⎝⎭的展开式二项式系数和为256,则展开式中系数最大的项为()A .第5项B .第6项C .第7项D .第8项1.(2023·上海嘉定·一模)已知6(12)x +的二项展开式中系数最大的项为.1.(2024·湖北·模拟预测)20242被9除的余数为()A .1B .4C .5D .82.(2024·甘肃张掖·三模)已知今天是星期四,则761-天后是()A .星期一B .星期二C .星期三D .星期五1.(24-25高三上·河南焦作·开学考试)203被10除的余数为.2.(2024·贵州黔南·二模)我国农历用“鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪”这12种动物按顺序轮流代表各年的生肖年号,今年2024年是龙年.那么从今年起的()14131+年后是()A .虎年B .马年C .龙年D .羊年1.(2024·宁夏·二模)杨辉是中国南宋末年的一位杰出的数学家、教育家.杨辉三角是杨辉的一项重要研究成果,它的许多性质与组合数的性质有关,杨辉三角中蕴藏了许多规律,如图是一个5阶杨辉三角.若第n 行中从左到右第3个数与第5个数的比为3:5,则n 的值为.2.(2023·海南·三模)(多选)“杨辉三角”是二项式系数在三角形中的一种几何排列,在中国南宋数学家杨辉1261年所著的《详解九章算法》一书中就有出现,比欧洲发现早500年左右.如图所示,在“杨辉三角”中,除每行两边的数都是1外,其余每个数都是其“肩上”的两个数之和,例如第4行的6为第3行中两个3的和.则下列命题中正确的是()A .在“杨辉三角”第6行中,从左到右第6个数是15B .由“第n 行所有数之和为2n ”猜想:012C C C C 2n nn n n n ++++= C .222234510C C C C 164+++⋅⋅⋅+=D .存在k *∈N ,使得{}1C C k kn n +-为等差数列3.(23-24高二上·山东青岛·期末)(多选)我国南宋数学家杨辉1261年所著的《详解九章算法》一书中展示了二项式系数表,数学爱好者对杨辉三角做了广泛的研究.则下列结论正确的是()A .第6行、第7行、第8行的第7个数之和为第9行的第8个数B .123356781C C C C +++=C .第2020行的第1010个数最大D .第12行中从左到右第2个数与第3个数之比为2:111.(2023·安徽黄山·二模)如图给出的三角形数阵,图中虚线上的数1、3、6、10、L ,依次构成数列{}n a ,则1210111a a a +++= .2.(2024·河南新乡·三模)如图所示的“分数杨辉三角形”被我们称为莱布尼茨三角形,是将杨辉三角形中的C rn换成1(1)C r nn +得到的,根据莱布尼茨三角形,下列结论正确的是()A .11111C C (1)C r r r n n n n n n +++=-B .11111C C (1)C r r r n n n n n n +-+=-C .11111(1)C (1)C C r r r n n n n n n +++=++D .11111(1)C (1)C C r r n n r n n n n +-+=++3.(2023·黑龙江哈尔滨·模拟预测)(多选)“杨辉三角”是二项式系数在三角形中的一种几何排列,在中国南宋数学家杨辉1261年所著的《详解九章算法》一书中就有出现.如图所示,在“杨辉三角”中,除每行两边的数都是1外,其余每个数都是其“肩上”的两个数之和,例如第4行的6为第3行中两个3的和.则下列命题中正确的是()A .在第10行中第5个数最大B .22222348C C C C 84++++= C .第8行中第4个数与第5个数之比为4:5D .在杨辉三角中,第n 行的所有数字之和为12n -一、单选题1.(2024·山东菏泽·模拟预测)在42120x x ⎛⎫+ ⎪⎝⎭的展开式中,2x 的系数为()A .80B .240C .1600D .24002.(2024·山西太原·三模)()51x y +-的展开式中2xy 的系数为()A .-20B .20C .-30D .303.(2024·辽宁鞍山·模拟预测)已知212nx x ⎛⎫+ ⎪⎝⎭的展开式中第3项的二项式系数等于36,则该展开式中的常数项为()A .212B .6316C .2116D .9324.(2024·陕西·模拟预测)若()201221nn n x a a x a x a x +=++++ 的展开式中的各项系数和为243,则122222n na a a +++= ()A .32B .31C .16D .15二、多选题5.(2024·吉林·模拟预测)在61x ⎛- ⎝的展开式中,下列说法正确的是()A .各二项式系数的和为64B .各项系数的绝对值的和为729C .有理项有3项D .常数项是第4项6.(23-24高二下·广东深圳·期中)若8280128(1)(1)(1)x a a x a x a x =+-+-++-L ,其中0128,,,,a a a a 为实数,则()A .01a =B .656a =C .1357128a a a a +++=D .2468127a a a a +++=三、填空题7.(2024·湖北襄阳·模拟预测)81x ⎫⎪⎭的展开式中4x -的系数为.8.(2024·浙江嘉兴·模拟预测)若52345012345(1)x a a x a x a x a x a x -=+++++,则2a =.9.(2024·广东佛山·模拟预测)8的展开式中常数项是.(用数字作答)10.(2024·福建南平·模拟预测)在()6122x x x ⎛⎫+- ⎪⎝⎭的展开式中,3x 的系数为.一、单选题1.(2024·山东·二模)811x y ⎛⎫+- ⎪⎝⎭展开式中22x y -的系数为()A .840-B .420-C .420D .8402.(2024·湖北·模拟预测)若1nx ⎛⎫ ⎪⎝⎭的二项展开式中,当且仅当第5项是二项式系数最大的项,则其展开式中51x 的系数为()A .8B .28C .70D .2523.(2024·河北邢台·二模)已知在n⎫⎪⎭的二项展开式中,第6项为常数项,若在展开式中任取3项,其中有理项的个数为ξ,则()E ξ=()A .811B .1211C .911D .8554.(2024·江西鹰潭·二模)第14届国际数学教育大会在上海华东师范大学举行,如图是本次大会的会标,会标中“ICME-14”的下方展示的是八卦中的四卦3、7、4、4,这是中国古代八进制计数符号,换算成现代十进制是3210387848482020⨯+⨯+⨯+⨯=,正是会议计划召开的年份,那么八进制数87777⋅⋅⋅ 个换算成十进制数,则换算后这个数的末位数字是()A .1B .3C .5D .7二、多选题5.(2024·江苏·模拟预测)若()10223200123202x x a a x a x a x a x +-=+++++ ,则()A .01024a =B .11a =C .1910a =D .13519512a a a a ++++=- 6.(2024·河北·二模)已知()423401234m x a a x a x a x a x +=++++,()()423450123451x m x b b x b x b x b x b x -+=+++++,其中m ∈R ,0m ≠.若223a b =,则()A .2m =B .0123481++++=a a a a a C .1234516b b b b b ++++=-D .12345234580b b b b b ++++=7.(2024·山西·三模)已知函数()()122120121241f x x a a x a x a x =-=+++⋅⋅⋅+,则()A .333124C a =⨯B .()f x 展开式中,二项式系数的最大值为612C C .12123123a a a a +++⋅⋅⋅+=D .()5f 的个位数字是1三、填空题8.(2024·山西朔州·一模)5y ⎫⎪⎭的展开式中y 的系数为.9.(2024·河北·模拟预测)已知()2311n nx x x x +⎛⎫-++ ⎪⎝⎭的展开式中各项系数和为8,则展开式中常数项为.10.(2024·江西景德镇·三模)若关于x ,y 的三项式()221cos sin nx y θθ++的展开式中各项系数之和为64,则n =;其中xy 项系数的最大值为.1.(2024·北京·高考真题)在(4x 的展开式中,3x 的系数为()A .6B .6-C .12D .12-2.(2024·上海·高考真题)()61x -展开式中4x 的系数为.3.(2024·全国·高考真题)1013x ⎛⎫+ ⎪⎝⎭的展开式中,各项系数中的最大值为.4.(2024·天津·高考真题)在63333x x⎛⎫+ ⎪⎝⎭的展开式中,常数项为.5.(2023·天津·高考真题)在6312x x ⎛⎫- ⎪⎝⎭的展开式中,2x 的系数为.6.(2022·北京·高考真题)若443243210(21)x a x a x a x a x a -=++++,则024a a a ++=()A .40B .41C .40-D .41-7.(2022·浙江·高考真题)已知多项式42345012345(2)(1)x x a a x a x a x a x a x +-=+++++,则2a =,12345a a a a a ++++=.8.(2022·全国·高考真题)81()y x y x ⎛⎫-+ ⎪⎝⎭的展开式中26x y 的系数为(用数字作答).9.(2022·天津·高考真题)在523x ⎫+⎪⎭的展开式中,常数项是.10.(2021·北京·高考真题)在341()x x-的展开式中,常数项为.11.(2021·天津·高考真题)在6312x x ⎛⎫+ ⎪⎝⎭的展开式中,6x 的系数是.12.(2021·浙江·高考真题)已知多项式344321234(1)(1)x x x a x a x a x a -++=++++,则1a =,234a a a ++=.13.(2020·天津·高考真题)在522x x ⎛⎫+ ⎪⎝⎭的展开式中,2x 的系数是.14.(2020·全国·高考真题)25()()x x y xy ++的展开式中x 3y 3的系数为()A .5B .10C .15D .2015.(2020·北京·高考真题)在52)-的展开式中,2x的系数为().A .5-B .5C .10-D .1016.(2020·浙江·高考真题)设52345123456(12)x a a x a x a x a x a x +=+++++,则5a =;123a a a ++=.17.(2020·全国·高考真题)262()x x+的展开式中常数项是(用数字作答).。
2021年高考历史10年真题3年模拟题练习:考点31 第一次工业革命(解析版)
考点31 第一次工业革命【十年真题】1.(2019·新课标全国Ⅰ卷高考·34)工业革命前,英国矿井里使用蒸汽唧筒抽水。
1765年,修理过唧筒的瓦特发明了一种单动式蒸汽机,后在工厂主的合作和资助下,终于改进制成“万能蒸汽机”,并广泛使用到工业领域。
该过程表明,第一次工业革命期间生产领域的主要发明创造()A.源自于劳动实践 B.依赖于科学理论的突破C.取决于资金保障 D.得益于各阶层广泛参与【答案】A【解析】材料“英国矿井里使用蒸汽唧筒抽水。
1765年,修理过唧筒的瓦特发明了一种单动式蒸汽机”说明发明创造源自于劳动实践,故选A项;材料“修理过唧筒的瓦特发明了一种单动式蒸汽机”说明来源于劳动实践而不是科学理论,排除B项;材料“后在工厂主的合作和资助下,终于改进制成‘万能蒸汽机’”说明资金不是决定原因,排除C项;材料中瓦特和工厂主并不能说明各阶级广泛参与,排除 D项。
2.(2019.4·浙江高考·20)阅读下列示意图表,结合所学判断,对此解读正确的是()A.生铁产量的增加与蒸汽机的广泛应用密不可分B.生铁产量的不断增加催生了大工厂制度C.电力的广泛使用推动了生铁产量的增加D.生铁产量的变化改变了英国产业结构和世界市场格局【答案】A【解析】根据图表信息,1788年英国生铁产量不断增加,结合所学,1785年蒸汽机在工厂开始使用,极大推动了生产力的进步,故选A项;第一次工业革命在组织形式上,产生了工厂制度,排除B项;19世纪七十年代,第二次工业革命电力广泛使用,排除C项;图表信息不能表明生铁产量增加对英国产业结构和世界市场格局的影响,排除D项。
2.(2018·新课标全国Ⅰ卷高考·34)传统观点认为,英国成为工业革命发源地,是因为英国最早具备了技术、市场等经济条件;后来有研究者认为,其主要原因是英国建立了君主立宪制度;又有学者提出,煤铁资源丰富、易于开采等自然条件是其重要因素。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章-变态心理学与健康心理学知识 近年考点分布与真题练习 第一节-变态心理学概述: 三级:人的心理活动、变态心理学的研究对象(多次考到)、变态心理学和精神病学的区别、精神分析对心理异常现象的解释(两个命题、五个推论、对异常现象的解释,三级二级均多次考到) 二级:精神病性的概念、精神分析对心理异常现象的解释(两个命题、五个推论、对异常现象的解释,三级二级均多次考到)、人本主意对心理异常现象的解释(存在焦虑,二级多次考到)
(2012.5三级)47、关于人的心理活动,下列陈述中正确的是( )。 (A)有正常和异常心理活动两个方面 (B)心理健康水平不高就属于心理异常 (C)精神障碍者的心理活动是完全异常的 (D)正常和异常心理活动之间无法转换 A,P289:人的心理活动存在正常心理活动和异常心理活动,由此形成了心理正常的群体和心理异常的群体。
(2010.5三级)32、变态心理学与精神病学共同的研究对象是( )。 (A)心理与行为的联系 (B)心理与行为的异常 (C)各种不良行为模式 (D)各种脑器质性病变 B,p289:变态心理学是一门以心理与行为异常表现为研究对象的心理学分支学科。与精神病学对象相同,但两门学科各自的侧重点不同。
(2010.5三级)120、变态心理学的研究对象包括( )。(多选) (A)变态心理的定义 (B)变态心理的种类 (C)异常心理的特点 (D)异常心理的转归 ABC,p289,多次考到的考点,要引起重视。选项D是精神医学的研究对象。
(2011.11二级)47、根据ICD-10,并非由焦虑和抑郁引起的严重而持久的社会性退缩属于( )。 (A)精神病性症状 (B)焦虑发作 (C)神经症性症状 (D)精神迟滞 A,p289,精神病性用于描述存在:幻觉;妄想;显著的兴奋和活动过多;并非由于抑郁或焦虑引起的严重而持久的社会性退缩;显著的精神运动性迟滞;紧张症性行为。
(2010.11三级)50、变态心理学研究的侧重点是心理异常的( )。 (A)性质 (B)治疗 (C)诊断 (D)预防 A,p290变态心理学是心理学的分支学科,侧重研究和说明心理异常的基本性质与特点,研究个体心理差异以及生存环境对心理异常发生、发展影响。精神病学作为医学的分支,着重异常心理的诊断、治疗、转归(指病情的转移和发展的意思)和预后以及精神障碍的预防与康复。
(2011.5三级) 48、经典精神分析认为,人类的生物本能是心理活动的( )。 (A)过程 (B)潜意识 (C)动力 (D)前意识 C,P291,考点:弗洛伊德的五个判断:1.力必多;2.三个发展期:口欲期、肛欲期、生殖器期;3.心理结构游潜意识、前意识和意识构成;与此对应的人格则由本我、自我和超我构成;4.本我遵循快乐原则,自我遵循现实原则,超我遵循道德原则;5.防御机制
(2010.11三级)51、精神分析理论认为,心理健康的充分和必要条件是( )。 (A)力比多发育良好 (B)合理地解释各种本能的欲望 (C)完善的防御机制 (D)合理度过性心理发展各阶段 D,p291:合理地度过“性心理”发展的每个阶段,是未来心理健康的充分和必要条件。精神分析理论对心理异常现象的解释:1.“固着”:“性心理发展阶段”受挫;2.焦虑:“本我”和“超我”之间的冲突矛盾引起焦虑;3.压抑:压抑的痛苦在潜意识中变相表达。
(2009.11二级)53、弗洛伊德认为,神经症和精神病的重要起因是( ) (A)防御机制 (B)动机冲突 (C)性的冲突 (D)克制能力 C,P291,精神分析理论解释异常心理现象的两个基本命题:1.心理过程主要是潜意识的;2.性的冲动是神经症和精神并的重要起因。
(2010.11二级)50、马斯洛认为,心理异常最基本的表现是( )。 (A)存在焦虑 (B)潜能受阻 (C)责任冲突 (D)自由选择 A,P292,马斯洛认为心理异常最基本的表现是“存在焦虑”。
(2011.11二级)114、马斯洛认为,心理异常的原因是( )的冲突。(多选) (A)存在 (B)兴奋 (C)责任 (D)抑制 AC,P292,马斯洛认为心理异常最基本的表现是“存在焦虑”,这种“存在焦虑”就是“存在”和“责任”的冲突。
(2010.11二级)51、区分心理正常与异常的医学标准把心理问题视为( )。 (A)常态分布 (B)行为的反映 (C)内省经验 (D)疾病的症状 D,P293,医学标准将精神障碍的心理或行为表现视为疾病的症状。
第二节-心理正常与心理异常: 三级:正常的心理活动的功能、心理正常与心理异常的关系(相互转化)、各类标准化的区分(二级三级多次考到,很重要,二级医学标准、内省经验标准和社会适应标准都出过考题,三级出过社会适应标准的考题。)、心理学的区分原则(三条原则是重点,二级三级必考的考点) 二级:各类标准化的区分(二级三级多次考到,很重要,二级医学标准、内省经验标准和社会适应标准都出过考题,三级出过社会适应标准的考题。)、心理学的区分原则(三条原则是重点,二级三级必考的考点)
(2009.11三级)104、正常心理活动能保证我们( )。(多选) (A)顺利适应环境 (B)维持生理机能 (C)进行人际交往 (D)认识客观世界 ACD,p293正常心理活动的功能包括:1.顺利地适应环境,健康地生存发展;2.正常地进行人际交往;3.正常地反映、认识客观世界。 (2012.5三级)49、判断正常心理与异常心理的心理学原则不包括( )。 (A)主客观世界统一原则 (B)心理活动的内在协调性原则 (C)个人需求与社会需求一致性原则 (D)人格的相对稳定性原则 C,P294:区分正常异常心理的三原则:主观世界与客观世界的统一性原则;心理活动的内在协调性原则;人格的相对稳定性原则
(2008.11三级)49、将心理异常理解为对社会准则的破坏,这是( )的观点。 (A)认知心理学 (B)统计学 (C)文化人类学 (D)社会学
D,P294:正常人的行为符合社会的准则,能根据社
会要求和道德规范行事。
(2010.11三级)100、郭念峰认为,心理学确定心理正常和异常的原则包括( )。(多选) (A)主观和客观统一性 (B)心理活动灵活性 (C)人格的相对稳定性 (D)心理活动平衡性 AC,P294,郭念峰提出的病与非病三原则: 1.主客观世界统一性原则; 2.心理活动的内在协调性原则; 3.人格的相对稳定性原则。 这个非常重要,务必要记住,在诊断考题中可以作为鉴别诊断的主要依据。
(2011.11二级)37、区分正常与异常心理的内省经验标准的缺陷是( )。 (A)受到文化制约 (B)客观性 (C)操作过于复杂 (D)主观性 D,P294 内省经验标准判断具有很大的主观性,不同的观察者有各自的经验,所以评定行为的标准也就各不相同。
(2010.5二级)106、根据区分心理活动正常与异常的社会适应标准,正常人的行为一般应该( )。(多选) (A)符合社会准则 (B)能按照社会认可的方式行事 (C)遵守道德规范 (D)能完成社会要求的各种活动 AB,P294,在社会适应标准下,正常人的行为符合社会的准则,能根据社会要求和道德规范行事,这时,我们说他的行为是一种社会适应性行为。
(2009.11二级)73、区分心理正常与异常的心理学原则中,人格相对稳定性原则认为( )。 (A)无明显原因的人格改变提示异常 (B)心理过程通过人格表现出来 (C)人格在各种条件下都应是稳定的 (D)人格是各种心理过程的总和 A,P295,如果在没有明显外部原因的情况下,一个人的人格相对稳定性出现问题,我们也要怀疑这个人的心理活动出现了异常。
第三节-常见心理异常的症状: 各类症状的分类、定义、区别。
(2011.5三级)49、病理性错觉的特点是( )。 (A)能够进行自我校正 (B)属于感知综合障碍 (C)不能接受现实检验 (D)属于思维形式障碍 C,p296正常人的错觉经现实验证后,可以加以纠正,精神疾病患者的错觉不能接受现实检验。 (2009.5三级)54、精神疾病患者错觉的特点是( )。 (A)能够进行自我校正 (B)感知综合障碍 (C)不能接受现实检验 (D)感觉功能障碍 C,P296,错觉属于知觉障碍,病理性错觉的特点是不能接受现实检验。
(2010.11三级)52、人在抑郁状态下出现的病理性感觉阈限增高在临床上的表现是( )。 (A)感觉过敏 (B)感觉减退 (C)感觉适应 (D)感觉不适 B,p296,感觉阈限增高就是说对外界刺激的感受迟钝(能引起感觉的刺激强度要比以往增强)。选项C感觉适应也是一种感觉阈限增高,但它属于正常人的反应。
52、由强烈的精神刺激引发的幻觉是( )。 (A)真性幻觉 (B)心因性幻觉 (C)假性幻觉 (D)功能性幻觉 B,P297,心因性幻觉是指由强烈的精神刺激引发的幻觉,幻觉内容与精神刺激的因素有密切的联系。
(2011.11二级)48、经历强烈地震后出现的幻觉是( )。 (A)真性幻觉 (B)心因性经常 (C)假性幻觉 (D)功能性幻觉 B,P297,心因性幻觉指由强烈的精神刺激引发的幻觉,幻觉的内容与精神刺激的因素有密切的联系。此幻觉仅见于应激相关精神障碍、癔症等。
(2008.11三级)50、无对象性的知觉是( )。 (A)幻觉 (B)错觉 (C)妄想 (D)谵妄
