习题讲解2hcy
结构化学第四章习题讲解

《结构化学》第四萃习题4001厶和人不是独立的对称元素• I大1为心___ ,/6= ________4002判断:既不存在G轴.又不存在6时,久轴必不存在。
--------------------- ()4003判断:在任何情况下,S^E。
------------------------- ()4004判断:分子的对称元素仅7种,即o , i及轴次为1. 2. 3, 4, 6的旋转轴和反轴。
4005下面说法正确的是:------------------- ()(A)分子中各类对称元素的完全集合构成分子的对称群(B)同一种分子必然同属于一个点群.不同种分子必然属于不同的点群(C)分子中有&轴.则此分子必然同时存在G轴和6面(D)tfirfliod —定也是镜而64006下面说法正确的是:------------------- ()(A)如构成分子的各类原子均是成双出现的,则此分子必有对称中心(B)分子中若有C,又有i,则必有o(C)凡是平面型分子必然属于C,群(D)在任何情况下,= E4008对称元素G与6组合•得到 ___________________ : C”次轴与垂直它的G组合,得到.4009如果图形中有对称元素S6,那么该图形中必然包含:(A) a. 6 (B)C3,Qh (C)G,i (D)Cj i4010判断:因为映轴是旋转轴与垂直于轴的面组合所得到的对称元素.所以点群分子中必有对称元素6 和Cno ----------------------------- ()4011给出下列点群所具有的全部对称元素:(l)C2h (2) C JV⑶⑺⑷0⑸C引4012假定CuCl卩原來属于门点群,四个C1原子的编号如下图所示。
十出现下面的变化时•点群将如何变化(写出分子点群)。
(1)Cu-Cl(l)键长缩短(2)Cu-Cl(l)和Cu—C1⑵缩短同样长度(3)Cu-Cl(l)和Cu-Cl(2)缩短不同长度(4)0(1)和Cl(2)两原子沿这两原子(5)C1 (1)和CK2)沿其连线逆向移动相同距离.0(3)和Cl(4)亦沿其连线如上同样距离相向移动ci2--Cu-CL (Ch和Cb在纸面以上,X I C12和CX在纸面以下)4013d'(d._ 如.d 2-.2)sp4)杂化的几何构型属于 _________________ 点群°4014已知络合物MAaB:的中心原子M是dtp]杂化.该分子有多少种界构体?这些界构体备属什么点群?4015有一个AB.分子,实验测得其偶极矩为零且有一个三重轴,则此分子所属点群是4016有两个分子,NDH B和CHF"它们都为非极性,且为反磁性,则N3B3H6几何构型 __________________ 点群__________ o C1H4F2几何构型________ ,点群__________ 。
(NEW)克鲁格曼《宏观经济学》(第2版)课后习题详解

答:税后平均个人收入的增长率为:(33705-6517)/6517=4.17。
学费、住宿费以及生活费总数的增长率为:(135892038)/2038=5.67。
由此可知,学费的增长率大于税后平均收入的增长率,学费的上升使得 学生支付大学学费更困难了。
11每年5月,《经济学家》杂志会刊登巨无霸汉堡包在不同国家的价格 以及汇率数据。下表列出了2003年和2007年的部分数据。请利用这些信 息回答下面的问题。
全景综览第23章宏观经济学循迹第24章失业和通货膨胀第11部分长期经济增长第25章长期经济增长第26章储蓄投资和金融系统第12部分短期经济第27章收入和支出第27章附录乘数的代数推导第28章总供给和总需求第13部分稳定政策第29章财政政策第29章附录税收与乘数第30章货币银行业和美国联邦储备体系第31章货币政策第32章通货膨胀通货膨胀减缓和通货紧缩第14部分事件和思想第33章宏观经济学
b.这个问题属于宏观经济学的研究范围。因为它考虑了消费者的总支 出与经济衰退之间的关系。
c.这个问题属于微观经济学的研究范围。它研究了单一市场上价格的 影响因素。
湘潭大学出版社计量经济学课后习题讲解

第二章2.4 以下是某城市10个市场苹果需求(Y )和价格(X )的数据: Y 99 91 70 79 60 55 70 101 81 67X 22 24 23 26 27 24 25 2322 26 (1)计算22, , yx xy ∑∑∑。
(2)假设12Y X u ββ=++,计算系数的OLS 估计量12ˆˆ,ββ。
(3)做出散点图和样本回归线(利用统计软件)。
(4)估计苹果在本均值点(,)X Y 的需求弹性(Y X Y X Y X X Y∆∆∆÷=⋅∆)。
答:(1)(2224232627242523+22+26)1024.2X =+++++++= (999170796055701018167)/1077.3Y =+++++++++=22y ()470.89+187.69+53.29+2.89+299.29+497.29+53.29+561.69+13. 69+106.09=2246.1Y Y =-=∑∑22() 4.840.04 1.44 3.247.840.040.64 1.44 4.84 3.2427.6x X X =-=+++++++++=∑∑ ()()47.74 2.748.76 3.0648.44 4.46 5.8428.448.1418.54143.6xy X X Y Y =--=--++-+----=-∑∑(2)22143.6ˆ== 5.20327.6i i i x y x β-=-∑∑ 12ˆˆ=77.3 6.3824.2=203.2126Y X ββ=-- (3)散点图和样本回归线如下图所示:50607080901001102122232425262728X Y(4)224.25.203 1.6377.3Y X Y X X Y X X Y Y β∆∆∆÷=⋅=-⨯=-⨯=-∆ 2.5 DATA1-1给出了中国2011年各省市GDP (Y )和投资(X )的数据。
物理化学核心教程第二版(沈文霞)课后习题答案详细讲解

物理化学核心教程第二版(沈文霞)课后习题答案详细讲解....课后习题答案第一章气体一.基本要求1.了解低压下气体的几个经验定律;2.掌握理想气体的微观模型,能熟练使用理想气体的状态方程;3.掌握理想气体混合物组成的几种表示方法,注意Dalton分压定律和Amagat分体积定律的使用前提;4.了解真实气体pVm图的一般形状,了解临界状态的特点及超临界流体的应用;5.了解vanderWaal气体方程中两个修正项的意义,并能作简单计算。
二.把握学习要点的建议本章是为今后用到气体时作铺垫的,几个经验定律在先行课中已有介绍,这里仅是复习一下而已。
重要的是要理解理想气体的微观模型,掌握理想气体的状态方程。
因为了解了理想气体的微观模型,就可以知道在什么情况下,可以把实际气体作为理想气体处理而不致带来太大的误差。
通过例题和习题,能熟练地使用理想气体的状态方程,掌握p,V,T和物质的量n几个物理量之间的运算。
物理量的运算既要进行数字运算,也要进行单位运算,一开始就要规范解题方法,为今后能准确、规范地解物理化学习题打下基础。
掌握Dalton分压定律和Amagat分体积定律的使用前提,以免今后在不符合这种前提下使用而导致计算错误。
在教师使用与“物理化学核心教程”配套的多媒体讲课软件讲课时,要认真听讲,注意在PowerPoint动画中真实气体的pVm图,掌握实际气体在什么条件下才能液化,临界点是什么含义等,为以后学习相平衡打下基础。
三.思考题参考答案1.如何使一个尚未破裂而被打瘪的乒乓球恢复原状?采用了什么原理?答:将打瘪的乒乓球浸泡在热水中,使球的壁变软,球中空气受热膨胀,可使其恢复球状。
采用的是气体热胀冷缩的原理。
专注专业....2.在两个密封、绝热、体积相等的容器中,装有压力相等的某种理想气体。
试问,这两容器中气体的温度是否相等?答:不一定相等。
根据理想气体状态方程,若物质的量相同,则温度才会相等。
3.两个容积相同的玻璃球内充满氮气,两球中间用一根玻管相通,管中间有一汞滴将两边的气体分开。
程稼夫电磁学第二版第二章习题解析
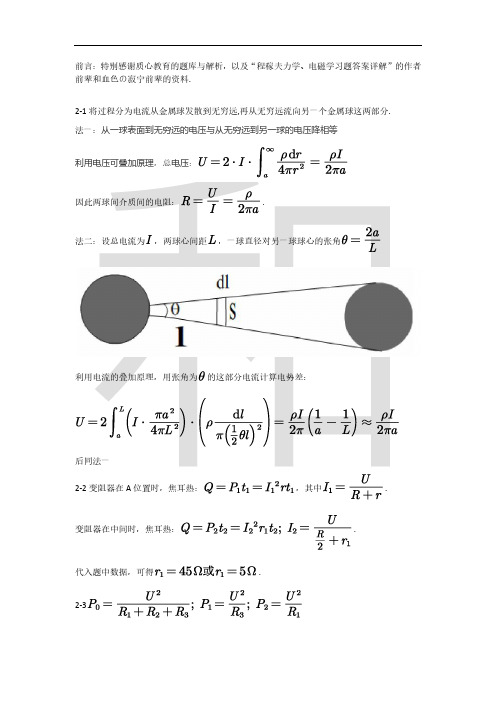
前言:特别感谢质心教育的题库与解析,以及“程稼夫力学、电磁学习题答案详解”的作者前辈和血色の寂宁前辈的资料.2-2变阻器在A位置时,焦耳热:,其中.变阻器在中间时,焦耳热:.代入题中数据,可得.2-32-4(1)即,在图中作出该直线,交伏安特性曲线于.两端电压.(2)电源功率之比就等于干路电流之比,即总电阻之反比,设总电阻分别为,则.2-7未烧断前总电阻,烧断后,故干路电流之比为22AB2-10注意电阻温度系数的基准是0℃,得.负载时,负载时,联立解得:.2-11题设是默认加热间断时间相等的,设为.即110V为A、B串联时的工作电压的等差中项作伏安特性曲线关于直线的对称图像,分别交另一曲线于和.得.2-15(1)电容器极板带电量,极板间电流保持为电势差为0时,极板不带电,所以.(2)最大动能的电子到达上极板时动能全部转化为电势能所以,得.K断开时,R与R1串联,该支路总电压该支路与R2并联,为R2两端电压,又R2,R3串联,R3两端电压为可以列出:两式联立,代入数据可解得:.2-18(1)由基尔霍夫方程知:.(2)沿n个电源这一路计算:2-22注意看题,不要啥都不想直接Y-△变换了设从1向O流的电流为,从2向O流的电流为,则从O向3流的电流为则可由三点的电势得到:2-即2-将等效内阻,等效电源. 2-25设有x组电池组串联,每组内有y个电池并联.法一:电源最大输出功率,电池个数.要使电源达到最大输出功率,则必有内阻与负载相等:解得法二:回路内满足:到的是Y-△变换的Y型电路(b),设出电阻即可求解,然后用Y-△变换得到△型电路(a).2-27上式联立解得.2-28(i)由知122’1’回路为电路干路而无支路,该干路总电阻;1 2与1’2’间若有电阻,则应被导线短路.(ii)由知1 2与1’2’间确有电阻,设为;由于要求电路最简,不妨设12间仅有一个电阻;故此情况中两电阻并联:代入数据得:,带回各条件检查,满足.故电路图如下:所以安培表示数.2-30题意即5两端接电源.电压表示数是由其上电流决定的,所以可以把电压表全看成电阻,求其上电流比例.由分析,电路可简化为如下图:由节点方程可知流经并联两表中电压表的电流欧姆定律:得. 2-33由每个量程达到满偏时通过电流计的电流相同得:,干路电流为,而B,C间的电流为,即100kΩ电阻和电压表各分得干路电流的一半,可知电压表内阻也为100kΩ.在图(b)中,200kΩ电阻与电压表并联后的电阻为,电压表读数为A、B间所分的电压为.由本题推广,可以证明,电压表接入串联电路测得的数值与所测部分电阻成正比,此性质与电压表内阻无关.2-36首先说明,若测量过程中测得某两点间电阻为1Ω,由对称性及电阻串并联等效可以判断:特异电阻被短路,连接在另外两端点间.2-38等效电路图如下:其中,由电桥平衡条件,有,解得.2-39第一次实验,B端电压为40V,即电阻R分压40V,则左段电缆电阻为第二次实验,A端电压为40V,即电阻R分压40V,则右段电缆电阻为左右电缆的电阻之比为:由于电缆的电阻与长度成正比,可知左段电缆长度为由此得:2-41,解得,解得;对于上述两支路的交点A,列节点方程:;由欧姆定律,图中B点的电势为:.显然U1与U3所在支路的电流为0;由于电容所在支路电流为0,由节点方程,图中B与C之间的支路上电流为;对图中红圈内的部分列节点方程(以向下为正方向):.2-42设该平行板电容器极板面积为S,极板间距为d,漏电流为I.由平行板电容器的电容公式,得玻璃的电阻为.由高斯2-44首先明确,无论短接哪个电阻,总电阻一定变小将五个电阻分两类,一类是四周的4 个电阻臂,一类是中间的100Ω桥上电阻.短接桥上电阻,总电阻变为203Ω;短接一支电阻臂,以500Ω的为例:两个100Ω的并联后与200Ω的串联再与300Ω的并联.可以看出300Ω的在这里与其他所有电阻并联,而并联电路中的总电阻不超过最小的电阻,故让100Ω与其他电阻并联可以使变化最大.2-45等效电阻整理得,故或.2-46本题为无穷网络等效电阻题.先分析对称性:电路呈轴对称,可将图中各个处于对称轴上的中点断开,于是电路转化为:转化为:再将A,B两点左侧网络“翻折”至右侧:单电路:,即两导线间电压为零.2-51本题为无穷网络等效电阻题,解题关键在于网络的自相似性.记A点左侧无穷网络等效电阻为R1.分析电路可知:故只需求出R1.分析R1结构可知:除去三个电阻r后剩余部分仍为一无穷网络R1:2-52(1)本题中的三角形电阻网络具有高度对称性,可将分割n次后的电阻网络(设其两顶点之间的电阻为;图中未画出分割后电阻网络的全貌;最初的只有三条边的三角形当作分割了0次)等效为如下的Y形网络:其中每个电阻的大小均为则下一次分割所得的电阻网络可以等效为三个上图所示的网络相连接而成(每个电阻变为一半),如下图所示:其中每个电阻大小为.这是一个简单的电阻网络,我们可以依据串并联关系计算其两端点间的电阻:(2,解得.2-53本题为等效电容题.(a)图中三电容实为并联;(b)图为中心对称图形,由对称性可知中间的C0等价为断路:整个线路和原来的线路完全一样,线路结构没有改变,各线上电流、各点的电势均无改变.可见,由点2到点n−1这n−2个点是完全等价的.因此,上述n−2个点的电势必然完全相同,从而这些点之间的连线上都没有电流,在考虑本题所问时,这些连线可以全部撤去,于是可得.2-58(1)电阻网络E、G两点间电压可表示为从图中的二极管D的正向伏安曲线中可査得,电压UDI对应的电流I1为25.0mA,此电流就是流过电阻R及由E点流入电阻网络的电流,将数据代入上式得由对称性可得H、A、C、F电势相等,其等效电路如图13-13所示(除两只电阻为外,(2)当引线两端P、Q与电阻网络B、D两点相接时,等效电路仍如图所示,易得通过二极管DD的电流与二极管两端电压有关系代入数据得这是一条联系UD与ID的方程,但是UD与ID又必须满足二极管的伏安特性曲线,在图中绘出上式所述直线,它与曲线的交点的纵坐标即为通过二极管的电流ID,由图中读出由对称性,,,则.2-59本题为图像分析题,同时需要用到“负载功率最大时,路端电压等于电源电动势的一半”的结论(此处证明从略).图像显示电源可视为两个负载电流范围不同的电源``拼接''而成,分段讨论即可.电流小于0.26A时,电源电动势等于6.2V,故路端电压等于3.1V时(由(2)(3)C1电荷变化量C2电荷变化量故由a到b流过K的正电荷.2-62本题为含电容的电路分析题,只需分析始末状态和电量变化即可.通过K的电量即通过R的电量.闭合K前,两电容器不带电;闭合K并稳定后,两电容器靠近电键K的极板上均沿回路列出方程:联立解得代入数据.忽略接地信息的解法得到的答案与此一致,但无视了与大地间的电流和电位.。
同型半胱氨酸(HCY)检测试剂方法学比较

直接法优点
➢ 原理设计
• 胱硫醚循环酶法(简称间接法)的Hcy检测试剂在基本的 设计上存在着问题,其检验是靠测量Hcy转化为β-胱硫醚 时产生的胱硫醚,但是却不能够消除内生β-胱硫醚,而 恰恰有很多人,尤其是肾脏疾病患者的内生β-胱硫醚水 平非常高(可高达>300μmol/L,大部份< 20μmol/L)。 间接法的Hcy试剂受到了内生胱硫醚的明显干扰。它测的 是同型半胱氨酸(Hcy)与内源性胱硫醚的总和,因此被称 为是很好的检测胱硫醚的试剂而非检测Hcy的试剂。
Hcy自发形成的巯基内酯化合物,可以和反式视黄酸共同 引起血小板的凝集,与此同时,同型半胱氨酸巯基内酯还 可引起血栓素(TXB2)的形成。
同型半胱氨酸巯基内酯,与低密度脂蛋白形成复合体,随 后被巨噬细胞吞噬,形成泡沫细胞。促进血凝块的形成, 从而引起临床上常见的梗塞性疾病。
同型半胱氨酸(Hcy)简介
直接法优点
➢ 目前国际市场上,能够在生化分析仪器上使用的 Hcy试剂有两种,都是循环酶法。一种为直接法 (水解酶循环酶法),另一种为间接法(胱硫醚 循环酶法)。
➢ 水解酶循环酶法,该法特异性高、抗干扰力强、 适用于各种生化仪,该类产品被国际大公司(如 罗氏, 奥林帕斯等)广泛采用。
如何区分两种方法学的试剂
参考文献:同型半胱氨酸检测技术的研究进展及评价;谭功军等,实用预防医学, 2010,11(24):2334-2337
直接法测定Hcy原理
同型半胱氨酸在体内的主要代谢途径: 间接法(胱硫醚法)
数据来源:www.kegg.jp
直接法(水解酶法)
直接法测定Hcy原理
① ATP + L-methionine + H2O = phosphate + diphosphate + S-methyl-L-methionine ② S-methyl-L-methionine + L-homocysteine = L-methionine+S-adenosyl-L-homocysteine ③ S-adenosyl-L-homocysteine + H2O = L-homocysteine + adenosine ④ adenosine + H2O = inosine + NH3 ⑤ 2-oxoglutarate + NH3 + NADH+ H+= L-glutamate + H2、间接法检测准确性及线性范围存在问题 •间接法的试剂检测线性范围窄,对于高于50 μmol/L的样本 中报告出假阴性结果,往往无法给出正确的结果,试验很可 能只报告出30μmol/L或更低。
习题讲解2hcy

*
M 1
16 10 9 24 2 7 mod26 24 11 4 (detM ) 1 M * (mod26) 21 16 3 20 15 0 6 3 0 22 23 22 25 24 2 7 11 2 19 24 11 4 mod26 5 23 25 19 1 15 7 23 18 3 0 22 20 7 17
K C M
1
8 6 24 7 16 0 mod26 5 9 1 8 25 3
验证:取明文分组(n,n)
16 0 13 0 a K M (mod26) mod26 25 3 13 0 a
所对应的数字序列为(3,8,11,8,6,4,13,2,4) 将明文按照每9个字母进行分组,并转换成与之对应的 数字,加密过程如下:
明 w e a
密 D I
r
e
4
c r
y p t
E D
o g r a p h e r
I L I G E N C E
文 22 4 0 17 L I
2 17 24 15 19 14 6 17 0 15 7 4 17 N C 4 e
K C M 1
经验证,该密钥正确。
3-4 什么是Feistel密码结构,主要有什么好处?
Li-1
Ki
Ri-1
×
F
Li
Ri
其中: Li Ri 1
Ri Li 1 f Ri 1 , K i
好处:加解密完全相同,除了所使用的子密钥的顺序正好 相反;且每一轮都只是对一半的明文进行加密。
15 20 15 8 * 又 M 17 8 17 20
有机化学_第二版_徐寿昌_课后习题参考答案(全)

徐寿昌编《有机化学》第二版习题参考答案第二章烷烃1、用系统命名法命名下列化合物(1)2,3,3,4-四甲基戊烷(2)3-甲基-4-异丙基庚烷(3)3,3,-二甲基戊烷(4)2,6-二甲基-3,6-二乙基辛烷(5)2,5-二甲基庚烷(6)2-甲基-3-乙基己烷(7)2,2,4-三甲基戊烷(8)2-甲基-3-乙基庚烷2、试写出下列化合物的结构式(1) (CH3)3CC(CH2)2CH2CH3(2) (CH3)2CHCH(CH3)CH2CH2CH2CH3(3) (CH3)3CCH2CH(CH3)2(4) (CH3)2CHCH2C(CH3)(C2H5)CH2CH2CH3(5)(CH3)2CHCH(C2H5)CH2CH2CH3(6)CH3CH2CH(C2H5)2(7) (CH3)2CHCH(CH3)CH2CH3(8)CH3CH(CH3)CH2CH(C2H5)C(CH3)33、略4、下列各化合物的系统命名对吗?如有错,指出错在哪里?试正确命名之。
均有错,正确命名如下:(1)3-甲基戊烷(2)2,4-二甲基己烷(3)3-甲基十一烷(4)4-异丙基辛烷(5)4,4-二甲基辛烷(6)2,2,4-三甲基己烷5、(3)>(2)>(5)>(1) >(4)6、略7、用纽曼投影式写出1,2-二溴乙烷最稳定及最不稳定的构象,并写出该构象的名称。
H交叉式最稳定重叠式最不稳定8、构象异构(1),(3)构造异构(4),(5)等同)2),(6)9、分子量为72的烷烃是戊烷及其异构体(1) C(CH3)4(2) CH3CH2CH2CH2CH3 (3) CH3CH(CH3)CH2CH3(4) 同(1)10、分子量为86的烷烃是己烷及其异构体(1)(CH3)2CHCH(CH3)CH3(2) CH3CH2CH2CH2CH2CH3 , (CH3)3CCH2CH3 (3)CH3CH2CH(CH3)CH2CH3(4)CH3CH2CH2CH(CH3)214、(4)>(2)>(3)>(1)第三章 烯烃1、略2、(1)CH 2=CH — (2)CH 3CH=CH — (3)CH 2=CHCH 2— CH 2CH CH 3M eH H i-P rE t M en-P rM e M e E t i-P rn-P r (4)(5)(6)(7)3、(1)2-乙基-1-戊烯 (2) 反-3,4-二甲基-3-庚烯 (或(E)-3,4-二甲基-3-庚烯 (3) (E)-2,4-二甲基-3-氯-3-己烯 (4) (Z)-1-氟-2-氯-2-溴-1-碘乙烯(5) 反-5-甲基-2-庚烯 或 (E)-5-甲基-2-庚烯 (6) 反-3,4-二甲基-5-乙基-3-庚烯 (7) (E) -3-甲基-4-异丙基-3-庚烯 (8) 反-3,4-二甲基-3-辛烯 4、略 5、略 6、CH 3CH 2CHC H 2CH 3CH 3CH 2CCHC H 3CH 3OH BrCH 3CH 2CCHC H3CH 3Cl ClCH 3CH 2C CHC H3CH 3OH OHCH 3CH 2CHCHC H 3CH 3OHCH 3CH 2COCH3CH 3CHOCH 3CH 2CHCHC H 3CH 3Br(1)(2)(3)(4)(5)(6)(7)7、活性中间体分别为:CH 3CH 2+ CH 3CH +CH 3 (CH 3)3C + 稳定性: CH 3CH 2+ > CH 3CH +CH 3 > (CH 3)3C + 反应速度: 异丁烯 > 丙烯 > 乙烯8、略9、(1)CH 3CH 2CH=CH 2 (2)CH 3CH 2C(CH 3)=CHCH 3 (有顺、反两种) (3)CH 3CH=CHCH 2CH=C(CH 3)2 (有、反两种)用KMnO 4氧化的产物: (1) CH 3CH 2COOH+CO 2+H 2O (2)CH 3CH 2COCH 3+CH 3COOH (3) CH 3COOH+HOOCCH 2COOH+CH 3COCH 310、(1)HBr ,无过氧化物 (2)HBr ,有过氧化物 (3)①H 2SO 4 ,②H 2O (4)B 2H 6/NaOH-H 2O 2 (5)① Cl 2,500℃ ② Cl 2,AlCl 3(6)① NH 3,O 2 ② 聚合,引发剂 (7)① Cl 2,500℃,② Cl 2,H 2O ③ NaOH 11、烯烃的结构式为:(CH 3)2C=CHCH 3 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
c5
k
14
mod
26
c6 17
c7 4
c8
k
12
mod 26
c9 14
c10 13
c11
k
4
mod
26
c12 24
17 17 5
∵ k 21 18 21
2 2 19
∴代入得
c1 11
l
c2
13
mod
26
n
c3 18
s
c4 7
h
c5
3
mod
26
d
解: LHTEHLIO YSTCORSP EYISSTNM EOUTRSEC
1.
π = (4,1,6,2,7,3,8,5)
可求出 π-1 =(2,4,6,1,8,3,5,7)
2. (LHTEHLIO)
π-1
(HELLOTHI)
(YSTCORSP)
π-1
(SCRYPTOS)
(EYISSTNM)
π-1
(YSTEMISN)
由于密钥是3×3阶的矩阵,所以将将明文分成四组: (p, a, y), (m, o, r), (e, m, o), (n, e, y) 即:
(15,0,24), (12,14,17), (4,12,14), (13,4,24)
加密过程如下:
c1 15
c2
k
0
mod 26
c3 24
c4 12
(EOUTRSEC)
π-1
(OTSECURE)
∴明文为:HELLOTHISCRYPTOSYSTEMISNOTSECURE
2-12 如果给出了充分多的明文/密文对,Hill密码就经 不住已知明文攻击。如果实施一种选择明文攻击,甚 至更容易解开Hill密码,请描述这种攻击。
答:假定密码分析者知道加密分组长度n值,且有至 少N(N>n)个不同的明文/密文对,利用n个已知的明 文/密文分组对定义两个n×n方阵
解:明文长度为24,可能的加密分组长度n值有
n 2 3 4 68
N 12 8 6 4 3 N表示不同的明文/密文分组对,且n<N。所以加 密分组长度只能取2, 3或4
由于C = K ·M(mod 26),所以只要M-1存在,则加密
密钥K = C ·M-1,最后选用一个明文密文验证密钥的 正确性。
(1) n=2时,将明文,密文划分为12组
习题讲解
韩彩芸
2-3 试给出定义在Z26上的位移密码体制中的所 有对合密钥
位移密码体制中
加密变换E 解密变换D
E:Ek m D:Dk c
m kmod26 c c kmod26 m
mM, c C, k
kK
K
解:由题意对合密钥的定义知:
m kmod 26 c kmod 26且m c
∴ 2k mod 26 = 0
∴ k = 0 或 k = 13
2-4 用弗吉尼亚密码加密“we are cryptographer”, 密钥“DILLGENCE”
解:由密钥k= DILLGENCE可得分组长度n=9,密钥
所对应的数字序列为(3,8,11,8,6,4,13,2,4) 将明文按照每9个字母进行分组,并转换成与之对应的 数字,加密过程如下:
明 wea r e c r y p t o g r a p he r 文 22 4 0 17 4 2 17 24 15 19 14 6 17 0 15 7 4 17 密 DI L I GE NC ED I L I GENCE 钥 3 8 11 8 6 4 13 2 4 3 8 11 8 6 4 13 2 4 密 25 12 11 25 10 6 4 0 19 22 22 17 25 6 19 20 6 21 文 z m l z kg e a t ww r z g t u gv
2-5 用Hill密码加密消息“pay more money”, 设加密密钥矩阵是:
17 17 5 k 21 18 21
2 2 19
Hill密码加密变换:C = K M (mod26) 解密变换:M = K-1 C(mod26)
解: p a y m o r e m o n e y
15 0 24 12 14 17 4 12 14 13 4 246来自9K20 17
15
8
记明文矩阵 20
17
185为M
det(M)=(20×8-15×17)mod26=9 ∵ gcd(9,26) = 1
明文矩阵 行列式
∴ 9-1mod26存在,且9-1mod26=3
求乘法逆元
又
M
*
20 17
15* 8
8
17
15
20
求伴随矩阵
M
1
(detM
)1
M
* (mod26)
M (M1M 2M3 M n )
C (C1C2C3 Cn )
有矩阵方程C K M (mod26)
若提供的矩阵M可逆,则能计算出K = C ·M-1, 从而破译该密码体制。
若M关于模26不可逆,可通过其他明文/密文对 产生新的方阵,找到可逆明文矩阵M就可破译Hill密 码。
补充题:已知Hill密码明文密文对, 明文:your pin no is four one two six 密文:WGIFG JTMRL HHXTH WBXZP SBRB 试分析出加密密钥矩阵K
c6 11
l
c7 4
e
c8
22
mod
26
w
c9 12
m
c10 19
t
c11
17
mod
26
r
c12 22
w
因此密文为: lns hdl ewm trw
2-10 设π 为集合{1,2,3,4,5,6,7,8}上的置换,
π = (4,1,6,2,7,3,8,5) (1)求出逆置换π-1 (2)解密如下使用n=8置换密码加密的密文,密钥为(1)中 的π-1
① 利用一、二组明文密文对,构造矩阵方程:
22
6
8 5
K
24 14
20 17
记明文矩阵 24
14
1270为M
det(M)=(24×17-20×17)mod26=24
∵ gcd(24,26) ≠ 1 ∴ 24-1mod26不存在,矩阵M关于模26不可逆.
② 利用二、三组明文密文对,构造矩阵方程:
8 5
