缓和曲线的定义及公式推导
《缓和曲线测设》课件

该案例展示了缓和曲线测设在高速公路建 设中的重要性和实际应用,强调了精确测 设对道路安全和使用寿命的影响。
某铁路线缓和曲线测设案例
案例概述
某铁路线在改造过程中,需要对原有的缓和曲线进行测设,以确保列 车的安全运行。
测设难点
既有线路的线形和参数较为复杂,需考虑列车的行驶速度和安全性。
解决方案
采用轨道测量技术和数据分析方法,对既有缓和曲线进行精确测量和 分析。
切线支距法测设法
总结词
通过已知的起点、终点坐标和曲线半径,计算出曲线上各点的切线支距,并利用钢尺或光电测距仪进 行实地测设。
详细描述
切线支距法测设法是一种简单易行的缓和曲线测设法。首先根据起点、终点坐标和曲线半径,计算出 曲线上各点的切线支距。然后使用钢尺或光电测距仪,将切线支距在实地标定出来,并进行必要的调 整和修正,完成缓和曲线的测设。
缓和曲线能够使道路线形更加自然、 流畅,提高道路的美观性。
缓和曲线测设的基本原则
01
02
03
保证车辆行驶平稳
缓和曲线的设置应保证车 辆在过渡过程中行驶平稳 ,减小侧向位移和离心力 对车辆行驶的影响。
满足道路设计规范
缓和曲线的长度、曲率半 径、曲率等参数应满足道 路设计规范的要求。
考虑地形条件
在满足设计要求的前提下 ,应尽量利用地形条件, 减小工程量,降低工程造 价。
采用GPS定位技术和施工监测系统,对桥墩的位置和线形进行 实时监测和控制。
该案例展示了缓和曲线测设在桥梁工程建设中的重要性和实际 应用,强调了精确测设对桥梁安全和施工精度的影响。
THANKS FOR WATCHING
感谢您的观看
根据缓和曲线方程,计算曲线上各点 的坐标。
缓和曲线公式
用回旋线(放射螺旋型)作为缓和曲线。
回旋线是一种曲率随曲线长度成比例变化的曲线,不仅可以使线形更加美观,而且与驾驶员匀速转动方向盘由圆曲线驶入直线或者由直线驶入圆曲线的轨迹线相符合。
其基本公式为:rl=A2;其中:r—回旋线上某点曲率半径(m);l—回旋线上其点到原点的曲线长(m);A—回旋线参数;由于rl是长度的二次方,故令C=A2,A表征曲率变化的缓急程度,因此在缓和曲线上,r随l的变化而变化,在缓和曲线的终点处,l=L s,r=R,RL s=A2,即A=√(RL s);其中:R—回旋线所连接的圆曲线半径;L s—回旋线形的缓和曲线长度。
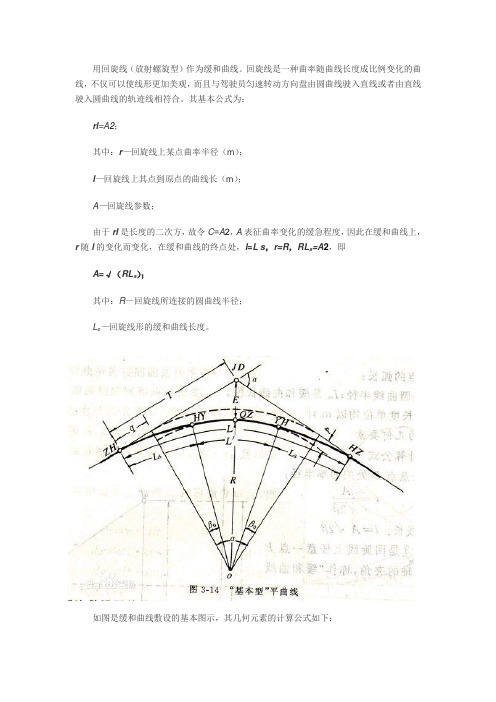
如图是缓和曲线敷设的基本图示,其几何元素的计算公式如下:q =L s/2-L s3/(240×R2) (m);p=L s2/(24R)-L s4/(2384×R3) (m);β=28.6479L s/R(。
);T=(R+p)tan(α/2)+q(m);L=(α-2β)πR/180+2Ls(m);E=(R+p)/cos(α/2) -R(m);J=2T-L(m);其中:α—路线转角(。
);β—圆曲线对应角度(。
);q—偏移值(m);p—原曲线与直线偏移值(m);T—切线长(m);E—外移值(m);J—里程差(m);[式中α为路线设计参数,R值对于设计道路可查相关规范][1-2]缓和曲线的作用:p(1)曲率连续变化,便于车辆遵循。
(2)离心加速度逐渐变化,旅客感觉舒适。
(3)超高横坡度及加宽逐渐变化,行车更加稳定。
(4)与圆曲线配合,增加线形美观。
缓和曲线计算公式

缓和曲线计算公式当前的位置】:工程测量→第十一章→ 第四节圆曲线加缓和曲线及其主点测设第四节圆曲线加缓和曲线及其主点测设§11—4 圆曲线加缓和曲线及其主点测设一、缓和曲线的概念二、缓和曲线方程三、缓和曲线常数四、圆曲线加缓和曲线的综合要素及主点测设一、缓和曲线的概念1、为什麽要加入缓和曲线?(1)在曲线上高速运行的列车会产生离心力,为克服离心力的影响,铁路在曲线部分采用外轨超高的办法,即把外轨抬高一定数值.使车辆向曲线内倾斜,以平衡离心力的作用,从而保证列车安全运行。
图11-10(a).(b)为采用外轨超高前、后的情况。
外轨超高和内轨加宽都是逐渐完成,这就需要在直线与圆曲线之间加设一段过渡曲线——缓和曲线.缓和曲线: 其曲率半径ρ 从∞逐渐变化到圆曲线的半径R 。
2、缓和曲线必要的前提条件(性质):在此曲线上任一点P 的曲率半径ρ与曲线的长度l成反比,如图11-12所示,以公式表示为:ρ ∝1l 或ρ. l = C (11-4)式中: C 为常数,称曲线半径变更率。
当l= l o时,ρ= R ,按(11-4)式,应有C = ρ.l= R .l o (11-5)符合这一前提条件的曲线为缓和曲线,常用的有辐射螺旋线及三次抛物线,我国采用辐射螺旋线。
3、加入缓和曲线后的铁路曲线示意图(见图11-J)二、缓和曲线方程1、加入缓和曲线后的切线坐标系坐标原点:以直缓(ZH)点或缓直(HZ)点为原点;X坐标轴:直缓(ZH)点或缓直(HZ)点到交点(JD)的切线方向;Y坐标轴:过直缓(ZH)点或缓直(HZ)点与切线垂直的方向。
其中:x、y 为P点的坐标;x o、y o为HY点的坐标;ρ 为P 点上曲线的曲率半径;R 为圆曲线的曲率半径l 为从ZH点到P 点的缓和曲线长;l o为从ZH点到HY点的缓和曲线总长;2、缓和曲线方程式:根据缓和曲线必要的前提条件推导出缓和曲线上任一点的坐标为实际应用时, 舍去高次项, 代入C=R*l o,采用下列公式:式中:l 为缓和曲线上任一点P 到直缓(ZH)点的曲线长;R 为圆曲线半径;l o为缓和曲线总长度。
《缓和曲线的测设》课件

某铁路线缓和曲线的测设
铁路线缓和曲线长度
根据铁路设计规范和曲线半径,确定缓和曲线的长度,以确保列 车行驶的平顺性和安全性。
铁路线缓和曲线要素
根据缓和曲线的长度,计算缓和曲线的要素,包括切线长、外距、 内距等,以确保测设的准确性。
铁路线缓和曲线测设方法
采用轨道测量仪、全站仪等测量设备,按照计算出的要素进行实地 测设,并确保精度满足规范要求。
缓和曲线应与道路线形相 协调,避免出现急转弯或 陡坡,以免影响行车安全 。
缓和曲线应设置合适的超 高和加宽,以保持车辆行 驶的稳定性。
保证曲线长度符合设计要求
01
在测设缓和曲线时,应严格按照设计图纸的要求,确保缓和曲 线的长度满足规范要求。
02
若实际地形条件限制,无法满足设计长度要求,应与设计单位
三次抛物线
三次抛物线也是一种常用的缓和曲 线,其特点是曲率随曲线长度逐渐 减小,直到与圆曲线曲率相等。
其他类型
除了回旋线和三次抛物线外,还有 多种类型的缓和曲线,如指数曲线 、双曲线等,可根据实际情况选择 使用。
缓和曲线的作用
01
02
03
改变方向
缓和曲线能够使车辆逐渐 改变行驶方向,从直线过 渡到圆曲线或从圆曲线过 渡到直线。
详细描述
弦线法是通过测量缓和曲线起点和终点的弦线长度,以及各控制点的弦线距离,计算出缓和曲线上各 点的坐标值。该方法操作简单,精度较低,适用于缓和曲线长度较短且精度要求不高的场合。
03
缓和曲线测设的注意事项
保证行车安全
缓和曲线长度应满足设计 要求,避免过短或过长, 以确保车辆在缓和曲线上 的行驶安全。
04
缓和曲线测设的实例分析
某高速公路缓和曲线的测设
缓和曲线计算公式

课间休息
音乐欣赏:
1、痴心绝对 2、给我新鲜
三、带有缓和曲线的圆曲线详细测设
1、切线支距法 (tangent off-set method)
要注意:点是位于缓和曲线上,还是位于圆曲线上。
位于缓和曲线
41.96m
EH
(R
p) sec
2
R 1.33m
(二)计算里程
ZH=K0+497.54;HY=K0+507.54;QZ=K0+518.52; HZ=K0+539.50;YH=K0+529.50
(三)主点测设
1.架仪JDi,后视JDi-1,量取TH,得ZH点;后视JDi+1, 量取TH,得HZ点;在分角线上量取EH,得QZ点。
b0
2 0
ls 3R
此外还有极坐标法、弦线支距法、长弦偏角 法。
概念及基本公式1概念为缓和行车方向的突变和离心力的突然产生与消失需要在直线超高为0与圆曲线超高为h之间插入一段曲率半径由无穷大逐渐变化至圆曲线半径的过渡曲线使超高由0变为h此曲线为缓和曲线
讲题:缓和曲线的测设
内容提要:
§8.3 缓和曲线的测设
一.概念及基本公式 二.主点的测设 三.带有缓和曲线的圆曲线详细测设
位于圆曲线
(1)当点位于缓和曲线上,有:
x y
l l5
40R
2l
2 s
l3 l7 6Rls 336R
3l
3 s
(2)当点位于圆曲线上,有:
x Rsin q y R(1 cos) p
缓和曲线计算公式

p=0.04m;q=5.00m;
0
ls 1800
2R
205153
x0
ls
ls3 40R2
10.00m
y0
ls 2 6R
0.17m
TH (R p)tg 2 q 21.12m
LH
R(
20
)
180
2ls
1、测设元素的计算
(1)内移距p 和切线增长q的计算:
p
l
2 s
24R
q ls
l
3 s
2 240R2
2、主点的测设
(1)里程的计算
ZH=JD-TH;HY=ZH+ls; QZ=ZH+LH/2;HZ=ZH+LH;YH=HZ-ls
(2)测设方法。(见例题)
例题:如图,设某公路的交点桩号为K0+518.66,右转 角αy=180018'36",圆曲线半径R=100m,缓和曲线长 ls=10m,试测设主点桩。(作为实习课内容)
2.分别在ZH、HZ点架仪,后视JDi方向,量取x0,再在 此方向垂直方向上量取y0,得HY和YH点。
课间休息
音乐欣赏:
1、痴心绝对 2、给我新鲜
三、带有缓和曲线的圆曲线详细测设
1、切线支距法 (tangent off-set method)
要注意:点是位于缓和曲线上,还是位于圆曲线上。
位于缓和曲线
讲题:缓和曲线的测设
内容提要:
§8.3 缓和曲线的测设
一.概念及基本公式 二.主点的测设 三.带有缓和曲线的圆曲线详细测设
3-3缓和曲线

α1
2
JD a
线时:
)
T1
a2
T2 = R tan
α2
2
D( ZY )
T1 A(
B(
JD b
)
T2
) YZ E(
T1 + T2 = R tan
α1
2
+ R tan
α1
2
R
a1
a2
O
R
R= tan
α1
T1 + T2 + tan
α2
2 2 计算出R后,按单圆曲线 计算
虚交单 曲线
四,直角坐标与缓和曲线常数
Y
O
R
距离
1 Ls 3 Tk = Ls + 3 126 R 2
ZH
Δh
d
Ch
HY
h
k
Tk—缓和曲线终点至Q点的 距离 β 1 2
= 3 Ls ( )
Q
h
X
Δ—缓和曲线上任意点的 偏角 β
h = 3
C h = X h sec h = Ls
缓和曲线起点,终点的切线 相交于Q点 3 Ls
90 R 2
Δh—缓和曲线总 偏角
O
α
R+p R+p
R
R=∞
q:设有缓和曲 线后圆曲线的 内移值 ZH
R+p R
Ls 2 p= 24 R
0
QZ HY
Ls Ls 3 q= 2 240 R 2
h
YH
JD
HZ
(三)缓和曲线常数
R= ∞
E0
四,直角坐标与缓和曲线常数
(三)缓和曲线常数
2 11 Ls 3 Td = Ls + 3 360 R 2 Td—缓和曲线起点至Q点的
平面设计-缓和曲线、平面线形组合设计

平面设计-缓和曲线、平面线形组合设计缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间,由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。
缓和曲线的主要特征是曲率均匀变化。
一、设置缓和曲线的目的和条件(一)设置缓和曲线的条件《公路工程技术标准》规定:直线与小于不设超高的圆曲线最小半径相衔接处,应设置缓和曲线(回旋线);四级公路的直线与小于不设超高的圆曲线最小半径相衔接处,可不设置缓和曲线(回旋线),用超高、加宽缓和段径相连接。
(二)设置缓和曲线的目的1.有利于驾驶员操纵方向盘2.消除离心力的突变,提高舒适性3.完成超高和加宽的过渡4.与圆曲线配合得当,增加线形美观二、缓和曲线的性质(一)汽车转弯时行驶的理论轨迹方程图2—4 汽车进入曲线行驶轨迹图假定汽车是等速行驶,驾驶员匀速转动方向盘,当方向盘转动角度为φ 时,前轮相应转动角度为φ,通过理论推导得出弧长和曲率半径的关系有:=式中:K为小于1的系数;ω—方向盘转动的角速度(rad /s);t —行驶时间(s); d —汽车前后轴轮距;-汽车匀速行驶的速度(m/s)。
鉴于、d 、K、ω均为常数,可令C= ,则有:= ;此为汽车车轮行驶的轨迹方程。
式中:—汽车自直线终点进入曲线经t 时间后行驶的弧长,m;ρ—汽车行驶经t 时间后行驶的弧长处相对应的曲率半径,m;C—常数(二)回旋线作为缓和曲线根据回旋线的数学定义:其曲率半径随曲线上某一点至该曲线起点之距离成反比。
即:ρ=A2式中A为曲率与曲线长度的比例常数;若令,通过对汽车行驶理论方程与回旋线基本方程的比较可知,它们的形式是相符的,因此《标准》规定缓和曲线采用回旋线。
回旋线参数A 的确定:R LS = A2 A=式中:R—圆曲线半径 m ;LS—缓和曲线长度m ;三、缓和曲线最小长度缓和曲线最小长度应满足:(1)使汽车平顺地由直线段过渡到到圆曲线段,并对离心力的增长有一定的限制;(2)驾驶员操纵方向盘所需的必要时间以利驾驶员顺适地操纵放向盘;(3)满足道路设置超高与加宽过渡的要求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 / 8
缓和曲线计算公式的推导
对于搞公路铁路工程的人来说,缓和曲线并不陌生,它是在直
线和圆曲线之间的一段过渡曲线,其目的是使曲线的曲率半径连续
变化,从而使车辆的向心加速度变化连续,降低旅客由车辆转弯引
起的不适感。缓和曲线类型有回旋线、三次抛物线、Bloss曲线、
正弦一波型、半波正弦型等曲线。而在我国回旋线被广泛采用,故
本文详细介绍回旋线作为缓和曲线的计算方法,顺便讲一点有趣的
历史。
一、回旋线的定义
回旋线(clothoid)又称为欧拉螺旋
线(Euler spiral)、羊角螺旋
(Cornu spirals),菲涅尔螺旋
(Fresnel spirals)、辐射螺旋线
(Radiation helix),它被定义为:
线上任意点的曲率半径与该点到坐标
原点的曲线长成反比的曲线。
二、为什么需要缓和曲线
回旋线最重要的性质—曲率随弧长线性变化
回旋线的曲率是随弧长线性变化的,这也是它能作为缓和曲线
的原因,下面将给出证明。
三、预备一些数学背景知识
1、任意曲线的弧长微分公式推导
2 / 8
如图所示,笛卡尔坐标系下,在曲
线上任取一段弧微元ds,当ds足够小
时,可认为弧线和弦线相等,则有:
ⅆ𝑠=√(ⅆ𝑥)2+(ⅆ𝑦
)
2
而ⅆ𝑦=𝑦
′
ⅆ𝑥,则有:
ⅆ𝑠=√(ⅆ𝑥)2+(𝑦′ⅆ𝑥
)
2
=√1+(𝑦′)2ⅆ𝑥
特别的,当曲线为参数方程形式时
𝑥=𝑓(𝑡)
𝑦=𝑔(𝑡)
ⅆ𝑠=√𝑓′2(𝑡)+𝑔′2(𝑡)ⅆ𝑡
2、任意曲线的曲率公式
曲线的曲率(curvature)是单位
切向量对于弧长的旋转速度,也就是
弧的切线偏转角与该弧长之比的绝对
值,通过微分来定义,曲率表明曲线
某一点附近的弯曲程度。其表达式
为:
𝑘=|ⅆ𝜃ⅆ𝑠|
式中:𝑘表示曲率,ⅆ𝜃表示曲线在该点处切线与𝑥轴夹角的变化
微元,也等于曲线在该点处的偏转角微元,ⅆ𝑠表示曲线的长度变化
3 / 8
微元,加绝对值是为了保证曲率是正值。
下面将给出曲率求解过程:
设曲线的方程为𝑦=𝑓(𝑥),且具有二阶导数,则曲线在点M处
的切线斜率为:
𝑦′=𝑡𝑎𝑛𝜃
则𝑦′′=ⅆ(𝑡𝑎𝑛𝜃)ⅆ𝜃ⅆ𝜃ⅆ𝑥=𝑠𝑒𝑐2𝜃ⅆ𝜃ⅆ𝑥
即ⅆ𝜃ⅆ𝑥=𝑦′′1+𝑡𝑎𝑛2𝜃=𝑦′′1+𝑦′2
又ⅆ𝑠=√1+(𝑦
′)2
ⅆ𝑥,故𝑦=𝑓(𝑥)在点M处的曲率为:
𝑘=|ⅆ𝜃ⅆ𝑠|
=
|𝑦′′1+𝑦′2ⅆ𝑥√1+𝑦′2ⅆ𝑥|
=|𝑦′′(1+𝑦′2)32|
这就是曲率方程的一般形式,特别地,当曲线为参数方程形式
时
𝑥=𝑓(𝑡)
𝑦=𝑔(𝑡)
𝑘=
|𝑓′(𝑡)𝑔′′(𝑡)−𝑔′(𝑡)𝑓′′(𝑡)(𝑓′2(𝑡)+𝑔′2(𝑡))32|
三、回旋线方程的推导
我们从回旋线的定义可以得到它的重要性质,即曲线上任意点
4 / 8
的曲率半径与该点到坐标原点的曲线长成反比。
即
𝑙∝
1
𝜌
式中:𝜌为曲线上一点的曲率半径;
𝑙为曲线上一点距坐标原点的曲线长
我们不妨设这个比例系数为𝐶
即
𝜌𝑙=𝐶
对于任意曲线我们可以列出以下微分方程:
ⅆ𝑙=𝜌⋅ⅆ𝛽 (1)
ⅆ𝑥=ⅆ𝑙⋅𝑐𝑜𝑠𝛽 (2)
ⅆ𝑦=ⅆ𝑙⋅𝑠𝑖𝑛𝛽 (3)
式中:ⅆ𝑙为曲线上任意一点附近的弧微分
ⅆ𝛽为曲线上任意一点的切向量偏转角的微分
𝛽为曲线上任意一点的切线与𝑥轴正方向的夹角
在这里,只要我们以𝜌𝑙=𝐶代入(1),就可以让回旋线独有的
5 / 8
性质与一般曲线的性质得到综合。
即
ⅆ𝑙=𝐶𝑙⋅ⅆ𝛽
𝑙 ⅆ𝑙=𝐶⋅ⅆ𝛽
在这里,只要我们对两边同时积分,就可以将ⅆ𝛽、ⅆ𝑙转化为
𝛽、𝑙,从而建立起𝛽、𝑙的直接关系,当把这个关系应用到(2)(3)
时,方程的数量将会减少,这才是我们的目的。
即
∫𝑙 ⅆ𝑙=∫𝐶⋅ⅆ𝛽
𝑙
2
2
=𝐶⋅𝛽
𝛽=
𝑙
2
2𝐶
在这里,我们对𝑠𝑖𝑛𝛽, 𝑐𝑜𝑠𝛽应用泰勒展开:
ⅆ𝑥=ⅆ𝑙⋅𝑐𝑜𝑠𝛽
=(1−𝛽22!+𝛽44!−𝛽66!+⋯)ⅆ𝑙
将𝛽=𝑙22𝐶代入上式得:
=(1−12(𝑙22𝐶)2+124(𝑙22𝐶)4−1720(𝑙22𝐶)6+⋯)ⅆ𝑙
=(1−𝑙48𝐶2+𝑙8384𝐶4−𝑙1246080𝐶6+⋯)ⅆ𝑙
同理,可得
ⅆ𝑦=ⅆ𝑙⋅𝑠𝑖𝑛𝛽
6 / 8
=(𝑙22𝐶2−𝑙648𝐶3+𝑙103840𝐶5−𝑙14645120𝐶7+⋯)ⅆ𝑙
对ⅆ𝑥,ⅆ𝑦的泰勒展开式两边同时进行积分得:
𝑥=∫ⅆ𝑥=∫(1−𝑙48𝐶2+𝑙8384𝐶4−𝑙1246080𝐶6+⋯)ⅆ𝑙
=𝑙−𝑙540𝐶2+𝑙93456𝐶4−𝑙13599040𝐶6+⋯
同理可得:
𝑦=∫ⅆ𝑦=∫(𝑙22𝐶−𝑙648𝐶2+𝑙103840𝐶4−𝑙14645120𝐶7+⋯)ⅆ𝑙
=𝑙36𝐶−𝑙7336𝐶2+𝑙1142240𝐶4−𝑙159676800𝐶7+⋯
这里有一个问题,不知各位发现没有?在(2)(3)式得出后,
为什么不直接对两边进行积分,而是先进行泰勒展开,使之成多项
式相加的形式,再进行积分,这样岂不是多此一举?不妨让我们直
接对(2)(3)式进行积分,看看会有什么结果,究竟哪一种更为简
单。
ⅆ𝑥=ⅆ𝑙⋅𝑐𝑜𝑠𝛽
对等号两边同时进行积分
∫ⅆ𝑥=∫ⅆ𝑙⋅𝑐𝑜𝑠𝛽
将将𝛽=𝑙22𝐶代入上式得:
𝑥=∫𝑐𝑜𝑠𝑙22𝐶ⅆ𝑙 (4)
用换元法进行积分,令𝑡=𝑙22𝐶,则
ⅆ𝑡=ⅆ(𝑙22𝐶)=𝑙𝐶ⅆ𝑙 (5)
将(5)代入(4)得:
7 / 8
𝑥=𝐶𝑙∫𝑐𝑜𝑠𝑡2ⅆ𝑡
同理,你也将得到
𝑦=𝐶𝑙∫𝑠𝑖𝑛𝑡2ⅆ𝑡
值得注意的是,积分式前面的系数𝐶𝑙恰好是曲率半径𝜌。计算到
这一步,我们遇到了困难,因为∫𝑐𝑜𝑠𝑡
2ⅆ𝑡,∫𝑠𝑖𝑛𝑡2
ⅆ𝑡的结果根本不
是初等函数,它们就是所谓的菲涅尔积分(Fresnel integral),这
也是回旋线被称为菲涅尔积分曲线的原因,事实上,菲涅尔积分的形
式才是回旋线真正严密的表达式。关于这个积分函数的解法,不是
本篇文章的主题,感兴趣的同学可以下来自己了解一下,我们这里
给出这个函数,菲涅尔积分函数有两种,分别定义为:
𝐶(𝑥)=∫𝑐𝑜𝑠𝑡2ⅆ𝑡𝑥0=∑(−1
)
𝑛
𝑥
4𝑛+1
2𝑛!(4𝑛+1
)
∞
0
𝑆(𝑥)=∫𝑠𝑖𝑛ⅆ𝑡𝑥0=∑(−1
)
𝑛
𝑥
4𝑛+3
(2𝑛+1)!(4𝑛+3)
∞
0
如图所示,𝐶(𝑥) (橘黄色), 𝑆(𝑥)(蓝色)都是奇函数,它们
105510
0.5
0.5
8 / 8
的函数值会收敛于±√𝜋8。这个函数的积分上限是一个变量,因此很
难求解。这也就是我们在(2)(3)式先进行泰勒展开,后积分的原
因,这样将巧妙地避开十分复杂的菲涅尔函数。
[文档可能无法思考全面,请浏览后下载,另外祝您生活愉快,工作顺利,万事如意!]
