国密SM9中R-ate双线性对快速计算
国密是什么

国密是什么
国密即国家密码局认定的国产密码算法,即商用密码。
国密主要有SM1,SM2,SM3,SM4。
密钥长度和分组长度均为128位。
1、SM1 为对称加密。
其加密强度与AES(高级加密标准,Advanced Encryption Standard)相当。
该算法不公开,调用该算法时,需要通过加密芯片的接口进行调用。
2、SM2为非对称加密,基于ECC。
该算法已公开。
由于该算法基于ECC,故其签名速度与秘钥生成速度都快于RSA。
ECC 256位(SM2采用的就是ECC 256位的一种)安全强度比RSA 2048位高,但运算速度快于RSA。
3、SM3为消息摘要。
可以用MD5作为对比理解。
该算法已公开。
校验结果为256位。
4、SM4为无线局域网标准的分组数据算法。
对称加密,密钥长度和分组长度均为128位。
由于SM1、SM4加解密的分组大小为128bit,故对消息进行加解密时,若消息长度过长,需要进行分组,要消息长度不足,则要进行填充。
国密应用
商用密码的应用领域十分广泛,主要用于对不涉及国家秘密内容但又具有敏感性的内部信息、行政事务信息、经济信息等进行加
密保护。
商用密码可用于企业门禁管理、企业内部的各类敏感信息的传输加密、存储加密,防止非法第三方获取信息内容;也可用于各种安全认证、网上银行、数字签名等。
例如:在门禁应用中,采用SM1算法进行身份鉴别和数据加密通讯,实现卡片合法性的验证,保证身份识别的真实性。
安全是关系国家、城市信息、行业用户、百姓利益的关键问题。
国标商密算法

国标商密算法
国标商密算法是指中国国家密码管理局制定的商用密码算法。
该算法主要用于保护商业机密和个人隐私信息的安全。
国标商密算法包括了多种密码算法,如SM1、SM2、SM3、SM4等。
- SM1是一种对称密码算法,用于数据的加密和解密,可以保护商业机密数据的安全传输。
- SM2是一种非对称密码算法,用于数字签名和密钥交换,可以保护个人隐私信息的安全传输。
- SM3是一种密码杂凑算法,用于对数据进行哈希计算,可以保护数据的完整性和防止篡改。
- SM4是一种分组密码算法,用于数据的加密和解密,可以保护商业机密数据的安全传输。
国标商密算法采用了先进的密码技术和安全性设计,经过了严格的安全评估和认证。
它不仅满足了商业机密和个人隐私信息的安全需求,还具有高效性和可靠性的特点。
国密标准标识密码算法

国密标准标识密码算法
国密标准标识密码算法主要包括SM1、SM2、SM3、SM4四个算法。
- SM1是中国自主研发的对称密码算法,用于对称加密和数据传输保密。
- SM2是基于椭圆曲线密码算法(ECC)的公钥密码算法,提供数字签名和密钥交换功能。
- SM3是中国自主研发的哈希算法,用于数字签名和消息认证码的生成。
- SM4是中国自主研发的分组密码算法,用于对称加密和数据传输保密。
这些算法都由中国密码学专家根据国家密码管理局的要求进行研发,主要用于国内政府和商业机构的信息安全保护。
rsa 原理

rsa 原理
RSA加密算法是一种非对称加密算法,也就是说它使用了两
个密钥:公钥和私钥。
其基本原理是利用大数分解的困难性来保证信息的安全性。
具体而言,RSA算法的生成过程如下:
1. 随机选择两个质数p和q,并计算它们的乘积n = p * q,n
被称为模数。
2. 计算欧拉函数φ(n) = (p - 1) * (q - 1),欧拉函数表示小于n
且与n互质的正整数的个数。
3. 选择一个与φ(n)互质的正整数e作为公钥,通常选择65537(即2^16 + 1)作为公钥,因为它是一个较小的质数,且满足了一些加密要求。
4. 计算与e关于模φ(n)的乘法逆元d,即d满足(e * d) mod φ(n) = 1,d作为私钥。
5. 公钥是(n, e),私钥是(n, d)。
对于明文M的加密过程如下:
1. 将明文M转化为一个整数m,要求m小于模数n。
2. 加密过程为密文C = (m^e) mod n,即C = (M^e) mod n。
对于密文C的解密过程如下:
1. 解密过程为明文M = (C^d) mod n,即M = (C^d) mod n。
RSA算法的安全性依赖于大数分解的困难性,也就是说,如
果有人能够在合理的时间内将n分解为p和q,那么就能够计
算出私钥d,进而解密密文。
然而对于较大的n,目前的计算
机技术并不足以快速分解它,因此RSA算法被认为是安全的。
需要注意的是,RSA算法是一种非对称加密算法,加密过程
中使用公钥进行加密,解密过程中使用私钥进行解密。
同时,RSA算法还可以用于数字签名和密钥交换等安全领域中。
RSA和DES加密算法详解

RSA和DES加密算法详解RSA加密算法:RSA是一种非对称加密算法,它的安全性基于大数的因数分解难题。
RSA算法的原理如下:1.选择两个不同的质数p和q,并计算它们的乘积n=p*q。
n被称为RSA算法的模数。
2.计算n的欧拉函数φ(n)=(p-1)*(q-1)。
3.选择一个整数e,使得1<e<φ(n),且e和φ(n)互质。
e被称为RSA算法的公钥指数。
4. 计算整数d,使得d*e ≡ 1 (mod φ(n))。
d被称为RSA算法的私钥指数。
5.公钥为(n,e),私钥为(n,d)。
6. 加密消息m时,将m的整数表示x,计算密文c ≡ x^e (mod n)。
7. 解密密文c时,计算明文m ≡ c^d (mod n)。
RSA算法的优点是加密速度较快,且在典型情况下很难被破解。
其主要应用领域包括数据传输中的身份认证、数字签名、数字证书等。
DES加密算法:DES(Data Encryption Standard)是一种对称加密算法,它采用64位的分组长度和56位的密钥长度。
DES算法的原理如下:1.初始置换(IP):将输入的64位明文分为左右两个32位部分。
2.迭代运算:通过16次的迭代运算,先对右半部分进行扩展和异或运算,然后经过S盒置换和P盒置换,最后与左半部分进行异或运算。
3.逆初始置换(IP-1):将得到的64位结果进行逆初始置换得到密文。
4.这里的迭代运算中,用到了轮密钥生成算法。
DES算法的密钥扩展过程中,通过对56位密钥进行位移、选择和置换操作生成各轮所使用的子密钥。
DES算法的缺点是安全性较低,主要是由于其算法密钥长度较短,易受到穷举攻击。
因此在实际应用中,通常采用3DES算法,即对DES算法进行三次加密。
1.对称加密算法DES的加密速度较快,而非对称加密算法RSA的加密速度较慢。
这是因为RSA算法涉及大数的运算,而DES算法仅涉及位运算。
2.DES算法的密钥长度较短,容易受到穷举攻击,安全性较低。
简单的rsa加密解密计算

简单的rsa加密解密计算
RSA加密算法是一种非对称加密算法,它使用一对密钥(公钥
和私钥)来加密和解密数据。
下面我将简单介绍RSA加密和解密的
计算过程。
1. 生成密钥对,首先,选择两个不同的大质数p和q,并计算
它们的乘积n=pq。
然后选择一个整数e,使得e与(p-1)(q-1)互质,并计算出e的模反元素d。
公钥是(n, e),私钥是(n, d)。
2. 加密,假设要加密的消息为M,首先将消息M转换为整数m,满足0≤m<n。
然后使用公钥(n, e)进行加密,加密后的密文C等于
m的e次方再对n取模,即C≡m^e (mod n)。
3. 解密,接收到密文C后,使用私钥(n, d)进行解密,解密后
的明文M等于C的d次方再对n取模,即M≡C^d (mod n)。
下面我举一个简单的例子来说明RSA加密和解密的计算过程:
假设我们选择两个质数p=11和q=3,计算n=pq=33,然后选择
e=3,并计算d=7。
这样我们得到公钥(n, e)=(33, 3)和私钥(n,
d)=(33, 7)。
现在假设要加密的消息为M=5,将其转换为整数m=5。
使用公钥进行加密,计算C≡5^3 (mod 33),得到C=5。
接收到密文C=5后,使用私钥进行解密,计算M≡5^7 (mod 33),得到M=5。
因此,我们成功地将消息M=5加密为密文C=5,然后再解密回到原始消息M=5。
这就是RSA加密和解密的简单计算过程。
国密算法 同态运算

国密算法同态运算国密算法国密算法是指由中国密码学专家自主研发的一种密码算法体系,主要用于保护国家机密和个人隐私。
它包括了对称加密算法、非对称加密算法、哈希算法、数字签名算法等多种密码学算法。
对称加密算法是指加密和解密使用同一个密钥的算法,其代表算法是SM4。
SM4算法是一种分组密码算法,其分组长度为128位,密钥长度为128位、192位或256位。
SM4算法具有加密速度快、安全性高、抗攻击能力强等优点,已被广泛应用于各种领域。
非对称加密算法是指加密和解密使用不同密钥的算法,其代表算法是SM2。
SM2算法是一种基于椭圆曲线密码学的公钥密码算法,具有安全性高、计算量小等优点,已被应用于数字证书、数字签名等领域。
哈希算法是指将任意长度的消息压缩成一个固定长度的摘要信息的算法,其代表算法是SM3。
SM3算法具有抗碰撞能力强、安全性高等优点,已被广泛应用于数字签名、消息认证等领域。
数字签名算法是指用于保证数字信息的完整性、真实性和不可抵赖性的算法,其代表算法是SM2和SM3。
SM2和SM3结合使用可以实现数字签名的功能。
同态运算同态运算是指在加密状态下对密文进行运算,得到的结果与对明文进行同样运算后所得的结果相同或相似的运算。
同态运算分为完全同态运算和部分同态运算两种。
完全同态运算是指在加密状态下进行加法和乘法运算,得到的结果与对明文进行同样运算后所得的结果完全相同。
完全同态运算可以实现在不暴露明文的情况下对密文进行计算,从而保护数据的隐私性。
部分同态运算是指在加密状态下进行加法或乘法运算,得到的结果与对明文进行同样运算后所得的结果相似但不完全相同。
部分同态运算可以实现在不暴露明文的情况下对密文进行计算,但是需要在一定程度上暴露部分信息。
同态运算在云计算、大数据分析等领域有着广泛的应用,可以实现在不暴露数据隐私的情况下进行计算和分析。
谈谈PBOC3.0中使用的国密SM2算法.
谈谈PBOC3.0中使⽤的国密SM2算法.谈谈PBOC3.0中使⽤的国密SM2算法⼀知识准备SM2是国密局推出的⼀种他们⾃⼰说具有⾃主知识产权的⾮对称商⽤密码算法。
本⾝是基于ECC椭圆曲线算法的,所以要讲sm2, 先要弄懂ECC。
完全理解ECC算法需要⼀定的数学功底,因为涉及到射影平⾯坐标系,齐次⽅程求解, 曲线的运算规则等概念。
这⾥不做过多的数学分析(主要是我⾃⼰也没有完全整明⽩)。
想要深⼊了解ECC的我推荐⽹名为ZMWorm的⼤⽜在多年前写的<<椭圆曲线ECC加密算法⼊门介绍>>。
此⼈是早年看雪论坛中的⼀个版主,对算法和密码学很有研究。
本篇的主旨还是希望能以简单通俗的语⾔,讲清楚PBOC3.0认证过程中,所⽤到的SM2的相关概念,包括它的实现,使⽤等。
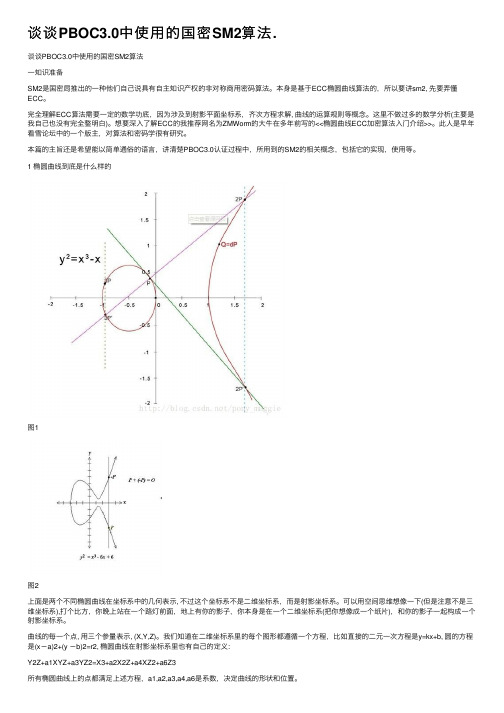
1 椭圆曲线到底是什么样的图1图2上⾯是两个不同椭圆曲线在坐标系中的⼏何表⽰, 不过这个坐标系不是⼆维坐标系,⽽是射影坐标系。
可以⽤空间思维想像⼀下(但是注意不是三维坐标系),打个⽐⽅,你晚上站在⼀个路灯前⾯,地上有你的影⼦,你本⾝是在⼀个⼆维坐标系(把你想像成⼀个纸⽚),和你的影⼦⼀起构成⼀个射影坐标系。
曲线的每⼀个点, ⽤三个参量表⽰, (X,Y,Z)。
我们知道在⼆维坐标系⾥的每个图形都遵循⼀个⽅程,⽐如直接的⼆元⼀次⽅程是y=kx+b, 圆的⽅程是(x-a)2+(y -b)2=r2, 椭圆曲线在射影坐标系⾥也有⾃⼰的定义:Y2Z+a1XYZ+a3YZ2=X3+a2X2Z+a4XZ2+a6Z3所有椭圆曲线上的点都满⾜上述⽅程,a1,a2,a3,a4,a6是系数,决定曲线的形状和位置。
⼆维坐标和射影坐标有⼀个对应关系,即x=X/Z, y=Y/Z, 这样就可以把上⾯的⽅程转成普通的⼆维坐标系⽅程:y2+a1xy+a3y= x3+a2x2+a4x+a62 离散的椭圆曲线上⾯的坐标系都是基于实数的,椭圆曲线看起来都是平滑的,如果我们限制曲线的点都必须是整数,曲线就变成离散的了,如图3所⽰:图3再进⼀步限制,要求整数必须⼤于0, ⼩于某个⼤整数P, 这样就形成了⼀个有限域F p.然后我们在这个有限域⾥定义⼀些点与点之间的加减乘除运算规则,⽐如A点加B点得到C点(记做A+B≡C (mod p)),或者A点乘以n得到K点(记做A×n≡K (mod p))。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第45卷第6期Vob45No.62019年6月June2019计算机工程Computer Engineering-安全技术-文章编号:1000-3428(2019)06-0171-04文献标志码:A中图分类号:TP399国密SM9中R-atr双线性对快速计算甘植旺1,廖方圆2(1.中国电子科技集团公司信息科学研究院,北京100086;2.中国电子科技集团有限公司,北京100846)摘要:R-ate是国密SM9标识密码算法中一种重要的双线性映射,其计算性能对SM9密码体制的应用至关重要%为提升R-ate双线性对的计算效率,提岀一种快速计算算法%通过对BN曲线上R-ate双线性对的计算过程和其中涉及的逆运算原理进行分析,改变计算中同构映射的作用顺序,将大部分逆运算从大特征域转到小特征域,以降低逆元求解的计算损耗%以SM9的系统参数为计算实例进行实验,结果表明,该算法的运行时间低至1.8.105mt%关键词:国密SM9;双线性对;R-ate计算;标识密码算法;椭圆曲线对开放科学(资源服务)标志码(OSID):UHj中文引用格式:甘植旺,廖方圆•国密SM9中R-ate双线性对快速计算:J).计算机工程,2019,45(6):171-174.英文弓丨用格式:GAN Zhiwang,LIAO Fangyuan.Rapid calculation of R-ate bilinear pairing in China state cryptography standard SM9(J).Computer Engineering,2019,45(6):171-174.Rapin Calculation of R-ate Bilinear Pairing inChina State Cryptography Standard SM9GAN Zhiwang1,LIAO Fangyuan2(1$Information ScienceAcademy ofChinaElectronicsTechnology Group Corporation,Beieing100086,China;2$China Electronics Technology Group Corporation,Beieing100846,China)+Abstract]R-ate is an impoSant bilinear mapping in the Identity-Based Cryptography(IEC)algorithm of China state cryptography standard SM9.Ct computational performance is very impoSant to the application of SM9cryptosystem.To improve the computational efficiency of R-ate bilinear pairing,a fast computational algorithm is proposed.By analyzingthe computation proces s of R-ate bilinear pairing on BN curvet and the involved principle of inverse operations,the orderin which isomorphic mapping takes effect in computation is changed,and most of the inverse operations are transferredfrom th+larg+f+atur+domain to sma l f+atur+domain to r+duc+th+computation loss of inv+rs++l m+n tsolu tion.Th+ systm param+trs of SM9ar+tak+n asan+xampl to ca r y ou t+xp+rim+n ts.R+sul ts show tha t th+running tim+ofth+ proposed algorithm is only1.8x105mt.+Key words]China state cryptography standard SM9;bilinear pairing;R-ate computing;Identity-Based Cryptography (IEC)algorithm;aiiptic curve pairingDOn:10.19678/j.issn.1000-3428.00541230概述根据加密过程与解密过程的密钥是否相同,密码体制可以分为对称加密体制和非对称加密体制。
非对称加密体制⑴于'976年被提出,其拥有完全不同的加密密钥和解密密钥,具有算法性能强、安全性高的特点,通常应用于对称加密过程的密钥加密%典型的非对称密码体制包括RSA、Elgamal、ECC等[2'3]%为保证公钥信息的真实性,非对称加密一般需要引入可信第三方认证中心(CeSificate AuthoSty,/A)o在每次加解密的过程中,用户都需要向CA中心申请认证,通过CA中心发放CA证书以确认通信双方的可信性。
CA证书包含公钥信息、用户注册信息、CA签名等认证信息。
因此,在传统的非对称加解密过程中,CA认证中心充当加解密双方的信任媒介,认证过程的通信量大小也直接影响加解密的效率%为解决由非对称加密体制高频认证引发的通信堵塞问题,文献[5]提出标识密码(Identity-Based基金项目:中国电科网络安全和信息化行动计划项目%作者简介:甘植旺(1988―),男,工程师、博士,主研方向为网络与信息安全;廖方圆,高级工程师收稿日期:2019-03-06修回日期:2019-04-17E-mail:ganzhiwang@172计算机工程2019年6月15日Cryptography,ITC)的概念,并设计一种基于标识的签名算法%文献(6]使用椭圆曲线对构造一种标识密钥共享方案,文献(7-8]先后提出基于椭圆曲线对的ITC算法。
在ITC算法中,密钥生成中心(Key Generation Centr,KGC)通过随机数生成主密钥,在主密钥与用户公开标识的基础上生成私钥,而用户公钥由其公开标识唯一确定。
用户的公开标识可以是用户昵称、邮件地址、电话号码等公开信息,无需经过第三方交换与复杂运算。
与基于证书的非对称密码体制相比,IBC体制能够简化公钥密码系统的密钥管理环节,减少公钥认证的通信量,降低真实性认证成本,具有易部署、易管理的优点,因此,在互联网、物联网等密码服务领域具有广阔的应用前景[9'10]%我国国家密码管理局于2008年正式颁布商用标识密码算法型号:SM9(商密九号算法),并于2016年3月28日发布并实施SM9标识密码算法标准[11L2]%国密SM9标识密码算法是一种基于椭圆曲线双线性对的商用标识密码标准%双线性对是一类具有非退化性的二元映射,常见的双线性对有Weil对、Tate对、R e te对[13L5]等%双线性对计算是SM9标识密码算法的关键步骤,其计算效率决定着整个密码体制的效率%双线性对的计算量巨大,Miller算法[16]是计算双线性对的有效算法%文献[17-19]通过构造具有特殊结构的椭圆曲线、减少Miller算法中的循环次数与扩域中的运算次数、优化幂乘运算等来优化双线性对计算%文献[20]提出一种新的R—te对参数选择方式,其通过降低Atel方程的域特征来减少Miller算法的循环次数,从而提升计算效率%本文对SM9中 BN(Ba r eto and Naehr0g)曲线上的R—S双线对计算进行研究,利用同构映射的性质,将双线性对计算中涉及的逆运算从大特征域转到小特征域,以减少扩域中的逆运算次数,提升R—o双线对的计算效率%1有限域与椭圆曲线1-1素域设7表示素数,记集合J p=10,1,…,p-12%对于55,6"J p,分别定义J p上的加法运算和乘法运算,如下:5+6=(5+6)mod p5-6=(5-6)mod p根据上述运算定义,且0和1分别为J p的加法单位元和乘法单位元,可以得出J p在上述加法和乘法定义下封闭%定义1集合J p是特征为p的素域%1-2有限域记J p[—是定义在素域J p上的关于-的多项式集合,设<—"J p[—为素域J p上的8次不可约多项式。
记J p”为J p[—模<—的剩余类,J p”是由8-1次多项式组成的集合%对于5"J””,5= 58一;—-1+58_2—「23…35]—350,5可以简记为(58-1,58-2,…,51,50)%对于55=( 5...-1,58一2,...,51,50),6=(6 (1)6『2,-,6],60)"J””,定义J””上的二元运算如下:536=(5...-136...-1,5”一236”一2, (51361)50+60)2(”-1)5-!(八M+0=5«-6N) mod<—)J p”根据加法和乘法构成域,称J p”为含有卩”个元素的有限域%根据上述运算定义,则0和]分别为有限域J p”的加法单位元和乘法单位元。
记J p*”= J p”\|02,有以下性质:性质1J#”关于乘法构成循环群%性质255"J;”,5P”-1=1%性质355"J#”,5-1=5p8-2%性质3给出在有限域上求解逆元的一种计算方法%由性质3可知,有限域上的逆元运算可以转化为指数运算,参数8的取值越大,逆元求解的运算量越大%算法1为一种逆元求解算法伪代码%算法145)输入5"J p#”输出5-11•分解p'-2=!F2t,其中,i=12.令x=a3•对于i从L-1到0,执行:1)x=x22)若i t=1,贝勺x=a*x4.输出x对于有限域J p”上的非零元素5,若使用算法1进行逆元求解运算,则其时间复杂度为Id(p”-2)%1-3椭圆曲线设p>3是素数,5、6"J””,满足453+2762( 0,有:*:.2=—35—+6为在J p”上定义椭圆曲线方程,将*上的无穷远点记为O%则有:*(J p”)=1(—.)72=—+5—+6,—."J p”2U10定义*(J p”)上的加法运算规则如下:1) 57"*(J p…),7+0=0+7=7%2) 57=(—.)"*(J p»),-7=(—,-.),7+ (-7)=O%3)57]=(-,.])"*(J p”)\02,72=(—2,.)" *(J p”)\02%记:入=<21」,—1(—3—1+52.1,12,71+72(0则7]+72=(—3,.3),其中有:第45卷第6期甘植旺,廖方圆:国密SM9中R—te双线性对快速计算173-3='2--1--2].3='(-]--3)-.]性质4*(J”)关于上述加法运算规则构成交换群%*(J”)上的加法运算在求解因子'时需要进行除法运算,此处的除法运算相当于先求除数逆元,然后再做乘法%参数8的取值越大,除法运算与加法运算的运算量也越大%2BN曲线上的R-ate双线性对对于BN曲线(2])*:.2=-3+6,曲线*存在定义在J2上的扭曲线*':.2=-3+06,其中,0"©,且满足%/28J2,%/38J2%BN曲线上的R-ate是SM9密码算法中的一类重要双线性对[11],改进并降低R-ate的运算量是提升SM9算法应用效率的重要途径%$:(-,.)7(0-]/3-,0-]/2.)为*到*的同构映射%定义1(Q#:(-,.)7(-1,-1),G nq(7#: *(J12)7J12%则BN曲线上的R-ate双线性对可以由算法2进行计算%&壮(7)的详细计算不影响本文算法的过程,故此处不再赘述,其具体计算可以参见文献[1']%算法2e(7,Q)输入7"*(J),Q"*(J”,),整数5,%输出/"J"1.分解a=i i a i2s,其中,-l=12.令Q=$(Q),T=Q,f=13.对于i从L-l到0,执行:1)f=f2-g T,T(P),T=T+T2)若-j=1,则f=f•g T,Q(P),T=T+Q4.令Q i="p(Q),Q2=-"2(Q),计算:1)f=f•/t,Q](P),T=T+Q'2)f=f•g;,q2(P),T=T3Q25.输出3算法改进由于0/28J12,0①8J12,因此$运算需要在J12的6次扩域J12下进行,则对于点Q"*(J12),有$(Q)"*(J12)%算法2的计算都在*(J]2)下进行,在步骤3中计算椭圆曲线上点的加法时,涉及有限域上点的逆运算%根据性质3,计算有限域上的逆元需要进行指数为1”-2的幂乘运算%因此,算法2中的椭圆曲线点运算涉及大量的51'2-2运算,计算效率极低%注意到映射$是*'(J12)到*(J12)的同构映射,对于5-,."*'(J12),都有$(-)+$(.)= $(-+.),因此,可以先在*'(J12)中进行点加法运算,在计算完成后再映射回*(J12)%通过改变同构映射的顺序,将算法2步骤3中涉及的点加运算所在的域特征从112改为12,将一次*(J]2)中的加法改为一次*'(J12)中的加法和一次乘法映射,从而大幅缩短算法的运算时间%改进算法伪代码如下:算法3e_8(7,Q)输入7"*(J),Q"*'(J”,),整数5,%输出/"J"1•分解-=!f2t,其中,1='2.令Q'=$(Q),T=Q,f=]3.对于i从L-]到0,执行:1);=$(T),f=f•g i,T(P),T=T+T2)若-j=1,则T=$(T),f=f•g;P),T=T+Q4.令Q1="p(Q'),Q2=-"2(Q'),T=$(T),计算:])f=f•g;,Q'(P),T=T+Q12)f=f•g;,q.(P)5.输出4性能分析由于算法3中步骤3、步骤4所涉及的椭圆曲线加法运算是在域J,上进行,其运算量主要来自椭圆曲线上的点加运算%根据1.3节的分析可知,椭圆点加运算涉及有限域上的匀速逆元求解%如使用算法1进行逆元运算,则算法2步骤3中单步循环涉及的点逆运算复杂度为0(lb(112-2))%算法3通过改变同构映射的作用顺序,将步骤3中涉及的点逆运算从大特征域转换到小特征域,使其中的点逆运算从51'2-2变为51%-2,单次点逆运算时间复杂度从0(lb(112-2))降低到0(lb(12-2)),且算法3未增加点逆运算次数其时间复杂度也从0('•lb(112-2))降为0('•lb(12-2))%以SM9给定的系统参数为例进行实验比较与分析,其中,椭圆曲线方程为=-3+5,扭曲线参数0为槡一%为方便结果展示,下文的参数如无特别说明,都是使用'6进制进行表示,左边为高位,右边为低位%1)基域特征1:B640000002A3A6F1D603AB4F F58EC74521F2934B1A7AEEDB E56F9B27E351457D2)整数5:00000002400000000215D93E3)整数%:B640000002A3A6F1D603AB4F F58EC74449F2934B18EA8BEE E56EE19C D69ECF254)点7:(-7,.)-7:93DE051D62BF718F F5ED0704487D01D6 E l E4086909DC3280E8C4E4817C66DDDD.7:21FE8DDA4F21E607631065125C395BBC 1C l C00CB FA6024350C464CD70A3EA6165)点Q:(-Q,.q)-Q:(9F64080B3084F733E48AFF4B41B56501 1CE0711C5E392CFB0AB1B6791B94C408,29DBA116152D1F786CE843ED24A3B573 414D2177386A92DD8F14D65696EA5E32) .Q:(69850938ABEA0112B57329F447E3A0CB174计算机工程2019年6月15日AD3E2FDB1A77F335E89E1408D0EF1C25,41E00A53 DDA532DA1A7CE027B7A46F741006E85F5CDFF073 0E75C05F B4E3216D)实验使用的计算机CPU为酷睿S—510U,操作系统为windows7旗舰版%分别使用算法2、算法3进行计算,所得到的结果e(7,Q)与e_8(7,Q)完全一致%算法2的计算时间为339956ms,而本文改进算法3的运行时间仅为184418ms,时间缩短了45.75%%5结束语本文提出一种R—o双线性对快速计算算法,通过改变R—w双线性对计算过程中所涉及的同构映射作用顺序,将其中的椭圆曲线加法运算从大特征域转到小特征域,从而缩短R—w双线性对的计算时间。
