1.向量的物理背景与概念及向量的几何表示最后更新
向量

例1.如图设O是正六边形ABCDEF的中心,写出图中
与向量OA相等的向量。 OA = DO = CB 变式一:与向量OA长度相等的向量 有多少个? 11个 变式二:是否存在与向量OA长度相等,方向 相反的向量? 存在,为 FE
变式三:与向量OA长度相等的共线向量有哪些?
CB、DO、FE
向量的概念:
(1)模相等的两个平行向量是相等的向量;
(2)若 a和b都是单位向量,则 a = b;
(3)若|a|>|b| ,则a > b (4)若a = b,b = c,则a = c。
(5) 若 a ∥ b, b ∥ c, 则a ∥c 问:在平面上把所有单位向量的起点平移到同一
× × × √ ×
点P,那么它们的终点的集合组成什么图形?
向量的表示方法: 零向量、单位向量概念: 平行向量定义: 相等向量定义:
共线向量与平行向量关系:
2.1.1
向量的物理背景与概念
2.1.2 向量的几何表示 2.1.3 相等向量与共线向量
嘻嘻!大笨 猫!
A B
唉, 哪儿 去了?
猫以5m/s的速率追赶一只以2m/s逃跑的小老鼠……
箱子的质量m
(1)
手对球的压力F
(2)
地面对球的支持力F1
观察上述三个量有什么区别? 在我们生活中,有哪些量是 数量,哪些是向量? 向量:既有大小,又有方向的量。 数量:只有大小,没有方向的量。
如: a, b, c……
判断题
1.温度含零上和零下温度,所以温度是向量( 2.向量的模是一个正实数。( 3.若|a|=0
思 考 与 判 断
1相等向量一定是平行向量吗? 2平行向量一定是相等向量吗? 3.若AB//CD ,那么非零向量AB//CD吗? 4.若非零向量AB//CD ,那么AB//CD吗?
向量的实际背景及基本概念

B(终点)
有向线段:在线段AB的两个端点
中,规定一个顺序,假设A为起点,
B为终点,我们就说线段AB具有方
A(起点)
向。具有方向的线段叫做有向线段。
有向线段的三个要素:起点、方向、长度
1、向量的几何表示:用有向线段表示。
记作:a = b
D
C
规定:0 = 0
A
B
A
B
D
a b
.
o
相等向量一定是平行向量吗?
向量相等 平行向量一定是相等向量吗?
C
向量平行
例1.如图设O是正六边形ABCDEF的中心,写出图中
与向量OA相等的向量。 OA = DO = CB
变式一:与向量OA长度相等的向量 有多少个? 11个
变式二:是否存在与向量OA长度相等,方向 相反的向量? 存在,为 FE
)
A.0 B. 1
D
C
C. 2
D. 3
C
D
变:若 a ∥ b, b ∥ c, 则a ∥c
当b ≠ 0时成立。概念: 向量的表示方法: 零向量、单位向量概念:
平行向量定义: 相等向量定义: 共线向量与平行向量关系:
(×)
2.下面几个命题:
(1)若a = b,b = c,则a = c。
(2)若|a|=0,则a = 0
(3)若|a|=|b|,则a = b |a|=|b|
(4)两个向量a、b相等的充要条件是 a ∥b
(5)若A、B、C、D是不共线的四点,则AB=DC是
四边形ABCD是平形四边形的充要条件。
其中正确的个数是(
向量知识点

、向量的物理背景与概念1、了解四种常见向量:力、位移、速度、加速度.2、既有大小又有方向的量叫做向量.§ 2.1.2>向量的几何表示1、带有方向的线段叫做有向线段,有向线段包含三个要素:起点、方向、长度.2、向量扇的大小,也就是向量扇的长度(或称模),记作|AB|;长度为零的向量叫做零向量;长度等于1个单位的向量叫做单位向量.3、方向相同或相反的非零向量叫做平行向量(或共线向量).规定:零向量与任意向量平行.、相等向量与共线向量1、长度相等且方向相同的向量叫做相等向量.、向量加法运算及其几何意义1、三角形加法法那么和平行四边形加法法那么.―► —►—► —►a +b a + b.2、§2. 2. 2、向量减法运算及其几何意义1、与。
长度相等方向相反的向量叫做。
的相反向量.2、三角形减法法那么和平行四边形减法法三角形遍法法那平行边形遍法法那§2. 2. 3、向量数乘运算及其几何意义1、规定:实数人与向量。
的积是一个向量,这种运算叫做向量的数乘.记作:膈,它的长度和方向规定如下:(1)Aai = l/lLL⑵当;I >0时,的方向与。
的方向相同;当2<0时,人]的方向与。
的方向相反.2、平面向量共线定理:向量a[a 6)与片共线,当且仅当有唯一个实数人,使方= 4".§2. 3.1、平面向量根本定理1、平面向量根本定理:如果。
],勺是同一平面内的两个不共线向量,那么对于这一平面内(l)a-b = x }x 2 + y 2 ⑵ a =+ y} a Lb a^b = Q x x x 2 + ^^2 =。
―► —► —► —►任一向量。
,有且只有一对实数2] , 22 ,使"=人]弓+人2。
2 • § 2. 3. 2>平面向量的正交分解及坐标表示 a = xi + yj = (x, y) •、平面向量的坐标运算 1、 1、设a = (x i ,y i \b = (x 2,y 2),那么:(& +万=(邑 +x 2^Ji +.2),一&=3 一知、 一无),(3)人1 =(入],人乂),^a//b<^>x x y 2 =x 2y r设 A (M , 乂), 3(听,光),贝土 AB= (X 22、 1、设 A(%!, yj), B(X 2 , y 2 \ C(x 3, y 3),那么 ⑴线段AB 中点坐标为。
2.1.1 向量的物理背景与概念及向量的几何表示

2.1.1 向量的物理背景与概念及向量的几何表示教学目标:1. 了解向量的实际背景,理解平面向量的概念和向量的几何表示;掌握向量的模、零向量、单位向量、平行向量、相等向量、共线向量等概念;并会区分平行向量、相等向量和共线向量. 2. 通过对向量的学习,使学生初步认识现实生活中的向量和数量的本质区别.3. 通过学生对向量与数量的识别能力的训练,培养学生认识客观事物的数学本质的能力. 教学重点:理解并掌握向量、零向量、单位向量、相等向量、共线向量的概念,会表示向量. 教学难点:平行向量、相等向量和共线向量的区别和联系.学 法:本节是本章的入门课,概念较多,但难度不大.学生可根据在原有的位移、力等物理概念来学习向量的概念,结合图形实物区分平行向量、相等向量、共线向量等概念. 教学思路: (一) 一、情景设置:如图,老鼠由A 向西北逃窜,猫在B 处向东追去,设问:猫能否追到老鼠?(画图) 结论:猫的速度再快也没用,因为方向错了.分析:老鼠逃窜的路线AC 、猫追逐的路线BD 实际上都是有方向、有长短的量.引言:请同学指出哪些量既有大小又有方向?哪些量只有大小没有方向? 二、新课学习:(一)向量的概念:我们把既有大小又有方向的量叫向量。
(二)(教材P74面的四个图制作成幻灯片)请同学阅读课本后回答:(7个问题一次出现) 1、数量与向量有何区别?(数量没有方向而向量有方向) 2、如何表示向量?3、有向线段和线段有何区别和联系?分别可以表示向量的什么?4、长度为零的向量叫什么向量?长度为1的向量叫什么向量?5、满足什么条件的两个向量是相等向量?单位向量是相等向量吗?6、有一组向量,它们的方向相同或相反,这组向量有什么关系?7、如果把一组平行向量的起点全部移到一点O ,这是它们是不是平行向量? 这时各向量的终点之间有什么关系?(三)探究学习1、数量与向量的区别:数量只有大小,是一个代数量,可以进行代数运算、比较大小; 向量有方向,大小,双重性,不能比较大小. 2.向量的表示方法:①用有向线段表示; ②用字母a、b(黑体,印刷用)等表示;ABCDA(起点)B(终点)a③用有向线段的起点与终点字母:AB;④向量AB的大小―长度称为向量的模,记作|AB|.3.有向线段:具有方向的线段就叫做有向线段,三个要素:起点、方向、长度.向量与有向线段的区别:(1)向量只有大小和方向两个要素,与起点无关,只要大小和方向相同,这两个向量就是相同的向量;(2)有向线段有起点、大小和方向三个要素,起点不同,尽管大小和方向相同,也是不同的有向线段.4、零向量、单位向量概念:①长度为0的向量叫零向量,记作0.0的方向是任意的. 注意0与0的含义与书写区别.②长度为1个单位长度的向量,叫单位向量.说明:零向量、单位向量的定义都只是限制了大小.5、平行向量定义:①方向相同或相反的非零向量叫平行向量;②我们规定0与任一向量平行.说明:(1)综合①、②才是平行向量的完整定义;(2)向量a、b、c平行,记作a∥b∥c. (四)理解和巩固:例1 书本75页例1.例2判断:(1)平行向量是否一定方向相同?(不一定)(2)与任意向量都平行的向量是什么向量?(零向量)(3)若两个向量在同一直线上,则这两个向量一定是什么向量?(平行向量)课堂练习:书本77页练习1、2、3题三、小结:1、描述向量的两个指标:模和方向.2、平面向量的概念和向量的几何表示;3、向量的模、零向量、单位向量、平行向量等概念。
2.1向量的物理背景与概念及向量的几何表示

4.向量AB 的大小,也就是向量AB 长度(或称模), 向量 的大小, 长度(或称模), 记作: 记作: AB 向量和有向线段的联系和区别? 向量和有向线段的联系和区别?3、向量Biblioteka 相关定义(2) 、向量的相关定义( )
r 1. 零向量 : 长度为零 的向量叫做零向量 记作 0 零向量: 长度为零的向量叫做零向量 的向量叫做零向量.记作
3、向量的相关定义(1) 、向量的相关定义( ) 1.向量定义:既有大小又有方向的量叫做向量. 向量定义:既有大小又有方向的量叫做向量. 大小又有方向的量叫做向量 方向. 2.向量特点:有大小,又有方向. 向量特点: 大小,又有方向
r r r 向量表示法: 表示; 3.向量表示法:也可用字母 a ,b ,c 表示;还可用 有向线段起点和终点字母表示 AB , CD .
五 课堂小结
(1)向量的定义 )向量的定义——既有大小又有方向的量叫做向量; 既有大小又有方向的量叫做向量
(2)向量的表示方法 )向量的表示方法—— 可以用有向线段表示;也可用字母表示;还可 可以用有向线段表示;也可用字母表示; 用有向线段起点和终点字母表示 ; 相等向量,平行向量 (3)两个向量之间的关系 )两个向量之间的关系——相等向量 平行向量 相等向量 向量可平移, 这是向量的本质特征. 向量可平移 这是向量的本质特征 注意对平行向量也叫做共线向量的理解
——课本第 页例题 课本第85页例题 课本第
某人从A 点出发向西走了200 到达B 200m 例 3 某人从 A 点出发向西走了 200m 到达 B 点 , 然 后 改 变 方 向 向 西 偏 北 60 度 走 了 450m到达C 最后又向东走了200 200m 450m到达C点,最后又向东走了200m到达 D 点. uuu uuu uuu r r r (1)作出向量 AB , BC , CD(用1cm表示100m ); uuu v (2)求|DA | .
平面向量的概念课件(共34张PPT)-高一下学期数学人教A版(2019)必修第二册

长度
方向
______表示向量的大小,有向线段的______表示向量的方向.如
, .
(2)向量的字母表示:向量可以用黑体小写字母,,,…表示,书写时,
→ → →
用带箭头的小写字母 , , ,…表示.
课前预习
3.向量的相关概念
=
(5 2)2 − 52 = 5 m .
△ 是直角三角形,其中∠ = 90∘ , = 3 m, = 5 m,
所以 = 32 + 52 = 34(m),故|| = 34 m.
课中探究
[素养小结]
在画图时,向量是用有向线段来表示的,用有向线段的长度表示向
量的大小,用箭头所指的方向表示向量的方向.应该注意的是有向
课前预习
知识点三 相等向量与共线向量
相同或相反
非零向量
1.平行向量:方向____________的__________叫作平行向量.向量与
//
平行,记作______.规定:零向量与任意向量平行.
相等
相同
2.相等向量:长度______且方向______的向量叫作相等向量.向量与
相等,记作 = .
课中探究
[解析] 因为,,为非零向量,且//,所以与方向相同或相反,
又//,所以与方向相同或相反,因此与方向相同或相反,所
以//,故A正确;
两个相等的非零向量的起点与终点也可能在一条直线上,故B不正确;
易知C正确;有相同起点的两个非零向量有可能是平行向量,故D不正确.
以//,且 = .
由图可知,与向量相等的向量有.
课中探究
,
(2)与向量相反的向量有_________;
2.1向量的物理背景概念几何表示

思考6:对于一个实数,可以用数轴上的 点表示;对于一个角的正弦、余弦和正 切,可以用三角函数线表示;对于一个 二次函数,可以用一条抛物线表示….数 学中有许多量都可以用几何方式表示, 你认为如何用几何方式表示向量最合适?
自学提纲 1.有向线段的概念,怎么画有向线段 2.有向线段的长度?如何记法? 3.有向线段的三要素 4.知道了有向线段的()()和() 它的终点就唯一确定的 5.向量可以用什么表示?什么叫做向量 的长度(模)如何记法?向量能比较大 小吗? 6.什么叫做零向量,单位向量?
(2)写出与向量OC 共线的向量
B A
O
C D E F
2、如图,四边形ABCD为正方形,△BCE为等 腰直角三角形.以图中各点为起点和终点,写 出与向量AB 模相等的所有向量.
D C
A
B
E
1.在物理中,位移与距离是同一个概 念吗?为什么?
2.现实世界中有各种各样的量,如年 龄、身高、体重、力、速度、面积、体 积、温度等,在数学上,为了正确理解、 区分这些量,我们引进向量的概念.
探究(一):向量的物理背景与概念
思考1:在物理中,怎样区分作用于同一 点的两个力? 力的大小和力的方向
思考2:物体受到的重力、物体在液体中 受到的浮力的方向分别如何?受力的大 小分别与哪些因素有关?
③任一向量与它的相反向量不相等;
④四边形ABCD是平行四边形的充要条件是 AB CD = ⑤ 若 a // b , b // c , 则a // c . ⑥ 若 | a | | b |, 则a b . ⑦共线的向量,若点不同,则终点一定不同。
例2.如图,设O是正六边形ABCDEF的中 OB OC 心(1)分别写出图中与向量 OA 、 、 相等的向量;
人教A版2025高中数学必修二6.1 平面向量的概念 课件
的区别及联系:0是一个实数, 是一个向量,并
且| |=0,书写时 0 表示零向量,一定不能忘记上面的箭头.
③单位向量有无数个,它们大小相等,但是方向不一定相同.
④在平面内,将表示所有单位向量的有向线段的起点平移到
同一点,则它们的终点就会构成一个半径为1的圆.
3
相等向量与共线向量
②错误,向量的模相等,大小未必相同,不一定是相等向量;
③错误,平行与模大小没有必然关系;
综上,正确答案选A.
题①
下列几个结论:
①温度有零上和零下之分,所以温度是向量;
②向量 ≠ ,则 和 的方向不同;
③若 >|| ,则 > ;
④若向量 是单位向量,向量 也是单位向量,则它们共线;
与 不一定平行.
混淆向量相等、平行、模相等
坑②
给出下列几个说法:①若 || = ,则 = 0 ;②若|| = ||,则 = ;
③若 // ,则 || = ||.其中说法正确的有(
A. 0
B. 1
C. 2
)个.
D. 3
【错解】①②对,③错,选C
【正解】①错误,正确的写法应该是 = ;
定,任意两个相等的非零向量都能用同一个有向线段表示.
共线
向量
向量 = 就意
味着|| = ||并且它
们的方向相同,但是
|| = ||只能说明它
任何一组平行向量都能平移到同一条直线上,因此, 们的模相等,方向未
平行向量也叫做共线向量,同一直线上的向量平行.
必相同.
3
相等向量与共线向量
概念辨析
【3】向量可以用有向线段来表示,但是向量不是有向线段,也不能说有向线段
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
思考4:力既有大小,又有方向,在物理 学中称为矢量,你还能指出哪些物理量是 矢量吗?
思考5:数学中,把既有大小,又有方向 的量叫做向量,把只有大小,没有方向 的量称为数量.那么年龄、身高、体重、 面积、体积、温度、时间、路程是向量 吗?
合作探究
1. 向量的概念: 我们把既有大小又有方向的量叫向量.
合作探究
2. 数量与向量的区别: 数量只有大小,是一个代数量,可以 进行代数运算、比较大小;向量有方向, 大小,双重性,不能比较大小.
a A(起点) B (终点)
思考6:对于一个实数,可以用数轴上的 点表示;对于一个角的正弦、余弦和正 切,可以用三角函数线表示;对于一个 二次函数,可以用一条抛物线表示….数 学中有许多量都可以用几何方式表示, 你认为如何用几何方式表示向量最合适?
说明:
零向量、单位向量的定义都只是限制 了大小.
合作探究
6.平行向量定义: ①方向相同或相反的非零向量叫平行向量; ②我们规定0与任一向量平行. a b c
合作探究
6.平行向量定义: ①方向相同或相反的非零向量叫平行向量; ②我们规定0与任一向量平行. a b c
说明:
(1) 综合①、②才是平行向量的完整定义; (2) 向量a、b、c平行,记作a∥b∥c.
A D C
东
练习.如图,四边形ABCD为正方形,△BCE为 等腰直角三角形.以图中各点为起点和终点, 写出与向量 AB 模相等的所有向量.
D C
A
B
E
课堂小结
1.描述向量的两个指标:模和方向. 2. 平面向量的概念和向量的几何表示; 3. 向量的模、零向量、单位向量、平行
向量等概念.
限时抢答
C
合作探究
3. 向量的表示方法: ①用有向线段表示;
②用字母a、b(黑体,印刷用)等表示;
③用有向线段的起点与终点字母: AB ; 向量 AB 的大小——长度称为向量的模,
记作 AB .
合作探究
4. 有向线段: 具有方向的线段就叫做有向线段, 三个要素:起点、方向、长度.
合作探究
4. 有向线段: 具有方向的线段就叫做有向线段, 三个要素:起点、方向、长度. 向量与有向线段的区别:
理论迁移
练习. 判断: (1) 平行向量是否一定方向相同? 不一定
(2) 与任意向量都平行的向量是什么向量?
零向量
(3) 若两个向量在同一直线上,则这两个向
量一定是什么向量? 平行向量
理论迁移
例2. 如图,试根据图 中的比例尺以及三地 的位置,在图中分别
A
B C
用向量表示A地至B、
C两地的位移,并求
出A地至B、C两地的
实际距离(精确到1km).
理论迁移
例3.已知飞机从A地按北偏东30°方 向飞行2000km到达B地,再从B地按南偏 东30°方向飞行2000km到达C地,再从C 地按西南方向飞行1000 2 km到达D地. (1)画图表示向量 AB, BC , CD; (2)求飞机从A地到达D地的位移所对应 北 B 的向量的模和方向.
合作探究
请同学指出哪些量既有大小又有方向? 哪些量只有大小没有方向?
探究(一):向量的物理背景与概念
思考1:在物理中,怎样区分作用于同一 点的两个力? 力的大小和力的方向
思考2:物体受到的重力、物体在液体中 受到的浮力的方向分别如何?受力的大 小分别与哪些因素有关?
F G
思考3:在如图所示的弹簧中,被拉长或 压缩的弹簧的弹力方向如何?在弹性限 度内,弹力的大小与什么因素有关?
理论迁移
例1.判断下列命题是否正确,若不正确, 请简述理由.
①向量 AB 与 CD 是共线向量,则A、B、C、D 四点必在一直线上; ②单位向量都相等; ③任一向量与它的相反向量不相等; ④四边形ABCD是平行四边形的充要条件是 AB = CD ⑤若a / /b, b / / c, 则a / / c. ⑥若 | a || b |, 则a b. ⑦共线的向量,若起点不同,则终点一定不同。
合作探究
5. 零向量、单位向量概念: ①长度为0的向量叫零向量,记作0. 0的方向是任意的. 注意0与0的含义与书写区别.
②长度为1个单位长度的向量, 叫单位向量.
合作探究
5. 零向量、单位向量概念: ①长度为0的向量叫零向量,记作0. 0的方向是任意的. 注意0与0的含义与书写区别.
②长度为1个单位长度的向量, 叫单位向量.
的向量叫什么向量?
自主学习 阅读教材,回答下列问题:
(5)有向线段的三要素: (6)知道了有向线段的起点、长度和 方向它的终点就唯一确定的。
(7)向量可以用什么表示?什么叫做 向量的长度(模)如何记法?向 量能比较大小吗?
自主学习
(8)满足什么条件的两个向量是相等向量? 满足什么条件的两个向量是相反向量? 如何表示?单位向量是相等向量吗? (9)有一组向量,它们的方向相同或相反, 这组向量有什么关系?如何表示? (10)如果把一组平行向量的起点全部移到一 点O,这时它们是不是平行向量?这时 各向量的终点之间有什么关系? 什么是共线向量(平行向量)?
合作探究
4. 有向线段: 具有方向的线段就叫做有向线段, 三个要素:起点、方向、长度. 向量与有向线段的区别: (1)向量只有大小和方向两个要素,与起点 无关,只要大小和方向相同,这两个向 量就是相同的向量; (2)有向线段有起点、大小和方向三个素, 起点不同,尽管大小和方向相同,也是 不同的有向线段.
2.1向量的物理背景与
概念及几何表示
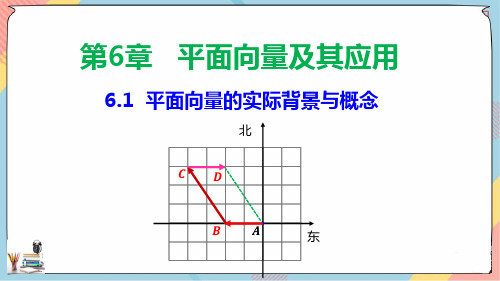
问题提出 1. 老鼠由A向西北逃窜,猫在B处向东追 去,设问:猫能否追到老鼠?
C
结论:猫的速度再Biblioteka 也没用,因为方向 错了.A
B
D
问题提出
2.在物理中,位移与距离是同一个概 念吗?为什么?
3.现实世界中有各种各样的量,如年 龄、身高、体重、力、速度、面积、体 积、温度等,在数学上,为了正确理解、 区分这些量,我们引进向量的概念.
限时抢答
B
限时抢答
B
课后作业
练习.教材P.77练习第1、2、3题. (做在书上) P77习题2.1A组:1,2.
讲授新课
1. 向量的概念:
我们把既有大小又有方向的量叫向量.
自主学习 阅读教材74~76,回答下列问题:
(1)数量与向量有何区别? (2)如何表示向量?
(3)有向线段和线段有何区别和联系?分别 有向线段的长度?如何记法?
(4)长度为零的向量叫什么向量?长度为1
可以表示向量的什么?如何画有向线段?
