《时间序列分析》第二章 时间序列预处理习题解答[1]
人大版时间序列分析基于R(第2版)习题答案
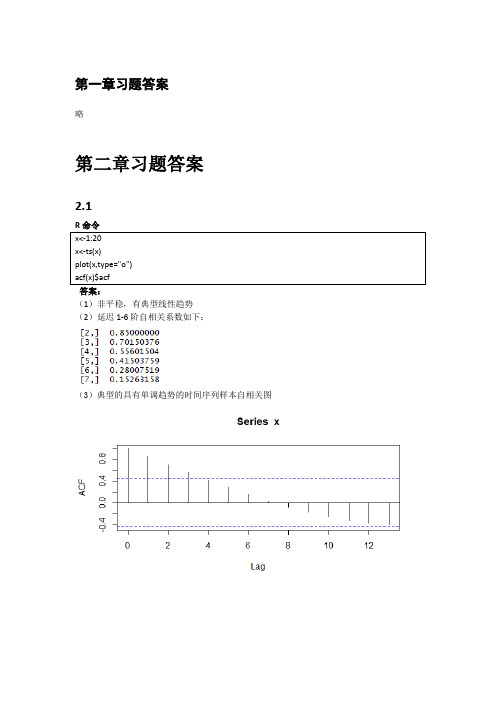
第一章习题答案略第二章习题答案2.1答案:(1)非平稳,有典型线性趋势(2)延迟1-6阶自相关系数如下:(3)典型的具有单调趋势的时间序列样本自相关图2.2(1)非平稳,时序图如下(2)1-24阶自相关系数如下(3)自相关图呈现典型的长期趋势与周期并存的特征2.3R命令答案(1)1-24阶自相关系数(2)平稳序列(3)非白噪声序列Box-Pierce testdata: rainX-squared = 0.2709, df = 3, p-value = 0.9654X-squared = 7.7505, df = 6, p-value = 0.257X-squared = 8.4681, df = 9, p-value = 0.4877X-squared = 19.914, df = 12, p-value = 0.06873X-squared = 21.803, df = 15, p-value = 0.1131X-squared = 29.445, df = 18, p-value = 0.04322.4答案:我们自定义函数,计算该序列各阶延迟的Q统计量及相应P值。
由于延迟1-12阶Q统计量的P值均显著大于0.05,所以该序列为纯随机序列。
2.5答案(1)绘制时序图与自相关图(2)序列时序图显示出典型的周期特征,该序列非平稳(3)该序列为非白噪声序列Box-Pierce testdata: xX-squared = 36.592, df = 3, p-value = 5.612e-08X-squared = 84.84, df = 6, p-value = 3.331e-162.6答案(1)如果是进行平稳性图识别,该序列自相关图呈现一定的趋势序列特征,可以视为非平稳非白噪声序列。
如果通过adf检验进行序列平稳性识别,该序列带漂移项的0阶滞后P值小于0.05,可以视为平稳非白噪声序列Box-Pierce testdata: xX-squared = 47.99, df = 3, p-value = 2.14e-10X-squared = 60.084, df = 6, p-value = 4.327e-11(2)差分序列平稳,非白噪声序列Box-Pierce testdata: yX-squared = 22.412, df = 3, p-value = 5.355e-05X-squared = 27.755, df = 6, p-value = 0.00010452.7答案(1)时序图和自相关图显示该序列有趋势特征,所以图识别为非平稳序列。
时间序列分析(第一章、第二章)2

自协方差函数的周期性分析
例 3.1
AR(4)模型1的谱密度
2.5 2 lamda=2.07 lamda=1.1
1.5
1
0.5
0
0
0.5
1
1.5
2
2.5
3
3.5
3 2.5 2 1.5 1 0.5 0 -0.5 -1 -1.5
0
5
10
15
20
25
AR(4)模型1、2、3的谱密度
4
3
2
1
0
-1
-2
-3 0
10
20
30
40
50
60
70
80
§2.3
AR( p) 序列的谱密度
Yule-Walker方程 自协方差的收敛性 自协方差的正定性 时间序列的完全可预测性
谱密度的自协方差函数反演公式
定理3.1的证明
白噪声列与平稳解的关系
Yule-Walker方程
Yule-Walker系数的最小相位性(2)
Levinson递推公式
偏相关系数
AR序列的偏相关系数
AR序列的充分必要条件
定理4.3的证明(1)
定理4.3的证明(2)
定理4.3的证明(3)
定理4.3的证明(4)
本节内容的应用意义
§例5.1 AR(1)序列
X t 0.85X t 1 t ,
250
300
350
400
450
4 gamma=3.6036 3.5 3 2.5 2 1.5 1 0.5 0
0
5
10
15
20
25
8 7 6 5 4 3 2 1 0 f(0)=7.0736
第二章PPT时间序列分析

❖ 联合概率分布通常涉及非常复杂的数学运算。
解决方案 研究该序列的低阶矩(均值、方差、自协方差、
自相关系数,也称为特征统计量)
特征统计量
❖ 均值
对于时间序列Xt ,t T,任意时刻的序列值 X t 都是一个随
机变量,记它的分布函数为 Ft (x) ,若满足
▪ 随机变量族X t 的所有统计特性完全由它们的联合
分布函数或联合密度函数决定。
时间序列的概率分布
❖对于时间序列Xt ,t T,它的概率分布定义如下: ❖任取正整数m ,任取 t1,t2,..., tm T ,则m 维随机向量
(Xt1 , Xt2 ,..., Xtm )' 的联合概率分布定义为
Ft1,t2 ,...,tm (x1, x2 ,..., xm ) = P( X t1 x1, X t2 x2 ,..., X tm xm )
正态时间序列
时间序列 Xt ,t T为正态时间序列,如果任取正整数n,任
取 t1,t2,..., tn T ,相对应的有限维随机变量 X1, X 2,..., X n 服从n
维正态分布,密度函数为
ft1 ,t2
,,tn
(~xn )
=
−n
(2 ) 2
n
−1 2
exp[ −
1 2
(~xn
−
~n )n−1(~xn
由这些有限维分布函数构成的全体
{ Ft1,t2 ,...,tm (x1, x2 ,..., xm ), m 正整数,t1, t2 ,..., tm T }
就称为时间序列 Xt ,t T的概率分布族。
❖ 例如:
所有的一维分布(m=1)是 Ft1 (x1), Ft2 (x2 ), Ft3 (x3 ),....
完整word版时间序列测验2解答1北师珠时间序列

=2 测试2解答(第三、四章)1.设{ X t }为一时间序列,且■^X t =X t —X t-1,▽ PX ^7p-1(7x t ),J X t = X t — X t-k ,Bx t =Xt-1,记 V (72x t )二①(B) X t ,则①(B ) =?解:根据k 步差分和P 阶差分与延迟算子之间的关系,得①(B)=(1-B3 4 5 6)(1-B)22.已知 AR (1)模型为:X t =0.7X t-1 + 名t ,街 ~WN(0,cr ;) o(P )模型平稳性的特征根判别法要求所有特征根绝对值小于 1; (1) 模型平稳性的平稳域判别法要求|% |<1, (2) 模型平稳性的平稳域判别法要求:|% |<1,聽±% <1 0 二1 =弋.8特征根判别法:平稳;I % |=0.8<1,平稳域判别法:=1.3特征根判别法:非平稳; ® | = 1.3:>1,平稳域判别法:21特征方程为: 6入—k — 1 = 0 即(2入—1)(3入中1) = 0,礼=――,3由特征根判别法:平稳;11|=- ", $2=— <1, ©2 =0",平稳域判别法:平稳;63⑷ 特征方程为:A 2 — A —2 = 0即a + 1)a —2)= 0,人=—1,几2 由特征根判别法:非平稳;|纟|=2>1, *2中°1=3》1, *2-^=1不小于1,平稳域判别法:非平稳。
P . 46其中, g t }均为服从标准正态分布的白噪声序列。
求: E(x t ), Var(x t ),P 2和 *22。
解: (1) 由平稳序列E (x t) *0=E ( X t-1)和 E (名t ) = 0,得 E ( X t ) = 0_=0 (-% =0) P或 - A.Var(X t ) =0.72Var(X t 」)+Var(g t ) = 0.49Var (X t )+^72 2bpCT 2V a rx t)=——j 止 1.96° -1 -0.49 0.51 E(k > 0),p 2 =转(1)模型偏自相关系数截尾:AR (1)模型P k =样 AR=0.72 P. 47P.49= 0.49P.503.分别用特征根判别法和平稳域判别法检验下列四个AR 模型的平稳性。
人大PPT讲义 第二章 时间序列的预处理

例2.3时序图
例2.3自相关图
2.2 纯随机性检验
纯随机序列的定义 纯随机性的性质 纯随机性检验
纯随机序列的定义
纯随机序列也称为白噪声序列,它满足 如下两条性质
(1) EX t , t T 2 , t s (2) (t , s ) , t , s T 0, t s
标准正态白噪声序列时序图
白噪声序列的性质
纯随机性
(k) 0,k 0
各序列值之间没有任何相关关系,即为 “没有记 忆”的序列
方差齐性
DX t (0) 2
根据马尔可夫定理,只有方差齐性假定成立时,用 最小二乘法得到的未知参数估计值才是准确的、有 效的
纯随机性检验
{Ft1 ,t2 ,,tm ( x1 , x2 ,, xm )} m (1,2,, m), t1 , t2 ,, tm T
实际应用的局限性
特征统计量
均值 方差
t EX t xdFt ( x)
DX t E( X t t ) ( x t ) dFt ( x)
自相关图检验
例题
例2.1
检验1964年——1999年中国纱年产量序列的平稳性 检验1962年1月——1975年12月平均每头奶牛月产 奶量序列的平稳性 检验1949年——1998年北京市每年最高气温序列的 平稳性
例2.2
例2.3
例2.1时序图
例2.1自相关图
例2.2时序图
例2.2 自相关图ቤተ መጻሕፍቲ ባይዱ
时间序列分析参考答案

时间序列分析参考答案时间序列分析参考答案时间序列分析是一种研究随时间变化的数据模式和趋势的统计方法。
它可以帮助我们理解数据的变化规律,预测未来的趋势,以及制定相应的决策。
在本文中,我们将探讨时间序列分析的基本概念、方法和应用。
一、时间序列分析的基本概念时间序列是按照时间顺序排列的一系列数据观测值。
它可以是连续的,比如每天的股票价格,也可以是离散的,比如每月的销售额。
时间序列分析的目标是找出数据中的模式和趋势,以便进行预测和决策。
时间序列分析的基本概念包括趋势、季节性和周期性。
趋势是指数据在长期内的整体变化方向,可以是上升、下降或平稳。
季节性是指数据在一年中周期性重复出现的变化模式,比如节假日销售额的增长。
周期性是指数据在较长时间内出现的波动,通常周期长度大于一年。
二、时间序列分析的方法时间序列分析的方法包括描述性分析、平稳性检验、模型建立和预测等。
描述性分析是对时间序列数据进行可视化和统计分析,以了解数据的基本特征。
常用的描述性分析方法包括绘制折线图、直方图和自相关图等。
折线图可以显示数据的整体趋势和季节性变化,直方图可以展示数据的分布情况,自相关图可以帮助我们发现数据的相关性。
平稳性检验是判断时间序列数据是否具有平稳性的方法。
平稳性是指数据的均值和方差在时间上保持不变。
常用的平稳性检验方法包括单位根检验和ADF检验等。
模型建立是根据时间序列数据的特征,选择合适的模型来描述数据的变化规律。
常用的模型包括AR模型、MA模型和ARMA模型等。
AR模型是自回归模型,表示当前观测值与过去观测值之间的线性关系;MA模型是移动平均模型,表示当前观测值与过去观测值的误差之间的线性关系;ARMA模型是自回归移动平均模型,综合考虑了自回归和移动平均的效果。
预测是利用已知的时间序列数据,通过建立模型来预测未来的观测值。
常用的预测方法包括滚动预测、指数平滑法和ARIMA模型等。
滚动预测是指根据当前观测值和过去观测值的模型,逐步预测未来的观测值;指数平滑法是基于历史数据的加权平均值,对未来的观测值进行预测;ARIMA模型是自回归移动平均差分整合模型,可以处理非平稳的时间序列数据。
时间序列分析版
第2章时间序列得预处理拿到一个观察值序列之后,首先要对它得平稳性与纯随机性进行检验,这两个重要得检验称为序列得预处理。
根据检验得结果可以将序列分为不同得类型,对不同类型得序列我们会采用不同得分析方法、2、1 平稳性检验2、1、1 特征统计量平稳性就是某些时间序列具有得一种统计特征。
要描述清楚这个特征,我们必须借助如下统计工具。
一、概率分布数理统计得基础知识告诉我们分布函数或密度函数能够完整地描述一个随机变量得统计特征。
同样,一个随机变量族得统计特性也完全由它们得联合分布函数或联合密度函数决定。
对于时间序列{,t∈},这样来定义它得概率分布:任取正整数m,任取∈,则m维随机向量()’得联合概率分布记为,由这些有限维分布函数构成得全体。
{,∀m∈正整数,∀∈}就称为序列{}得概率分布族。
概率分布族就是极其重要得统计特征描述工具,因为序列得所有统计性质理论上都可以通过概率分布推测出来,但就是概率分布族得重要性也就停留在这样得理论意义上。
在实际应用中,要得到序列得联合概率分布几乎就是不可能得,而且联合概率分布通常涉及非常复杂得数学运算,这些原因使我们很少直接使用联合概率分布进行时间序列分析。
二、特征统计量一个更简单、更实用得描述时间序列统计特征得方法就是研究该序列得低阶矩,特别就是均值、方差、自协方差与自相关系数,它们也被称为特征统计量。
尽管这些特征统计量不能描述随机序列全部得统计性质,但由于它们概率意义明显,易于计算,而且往往能代表随机序列得主要概率特征,所以我们对时间序列进行分析,主要就就是通过分析这些统计量得统计特性,推断出随机序列得性质。
1.均值对时间序列{,t∈}而言,任意时刻得序列值都就是一个随机变量,都有它自己得概率分布,不妨记为。
只要满足条件就一定存在着某个常数,使得随机变量总就是围绕在常数值附近做随机波动。
我们称为序列{}在t时刻得均值函数。
==当t取遍所有得观察时刻时,就得到一个均值函数序列{,t∈}。
时间序列分析习题答案
时间序列分析习题答案时间序列分析习题答案时间序列分析是一种广泛应用于统计学和经济学领域的方法,用于研究随时间变化的数据。
通过对时间序列数据的建模和分析,我们可以揭示数据背后的规律和趋势,从而进行预测和决策。
下面我将给出一些时间序列分析习题的答案,希望能对大家的学习和理解有所帮助。
1. 什么是时间序列?时间序列是按照时间顺序排列的一系列数据观测值。
它可以是连续的,比如每天的股票价格,也可以是离散的,比如每个月的销售额。
时间序列分析的目标是通过对这些数据的分析和建模,揭示数据背后的规律和趋势。
2. 时间序列分析的步骤是什么?时间序列分析一般包括以下几个步骤:- 数据收集:收集并整理时间序列数据,确保数据的准确性和完整性。
- 数据可视化:通过绘制时间序列图,观察数据的趋势、季节性和周期性等特征。
- 数据平稳性检验:通过统计检验方法,判断时间序列数据是否平稳。
如果不平稳,需要进行差分处理。
- 模型选择:根据数据的特征和目标,选择适合的时间序列模型,比如ARIMA模型、季节性ARIMA模型等。
- 模型拟合:利用选定的模型,对时间序列数据进行拟合和参数估计。
- 模型诊断:对拟合的模型进行诊断,检验模型的残差序列是否符合模型假设。
- 模型预测:利用已拟合的模型,对未来的数据进行预测。
3. 如何判断时间序列数据的平稳性?平稳性是时间序列分析的基本假设之一,它要求时间序列的均值、方差和自相关函数在时间上都是常数。
常用的平稳性检验方法有:- 绘制时间序列图:观察数据是否具有明显的趋势、季节性和周期性。
- 平稳性统计检验:常用的统计检验方法有ADF检验、KPSS检验等。
这些检验方法的原理是基于单位根检验,判断序列是否存在单位根,从而判断序列的平稳性。
4. 如何选择适合的时间序列模型?选择适合的时间序列模型需要考虑数据的特征和目标。
常用的时间序列模型有:- AR模型:自回归模型,利用过去的观测值对当前值进行预测。
- MA模型:移动平均模型,利用过去的白噪声误差对当前值进行预测。
时间序列分析答案
由于P值显著大于显著性水平所以该序列不能拒绝纯随机的原假设•换言之,我们可以认为该序列的波动没有任何规律可循,所以该序列为纯随机序列5.(1)时序图data example2_9;in put price;time=intnx ( 'month' , '01jan2000'd , _n_- 1);format time date. ; |cards ;153 187 234 212 300 221 201175123 104 85 78134 175 243 227 298 256 237165124 106 87 74145 203 189 214 295 220 231174119 85 67 75117 178 149 178 248 202 162135120 96 90 63procgplot data =example2_9;plot price*time= 1; |symbol1c =gree n v=star i =spli ne;run ;data example2_9_1; in put freq@@; month=intnx ( 'month', '1jan2000'd, _n_-1);format year year4.; cards ;153 187 234 212 300 221 201 175 123 104 85 78 134 175 243 227 298 256 237 165 124 106 87 74 145 203 189 214 295 220 231 174 119 85 67 75 117 178 149 178 248 202 162 135 120 96 90 63procarima data =example2_9_1; iden tifyvar =freq; run ;(2)该序列不是平稳性序列.⑶纯随机性检验()延迟Q LB 统计量检验Q LB 统计量值P 值 延迟6期 95.84 <0.0001 延迟12期190.40<0.0001检验结果显示,在各延迟阶下LB 检验统计量的P 值都非常小(<0.0001),所以我 们可以Lag Coviri ernce4202.$73 1,009000 ■俪Q弗刪4E H {事恸臓31M.Q14 9-CJ4433S 1920.888 0*45704 »0*208852 341.398 0.D8123 常麻■ 0.228741 -1345.I6E -.920060.229342 -2600.731 -,61936 illi_iill1111 r illi, i ill li iLcili 1.3 i|ii^ iipuyiif iyii- i ip ip j|i i a■ 0.2384SG -3030.168 -+理舶8 山』'山 山■山 QJ B I JH ■:H I ■>■■0.268653 -2844.965 -.62332 ■ Li Hi ■ I ■HiillH K U J HLiC.307374 -1427.302 -.33380 ■ ppd 爪昂肝MM0.333188 47.54^424 0,01136 ■(1.340274 1402.572 0.33372 s0.W2S2 243G.343 Q.579Cd 4 弗榊躍笊當榊當窃寧世■ C.347033 3071.366 0*73092■出壯阳常出為申州器附常岀勒岸附O^S6E52Autocorre lai ionsCorrelationStd Errormarks two stftrtdard errors以很大的把握(置信水平>99.999%)断定该公司销售量属于非白噪声序列,即该公司的销售量不是纯随机的.。
第2章时间序列的预处理PPT课件
第(1)条是OLS估计的需要 第(2)条是为了满足统计推断中大样本下的“一致
性”特性:
Plim(ˆ) n
▲如果X是非平稳数据(如表现出向上的趋势), 则(2)不成立,回归估计量不满足“一致性”, 基于大样本的统计推断也就遇到麻烦。
nk t1
(xt
x)(xtk
x),0kn
n1ktkn1(xt x)(xtk x),0kn
或 ˆ*(k)1 nn t 1 k(xtx)(xtkx),0kn
可以证明
E[ˆ(k)](k)O(1)
n
E[ˆ*(k)](1k)(k)(1k)O(1)
n
nn
所以,ˆ ( k ) 是 ( k ) 的渐近无偏估计,而 ˆ * ( k ) 是 ( k )
第二章 时间序列的预处理
一、问题的引出:非平稳变量与经典回归模型
⒈常见的数据类型
到目前为止,经典计量经济模型常用到的数据有: 时间序列数据(time-series data) 截面数据(cross-sectional data) 平行/面板数据(panel data/time-series cross-section
自协方差 (t,s ) E (X tt)X (ss)
自相关系数 (t,s) (t,s)
DXt DXs
2.平稳时间序列的定义
(1)严平稳
严平稳是一种条件比较苛刻的平稳性定义,它认为 只有当序列所有的统计性质都不会随着时间的推移 而发生变化时,该序列才能被认为平稳。
(2)宽平稳
宽平稳是使用序列的特征统计量来定义的一种平稳 性。它认为序列的统计性质主要由它的低阶矩决定, 所以只要保证序列低阶矩平稳(二阶),就能保证 序列的主要性质近似稳定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∧
(2)当延迟期数即 k (本题取值 1 2 3 4 5 6)远小于样本容量 n (本题为 20)时,自相关系数 ρ k 计算公式为
∧
ρk ≈
∧
∑(X
t =1
n−k
t n
− X )( X t + k − X )
t
∑(X
t =1
0<k <n
− X)
∧
2
即计算得 ρ1 = 0.8500 , ρ 2 = 0.7015 , ρ3 = 0.5560 , ρ 4 = 0.4150 , ρ5 = 0.2805 ,
number 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 01JAN80 01JAN81 01JAN82 01JAN83 01JAN84 01JAN85 01JAN86 01JAN87 01JAN88 01JAN89 01JAN90 01JAN91 01JAN92 01JAN93 01JAN94 01JAN95 01JAN96 01JAN97 01JAN98 01JAN99 time
ppm 342 341 340 339 338 337 336 335 334 333 332 331 330 329 328 01JAN75 01MAY75 01SEP75 01JAN76 01MAY76 01SEP76 01JAN77 01MAY77 01SEP77 01JAN78 01MAY78 01SEP78 01JAN79 01MAY79 01SEP79 01JAN80 01MAY80 01SEP80 01JAN81 time
340.57 336.63 333.61 329.41 334.82 330.18 33 36.44 332.05 337.65 5 333.59 3 339.06 335 5.05 341.19 337.74 333.55 330.63 334.32 331.50 33 35.99 333.53 337.57 7 334.76 3 338.95 336 6.53 340.87 338.36 ; pro oc arima data=examp d ple2; identify var r=ppm; run n;
4、若序列长度为 100,前 12 个样本自相关系数如:
ρ1 = 0.02 ρ2 = 0.05 ρ3 = 0.10 ρ4 = −0.02 ρ5 = 0.05 ρ6 = 0.01 ρ7 = 0.12 ρ8 = −0.06 ρ9 = 0.08 ρ10 = −0.05 ρ11 = 0.02 ρ12 = −0.05
∧
330.97 330.05 332.46 330.87 333.23 332.41 335.07 334.39 336.44 335.71 338.16 337.19 331.64 328.58 333.36 329.24 334.55 331.32 336.33 332.44 337.63 333.68 339.88 335.49 332.87 328.31 334.45 328.87 335.82 330.73 337.39 332.25 338.54 333.69 340.57 336.63 333.61 329.41 334.82 330.18 336.44 332.05 337.65 333.59 339.06 335.05 341.19 337.74 333.55 330.63 334.32 331.50 335.99 333.53 337.57 334.76 338.95 336.53 340.87 338.36 ; proc gplot data=example2; plot ppm*time=1; symbol1 c=black v=star i=join; run;
《时间序列分析》习题解答
习题 2.3
1.考虑时间序列{1,2,3,4,5,…,20}: (1)判断该时间序列是否平稳; (2)计算该序列的样本自相关系数 ρ k (k=1,2,…,6); (3)绘制该样本自相关图,并解释该图形. 解: (1)根据时序图可以看出,该时间序列有明显的递增趋势,所以它一定不是 平稳序列, 即可判断该时间序是非平稳序列,其时序图程序见后。
该序列能否视为纯随机序列? 检验问题如下 原 假 设:延迟期数小于或等于 12 期的序列值之间相互独立 (即纯随机序列 WN,也就是非白噪声序列 white noise series) 备择假设:延迟期数小于或等于 12 期的序列值之间有相关性 (非纯随机序列或非 WN, 也就是非白噪声序列) 数学语言描述即为
∧
∧
∧
∧
ρ6 = 0.1526
MATLAB 计算程序: clear all; close all; X_t=[1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20]; %时间序列值 k=6; %拟计算的自相关延迟期数值 rou_hat=zeros(k,1); %为拟计算的中阶自相关系数预留数组空间 Time_mean=mean(X_t); %计算时间序列值的样本均值 %计算自相关系数计算公式的分母部分 SST=0; for t=1:20 SST=SST+(X_t(t)-Time_mean)^2; end %计算对应 K 阶自相关系数 for i=1:k S=0; for t=1:20-i S=S+(X_t(t)-Time_mean)*(X_t(t+i)-Time_mean); %计算公式分子部分 end rou_hat(i,1)=S/SST; end rou_hat=rou_hat %输出相关系数值
(2 ) ρ 0.8 85,,ρ 0.70,ρ 0.56,ρ 0.41,ρ 0 ; 0.28
年 那罗亚火山 ( (Mauna Loa) 每月释放的 CO2 数据如 如下 (单位: ppm) 2. 1975—1980 年夏威夷莫那 见教材 P34 表 2-7. 见 (1) ) 绘制该序 序列时序图,并判断该系 系列是否平稳 稳; (2) ) 计算该序 序列的样本自 自相关系数 ρ k (k=1,2,…,24); (3) ) 绘制该样 样本自相关图 图,并解释该 该图形. 解:时序图的描 描述 dat ta example e2; input ppm@@; tim me=intnx('month','0 01jan1975'd, _n_-1); format time date.; cards; 330.45 331.90 331.63 333.05 33 32.81 334.65 334.66 6 336.25 3 335.89 337 7.41 337.81 339.25
运行结果 rou_hat = 0.8500 0.7015 0.5560 0.4150 0.2801 0.1526
∧
(3) 绘制该 该样本自相关 关图
dat ta example e1; input number r@@; tim me=intnx('year','01 1jan1980'd d, _n_-1); format year year4.; cards; 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 ; pro oc arima data=examp d ple1; identify var r=number; run n;
97.0 105.4
proc print data=example2_3; proc arima data=example2_3; identify var=rain; run;
分析: (1) 如上图所示: (2) 根据样本时序图和样本自相关图可知,该序列平稳 (3) 根据白噪声检验,P 值都较大,可以判断该序列为白噪声序列,即该序列具有纯随 机性。
∧
, 24)
225.0 131.6 63.2 86.4
95.3 112.8 181.6 136.9
1 100.6 8 81.8 7 73.9 3 31.5
48.3 31.0 64.8 35.3
112.3 160.8 52.3 ; 26.2 112.8
143.0 80.5 144.3 62.5 49.5 158.2 116.1 7.6 165.9 54.1 106.7 92.2 63.2 67.3 77.0 148.6 159.3 85.3 59.4
data example2; input ppm@@; time=intnx('month','01jan1975'd, _n_-1); format year year4.; cards; 330.45 331.90 331.63 333.05 332.81 334.65 334.66 336.25 335.89 337.41 337.81 339.25 330.97 330.05 332.46 330.87 333.23 332.41 335.07 334.39 336.44 335.71 338.16 337.19 331.64 328.58 333.36 329.24 334.55 331.32 336.33 332.44 337.63 333.68 339.88 335.49 332.87 328.31 334.45 328.87 335.82 330.73 337.39 332.25 338.54 333.69
