时间序列分析的预处理
高效处理时间序列数据的技巧和方法

高效处理时间序列数据的技巧和方法时间序列数据是一种按时间顺序排列的数据,通常是用来描述某一现象在不同时间点上的变化情况。
时间序列数据在很多领域都有着重要的作用,比如金融、经济学、气象学、医学等领域都广泛使用时间序列数据进行分析和预测。
处理时间序列数据需要掌握一些高效的技巧和方法,本文将介绍一些处理时间序列数据的技巧和方法,以及它们在实际应用中的作用。
一、数据预处理在处理时间序列数据之前,首先要对原始数据进行预处理,以确保数据的准确性和可靠性。
数据预处理的步骤包括数据清洗、缺失值处理、异常值处理和数据重采样等。
1.数据清洗数据清洗是指对原始数据进行筛选和处理,去除不需要的数据或者错误的数据。
在处理时间序列数据时,数据清洗的过程包括去除重复数据、去除不必要的字段、对数据进行格式转换等。
清洗后的数据能够更好地反映原始数据的特征,同时也减少了数据处理的难度。
2.缺失值处理时间序列数据中经常会出现缺失值,这些缺失值可能是由于数据采集的问题或者数据损坏等原因造成的。
处理缺失值的方法包括删除缺失值、插值处理和填充处理等。
不同的处理方法会对后续的数据分析和建模产生不同的影响,因此需要根据实际情况选择合适的处理方法。
3.异常值处理异常值是指与其他数据明显不同的数值,可能是由于数据采集错误或者异常事件引起的。
处理异常值的方法包括删除异常值、替换异常值和转换异常值等。
对异常值进行处理可以减少对数据分析的干扰,使得分析结果更加准确。
4.数据重采样数据重采样是指将原始数据的时间间隔进行调整,使得数据变得更加平滑或者更加精细。
数据重采样的方法包括向前采样、向后采样、插值重采样和汇总重采样等。
选择合适的重采样方法可以更好地反映数据的变化趋势,提高数据分析的准确性。
二、特征提取在进行时间序列数据分析之前,需要对数据进行特征提取,以提取出数据的关键特征,为后续的建模和预测提供支持。
特征提取的方法包括统计特征提取、时域特征提取和频域特征提取等。
《时间序列分析》第二章 时间序列预处理习题解答

《时间序列分析》习题解答�0�2习题2.3�0�21考虑时间序列12345…201判断该时间序列是否平稳2计算该序列的样本自相关系数kρ∧k12… 6 3绘制该样本自相关图并解释该图形. �0�2解1根据时序图可以看出该时间序列有明显的递增趋势所以它一定不是平稳序列�0�2即可判断该时间序是非平稳序列其时序图程序见后。
�0�2 时间序描述程序data example1 input number timeintnxyear01jan1980d _n_-1 format time date. cards 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 proc gplot dataexample1 plot numbertime1 symbol1 cblack vstar ijoin run�0�2�0�2�0�22当延迟期数即k本题取值1 2 3 4 5 6远小于样本容量n本题为20时自相关系数kρ∧计算公式为number1234567891011121314151617181920time01JAN8001J AN8101JAN8201JAN8301JAN8401JAN8501JAN8601JAN870 1JAN8801JAN8901JAN9001JAN9101JAN9201JAN9301JAN9 401JAN9501JAN9601JAN9701JAN9801JAN99121nkttktknttX XXXXXρ�6�1∧�6�1�6�1≈�6�1∑∑ 0kn4.9895�0�2注20.05125.226χ接受原假设认为该序列为纯随机序列。
�0�2解法三、Q统计量法计算Q统计量即12214.57kkQnρ∑�0�2�0�2�0�2�0�2�0�2�0�2�0�2�0�2�0�2�0�2查表得210.051221.0261χ�6�1由于Q统计量值4.57Q小于查表临界值即可认为接受原假设即该序列可视为纯随机序列为白噪声序列 5表2——9数据是某公司在2000——2003年期间每月的销售量。
简述时间序列预测的步骤

简述时间序列预测的步骤
时间序列预测的步骤通常包括以下几个方面:
1. 数据收集与预处理:收集时间序列数据,并进行预处理,如处理缺失值、异常值、平滑数据等。
2. 可视化与探索性分析:对时间序列数据进行可视化,包括绘制时间序列图、自相关图、偏自相关图等,以便了解数据的趋势、季节性、周期性等特征。
3. 模型选择和参数估计:根据数据的特点选择合适的时间序列模型,如ARIMA、ARMA、AR、MA等模型,并通过最大似然估计、最小二乘估计等方法估计模型的参数。
4. 模型诊断与改进:对所选模型进行诊断,包括检验模型的残差序列是否为白噪声、检验模型的拟合优度等。
如果模型不符合要求,则需要改进模型或选择其他合适的模型。
5. 模型评估与验证:使用历史数据来评估模型的性能,可以计算平均绝对误差(MAE)、均方根误差(RMSE)、平均绝对百分比误差(MAPE)等指标。
还可以使用交叉验证等方法来验证模型的泛化能力。
6. 预测与评估:使用训练好的模型对未来一段时间的数据进行预测,同时计算预测误差,并评估预测的准确性和可靠性。
7. 模型应用和监控:根据预测结果制定相应的策略和决策,同
时对模型的性能进行监控,及时更新模型或调整参数以适应数据的变化。
时间序列的预处理教材

时间序列的预处理教材时间序列的预处理是在进行时间序列分析之前的必要步骤。
它包括数据收集、数据清洗、数据转换和缺失值处理等过程,以确保时间序列数据的准确性和一致性。
本文将逐步介绍时间序列预处理的重要步骤。
1. 数据收集:在时间序列预处理的第一步,需要确定数据来源和收集数据。
数据可以从各种渠道获取,如公共数据库、传感器设备或实时数据流等。
确保数据的质量和完整性非常重要,因此应该选择可靠的数据源。
2. 数据清洗:数据清洗是时间序列预处理的关键步骤,旨在处理异常值、噪声和重复数据等问题。
首先,检查数据集中是否存在缺失值、异常值或错误值。
可以使用统计方法、可视化工具或专门的算法来检测这些问题。
一旦发现异常值,可以删除、替换或修正它们。
3. 数据转换:在某些情况下,时间序列可能会显示出非常不规则的波动,这会对后续的分析造成困扰。
数据转换可以通过应用平滑技术(如移动平均法或指数平滑法)或差分操作来减少数据波动。
这些转换操作可以使数据变得更加稳定,更容易分析。
4. 缺失值处理:在时间序列中,经常会遇到缺失值的情况。
这些缺失值可能会对分析结果产生不良影响,因此需要采取适当的处理方法来填补这些缺失值。
常见的方法包括用平均值、中值或插值等方法来填补缺失值。
但在填补缺失值之前,需要对缺失数据进行详细的分析,了解缺失的原因和模式。
5. 数据标准化:标准化是时间序列预处理的另一个重要步骤。
通过标准化,可以将不同尺度的数据转换为具有相似分布的数据。
这样可以确保不同时间序列的比较是可靠的。
一种常见的标准化方法是Z得分标准化,通过减去均值并除以标准差,将数据转换为标准正态分布。
总之,时间序列预处理是进行时间序列分析的必要步骤。
通过数据清洗、转换和标准化等处理,可以确保时间序列数据的准确性和稳定性。
在进行时间序列预处理之后,可以继续进行各种分析方法,如趋势分析、周期性分析和季节性分析等。
6. 噪声去除:在时间序列预处理中,噪声是造成数据不准确和干扰分析结果的主要因素之一。
时间序列预处理实验报告
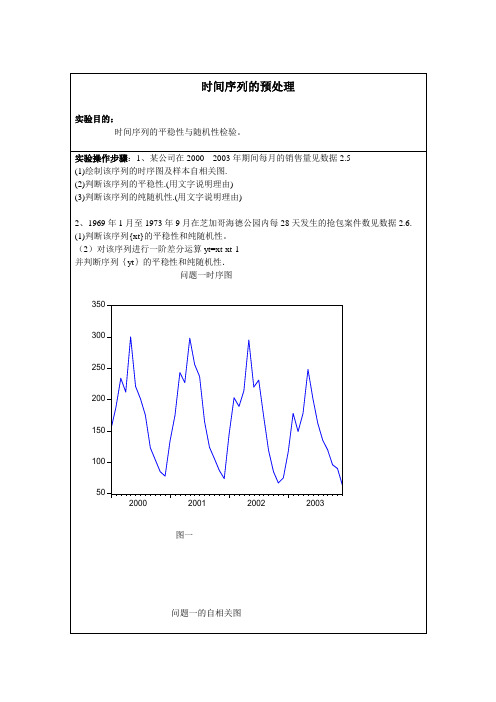
2、1969年1月至1973年9月在芝加哥海德公园内每28天发生的抢包案件数见数据2.6.
(1)判断该序列{xt}的平稳性和纯随机性。
(2)对该序列进行一阶差分运算yt=xt-xt-1
并判断序列{yt}的平稳性和纯Leabharlann 机性.问题一时序图图一
问题一的自相关图
差分方程的自相关性
结果分析:问题一:2000---2003年期间每月的销售量
图一的时序图提供的信息非常明确,销售量的是成周期变化的。所以是平稳序列
图二中自相关图的横轴表示自相关系数,纵轴表示延迟时期数,用水平方向的垂线表示自相关系数的大小。自相关系数有时为正,有时为负,逐渐趋于零。具有单调趋势的非平稳序列的一种典型的自相关图形式。
问题二:
时序图显示序列数据明显集中在均值附近,所以没有平稳;
样本自相关图显示该序列的自相关系数有时为正,有时为负。没有平稳性和随机性。
差分方程:由差分方程的时序图可以明显看到围绕在一个常数上下波动的。而且有周期的波动。所以是平稳序列
自相关性可以看到P值小于0.0005的有十个。所以
附:实验程序
注:可以任意添加页数。
所以是平稳序列图二中自相关图的横轴表示自相关系数纵轴表示延迟时期数用水平方向的垂线表示自相关系数的大小
时间序列的预处理
实验目的:
时间序列的平稳性与随机性检验。
实验操作步骤:1、某公司在2000---2003年期间每月的销售量见数据2.5
(1)绘制该序列的时序图及样本自相关图.
(2)判断该序列的平稳性.(用文字说明理由)
图二
问题二的时序图
图三
问题二的自相关性
(1)yt=xt-xt-1的结果:
第二章时间序列的预处理

),,(),,(21,,21,,2121m t t t m t t t x x x F x x x F m m τττ+++=第二章 时间序列的预处理 2.1 平稳性检验 2.1.1 特征统计量 一、概率分布对时间序列},{T t X t ∈,,,,,21T t t t N m m ∈∀∈∀ 联合概率分布记为),,(21,,21m t t t x x x F m,由这些有限维分布函数构成的全体记为:},,,),,2,1(),,,({2121,,21T t t t m m x x x F m m t t t m ∈∀∈∀成为序列}{t X 的概率分布族二、特征统计量对时间序列},{T t X t ∈,取T s t ∈∀, 1、均值t t EX =μ为}{t X 在t 时刻的均值函数,},{T t t ∈μ反映},{T t X t ∈每时每刻的平均水平 2、方差2)(t t t X E DX μ-=3、自协方差函数(autocovariance function)和自相关函数(autocorrelatioi function) 定义 ),(s t γ为}{t X 的协方差函数:))((),(s s t t X X E s t μμγ--= 定义),(s t ρ为}{t X 的自相关系数,ACF. st DXDX s t s t ⋅=),(),(γρ2.1.2 平稳时间序列的定义 一、严平稳只有当序列所有的统计性质都不会随着时间的推移而发生变化时,该序列才能被认为是严平稳的。
定义 2.1 设}{t X 为一时间序列,对任意正整数m ,任取T t t t m ∈ ,,21,对任意整数τ 有则称时间序列}{t X 为严平稳时间序列。
二、宽平稳定义 2.2 如果}{t X 满足如下三个条件: (1)任取∞∈ 2,tEX T t 有;(2)任取μμ,,=∈tEXT t 有为常数;(3)任取),(),(T,t -s k T,k s,t,t s k k s t -+=∈+∈γγ有且; 则称}{t X 为宽平稳时间序列。
如何使用Matlab进行时间序列分析和预测模型构建
如何使用Matlab进行时间序列分析和预测模型构建引言时间序列分析和预测在许多领域都具有重要的应用价值,如金融、经济、气象等。
而Matlab作为一种功能强大的数学软件,提供了丰富的工具和函数用于时间序列分析和预测模型的构建。
本文将介绍如何使用Matlab进行时间序列分析和预测模型构建,帮助读者快速掌握这一有用的技能。
一、数据预处理在进行时间序列分析和预测之前,首先需要对数据进行预处理。
常见的预处理方法包括数据清洗、缺失值处理、异常值检测等。
1. 数据清洗数据清洗是指对数据进行筛选和剔除,以保证数据的质量和准确性。
在Matlab 中,可以使用各种函数进行数据清洗,如isnan、isinf等。
例如,可以通过isnan函数判断数据是否含有缺失值,并使用isnan函数将缺失值替换为NaN。
2. 缺失值处理缺失值是指数据中的某些观测值缺失或无法获取。
在时间序列分析中,缺失值会对模型的预测产生较大影响。
因此,对于缺失值的处理是非常重要的。
在Matlab中,可以使用一些统计函数,如mean、median等,来对缺失值进行插补或填充。
例如,可以使用mean函数将缺失值替换为数据的均值。
3. 异常值检测异常值是指与其他观测值相比,具有异常数值的观测值。
异常值可能由于测量误差、数据录入错误或其他原因造成。
在时间序列分析中,异常值会对模型的精度和可靠性产生较大影响。
因此,需要对异常值进行检测并进行相应的处理。
在Matlab中,可以使用箱线图、离群点检测等方法来检测异常值,并使用插补或删除等方法进行处理。
二、时间序列分析时间序列分析是指对一系列时间上连续观测值的统计分析与建模。
时间序列分析常用于探索数据的内在规律和结构,并建立相应的数学模型。
1. 数据可视化数据可视化是进行时间序列分析的重要步骤,可以帮助我们直观地了解数据的特征和趋势。
在Matlab中,可以使用plot、scatter等函数进行数据可视化。
例如,可以使用plot函数绘制时间序列的折线图,以展示数据的趋势和变化。
时序预测中常见的数据预处理方法(六)
时序预测中常见的数据预处理方法时序预测是一种重要的数据分析方法,它通过对历史数据的分析和建模,来预测未来的趋势和变化。
在进行时序预测之前,需要对原始数据进行预处理,以提高模型的准确性和可靠性。
本文将介绍时序预测中常见的数据预处理方法。
1. 数据清洗数据清洗是时序预测中非常重要的一步。
原始数据可能存在缺失值、异常值和重复值,这些数据问题会对预测模型的准确性造成影响。
因此,首先需要对数据进行清洗,以确保数据的完整性和准确性。
对于缺失值,可以选择删除或填充。
删除缺失值可能会减少数据量,但可以保证数据的准确性。
填充缺失值则可以保持数据完整性,常见的填充方法包括均值填充、中位数填充和插值填充。
对于异常值和重复值,可以通过数据可视化和统计方法进行识别和处理。
2. 数据平稳化时序数据中常常存在非平稳性,即数据的均值和方差会随着时间变化而发生变化。
非平稳性数据会影响预测模型的准确性,因此需要对数据进行平稳化处理。
常见的数据平稳化方法包括差分法和对数变换法。
差分法通过计算相邻时间点数据的差值来消除数据的趋势和季节性。
对数变换法则通过取数据的对数来减小数据的波动。
这些方法可以使数据更加稳定,有利于建立准确的预测模型。
3. 数据归一化时序数据的数值范围可能存在差异,这会对模型的训练和预测造成影响。
因此,需要对数据进行归一化处理,使数据的数值范围在一定范围内。
常见的数据归一化方法包括最大-最小归一化和Z-score归一化。
最大-最小归一化通过对数据进行线性变换,将数据的数值范围缩放到[0, 1]之间。
Z-score归一化则通过计算数据的均值和标准差,将数据进行标准化处理。
这些方法可以有效地减小数据的数值差异,提高模型的训练和预测效果。
4. 特征工程特征工程是时序预测中非常重要的一环,它可以通过对原始数据进行特征提取和变换,来构建更加有效的特征集合。
常见的特征工程方法包括滞后特征、移动平均特征和季节性特征。
滞后特征是指将时间序列数据向后移动一定的时间步长,来构建新的特征。
时间序列法的具体方法
时间序列法的具体方法
1. 数据收集,首先,我们需要收集时间序列数据,这些数据可以是一段时间内的观测值,比如销售额、股票价格、气温等。
2. 数据预处理,在进行时间序列分析之前,我们需要对数据进行预处理,包括去除异常值、填补缺失值、平稳化处理等,以确保数据的准确性和可靠性。
3. 时间序列图形化,接下来,我们可以通过绘制时间序列图来观察数据的趋势、季节性和周期性变化,以便更好地理解数据的特点。
4. 模型选择,根据时间序列数据的特点,我们可以选择合适的时间序列模型,比如ARIMA模型、指数平滑模型等,来描述数据的变化规律。
5. 参数估计,对于所选择的模型,我们需要对模型的参数进行估计,以便建立准确的模型。
6. 模型诊断,在建立模型之后,我们需要对模型进行诊断,检
验模型的拟合度和预测能力,以确保模型的有效性。
7. 模型预测,最后,我们可以利用建立的时间序列模型对未来的数据进行预测,从而为决策提供参考。
通过以上具体方法,时间序列法可以帮助我们更好地理解时间序列数据的规律,并进行有效的预测和决策。
时间序列的预处理(平稳性检验和纯随机性检验)
1、时序图的绘制
在SAS系统中,使用GPLOT程序可以绘 制多种精美的时序图。
可以设置坐标轴、图形颜色、观察值点 的形状及点之间的连线方式等
例2-1
data example2_1;
input price1 price2;
time=intnx('month','01jul2004'd,_n_-1);
format time date.;
cards;
12.85 15.21
13.29 14.23
12.41 14.69
15.21 13.27
14.23 16.75
13.56 15.33
;
proc gplot data= example2_1; \\绘图过程开始
plot price1*time=1 price2*time=2/overlay; //确定纵横轴,按两种
时间序列分析之
试验二
时间序列的预处理 (平稳性检验和纯随机性检验)
一、平稳性检验
时序图检验
根据平稳时间序列的均值、方差
及周期特征。
自相关图检验
根据平稳时间序列的短期相关性, 其自相关图中随着延迟期数 的增加,自相关系数会很快 地衰减向零。
cards;
97 154 137.7 149 164 157 188 204 179 210 202 218 209
204 211 206 214 217 210 217 219 211 233 316 221 239
215 228 219 239 224 234 227 298 332 245 357 301 389
平稳时间序列的时序图与自相关图
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. Analyze—Nonparametric Tests—Runs
变量gnp进入“Test Variable list”栏 内 选中“cut point”栏中“mean”选项→OK
输出结果分析:因为P 值(sig.)极大,所以不拒绝 零假设,故不能拒绝原序列是平稳的。
时序图检验法
• 1)给出一个随机时间序列,首先可通过该序 列的时间路径图(时序图)来粗略地判断它是 否是平稳的。
优点:简便、直观。对于那些明显为非平稳的时间序 列,可以采用这种方法。
缺点:对于一般的时间序列是否平稳,不易用这种方 法判断出来。
(1)时序图检验(判断准则)
根据平稳时间序列均值、方差为常数的性质
,平稳序列的时序图应该显示出该序列始终在 一个常数值附近随机波动,而且波动的范围有 界、无明显趋势及无周期特征
Z r E(r) D(r)
判定:若-z α<z<+z α,则不能拒绝零假设,即不能拒 绝序列是平稳的;否则拒绝零假设,序列是非平稳的。
非参数检验可以很方便的通过SPSS软件进行, 实例:用游程检验检验第一讲的数据的平稳性; 步骤如下: 1.打开SPSS输入数据 2.依次单击Analyze—Nonparametric Tests—Runs; 打开Runs对话框。 3.在原变量对话框中选择变量进入“Test Variable list”栏内 4.选中“cut point”栏中“mean”选项 5.单击“OK”按纽,开始进行统计分析。
时间序列的预处理(续)
获
得 观 察 值 序
平稳性 检验
N
Y 纯随机 检验
N
Y分 析 结 束
列 差分 运算
拟合
ARMA 模型
四、 平稳性检验
1.平稳性定义——知识回顾
若时间序列有有穷的二阶矩,且 Xt 满足如下两个条件:
(1)t EXt c (2) (t, s) E(Xt c)(X s c) (t s,0)
平方根变换等。
3. 平稳性检验方法
非参数检验法 特征根检验法 单位根检验法
(1)通过时间序列的趋势图来判断
(2)通过自相关函数(ACF)判断
图检验方法
非参数检验法:游程检验
(1) 什么是游程
一个游程定义为一个具有相同符号的连续串,在它前 后相接的是与其不同的符号或完全无符号。
表,得出抽样分布的临界值rL、rU 判定:若rL <r< rU 则不能拒绝零假设,即不能拒绝序列是
平稳的;若r> rU 或r< rL则拒绝零假设,序列是非平稳的。
b.大样本情况 零假设H0:加号和减号以随机的方式出现 检验方法:给定显著性水平α(一般取0.05)查标准正态分布
表,得出抽样分布的临界值-zα,+zα。并计算统计量:
如果符号序列是随机的,那么“+”和“-”将随机出 现,因此它的游程数既不会太多,又不会太少;反 过来说如果符号序列的游程总数太少或太多,我们 就可以认为时间序列存在某种趋势性或周期性。
设序列长度为N , N N1 N 2 , N1和N 2分别 为记号序列中""与""出现的次数,游程
总数为r,对于随机序列可以证明 : 游程总
(2)自相关图检验(判断准则)
平稳序列通常具有短期相关性。该性质用自相关系数来 描述就是随着延迟期数的增加,平稳序列的自相关系数会 很快地衰减向零。 若时间序列的自相关函数在k>3时都落入置信区间,且 逐渐趋于零,则该时间序列具有平稳性; 若时间序列的自相关函数更多地落在置信区间外面,则 该时间序列就不具有平稳性。
数r的期望和方差分别如下:
E(r) 2N1N2 1 N1 N2
D(r)
2N1N2 (2N1N2 N 2 (N 1)
1)
在大样本情况下(N1或N 2大于15)有 : Z r E(r)
D(r)
渐近服从N (0,1)服布.
(3)检验方法
a.小样本情况 零假设H0:加号和减号以随机的方式出现 检验方法用举例
•例1 时序图 •检验1951年——2005年我国居民住院消费价格指数 的平稳性 •例2 时序图
–检验1990年1月——1997年12月我国药品总产值序 列的平稳性
例1 居民住院消费价格指数时序图
平 稳 序 列
例2 药品总产值时序图
则称该时间序列为平稳序列。
包括严平稳序列和宽平稳序列。
2. 关于非平稳序列的处理
• 在对实际的时间序列进行建模之前,应首先检验 序列是否平稳,若序列非平稳,应先通过适当变 换将其化为平稳序列,然后再进行模型的建立。
• 序列的非平稳包括均值非平稳和方差非平 稳。
• 均值非平稳序列平稳化的方法:差分变换。 • 方差非平稳序列平稳化的方法:对数变换、
例如,观察的结果用加、减标志表示,得到一组这样 的记录顺序:
+ +- - - + - - - -+ + - + 这个样本的观察结果共有7个游程。
(2) 游程检验的基本思想
对于一个时间序列{xt }, 设其样本均值为x , 对序列中比x小的观察值记为" "号,比x大 的观察值记为" "号, 这样就形成了一个符 号序列.并可求出这个序列的游程数.
• 一个平稳的时间序列在图形上往往表现出一种 围绕其均值不断波动的过程;
• 而非平稳序列则往往表现出在不同的时间段具 有不同的均值(如持续上升或持续下降)。
Xt
Xt
t
t
(a)
(b)
图 9.1 平稳时间序列与非平稳时间序列图
这种方法通过观察时间序列的趋势图来判断时间序列 是否存在趋势性或周期性。
若序列无趋势,但是具有季节性,那末对于按月采 集的数据,时滞12,24,36……的自相关系数达到最 大(如果数据是按季度采集,则最大自相关系数出现在 4,8,12, ……),并且随着时滞的增加变得较小。
若序列是有趋势的,且具有季节性,其自相关函数特 性类似于有趋势序列,但它们是摆动的,对于按月数 据,在时滞12,24,36,……等处具有峰态;如果时 间序列数据是按季节的,则峰出现在时滞4,8, 12, ……等处。
