第09讲 因式分解
《 因式分解法》PPT课件

精彩一题 解:令 x2-x=y,则原方程可化为 y2-4y-12=0, 即(y+2)(y-6)=0.所以 y+2=0 或 y-6=0, 解得 y1=-2,y2=6. 当 y=-2 时,x2-x=-2,即 x2-x+2=0,此方程无实数解; 当 y=6 时,x2-x=6,即(x+2)(x-3)=0, 解得 x1=-2,x2=3. 所以原方程的解为 x1=-2,x2=3.
当 0≤x<1 时,12x2=0,解得 x1=x2=0;
当-1≤x<0 时,12x2=-1,方程没有实数解;
当-2≤x<-1 时,12x2=-2,方程没有实数解;
所以方程[x]=12x2 的解为 0 或 2. 【答案】A
课堂导练 12.已知下列方程,请把它们的序号填在最适当的解法后的横线
上.
①2(x-1)2=6;
精彩一题
(1)在由方程 x4-x2-6=0 得到方程①的过程中,利用__换__元____ 法达到了降次的目的,体现了___转__化___的数学思想.
【思路点拨】根据换元法解一元二次方程的特点即可得出结论;
精彩一题 (2)利用本题的解题方法,解方程(x2-x)2-4(x2-x)-12=0. 【思路点拨】设 x2-x=y,于是原方程可变为 y2-4y-12=0, 解方程可求出 y 值,再将其代入 x2-x=y 中即可求出 x 的值.
解: 3x(x-2)=x-2, 3x(x-2)-(x-2)=0, (x-2)(3x-1)=0. ∴x1=2,x2=13.
课后训练 (2)x2-( 2+ 3)x+ 6=0;
解:x2-( 2+ 3)x+ 6=0, (x- 2)(x- 3)=0. ∴x1= 2,x2= 3.
课后训练 (3)(2x+1)2-3(2x+1)-28=0.
第9讲 因式分解(一)

第九讲 因式分解(一) 知识模块一、因式分解的概念 知识梳理: 定 义 示 例 剖 析 定义:把一个多项式化成几个整式的积的形式,这种式子变形叫做因式分解,又叫分解因式。 a+a2=a(1+a);4x2+2x3=2x2(2+x)
3a3b+6a2b+3ab=3ab(a2+2a+1)=3ab(a+1)2 实质:是一种恒等变形,是一种化和为积的变形。 因式分解与整式乘法是相反方向的变形 ma+mb+mc 因式分解整式乘法m(a+b+c)
多项式因式分解整式乘法整式乘积 分解因式的注意事项 1、结果一定是乘积的形式; 2、每一个因式都是整式; 3、相同的因式的积要写成幂的形式; 4、没有大括号和中括号; 5、每个因式中不能含有同类项,如果有需要合并的同类项,合并后要注意能否再分解; 6、单项式因式写在多项式因式的前面; 7、每个因式第一项系数一般不为负; 8、若不特别说明,分解因式的结果必须是每个因式在有理数范围内不能再分解为止。
如:x+1=x(1+1x)不是因式分解
x2−1=(x+1)(x−1)是因式分解 (x+y)(x−y)=x2−y2不是因式分解
x2+3x−2=x(x+3)−2不是因式分解
例1.下列各式从左边到右边的变形中,是因式分解的是( ) A.3ab(a+b)=3a2b+3ab2 B.2x2+4x=2x2(1+2x) C.a2−4b2=(a+2b)(a−2b) D.3x2−6xy+3x=3x(x−2y)+3x
例2.(1)一个多项式分解因式的结果是(b3+2)(2−b3),那么这个多项式是( )
A.b6−4 B.4−b6 C.b6+4 D.−b6−4 (2)若多项式x2+ax+b可因式分解为(x+1)(x−2),求a+b的值为 。
知识模块二、提公因式法 知识梳理: 定 义 示 例 剖 析 如果多项式的各项有公因式,一般要将公因式提到括号外面进行因式分解。 确定公因式的方法:
如:ma +mb + mc =m(a+b+c);
因式分解ppt

因式分解ppt作为一名数学学者,我认为因式分解是数学中的基本算法之一,也是许多高级数学领域的基础。
在学校的数学教育中,因式分解通常作为代数学的一部分来学习。
因此,本文将从代数学的角度阐述因式分解的相关知识和应用。
首先,让我们来看看因式分解的定义。
因式分解是将一个多项式分解成若干个较简单的因子的乘积的过程。
可以分解的多项式通常具有以下形式:$a^2-b^2$,$ax^2 + bx + c$等。
接下来,让我们来看一些常见的因式分解方法。
首先是提公因式法,该方法可以从一个多项式中提取一个公共因子。
例如,对于式子$3x^2 + 9x$,我们可以提取出3x,得到$3x(x+3)$。
其次是求平方差法,该方法可以将形如$a^2-b^2$的多项式分解为$(a+b)(a-b)$。
例如,$9-4$可以分解为$(3+2)(3-2)$。
最后是配方法,这是一种用于分解三次或更高次多项式的方法。
例如,对于式子$x^3+3x^2+3x+1$,我们可以使用配方法将其分解为$(x+1)^3$。
除了以上方法外,还有一些其他的因式分解技巧,如因式定理、差积公式等,都可以有效地帮助我们完成因式分解。
事实上,因式分解在数学中有着广泛的应用。
在高等数学领域,因式分解是许多理论研究的基础,如线性代数、物理学、工程学等都有广泛的应用。
在实际计算中,因式分解也有许多应用,如多项式插值、信号处理、图像处理等。
此外,在金融等领域中,因式分解也有不少应用,如投资分析、财务报告分析等。
总之,因式分解是一种基本的数学算法,在数学教育中具有重要的地位。
通过学习和掌握因式分解的方法和应用,不仅能够提高代数学的水平,也能够更好地应用于实际计算和理论研究中。
第09讲 一元二次方程

方米的矩形草坪,它的长比宽多10米,设草坪的宽为x米,则
可列方程为( )
(A)x(x-10)=200
(C)2x+2(x+10)=200
(B)2x+2(x-10)=200
(D)x(x+10)=200
【解析】选D.宽为x米,则长为(10+x)米, 可得x(x+10)=200.
10.(2012·湘潭中考)如图,某中学准备在校园里利用围墙的
一元二次方程的基本概念
◆中考指数:★★★★☆
1.一元二次方程的三个特点 (1)只含有一个未知数;(2)未知数的最高次数是2;(3)是 整式方程. 2.要判断一个方程是否为一元二次方程,先看它是否为整 式方程,若是,再对它进行整理.如果能整理为 ax2+bx+c=0(a≠0)的形式,则这个方程就是一元二次方程.
解二元一次方程组
结果
选D
【对点训练】
1.(2011·兰州中考)下列方程中是关于x的一元二次方程的
是( ) (B)ax2+bx+c=0 (D)3x2-2xy-5y2=0
x
(A) x 2 12 0 (C)(x-1)(x+2)=1
【解析】选C.A项分母中含有未知数,不一定是一元二次方程; B项中未强调a≠0,不一定是一元二次方程;D项中含有两个未 知数,不是一元二次方程.
2 1 2 的值为( ) 2 a 1 a a (A) 1 5 (B) 1 5 2 2
(C)-1
(D)1
【解析】选D.根据题意,得a2+a-1=0,∴a2+a=1. ∴原式=
2a a 1 a a 1 a 1 a a 1 (a 1) a 1 1 1 2 1. a a 1 a 1 a a 1 a a
【北师大版初三数学】第9讲:因式分解法解一元二次方程-教案
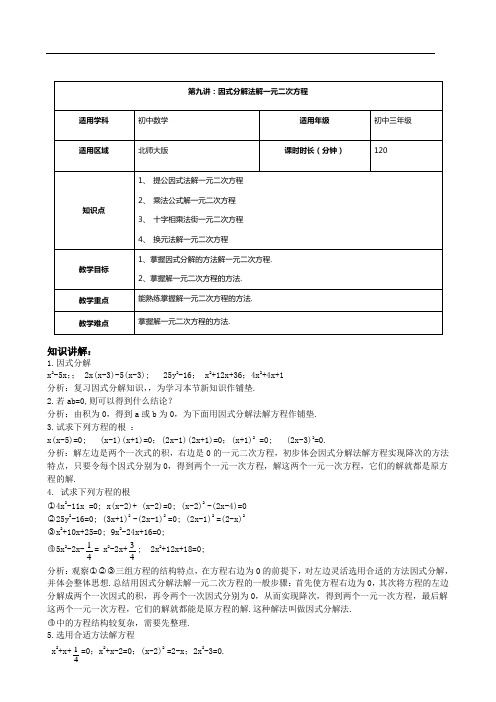
知识讲解:1.因式分解x 2-5x ;; 2x(x-3)-5(x-3); 25y 2-16; x 2+12x+36;4x 2+4x+1分析:复习因式分解知识,,为学习本节新知识作铺垫.2.若ab=0,则可以得到什么结论?分析:由积为0,得到a 或b 为0,为下面用因式分解法解方程作铺垫.3.试求下列方程的根 :x(x-5)=0; (x-1)(x+1)=0;(2x-1)(2x+1)=0;(x+1)2 =0; (2x-3)2=0.分析:解左边是两个一次式的积,右边是0的一元二次方程,初步体会因式分解法解方程实现降次的方法特点,只要令每个因式分别为0,得到两个一元一次方程,解这两个一元一次方程,它们的解就都是原方程的解.4. 试求下列方程的根○14x 2-11x =0; x(x-2)+ (x-2)=0; (x-2)2 -(2x-4)=0 ○225y 2-16=0; (3x+1)2 -(2x-1)2 =0; (2x-1)2 =(2-x)2 ○3x 2+10x+25=0; 9x 2-24x+16=0; ○45x 2-2x-41= x 2-2x+43; 2x 2+12x+18=0; 分析:观察○1○2○3三组方程的结构特点,在方程右边为0的前提下,对左边灵活选用合适的方法因式分解,并体会整体思想.总结用因式分解法解一元二次方程的一般步骤:首先使方程右边为0,其次将方程的左边分解成两个一次因式的积,再令两个一次因式分别为0,从而实现降次,得到两个一元一次方程,最后解这两个一元一次方程,它们的解就都能是原方程的解.这种解法叫做因式分解法.○4中的方程结构较复杂,需要先整理. 5.选用合适方法解方程x 2+x+41=0;x 2+x-2=0;(x-2)2 =2-x ;2x 2-3=0.分析:四个方程最适合的解法依次是:利用完全平方公式,求根公式法,提公因式法,直接开平方法或利用平方差公式.归纳:配方法要先配方,再降次;公式法直接利用求根公式;因式分解法要先使方程一边为两个一次因式相乘,另一边为0,再分别使各一次因式等于0.配方法、公式法适用于所有一元二次方程,因式分解法用于某些一元二次方程. 解一元二次方程的基本思路:化二元为一元,即降次.课堂练习:考点一:用提公因式法解一元二次方程【例题】 1、用因式分解法解一元二次方程0)1(2)1(=---x x x ,正确的步骤是( )A .0)2)(1(=++x xB .0)2)(1(=-+x xC .0)2)(1(=--x xD .0)2)(1(=+-x x2、一元二次方程x 2=3x 的解是:【答案】1、D【解析】根据题意,可将方程化为x(x-1)+2(x-1)=0,提公因式(x-1),有(x-1)(x+2)=0.试题分析:因式分解的一般步骤是:第一,看能不能用提公因式法;第二,公式法,平方差公式和完全平方公式;第三步,对于二次三项式,看能不能用十字相乘法.考点:因式分解.2、x 1=0,x 2=3.【解析】试题分析:利用因式分解法解方程.试题解析:x 2=3x ,x 2-3x=0,x (x-3)=0,x 1=0,x 2=3.考点:解一元二次方程-因式分解法.【练习】1、方程x(x-2)=2-x 的根是( )A .x=-1B .x=2C .120,2x x == D .121,2x x =-=2、解方程2(2)3(2)x x +=+【答案】1、D 2、122,1x x =-=考点二:用乘法公式解一元二次方程【例题】1、一元二次方程(2x -1)2=(3-x)2的解是_______________________.2、写出一个既能直接开方法解,又能用因式分解法解的一元二次方程是__________。
七年级数学第九章:因式分解 第1、2小节北京实验版知识精讲

初一数学第九章:因式分解第1、2小节实验版【本讲教育信息】一. 教学内容:第九章:因式分解第1小节:因式分解第2小节:提取公因式法教学要求:1. 初步了解分解因式是将一个多项式化为几个整式的积的形式,理解因式分解和整式乘法的互逆关系;2. 掌握提公因式法分解因式,能正确找到多项式各项的公因式,并正确地提出公因式;3. 在分解因式的过程中理解并应用换元思想;4. 初步学会将分组的手段运用于分解因式的过程中。
二. 重点、难点1. 重点:(1)理解因式分解和整式乘法的互逆关系。
(2)会用提公因式法分解因式。
2. 难点:(1)正确找到多项式各项的公因式。
(2)换元思想在分解过程中的应用。
课堂教学:(一)知识要点:1. 因式分解:把一个多项式化为几个整式的乘积的形式,叫做把这个多项式因式分解,也叫做将多项式分解因式。
因式分解和整式乘法的互逆关系:2. 公因式:把多项式各项都含有的因式叫多项式各项的公因式。
公因式的组成:注:多项式首项为负,则公因式为负,多项式首项为正,则公因式为正。
3. 提取公因式法分解因式:将多项式的公因式提取出来,写成公因式与另一个多项式因式乘积的形式,这种因式分解的方法叫提取公因式法。
基本形式:提取公因式法分解因式的一般步骤:(1)找到多项式各项的公因式(2)将多项式的各项分别写成公因式和另一个因式乘积的形式(3)提取公因式:将公因式提到括号外,括号里的各项是上一步中另一个因式的代数和注:(1)若多项式因式的首项不能为负,若多项式首项为负,可通过公因式的符号加以解决。
(2)若多项式某项为公因式或公因式的相反数,则多项式因式对应项为1或-1。
(3)多项式因式的项数和多项式的项数相同。
(4)公因式可为单项式,也可为多项式,亦可以单项式与多项式的乘积。
(5)在找公因式的过程中,不要漏掉某些因式,否则提取公因式后,多项式因式仍可继续提公因式法分解因式。
4. 分组手段在提取公因式法分解因式中的应用步骤:先分组,再分解。
因式分解ppt(共22张PPT)
规律总结
• 对多项式分解因式与整式乘法是方向相反的两种恒等变 形.
• 整式的乘法运算是把几个整式的积变为多项式的形式,
特征是向着积化和差的形式发展;
• 多项式的分解因式是把一个多项式化为几个整式乘积的
形式,特征是向着和差化积的形式发展.
• 因式分解要注意以下几点: 1.分解的对象必须是多项式.
• 把一个多项式化成几个整式的积的形式,这 种变形叫做因式分解。
• 因式分解也可称为分解因式。
因分解的结果要以积的形式表示
2.每个因式必须是整式,且每个因式的次数 都要低于原多项式的次数。
3.必须分解到每个多项式不能分解为止(具 体由所在的数集决定)。
想一想: 因式分解与整式乘法有什么联系?
2.分解的结果一定是几个整式的乘积的形式.
2:计算
(1) 8728713 (2) 1012992
=87(87+13) =8700
=(101+99)(101-99) =200×2 =400
3.若 x101,y99则 x22xyy2_ 4_
动脑筋
n2+n是奇数还是偶数?
2517-532能被120整除吗? 若n是整数,证明 (2n+1)2-(2n-1)2是8的倍数.
多项式的因式分解与整式乘法是方向相反的恒等式.
整式乘法
3x(x-1)= _____
(3).(5a-1) =25a -10a+1 解: ab-ac=a(b-c)
a(a+1)(a-1) a3-a=a(a+1)(a-1)
2
2
整式乘法
答: 由a(a+1)(a-1)得到a3-a的变形是整式乘法,由a3-a得到a(a+1)(a-1)的变形是把一个多项式化成几个整式的积的形式.
因式分解法(教学课件)—2025学年人教版数学九年级上册
即
10x-4.9x2.
配方法解方程 10x - 4.9x2 = 0
解: x2 100 x 0, 49
x2
100 49
x
50 49
2
0
50 49
2
x
50 49
2
50 49
2
,
x 50 50,
49 49
x1
100 , 49
x2 0.
【注意】不能随意在方程两边约去含未知数的代数式, 如 x(x - 1) = x,若约去 x,则会丢失 x = 0这个根.
几种常见的用因式分解法求解的方程:
(1)形如 x2 +bx = 0 的一元二次方程,将左边运用提公因式法因
式分解为 x(x+b) = 0,则 x = 0 或 x+b = 0,即 x1= 0, x2 = -b.
A. x 2
B. x 3
C. x1 2 , x2 3
D. x1 2 , x2 3
解析:因为 (x 2)(x 3) 0 ,所以 x 2 0 或 x 3 0 , 解得 x1 2 , x2 3 .故选 D.
练习 3 已知某一元二次方程的两根分别为 x1 3 , x2 4 ,则这个
方程可能为( C )
A. (x 3)(x 4) 0 C. (x 3)(x 4) 0
B. (x 3)(x 4) 0 D. (x 3)(x 4) 0
解析:A、 (x 3)(x 4) 0 ,解得: x1 3 , x2 4 ,符合题意; B、 (x 3)(x 4) 0 ,解得: x1 3, x2 4 ,不符合题意; C、 (x 3)(x 4) 0 ,解得: x1 3, x2 4 ,不符合题意; D、 (x 3)(x 4) 0 ,解得: x1 3, x2 4 ,不符合题意; 故选:A.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
让我们为全力打造甘肃名校—甘肃省华亭县皇甫学校而共同努力吧! 走进奥数,成就辉煌—皇甫学校培优竞赛教程(李敬之个人竞赛空间) 47
第9讲 因式分解 如果你想学会游泳,你必须下水;如果想成为解题能手,你必须解题。 ——波利亚
知识方法扫描 将一个多项式化为几个整式的积的形式,叫做因式分解。因式分解是一种重要的恒等变形,在数学中有广泛的应用。 因式分解的方法比较多,除了课本介绍的提公因式法,公式法,十字相乘法,分组分解法外,我们还要掌握换元法,主元法,配方法, 待定系数法等。 1.换元法. 在解题的过程中,我们常把某个比较复杂的代数式看成一个整体,将它用一个字母来代替,从而简化这个代数式的结构,这种方法就是换元法. 在因式分解中用换元法,又可细分为整体代换,对称代换,倒数代换,平均代换等. 2.主元法 在分解一个含有多个字母的多项式时,我们常选择一个字母作为主要元素,将其他字母看作常数,然后将多项式按选定的字母降幂排列,这种方法叫做主元法。用主元法往往可以得到恰当的分组,从而找出公因式来。 3.配方法 通过添项,拆项利用公式将一个多项式配成一个完全平方,是一种常用的恒等变形技巧,以便利用公式来分解因式。 4.待定系数法 在解决有关多项式时,可先假定问题的结果已经求出,其中含有未知系数,然后根据多项式恒等的定义或性质,列出含有这些未知数的方程或方程组,通过解方程或方程组,求出未知系数的值,从而解决问题的方法。
经典例题解析 例1 (1994年第6届“五羊杯”数学竞赛试题)在有理数范围内分解因式: (1)16(6x-1)(2x-1)(3x+1)(x-1)+25= . (2)(6x-1)(2x-1)(3x-1)(x-1)+x2= . (3)(6x-1)(4x-1)(3x-1)(x-1)+9x4= . 解 (1)原式=(6x-1)(4x-2)(6x+2)(4x+4)+25=(24x2-16x+2) (24x2-16x-8)+25 设 24x2-16x+2=t, 原式=t(t-10)+25=(t-5)2=(24x2-16x-3)2
(2)原式=(6x-1) (x-1) (2x-1)(3x-1) +x2=(6x2-7x+1)(6x2-5x+1) +x2 设6x2-7x+1=t, 原式=t(t-2x) +x2=(t-x)2=(6x2-6x+1)2 (3)原式=(6x-1) (x-1) (4x-1)(3x-1) +9x4=(6x2-7x+1) (12x2-7x+1)+ 9x4 设6x2-7x+1=t, 原式=t(6x2+t)+ 9x4=(t+3x2)2=(9x2-7x+1)2 评注 换元法是因式分解的常用方法,需要根据具体的题目选择恰当的方式换元。 例2 (2000年第12届“五羊杯”数学竞赛试题) 分解因式:(2x –3y)3 + (3x –2y)3
–125(x–y)3= .
解 设2x –3y=a, 3x –2y=b, -5x+5y=c,显然a+b+c=0. 让我们为全力打造甘肃名校—甘肃省华亭县皇甫学校而共同努力吧! 走进奥数,成就辉煌—皇甫学校培优竞赛教程(李敬之个人竞赛空间) 48
由公式 a3+b3+c3-3abc=(a+b+c)(a2+b2+c2-bc-ca-ab) 知此时有a3+b3+c3=3abc,故原式=3(2x –3y) (3x –2y) (-5x+5y)=-15(2x –3y) (3x –2y)(x-y) 例3.(1997-1998年天津市初二数学竞赛决赛试题)分解因式
xy(xy+1)+(xy+3)-2(x+y+12)-(x+y-1)2 解 设xy=a, x+y=b,则 原式=a(a+1)+(a+3)-2b-1-( b-1)2
=a2+2a+1-b2=(a+1)2-b2=(a+1+b)(a+1-b) =(xy+1+x+y)(xy+1-x-y)=(x+1)(y+1)(x-1)(y-1) 评注 这种方法叫做对称代换,一般对于对称式,适于采用对称代换法换元。 例4.(1991年贵州省初中数学竞赛试题)分解因式:x4+x3-4x2+x+1。
解 原式=2222221111(4)()()4xxxxxxxxxx。
设1,xtx则22212xtx,则 原式=x2(t+t2-2-4)= x2(t+3)(t-2)=211(3)(2)xxxxx=(x2+3x+1)(x-1)2。 评注 这种方法叫做倒数代换,适用于系数降幂排列时系数对称的多项式。 例5.(1994年石家庄市初中数学竞赛试题)分解因式 (x+1)4+(x+3)4-272。 解 设x+2=t, 则 原式=(t-1)4+(t+1)4-272=2t4+12t2-270=2(t2+15)( t2-9) =2(x2+4x+19)(x+5)(x-1) 评注 这种方法叫做平均代换,平均代换的目的是为了消去四项式中的奇数项,以便利用二次三项式的方法分解。 例6.(1998-1999年天津市初二数学竞赛预赛试题)分解因式: 2x3-x2z-4x2y+2xyz+2xy2-y2z 。 解 原式=(2x-z)y2-2(2x-z)xy+(2x-z)x2=(2x-z)(y-x)2 评注 按一个字母降幂排列,是此类形式的多项式采用分组分解法来分解因式的分组根据。 例7.(1986年扬州市数学竞赛试题)因式分解:(1+y)2-2x2(1+y2)+x4(1-y)2。解 原式=[(1+y)2+2x2(1-y2)+x4(1-y)2]-4x2=[(1+y)+x2(1-y)]2-(2x)2
=[(1+y)+x2(1-y)+2x] [(1+y)+x2(1-y)-2x]=[(x+1)2-y(x2-1)] [(x-1)2-y(x2-1)] =(x+1)(x-xy+y+1)(x-1)(x-xy-y-1)。 评注 配方法也是因式分解的重要方法,配方后就有利于应用公式来解题。 例8.(2002年太原市初中数学竞赛试题)关于x,y的二次式 x2+7xy+my2-5x+43y-24可分解为两个一次因式的乘积,则m的值是 . 解 设x2+7xy+my2-5x+43y-24=(x+ay+b)(x+cy+d),即 x2+7xy+my2-5x+43y-24=x2+(a+c)xy+acy2+(b+d)x+(ad+bc)y+bd 比较对应项的系数,得 a+c = 7 (1) ac = m (2) b+d = -5 (3) 让我们为全力打造甘肃名校—甘肃省华亭县皇甫学校而共同努力吧! 走进奥数,成就辉煌—皇甫学校培优竞赛教程(李敬之个人竞赛空间) 49
ad+bc = 43 (4) bd = -24 (5) 由(3),(5)解得 b = 3,d = -8 或b = -8,d = 3 当b = 3,d = -8 时,(4)式为 -8a+3c=43 (6) 由(1),(6)解得 a=-2,c=9. 故m=ac=-18 当b = -8,d = 3时,可以得到同样的结果。
同步训练 一 选择题 1.(1999年北京市中学生数学邀请赛试题)x2+2x-99等于( ) (A)(x-9)(x-11)(B)(x+9)(x-11)(C)(x-9)(x+11)(D)(x+9)(x+11) 2.(2002年第13届“希望杯”数学竞赛试题)下列各式分解因式后,可表示为一次因式乘积的是( ). (A) x3-9x2+27x-27(B)x3-x2+27x-27(C)x4-x3+27x-27(D)x3-3x2+9x-27 3.(1985年上海市初中数学竞赛试题)x2y-y2z+z2x-x2z+y2x+z2y-2xyz因式分解之后,正确的结果为( ). (A) (y-z)(x+y)(x-z) (B) (y-z)(x-y)(x+z) (C) (y+z)(x-y)(x+z) (D) (x+z) (x+y) (x-z) 4. (1997年第8届“希望杯”数学竞赛初二第二试试题)把多项式x2-y2-2x-4y-3因式分解之后,正确的结果是( ). (A) (x+y+3)(x-y-1) (B) (x+y-1)(x-y+3) (C) (x+y-3)(x-y+1) (D) (x+y+1)(x-y-3) 5.(2002年北京市数学竞赛预赛试题)a4+4分解因式的结果是( ). (A) (a2+2a-2)(a2-2a+2) (B) (a2+2a-2)(a2-2a-2) (C) (a2+2a+2)(a2-2a-2) (D) (a2+2a+2)(a2-2a+2) 二 填空题 6.(2000年第12届“五羊杯”数学竞赛试题)分解因式:(x –2)3 – (y –2)3
–(x–y)3= .
7.(2002年河南省数学竞赛试题)分解因式:x4+2x3+3x2+2x+1= . 8.(1998年第9届“希望杯”数学竞赛初二第二试试题)把代数式(x+y-2xy)(x+y-2)+(xy-1)2分解成因式的乘积应当是 . 9.(2000年第13届“五羊杯”数学竞赛试题)分解因式:(x4-4x2+1)(x4+3x2+1)+10x4= . 10.(1999年天津市数学竞赛试题)k为 时,多项式x2-2xy+ky2+3x-5y+2能分解为两个一次因式的乘积。 三、解答题 11.(1998年天津市数学竞赛试题)分解因式:(x+1)(x+2)(x+3)(x+6)+x2
12.(1992年沈阳市数学竞赛试题)分解因式:x4+y4 +z4-2x2y2-2y2z2-2z2x2 13.(1996年北京市数学竞赛试题)一个自然数a恰好等于另一个自然数b的平方,则称自然数a为完全平方数,如64=82,64就是一个完全平方数,若a=19952+19952×19962+19962,求证:a是一个完全平方数。 14.(1994年“祖冲之杯”数学邀请赛试题)已知乘法公式 a5+b5=(a+b)(a4-a3b+a2b2-ab3+b4),a5-b5=(a-b)(a4+a3b+a2b2+ab3+b4),利用或不利用上
