绕y轴旋转体侧面积公式
一般旋转体的体积和侧面积计算公式

积 怎 样 计 算 ?不 少 人 认 为 利 用 坐 标 变 换 , 任 意 轴 L( 转 轴 )为 X 轴 建 立 新 的 坐 标 系 , 利 用 常 规 法 以 旋 再 进 行 求 解 即 可 。 理 论 上 讲 , 种 方 法 能 得 到 最 终 的 结 果 , 事 实 上 , 于 曲 线 一 f( 从 这 但 由 z)经 坐 标 变 换 后 ,
曲 边 梯 形 绕 直 线 一 z + m 旋 转 所 生 成 的 立 体 体 积 为 :
V一 二l 厂z一 一m 厂() d _ _ [() 丽 ]l +1 - z lz
I PP,l 一
证 明 如 图 2设 M 、 在 直 线 L 上 的 射 影 分 别 为 t t, 过 N , 通
图 1
N
X
轴 上 的 任 意 点 z 与 z+ △ z分 别 作 垂 直 于 x 轴 的 直 线 , 们 在 曲 线 它 M , 上 截 出 一 段 △ l 为 下 面 证 明 方 便 , 为 AB), △ z 任 取 一 点 、 , ( 记 在 上
V
PA ' l
/
P ( ), 在 直 线 L 的 射 影 为 P 由 于 函 数 一 厂( z, P , z)在 [ 6 ,]上 连
维普资讯
20 0 8年 5月 第 1 第 2期 4卷
安 庆 师范 学院 学报 ( 自然 科 学版)
Junl f n i e cesc Ig ( aua c neE io ) ora o A qn T a h r oI e N trI i c dt n g e S e i
旋转体侧面积与体积的计算

对于上述 Ⅱ+1 个区间中的任意一个[ , ]V tt , t∈( , … t
, t ≠0 则X()>0 ()<0不防设 ()> , 或 t . t 0 当平面曲线 C 的直角坐标方程为, . ,n ≤6 , 一 厂 (≤ ( ) )如 t ) 有 () , t
则 ( 在区间 , 严格增加 因 = ( 在区 f = t ) t …] . 此, xt ) 问[ , l
^ 8 — 一 — —— 一 — — 8
s 2 y) ( +t ,=ryt £ d =7 (l £ y( V 7 2) ) t r f ) 2 伽c f ( ‘ (l.
J转体的侧面积和体积的计
算方法.
1 光滑 曲线的定义
证明: ,) 设在( 内使 ()=0 有n f t …, 满足 t 的t 个:, , t £ <t l 2<… <t, f , = 则它们将[ p 分成 n 且设 0= t , ,]
体 的侧 面积 和 体 积 的计 算 方 法.
关键词 : 光滑曲线 ; 旋转体 ; 角坐标 方程; 直 参数方程; 坐标方程 极 中图分类号: 8 012 文献标识码 : A 文章编号 :6 1— 3 5 2 0 )2一o 2 0 17 5 6 (0 8 l 04— 3
0 引言
2 绕 轴旋转的情形
到的旋转体的侧面积和体积分别为 S, 一S 和 , 一 oS , ,
.
,t( ≤t )如果 : t, )t都是连续可微函数, ()o ≤ . t ()y= ) ( 则 称曲线 C为光滑曲线 J . 果 一 fx 是连续可微函数, () 则曲线 C为光滑曲线.
则 S=S S +… + V= + +… + . o+ l 5和 l
收稿 日期 :0 8— 4—1 20 0 0
-体积、旋转体的侧面积、一些物理量的计算
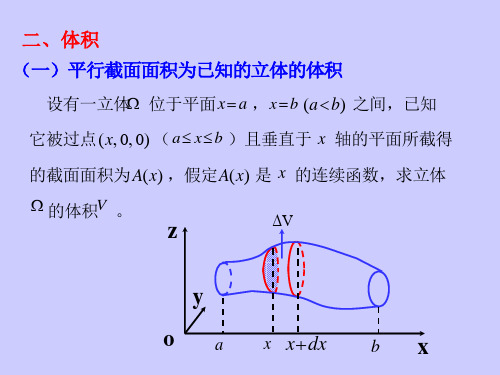
dV A(x)dx,
b
V a A(x)dx.
例 1.设有半径为R 的正圆柱体,被通过其底的直径
而与底面交成 的平面所截,求截得的圆柱楔的体积。
解:如图建立坐标系,
y tan
R
则底圆的方程为x2 y2 R2 。
x y
x[R, R] ,用过点x 且垂直于x 轴 o
x2
)dx
a
V
a a
b2 a2
(a
2
x2
)dx
ox
b
Байду номын сангаасax
x dx
2
b2 a2
a 0
(a2 x2)dx
2b2 a2
(a
2
x
1 3
x3
)
a 4 ab2. 03
例 3.已知圆台的上底半径为 r1 ,下底半径为r2 ,高为h ,
求它的体积。
解:如图选择坐标系,母线 AB 的方程为
y
0
r1
h r2
y
o a x xdx b x
设[x,x dx] 是[a,b] 上的代表小区间,相应的一小块立体
的体积记为V ,设 A(x) 在[x,x dx] 上的最小值和最大值分
别为m 和 M ,则 mdxV Mdx,
取近似
V A(x)dx,
其误差为 V A(x)dx (M m)dx ,
∵当dx0 时,(M m) 0 ,
则 dA 2f (x)dL ,
oa
故
A 2
b
f (x)
1 y2 dx.
a
y f (x) x x dx b x
[ 圆台的侧面积= 母线长 (上底半径 下底半径 ) 。在极限 状态,母线长是弧微元dL ;上底半径 下底半径 2f(x) 。]
定积分在几何学上的应用

成的图形的面积.
解 两曲线的交点
y2 2x y x4
(2 , 2 )(,8 ,4 ).
yx4
y2 2x
选 y为积分变量 y[2,4]
dAy4y2dy
4
A dA18.
2
2
整理ppt
6
如果曲边梯形的曲边为参数方程
x y
(t) (t)
曲边梯形的面积 A t2(t)(t)d.t t1
( 其 中 t 1 和 t 2 对 应 曲 线 起 点 与 终 点 的 参 数 值 )
就得半径为a
的球体的体积
4 3
a3
.
整理ppt
21
2
2
2
例 9 求星形线 x 3 y 3 a 3 (a 0)绕 x轴旋转
构成旋转体的体积.
y
2
2
2
解 y3 a3 x3,
y2
a32
2
x3
3
a
x[a,a]
o
ax
旋 转 体 的 体 积
V
aaa32
2
x3
3
dx
32 a3 105
.
整理ppt
22
25
绕 y 轴 旋 转 的 旋 转 体 体 积 2ayC B xx2(y)
可看作平面图OABC与OBC o xx1(y)
A
2a x
分别绕y轴旋转构成旋转体的体积之差.
Vy
2ax22(y)dt
0
2ax12(y)dt
0
a2(tsit)n 2asitn dt 2 a2(tsit)n 2asitn dt 0
0
整理ppt
28
例 求曲线 y3x21 与 x 轴围成的封闭图形
侧面积公式推导

定积分在几何上的应用3——求旋转体的侧面积
设旋转体是曲线y=f(x)(≥0,a≤x≤b),直线x=a,x=b绕x轴旋转而生成.任取一微区间[x,x+dx],如图1.有P(x,y),Q(x+dx,y+Δy),由弧微分中的讨论知:
弧长=Δs=ds+o(dx) ①
线段=+o(dx)=ds+o(dx) ②
因为绕x轴旋转生成的旋转体的侧面积是侧面积量A的增量ΔA,线段PQ绕x轴旋转生成的面积恰好是上、下底面半径为y和y+Δy,侧高为的圆台的侧面积Δ∑.由圆台侧面积公式可知后者等于
Δ∑=π(y+y+Δy)
=π[2y+dy+o(dx)][ds+o(dx)]
=2πyds+o(dx),
显然ΔA=Δ∑+o(dx),故有
从而旋转体的侧面积为
相应地也可写出曲线在参数坐标和极坐标下的侧面积公式,这里不列出了.例18 求抛物线y2=2px(0≤x≤a)绕x轴旋转生成的旋转体的侧面积.
由⑤式得侧面积为
例19 求由圆x2+(y-a)2=r2(r<a)绕x轴旋转而成的环体的表面积.
故对哪个半圆周都有
代入公式⑤即得所求表面积为
解采用参数坐标较为方便.令x=acost,y=bsint 0≤t≤2π弧长微分
故表面积为
我们说过椭圆的周长不能准确计算,但椭圆的旋转面积却能准确算出来.当e
习题
29.求抛物线y2=4x,直线x=8所围成图形绕x轴旋转所得旋转体的侧面积.求旋转下列曲线所成曲面的面积
33.x=a(t-sint),y=a(1-cost)(0≤t≤2π)分别绕x轴和y轴.
答案
如有侵权请联系告知删除,感谢你们的配合!。
古尔丁定理求旋转体表面积

古尔丁定理求旋转体表面积古尔丁定理求旋转体表面积一、引言在数学中,旋转体是一个非常重要的概念,它是由一个平面图形绕着某个轴线旋转而成的立体图形。
旋转体广泛应用于各种领域,比如建筑设计、机械制造、航空航天等。
在计算旋转体表面积时,古尔丁定理是一个非常有用的工具。
二、古尔丁定理的定义古尔丁定理是指,在平面上存在一条曲线,将其绕某个轴线旋转一周所得到的旋转体表面积等于该曲线沿轴线方向上的长度与该曲线绕轴线旋转一周所得到的螺旋线长度之积。
三、古尔丁定理的证明为了证明古尔丁定理,我们需要从几何和微积分两个角度进行分析。
1. 几何分析设平面上存在一条曲线L,并以y轴为轴将L绕x轴逆时针旋转一周所得到的立体图形为S。
我们可以将S划分成无数个小块,每个小块都可以看作一个圆台。
设第i个小块半径为ri,高为hi,底面圆周长为Li,则该小块的表面积为:Si = πri^2 + πriLi将该小块绕x轴旋转一周所得到的螺旋线长度为:di = 2πrihi则整个立体图形S的表面积为:S = ∑Si = ∑(πri^2 + πriLi) = π∑(ri^2 + riLi)将该曲线L沿y轴方向上的长度表示为L,则有:L = ∫[a,b]√(1+(dy/dx)^2)dx其中a和b分别表示曲线L在x轴上的两个交点。
我们可以通过微积分方法求出该曲线绕y轴旋转一周所得到的螺旋线长度,即:d = 2π∫[a,b]√(1+(dy/dx)^2)dx因此,根据古尔丁定理可得:S = Ld即旋转体表面积等于曲线沿轴线方向上的长度与曲线绕轴线旋转一周所得到的螺旋线长度之积。
2. 微积分分析古尔丁定理还可以通过微积分方法进行证明。
设平面上存在一条曲线L,并以y轴为轴将L绕x轴逆时针旋转一周所得到的立体图形为S。
我们可以将该曲线表示为y=f(x),则有:S = 2π∫[a,b]f(x)√(1+(dy/dx)^2)dx其中a和b分别表示曲线L在x轴上的两个交点。
定积分的几何应用公式总结

定积分在几何上的应用公式及其应用定积分的几何应用公式主要包括以下几种:
1.曲线长度公式:设曲线L的参数方程为x=f(t),y=g(t),t∈[a,b],则曲线
L的长度L可表示为定积分形式:L = ∫[a,b]√[f'(t)² + g'(t)²] dt。
2.曲线旋转体体积公式:设曲线L的参数方程为x=f(t),y=g(t),t∈[a,b],
绕x轴旋转一周生成的曲面的体积V可表示为定积分形式:V = π∫[a,b] [f(t)]^2 dt。
3.平面图形面积公式:如果平面区域D由曲线y=f(x)和直线x=a,x=b以及
x轴围成,则该平面图形的面积为A = ∫(a,b) [f(x)] dx。
4.旋转体侧面积公式:设曲线y=f(x)在[a,b]上非负、连续、且f(0)=0,则由
该曲线及直线y=0,x=a,x=b所围成的柱体的侧面积为S = ∫(a,b) [2πxf(x)] dx。
这些公式都是定积分在几何上的重要应用,可以通过这些公式解决实际问题。
考研数学旋转体表面积公式

考研数学旋转体表面积公式
旋转体是指一个平面图形绕着某条轴线旋转一周形成的立体图形。
求解旋转体的表面积需要根据具体的旋转体形状来选择相应的公式。
常见的旋转体包括圆锥、圆柱和圆盘等。
下面分别介绍它们的表面积公式:
1. 圆锥的表面积公式:
圆锥的侧面积为 L = πrl,其中 r 为底面半径,l 为母线长度。
圆锥的底面积为 B = πr²,其中 r 为底面半径。
圆锥的总表面积为 S = L + B = πrl + πr²。
2. 圆柱的表面积公式:
圆柱的侧面积为 L = 2πrh,其中 r 为底面半径,h 为高度。
圆柱的底面积为 B = πr²。
圆柱的总表面积为 S = L + 2B = 2πrh + 2πr²。
3. 圆盘的表面积公式:
圆盘的侧面积为 L = 2πrh,其中 r 为半径,h 为高度。
圆盘的底面积为 B = πr²。
圆盘的总表面积为 S = L + B = 2πrh + πr²。
需要注意的是,以上公式中的 r 和 h 分别表示旋转体的半径和高度,具体应根据题目给出的条件进行替换计算。
另外,如
果旋转体的形状与以上所列的不同,可能需要其他相关公式来计算表面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绕y轴旋转体侧面积公式
椭圆体的体积v=(4/3)πabc 椭圆是平面内到定点f1、f2的距离之和等于常数(大于|f1f2|)的动点p的轨迹,f1、f2称为椭圆的两个焦点。
其数学表达式为:
|pf1|+|pf2|=2a(2a\ue|f1f2|)。
a与b,c分别代表x轴、y轴、z轴的一半。
椭圆是圆锥曲线的一种,即圆锥与平面的截线。
椭圆围绕它的长轴或短轴旋转一周所围成的几何体。
椭圆是圆锥曲线的一种,即圆锥与平面的截线。
椭圆上的任何一点到椭圆的两个焦点距离只和相等。
椭圆的面积就是πab。
椭圆可以看做圆在某方向上的弯曲,它的参数方程就是:
x=acosθ ,y=bsinθ
椭圆围绕它的长轴或短轴旋转一周所围成的几何体,椭圆体近似公式:
① s=πb/(a)(17a+3b)^2
② s=4πb(sin45°(a-b)+b)
如果不建议很高的精度,①②两公式基本满足用户。
如果需要更高精度,则用下列公式即可,(此公式包含了割圆术公式)
s=πb/(a)(16.9a+3.1b)2((a-b)/a)6/arctg((a-b)/a)6
椭圆与其他两种形式的圆锥截面有很多相似之处:抛物线和双曲线,两者都是开放的和无界的。
圆柱体的横截面为椭圆形,除非该截面平行于圆柱体的轴线。
