数学试卷98年普通高等国统一考试(上海卷)数学试题

1999年高考数学试题及答案(全国理)

1999年普通高等学校招生全国统一考试数学（理工农医类）本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分。

第I 卷第1至 2页。

第II 卷3至8页。

共150分。

考试时间120分钟。

第I 卷（选择题共60分）注意事项1．答第I 卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。

2．每小题选出答案后，用铅笔把答题卡对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上。

3．考试结束，监考人将本试卷和答题卡一并收回。

参考公式：三角函数的积化和差公式()()[]βαβαβα-++=sin sin 21cos sin()()[]βαβαβα--+=sin sin 21sin cos()()[]βαβαβα-++=cos cos 21cos cos()()[]βαβαβα--+-=cos cos 21sin sin正棱台、圆台的侧面积公式()l c c S +'=21台侧其中c '、c 分别表示上、下底面周长，l 表示斜高或母线长台体的体积公式()h S S S S V +'+'=31台体其中S '、S 分别表示上、下底面积，h 表示高一、选择题：本大题共14小题；第（1）—（10）题每小题4分，第（11）—（14）题每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）如图，I 是全集，M 、P 、S 是I3个子集，则阴影部分所表示的集合是（A ）（M ∩P ）∩S （B ）（M ∩P ）∪S（C ）（M ∩P ）∩S （D ）（M ∩P ）∪S（2）已知映射f ：B A →，其中，集合{},4,3,2,1,1,2,3---=A射f 下的象，且对任意的,A a ∈在B （A ）4 （B ）5 （C ）6 （D ）7 （3）若函数()x f y =的反函数是()()0,,≠==ab b a f x g y ，则()b g 等于（A ）a （B ）1-a （C ）b （D ）1-b（4）函数()()()0sin >+=ωϕωx M x f 在区间[]b a ,上是增函数，且 ()(),,M b f M x f =-=则函数()()ϕω+=x M x g cos在[]b a ,上（A ）是增函数（B ）是减函数（C ）可以取得最大值M （D ）可以取得最小值M - （5）若()x x f sin 是周期为π的奇函数，则()x f 可以是（A ）x sin （B ）x cos （C ）x 2sin （D ）x 2cos（6）在极坐标系中，曲线⎪⎭⎫ ⎝⎛-=3sin 4πθρ关于（A ）直线3πθ=轴对称（B ）直线πθ65=轴对称（C ）点⎪⎭⎫⎝⎛3,2π中心对称（D ）极点中心对称（7）若干毫升水倒入底面半径为cm 2的圆柱形器皿中，量得水面的高度为cm 6，若将这些水倒入轴截面是正三角形的倒圆锥形器皿中，则水面的高度是（A ）cm 36 （B ）cm 6 （C ）cm 3182 （D ）cm 3123（8）若(),323322104x a x a x a a x +++=+则()()2312420a a a a a +-++的值为（A ）1 （B ）1- （C ）0 （D ）2 （9）直线0323=-+y x 截圆422=+y x 得的劣弧所对的圆心角为（A ）6π （B ）4π （C ）3π （D ）2π （10）如图，在多面体ABCDEF 中，已知面ABCD 是边长为3的正方形，EF ∥AB ，EF 23=，EF 与面AC 的距离为2，则该多面体的体积为（A ）29 （B ）5 （C ）6 （D ）215（11）若,22sin ⎪⎭⎫ ⎝⎛<<->>παπαααctg tg 则∈α（A ）⎪⎭⎫ ⎝⎛--4,2ππ （B ）⎪⎭⎫⎝⎛-0,4π （C ）⎪⎭⎫ ⎝⎛4,0π （D ）⎪⎭⎫⎝⎛2,4ππ（12）如果圆台的上底面半径为5，下底面半径为R ，中截面把圆台分为上、下两个圆台，它们的侧面积的比为1：2，那么R=（A ）10 （B ）15 （C ）20 （D ）25（13）已知两点,45,4,45,1⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛N M 给出下列曲线方程：①0124=-+y x ②322=+y x ③1222=+y x ④1222=-y x 在曲线上存在点P 满足|MP|=|NP|的所有曲线方程是（A ）①③ （B ）②④ （C ）①②③ （D ）②③④（14）某电脑用户计划使用不超过500元的资金购买单价分别为60元、70元的单片软件和盒装磁盘，根据需要，软件至少买3片，磁盘至少买2盒，则不同的选购方式共有（A ）5种（B ）6种（C ）7种（D ）8种1999年普通高等学校招生全国统一考试数学（理工农医类）第II 卷（非选择题共90分）注意事项：1．第II 卷共6页，用钢笔或圆珠笔直接写答在试题卷中。

1999年高考数学试题及答案(全国理)

1999年普通高等学校招生全国统一考试数学（理工农医类）本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分。

第I 卷第1至 2页。

第II 卷3至8页。

共150分。

考试时间120分钟。

第I 卷（选择题共60分）注意事项1．答第I 卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。

2．每小题选出答案后，用铅笔把答题卡对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上。

3．考试结束，监考人将本试卷和答题卡一并收回。

参考公式：三角函数的积化和差公式()()[]βαβαβα-++=sin sin 21cos sin()()[]βαβαβα--+=sin sin 21sin cos()()[]βαβαβα-++=cos cos 21cos cos()()[]βαβαβα--+-=cos cos 21sin sin正棱台、圆台的侧面积公式()l c c S +'=21台侧其中c '、c 分别表示上、下底面周长，l 表示斜高或母线长台体的体积公式()h S S S S V +'+'=31台体其中S '、S 分别表示上、下底面积，h 表示高一、选择题：本大题共14小题；第（1）—（10）题每小题4分，第（11）—（14）题每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）如图，I 是全集，M 、P 、S 是I3个子集，则阴影部分所表示的集合是（A ）（M ∩P ）∩S （B ）（M ∩P ）∪S（C ）（M ∩P ）∩S （D ）（M ∩P ）∪S（2）已知映射f ：B A →，其中，集合{},4,3,2,1,1,2,3---=A射f 下的象，且对任意的,A a ∈在B （A ）4 （B ）5 （C ）6 （D ）7 （3）若函数()x f y =的反函数是()()0,,≠==ab b a f x g y ，则()b g 等于（A ）a （B ）1-a （C ）b （D ）1-b（4）函数()()()0sin >+=ωϕωx M x f 在区间[]b a ,上是增函数，且 ()(),,M b f M x f =-=则函数()()ϕω+=x M x g cos在[]b a ,上（A ）是增函数（B ）是减函数（C ）可以取得最大值M （D ）可以取得最小值M - （5）若()x x f sin 是周期为π的奇函数，则()x f 可以是（A ）x sin （B ）x cos （C ）x 2sin （D ）x 2cos（6）在极坐标系中，曲线⎪⎭⎫ ⎝⎛-=3sin 4πθρ关于（A ）直线3πθ=轴对称（B ）直线πθ65=轴对称（C ）点⎪⎭⎫⎝⎛3,2π中心对称（D ）极点中心对称（7）若干毫升水倒入底面半径为cm 2的圆柱形器皿中，量得水面的高度为cm 6，若将这些水倒入轴截面是正三角形的倒圆锥形器皿中，则水面的高度是（A ）cm 36 （B ）cm 6 （C ）cm 3182 （D ）cm 3123（8）若(),323322104x a x a x a a x +++=+则()()2312420a a a a a +-++的值为（A ）1 （B ）1- （C ）0 （D ）2 （9）直线0323=-+y x 截圆422=+y x 得的劣弧所对的圆心角为（A ）6π （B ）4π （C ）3π （D ）2π （10）如图，在多面体ABCDEF 中，已知面ABCD 是边长为3的正方形，EF ∥AB ，EF 23=，EF 与面AC 的距离为2，则该多面体的体积为（A ）29 （B ）5 （C ）6 （D ）215（11）若,22sin ⎪⎭⎫ ⎝⎛<<->>παπαααctg tg 则∈α（A ）⎪⎭⎫ ⎝⎛--4,2ππ （B ）⎪⎭⎫⎝⎛-0,4π （C ）⎪⎭⎫ ⎝⎛4,0π （D ）⎪⎭⎫⎝⎛2,4ππ（12）如果圆台的上底面半径为5，下底面半径为R ，中截面把圆台分为上、下两个圆台，它们的侧面积的比为1：2，那么R=（A ）10 （B ）15 （C ）20 （D ）25（13）已知两点,45,4,45,1⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛N M 给出下列曲线方程：①0124=-+y x ②322=+y x ③1222=+y x ④1222=-y x 在曲线上存在点P 满足|MP|=|NP|的所有曲线方程是（A ）①③ （B ）②④ （C ）①②③ （D ）②③④（14）某电脑用户计划使用不超过500元的资金购买单价分别为60元、70元的单片软件和盒装磁盘，根据需要，软件至少买3片，磁盘至少买2盒，则不同的选购方式共有（A ）5种（B ）6种（C ）7种（D ）8种1999年普通高等学校招生全国统一考试数学（理工农医类）第II 卷（非选择题共90分）注意事项：1．第II 卷共6页，用钢笔或圆珠笔直接写答在试题卷中。

上海普通高等学校招生数学统一考试答案.doc

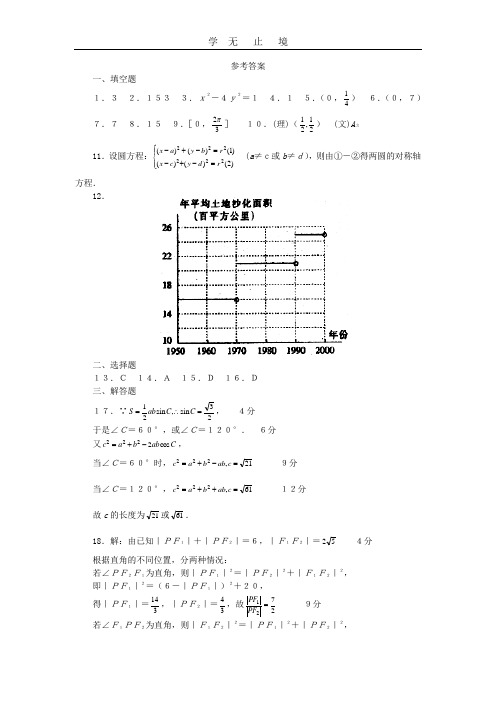
参考答案一、填空题１．３２．１５３３．ｘ２－４ｙ２＝１４．１５．（０，41）６．（０，７）７．７８．１５９．［０，32π］１０．(理)（21,21） (文)A ３11．设圆方程：⎪⎩⎪⎨⎧=-+-=-+-)2()()()1()()(222222r d y c x r b y a x (a ≠ｃ或b ≠ｄ），则由①－②得两圆的对称轴方程．12．二、选择题１３．Ｃ１４．Ａ１５．Ｄ１６．Ｄ三、解答题１７．∵23sin ,sin 21=∴=C C ab S ，４分于是∠Ｃ＝６０°，或∠Ｃ＝１２０°．６分又C ab b a c cos 2222-+=，当∠Ｃ＝６０°时，21,222=-+=c ab b a c ９分当∠Ｃ＝１２０°，61,222=++=c ab b a c １２分故c 的长度为21或61．18．解：由已知｜ＰＦ１｜＋｜ＰＦ２｜＝６，｜Ｆ１Ｆ２｜＝52 ４分根据直角的不同位置，分两种情况：若∠ＰＦ２Ｆ１为直角，则｜ＰＦ１｜２＝｜ＰＦ２｜２＋｜Ｆ１Ｆ２｜２，即｜ＰＦ１｜２＝（６－｜ＰＦ１｜）２＋２０，得｜ＰＦ１｜＝314，｜ＰＦ２｜＝34，故2721=PF PF ９分若∠Ｆ１ＰＦ２为直角，则｜Ｆ１Ｆ２｜２＝｜ＰＦ１｜２＋｜ＰＦ２｜２，即２０＝｜ＰＦ１｜２＋（６－｜ＰＦ１｜）２，得｜ＰＦ１｜＝４，｜ＰＦ２｜＝２，故.221=PF PF １２分(说明：两种情况，缺少一种扣3分)19．(1)证明：如图，以O 为原点建立空间直角坐标系，设AE ＝ＢＦ＝ｘ，则A ′(a ,0,a )、F (a -x ,a ,0)、C ′(0,a ,a )、E (a ,x ,0),F A '＝｛-x ,a ,-a ｝,E C ' ={a ,x-a ,-a },4分∵F A '·E C '＝－xa +a (x-a )+a ２＝０，∴Ａ′Ｆ⊥Ｃ′Ｅ． 6分(2)解：记BF=x,BE=y ，则x+y=a , 三棱锥B ′－ＢＥＦ的体积V ＝xya 61≤32241)2(6a y x a =+．当且仅当x =y=2a时，等号成立．因此，三棱锥B ′－ＢＥＦ的体积取得最大值时，ＢＥ＝ＢＦ＝2a１０分过B 作BD ⊥EF 交EF 于D ，连B ′D ，可知B ′Ｄ⊥ＥＦ． ∴∠Ｂ′ＤＢ是二面角B ′－ＥＦ－Ｂ的平面角．在直角三角形BEF 中，直角边BE ＝ＢＦ＝2a，BD 是斜边上的高，∴22tg ,42='='=BDB B DB B a BD ．故二面角Ｂ′－ＥＦ－Ｂ的大小为arctg ２2．１４分20．(理)解：(1)∵α是方程0122=+-x x 的根， ∴)1(22)1(2221i i +=+=αα或２分当)1(221i +=α时， ∵21α＝ｉ，1121121)(ααnn n i a a ==-， ∴Ｍa1＝｛11111,,1,a a i a a i --｝＝｛)1(22),1(22),1(22),1(22i i i i -+---+｝. 当α２＝,,)1(2222i i -=-αΘ时∴M a2＝122221,,1,αααααM i i =⎭⎬⎫⎩⎨⎧--. 因此，不论α取哪一个值，集合αM 是不变的，即⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧-+---+=)1(22),1(22),1(22),1(22i i i i M α. 8分于是P ＝31224=C ．１０分 (2)证明：∵ω∈Ｍｚ，∴存在m ∈Ｎ，使得ω＝ｚ２ｍ－１． 12分于是对任意n ∈Ｎ，ω２ｎ－１＝ｚ（２m -1）(2n -1),由于(2m -1)(2n -1)是正奇数，ω２ｎ－１∈Ｍｚ，所以M ω⊆Ｍｚ．１４分 (文)解：(1)∵ｚ是方程x ２＋１＝０的根， ∴ｚ１＝ｉ或z ２＝－ｉ．２分不论z １＝ｉ或z ２＝－ｉ，M ｚ＝｛ｉ，ｉ２，ｉ３，ｉ４｝＝｛ｉ，－１，－ｉ，１｝．８分于是P ＝31224=C ．１０分(2)取z ＝－i 2321+，则i Z 23212--=及ｚ3=1.于是{}.,,32Z Z Z M z = １４分或取z ＝i 2321--．（说明：只需写出一个正确答案）． 21．解：(1)f (0)=1表示没有用水洗时，蔬菜上的农药量将保持原样． 2分(2)函数f (x )应该满足的条件和具有的性质是：f (0)=1,f (1)=21,在［０，＋∞)上f (x )单调递减，且0＜f (x )≤１．８分 (3)设仅清洗一次，残留的农药量为f １＝211a +，清洗两次后，残留的农药量为f ２＝,)4(16)2(112222a a +=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+ １２分则2222222221)4)(1()8()4(1611a a a a a a f f ++-=+-+=-．于是，当a ＞２2时，f １＞ｆ２；当a =２2时，f １＝ｆ２；当0＜ａ＜２2时，f １＜ｆ２．因此，当a ＞２时，清洗两次后残留的农药量较少；当a=２2时，两种清洗方法具有相同的效果；当0＜ａ＜２2时，一次清洗残留的农药量较少．１６分 22.解：(1)∵f(x )的定义域D =（－∞，－１）∪（－１，＋∞），∴数列｛ｘｎ｝只有三项：x １＝1,51,191132-==x x . 3分(2)023,124)(2=+-=+-=x x x x x x f 即Θ, ∴x =1或x =2即当x ０＝１或2时,.1124n n n n x x x x =+-=+ 故当x ０＝１时，x ｎ＝１；当x ０＝２时，x ｎ＝２（ｎ∈Ｎ）９分 (3)(理)解不等式x ＜124+-x x ，得x ＜－１或1＜ｘ＜２．要使x １＜ｘ２，则x １＜－１或1＜ｘ１＜２．１２分对于函数164124)(+-=+-=x x x x f ,若x １＜－１，则x ２＝f(x １)＞４，ｘ３＝f(x ２)＜ｘ２．１5分当1＜ｘ１＜２时，x ２＝f(x )＞x １，且1＜ｘ２＜2，依次类推，可得数列｛ｘｎ｝的所有项均满足x ｎ＋１＞ｘｎ（ｎ∈Ｎ）综上所述，x １∈（１，２），由x １＝f(x ０)，得x ０∈（１，２）．１８分 (文)证明：设x ｎ＜０（ｎ∈Ｎ）．由124001+-=x x x ＜０，得－１＜ｘ０＜21，151014002--=x x x ＜０，得51＜ｘ０＜75，1119)1923(2003--=x x x ＜０，得231919110ππx ．∵191121π，∴同时使x １、ｘ２、ｘ３为负数的x ０不存在．故所求的x ０不存在．１８分。

全国统一考试数学及答案(上海卷文)

全国统一考试数学及答案（上海卷文）_年全国高等学校招生统一考试数学(上海·文)试题考生注意:1．答卷前,考生务必将姓名.高考准考证号.校验码等填写清楚．2．本试卷共有22道试题,满分 150分．考试时间120分钟．请考生用钢笔或圆珠笔将答案直接写在试卷上．一．填空题(本大题满分48分)本大题共有12题,只要求直接填写结果,每个空格填对得4分,否则一律得零分．1．函数f(_)=log4(_+1)的反函数f(_)=．2．方程4_+2_-2=0的解是．3．若_,y满足条件_+y≤3y≤2_ ,则z=3_+4y的最大值是．4．直角坐标平面_oy中,若定点A(1,2)与动点P(_,y)满足=4.则点P的轨迹方程是．5．函数y=cos2_+sin_cos_的最小正周期T= ．6．若cosα=,α∈(0.),则cos(α+)=．7．若椭圆长轴长与短轴长之比为2,它的一个焦点是(2,0),则椭圆的标准方程是．8．某班有50名学生,其中 15人选修A课程,另外35人选修B课程．从班级中任选两名学生,他们是选修不同课程的学生的慨率是．(结果用分数表示)9．直线y=_关于直线_＝1对称的直线方程是．10．在△ABC中,若∠A＝120°,AB=5,BC＝7,则 AC＝．11．函数f(_)=sin_+2,_∈[0,2π]的图象与直线y=k有且仅有两个不同的交点,则k的取值范围是．12．有两个相同的直三棱柱,高为,底面三角形的三边长分别为3a.4a.5a(a_gt;0).用它们拼成一个三棱柱或四棱柱,在所有可能的情况中,全面积最小的是一个四棱柱,则a的取值范围是．二．选择题(本大题满分16分)本大题共有4题,每题都给出代号为A.B.C.D的四个结论,其中有且只有一个结论是正确的,必须把正确结论的代号写在题后的圆括内,选对得4分,不选.选错或者选出的代号超过一个(不论是否都写在圆括内),一律得零分．13．若函数f(_)=, 则该函数在(-∞,+∞)上是[答]( )(A)单调递减无最小值(B) 单调递减有最小值(C)单调递增无最大值(D) 单调递增有最大值14．已知集合M={_│≤, _∈R},P={_│≥1, _∈Z},则M∩P等于[答]( )(A){_│0_lt;_≤3, _∈Z}(B) {_│0≤_≤3, _∈Z}(C) {_│-1≤_≤0, _∈Z}(D) {_│-1≤__lt;0, _∈Z}15．条件甲:〝_gt;1〞是条件乙:〝〞的[答]( )(A)既不充分也不必要条件(B) 充要条件(C) 充分不必要条件(D)必要不充分条件16．用n个不同的实数a1,a2,┄an可得n!个不同的排列,每个排列为一行写成1 23一个n!行的数阵.对第i行ai1,ai2,┄ain,记bi=- ai1+2ai2-3 ai3+┄+(-1)nnain, 1 32i=1,2,3,┄,n!.用1,2,3可你数阵如右,由于此数阵中每一列各数之和都 2 13是12,所以,b1+b2+┄+b6=-12+212-312=-24.那么,在用1,2,3,4,5形成 2 3 1的数阵中, b1+b2+┄+b120等于31 232 1[答]( )(A)-3600 (B)1800(C)-1080(D)-720三．解答题(本大题满分86分)本大题共有6题,解答下列各题必须写出必要步骤.17．(本题满分12分)已知长方体ABCD-A1B1C1D1中,M.N分别是BB1和BC的中点,AB=4,AD=2.B1D与平面ABCD所成角的大小为60°,求异面直线B1D与MN所成角的大小.(结果用反三角函数值表示)[解]18．(本题满分12分)在复数范围内解方程(i为虚数单位) [解]19．(本题满分14分)本题共有2个小题,第1小题满分6分, 第2小题满分8分.已知函数f(_)=k_+b的图象与_.y轴分别相交于点A.B,( .分别是与_.y轴正半轴同方向的单位向量), 函数g(_)=_2-_-6.(1)求k.b的值;(2)当_满足f(_)_gt; g(_)时,求函数的最小值.[解]20．(本题满分14分)本题共有2个小题,第1小题满分6分, 第2小题满分8分. 假设某市_年新建住房400万平方米,其中有250万平方米是中低价房.预计在今后的若干年内,该市每年新建住房面积平均比上一年增长8%.另外,每年新建住房中,中低价房的面积均比上一年增加50万平方米.那么,到哪一年底,(1)该市历年所建中低价房的累计面积(以_年为累计的第一年)将首次不少于4750万平方米?(2)当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%?[解]21．(本题满分16分)本题共有3个小题,第1小题满分4分, 第2小题满分6分, 第3小题满分6分.已知抛物线y2=2p_(p_gt;0)的焦点为F,A是抛物线上横坐标为4.且位于_轴上方的点,A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M.(1)求抛物线方程;(2)过M作MN⊥FA, 垂足为N,求点N的坐标;(3)以M为圆心,MB为半径作圆M.当K(m,0)是_轴上一动点时,丫讨论直线AK与圆M的位置关系.[解]22．(本题满分18分)本题共有3个小题,第1小题满分4分, 第2小题满分8分, 第3小题满分6分.对定义域分别是Df.Dg的函数y=f(_) .y=g(_),f(_)·g(_)当_∈Df且_∈Dg规定: 函数h(_)= f(_)当_∈Df且_Dgg(_) 当_Df且_∈Dg(1)若函数f(_)=-2_+3,_≥1; g(_)=_-2,_∈R,写出函数h(_)的解析式;(2)求问题(1)中函数h(_)的最大值;(3)若g(_)=f(_+α), 其中α是常数,且α∈[0,π],请设计一个定义域为R的函数y=f(_),及一个α的值,使得h(_)=cos2_,并予以证明.[解]上海数学(文史类)参考答案一.1. 4-12._=0 3. 11 4. _+2y-4=0 5. π 6. - 7.8. 9._+2y-2=0 10. 3 11. 1_lt;k_lt;3 12. 0_lt;a_lt;二.13.A 14.B 15. B 16.C三.17. [解]联结B1C,由M.N分别是BB1和BC的中点,得B1C∥MN,∴∠DB1C就是异面直线B1D与MN所成的角.联结BD,在Rt△ABD中,可得BD=2,又BB1⊥平面ABCD, ∠B1DB是B1D与平面ABCD 所成的角, ∴∠B1DB=60°.在Rt△B1BD中, B1B=BDtan60°=2,又DC⊥平面BB1C1C, ∴DC⊥B1C,在Rt△DB1C中, tan∠DB1C=,∴∠DB1C=arctan.即异面直线B1D与MN所成角的大小为arctan.18. [解]原方程化简为,设z=_+yi(_.y∈R),代入上述方程得 _2+y2+2_i=1-i,∴_2+y2=1且2_=-1,解得_=-且y=±,∴原方程的解是z=-±i.19. [解](1)由已知得A(,0),B(0,b),则={,b},于是=2,b=2.∴k=1,b=2.(2)由f(_)_gt; g(_),得_+2_gt;_2-_-6,即(_+2)(_-4)_lt;0,得-2_lt;__lt;4,==_+2+-5由于_+2_gt;0,则≥-3,其中等号当且仅当_+2=1,即_=-1时成立∴的最小值是-3.20. [解](1)设中低价房面积形成数列{an},由题意可知{an}是等差数列,其中a1=250,d=50,则Sn=250n+=25n2+225n,令25n2+225n≥4750,即n2+9n-190≥0,而n是正整数, ∴n≥10.到_年底,该市历年所建中低价房的累计面积将首次不少于4750万平方米.(2)设新建住房面积形成数列{bn},由题意可知{bn}是等比数列,其中b1=400,q=1.08,则bn=400·(1.08)n-1·0.85.由题意可知an_gt;0.85 bn,有250+(n-1)·50_gt;400·(1.08)n-1·0.85.由计箅器解得满足上述不等式的最小正整数n=6.到_年底,当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%.21. [解](1) 抛物线y2=2p_的准线为_=-,于是4+=5, ∴p=2.∴抛物线方程为y2=4_.(2)∵点A是坐标是(4,4), 由题意得B(0,4),M(0,2),又∵F(1,0), ∴kFA=;MN⊥FA, ∴kMN=-,则FA的方程为y=(_-1),MN的方程为y-2=-_,解方程组得_=,y=, ∴N的坐标(,).(4)由题意得, ,圆M.的圆心是点(0,2), 半径为2,当m=4时, 直线AK的方程为_=4,此时,直线AK与圆M相离.当m≠4时, 直线AK的方程为y=(_-m),即为4_-(4-m)y-4m=0,圆心M(0,2)到直线AK的距离d=,令d_gt;2,解得m_gt;1∴当m_gt;1时, AK与圆M相离;当m=1时, AK与圆M相切;当m_lt;1时, AK与圆M相交.22. [解](1)h(_)= (-2_+3)(_-2) _∈[1,+∞)_-2_∈(-∞,1)(2) 当_≥1时, h(_)= (-2_+3)(_-2)=-2_2+7_-6=-2(_-)2+∴h(_)≤;当__lt;1时, h(_)_lt;-1,∴当_=时, h(_)取得最大值是(3)令f(_)=sin_+cos_,α=则g(_)=f(_+α)=sin(_+)+cos(_+)=cos_-sin_,于是h(_)= f(_)·f(_+α)=(sin_+cos_)( cos_-sin_)=cos2_. 另解令f(_)=1+sin_, α=π,g(_)=f(_+α)=1+sin(_+π)=1-sin_,于是h(_)= f(_)·f(_+α)=(1+sin_)( 1-sin_)=cos2_.。

1998年全国高考数学试题

1998年普通高等学校招生全国统一考试数学(理工农医类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟.第Ⅰ卷(选择题共65分)一、选择题:本大题共15小题;第(1) (10)题每小题4分,第(11) (15)题每小题5分,共65分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)设集合M=｛x │0≤x<2｝,集合N=｛x │x 2-2x-3<0｝,集合M ∩N 为(A)｛x │0≤x<1｝ (B)｛x │0≤x<2｝(C)｛x │0≤x ≤1｝ (D)｛x │0≤x ≤2｝[Key] B(2)如果直线ax+2y+2=0与直线3x-y-2=0平行,那么系数a 为32)(23)(6)(3)(D C B A ---[Key] B(3)函数)x 31x 21(tg y -=在一个周期内的图象是[Key] A(4)已知三棱锥D-ABC 的三个则面与底面全等，且AB=AC=3，BC=2，则BC 为棱,以面BCD 与面BCA 为面的二面角的大小是32)D (2)C (31arccos )B (33arccos )A (ππ[Key] C（5）函数x 2cos )x 23sin(y +-π=的最小正周期是ππππ4)D (2)C ()B (2)A ([Key] B(6)满足arccos(1-x)≥arccosx 的x 的取值范围是]1,21)[(]21,0)[(]0,21)[(]21,1)[(D C B A --[Key] D(7)将y=2x 的图象(A)先向左平行移动1个单位 (B)先向右平行移动1个单位(C)先向上平行移动1个单位 (D)先向下平行移动1个单位再作关于直线y=x 对称的图象,可得到函数y=log 2(x+1)的图象.[Key] D(8)长方体一个顶点上三条棱的长分别是3,4,5,且它的八个顶点都在同一个球面上,这个球的表面积是ππππ200)(50)(225)(220)(D C B A[Key] C(9)曲线的参数方程⎪⎩⎪⎨⎧-=-=2111t y t x （t 是参数，t ≠0）,它的普通方程是11)(1)1(1)()1()2()(1)1()1)((2222+-=--=--==--x x y D x y C x x x y B y x A[Key] B(10)函数y=cos 2x-3cosx+2的最小值为6)(41)(0)(2)(D C B A -[Key] B(11)椭圆C 与14)2(9)3(22=-+-y x 椭圆关于直线x+y=0对称，椭圆C 的方程是 (A) 19)3(4)2(22=+++y x(B) 14)3(9)2(22=-+-y x (C) 14)3(9)2(22=+++y x (D) 19)3(4)2(22=-+-y x[Key] A(12)圆台上、下底面积分别为π、4π,侧面积为6π,这个圆台的体积是337)(637)(32)(332)(ππππD C B A[Key] D(13)定义在区间(-∞,+∞)的奇函数f(x)为增函数；偶函数g(x)在区间［0,+∞)的图象与f(x)的图象重合.设a>b>0,给出下列不等式①f(b)-f(-a)>g(a)-g(-b); ②f(b)-f(-a)<g(a)-g(-b);③f(a)-f(-b)>g(b)-g(-a); ④f(a)-f(-b)<g(b)-g(-a),其中成立的是(A)①与④ (B)②与③ (C)①与③ (D)②与④[Key] C（14）不等式组⎪⎩⎪⎨⎧+->+->x x x x x 22330的解集是 (){}20<<x x A (){}5.20<<x x B (){}60<<x x C (){}30<<x x D[Key] C(15)四面体的顶点和各棱中点共10个点,在其中取4个不共面的点,不同的取法共有(A)150种 (B)147种 (C)144种 (D)141种[Key] D(16)已知92⎪⎪⎭⎫ ⎝⎛-x x a 的展开式中x 3的系数为49，常数a 的值为_________. [Key] 4(17)已知直线的极坐标方程22)4sin(=+πθρ则极点到该直线的距离是_______。

1998年普通高等学校招生全国统一考试数学文.pdf

【学习目标】1、整体把握课文，把握四位作家的外貌特征和性格特点2、学习人物描写的方法，让学生仔细描摹，比较几个人物的不同写法3、学习本文行文顺序、材料剪裁方面的特点4、课文语言丰富，让学生细细品味，注意积累【学习重点】【学习难点】1．按拼音写汉字。

bèng（）发qiào（）起 zòng（）观lǚ（）着淹mò（）fù（）盖滑jī（）荒miù（）和ǎi（）一拍jí（）合【自疑】自主阅读全文，提出疑问 1、 2、【自探】 1、熟读课文，分别概括福楼拜、屠格涅夫、都德和左拉的肖像、语言、行动和性格的特点，并用表格说明。

人物肖像语言动作性格福楼拜?｝??屠格涅夫 ????都德????左拉???? 让学生揣摩课文中人物描写的句子，比较几个人物不同的写法。

作者善于抓住四位作家的性格上的特点，各有侧重地描写他们的肖像、行动和语言。

哪个作家在哪一方面最有特点，就着重写哪一方面。

描写中间，插入一些抒情和议论，有什么作用？体味莫泊桑在本文中所运用的准确而生动的语言，从文中找出例子来分析说明【自结】【自测】你对课文了解吗？（1）《福楼拜家的星期天》作者是 ________，法国 ________，被称为 ________。

其代表作有 ________、________等。

文中的人物________是他的启蒙老师。

（2）全文好像是一出舞台剧。

时间： ________。

地点： ________；人物： ________；主要内容： ________。

（3）按课文内容填空，体味其表现了人物怎样的性格特点。

这时只见福楼拜做着________的动作（就像他要飞起来似的），从这个人面前一步________到那个人面前，带动得他的衣裤________起来，像一条渔船上的风帆。

他时而 ________，时而________；有时________，有时 ________。

【精品试卷】98普通高等学校招生统一考试(上海卷)复习专用试卷

A B Cv A （a ）t t c /2t c O v v c t t c /2t c O v v c tt c /2t c O vv c t t c /2t c O v v c A B C D高中物理学习材料（精心收集**整理制作）1998年全国普通高等学校招生统一考试上海物理试题一、（24分）单项选择题。

本大题共6小题，每题4分。

每小题给出的四个答案中，只有一个是正确的。

把正确答案前面的字母填写在题后的方括号内，选对的得4分，选错的或不答的，得0分；选两个或两个以上的，得0分。

填写在方括号以外的字母，不作为选出的答案。

1．下列实验中，能证实光具有粒子性的是A ．光电效应实验B ．光的双缝干涉实验C ．炮的圆孔衍射实验D ．α粒子散射实验2．下列核反应方程中正确的是H Th U .A 212349023892+→ n C H B .B 10126e 42e 94+→+e P Th .C 01a 2349023490-+→ e S P .D 01i 30143115+→3．有两个光滑固定的斜面AB 和BC ，A 和C 两点在同一水平面上，斜面BC 比斜面AB 长[如图（a ）所示]。

一个滑块自A 点以速度v A 上滑，到达B 点时速度减小为零，紧接着沿BC 滑下。

设滑块从A 点到C 点的总时间是t C ，那么下列四个图[图（b ）]中，正确表示滑块速度的大小v 随时间t 变化的规律的是4．如图电路中，电源E 的电动势为3.2V ，电阻R 的阻值为30Ω，小灯泡L 的额定电压为3 V ，额定功率为4.5W 。

当电键S 接位置1时，A OB P Q a bC (a ) i i i i t t t (b ) t A B CD 电压表的读数为3V ，那么当电键S 接到位置2时，小灯泡L 的发光情况是A ．很暗，甚至不亮B ．正常发光C ．比正常发光略亮D ．有可能被烧坏5．如图（a ）电路中，L 是电阻不计的电感器，C 是电容器。

1999年高考数学试题及答案(全国理)

1999年高考数学试题及答案(全国理)1999年普通高等学校招生全国统一考试数学（理工农医类）本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分。

第I 卷第1至 2页。

第II 卷3至8页。

共150分。

考试时间120分钟。

第I 卷（选择题共60分）注意事项1．答第I 卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。

2．每小题选出答案后，用铅笔把答题卡对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上。

3．考试结束，监考人将本试卷和答题卡一并收回。

参考公式：三角函数的积化和差公式()()[]βαβαβα-++=sin sin 21cos sin()()[]βαβαβα--+=sin sin 21sin cos()()[]βαβαβα-++=cos cos 21cos cos()()[]βαβαβα--+-=cos cos 21sin sin正棱台、圆台的侧面积公式()l c c S +'=21台侧其中c '、c 分别表示上、下底面周长，l 表示斜高或母线长台体的体积公式()h S S S S V +'+'=31台体其中S '、S 分别表示上、下底面积，h 表示高一、选择题：本大题共14小题；第（1）—（10）题每小题4分，第（11） —（14）题每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）如图，I 是全集，M 、P 、S 是I3个子集，则阴影部分所表示的集合是（A ）（M ∩P ）∩S （B ）（M ∩P ）∪S（C ）（M ∩P ）∩S （D ）（M ∩P ）∪S（2）已知映射f ：B A →，其中，集合{,2,3---=A都是A 中元素在映射f 下的象，且对任意的,A a ∈在B 中和它对应的元素是a ，则集合B 中元素的个数是（A ）4 （B ）5 （C ）6 （D ）7 （3）若函数()x f y =的反函数是()()0,,≠==ab b a f x g y ，则()b g 等于（A ）a （B ）1-a （C ）b （D ）1-b （4）函数()()()0sin >+=ωϕωx M x f 在区间[]b a ,上是增函数，且()(),,M b f M x f =-=则函数()()ϕω+=x M x g cos 在[]b a ,上（A ）是增函数（B ）是减函数（C ）可以取得最大值M （D ）可以取得最小值M - （5）若()x x f sin 是周期为π的奇函数，则()x f 可以是（A ）x sin （B ）x cos （C ）x 2sin （D ）x 2cos（6）在极坐标系中，曲线⎪⎭⎫ ⎝⎛-=3sin 4πθρ关于（A ）直线3πθ=轴对称（B ）直线πθ65=轴对称（C ）点⎪⎭⎫⎝⎛3,2π中心对称（D ）极点中心对称（7）若干毫升水倒入底面半径为cm 2的圆柱形器皿中，量得水面的高度为cm 6，若将这些水倒入轴截面是正三角形的倒圆锥形器皿中，则水面的高度是（A ）cm 36 （B ）cm 6 （C ）cm 3182 （D ）cm 3123（8）若(),323322104x a x a x a a x +++=+则()()2312420a a a a a +-++的值为（A ）1 （B ）1- （C ）0 （D ）2 （9）直线0323=-+y x 截圆422=+y x 得的劣弧所对的圆心角为（A ）6π （B ）4π （C ）3π （D ）2π （10）如图，在多面体ABCDEF 中，已知面ABCD是边长为3的正方形，EF ∥AB ，EF 23=，EF 与面AC 的距离为2，则该多面体的体积为（A ）29（B ）5 （C ）6 （D ）215 （11）若,22sin ⎪⎭⎫ ⎝⎛<<->>παπαααctg tg 则∈α（A ）⎪⎭⎫ ⎝⎛--4,2ππ （B ）⎪⎭⎫ ⎝⎛-0,4π （C ） ⎪⎭⎫ ⎝⎛4,0π （D ）⎪⎭⎫⎝⎛2,4ππ（12）如果圆台的上底面半径为5，下底面半径为R ，中截面把圆台分为上、下两个圆台，它们的侧面积的比为1：2，那么R=（A ）10 （B ）15 （C ）20 （D ）25（13）已知两点,45,4,45,1⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛N M 给出下列曲线方程：①0124=-+y x ②322=+y x ③1222=+y x ④1222=-y x 在曲线上存在点P 满足|MP|=|NP|的所有曲线方程是（A ）①③ （B ）②④ （C ）①②③ （D ）②③④（14）某电脑用户计划使用不超过500元的资金购买单价分别为60元、70元的单片软件和盒装磁盘，根据需要，软件至少买3片，磁盘至少买2盒，则不同的选购方式共有（A ）5种（B ）6种（C ）7种（D ）8种1999年普通高等学校招生全国统一考试数学（理工农医类）第II 卷（非选择题共90分）注意事项：1．第II 卷共6页，用钢笔或圆珠笔直接写答在试题卷中。

普通高等学校招生全国统一考试上海数学试卷

普通高等学校招生全国统一考试上海数学试卷一、填空题（本大题共有12题，满分54分，第16题每题4分，第712题每题5分）1. 行列式4125的值为．【解析】18．2.双曲线2214x y -=的渐近线方程为．【解析】12y x =±．3.在()71x +的二项展开式中，2x 项的系数为．【解析】21．4.设常数a ∈R ，函数()()2log f x x a =+．若()f x 的反函数的图像经过点()3,1，则a =．【解析】7．5. 已知复数z 满足()()117i z i i +=-是虚数单位，则z =．【解析】5．6.记等差数列{}n a 的前n 项和为n S ．若30a =，6714a a +=，则7S =．【解析】14．7.已知112,1,,,1,2,322α⎧⎫∈---⎨⎬⎩⎭．若幂函数()f x x α=为奇函数，且在()0,+∞上递减，则α=．【解析】1-．8. 在平面直角坐标系中，已知点()1,0A -、()2,0B ，E 、F 是y 轴上的两个动点，且2EF =，则AE BF ⋅的最小值为．【解析】3-．9. 有编号互不相同的五个砝码，其中5克、3克、1克砝码各一个，2克砝码两个．从中随机选取三个，则这三个砝码的总质量为9克的概率是．【解析】15．10.设等比数列{}n a 的通项公式为()1*1n n a a q n -=∈N ，前n 项和为n S ．若11lim 2n n n S a →∞+=，则q =．【解析】3q =．11. 已知常数0a >，函数()22xxf x ax =+的图像经过点61,,55P p Q q ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭、．若236p qpq +=，则a =．【解析】6a =．12.22111x y +=，22221x y +=，12120.5x x y y +=的最大值为．【解析】利用两向量乘积、单位圆、点到直线:10l x y +-=二、选择题（本大题共有4题，满分20分，每题5分）13. 设P 是椭圆22153x y +=上的动点，则P 到该椭圆的两个焦点的距离之和为（）．（A）B）C）D）【解析】（C ）14. 已知a ∈R ，则“1a >”是“11a<”的（）．（A ）充分非必要条件（B ）必要非充分条件（C ）充要条件（D ）既非充分又非必要条件【解析】（A ）15. 《九章算术》中，称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马．设1AA 是正六棱柱的一条侧棱，如图，若阳马以该正六棱柱的顶点为顶点，以1AA 为底面矩形的一边，则这样的阳马的个数是（）．（A ）4 （B ）8 （C ）12 （D ）16 【解析】（D ）16. 设D 是含数1的有限实数集，()f x 是定义在D 上的函数．若()f x 的图像绕原点逆时针旋转6π后与原图像重合，则在以下各项中，()1f 的可能取值只能是（）．（AB（C）（D ）0 【解析】（B ）三、解答题（本大题共有5题，满分76分）17. （本题满分14分，第1小题满分6分，第2小题满分8分）已知圆锥的顶点为P ，底面圆心为O ，半径为2，（1）设圆锥的母线长为4，求圆锥的体积；（2）设4PO =，OA OB 、是底面半径，且90AOB ∠=，M 为线段AB 的中点，如图，求异面直线PM 与OB 所成的角的大小．【解析】（1）V =；（2）O MPBA18. （本题满分14分，第1小题满分6分，第2小题满分8分）设常数a ∈R ，函数()2sin 22cos f x a x x =+．（1）若()f x 为偶函数，求a 的值；（2）若14f π⎛⎫=+ ⎪⎝⎭，求方程()1f x =-在区间[],ππ-上的解．【解析】（1）0a =；（2）115131924242424x ππππ=--、、、． 19. （本题满分14分，第1小题满分6分，第2小题满分8分）某群体的人均通勤时间，是指单日内该群体中成员从居住地到工作地的平均用时．某地上班族S 中的成员仅以自驾或公交方式通勤．分析显示：当S 中()%0100x x <<的成员自驾时，自驾群体的人均通勤时间为：()()30,0301800290,30100x f x x x x <≤⎧⎪=⎨+-<<⎪⎩单位：分钟，而公交群体的人均通勤时间不受x 影响，恒为40分钟．试根据上述分析结果回答下列问题：（1）当x 在什么范围时，公交群体的人均通勤时间少于自驾群体的人均通勤时间？（2）求该地上班族S 的人均通勤时间()g x 的表达式；讨论()g x 的单调性，并说明其实际意义．【解析】（1）45100x <<；（2）()240,0301011358,301005010x x g x x x x ⎧-<≤⎪⎪=⎨⎪-+<<⎪⎩，()g x 在(]0,32.5x ∈时单调递减，在[)32.5,100x ∈时单调递增．实际意义为：当S 中32.5%的成员自驾时，该地上班族S 的人均通勤时间达到最小值36.875分钟．20.（本题满分18分，第1小题满分4分，第2小题满分6分，第3小题满分8分）给定无穷数列{}n a ，若无穷数列{}n b 满足：对任意n ∈*N ，都有1n n b a -≤，则称{}n b 与{}n a “接近”．（1）设{}n a 是首项为1，公比为12的等比数列，11n n b a +=+，n ∈*N ，判断数列{}n b 是否与{}n a 接近，并说明理由；（2）设数列{}n a 的前四项为：11a =，22a =，34a =，48a =，{}n b 是一个与{}n a 接近的数列，记集合{}|,1,2,3,4i M x x b i ===，求M 中元素的个数m ；（3）已知{}n a 是公差为d 的等差数列，若存在数列{}n b 满足：{}n b 与{}n a 接近，且在21b b -，32b b -，…，201200b b -中至少有100个为正数，求d 的取值范围．【解析】（1）1112n n n b a -=-≤，所以{}n b 与{}n a “接近”；（2）[]10,2b ∈，[]21,3b ∈，[]33,5b ∈，[]47,9b ∈， {}|,1,2,3,4i M x x b i ===元素个数34m =或；（3）2d =-时，10,1,2,,200k k b b k +-≤=，即21b b -，32b b -，…，201200b b -中没有正数；当2d >-时，存在12201,,,b b b 使得210b b ->，320b b -<，430b b ->，540b b -<…，2001990b b ->，2012000b b -<，即有100个正数，故2d >-．21.（本题满分16分，第1小题满分4分，第2小题满分6分，第3小题满分6分）设常数2t >，在平面直角坐标系xOy 中，已知点()2,0F ，直线l ：x t =，曲线Γ：28y x =()0,0x t y ≤≤≥，l与x 轴交于点A、与Γ交于点B ，P 、Q 分别是曲线Γ与线段AB上的动点．（1）用t 表示点B 到点F 的距离；（2）设3t =，2FQ =，线段OQ 的中点在直线FP 上，求△AQP 的面积；（3）设8t =，是否存在以FP 、FQ 为邻边的矩形FPEQ ，使得点E 在Γ上？若存在，求点P 的坐标；若不存在，说明理由．【解析】（1）2BF t =+；（2）AQP S =△；（3）25P ⎛ ⎝⎭．高考理科数学试题及答案（考试时间：120分钟试卷满分：150分）一、选择题：本题共12小题，每小题5分，共60分。

普通高等学校招生全国统一考试上海数学试卷

普通高等学校招生全国统一考试上海数学试卷一、填空题（本大题共有12题，满分54分，第16题每题4分，第712题每题5分）1. 行列式4125的值为．【解析】18．2.双曲线2214x y -=的渐近线方程为．【解析】12y x =±．3.在()71x +的二项展开式中，2x 项的系数为．【解析】21．4.设常数a ∈R ，函数()()2log f x x a =+．若()f x 的反函数的图像经过点()3,1，则a =．【解析】7．5. 已知复数z 满足()()117i z i i +=-是虚数单位，则z =．【解析】5．6.记等差数列{}n a 的前n 项和为n S ．若30a =，6714a a +=，则7S =．【解析】14．7.已知112,1,,,1,2,322α⎧⎫∈---⎨⎬⎩⎭．若幂函数()f x x α=为奇函数，且在()0,+∞上递减，则α=．【解析】1-．8. 在平面直角坐标系中，已知点()1,0A -、()2,0B ，E 、F 是y 轴上的两个动点，且2EF =，则AE BF ⋅的最小值为．【解析】3-．9. 有编号互不相同的五个砝码，其中5克、3克、1克砝码各一个，2克砝码两个．从中随机选取三个，则这三个砝码的总质量为9克的概率是．【解析】15．10.设等比数列{}n a 的通项公式为()1*1n n a a q n -=∈N ，前n 项和为n S ．若11lim 2n n n S a →∞+=，则q =．【解析】3q =．11. 已知常数0a >，函数()22xxf x ax =+的图像经过点61,,55P p Q q ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭、．若236p qpq +=，则a =．【解析】6a =．12.22111x y +=，22221x y +=，12120.5x x y y +=的最大值为．【解析】利用两向量乘积、单位圆、点到直线:10l x y +-=二、选择题（本大题共有4题，满分20分，每题5分）13. 设P 是椭圆22153x y +=上的动点，则P 到该椭圆的两个焦点的距离之和为（）．（A）B）C）D）【解析】（C ）14. 已知a ∈R ，则“1a >”是“11a<”的（）．（A ）充分非必要条件（B ）必要非充分条件（C ）充要条件（D ）既非充分又非必要条件【解析】（A ）15. 《九章算术》中，称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马．设1AA 是正六棱柱的一条侧棱，如图，若阳马以该正六棱柱的顶点为顶点，以1AA 为底面矩形的一边，则这样的阳马的个数是（）．（A ）4 （B ）8 （C ）12 （D ）16A 1A【解析】（D ）16. 设D 是含数1的有限实数集，()f x 是定义在D 上的函数．若()f x 的图像绕原点逆时针旋转6π后与原图像重合，则在以下各项中，()1f 的可能取值只能是（）．（AB（C）（D ）0 【解析】（B ）三、解答题（本大题共有5题，满分76分）17. （本题满分14分，第1小题满分6分，第2小题满分8分）P已知圆锥的顶点为P ，底面圆心为O ，半径为2，（1）设圆锥的母线长为4，求圆锥的体积；（2）设4PO =，OA OB 、是底面半径，且90AOB ∠=，M 为线段AB 的中点，如图，求异面直线PM 与OB 所成的角的大小．【解析】（1）V =；（2） 18. （本题满分14分，第1小题满分6分，第2小题满分8分）设常数a ∈R ，函数()2sin 22cos f x a x x =+．（1）若()f x 为偶函数，求a 的值；（2）若14f π⎛⎫=+ ⎪⎝⎭，求方程()1f x =-在区间[],ππ-上的解．【解析】（1）0a =；（2）115131924242424x ππππ=--、、、． 19. （本题满分14分，第1小题满分6分，第2小题满分8分）某群体的人均通勤时间，是指单日内该群体中成员从居住地到工作地的平均用时．某地上班族S 中的成员仅以自驾或公交方式通勤．分析显示：当S 中()%0100x x <<的成员自驾时，自驾群体的人均通勤时间为：()()30,0301800290,30100x f x x x x <≤⎧⎪=⎨+-<<⎪⎩单位：分钟，而公交群体的人均通勤时间不受x 影响，恒为40分钟．试根据上述分析结果回答下列问题：（1）当x 在什么范围时，公交群体的人均通勤时间少于自驾群体的人均通勤时间？（2）求该地上班族S 的人均通勤时间()g x 的表达式；讨论()g x 的单调性，并说明其实际意义．【解析】（1）45100x <<；（2）()240,0301011358,301005010x x g x x x x ⎧-<≤⎪⎪=⎨⎪-+<<⎪⎩，()g x 在(]0,32.5x ∈时单调递减，在[)32.5,100x ∈时单调递增．实际意义为：当S 中32.5%的成员自驾时，该地上班族S 的人均通勤时间达到最小值36.875分钟．20.（本题满分18分，第1小题满分4分，第2小题满分6分，第3小题满分8分）给定无穷数列{}n a ，若无穷数列{}n b 满足：对任意n ∈*N ，都有1n n b a -≤，则称{}n b 与{}n a “接近”．（1）设{}n a 是首项为1，公比为12的等比数列，11n n b a +=+，n ∈*N ，判断数列{}n b 是否与{}n a 接近，并说明理由；（2）设数列{}n a 的前四项为：11a =，22a =，34a =，48a =，{}n b 是一个与{}n a 接近的数列，记集合{}|,1,2,3,4i M x x b i ===，求M 中元素的个数m ；（3）已知{}n a 是公差为d 的等差数列，若存在数列{}n b 满足：{}n b 与{}n a 接近，且在21b b -，32b b -，…，201200b b -中至少有100个为正数，求d 的取值范围．【解析】（1）1112n n nb a -=-≤，所以{}n b 与{}n a “接近”；（2）[]10,2b ∈，[]21,3b ∈，[]33,5b ∈，[]47,9b ∈， {}|,1,2,3,4i M x x b i ===元素个数34m =或；（3）2d =-时，10,1,2,,200k k b b k +-≤=，即21b b -，32b b -，…，201200b b -中没有正数；当2d >-时，存在12201,,,b b b 使得210b b ->，320b b -<，430b b ->，540b b -<…，2001990b b ->，2012000b b -<，即有100个正数，故2d >-．21.（本题满分16分，第1小题满分4分，第2小题满分6分，第3小题满分6分）设常数2t >，在平面直角坐标系xOy 中，已知点()2,0F ，直线l ：x t =，曲线Γ：28y x =()0,0x t y ≤≤≥，l与x 轴交于点A、与Γ交于点B ，P 、Q 分别是曲线Γ与线段AB上的动点．（1）用t 表示点B 到点F 的距离；（2）设3t =，2FQ =，线段OQ 的中点在直线FP 上，求△AQP 的面积；（3）设8t =，是否存在以FP 、FQ 为邻边的矩形FPEQ ，使得点E 在Γ上？若存在，求点P 的坐标；若不存在，说明理由．【解析】（1）2BF t =+；（2）AQP S =△；（3）25P ⎛ ⎝⎭．高考理科数学试卷普通高等学校招生全国统一考试注意事项： 1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至3页，第Ⅱ卷3至5页. 2.答题前，考生务必将自己的姓名、准考证号填写在本试题相应的位置. 3.全部答案在答题卡上完成，答在本试题上无效. 4.考试结束后，将本试题和答题卡一并交回.第Ⅰ卷22. 选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.（1）已知集合{1,}A =2,3，{|(1)(2)0,}B x x x x =+-<∈Z ，则AB =（A ）{1}（B ）{12}，（C ）{0123}，，，（D ）{10123}-，，，，（2）已知(3)(1)i z m m =++-在复平面内对应的点在第四象限，则实数m 的取值范围是（A ）(31)-，（B ）(13)-，（C ）(1,)∞+（D ）(3)∞--，（3）已知向量(1,)(3,2)m =-，=a b ，且()⊥a +b b ，则m= （A ）－8（B ）－6 （C ）6 （D ）8（4）圆2228130x y x y +--+=的圆心到直线10ax y +-=的距离为1，则a= （A ）43-（B ）34-（C ）3（D ）2（5）如图，小明从街道的E 处出发，先到F 处与小红会合，再一起到位于G 处的老年公寓参加志愿者活动，则小明到老年公寓可以选择的最短路径条数为（A ）24 （B ）18 （C ）12 （D ）9（6）右图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为（A ）20π（B ）24π（C ）28π（D ）32π（7）若将函数y=2sin 2x 的图像向左平移π12个单位长度，则评议后图象的对称轴为（A ）x=kπ2–π6 (k ∈Z) （B ）x=kπ2+π6 (k ∈Z) （C ）x=kπ2–π12 (k ∈Z) （D ）x=kπ2+π12 (k ∈Z)（8）中国古代有计算多项式值的秦九韶算法，右图是实现该算法的程序框图.执行该程序框图，若输入的x=2，n=2，依次输入的a 为2，2，5，则输出的s= （A ）7 （B ）12 （C ）17 （D ）34 （9）若cos(π4–α)=35，则sin 2α=（A ）725（B ）15（C ）–15（D ）–725（10）从区间[]0,1随机抽取2n 个数1x ,2x ，…，nx ，1y ，2y ，…，ny ，构成n 个数对()11,x y ，()22,x y ，…，(),n n x y ，其中两数的平方和小于1的数对共有m 个，则用随机模拟的方法得到的圆周率π的近似值为（A ）4n m （B ）2n m （C ）4m n （D ）2m n（11）已知F1，F2是双曲线E 22221x y a b-=的左，右焦点，点M 在E 上，M F1与x 轴垂直，sin 2113MF F ∠=,则E 的离心率为（AB ）32（CD ）2（12）已知函数学.科网()()f x x ∈R 满足()2()f x f x -=-，若函数1x y x+=与()y f x =图像的交点为1122(,),(,),,(,),m m x y x y x y ⋅⋅⋅则1()mi i i x y =+=∑（A ）0 （B ）m （C ）2m （D ）4m第II 卷本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题，每个试题考生都必须作答.第(22)题~第(24)题为选考题，考生根据要求作答.二、填空题：本大题共3小题，每小题5分(13)△ABC 的内角A 、B 、C 的对边分别为a 、b 、c ，若cos A=45，cos C=513，a=1，则b=. (14)α、β是两个平面，m 、n 是两条直线，有下列四个命题：（1）如果m ⊥n ，m ⊥α，n ∥β，那么α⊥β. （2）如果m ⊥α，n ∥α，那么m ⊥n.（3）如果α∥β，m ⊂α，那么m ∥β. （4）如果m ∥n ，α∥β，那么m 与α所成的角和n 与β所成的角相等.其中正确的命题有.(填写所有正确命题的编号）（15）有三张卡片，分别写有1和2，1和3，2和3。