2017-2018年山东省枣庄市薛城区八年级(上)期中数学试卷(解析版)
2017-2018年山东省枣庄市山亭区八年级上学期期中数学试卷和答案

2017-2018学年山东省枣庄市山亭区八年级(上)期中数学试卷一、选择题(本大题共12小题,每小题3分,共36分)1.(3分)在实数0、3、﹣、、π、、3.14中无理数的个数是()个.A.1 B.2 C.3 D.42.(3分)下列各组数中,不能构成直角三角形的一组是()A.1,2,B.1,2,C.3,4,5 D.6,8,123.(3分)下列各式中计算正确的是()A.B.C. D.4.(3分)在平面直角坐标系中,点A(3,﹣5)所在象限为()A.第一象限B.第二象限C.第三象限D.第四象限5.(3分)下列函数中,一次函数为()A.y=x3 B.y=﹣2x+1 C.y= D.y=2x2+16.(3分)若k<<k+1(k是整数),则k=()A.6 B.7 C.8 D.97.(3分)若点A(2,4)在函数y=kx﹣2的图象上,则下列各点在此函数图象上的是()A.(1,1) B.(﹣1,1)C.(﹣2,﹣2)D.(2,﹣2)8.(3分)已知直角三角形两边的长为3和4,则此三角形的周长为()A.12 B.7+C.12或7+D.以上都不对9.(3分)如图,一场大风后,一棵大树在高于地面1米处折断,大树顶部落在距离大树底部3米处的地面上,那么树高是()A.4m B.m C.(+1)m D.(+3)m10.(3分)点P为第三象限的点,P到x轴的距离是2,到y轴的距离是5,那么P点坐标是()A.(5,2) B.(﹣5,﹣2)C.(﹣5,2)D.(5,﹣2)11.(3分)已知y=(m2+2m),如果y是x的正比例函数,则m的值为()A.2 B.﹣2 C.2,﹣2 D.012.(3分)已知正比例函数y=kx(k≠0)中,y随x的增大而减小,那么一次函数y=kx﹣k的图象大致是如图中的()A.B.C.D.二、填空题(本大题共6小题,每小题4分,共24分)13.(4分)已知x的平方根是±8,则x的立方根是.14.(4分)在电影院5排3号用(5,3)表示,那么6排2号可表示为.15.(4分)已知=0,则M(a,b)关于x轴对称的点的坐标为.16.(4分)已知一次函数y=﹣x+2的图象经过点P1(x1,1),P2(x2,﹣1),那么x1与x2的大小关系为:x1x2(用“>、<或=”填空).17.(4分)如图,将Rt△ABC放置在平面直角坐标系中,C与原点重合,CB在x轴上,若AB=2,点B的坐标为(4,0),则点A的坐标为.18.(4分)如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B,O分别落在点B1,C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(,0),B(0,4),则点B2018的横坐标为.三、解答题(本大题共60分)19.(12分)计算:(1)(2)(2﹣)2(3)+6﹣(4)(2﹣3)×﹣3.20.(6分)已知2a﹣1的平方为9,b﹣1的算术平方根是2,c是的整数部分,求a﹣b+c的值.21.(6分)如图,在平面直角坐标系xOy中,A(﹣1,5),B(﹣1,0),C(﹣4,3),(1)求出△ABC的面积.(2)在图中作出△ABC关于y轴的对称图形△A1B1C1.(3)直接写出点A1、B1、C1的坐标.22.(8分)已知一个正比例函数和一个一次函数的图象交于点P(﹣2,2)且一次函数的图象与y轴交于点Q(0,4).(1)求这两个函数的表达式;(2)在同一坐标系中,分别画出这两个函数的图象;(3)求三角形△PQO的面积.23.(8分)葛藤是一种刁钻的植物,它的腰杆不硬,为了争夺雨露阳光,常常绕着树干盘旋而上,它还有一手绝招,就是它绕树盘升的路线总是沿最短路线﹣﹣螺旋前进的,难道植物也懂数学?通过阅读以上信息,解决下列问题:(1)如果树干的周长(即图中圆柱体的底面周长)为30cm,绕一圈升高(即圆柱的高)40cm,则它爬行一圈的路程是多少?(2)如果树干的周长为80cm,绕一圈爬行100cm,它爬行10圈到达树顶,则树干高多少?24.(10分)如图,l A l B分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.(1)B出发时与A相距千米.(2)走了一段路后,自行车发生故障进行修理,所用的时间是小时.(3)B出发后小时与A相遇.(4)求出A行走的路程S与时间t的函数关系式.(写出计算过程)(5)请通过计算说明:若B的自行车不发生故障,保持出发时的速度前进,何时与A相遇?25.(10分)某苹果基地销售优质苹果,该基地对需要送货且购买量在2000kg ∽5000kg(含2000kg和5000kg)的客户有两种销售方案(客户只能选择其中一种方案):方案A:每千克5.8元,由基地免费送货.方案B:每千克5元,客户需支付运费2000元.某客户购买x(2000≤x≤5000)kg苹果,应付款y(元).(1)请分别写出按方案A,方案B购买这种苹果的应付款y(元)与购买量x(kg)之间的函数表达式;(2)求x=2200时,方案A和方案B哪种付款少?(3)某水果批发商计划用20000元,选用这两种方案中的一种,购买尽可能多的这种苹果,他应选择哪种方案?2017-2018学年山东省枣庄市山亭区八年级(上)期中数学试卷参考答案与试题解析一、选择题(本大题共12小题,每小题3分,共36分)1.(3分)在实数0、3、﹣、、π、、3.14中无理数的个数是()个.A.1 B.2 C.3 D.4【解答】解:无理数有:﹣,,π共有3个.故选:C.2.(3分)下列各组数中,不能构成直角三角形的一组是()A.1,2,B.1,2,C.3,4,5 D.6,8,12【解答】解:根据勾股定理的逆定理知,三角形三边满足c2=a2+b2,三角形就为直角三角形,四个选项,只有D中不满足,故选D.3.(3分)下列各式中计算正确的是()A.B.C. D.【解答】解:A、=9,故选项错误;B、=5,故选项错误;C、=﹣1,故选项正确;D、(﹣)2=2,故选项错误.故选:C.4.(3分)在平面直角坐标系中,点A(3,﹣5)所在象限为()A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:点A(3,﹣5)所在象限为第四象限.故选:D.5.(3分)下列函数中,一次函数为()A.y=x3 B.y=﹣2x+1 C.y= D.y=2x2+1【解答】解:A、不是一次函数,故此选项错误;B、是一次函数,故此选项正确;C、不是一次函数,故此选项错误;D、不是一次函数,故此选项错误;故选:B.6.(3分)若k<<k+1(k是整数),则k=()A.6 B.7 C.8 D.9【解答】解:∵k<<k+1(k是整数),9<<10,∴k=9.故选:D.7.(3分)若点A(2,4)在函数y=kx﹣2的图象上,则下列各点在此函数图象上的是()A.(1,1) B.(﹣1,1)C.(﹣2,﹣2)D.(2,﹣2)【解答】解:∵点A(2,4)在函数y=kx﹣2的图象上,∴2k﹣2=4,解得k=3,∴此函数的解析式为:y=3x﹣2,A、∵3×1﹣2=1,∴此点在函数图象上,故本选项正确;B、∵3×(﹣1)﹣2=﹣5≠1,∴此点在不函数图象上,故本选项错误;C、∵3×(﹣2)﹣2=﹣7≠﹣2,∴此点在不函数图象上,故本选项错误;D、∵3×2﹣2=4≠﹣2,∴此点在不函数图象上,故本选项错误.故选:A.8.(3分)已知直角三角形两边的长为3和4,则此三角形的周长为()A.12 B.7+C.12或7+D.以上都不对【解答】解:设Rt△ABC的第三边长为x,①当4为直角三角形的直角边时,x为斜边,由勾股定理得,x=5,此时这个三角形的周长=3+4+5=12;②当4为直角三角形的斜边时,x为直角边,由勾股定理得,x=,此时这个三角形的周长=3+4+,故选:C.9.(3分)如图,一场大风后,一棵大树在高于地面1米处折断,大树顶部落在距离大树底部3米处的地面上,那么树高是()A.4m B.m C.(+1)m D.(+3)m【解答】解:根据勾股定理可知:折断的树高==米,则这棵大树折断前的树高=(1+)米.故选:C.10.(3分)点P为第三象限的点,P到x轴的距离是2,到y轴的距离是5,那么P点坐标是()A.(5,2) B.(﹣5,﹣2)C.(﹣5,2)D.(5,﹣2)【解答】解:∵点P到x轴的距离为2,到y轴的距离为5,∴点的纵坐标是±2,横坐标是±5,又∵第三象限内的点横坐标小于0,纵坐标小于0,∴点的横坐标是﹣5,纵坐标是﹣2.故此点的坐标为(﹣5,﹣2).故选:B.11.(3分)已知y=(m2+2m),如果y是x的正比例函数,则m的值为()A.2 B.﹣2 C.2,﹣2 D.0【解答】解;由正比例函数的定义可得:m2+2m≠0,m2﹣3=1,解得;m=2.故选:A.12.(3分)已知正比例函数y=kx(k≠0)中,y随x的增大而减小,那么一次函数y=kx﹣k的图象大致是如图中的()A.B.C.D.【解答】解:∵正比例函数y=kx(k≠0)中,y随x的增大而减小,∴k<0,∴﹣k>0,∴一次函数y=kx﹣k的图象经过第一、二、四象限.故选:D.二、填空题(本大题共6小题,每小题4分,共24分)13.(4分)已知x的平方根是±8,则x的立方根是4.【解答】解:∵x的平方根是±8,∴x=(±8)2,∴x=64,∴==4,故答案是4.14.(4分)在电影院5排3号用(5,3)表示,那么6排2号可表示为(6,2).【解答】解:电影院5排3号用(5,3)表示,那么6排2号可表示为(6,2),故答案为:(6,2).15.(4分)已知=0,则M(a,b)关于x轴对称的点的坐标为(1,3).【解答】解:∵=0,∴a﹣1=0,b+3=0,解得:a=1,b=﹣3,则M(a,b)为:(1,﹣3),故M(a,b)关于x轴对称的点的坐标为:(1,3).故答案为:(1,3).16.(4分)已知一次函数y=﹣x+2的图象经过点P1(x1,1),P2(x2,﹣1),那么x1与x2的大小关系为:x1<x2(用“>、<或=”填空).【解答】解:根据题意,k=﹣<0,y随x的增大而减小,因为1>﹣1,所以x1<x2.故答案为<.17.(4分)如图,将Rt△ABC放置在平面直角坐标系中,C与原点重合,CB在x轴上,若AB=2,点B的坐标为(4,0),则点A的坐标为(3,).【解答】解:作AC⊥OB于C,如图所示:∵点B的坐标为(4,0),∴OB=4,∵∠OAB=90°,AB=2,∴OA==2,∵△OAB的面积=OB•AC=OA•AB,∴AC===,∴OC==3,∴A(3,);故答案为:(3,).18.(4分)如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B,O分别落在点B1,C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(,0),B(0,4),则点B2018的横坐标为10090.【解答】解:∵AO=,BO=4,∴AB=,∴OA+AB1+B1C2=+4+=10,∴B2的横坐标为:10,且B2C2=4,∴B4的横坐标为:2×10=20,∴点B2018的横坐标为:1009×10=10090.∴点B2018的纵坐标为:2.则B2018的横坐标是10090.三、解答题(本大题共60分)19.(12分)计算:(1)(2)(2﹣)2(3)+6﹣(4)(2﹣3)×﹣3.【解答】解:(1)===5;(2)(2﹣)2==8﹣4+3=11﹣4;(3)+6﹣==;(4)(2﹣3)×﹣3===.20.(6分)已知2a﹣1的平方为9,b﹣1的算术平方根是2,c是的整数部分,求a﹣b+c的值.【解答】解:2a﹣1的平方为9,∴2a﹣1=±3,解得:a=2或a=﹣1.∵b﹣1的算术平方根是2,∴b﹣1=4,解得b=5.∵c是的整数部分,∴c=3.当a=2时,a﹣b+c=2﹣5+3=0;当a=﹣1时,ab+c=﹣1﹣5+3=﹣3.21.(6分)如图,在平面直角坐标系xOy中,A(﹣1,5),B(﹣1,0),C(﹣4,3),(1)求出△ABC的面积.(2)在图中作出△ABC关于y轴的对称图形△A1B1C1.(3)直接写出点A1、B1、C1的坐标.【解答】解:(1)S=×5×3=7.5;△ABC(2)如图,△A1B1C1即为所求;(3)由图可知,A1(1,5),B1(1,0),C1(4,3);22.(8分)已知一个正比例函数和一个一次函数的图象交于点P(﹣2,2)且一次函数的图象与y轴交于点Q(0,4).(1)求这两个函数的表达式;(2)在同一坐标系中,分别画出这两个函数的图象;(3)求三角形△PQO的面积.【解答】解:设正比例函数解析式为y=mx,一次函数解析式为y=nx+4,将(﹣2,2)代入可得2=﹣2m,2=﹣2n+4,解得:m=﹣1,n=1,∴函数解析式为:y=﹣x;y=x+4.(2)根据过点(﹣2.2)及(0,4)可画出一次函数图象,根据(0,0)及(﹣2,2)可画出正比例函数图象.|=×2×4=4.(3)面积=|OQ|•|P横坐标23.(8分)葛藤是一种刁钻的植物,它的腰杆不硬,为了争夺雨露阳光,常常绕着树干盘旋而上,它还有一手绝招,就是它绕树盘升的路线总是沿最短路线﹣﹣螺旋前进的,难道植物也懂数学?通过阅读以上信息,解决下列问题:(1)如果树干的周长(即图中圆柱体的底面周长)为30cm,绕一圈升高(即圆柱的高)40cm,则它爬行一圈的路程是多少?(2)如果树干的周长为80cm,绕一圈爬行100cm,它爬行10圈到达树顶,则树干高多少?【解答】解:(1)将圆柱的侧面展开后,该侧面是矩形,AC=30cm,高是40cm,则BA=40cm,∴BC==50cm,故绕行一圈的路程为50cm,(2)因为底面圆的周长为80cm,即AC=80cm,绕一圈爬行100cm,则BC=100cm=60cm,∴树干高=60×10=600cm=6m故树干高为6m24.(10分)如图,l A l B分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.(1)B出发时与A相距10千米.(2)走了一段路后,自行车发生故障进行修理,所用的时间是1小时.(3)B出发后3小时与A相遇.(4)求出A行走的路程S与时间t的函数关系式.(写出计算过程)(5)请通过计算说明:若B的自行车不发生故障,保持出发时的速度前进,何时与A相遇?【解答】解:(1)根据函数图象可知,B出发时与A相距10千米,故答案为:10;(2)根据函数图象可知,走了一段路后,自行车发生故障进行修理,所用的时间是1.5﹣0.5=1小时,故答案为:1;(3)根据图象可知B出发后3小时时与A相遇;(4)根据函数图象可知直线l A经过点(0,10),(3,25).设直线l A的解析式为:S=kt+b,则解得,k=5,b=10即A行走的路程S与时间t的函数关系式是:S=5t+10;(5)设直线l B的解析式为:S=kt,∵点(0.5,7.5)在直线l B上,∴7.5=k×0.5得k=15∴S=15t.∴解得S=15,t=1.故若B的自行车不发生故障,保持出发时的速度前进,1小时时与A相遇.25.(10分)某苹果基地销售优质苹果,该基地对需要送货且购买量在2000kg ∽5000kg(含2000kg和5000kg)的客户有两种销售方案(客户只能选择其中一种方案):方案A:每千克5.8元,由基地免费送货.方案B:每千克5元,客户需支付运费2000元.某客户购买x(2000≤x≤5000)kg苹果,应付款y(元).(1)请分别写出按方案A,方案B购买这种苹果的应付款y(元)与购买量x(kg)之间的函数表达式;(2)求x=2200时,方案A和方案B哪种付款少?(3)某水果批发商计划用20000元,选用这两种方案中的一种,购买尽可能多的这种苹果,他应选择哪种方案?【解答】解:(1)由题意可得,方案A购买这种苹果的应付款y(元)与购买量x(kg)之间的函数表达式:y=5.8x,方案B 购买这种苹果的应付款y (元)与购买量x (kg )之间的函数表达式:y=5x +2000;(2)当x=2200时,方案A :y=5.8×2200=12760(元), 方案B :y=5×2200+2000=13000(元), ∵12760<13000, ∴方案A 付款少; (3)由题意可得,方案A 可以购买的苹果数量为:20000÷5.8≈3448(kg ), 方案B 可以购买的苹果数量为:(20000﹣2000)÷5=3600(kg ), ∵3600>3448,∴他应选择方案B 购买.赠送初中数学几何模型【模型一】“一线三等角”模型: 图形特征:60°60°60°45°45°45°运用举例:1.如图,若点B 在x 轴正半轴上,点A (4,4)、C (1,-1),且AB =BC ,AB ⊥BC ,求点B 的坐标;2.如图,在直线l 上依次摆放着七个正方形(如图所示),已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是1S 、2S 、3S 、4S ,则14S S += .ls 4s 3s 2s 13213. 如图,Rt △ABC 中,∠BAC =90°,AB =AC =2,点D 在BC 上运动(不与点B ,C 重合),过D 作∠ADE =45°,DE 交AC 于E . (1)求证:△ABD ∽△DCE ;(2)设BD =x ,AE =y ,求y 关于x 的函数关系式,并写出自变量x 的取值范围; (3)当△ADE 是等腰三角形时,求AE 的长.B4.如图,已知直线112y x =+与y 轴交于点A ,与x 轴交于点D ,抛物线212y x bx c =++与直线交于A 、E 两点,与x 轴交于B 、C 两点,且B 点坐标为 (1,0)。
2017-2018学年枣庄市薛城区八年级下期中数学试卷(含答案解析)

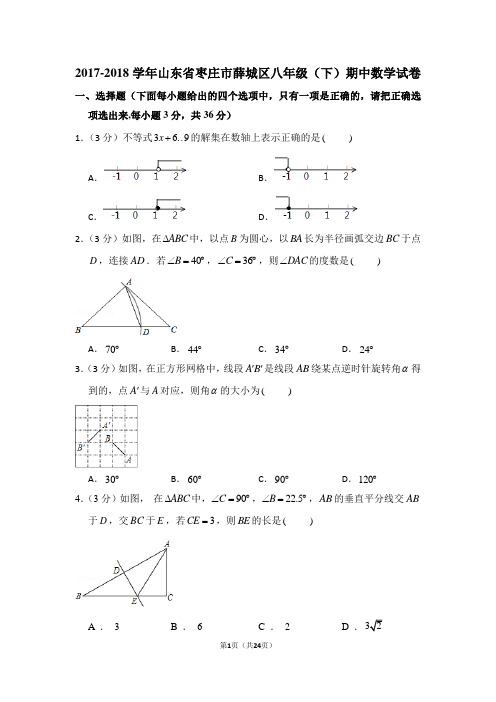
2017-2018学年山东省枣庄市薛城区八年级(下)期中数学试卷一、选择题(下面每小题给出的四个选项中,只有一项是正确的,请把正确选项选出来,每小题3分,共36分)1.不等式3x+6≥9的解集在数轴上表示正确的是()A.B.C.D.2.如图,在△ABC中,以点B为圆心,以BA长为半径画弧交边BC于点D,连接AD.若∠B=40°,∠C =36°,则∠DAC的度数是()A.70°B.44°C.34°D.24°3.如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转角α得到的,点A′与A对应,则角α的大小为()A.30°B.60°C.90°D.120°4.如图,在△ABC中,∠C=90°,∠B=22.5°,AB的垂直平分线交AB于D,交BC于E,若CE=3,则BE的长是()A.3B.6C.2D.35.如图,在方格纸中,△ABC经过变换得到△DEF,正确的变换是()A.把△ABC绕点C逆时针方向旋转90°,再向下平移2格B.把△ABC绕点C顺时针方向旋转90°,再向下平移5格C.把△ABC向下平移4格,再绕点C逆时针方向旋转180°D.把△ABC向下平移5格,再绕点C顺时针方向旋转180°6.不等式组的非负整数解的个数是()A.4B.5C.6D.77.实数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是()A.a﹣3>b﹣3B.﹣3c<﹣3d C.1﹣a>1﹣c D.b﹣d>08.图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是()A.①B.②C.③D.④9.如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.步骤1:以C为圆心,CA为半径画弧①;步骤2:以B为圆心,BA为半径画弧②,交弧①于点D;步骤3:连接AD,交BC延长线于点H.下列叙述正确的是()A.BH垂直平分线段AD B.AC平分∠BADC.S=BC•AH D.AB=AD△ABC10.若关于x的一元一次不等式组的解集是x<5,则m的取值范围是()A.m≥5B.m>5C.m≤5D.m<511.如图,在△ABC中,AB=AC,DE=DF,DE⊥AB,DF⊥AC,垂足分别是E、F.现有下列结论:①AD 平分∠BAC;②AD⊥BC;③AD上任意一点到AB、AC的距离相等;④AD上任意一点到BC两端点的距离相等.其中正确结论的个数有()A.1B.2C.3D.412.已知等边三角形的边长为3,点P为等边三角形内任意一点,则点P到三边的距离之和为()A.B.C.D.不能确定二、填空题(共6小题,每小题4分,满分24分)13.若等腰三角形的一个外角是110°,则其底角为.14.已知五个正数的和等于1.用反证法证明:这五个数中至少有一个大于或等于应先假设.15.关于x的一元一次不等式的解集为x≥4,则m的值为.16.如图,函数y1=﹣2x与y2=ax+3的图象相交于点A(m,2),则关于x的不等式﹣2x≤ax+3的解集是.17.如图在Rt△ABC中,∠ACB=90°,∠ABC=58°,将Rt△ABC绕点C旋转到Rt△A'B'C,使点B恰好落在A'B'上,A'C交AB于点D,则∠ADC的度数为°.18.为有效开展“阳光体育”活动,某校计划购买篮球和足球共50个,购买资金不超过3000元.若每个篮球80元,每个足球50元,则篮球最多可购买个.三、解答题(共7道大题,满分60分)19.(8分)如图所示,已知△ABC的角平分线BM,CN相交于点P.(1)判断AP能否平分∠BAC?请说明理由.(2)由此题你得到的结论是.20.(8分)已知关于x的方程3x﹣(2a﹣3)=5x+3(a+2)的解是非正数,求字母a的取值范围.21.(8分)同学们知道:“在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°.”(1)请写出它的逆命题;该逆命题是一个命题(填“真”或“假”)(2)若你的判断是真命题请写出证明过程(要求画图,并写出已知,求证).若是假命题,请说明理由.22.(8分)解不等式组请结合题意,完成本题解答过程.(1)解不等式①,得,依据是.(2)解不等式②,得.(3)解不等式③,得.(4)把不等式①,②和③的解集在数轴上表示出来.(5)从图中可以找出三个不等式解集的公共部分,得不等式组的解集.(6)根据不等式组的解集确立出该不等式组的最大整数解为.23.(8分)如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,2).请解答下列问题:(1)画出△ABC向左平移6个单位得到的△A1B1C1,并写出A1的坐标.(2)画出△ABC绕点B逆时针旋转90°后得到的△A2B2C2,并写出A2的坐标.(3)画出△A2B2C2关于原点O成中心对称的△A3B3C3,并写出A3的坐标.24.(10分)学校“百变魔方”社团准备购买A,B两种魔方,已知购买2个A种魔方和6个B种魔方共需130元,购买3个A种魔方和4个B种魔方所需款数相同.(1)求这两种魔方的单价;(2)结合社员们的需求,社团决定购买A,B两种魔方共100个(其中A种魔方不超过50个).某商店有两种优惠活动,如图所示.请根据以上信息,说明选择哪种优惠活动购买魔方更实惠.25.(10分)感知:如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°.判断DB与DC的大小关系并证明.探究:如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,DB与DC的大小关系变吗?请说明理由.应用:如图③,四边形ABDC中,∠B=45°,∠C=135°,DB=DC=a,则AB﹣AC=.(用含a的代数式表示)2017-2018学年山东省枣庄市薛城区八年级(下)期中数学试卷参考答案与试题解析一、选择题(下面每小题给出的四个选项中,只有一项是正确的,请把正确选项选出来,每小题3分,共36分)1.不等式3x+6≥9的解集在数轴上表示正确的是()A.B.C.D.【分析】根据解一元一次不等式基本步骤:移项、合并同类项、系数化为1可得.【解答】解:移项,得:3x≥9﹣6,合并同类项,得:3x≥3,系数化为1,得:x≥1,故选:C.【点评】本题主要考查解一元一次不等式的基本能力,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变.2.如图,在△ABC中,以点B为圆心,以BA长为半径画弧交边BC于点D,连接AD.若∠B=40°,∠C =36°,则∠DAC的度数是()A.70°B.44°C.34°D.24°【分析】由AB=BD,∠B=40°得到∠ADB=70°,再根据三角形的外角的性质即可得到结论.【解答】解:∵AB=BD,∠B=40°,∴∠ADB=70°,∵∠C=36°,∴∠DAC=∠ADB﹣∠C=34°.故选:C.【点评】本题考查了等腰三角形的性质,三角形内角和定理,掌握等边对等角是解题的关键,注意三角形外角性质的应用.3.如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转角α得到的,点A′与A对应,则角α的大小为()A.30°B.60°C.90°D.120°【分析】根据题意,由直线AB与直线A′B′的夹角是90°即可确定旋转角的大小.【解答】解:如图:延长AB、A′B′,直线AB与直线A′B′的夹角是90°,故旋转角α为90°.故选:C.【点评】考查了旋转的性质,解题的关键是能够根据题意确定旋转中心的知识,难度不大.4.如图,在△ABC中,∠C=90°,∠B=22.5°,AB的垂直平分线交AB于D,交BC于E,若CE=3,则BE的长是()A.3B.6C.2D.3【分析】利用线段的垂直平分线的性质计算.【解答】解:已知∠C=90°,∠B=22.5°,DE垂直平分AB.故∠B=∠EAB=22.5°,所以∠AEC=45°.又∵∠C=90°,∴△ACE为等腰三角形所以CE=AC=3,故可得AE=3.故选:D.【点评】本题考查的是线段的垂直平分线的性质(垂直平分线上任意一点,和线段两端点的距离相等),难度一般.5.如图,在方格纸中,△ABC经过变换得到△DEF,正确的变换是()A.把△ABC绕点C逆时针方向旋转90°,再向下平移2格B.把△ABC绕点C顺时针方向旋转90°,再向下平移5格C.把△ABC向下平移4格,再绕点C逆时针方向旋转180°D.把△ABC向下平移5格,再绕点C顺时针方向旋转180°【分析】观察图象可知,先把△ABC绕点C顺时针方向旋转90°,再向下平移5格即可得到.【解答】解:根据图象,△ABC绕点C顺时针方向旋转90°,再向下平移5格即可与△DEF重合.故选:B.【点评】本题考查了几何变换的类型,几何变换只改变图形的位置,不改变图形的形状与大小,本题用到了旋转变换与平移变换,对识图能力要求比较高.6.不等式组的非负整数解的个数是()A.4B.5C.6D.7【分析】先求出不等式组的解集,再求出不等式组的非负整数解,即可得出答案.【解答】解:∵解不等式①得:x≥﹣,解不等式②得:x<5,∴不等式组的解集为﹣≤x<5,∴不等式组的非负整数解为0,1,2,3,4,共5个,故选:B.【点评】本题考查了解一元一次不等式组和一元一次不等式组的整数解,能求出不等式组的解集是解此题的关键.7.实数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是()A.a﹣3>b﹣3B.﹣3c<﹣3d C.1﹣a>1﹣c D.b﹣d>0【分析】依据实数a,b,c,d在数轴上的对应点的位置,即可得到a,b,c,d的大小关系,进而利用不等式的基本性质得出结论.【解答】解:∵a<b,∴a﹣3<b﹣3,故A选项错误;∵c<d,∴﹣3c>﹣3d,故B选项错误;∵a<c,∴1﹣a>1﹣c,故C选项正确;∵b<d,∴b﹣d<0,故D选项错误;故选:C.【点评】本题考查了实数与数轴,观察数轴,逐一分析四个选项的正误是解题的关键.8.图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是()A.①B.②C.③D.④【分析】根据把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心,进而得出答案.【解答】解:当正方形放在③的位置,即是中心对称图形.故选:C.【点评】此题主要考查了中心对称图形的定义,正确把握定义是解题关键.9.如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.步骤1:以C为圆心,CA为半径画弧①;步骤2:以B为圆心,BA为半径画弧②,交弧①于点D;步骤3:连接AD,交BC延长线于点H.下列叙述正确的是()A.BH垂直平分线段AD B.AC平分∠BADC.S=BC•AH D.AB=AD△ABC【分析】根据已知条件可知直线BC是线段AD的垂直平分线,由此一一判定即可.【解答】解:A、正确.如图连接CD、BD,∵CA=CD,BA=BD,∴点C、点B在线段AD的垂直平分线上,∴直线BC是线段AD的垂直平分线,故A正确.B、错误.CA不一定平分∠BDA.C、错误.应该是S=•BC•AH.△ABCD、错误.根据条件AB不一定等于AD.故选:A.【点评】本题考查作图﹣基本作图、线段的垂直平分线的性质等知识,解题的关键是掌握证明线段垂直平分线的证明方法,属于基础题,中考常考题型.10.若关于x的一元一次不等式组的解集是x<5,则m的取值范围是()A.m≥5B.m>5C.m≤5D.m<5【分析】求出第一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了即可确定m的范围.【解答】解:解不等式2x﹣1>3(x﹣2),得:x<5,∵不等式组的解集为x<5,∴m≥5,故选:A.【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.11.如图,在△ABC中,AB=AC,DE=DF,DE⊥AB,DF⊥AC,垂足分别是E、F.现有下列结论:①AD 平分∠BAC;②AD⊥BC;③AD上任意一点到AB、AC的距离相等;④AD上任意一点到BC两端点的距离相等.其中正确结论的个数有()A.1B.2C.3D.4【分析】根据角平分线的逆定理可知①正确,利用等腰三角形底边上的中线、高线与顶角的角平分线三线合一,可得②④正确;利用角平分线上的点到角两边的距离相等,可得③.【解答】解:①∵DE=DF,DE⊥AB,DF⊥AC,∴AD平分∠BAC,故①正确;②∵AB=AC,AD平分∠BAC,∴AD⊥BC.故②正确;③∵AD是△ABC的角平分线,角平分线上的点到角两边的距离相等,∴AD上任意一点到边AB、AC的距离相等.故③正确;④∵AB=AC,AD平分∠BAC,∴BD=CD,即AD是BC的垂直平分线,∴AD上任意一点到BC两端点的距离相等;故④正确.所以①、②、③、④均正确,故选:D.【点评】本题考查了等腰三角形的性质、角平分线的性质等知识.根据相关知识对各选项进行逐个验证是正确解答本题的关键.12.已知等边三角形的边长为3,点P为等边三角形内任意一点,则点P到三边的距离之和为()A.B.C.D.不能确定【分析】作出图形,根据等边三角形的性质求出高AH的长,再根据三角形的面积公式求出点P到三边的距离之和等于高线的长度,从而得解.【解答】解:如图,∵等边三角形的边长为3,∴高线AH=3×=,S=BC•AH=AB•PD+BC•PE+AC•PF,△ABC∴×3•AH=×3•PD+×3•PE+×3•PF,∴PD+PE+PF=AH=,即点P到三角形三边距离之和为.故选:B.【点评】本题考查了等边三角形的性质,根据三角形的面积求点P到三边的距离之和等于等边三角形的高是解题的关键,作出图形更形象直观.二、填空题(共6小题,每小题4分,满分24分)13.若等腰三角形的一个外角是110°,则其底角为70°或55°.【分析】分这个外角为底角的外角和顶角的外角,分别求解即可.【解答】解:当110°外角为底角的外角时,则其底角为:180°﹣110°=70°;当110°外角为顶角的外角时,则其顶角为:70°,则其底角为:=55°,故答案为:70°或55°.【点评】本题主要考查等腰三角形的性质和三角形内角和定理的应用,掌握等腰三角形的两底角相等和三角形三个内角的和为180°是解题的关键.14.已知五个正数的和等于1.用反证法证明:这五个数中至少有一个大于或等于应先假设这五个数都小于.【分析】熟记反证法的步骤,直接从结论的反面出发得出即可.【解答】解:知五个正数的和等于1.用反证法证明:这五个数中至少有一个大于或等于应先假设这五个数都小于,故答案为:这五个数都小于【点评】此题主要考查了反证法,反证法的步骤是:(1)假设结论不成立;(2)从假设出发推出矛盾;(3)假设不成立,则结论成立.在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.15.关于x的一元一次不等式的解集为x≥4,则m的值为2.【分析】先用含有m的式子把原不等式的解集表示出来,然后和已知解集进行比对得出关于m的方程,解之可得m的值.【解答】解:解不等式得:x≥,∵不等式的解集为x≥4,∴=4,解得:m=2,故答案为:2.【点评】本题主要考查解一元一次不等式,当题中有两个未知字母时,应把关于某个字母的不等式中的字母当成未知数,求得解集,再根据解集进行判断,求得另一个字母的值.16.如图,函数y1=﹣2x与y2=ax+3的图象相交于点A(m,2),则关于x的不等式﹣2x≤ax+3的解集是x≥﹣1.【分析】首先利用待定系数法求出A点坐标,再以交点为分界,结合图象写出不等式﹣2x≤ax+3的解集即可.【解答】解:∵函数y1=﹣2x过点A(m,2),∴﹣2m=2,解得:m=﹣1,∴A(﹣1,2),∴不等式﹣2x<ax+3的解集为x≥﹣1.故答案为:x≥﹣1.【点评】此题主要考查了一次函数与一元一次不等式,关键是求出A点坐标.17.如图在Rt△ABC中,∠ACB=90°,∠ABC=58°,将Rt△ABC绕点C旋转到Rt△A'B'C,使点B恰好落在A'B'上,A'C交AB于点D,则∠ADC的度数为84°.【分析】首先由旋转的性质可知:△BB′C是等腰三角形,由三角形内角和定理可求得∠BCB′的度数,进而可求得∠BCD的度数,即可根据三角形的外角性质求得∠ADC的度数.【解答】解:由旋转的性质知:∠ABC=∠B′=58°,BC=B′C;在等腰△BCB′中,由三角形内角和定理知:∠BCB′=180°﹣2∠B′=64°,∴∠BCD=90°﹣∠BCB′=26°;∴∠ADC=∠ABC+∠BCD=58°+26°=84°;故∠ADC的度数为84°.【点评】此题主要考查了旋转的性质,还涉及到三角形内角和定理及三角形的外角性质,难度不大.18.为有效开展“阳光体育”活动,某校计划购买篮球和足球共50个,购买资金不超过3000元.若每个篮球80元,每个足球50元,则篮球最多可购买16个.【分析】设购买篮球x个,则购买足球(50﹣x)个,根据总价=单价×购买数量结合购买资金不超过3000元,即可得出关于x的一元一次不等式,解之取其中的最大整数即可.【解答】解:设购买篮球x个,则购买足球(50﹣x)个,根据题意得:80x+50(50﹣x)≤3000,解得:x≤.∵x为整数,∴x最大值为16.故答案为:16.【点评】本题考查了一元一次不等式的应用,根据各数量间的关系,正确列出一元一次不等式是解题的关键.三、解答题(共7道大题,满分60分)19.(8分)如图所示,已知△ABC的角平分线BM,CN相交于点P.(1)判断AP能否平分∠BAC?请说明理由.(2)由此题你得到的结论是三角形的三条内角平分线相交于一点.【分析】如图,作辅助线;证明PK=PL即可解决问题.【解答】解:(1)AP能平分∠BAC;理由如下:如图,过点P作PQ⊥BC、PK⊥AB、PL⊥AC;∵△ABC的角平分线BM、CN相交于点P,∴PK=PQ,PL=PQ,∴PK=PL,∴AP平分∠BAC;(2)结论:三角形的三条内角平分线相交于一点.故答案为:三角形的三条内角平分线相交于一点.【点评】该题主要考查了三角形的内角平分线的性质及其应用问题;作辅助线是解决该题的关键.20.(8分)已知关于x的方程3x﹣(2a﹣3)=5x+3(a+2)的解是非正数,求字母a的取值范围.【分析】依次移项,合并同类项,系数化为1,得到x关于a的解,根据方程的解为非正数,得到关于a 的一元一次不等式,解之即可.【解答】解:3x﹣(2a﹣3)=5x+3(a+2),移项得:3x﹣5x=3a+6+2a﹣3,合并同类项得:﹣2x=5a+3,系数化为1得:x=﹣,∵方程的解是非正数,∴﹣≤0,解得:a,即字母a的取值范围为:a.【点评】本题考查解一元一次不等式和一元一次方程的解,正确掌握解一元一次不等式和解一元一次方程的方法是解题的关键.21.(8分)同学们知道:“在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°.”(1)请写出它的逆命题在直角三角形中,如果一个锐角等于30度,那么它所对的直角边等于斜边的一半;该逆命题是一个真命题(填“真”或“假”)(2)若你的判断是真命题请写出证明过程(要求画图,并写出已知,求证).若是假命题,请说明理由.【分析】(1)写出逆命题,并判断是真命题;(2)首先写出已知、求证,画出图形,借助等边三角形的判定和性质证明或借助三角形的外接圆证明.【解答】解:(1)原命题的逆命题为:在直角三角形中,如果一个锐角等于30度,那么它所对的直角边等于斜边的一半,该逆命题是一个真命题;故答案为:在直角三角形中,如果一个锐角等于30度,那么它所对的直角边等于斜边的一半,真;(2)已知,在Rt△ABC中,∠A=30°,∠ACB=90°.求证:BC=AB.证明:证法一:如图1所示,延长BC到D,使CD=BC,连接AD,易证AD=AB,∠BAD=60°.∴△ABD为等边三角形,∴AB=BD,∴BC=CD=AB,即BC=AB.证法二:如图2所示,取AB的中点D,连接DC,有CD=AB=AD=DB,∴∠DCA=∠A=30°,∠BDC=∠DCA+∠A=60°.∴△DBC为等边三角形,∴BC=DB=AB,即BC=AB.证法三:如图3所示,在AB上取一点D,使BD=BC,∵∠B=60°,∴△BDC为等边三角形,∴∠DCB=60°,∠ACD=90°﹣∠DCB=90°﹣60°=30°=∠A.∴DC=DA,即有BC=BD=DA=AB,∴BC=AB.证法四:如图3所示,作△ABC的外接圆⊙D,∠C=90°,AB为⊙O的直径,连DC,有DB=DC,∠BDC=2∠A=2×30°=60°,∴△DBC为等边三角形,∴BC=DB=DA=AB,即BC=AB.【点评】本题考查的是直角三角形30度角的性质和等边三角形的判定、互逆命题的定义,熟练掌握直角三角形30度角的性质的证明是关键.22.(8分)解不等式组请结合题意,完成本题解答过程.(1)解不等式①,得x≥﹣3,依据是不等式两边都乘以(或除以)同一个负数,不等号的方向改变.(2)解不等式②,得x>﹣2.(3)解不等式③,得x<2.(4)把不等式①,②和③的解集在数轴上表示出来.(5)从图中可以找出三个不等式解集的公共部分,得不等式组的解集﹣2<x<2.(6)根据不等式组的解集确立出该不等式组的最大整数解为x=1.【分析】分别求出每一个不等式的解集,根据各不等式解集在数轴上的表示,确定不等式组的解集.【解答】解:(1)解不等式①,得x≥﹣3,依据是:不等式两边都乘以(或除以)同一个负数,不等号的方向改变.(2)解不等式②,得x>﹣2.(3)解不等式③,得x<2.(4)把不等式①,②和③的解集在数轴上表示出来如下:(5)从图中可以找出三个不等式解集的公共部分,得不等式组的解集:﹣2<x<2.(6)根据不等式组的解集确立出该不等式组的最大整数解为:x=1;故答案为:(1)x≥﹣3、不等式两边都乘以(或除以)同一个负数,不等号的方向改变;(2)x>﹣2;(3)x<2;(5)﹣2<x<2;(6)x=1.【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.23.(8分)如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,2).请解答下列问题:(1)画出△ABC向左平移6个单位得到的△A1B1C1,并写出A1的坐标.(2)画出△ABC绕点B逆时针旋转90°后得到的△A2B2C2,并写出A2的坐标.(3)画出△A2B2C2关于原点O成中心对称的△A3B3C3,并写出A3的坐标.【分析】(1)分别画出A、B、C的对应点A1、B1、C1即可;(2)分别画出A、B、C的对应点A2、B2、C2即可;(3)分别画出A2、B2、C2的对应点A3、B3、C3即可.【解答】解:(1)△A1B1C1,如图所示;A1(﹣4,2);(2)△A2B2C2如图所示;并写出A2(4,0),(3)△A3B3C3如图所示,A3(﹣4,0)、【点评】本题考查作图﹣旋转变换、平移变换等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.24.(10分)学校“百变魔方”社团准备购买A,B两种魔方,已知购买2个A种魔方和6个B种魔方共需130元,购买3个A种魔方和4个B种魔方所需款数相同.(1)求这两种魔方的单价;(2)结合社员们的需求,社团决定购买A,B两种魔方共100个(其中A种魔方不超过50个).某商店有两种优惠活动,如图所示.请根据以上信息,说明选择哪种优惠活动购买魔方更实惠.【分析】(按买3个A种魔方和买4个B种魔方钱数相同解答)(1)设A种魔方的单价为x元/个,B种魔方的单价为y元/个,根据“购买2个A种魔方和6个B种魔方共需130元,购买3个A种魔方和4个B种魔方所需款数相同”,即可得出关于x、y的二元一次方程组,解之即可得出结论;(2)设购进A种魔方m个(0<m≤50),总价格为w元,则购进B种魔方(100﹣m)个,根据两种活动方案即可得出w活动一、w活动二关于m的函数关系式,再分别令w活动一<w活动二、w活动一=w活动二和w活动一>w活动二,解出m的取值范围,此题得解.(按购买3个A种魔方和4个B种魔方需要130元解答)(1)设A种魔方的单价为x元/个,B种魔方的单价为y元/个,根据“购买2个A种魔方和6个B种魔方共需130元,购买3个A种魔方和4个B种魔方所需款数相同”,即可得出关于x、y的二元一次方程组,解之即可得出结论;(2)设购进A种魔方m个(0<m≤50),总价格为w元,则购进B种魔方(100﹣m)个,根据两种活动方案即可得出w活动一、w活动二关于m的函数关系式,再分别令w活动一<w活动二、w活动一=w活动二和w活动一>w活动二,解出m的取值范围,此题得解.【解答】(按买3个A种魔方和买4个B种魔方钱数相同解答)解:(1)设A种魔方的单价为x元/个,B种魔方的单价为y元/个,根据题意得:,解得:.答:A种魔方的单价为20元/个,B种魔方的单价为15元/个.(2)设购进A 种魔方m 个(0<m ≤50),总价格为w 元,则购进B 种魔方(100﹣m )个,根据题意得:w 活动一=20m ×0.8+15(100﹣m )×0.4=10m +600;w 活动二=20m +15(100﹣m ﹣m )=﹣10m +1500.当w 活动一<w 活动二时,有10m +600<﹣10m +1500,解得:m <45;当w 活动一=w 活动二时,有10m +600=﹣10m +1500,解得:m =45;当w 活动一>w 活动二时,有10m +600>﹣10m +1500,解得:45<m ≤50.综上所述:当m <45时,选择活动一购买魔方更实惠;当m =45时,选择两种活动费用相同;当m >45时,选择活动二购买魔方更实惠.(按购买3个A 种魔方和4个B 种魔方需要130元解答)解:(1)设A 种魔方的单价为x 元/个,B 种魔方的单价为y 元/个,根据题意得:,解得:. 答:A 种魔方的单价为26元/个,B 种魔方的单价为13元/个.(2)设购进A 种魔方m 个(0<m ≤50),总价格为w 元,则购进B 种魔方(100﹣m )个,根据题意得:w 活动一=26m ×0.8+13(100﹣m )×0.4=15.6m +520;w 活动二=26m +13(100﹣m ﹣m )=1300.当w 活动一<w 活动二时,有15.6m +520<1300,解得:m <50;当w 活动一=w 活动二时,有15.6m +520=1300,解得:m =50;当w 活动一>w 活动二时,有15.6m +520>1300,不等式无解.综上所述:当0<m <50时,选择活动一购买魔方更实惠;当m =50时,选择两种活动费用相同.【点评】本题考查了二元一次方程组的应用、一次函数的应用、解一元一次不等式以及解一元一次方程,解题的关键是:(1)找准等量关系,列出关于x 、y 的二元一次方程组;(2)根据两种活动方案找出w 活动一、w 活动二关于m 的函数关系式.25.(10分)感知:如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°.判断DB与DC的大小关系并证明.探究:如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,DB与DC的大小关系变吗?请说明理由.应用:如图③,四边形ABDC中,∠B=45°,∠C=135°,DB=DC=a,则AB﹣AC=a.(用含a的代数式表示)【分析】感知:判断出△ADC≌△ADB,即可得出结论;探究:欲证明DB=DC,只要证明△DFC≌△DEB即可.应用:先证明△DFC≌△DEB,再证明△ADF≌△ADE,结合BD=EB即可解决问题.【解答】感知:解:BD=DC,理由:∵AD平分∠BAC,∴∠DAC=∠DAB,∵∠B+∠C=180°,∠B=90°,∴∠C=90°=∠B,在△ADC和△ADB中,,∴△ADC≌△ADB(AAS),∴BD=DC;探究:证明:如图②中,DE⊥AB于E,DF⊥AC于F,∵DA平分∠BAC,DE⊥AB,DF⊥AC,∴DE=DF,∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,∴∠B=∠FCD,在△DFC和△DEB中,∴△DFC≌△DEB,∴DC=DB;应用:解;如图③连接AD、DE⊥AB于E,DF⊥AC于F,∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,∴∠B=∠FCD,在△DFC和△DEB中,∴△DFC≌△DEB,∴DF=DE,CF=BE,在Rt△ADF和Rt△ADE中,∴Rt△ADF≌Rt△ADE,∴AF=AE,∴AB﹣AC=(AE+BE)﹣(AF﹣CF)=2BE,在Rt△DEB中,∵∠DEB=90°,∠B=∠EDB=45°,BD=a,∴BE=BD=a,∴AB﹣AC=2BE=a.故答案为a.【点评】此题是四边形综合题,主要考查全等三角形的判定和性质、角平分线的性质、等腰直角三角形的性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形.。
2017 2018枣庄市薛城区八年级下期中数学试卷有答案

2017-2018学年山东省枣庄市薛城区八年级(下)期中数学试卷一、选择题(下面每小题给出的四个选项中,只有一项是正确的,请把正确选项选出来,每小题3分)36分,共x)的解集在数轴上表示正确的是(+6≥91.不等式3.A.BC.D.ABCBBABCDADB=40中,以点,连接为圆心,以°,长为半径画弧交边于点.若∠2.如图,在△DACC)°,则∠的度数是(∠36=A.70°B.44°C.34°D.24°α得到的,点′与对3.如图,在正方形网格中,线段′′是线段绕某点逆时针旋转角ABABAA)应,则角α的大小为(A.30°B.60°C.90°D.120°ABCCBABABDBCECE,若,交于4.如图,在△中,∠°,∠=90°,=22.5于的垂直平分线交),则的长是(3=BE A.3B.6 C.2 D.3).如图,在方格纸中,△5经过变换得到△,正确的变换是(ABCDEF.ABCC逆时针方向旋转90°,再向下平移A.把△2绕点格ABCC顺时针方向旋转90°,再向下平移.把△5绕点格B ABCC逆时针方向旋转180°.把△向下平移4格,再绕点CD.把△向下平移5格,再绕点顺时针方向旋转180°CABC6.不等式组的非负整数解的个数是()A.4B.5C.6D.7abcd在数轴上的对应点的位置如图所示,则正确的结论是(,7.实数),,abcdacbd>﹣D.30C.1﹣>1﹣A.3﹣>3 ﹣B.﹣3<﹣8.图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是()A.①B.②C.③D.④ABC,依下列步骤尺规作图,并保留作图痕迹.9.如图,已知钝角△CCA为半径画弧①;:以步骤1为圆心,BBAD;为半径画弧②,交弧①于点步骤2:以为圆心,步骤3:连接,交延长线于点.HADBC)下列叙述正确的是(.BHADACBAD平分∠B.A.垂直平分线段ABAHADSBC =C.D=.?ABC△的解集是<5,则的取值范围是()10.若关于的一元一次不等式组xxmmmmm>5D.B<5A..≥5C.≤5ABCABACDEDFDEABDFACEFAD①,,垂足分别是⊥.现有下列结论:在△11.如图,,中,、=⊥,=平分∠;②⊥;③上任意一点到、的距离相等;④上任意一点到两端点BCBCACADADABBACAD)的距离相等.其中正确结论的个数有(A.1 B.2 C.3 D.4PP为等边三角形内任意一点,,3点()12.则点已知等边三角形的边长为到三边的距离之和为CD.不能确定.B.A.4分,满分24分)二、填空题(共6小题,每小题13.若等腰三角形的一个外角是110°,则其底角为.14.已知五个正数的和等于1.用反证法证明:这五个数中至少有一个大于或等于应先假.设xxm的值为,则.的一元一次不等式的解集为≥415.关于yxyaxAmxxax+316.如图,函数≤的图象相交于点2=﹣与=+32的不等式﹣),则关于2,(21.的解集是17.如图在Rt△中,∠=90°,∠=58°,将Rt△绕点旋转到Rt△'',使点CABCACBABCACABCBBABACABDADC 的度数为于点'上,°.'恰好落在交',则∠18.为有效开展“阳光体育”活动,某校计划购买篮球和足球共50个,购买资金不超过3000元.若个.80每个篮球元,每个足球50元,则篮球最多可购买7道大题,满分60三、解答题(共分)ABCBMCNP.的角平分线相交于点,819.(分)如图所示,已知△APBAC?请说明理由.能否平分∠(1)判断(2)由此题你得到的结论是.xxaxaa的取值范围.)的解是非正数,求字母+3(分)已知关于8+2的方程3﹣(2﹣3)=5.(2021.(8分)同学们知道:“在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°.”;该逆命题是一个命题(填“真”或“假”)(1)请写出它的逆命题(2)若你的判断是真命题请写出证明过程(要求画图,并写出已知,求证).若是假命题,请说明理由.22.(8分)解不等式组请结合题意,完成本题解答过程.(1)解不等式①,得,依据是..2)解不等式②,得(.)解不等式③,得(3(4)把不等式①,②和③的解集在数轴上表示出来.(5)从图中可以找出三个不等式解集的公共部分,得不等式组的解集..)根据不等式组的解集确立出该不等式组的最大整数解为(6ABCA的三个顶点都在格点上,△2,8分)如图,在平面直角坐标系中,2点).请的坐标为(23.(解答下列问题:ABABCAC的坐标.向左平移6个单位得到的△(1)画出△,并写出1111的坐标.,并写出90绕点逆时针旋转°后得到的△(2)画出△ABCABCBA2222AOBACCAB的坐标.关于原点)画出△,并写出成中心对称的△(33223332ABAB种个种魔方和,个两种魔方,已知购买26.(2410分)学校“百变魔方”社团准备购买AB种魔方所需款数相同.43个个种魔方和130魔方共需元,购买(1)求这两种魔方的单价;(2)结合社员们的需求,社团决定购买,两种魔方共100个(其中种魔方不超过50个).某AAB商店有两种优惠活动,如图所示.请根据以上信息,说明选择哪种优惠活动购买魔方更实惠.分)感知:10.(25.ADBACBCBDBDC的大小关系并证明.与=,∠90+∠180=°,∠如图①,平分∠°.判断探究:如图②,平分∠,∠+∠=180°,∠<90°,与的大小关系变吗?请说明理DCDBABDACDADABDBAC由.应用:ABDCBCDBDCaABACa.(用含=﹣如图③,四边形,则==°,135=°,∠45=中,∠的代数式表示).2017-2018学年山东省枣庄市薛城区八年级(下)期中数学试卷参考答案与试题解析一、选择题(下面每小题给出的四个选项中,只有一项是正确的,请把正确选项选出来,每小题3分)36分,共)9≥的解集在数轴上表示正确的是(1.不等式3+6x..BA..DC可得.【分析】根据解一元一次不等式基本步骤:移项、合并同类项、系数化为1,﹣6【解答】解:移项,得:3≥9x,≥3合并同类项,得:3xx,11,得:≥系数化为C.故选:【点评】本题主要考查解一元一次不等式的基本能力,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变.BADBABCDABCB°,于点402.如图,在△,连接中,以点=为圆心,以.若∠长为半径画弧交边DACC)°,则∠∠的度数是(=36°.2434°D44.70°B.°C.A ADBBABBD°,再根据三角形的外角的性质即可得到结论.70=,∠=40°得到∠【分析】由=BABBD°,==,∠40【解答】解:∵ADB°,∴∠70=C°,36=∵∠°.==∠∴∠﹣∠34CDACADB.故选:C【点评】本题考查了等腰三角形的性质,三角形内角和定理,掌握等边对等角是解题的关键,注意三角形外角性质的应用.ABABAA对得到的,点′是线段′与绕某点逆时针旋转角.如图,在正方形网格中,线段3α′)α的大小为(应,则角A.30°B.60°C.90°D.120°ABAB′的夹角是90与直线【分析】根据题意,由直线°即可确定旋转角的大小.′【解答】解:如图:延长、′′,直线与直线′′的夹角是90°,故旋转角α为90°.BABABAABC.故选:【点评】考查了旋转的性质,解题的关键是能够根据题意确定旋转中心的知识,难度不大.ABCCBABABDBCECE,若于的垂直平分线交4.如图,在△中,∠于=90°,∠°,=22.5,交BE)的长是(=3,则A.3 B.6 C.2 D.3【分析】利用线段的垂直平分线的性质计算.CBDEAB.22.5°,【解答】解:已知∠=90°,∠垂直平分=BEAB=22.5=∠故∠°,AEC=45°.所以∠又∵∠=90°,C∴△为等腰三角形ACECEAC=3所以,=AE=3故可得.D.故选:【点评】本题考查的是线段的垂直平分线的性质(垂直平分线上任意一点,和线段两端点的距离相等),难度一般.ABCDEF,正确的变换是(.如图,在方格纸中,△)经过变换得到△5ABCC逆时针方向旋转90°,再向下平移A.把△2绕点格CABC5顺时针方向旋转°,再向下平移格B.把△90绕点180°C.把△向下平移4格,再绕点逆时针方向旋转CABC D180°.把△向下平移5格,再绕点顺时针方向旋转CABCABCC顺时针方向旋转绕点【分析】观察图象可知,先把△90°,再向下平移5格即可得到.ABCCDEF重合.【解答】解:根据图象,△5格即可与△顺时针方向旋转90绕点°,再向下平移B.故选:【点评】本题考查了几何变换的类型,几何变换只改变图形的位置,不改变图形的形状与大小,本题用到了旋转变换与平移变换,对识图能力要求比较高.6.不等式组的非负整数解的个数是()D..647B.5CA.【分析】先求出不等式组的解集,再求出不等式组的非负整数解,即可得出答案.【解答】解:x≥﹣,∵解不等式①得:解不等式②得:<5,xx<5≤,∴不等式组的解集为﹣0,1,2,3,4,共5个,∴不等式组的非负整数解为B.故选:能求出不等式组的解集是【点评】本题考查了解一元一次不等式组和一元一次不等式组的整数解,解此题的关键.)在数轴上的对应点的位置如图所示,则正确的结论是(,,7.实数,dcababcdacbd0 >﹣.D﹣1>﹣1.C3<﹣3.﹣B3 ﹣>3﹣.A.abcdabcd的大小关系,进而在数轴上的对应点的位置,即可得到【分析】依据实数,,,,,,利用不等式的基本性质得出结论.ababA选项错误;33<【解答】解:∵,故<,∴﹣﹣cdcdB选项错误;,故>﹣∵3<,∴﹣3acacC选项正确;1﹣<,故,∴1﹣∵>bdbdD选项错误;,故<<,∴0∵﹣C.故选:【点评】本题考查了实数与数轴,观察数轴,逐一分析四个选项的正误是解题的关键.8.图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它)与原来7个小正方形组成的图形是中心对称图形,这个位置是(A.①B.②C.③D.④【分析】根据把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心,进而得出答案.【解答】解:当正方形放在③的位置,即是中心对称图形.故选:.C【点评】此题主要考查了中心对称图形的定义,正确把握定义是解题关键.9.如图,已知钝角△,依下列步骤尺规作图,并保留作图痕迹.ABCCCA为半径画弧①;:以为圆心,步骤1BBAD;:以为半径画弧②,交弧①于点为圆心,2步骤HADBC.步骤3,交:连接延长线于点)下列叙述正确的是(BHADACBAD平分∠.B垂直平分线段.A.C.=?D.=ADSAHBCAB ABC△是线段【分析】根据已知条件可知直线的垂直平分线,由此一一判定即可.ADBC、、正确.如图连接,【解答】解:CDBDABDCACDBA,=,∵=ADCB的垂直平分线上,、点在线段∴点ADBC的垂直平分线,∴直线是线段A正确.故BCABDA.、错误.不一定平分∠CSBCAH.?、错误.应该是=?ABC△ABADD.不一定等于、错误.根据条件A.故选:【点评】本题考查作图﹣基本作图、线段的垂直平分线的性质等知识,解题的关键是掌握证明线段垂直平分线的证明方法,属于基础题,中考常考题型.xxm的取值范围是(,则)<510.若关于的一元一次不等式组的解集是mmmm5DA..≥5B.>5C.<≤5【分析】求出第一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小m的范围.无解了即可确定xxx<5,(【解答】解:解不等式﹣22),得:﹣1>3x<5,∵不等式组的解集为m,5≥∴.故选:A【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.11.如图,在△中,=,=,⊥,⊥,垂足分别是、.现有下列结论:①ADDFDEEDEABDFFACABCABACBACADBCADABA CADBC两端点平分∠;②⊥;③上任意一点到、的距离相等;④上任意一点到)的距离相等.其中正确结论的个数有(.A.1 B.2 C.3 D.4【分析】根据角平分线的逆定理可知①正确,利用等腰三角形底边上的中线、高线与顶角的角平分线三线合一,可得②④正确;利用角平分线上的点到角两边的距离相等,可得③.DEDFDEABDFAC,⊥【解答】解:①∵=⊥,,ADBAC,平分∠∴故①正确;ABACADBAC,,②∵平分∠=ADBC.∴⊥故②正确;ADABC的角平分线,角平分线上的点到角两边的距离相等,③∵是△∴上任意一点到边、的距离相等.ACABAD故③正确;ABACADBAC,④∵平分∠=,BDCD,=∴ADBC的垂直平分线,是即ADBC两端点的距离相等;∴上任意一点到故④正确.所以①、②、③、④均正确,故选:.D【点评】本题考查了等腰三角形的性质、角平分线的性质等知识.根据相关知识对各选项进行逐个验证是正确解答本题的关键.PP到三边的距离之和为)点(为等边三角形内任意一点,则点,12.已知等边三角形的边长为3.不能确定C.D.AB.PAH到【分析】作出图形,根据等边三角形的性质求出高的长,再根据三角形的面积公式求出点三边的距离之和等于高线的长度,从而得解.,【解答】解:如图,∵等边三角形的边长为3AH,=×3=∴高线=?=?+?+?,ACAHPEBCPFPDABBCS ABC△AHPDPEPF,3?+3?=××+×∴×3?3?PDPEPFAH=+∴,+=P到三角形三边距离之和为.即点B.故选:【点评】本题考查了等边三角形的性质,根据三角形的面积求点到三边的距离之和等于等边三角P形的高是解题的关键,作出图形更形象直观.二、填空题(共6小题,每小题4分,满分24分)110°,则其底角为70°或55°.13.若等腰三角形的一个外角是【分析】分这个外角为底角的外角和顶角的外角,分别求解即可.【解答】解:当110°外角为底角的外角时,则其底角为:180°﹣110°=70°;70°,则其底角为:=55110当°外角为顶角的外角时,则其顶角为:°,°.55°或故答案为:70掌握等腰三角形的两底角相本题主要考查等腰三角形的性质和三角形内角和定理的应用,【点评】°是解题的关键.180等和三角形三个内角的和为这14.已知五个正数的和等于应先假设.用反证法证明:这五个数中至少有一个大于或等于1.五个数都小于【分析】熟记反证法的步骤,直接从结论的反面出发得出即可.【解答】解:知五个正数的和等于1.用反证法证明:这五个数中至少有一个大于或等于应先假,设这五个数都小于故答案为:这五个数都小于【点评】此题主要考查了反证法,反证法的步骤是:(1)假设结论不成立;(2)从假设出发推出矛盾;(3)假设不成立,则结论成立.在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定..2 ,则的解集为≥4的值为15.关于的一元一次不等式mxxmm的方的式子把原不等式的解集表示出来,【分析】先用含有然后和已知解集进行比对得出关于m 的值.程,解之可得x≥,【解答】解:解不等式得:x≥4,∵不等式的解集为,=4∴m=2,解得:故答案为:2.【点评】本题主要考查解一元一次不等式,当题中有两个未知字母时,应把关于某个字母的不等式中的字母当成未知数,求得解集,再根据解集进行判断,求得另一个字母的值.16.如图,函数=﹣2与=+3的图象相交于点,2),则关于的不等式﹣2≤+3(mxAxaxyaxyx21x.的解集是1 ≥﹣【分析】首先利用待定系数法求出点坐标,再以交点为分界,结合图象写出不等式﹣2≤+3axAx的解集即可.yxAm,2(【解答】解:∵函数2=﹣),过点1,=2∴﹣2mm,=﹣1解得:A),∴(﹣21,xaxx≥﹣1的解集为.2∴不等式﹣<+3x.1≥﹣故答案为:A点坐标.【点评】此题主要考查了一次函数与一元一次不等式,关键是求出ABCACBABCABCCABC,使点'△'绕点Rt.如图在△旋转到中,∠Rt=90°,∠△=58°,将Rt17BABACABDADC的度数为84 ',则∠交恰好落在°.'上,'于点【分析】首先由旋转的性质可知:△′是等腰三角形,由三角形内角和定理可求得∠′的BCBCBBBCDADC的度数.度数,进而可求得∠的度数,即可根据三角形的外角性质求得∠CBCBABCB【解答】解:由旋转的性质知:∠=°,;=∠′′=58BCB′中,由三角形内角和定理知:在等腰△BCBB′=64∠°,′=180°﹣∠2BCDBCB′=26°;=90°﹣∠∴∠∴∠=∠+∠=58°+26°=84°;BCDADCABC故∠的度数为84°.ADC【点评】此题主要考查了旋转的性质,还涉及到三角形内角和定理及三角形的外角性质,难度不大.3000元.若18.为有效开展50个,购买资金不超过“阳光体育”活动,某校计划购买篮球和足球共每个篮球80元,每个足球50元,则篮球最多可购买16 个.xx)个,根据总价=单价×购买数量结合购买资金不﹣个,则购买足球(50【分析】设购买篮球x的一元一次不等式,解之取其中的最大整数即可.超过3000元,即可得出关于xx)个,50【解答】解:设购买篮球﹣个,则购买足球(根据题意得:80+50(50﹣)≤3000,xxx≤.解得:为整数,∵xx.16最大值为∴.16故答案为:【点评】本题考查了一元一次不等式的应用,根据各数量间的关系,正确列出一元一次不等式是解题的关键.分)道大题,满分60三、解答题(共7ABCBMCNP.分)如图所示,已知△19.(8相交于点的角平分线,APBAC?请说明理由.)判断能否平分∠1(.三角形的三条内角平分线相交于一点)由此题你得到的结论是2(.【分析】如图,作辅助线;证明=即可解决问题.PKPLAPBAC;理由如下:)能平分∠【解答】解:(1PPQBCPKABPLAC;、如图,过点、作⊥⊥⊥ABCBMCNP,的角平分线相交于点、∵△PKPQPLPQ,==,∴PKPL,=∴APBAC;平分∠∴(2)结论:三角形的三条内角平分线相交于一点.故答案为:三角形的三条内角平分线相交于一点.【点评】该题主要考查了三角形的内角平分线的性质及其应用问题;作辅助线是解决该题的关键.xxaxaa的取值范围.)的解是非正数,求字母)=5+2+320.(8分)已知关于的方程3(﹣(23﹣xa的解,根据方程的解为非正数,得到【分析】依次移项,合并同类项,系数化为关于1,得到的一元一次不等式,解之即可.关于aaxxa),5+3(+2【解答】解:3﹣(23﹣)=axxa,移项得:3﹣53=3+6+2﹣ax,+3=2合并同类项得:﹣5系数化为1得:,=﹣x ∵方程的解是非正数,∴﹣≤0,a,解得:aa.的取值范围为:即字母本题考查解一元一次不等式和一元一次方程的解,【点评】正确掌握解一元一次不等式和解一元一.次方程的方法是解题的关键.21.(8分)同学们知道:“在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°.”在直角三角形中,如果一个锐角等于30度,那么它所对的直角边等于斜(1)请写出它的逆命题边的一半命题(填“真”或“假”);该逆命题是一个真(2)若你的判断是真命题请写出证明过程(要求画图,并写出已知,求证).若是假命题,请说明理由.【分析】(1)写出逆命题,并判断是真命题;(2)首先写出已知、求证,画出图形,借助等边三角形的判定和性质证明或借助三角形的外接圆证明.【解答】解:(1)原命题的逆命题为:在直角三角形中,如果一个锐角等于30度,那么它所对的直角边等于斜边的一半,该逆命题是一个真命题;度,那么它所对的直角边等于斜边的一半,真;30故答案为:在直角三角形中,如果一个锐角等于ABCAACB=9030Rt△°,∠中,∠°.=2()已知,在BCAB.求证:=证明:BCDCDBCADADABBAD=60所示,延长到=,使°.=,∠,连接,易证证法一:如图1ABD为等边三角形,∴△ABBD,=∴BCCDABBCAB.∴,即===ABD,所示,取的中点证法二:如图2DCCDABADDB,==连接,有=∴∠=∠=30°,∠=∠+∠=60°.ADCAADCABDC∴△为等边三角形,DBC.∴==,即=.ABBCBCABDBABDBDBC,,使证法三:如图3所示,在=上取一点B°,∵∠60=∴△为等边三角形,BDC∴∠=60°,∠=90°﹣∠=90°﹣60°=30°=∠.ADCBDCBACDDCDABCBDDAAB,,即有==∴==ABBC.∴=ABCDCABO的直径,为⊙=所示,作△证法四:如图390的外接圆⊙°,,∠DCDBDCBDCA=2×30°=,∠60=2∠连°,,有=DBC为等边三角形,∴△∴===,即=.ABDBBCBCDAAB30度角的性质和等边三角形的判定、互逆命题的定义,熟练掌【点评】本题考查的是直角三角形握直角三角形30度角的性质的证明是关键.22.(8分)解不等式组请结合题意,完成本题解答过程.x≥﹣3 ,依据是不等式两边都乘以(或除以)同一个负数,不等号的(1)解不等式①,得.方向改变(2)解不等式②,得>﹣2 .xx<2 (3)解不等式③,得.(4)把不等式①,②和③的解集在数轴上表示出来.x<2 2<)从图中可以找出三个不等式解集的公共部分,得不等式组的解集(5.﹣x=1 (6)根据不等式组的解集确立出该不等式组的最大整数解为.确定不等式组的解集.根据各不等式解集在数轴上的表示,【分析】分别求出每一个不等式的解集,≥﹣3,依据是:不等式两边都乘以(或除以)同一个负数,)解不等式①,得【解答】解:(1x不等号的方向改变.x>﹣2.)解不等式②,得(2x.2<)解不等式③,得3(.(4)把不等式①,②和③的解集在数轴上表示出来如下:x<2.)从图中可以找出三个不等式解集的公共部分,得不等式组的解集:﹣2<(5x=1;(6)根据不等式组的解集确立出该不等式组的最大整数解为:故答案为:(1)≥﹣3、不等式两边都乘以(或除以)同一个负数,不等号的方向改变;x(2)>﹣2;xx<2)(3;x<22<;(5)﹣x=16).(【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.ABCA的坐标为().请2的三个顶点都在格点上,点,2△23.(8分)如图,在平面直角坐标系中,解答下列问题:ACABCAB的坐标.向左平移6个单位得到的△1()画出△,并写出1111ABCAABCB的坐标.°后得到的△90绕点,并写出逆时针旋转(2)画出△2222ACBACOAB的坐标.成中心对称的△(3)画出△关于原点,并写出3323232CABCAB即可;【分析】(1)分别画出、、、、的对应点111CBCABA即可;的对应点、2()分别画出、、、222CAABCB即可.的对应点、、(3)分别画出、、322332ACAB);【解答】解:(1,,如图所示;(﹣)△421111ABAC),2()△0,如图所示;并写出4(2222.(3)△如图所示,(﹣4,0)、ABCA3333【点评】本题考查作图﹣旋转变换、平移变换等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.24.(10分)学校“百变魔方”社团准备购买,两种魔方,已知购买2个种魔方和6个种BBAAAB种魔方所需款数相同.个种魔方和130元,购买3个4魔方共需(1)求这两种魔方的单价;(2)结合社员们的需求,社团决定购买,两种魔方共100个(其中种魔方不超过50个).某AAB 商店有两种优惠活动,如图所示.请根据以上信息,说明选择哪种优惠活动购买魔方更实惠.AB种魔方钱数相同解答)43【分析】(按买个个种魔方和买AxByAB个种魔方和2个,个种魔方的单价为6元/(1)设个,根据“购买种魔方的单价为/元xyAB 种魔方所需款数相同”,即可得出关于个种魔方和4的二130元,购买3种魔方共需个、元一次方程组,解之即可得出结论;AmmwBm)个,根据两100),总价格为种魔方()设购进(2元,则购进种魔方﹣个(0<≤50wwwwwwm的函数关系式,再分别令、<种活动方案即可得出、关于=活动二活动二活动一活动一活动一活动二wwm的取值范围,此题得解.>,解出和活动二活动一(按购买3个种魔方和4个种魔方需要130元解答)BAAxByAB个6种魔方和个2个,根据“购买/元种魔方的单价为个,/元种魔方的单价为)设1(.ABxy的二种魔方所需款数相同”,即可得出关于个、种魔方和4个种魔方共需130元,购买3元一次方程组,解之即可得出结论;AmmwBm)个,根据两﹣50),总价格为2)设购进种魔方(种魔方元,则购进个(0<100≤(wwwwwwm的函数关系式,再分别令=、、<种活动方案即可得出关于活动二活动二活动一活动一活动一活动二wwm的取值范围,此题得解.>和,解出活动二活动一AB种魔方钱数相同解答)个种魔方和买【解答】(按买3个4AxBy 元//个,个,解:(1)设种魔方的单价为种魔方的单价为元根据题意得:,解得:.AB种魔方的单价为15元/个,/答:个.种魔方的单价为20元(2)设购进种魔方个(0<≤50),总价格为元,则购进种魔方(100﹣)个,mBmAmwwmmm+60010;)×0.4×0.8+15(100根据题意得:﹣=20=活动一wmmmm+1500.)=﹣+15(100﹣10=20﹣活动二wwmm+1500,+600<<﹣时,有10当10活动二活动一m<45解得:;wwmm+1500,=﹣时,有1010当+600=活动二活动一解得:=45;mwwmm+15001010,+600当>﹣>时,有活动二活动一m≤50.解得:45<综上所述:当<45时,选择活动一购买魔方更实惠;当=45时,选择两种活动费用相同;当mmm时,选择活动二购买魔方更实惠.>45BA元解答)个130个(按购买3种魔方需要种魔方和4yBAx个,//元个,元解:(1)设种魔方的单价为种魔方的单价为,根据题意得:.解得:个.元//个,种魔方的单价为13元答:种魔方的单价为26BAmBmAmw)个,100≤50),总价格为﹣元,则购进(2)设购进种魔方0个(<种魔方(;+5200.4=15.6﹣×=根据题意得:260.8+13(100)×mmmw活动一mmmw.1300)=﹣﹣100(+1326=活动二当<时,有15.6+520<1300,mww活动二活动一解得:<50;mwwm+520=1300时,有当15.6=,活动二活动一m=50解得:;wwm+520>15.6当1300>,时,有活动二活动一不等式无解.mm=5050时,选择活动一购买魔方更实惠;当综上所述:当0<时,选择两种活动费用相同.<【点评】本题考查了二元一次方程组的应用、一次函数的应用、解一元一次不等式以及解一元一次xy的二元一次方程组;(2、方程,解题的关键是:(1)找准等量关系,列出关于)根据两种活wwm的函数关系式.、动方案找出关于活动二活动一25.(10分)感知:ADBACBCBDBDC的大小关系并证明.与=90,∠+∠°.判断=180如图①,°,∠平分∠探究:如图②,平分∠,∠+∠=180°,∠<90°,与的大小关系变吗?请说明理DCDBADACDBACABDABD 由.应用:ABDCBCDBDCaABACaa.(用含,则中,∠==45°,∠°,=135==﹣如图③,四边形的代数式表示)ADCADB,即可得出结论;【分析】感知:判断出△≌△=探究:欲证明,只要证明△≌△即可.DBDCDEBDFC应用:先证明△≌△,再证明△≌△,结合=即可解决问题.EBDFCADEDEBADFBDBDDC,=【解答】感知:解:ADBAC,理由:∵平分∠DACDAB,=∠∴∠BCB=90°,∠∵∠°,+∠=180CB,°=∠=90∴∠ADCADB,中,和△在△.ADCADBAAS),∴△(≌△BDDC;=∴探究:证明:如图②中,⊥于,⊥于,FDEDFABACE∵平分∠,⊥,⊥,ACBACABDADEDFDEDF,∴=BACDACDFCD=180∠°,∠=180°,∵∠++∠BFCD,∴∠=∠DFCDEB中,在△和△DFCDEB,∴△≌△DCDB;∴=应用:ADDEABEDFACF,,解;如图③连接于、⊥⊥于BACDACDFCD=180°,+∵∠∠+∠=180°,∠BFCD,=∠∴∠DFCDEB中,在△和△DFCDEB,∴△≌△DFDECFBE,,∴==在Rt△和Rt△中,ADEADFADFADE,Rt△∴Rt△≌AFAE,=∴ABACAEBEAFCFBE,﹣=(+2)﹣()=∴﹣DEBDEBBEDBBDa,°,=△在Rt45中,∵∠=90°,∠=∠=aBDBE,=∴=.==﹣∴2aBEABAC.故答案为a【点评】此题是四边形综合题,主要考查全等三角形的判定和性质、角平分线的性质、等腰直角三角形的性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形.。
2017-2018学年山东省枣庄市薛城区八年级(下)期中数学试卷
2017-2018学年山东省枣庄市薛城区八年级(下)期中数学试卷一、选择题(下面每小题给出的四个选项中,只有一项是正确的,请把正确选项选出来,每小题3分,共36分)1.(3分)不等式369x +…的解集在数轴上表示正确的是( ) A . B .C .D .2.(3分)如图,在ABC ∆中,以点B 为圆心,以BA 长为半径画弧交边BC 于点D ,连接AD .若40B ∠=︒,36C ∠=︒,则DAC ∠的度数是( )A .70︒B .44︒C .34︒D .24︒3.(3分)如图,在正方形网格中,线段A B ''是线段AB 绕某点逆时针旋转角α得到的,点A '与A 对应,则角α的大小为( )A .30︒B .60︒C .90︒D .120︒4.(3分)如图, 在ABC ∆中,90C ∠=︒,22.5B ∠=︒,AB 的垂直平分线交AB于D ,交BC 于E ,若3CE =,则BE 的长是( )A . 3B . 6C . 2D .5.(3分)如图, 在方格纸中,ABC ∆经过变换得到DEF ∆,正确的变换是()A . 把ABC ∆绕点C 逆时针方向旋转90︒,再向下平移 2 格B . 把ABC ∆绕点C 顺时针方向旋转90︒,再向下平移 5 格C . 把ABC ∆向下平移 4 格, 再绕点C 逆时针方向旋转180︒D . 把ABC ∆向下平移 5 格, 再绕点C 顺时针方向旋转180︒6.(3分)不等式组372291x x +⎧⎨-<⎩…的非负整数解的个数是( ) A .4 B .5 C .6 D .77.(3分)实数a ,b ,c ,d 在数轴上的对应点的位置如图所示, 则正确的结论是( )A .33a b ->-B .33c d -<-C .11a c ->-D .0b d ->8.(3分)图 1 和图 2 中所有的小正方形都全等, 将图 1 的正方形放在图 2中①②③④的某一位置, 使它与原来 7 个小正方形组成的图形是中心对称图形, 这个位置是( )A .①B .②C .③D .④9.(3分)如图, 已知钝角ABC ∆,依下列步骤尺规作图, 并保留作图痕迹 . 步骤 1 :以C 为圆心,CA 为半径画弧①;步骤 2 :以B 为圆心,BA 为半径画弧②, 交弧①于点D ;步骤 3 :连接AD ,交BC 延长线于点H .下列叙述正确的是( )A .BH 垂直平分线段ADB .AC 平分BAD ∠ C .ABC S BC AH ∆= D .AB AD =10.(3分)若关于x 的一元一次不等式组213(2)x x x m->-⎧⎨<⎩的解集是5x <,则m 的取值范围是( )A .5m …B .5m >C .5m …D .5m <11.(3分)如图,在ABC ∆中,AB AC =,DE DF =,DE AB ⊥,DF AC ⊥,垂足分别是E 、F .现有下列结论:①AD 平分BAC ∠;②AD BC ⊥;③AD 上任意一点到AB 、AC 的距离相等;④AD 上任意一点到BC 两端点的距离相等.其中正确结论的个数有( )A .1B .2C .3D .412.(3分)已知等边三角形的边长为3,点P 为等边三角形内任意一点,则点P到三边的距离之和为( )A .2B .2C .32D .不能确定二、填空题(共6小题,每小题4分,满分24分)13.(4分)若等腰三角形的一个外角是110︒,则其底角为 .14.(4分)已知五个正数的和等于 1 . 用反证法证明: 这五个数中至少有一个大于或等于15应先假设 . 15.(4分)关于x 的一元一次不等式223m x --…的解集为4x …,则m 的值为 . 16.(4分)如图, 函数12y x =-与23y ax =+的图象相交于点(,2)A m ,则关于x的不等式23x ax -+…的解集是 .17.(4分)如图在Rt ABC ∆中,90ACB ∠=︒,58ABC ∠=︒,将Rt ABC ∆绕点C旋转到Rt △A B C '',使点B 恰好落在A B ''上,A C '交AB 于点D ,则A D C ∠的度数为 ︒.18.(4分)为有效开展“阳光体育”活动, 某校计划购买篮球和足球共 50 个,购买资金不超过 3000 元 . 若每个篮球 80 元, 每个足球 50 元, 则篮球最多可购买 个 .三、解答题(共7道大题,满分60分)19.(8分)如图所示,已知ABC ∆的角平分线BM ,CN 相交于点P .(1)判断AP 能否平分BAC ∠?请说明理由.。
2017-2018学年山东省枣庄市薛城区八年级(下)期中数学试卷.

2017.2018学年山东省枣庄市薛城区八年级(下)期中数学试卷一、选择题(下面每小题给出的四个选项中,只有一项是正确的,请把正确选项选出来,每小题3分,共36分)1.(3分)不等式3x + 629的解集在数轴上表示正确的是( )2. (3分)如图,在MBC 中,以点"为圆心,以长为半径画弧交边8C 于点D,连接0?.若ZB = 40。
,ZC = 36°,则的度数是( )3. (3分)如图,在正方形网格中,线段4度是线段,48绕某点逆时针旋转角。
得到的,点4与X 对应,则角。
的大小为( )A. 30°B. 60°C. 90°D. 120°4. (3分)如图, 在LABC 中,ZC = 90°, 28 = 22.5。
,48的垂直平分线交于 D ,交BC 于E,A若 CE = 3,则BE 的长是()Q A . 3B .6C . 2D . 3>/25.(3分)如图,在方格纸中,MBC经过变换得到AD欣,正确的变换是()AA.把AABC绕点C逆时针方向旋转90。
,再向下平移2格B.把A/L9C绕点C顺时针方向旋转90。
,再向下平移5格C.把MBC向下平移4格,再绕点C逆时针方向旋转180。
D.把A4BC向下平移5格,再绕点C顺时针方向旋转180。
6.(3分)不等式组的非负整数解的个数是()2.r-9<1A.4B.5C. 6D.77.(3分)实数b,c,d在数轴上的对应点的位置如图所示,则正确的结论是O235-3-4A.a-3>b-3B.-3c<-3dC.\—a>1—cD.h—d>08.(3分)图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①®③④的某一位置,使它与原来7个小正方形组成的图形是中心对A.①B.②D.④9.(3分)如图,已知钝角依下列步骤尺规作图,并保留作图痕迹步骤1:以C为圆心,C4为半径画弧①:步骤2:以B为圆心,&4为半径画孤②,交弧①于点£):步骤3:连接AD,交8C延长线于点H.下列叙述正确的是()A.垂直平分线段SDB.4C平分/BADC.S mbc=BC,AHD.AB=AD10.(3分)若关于x的一元一次不等式组「x-l>3(x-2)的解集是工<5,则x<m〃,的取值范围是()A.B.m>5C.ni^5D.m<511.(3分)如图,在&8C中,AB=AC,DE=DF,DE LAB.DFlAC f垂足分别是E、F.现有下列结论:①血)平分ZBAC;©ADLBCx③♦。
2018-2019学年山东省枣庄市峄城区八年级(上)期中数学试卷(附答案详解)

2018-2019学年山东省枣庄市峄城区八年级(上)期中数学试卷1. 以下列各组数据为边长作三角形,其中能组成直角三角形的是( )A. 3,5,3B. 4,6,8C. 7,24,25D. 6,12,132. 如图,两个较大正方形的面积分别为225、289,则字母A所代表的正方形的面积为( )A. 4B. 8C. 16D. 643. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a ,较短直角边长为b.若ab =8,大正方形的面积为25,则小正方形的边长为( )A. 9B. 6C. 4D. 34. 如图,在△ABC 中,AC =10,DC =6,AD =8,BC =21,则AB 的长为( )A. 15B. 16C. 14D. 175. 与√37最接近的整数是( ) A. 5 B. 6 C. 7 D. 86. 下列实数中的无理数是( ) A. √1.21 B. √−83 C. √−332 D. 227 7. 下列计算正确的是( )A. 3√10−2√5=√5B. √711⋅(√117÷√111)=√11C. (√75−√15)÷√3=2√5D. 13√18−3√89=√28.如图所示,圆柱的高AB=3,底面直径BC=3,现在有一只蚂蚁想要从A处沿圆柱表面爬到对角C处捕食,则它爬行的最短距离是()A. 3√1+πB. 3√2C. 3√4+π22D. 3√1+π29.如图,若在中国象棋盘上建立平面直角坐标系,使“帅”位于点(−1,−2),“马”位于点(2,−2),则“兵”位于点()A. (−1,1)B. (−2,−1)C. (−3,1)D. (1,−2)10.若b>0,则一次函数y=−x+b的图象大致是()A. B. C. D.11.设正比例函数y=mx的图象经过点A(m,4),且y的值随x值的增大而减小,则m=()A. 2B. −2C. 4D. −412.已知一次函数y=32x+a与y=−12x+b的图象都经过点A(−2,0),且与y轴分别交于B,C两点,那么△ABC的面积是()A. 2B. 3C. 4D. 513.如图,小明将一张长为20cm,宽为15cm的长方形纸剪去了一角,量得AB=3cm,CD=4cm,则剪去的直角三角形的斜边长为______cm.14.一个正数的平方根分别是x+1和x−5,则x=______.15.我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个角形的三边长分别为a,b,c,则该三角形的面积为S=√14[a2b2−(a2+b2−c22)2],现已知△ABC的三边长分别为2,√6,3,则△ABC的面积为______.16.已知点M的坐标为(1,−2),线段MN=3,MN//x轴,点N在第三象限,则点N的坐标为______.17.如图,在平面直角坐标系中,A(4,0),B(0,3),以点A为圆心,AB长为半径画弧,交x轴的负半轴于点C,则点C坐标为______.18.甲、乙两车从A地出发,匀速驶向B地.甲车以80km/ℎ的速度行驶1h后,乙车才沿相同路线行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(ℎ)之间的函数关系如图所示.下列说法:①乙车的速度是120km/ℎ;②m=160;③点H的坐标是(7,80);④n=7.4.其中说法正确的是______(填写序号).19.解下列各题:(1)√144+√−83+|1−√3|−√3;(2)√20+√5√45−√13×√6;(3)(√6−2√3)2−(2√5+√2)(2√5−√2).20.全球气候变暖导致一些冰川融化并消失.在冰川消失12年后,一种低等植物苔藓就开始在岩石上生长.每一个苔藓都会长成近似圆形,苔藓的直径和其生长年限,近似地满足如下的关系式:d=7×√t−12(t≥12).其中d代表苔藓的直径,单位是厘米;t代表冰川消失的时间,单位是年.(1)计算冰川消失16年后苔藓的直径;(2)如果测得一些苔藓的直径是35厘米,问冰川约是在多少年前消失的?21.《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”翻译成数学问题是:如图所示,△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长.22.如图,在平面直角坐标系中,已知点A(0,3),B(2,4),C(4,0),D(2,−3),E(0,−4).(1)写出D,C,B关于y轴对称点F,G,H的坐标,并画出F,G,H点.(2)顺次平滑地连接A,B,C,D,E,F,G,H,A各点.23.小明一家利用元旦三天驾车到某景点旅游.小汽车出发前油箱有油36L,行驶若干小时后,途中在加油站加油若干升.油箱中余油量Q(L)与行驶时间t(ℎ)之间的关系如图所示.根据图象回答下列问题:(1)小汽车行驶______h后加油,中途加油______L;(2)求加油前油箱余油量Q与行驶时间t的函数关系式;(3)如果小汽车在行驶过程中耗油量速度不变,加油站距景点200km,车速为80km/ℎ,要到达目的地,油箱中的油是否够用?请说明理由.24.已知一次函数y=−2x−2(1)根据关系式画出函数的图象.(2)求出图象与x轴、y轴的交点A、B的坐标.(3)求A、B两点间的距离.(4)y的值随x值的增大怎样变化?答案和解析1.【答案】C【解析】解:A、32+32≠52;B、42+62≠82;C、72+242=252;D、62+122≠132.根据勾股定理7,24,25能组成直角三角形,故选C.欲求证是否为直角三角形,这里给出三边的长,只要满足勾股定理的逆定理即可.本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.勾股定理的逆定理:若三角形三边满足a2+b2=c2,那么这个三角形是直角三角形.2.【答案】D【解析】解:∵正方形PQED的面积等于225,∴即PQ2=225,∵正方形PRGF的面积为289,∴PR2=289,又△PQR为直角三角形,根据勾股定理得:PR2=PQ2+QR2,∴QR2=PR2−PQ2=289−225=64,则正方形QMNR的面积为64.故选:D.根据正方形的面积等于边长的平方,由正方形PQED的面积和正方形PRQF的面积分别表示出PR的平方及PQ的平方,又三角形PQR为直角三角形,根据勾股定理求出QR 的平方,即为所求正方形的面积.此题考查了勾股定理,以及正方形的面积公式.勾股定理最大的贡献就是沟通“数”与“形”的关系,它的验证和利用都体现了数形结合的思想,即把图形的性质问题转化为数量关系的问题来解决.能否由实际的问题,联想到用勾股定理的知识来求解是本题的关键.【解析】解:由题意可知:中间小正方形的边长为:a−b,∵每一个直角三角形的面积为:12ab=12×8=4,∴4×12ab+(a−b)2=25,∴(a−b)2=25−16=9,∴a−b=3,故选:D.由题意可知:中间小正方形的边长为:a−b,根据勾股定理以及题目给出的已知数据即可求出小正方形的边长.本题考查勾股定理,解题的关键是熟练运用勾股定理以及完全平方公式,本题属于基础题型.4.【答案】D【解析】【分析】先根据勾股定理的逆定理判断出△ADC的形状,再由勾股定理即可得出结论.本题考查的是勾股定理和勾股定理的逆定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.【详解】解:∵AC=10,DC=6,AD=8,DC2+AD2=62+82=100=102=AC2,∴△ADC是直角三角形,∴AD⊥BC,∴∠ADB=90°.在Rt△ABD中,∵AD=8,BD=BC−DC=21−6=15,∴AB=√AD2+BD2=√82+152=17.故选D.【解析】解:∵36<37<49,∴√36<√37<√49,即6<√37<7,∵37与36最接近,∴与√37最接近的是6.故选:B .由题意可知36与37最接近,即√36与√37最接近,从而得出答案.此题主要考查了无理数的估算能力,关键是整数与√37最接近,所以√36=6最接近.6.【答案】C【解析】【分析】此题主要考查了无理数的定义,注意带根号的要开不尽方才是无理数,无限不循环小数为无理数.如π,√6,0.8080080008…(每两个8之间依次多1个0)等形式.分别根据无理数、有理数的定义即可判定选择项.【解答】解:√1.21=1.1,√−83=−2,227是有理数,√−332是无理数, 故选C .7.【答案】B【解析】解:A 、3√10与−2√5不是同类二次根式,不能合并,此选项错误; B 、√711⋅(√117÷√111)=√711⋅√117×11=√711×117×11=√11,此选项正确; C 、(√75−√15)÷√3=(5√3−√15)÷√3=5−√5,此选项错误;D 、13√18−3√89=√2−2√2=−√2,此选项错误; 故选:B .根据二次根式的加减乘除运算法则逐一计算可得.本题主要考查二次根式的混合运算,解题的关键是掌握二次根式混合运算顺序和运算法则.8.【答案】C【解析】解:蚂蚁也可以沿A−B−C的路线爬行,AB+BC=6,把圆柱侧面展开,展开图如右图所示,点A、C的最短距离为线段AC的长.在Rt△ADC中,∠ADC=90°,CD=AB=3,AD为底面半圆弧长,AD=1.5π,所以AC=√AD2+CD2=√32+(3π2 )2=√9+9π2 4=3√4+π22<6,故选:C.要求最短路径,首先要把圆柱的侧面展开,利用两点之间线段最短,然后利用勾股定理即可求解.本题考查了平面展开−最短路径问题,解题的关键是会将圆柱的侧面展开,并利用勾股定理解答.9.【答案】C【解析】解:如图,“兵”位于点(−3,1).故选C.先利用“帅”位于点(−1,−2)画出直角坐标系,然后写出“兵”位于点的坐标.本题考查了坐标确定位置:平面内的点与有序实数对一一对应;记住直角坐标系中特殊位置点的坐标特征.10.【答案】C【解析】解:∵一次函数y=−x+b中k=−1<0,b>0,∴一次函数的图象经过一、二、四象限,故选:C.根据一次函数的k、b的符号确定其经过的象限即可确定答案.主要考查了一次函数的图象性质,要掌握它的性质才能灵活解题.一次函数y=kx+b的图象有四种情况:①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限;②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限;③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限;④当k<0,b<0时,函数y=kx+b 的图象经过第二、三、四象限.11.【答案】B【解析】【分析】本题考查了正比例函数的性质:正比例函数y=kx(k≠0)的图象为直线,当k>0时,图象经过第一、三象限,y值随x的增大而增大;当k<0时,图象经过第二、四象限,y值随x的增大而减小.直接根据正比例函数的性质和待定系数法求解即可.【解答】解:把x=m,y=4代入y=mx中,则m2=4,可得:m=±2,因为y的值随x值的增大而减小,所以m<0,故m=−2.故选:B.【解析】【分析】本题考查了用待定系数法求函数解析式以及一次函数与方程的关系,通过已知点的坐标来得出两函数的解析式是解题的关键.可先根据点A的坐标用待定系数法求出a,b的值,即求出两个一次函数的解析式,进而求出它们与y轴的交点,即B,C的坐标.那么三角形ABC中,底边的长应该是B,C纵坐标差的绝对值,高就应该是A点横坐标的绝对值,因此可根据三角形的面积公式求出三角形的面积.【解答】x+a,解:把点A(−2,0)代入y=32得:a=3,∴点B(0,3).x+b,把点A(−2,0)代入y=−12得:b=−1,∴点C(0,−1).∴BC=|3−(−1)|=4,×2×4=4.∴S△ABC=12故选:C.13.【答案】20【解析】解:延长AB、DC相交于F,则BFC构成直角三角形,运用勾股定理得BC2=(15−3)2+(20−4)2=122+162=400,所以BC=20.则剪去的直角三角形的斜边长为20cm.解答此题只要把原来的图形补全,构造出直角三角形解答.解答此题要延长AB、DC相交于F,则BFC构成直角三角形,再用勾股定理进行计算.【解析】解:根据题意知x+1+x−5=0,解得:x=2,故答案为:2.根据正数的两个平方根互为相反数列出关于x的方程,解之可得.本题主要考查的是平方根的定义和性质,熟练掌握平方根的定义和性质是解题的关键.15.【答案】√5【解析】解:∵△ABC的三边长分别为2,√6,3,∴△ABC的面积=√4[√2]=√5,故答案为:√5.根据三斜求积公式计算即可求解.本题考查了二次根式的应用,关键是熟悉三斜求积公式.16.【答案】(−2,−2)【解析】【分析】本题考查了坐标与图形性质,主要利用了平行于x轴的直线上点的纵坐标相等的性质.根据平行于x轴的直线上点的纵坐标相等求出点N的纵坐标,再分点N在点M的右边与左边两种情况求出点N的横坐标,然后根据点N在第三象限解答.【解答】解:∵点M的坐标为(1,−2),MN//x轴,∴点N的纵坐标为−2,∵MN=3,∴点N在点M的右边时,横坐标为1+3=4,此时,点N(4,−2),点N在点M的左边时,横坐标为1−3=−2,此时,点N(−2,−2),∵点N在第三象限,∴点N的坐标为(−2,−2).故答案为:(−2,−2).17.【答案】(−1,0)【解析】解:∵点A,B的坐标分别为(4,0),(0,3),∴OA=4,OB=3,在Rt△AOB中,由勾股定理得:AB=√32+42=5,∴AC=AB=5,∴OC=5−4=1,∴点C的坐标为(−1,0),故答案为:(−1,0),求出OA、OB,根据勾股定理求出AB,即可得出AC,求出OC长即可.本题考查了勾股定理和坐标与图形性质的应用,解此题的关键是求出OC的长,注意:在直角三角形中,两直角边的平方和等于斜边的平方.18.【答案】①②③④【解析】解:由图象可知,乙出发时,甲乙相距80km,2小时后,乙车追上甲.则说明乙每小时比甲快40km,则乙的速度为120km/ℎ.①正确;由图象第2−6小时,乙由相遇点到达B,用时4小时,每小时比甲快40km,则此时甲乙距离4×40=160km,则m=160,②正确;当乙在B休息1h时,甲前进80km,则H点坐标为(7,80),③正确;乙返回时,甲乙相距80km,到两车相遇用时80÷(120+80)=0.4小时,则n=6+1+ 0.4=7.4,④正确,故答案为:①②③④.根据题意,两车距离为函数,由图象可知两车起始距离为80,从而得到乙车速度,根据图象变化规律和两车运动状态,得到相关未知量.本题考查了一次函数的应用,考查双动点条件下,两点距离与运动时间的函数关系,解答时既要注意图象变化趋势,又要关注动点的运动状态.3+|1−√3|−√319.【答案】解:(1)√144+√−8=12−2+√3−1−√3=9;√20+√5√45−√13×√6=√5+√53√5√13×6=1−√2;(3)(√6−2√3)2−(2√5+√2)(2√5−√2)=6+12−4√18−[(2√5)2−(√2)2]=18−12√2−(20−2)=18−12√2−18=−12√2.【解析】(1)根据算术平方根,立方根,绝对值的性质化简,再进一步合并即可;(2)先化简二次根式,再进一步合并即可;(3)利用完全平方公式和平方差公式计算即可.此题考查实数的混合运算,注意先化简,再进一步利用公式和实数的运算法则计算.20.【答案】解:(1)当t=16时,d=7×√t−12=7×2=14cm;(2)当d=35时,√t−12=5,即t−12=25,解得t=37年.答:冰川消失16年后苔藓的直径为14cm,冰川约是在37年前消失的.【解析】(1)根据题意可知分别是求当t=16时,d的值,直接把对应数值代入关系式即可求解;(2)根据题意可知是求当d=35时,t的值,直接把对应数值代入关系式即可求解.本题主要考查了平方根、算术平方根概念的运用.会根据题意把数值准确的代入对应的关系式中是解题的关键.21.【答案】解:设AC=x,∵AC+AB=10,∴AB=10−x.∵在Rt△ABC中,∠ACB=90°,∴AC2+BC2=AB2,即x2+32=(10−x)2.解得:x=4.55,即AC=4.55.【解析】设AC=x,可知AB=10−x,再根据勾股定理即可得出结论.本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.22.【答案】解:(1)如图所示:F(−2,−3),G(−4,0),H(−2,4);(2)如图所示:【解析】(1)直接利用关于y轴对称点的性质,进而得出对应点的坐标即可;(2)将已知点顺次连接进而得出答案.此题主要考查了轴对称变换,正确得出对应点位置是解题关键.23.【答案】解:(1)从图中可知汽车行驶3h后加油,中途加油24L;(2)根据分析可知Q=−10t+36(0≤t≤3);(3)油箱中的油是够用的.∵200÷80=2.5(小时),需用油10×2.5=25L<30L,∴油箱中的油是够用的.【解析】本题考查了函数图象,观察函数图象的横坐标得出时间,观察函数图象的纵坐标得出剩余油量是解题关键,利用待定系数法求函数解析式.(1)观察图中数据可知,行驶3小时后油箱剩油6L,加油加至30L;(2)先根据图中数据把每小时用油量求出来,即:(36−6)÷3=10L,再写出函数关系式;(3)先要求出从加油站到景点需行几小时,然后再求需用多少油,便知是否够用.24.【答案】解:(1)在y=−2x−2中,令y=0可得x=−1,令x=0可得y=−2,∴A(−1,0),B(0,−2),其图象如图所示;(2)由(1)可知A(−1,0),B(0,−2);(3)∵A(−1,0),B(0,−2),∴OA=1,OB=2,∴AB=√OA2+OB2=√1+4=√5,即A、B两点间的距离为√5;(4)∵在y=−2x−2中,k=−2<0,∴y随x的增大而减小.【解析】(1)令x=0和y=0可先求得A、B的坐标,利用两点法可画出函数图象;(2)由(1)可求得A、B的坐标;(3)由A、B的坐标可求得OA、OB的长,利用勾股定理可求得AB的长;(4)由一次函数的性质可求得其变化情况.本题主要考查一次函数的图象及其性质,掌握一次函数的图象是一条直线及函数图象与坐标轴的交点的求法是解题的关键.。
【精编】2017-2018学年枣庄市薛城区八年级下期中数学试卷(有答案)
2017-2018学年山东省枣庄市薛城区八年级(下)期中数学试卷一、选择题(下面每小题给出的四个选项中,只有一项是正确的,请把正确选项选出来,每小题3分,共36分)1.不等式3x+6≥9的解集在数轴上表示正确的是()A.B.C.D.2.如图,在△ABC中,以点B为圆心,以BA长为半径画弧交边BC于点D,连接AD.若∠B=40°,∠C=36°,则∠DAC的度数是()A.70°B.44°C.34°D.24°3.如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转角α得到的,点A′与A对应,则角α的大小为()A.30°B.60°C.90°D.120°4.如图,在△ABC中,∠C=90°,∠B=22.5°,AB的垂直平分线交AB于D,交BC于E,若CE=3,则BE的长是()A.3B.6C.2D.35.如图,在方格纸中,△ABC经过变换得到△DEF,正确的变换是()A.把△ABC绕点C逆时针方向旋转90°,再向下平移2格B.把△ABC绕点C顺时针方向旋转90°,再向下平移5格C.把△ABC向下平移4格,再绕点C逆时针方向旋转180°D.把△ABC向下平移5格,再绕点C顺时针方向旋转180°6.不等式组的非负整数解的个数是()A.4B.5C.6D.77.实数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是()A.a﹣3>b﹣3B.﹣3c<﹣3d C.1﹣a>1﹣c D.b﹣d>08.图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是()A.①B.②C.③D.④9.如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.步骤1:以C为圆心,CA为半径画弧①;步骤2:以B为圆心,BA为半径画弧②,交弧①于点D;步骤3:连接AD,交BC延长线于点H.下列叙述正确的是()A.BH垂直平分线段AD B.AC平分∠BADC.S=BC•AH D.AB=AD△ABC10.若关于x的一元一次不等式组的解集是x<5,则m的取值范围是()A.m≥5B.m>5C.m≤5D.m<511.如图,在△ABC中,AB=AC,DE=DF,DE⊥AB,DF⊥AC,垂足分别是E、F.现有下列结论:①AD平分∠BAC;②AD⊥BC;③AD上任意一点到AB、AC的距离相等;④AD上任意一点到BC两端点的距离相等.其中正确结论的个数有()A.1B.2C.3D.412.已知等边三角形的边长为3,点P为等边三角形内任意一点,则点P到三边的距离之和为()A.B.C.D.不能确定二、填空题(共6小题,每小题4分,满分24分)13.若等腰三角形的一个外角是110°,则其底角为.14.已知五个正数的和等于1.用反证法证明:这五个数中至少有一个大于或等于应先假设.15.关于x的一元一次不等式的解集为x≥4,则m的值为.16.如图,函数y1=﹣2x与y2=ax+3的图象相交于点A(m,2),则关于x的不等式﹣2x≤ax+3的解集是.17.如图在Rt△ABC中,∠ACB=90°,∠ABC=58°,将Rt△ABC绕点C旋转到Rt△A'B'C,使点B恰好落在A'B'上,A'C交AB于点D,则∠ADC的度数为°.18.为有效开展“阳光体育”活动,某校计划购买篮球和足球共50个,购买资金不超过3000元.若每个篮球80元,每个足球50元,则篮球最多可购买个.三、解答题(共7道大题,满分60分)19.(8分)如图所示,已知△ABC的角平分线BM,CN相交于点P.(1)判断AP能否平分∠BAC?请说明理由.(2)由此题你得到的结论是.20.(8分)已知关于x的方程3x﹣(2a﹣3)=5x+3(a+2)的解是非正数,求字母a的取值范围.21.(8分)同学们知道:“在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°.”(1)请写出它的逆命题;该逆命题是一个命题(填“真”或“假”)(2)若你的判断是真命题请写出证明过程(要求画图,并写出已知,求证).若是假命题,请说明理由.22.(8分)解不等式组请结合题意,完成本题解答过程.(1)解不等式①,得,依据是.(2)解不等式②,得.(3)解不等式③,得.(4)把不等式①,②和③的解集在数轴上表示出来.(5)从图中可以找出三个不等式解集的公共部分,得不等式组的解集.(6)根据不等式组的解集确立出该不等式组的最大整数解为.23.(8分)如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,2).请解答下列问题:(1)画出△ABC向左平移6个单位得到的△A1B1C1,并写出A1的坐标.(2)画出△ABC绕点B逆时针旋转90°后得到的△A2B2C2,并写出A2的坐标.(3)画出△A2B2C2关于原点O成中心对称的△A3B3C3,并写出A3的坐标.24.(10分)学校“百变魔方”社团准备购买A,B两种魔方,已知购买2个A种魔方和6个B 种魔方共需130元,购买3个A种魔方和4个B种魔方所需款数相同.(1)求这两种魔方的单价;(2)结合社员们的需求,社团决定购买A,B两种魔方共100个(其中A种魔方不超过50个).某商店有两种优惠活动,如图所示.请根据以上信息,说明选择哪种优惠活动购买魔方更实惠.25.(10分)感知:如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°.判断DB与DC的大小关系并证明.探究:如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,DB与DC的大小关系变吗?请说明理由.应用:如图③,四边形ABDC中,∠B=45°,∠C=135°,DB=DC=a,则AB﹣AC=.(用含a的代数式表示)2017-2018学年山东省枣庄市薛城区八年级(下)期中数学试卷参考答案与试题解析一、选择题(下面每小题给出的四个选项中,只有一项是正确的,请把正确选项选出来,每小题3分,共36分)1.不等式3x+6≥9的解集在数轴上表示正确的是()A.B.C.D.【分析】根据解一元一次不等式基本步骤:移项、合并同类项、系数化为1可得.【解答】解:移项,得:3x≥9﹣6,合并同类项,得:3x≥3,系数化为1,得:x≥1,故选:C.【点评】本题主要考查解一元一次不等式的基本能力,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变.2.如图,在△ABC中,以点B为圆心,以BA长为半径画弧交边BC于点D,连接AD.若∠B=40°,∠C=36°,则∠DAC的度数是()A.70°B.44°C.34°D.24°【分析】由AB=BD,∠B=40°得到∠ADB=70°,再根据三角形的外角的性质即可得到结论.【解答】解:∵AB=BD,∠B=40°,∴∠ADB=70°,∵∠C=36°,∴∠DAC=∠ADB﹣∠C=34°.故选:C.【点评】本题考查了等腰三角形的性质,三角形内角和定理,掌握等边对等角是解题的关键,注意三角形外角性质的应用.3.如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转角α得到的,点A′与A对应,则角α的大小为()A.30°B.60°C.90°D.120°【分析】根据题意,由直线AB与直线A′B′的夹角是90°即可确定旋转角的大小.【解答】解:如图:延长AB、A′B′,直线AB与直线A′B′的夹角是90°,故旋转角α为90°.故选:C.【点评】考查了旋转的性质,解题的关键是能够根据题意确定旋转中心的知识,难度不大.4.如图,在△ABC中,∠C=90°,∠B=22.5°,AB的垂直平分线交AB于D,交BC于E,若CE=3,则BE的长是()A.3B.6C.2D.3【分析】利用线段的垂直平分线的性质计算.【解答】解:已知∠C=90°,∠B=22.5°,DE垂直平分AB.故∠B=∠EAB=22.5°,所以∠AEC=45°.又∵∠C=90°,∴△ACE为等腰三角形所以CE=AC=3,故可得AE=3.故选:D.【点评】本题考查的是线段的垂直平分线的性质(垂直平分线上任意一点,和线段两端点的距离相等),难度一般.5.如图,在方格纸中,△ABC经过变换得到△DEF,正确的变换是()A.把△ABC绕点C逆时针方向旋转90°,再向下平移2格B.把△ABC绕点C顺时针方向旋转90°,再向下平移5格C.把△ABC向下平移4格,再绕点C逆时针方向旋转180°D.把△ABC向下平移5格,再绕点C顺时针方向旋转180°【分析】观察图象可知,先把△ABC绕点C顺时针方向旋转90°,再向下平移5格即可得到.【解答】解:根据图象,△ABC绕点C顺时针方向旋转90°,再向下平移5格即可与△DEF重合.故选:B.【点评】本题考查了几何变换的类型,几何变换只改变图形的位置,不改变图形的形状与大小,本题用到了旋转变换与平移变换,对识图能力要求比较高.6.不等式组的非负整数解的个数是()A.4B.5C.6D.7【分析】先求出不等式组的解集,再求出不等式组的非负整数解,即可得出答案.【解答】解:∵解不等式①得:x≥﹣,解不等式②得:x<5,∴不等式组的解集为﹣≤x<5,∴不等式组的非负整数解为0,1,2,3,4,共5个,故选:B.【点评】本题考查了解一元一次不等式组和一元一次不等式组的整数解,能求出不等式组的解集是解此题的关键.7.实数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是()A.a﹣3>b﹣3B.﹣3c<﹣3d C.1﹣a>1﹣c D.b﹣d>0【分析】依据实数a,b,c,d在数轴上的对应点的位置,即可得到a,b,c,d的大小关系,进而利用不等式的基本性质得出结论.【解答】解:∵a<b,∴a﹣3<b﹣3,故A选项错误;∵c<d,∴﹣3c>﹣3d,故B选项错误;∵a<c,∴1﹣a>1﹣c,故C选项正确;∵b<d,∴b﹣d<0,故D选项错误;故选:C.【点评】本题考查了实数与数轴,观察数轴,逐一分析四个选项的正误是解题的关键.8.图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是()A.①B.②C.③D.④【分析】根据把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心,进而得出答案.【解答】解:当正方形放在③的位置,即是中心对称图形.故选:C.【点评】此题主要考查了中心对称图形的定义,正确把握定义是解题关键.9.如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.步骤1:以C为圆心,CA为半径画弧①;步骤2:以B为圆心,BA为半径画弧②,交弧①于点D;步骤3:连接AD,交BC延长线于点H.下列叙述正确的是()A.BH垂直平分线段AD B.AC平分∠BADC.S=BC•AH D.AB=AD△ABC【分析】根据已知条件可知直线BC是线段AD的垂直平分线,由此一一判定即可.【解答】解:A、正确.如图连接CD、BD,∵CA=CD,BA=BD,∴点C、点B在线段AD的垂直平分线上,∴直线BC是线段AD的垂直平分线,故A正确.B、错误.CA不一定平分∠BDA.C、错误.应该是S=•BC•AH.△ABCD、错误.根据条件AB不一定等于AD.故选:A.【点评】本题考查作图﹣基本作图、线段的垂直平分线的性质等知识,解题的关键是掌握证明线段垂直平分线的证明方法,属于基础题,中考常考题型.10.若关于x的一元一次不等式组的解集是x<5,则m的取值范围是()A.m≥5B.m>5C.m≤5D.m<5【分析】求出第一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了即可确定m的范围.【解答】解:解不等式2x﹣1>3(x﹣2),得:x<5,∵不等式组的解集为x<5,∴m≥5,故选:A.【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.11.如图,在△ABC中,AB=AC,DE=DF,DE⊥AB,DF⊥AC,垂足分别是E、F.现有下列结论:①AD平分∠BAC;②AD⊥BC;③AD上任意一点到AB、AC的距离相等;④AD上任意一点到BC两端点的距离相等.其中正确结论的个数有()A.1B.2C.3D.4【分析】根据角平分线的逆定理可知①正确,利用等腰三角形底边上的中线、高线与顶角的角平分线三线合一,可得②④正确;利用角平分线上的点到角两边的距离相等,可得③.【解答】解:①∵DE=DF,DE⊥AB,DF⊥AC,∴AD平分∠BAC,故①正确;②∵AB=AC,AD平分∠BAC,∴AD⊥BC.故②正确;③∵AD是△ABC的角平分线,角平分线上的点到角两边的距离相等,∴AD上任意一点到边AB、AC的距离相等.故③正确;④∵AB=AC,AD平分∠BAC,∴BD=CD,即AD是BC的垂直平分线,∴AD上任意一点到BC两端点的距离相等;故④正确.所以①、②、③、④均正确,故选:D.【点评】本题考查了等腰三角形的性质、角平分线的性质等知识.根据相关知识对各选项进行逐个验证是正确解答本题的关键.12.已知等边三角形的边长为3,点P为等边三角形内任意一点,则点P到三边的距离之和为()A.B.C.D.不能确定【分析】作出图形,根据等边三角形的性质求出高AH的长,再根据三角形的面积公式求出点P到三边的距离之和等于高线的长度,从而得解.【解答】解:如图,∵等边三角形的边长为3,∴高线AH=3×=,S=BC•AH=AB•PD+BC•PE+AC•PF,△ABC∴×3•AH=×3•PD+×3•PE+×3•PF,∴PD+PE+PF=AH=,即点P到三角形三边距离之和为.故选:B.【点评】本题考查了等边三角形的性质,根据三角形的面积求点P到三边的距离之和等于等边三角形的高是解题的关键,作出图形更形象直观.二、填空题(共6小题,每小题4分,满分24分)13.若等腰三角形的一个外角是110°,则其底角为70°或55°.【分析】分这个外角为底角的外角和顶角的外角,分别求解即可.【解答】解:当110°外角为底角的外角时,则其底角为:180°﹣110°=70°;当110°外角为顶角的外角时,则其顶角为:70°,则其底角为:=55°,故答案为:70°或55°.【点评】本题主要考查等腰三角形的性质和三角形内角和定理的应用,掌握等腰三角形的两底角相等和三角形三个内角的和为180°是解题的关键.14.已知五个正数的和等于1.用反证法证明:这五个数中至少有一个大于或等于应先假设这五个数都小于.【分析】熟记反证法的步骤,直接从结论的反面出发得出即可.【解答】解:知五个正数的和等于1.用反证法证明:这五个数中至少有一个大于或等于应先假设这五个数都小于,故答案为:这五个数都小于【点评】此题主要考查了反证法,反证法的步骤是:(1)假设结论不成立;(2)从假设出发推出矛盾;(3)假设不成立,则结论成立.在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.15.关于x的一元一次不等式的解集为x≥4,则m的值为2.【分析】先用含有m的式子把原不等式的解集表示出来,然后和已知解集进行比对得出关于m的方程,解之可得m的值.【解答】解:解不等式得:x≥,∵不等式的解集为x≥4,∴=4,解得:m=2,故答案为:2.【点评】本题主要考查解一元一次不等式,当题中有两个未知字母时,应把关于某个字母的不等式中的字母当成未知数,求得解集,再根据解集进行判断,求得另一个字母的值.16.如图,函数y1=﹣2x与y2=ax+3的图象相交于点A(m,2),则关于x的不等式﹣2x≤ax+3的解集是x≥﹣1.【分析】首先利用待定系数法求出A点坐标,再以交点为分界,结合图象写出不等式﹣2x≤ax+3的解集即可.【解答】解:∵函数y1=﹣2x过点A(m,2),∴﹣2m=2,解得:m=﹣1,∴A(﹣1,2),∴不等式﹣2x<ax+3的解集为x≥﹣1.故答案为:x≥﹣1.【点评】此题主要考查了一次函数与一元一次不等式,关键是求出A点坐标.17.如图在Rt△ABC中,∠ACB=90°,∠ABC=58°,将Rt△ABC绕点C旋转到Rt△A'B'C,使点B恰好落在A'B'上,A'C交AB于点D,则∠ADC的度数为84°.【分析】首先由旋转的性质可知:△BB′C是等腰三角形,由三角形内角和定理可求得∠BCB′的度数,进而可求得∠BCD的度数,即可根据三角形的外角性质求得∠ADC的度数.【解答】解:由旋转的性质知:∠ABC=∠B′=58°,BC=B′C;在等腰△BCB′中,由三角形内角和定理知:∠BCB′=180°﹣2∠B′=64°,∴∠BCD=90°﹣∠BCB′=26°;∴∠ADC=∠ABC+∠BCD=58°+26°=84°;故∠ADC的度数为84°.【点评】此题主要考查了旋转的性质,还涉及到三角形内角和定理及三角形的外角性质,难度不大.18.为有效开展“阳光体育”活动,某校计划购买篮球和足球共50个,购买资金不超过3000元.若每个篮球80元,每个足球50元,则篮球最多可购买16个.【分析】设购买篮球x个,则购买足球(50﹣x)个,根据总价=单价×购买数量结合购买资金不超过3000元,即可得出关于x的一元一次不等式,解之取其中的最大整数即可.【解答】解:设购买篮球x个,则购买足球(50﹣x)个,根据题意得:80x+50(50﹣x)≤3000,解得:x≤.∵x为整数,∴x最大值为16.故答案为:16.【点评】本题考查了一元一次不等式的应用,根据各数量间的关系,正确列出一元一次不等式是解题的关键.三、解答题(共7道大题,满分60分)19.(8分)如图所示,已知△ABC的角平分线BM,CN相交于点P.(1)判断AP能否平分∠BAC?请说明理由.(2)由此题你得到的结论是三角形的三条内角平分线相交于一点.【分析】如图,作辅助线;证明PK=PL即可解决问题.【解答】解:(1)AP能平分∠BAC;理由如下:如图,过点P作PQ⊥BC、PK⊥AB、PL⊥AC;∵△ABC的角平分线BM、CN相交于点P,∴PK=PQ,PL=PQ,∴PK=PL,∴AP平分∠BAC;(2)结论:三角形的三条内角平分线相交于一点.故答案为:三角形的三条内角平分线相交于一点.【点评】该题主要考查了三角形的内角平分线的性质及其应用问题;作辅助线是解决该题的关键.20.(8分)已知关于x的方程3x﹣(2a﹣3)=5x+3(a+2)的解是非正数,求字母a的取值范围.【分析】依次移项,合并同类项,系数化为1,得到x关于a的解,根据方程的解为非正数,得到关于a的一元一次不等式,解之即可.【解答】解:3x﹣(2a﹣3)=5x+3(a+2),移项得:3x﹣5x=3a+6+2a﹣3,合并同类项得:﹣2x=5a+3,系数化为1得:x=﹣,∵方程的解是非正数,∴﹣≤0,解得:a,即字母a的取值范围为:a.【点评】本题考查解一元一次不等式和一元一次方程的解,正确掌握解一元一次不等式和解一元一次方程的方法是解题的关键.21.(8分)同学们知道:“在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°.”(1)请写出它的逆命题在直角三角形中,如果一个锐角等于30度,那么它所对的直角边等于斜边的一半;该逆命题是一个真命题(填“真”或“假”)(2)若你的判断是真命题请写出证明过程(要求画图,并写出已知,求证).若是假命题,请说明理由.【分析】(1)写出逆命题,并判断是真命题;(2)首先写出已知、求证,画出图形,借助等边三角形的判定和性质证明或借助三角形的外接圆证明.【解答】解:(1)原命题的逆命题为:在直角三角形中,如果一个锐角等于30度,那么它所对的直角边等于斜边的一半,该逆命题是一个真命题;故答案为:在直角三角形中,如果一个锐角等于30度,那么它所对的直角边等于斜边的一半,真;(2)已知,在Rt△ABC中,∠A=30°,∠ACB=90°.求证:BC=AB.证明:证法一:如图1所示,延长BC到D,使CD=BC,连接AD,易证AD=AB,∠BAD=60°.∴△ABD为等边三角形,∴AB=BD,∴BC=CD=AB,即BC=AB.证法二:如图2所示,取AB的中点D,连接DC,有CD=AB=AD=DB,∴∠DCA=∠A=30°,∠BDC=∠DCA+∠A=60°.∴△DBC为等边三角形,∴BC=DB=AB,即BC=AB.证法三:如图3所示,在AB 上取一点D ,使BD =BC ,∵∠B =60°,∴△BDC 为等边三角形,∴∠DCB =60°,∠ACD =90°﹣∠DCB =90°﹣60°=30°=∠A .∴DC =DA ,即有BC =BD =DA =AB ,∴BC =AB .证法四:如图3所示,作△ABC 的外接圆⊙D ,∠C =90°,AB 为⊙O 的直径,连DC ,有DB =DC ,∠BDC =2∠A =2×30°=60°,∴△DBC 为等边三角形,∴BC =DB =DA =AB ,即BC =AB .【点评】本题考查的是直角三角形30度角的性质和等边三角形的判定、互逆命题的定义,熟练掌握直角三角形30度角的性质的证明是关键.22.(8分)解不等式组请结合题意,完成本题解答过程.(1)解不等式①,得 x ≥﹣3 ,依据是 不等式两边都乘以(或除以)同一个负数,不等号的方向改变 .(2)解不等式②,得 x >﹣2 .(3)解不等式③,得 x <2 .(4)把不等式①,②和③的解集在数轴上表示出来.(5)从图中可以找出三个不等式解集的公共部分,得不等式组的解集 ﹣2<x <2 .(6)根据不等式组的解集确立出该不等式组的最大整数解为 x =1 .【分析】分别求出每一个不等式的解集,根据各不等式解集在数轴上的表示,确定不等式组的解集.【解答】解:(1)解不等式①,得x ≥﹣3,依据是:不等式两边都乘以(或除以)同一个负数,不等号的方向改变.(2)解不等式②,得x >﹣2.(3)解不等式③,得x <2.(4)把不等式①,②和③的解集在数轴上表示出来如下:(5)从图中可以找出三个不等式解集的公共部分,得不等式组的解集:﹣2<x<2.(6)根据不等式组的解集确立出该不等式组的最大整数解为:x=1;故答案为:(1)x≥﹣3、不等式两边都乘以(或除以)同一个负数,不等号的方向改变;(2)x>﹣2;(3)x<2;(5)﹣2<x<2;(6)x=1.【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.23.(8分)如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,2).请解答下列问题:(1)画出△ABC向左平移6个单位得到的△A1B1C1,并写出A1的坐标.(2)画出△ABC绕点B逆时针旋转90°后得到的△A2B2C2,并写出A2的坐标.(3)画出△A2B2C2关于原点O成中心对称的△A3B3C3,并写出A3的坐标.【分析】(1)分别画出A、B、C的对应点A1、B1、C1即可;(2)分别画出A、B、C的对应点A2、B2、C2即可;(3)分别画出A2、B2、C2的对应点A3、B3、C3即可.【解答】解:(1)△A1B1C1,如图所示;A1(﹣4,2);(2)△A2B2C2如图所示;并写出A2(4,0),(3)△A3B3C3如图所示,A3(﹣4,0)、【点评】本题考查作图﹣旋转变换、平移变换等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.24.(10分)学校“百变魔方”社团准备购买A,B两种魔方,已知购买2个A种魔方和6个B 种魔方共需130元,购买3个A种魔方和4个B种魔方所需款数相同.(1)求这两种魔方的单价;(2)结合社员们的需求,社团决定购买A,B两种魔方共100个(其中A种魔方不超过50个).某商店有两种优惠活动,如图所示.请根据以上信息,说明选择哪种优惠活动购买魔方更实惠.【分析】(按买3个A种魔方和买4个B种魔方钱数相同解答)(1)设A种魔方的单价为x元/个,B种魔方的单价为y元/个,根据“购买2个A种魔方和6个B 种魔方共需130元,购买3个A种魔方和4个B种魔方所需款数相同”,即可得出关于x、y的二元一次方程组,解之即可得出结论;(2)设购进A种魔方m个(0<m≤50),总价格为w元,则购进B种魔方(100﹣m)个,根据两种活动方案即可得出w活动一、w活动二关于m的函数关系式,再分别令w活动一<w活动二、w活动一=w活动二和w活动一>w活动二,解出m的取值范围,此题得解.(按购买3个A种魔方和4个B种魔方需要130元解答)(1)设A种魔方的单价为x元/个,B种魔方的单价为y元/个,根据“购买2个A种魔方和6个B 种魔方共需130元,购买3个A种魔方和4个B种魔方所需款数相同”,即可得出关于x、y的二元一次方程组,解之即可得出结论;(2)设购进A 种魔方m 个(0<m ≤50),总价格为w 元,则购进B 种魔方(100﹣m )个,根据两种活动方案即可得出w 活动一、w 活动二关于m 的函数关系式,再分别令w 活动一<w 活动二、w 活动一=w 活动二和w 活动一>w 活动二,解出m 的取值范围,此题得解.【解答】(按买3个A 种魔方和买4个B 种魔方钱数相同解答)解:(1)设A 种魔方的单价为x 元/个,B 种魔方的单价为y 元/个,根据题意得:, 解得:.答:A 种魔方的单价为20元/个,B 种魔方的单价为15元/个.(2)设购进A 种魔方m 个(0<m ≤50),总价格为w 元,则购进B 种魔方(100﹣m )个, 根据题意得:w 活动一=20m ×0.8+15(100﹣m )×0.4=10m +600;w 活动二=20m +15(100﹣m ﹣m )=﹣10m +1500.当w 活动一<w 活动二时,有10m +600<﹣10m +1500,解得:m <45;当w 活动一=w 活动二时,有10m +600=﹣10m +1500,解得:m =45;当w 活动一>w 活动二时,有10m +600>﹣10m +1500,解得:45<m ≤50.综上所述:当m <45时,选择活动一购买魔方更实惠;当m =45时,选择两种活动费用相同;当m >45时,选择活动二购买魔方更实惠.(按购买3个A 种魔方和4个B 种魔方需要130元解答)解:(1)设A 种魔方的单价为x 元/个,B 种魔方的单价为y 元/个,根据题意得:, 解得:.答:A 种魔方的单价为26元/个,B 种魔方的单价为13元/个.(2)设购进A 种魔方m 个(0<m ≤50),总价格为w 元,则购进B 种魔方(100﹣m )个, 根据题意得:w 活动一=26m ×0.8+13(100﹣m )×0.4=15.6m +520;w 活动二=26m +13(100﹣m ﹣m )=1300.当w 活动一<w 活动二时,有15.6m +520<1300,解得:m <50;当w 活动一=w 活动二时,有15.6m +520=1300,解得:m =50;当w 活动一>w 活动二时,有15.6m +520>1300,不等式无解.综上所述:当0<m <50时,选择活动一购买魔方更实惠;当m =50时,选择两种活动费用相同.【点评】本题考查了二元一次方程组的应用、一次函数的应用、解一元一次不等式以及解一元一次方程,解题的关键是:(1)找准等量关系,列出关于x 、y 的二元一次方程组;(2)根据两种活动方案找出w 活动一、w 活动二关于m 的函数关系式.25.(10分)感知:如图①,AD 平分∠BAC ,∠B +∠C =180°,∠B =90°.判断DB 与DC 的大小关系并证明. 探究:如图②,AD 平分∠BAC ,∠ABD +∠ACD =180°,∠ABD <90°,DB 与DC 的大小关系变吗?请说明理由.应用:如图③,四边形ABDC 中,∠B =45°,∠C =135°,DB =DC =a ,则AB ﹣AC =a .(用含a 的代数式表示)【分析】感知:判断出△ADC ≌△ADB ,即可得出结论;探究:欲证明DB =DC ,只要证明△DFC ≌△DEB 即可.应用:先证明△DFC ≌△DEB ,再证明△ADF ≌△ADE ,结合BD =EB 即可解决问题.【解答】感知:解:BD =DC ,理由:∵AD 平分∠BAC ,∴∠DAC =∠DAB ,∵∠B +∠C =180°,∠B =90°,∴∠C =90°=∠B ,在△ADC 和△ADB 中,, ∴△ADC ≌△ADB (AAS ),∴BD =DC ;探究:证明:如图②中,DE⊥AB于E,DF⊥AC于F,∵DA平分∠BAC,DE⊥AB,DF⊥AC,∴DE=DF,∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,∴∠B=∠FCD,在△DFC和△DEB中,∴△DFC≌△DEB,∴DC=DB;应用:解;如图③连接AD、DE⊥AB于E,DF⊥AC于F,∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,∴∠B=∠FCD,在△DFC和△DEB中,∴△DFC≌△DEB,∴DF=DE,CF=BE,在Rt△ADF和Rt△ADE中,∴Rt△ADF≌Rt△ADE,∴AF=AE,∴AB﹣AC=(AE+BE)﹣(AF﹣CF)=2BE,在Rt△DEB中,∵∠DEB=90°,∠B=∠EDB=45°,BD=a,∴BE=BD=a,∴AB﹣AC=2BE=a.故答案为a.【点评】此题是四边形综合题,主要考查全等三角形的判定和性质、角平分线的性质、等腰直角三角形的性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形.。
山东省枣庄市山亭区2017-2018学年八年级数学上学期期中试题(扫描版) 青岛版
山东省枣庄市山亭区2017-2018学年八年级数学上学期期中试题2017—2018学年度第一学期阶段性检测八年级数学(2017.11)参考答案一、1-5.CDCDB.6-10.DACCB.11-12AA二、13 4 14. (6,2) 15. (1,3) 16. <17. (3,) 18. 10090三、解答题19. 解:(1)5 (2)11-4(3) 4)9-9…….每小题过程2分结果2分20. 解::∵2a-1的平方根是9∴2a-1=∴a=2或a=-1……………………………..2分∵b-1的算平方根是2,∴b-1=4∴b=5……………………………………………3分∵ c是的整数部分,∴c=3,……………………………………………4分当a=2时:a-b+c=2-5+3=0…………………………….6分当a=-1时:a-b+c=-1-5+3= -3………………………………8分21解:(1)或7.5……………2分(2)如图……………4分(3)A1(1,5),B1(1,0),C1(4,3)………6分22.解:(1)设正比例函数解析式为y=mx,一次函数解析式为y=nx+4………2分将(-2,2)代入可得2=-2m,2=-2n+4,解得:m =-1,n =1,∴函数解析式为:y=-x;y=x+4………4分(2)根据过点(-2,2)及(0,4)可画出一次函数图象,根据过点(0,0)及(-2,2)可画出正比例函数图象(如图)………6分(3)………8分23. 解:(1)如图,将圆柱的侧面展开,AC=30cm,高是40cm,则BA=40cm,BC==50 cm故绕行一圈的路程是50cm.………4分(2)因为底面圆的周长为80cm,即AC=80cm,……5分绕一圈爬行100cm,则BC=100cm=60cm……6分∴树干高=60×10=600cm=6m.故树干高6m.…8分24.解:1)10;………1分(2)1 ;………3分(3)3 ;………4分(4)解:设l A:s= kt + b ∵图象过(0,10)(3,25)解得A行走的路程S与时间t的函数关系式:s=5t + 10………7分(5)设l B:s= kt ∵点(0.5,7.5)在l B上,7.5=0.5k,解得k=15, s= 15t解得s=15,t=1若B的自行车不发生故障,保持出发时的速度前进,1小时与A相遇. ………10分25. 解:(1)方案A:函数表达式为………1分方案B:函数表达式为………3分(2)当x=2200时,方案A的费用为(元)方案B的费用为(元)因为12760<13000,所以方案A付款少. ………7分(3)方案A:苹果数量为20000 5.83448(kg)方案B:苹果数量为(20000-2000)5=3600(kg)所以他应选择方案B购买. ………10分。
2017-2018学年山东省枣庄市薛城区八年级(下)期中数学试卷
2017-2018学年山东省枣庄市薛城区八年级(下)期中数学试卷一、选择题(下面每小题给出的四个选项中,只有一项是正确的,请把正确选 项选出来,每小题3分,共36分)1. (3分)不等式3x 6-9的解集在数轴上表示正确的是()―I—I —右 I 鼻—I ------------------ >C. J 01 2 D. -1 0 1 22. (3分)如图,在厶ABC 中,以点B 为圆心,以BA 长为半径画弧交边BC 于点D ,连接AD .若.B =40,. C = 36,贝U • DAC 的度数是()3. (3 分)如图,在正方形网格中,线段A B 是线段AB 绕某点逆时针旋转角:得到的,点A •与A 对应,则角〉的大小为( )于D ,交BC 于E ,若CE=3,则BE 的长是(C. 34D . 24B . 60 C. 904. (3分)如图, 在 ABC 中,C =90 , B =22.5,AB 的垂直平分线交AB44A . 30A . 3B . 6C . 25. (3分)如图,在方格纸中,ABC经过变换得到.DEF,正确的变换是()AA .把ABC绕点C逆时针方向旋转90,再向下平移2格B .把ABC绕点C顺时针方向旋转90,再向下平移5格C .把ABC向下平移4格,再绕点C逆时针方向旋转180D .把ABC向下平移5格,再绕点C顺时针方向旋转180• 26. (3分)不等式组的非负整数解的个数是()2x-9 clA. 4B. 5C. 6D. 77. (3分)实数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是()a b c d―J-e --- --- •- ―1------------- • ---- >-5 -4 -3 -2 -1 0 1 2 3 4 5A . a _ 3 b - 3B . -3c ::: -3dC . 1-a・1-cD . b-d 08. (3分)图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是()图1 图2A .①B .②C .③D .④9. (3分)如图,已知钝角 ABC ,依下列步骤尺规作图, 并保留作图痕迹步骤1 :以C 为圆心,CA 为半径画弧①;步骤2 :以B 为圆心,BA 为半径画弧②, 交弧①于点D ;步骤3 :连接AD ,交BC 延长线于点H .B . AC 平分 BADD . AB = AD10. (3 分)若关于x 的一元一次不等式组 2X" "(x — 2)的解集是x :::5,则m的 I x < m取值范围是( )A . m r 511. (3 分)如图,在 ABC 中,AB 二 AC ,DE = DF ,DE _ AB ,DF _ AC , 垂足分别是E 、F .现有下列结论:①AD 平分.BAC :②AD _ BC :③AD 上任意一点到AB 、AC 的距离相等;④AD 上任意一点到BC 两端点的距离C . S AB C =BC L AHC . m, 5AD相等.其中正确结论的个数有(到三边的距离之和为()A. 1B. 2C. 3D. 412. (3分)已知等边三角形的边长为3,点P为等边三角形内任意一点,则点D •不能确定二、填空题(共6小题,每小题4分,满分24分)13. ____________________________________________________ (4分)若等腰三角形的一个外角是110,则其底角为________________________ .14. (4分)已知五个正数的和等于1 .用反证法证明:这五个数中至少有一1个大于或等于-应先假设15(4分)关于x的一元一次不等式巴分,-2的解集为x-4,则m的值为________316. (4分)如图,函数%=-2x与y2二ax・3的图象相交于点A(m,2),则关于x的不等式-2x, ax 3的解集是y;=ax+317. (4 分)如图在Rt ABC 中,ACB=90 , ABC = 58,将Rt ABC 绕点C旋转到Rt △ ABC,使点B恰好落在AB 上, AC交AB于点D,贝ADC的度数为_______ .18. (4分)为有效开展阳光体育”活动,某校计划购买篮球和足球共50个,购买资金不超过3000元.若每个篮球80元,每个足球50元,则篮球最多可购买____ 个.三、解答题(共7道大题,满分60分)19. (8分)如图所示,已知ABC的角平分线BM,CN相交于点P . (1)判断AP能否平分• BAC ?请说明理由.。
2017-2018学年山东省枣庄市薛城区八年级(下)期中数学试卷
2017-2018学年山东省枣庄市薛城区八年级(下)期中数学试卷一、选择题(下面每小题给出的四个选项中,只有一项是正确的,请把正确选项选出来,每小题3分,共36分)1.(3分)不等式3x+6N 9的解集在数轴上表示正确的是()A. -1 0C. -1 0D.0 122. (3分)如图,^AABC 中,以点B 为圆心,以长为半径画弧交边3C 于I I 点D,连接AD.若£6=40° , ZC=36° ,则ZDAC 的度数是( )44° C. 34° D. 24°3. (3分)如图,在正方形网格中,线段A' B'是线段A3绕某点逆时针旋转角a 得到的,点A'与A 对应,贝」角a 的大小为()A. 30°B. 60°C. 90°D. 120°4. (3 分)如图,在左ABC 中,ZC=90° , £8=22.5°,AB 的垂直平分线交AB 于。
,交BC 于■ E,若CE=3,则BE 的长是()D. 3扼5. (3分)如图,在方格纸中,AABC 经过变换得到△£>",正确的变换是()AA.把AABC绕点。
逆时针方向旋转90°,再向下平移2格B.把AABC绕点。
顺时针方向旋转90°,再向下平移5格C.把AABC向下平移4格,再绕点。
逆时针方向旋转180。
D.把AABC向下平移5格,再绕点。
顺时针方向旋转180°6.(3分)不等式组(3x+7>2的非负整数解的个数是()[2x-9<lA.4B.5C.6D.77.(3分)实数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论A. a一3〉b-3B.3cV-3dC.1-。
>1一cD.b一d>08.(3分)图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是()r"■•f~w i\®\②:o□^®o图1图2A.①B.②C.③D.④9.(3分)如图,已知钝角AABC,依下列步骤尺规作图,并保留作图痕迹.步骤1:以。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017-2018学年山东省枣庄市薛城区八年级(上)期中数学试卷 一、选择题(共12小题,每小题3分,满分36分) 1.(3分)在下列各数:、、0.、、、、0.303 003 0003…(每两个3之间增加1个0)中,无理数的个数是( ) A.2 B.3 C.4 D.5 2.(3分)(﹣2)2的平方根是( ) A.2 B.﹣2 C.± D.±2 3.(3分)如果P(m+3,2m+4)在y轴上,那么点P的坐标是( ) A.(﹣2,0) B.(0,﹣2) C.(1,0) D.(0,1) 4.(3分)下列三角形中,不是直角三角形的是( ) A.三角形三边分别是9,40,41 B.三角形三内角之比为1:2:3 C.三角形三内角中有两个角互余 D.三角形三边之比为2:3:4 5.(3分)如果P点的坐标为(a,b),它关于y轴的对称点为P1,P1关于x轴的对称点为P2,已知P2的坐标为(﹣2,3),则点P的坐标为( ) A.(﹣2,﹣3) B.(2,﹣3) C.(﹣2,3) D.(2,3) 6.(3分)一艘轮船在同一航线上往返于甲、乙两地.已知轮船在静水中的速度为15km/h,水流速度为5km/h.轮船先从甲地逆水航行到乙地,在乙地停留一段时间后,又从乙地顺水航行返回到甲地,设轮船从甲地出发后所用时间为t(h),航行的路程为s(km),则s与t的函数图象大致是( )
A. B. C. D. 7.(3分)将一次函数y=2x﹣3的图象沿y轴向上平移8个单位长度,所得直线的解析式为( ) A.y=2x﹣5 B.y=2x+5 C.y=2x+8 D.y=2x﹣8 8.(3分)实数a、b在数轴上对应点的位置如图所示,化简|a|﹣的结果是( )
A.﹣2a+b B.2a﹣b C.﹣b D.b 9.(3分)已知:如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中阴影部分的面积为( )
A.9 B.3 C. D. 10.(3分)对于任意的正数m、n定义运算※为:m※n=,计算(3※2)×(8※12)的结果为( ) A.2﹣4 B.2 C.2 D.20 11.(3分)一次函数y=kx+b满足kb>0,且y随x的增大而减小,则此函数的图象不经过( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 12.(3分)在如图所示的数轴上,点B与点C关于点A对称,A,B两点对应的实数分别是和﹣1,则点C所对应的实数是( ) A.1+ B.2+ C.2﹣1 D.2+1 二、填空题(共6小题,每小题4分,满分24分) 13.(4分)若a、b为实数,且满足|a﹣2|+=0,则b﹣a的值为 . 14.(4分)如图,直线l是一次函数y=kx+b的图象,若点A(3,m)在直线l上,则m的值是 .
15.(4分)如图,一只蚂蚁从长、宽都是3cm,高是8cm的长方体纸箱的A点沿纸箱表面爬到B点,那么它需要爬行的最短路线的长是 .
16.(4分)若一个正数的两个平方根分别为a+2与3a﹣1,则a= ,这个正数是 . 17.(4分)如图,数轴上点A、B对应的数分别是1,2,过点B作PQ⊥AB,以点B为圆心,AB长为半径作圆弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,当点M在点B的右侧时,点M对应的数是 .
18.(4分)如图,它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形的 较短的直角边长为a,较长的直角边长为b,那么(a+b)2的值为 . 三、解答题(共7小题,满分60分) 19.(10分)计算 (1)(2﹣1)2+(+2)(﹣2) (2)(﹣2)×﹣6.
20.(6分)已知x﹣2的平方根是±2,2x+y+7的立方根是3,求x2+y2的平方根. 21.(8分)阅读下面问题: ==﹣1;
==﹣ ==﹣2,根据以上解法 试求:(1)的值; (2)(n为正整数)的值 (3)+++…++的值. 22.(8分)如图,长方形ABCD中,AB=4,BC=5,F为CD上一点,将长方形沿折痕AF折叠,点D恰好落在BC上的点E处,求△CFE的面积.
23.(8分)在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村,设甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,请回答下列问题 (1)A、C两村间的距离为 km (2)求y1的关系式,并写出自变量x的取值范围; (3)求出图中点P的坐标,并解释该点坐标所表示的实际意义.
24.(10分)如图,正方形网格中的△ABC,若小方格边长为1,格点三角形(顶点是网格线交点的三角形)ABC的顶点A,C的坐标分别为(﹣1,1),(0,﹣2),请你根据所学的知识. (1)在如图所示的网格平面内作出平面直角坐标系; (2)作出三角形ABC关于y轴对称的三角形A1B1C1; (3)判断△ABC的形状,并求出△ABC的面积.
25.(10分)已知直线y=kx+b经过点A(0,6),且平行于直线y=﹣2x (1)求该函数的解析式,并画出它的图象; (2)如果这条直线经过点P(m,2),求m的值; (3)若O为坐标原点,求直线OP的解析式; (4)求直线y=kx+b和直线OP与x轴所围成的图形的面积. 2017-2018学年山东省枣庄市薛城区八年级(上)期中数学试卷 参考答案与试题解析
一、选择题(共12小题,每小题3分,满分36分) 1.(3分)在下列各数:、、0.、、、、0.303 003 0003…(每两个3之间增加1个0)中,无理数的个数是( ) A.2 B.3 C.4 D.5 【解答】解:、、0.303 003 0003…(每两个3之间增加1个0)是无理数, 故选:B.
2.(3分)(﹣2)2的平方根是( ) A.2 B.﹣2 C.± D.±2 【解答】解:∵(﹣2)2=4, 而2或﹣2的平方等于4, ∴(﹣2)2的平方根是±2. 故选:D.
3.(3分)如果P(m+3,2m+4)在y轴上,那么点P的坐标是( ) A.(﹣2,0) B.(0,﹣2) C.(1,0) D.(0,1) 【解答】解:∵P(m+3,2m+4)在y轴上, ∴m+3=0, 解得m=﹣3,2m+4=﹣2, ∴点P的坐标是(0,﹣2). 故选:B.
4.(3分)下列三角形中,不是直角三角形的是( ) A.三角形三边分别是9,40,41 B.三角形三内角之比为1:2:3 C.三角形三内角中有两个角互余 D.三角形三边之比为2:3:4 【解答】解:A、92+42=412,符合勾股定理的逆定理,是直角三角形; B、三角形三内角之比为1:2:3,可得三个内角分别为30°,60°,90°,是直角三角形; C、角形三内角中有两个角互余,则第三个角为90°,是直角三角形; D、22+32≠42,不是直角三角形, 故选:D.
5.(3分)如果P点的坐标为(a,b),它关于y轴的对称点为P1,P1关于x轴的对称点为P2,已知P2的坐标为(﹣2,3),则点P的坐标为( ) A.(﹣2,﹣3) B.(2,﹣3) C.(﹣2,3) D.(2,3) 【解答】解:∵P2的坐标为(﹣2,3),P1关于x轴的对称点为P2, ∴P1(﹣2,﹣3), ∵P点的坐标为(a,b),它关于y轴的对称点为P1, ∴a=2,b=﹣3, ∴点P的坐标为(2,﹣3), 故选:B.
6.(3分)一艘轮船在同一航线上往返于甲、乙两地.已知轮船在静水中的速度为15km/h,水流速度为5km/h.轮船先从甲地逆水航行到乙地,在乙地停留一段时间后,又从乙地顺水航行返回到甲地,设轮船从甲地出发后所用时间为t(h),航行的路程为s(km),则s与t的函数图象大致是( )
A. B. C. D. 【解答】解:逆流行驶用的时间长,中间停留路程没变化,顺流行驶用的时间短,故C符合题意; 故选:C.
7.(3分)将一次函数y=2x﹣3的图象沿y轴向上平移8个单位长度,所得直线的解析式为( ) A.y=2x﹣5 B.y=2x+5 C.y=2x+8 D.y=2x﹣8 【解答】解:由题意,得 y=2x﹣3+8, 即y=2x+5, 故选:B.
8.(3分)实数a、b在数轴上对应点的位置如图所示,化简|a|﹣的结果是( )
A.﹣2a+b B.2a﹣b C.﹣b D.b 【解答】解:由数轴可得: a<0,a﹣b<0, 则|a|﹣ =﹣a+(a﹣b) =﹣b. 故选:C.
9.(3分)已知:如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中阴影部分的面积为( ) A.9 B.3 C. D. 【解答】解:设以Rt△ABC的三边为斜边分别向外作等腰直角三角形的底边上的高分别为h1,h2,h3, 则h1=AC,h2=BC,h3=AB,
即:阴影部分的面积为:××AC×AC+××BC×BC+××AB×AB=(AC2+AB2+BC2), 在Rt△ABC中,由勾股定理可得:AC2+BC2=AB2,AB=3, 所以阴影部分的面积为:×2AB2=×32=, 故选:D.
10.(3分)对于任意的正数m、n定义运算※为:m※n=,计算(3※2)×(8※12)的结果为( ) A.2﹣4 B.2 C.2 D.20 【解答】解:∵3>2, ∴3※2=﹣, ∵8<12, ∴8※12=+=2×(+), ∴(3※2)×(8※12)=(﹣)×2×(+)=2. 故选:B.
11.(3分)一次函数y=kx+b满足kb>0,且y随x的增大而减小,则此函数的图象不经过( )
