人教版九年级数学上册24.4 弧长和扇形面积同步练习带答案【高分必备】

合集下载

人教版九年级上册数学 24.4 弧长和扇形面积同步训练(含答案)

人教版九年级数学24.4 弧长和扇形面积同步训练一、选择题（本大题共10道小题）1. 若扇形的圆心角为90°，半径为6，则该扇形的弧长为()A.πB.2πC.3πD.6π2. 如图，在边长为4的正方形ABCD中，以点B为圆心，AB长为半径画弧，交对角线BD于点E，则图中阴影部分的面积是(结果保留π)()A.8-πB.16-2πC.8-2πD.8-π3. 如图，在边长为4的正方形ABCD中，以点B为圆心，AB长为半径画弧，交对角线BD于点E，则图中阴影部分的面积是(结果保留π)()A．8－π B．16－2πC．8－2π D．8－1 2π4. 2018·宁夏用一个半径为30，圆心角为120°的扇形纸片围成一个圆锥(接缝处忽略不计)，则这个圆锥的底面圆半径是()A．10 B．20 C．10π D．20π5. 如图，已知一块圆心角为270°的扇形铁皮，用它做一个圆锥形的烟囱帽(接缝忽略不计)，圆锥底面圆的直径是60 cm，则这块扇形铁皮的半径是()A ．40 cmB ．50 cmC ．60 cmD ．80 cm6. (2019•温州)若扇形的圆心角为90°，半径为6，则该扇形的弧长为A ．B ．C ．D ．7. 如图，在△AOC 中，OA ＝3 cm ，OC ＝1 cm ，将△AOC 绕点O 顺时针旋转90°后得到△BOD ，则AC 边在旋转过程中所扫过的图形的面积为( )A.π2 cm2 B ．2π cm2C.17π8 cm2D.19π8 cm28. 如图，以AD 为直径的半圆O 经过Rt △ABC 斜边AB 的两个端点，交直角边AC 于点E.B ，E 是半圆弧的三等分点，BE ︵的长为2π3，则图中阴影部分的面积为( )图A.π9 B.3π9C.3 32－3π2D.3 32－2π39. 如图在扇形OAB 中，∠AOB ＝150°，AC ＝AO ＝6，D 为AC 的中点，当弦AC沿AB ︵运动时，点D 所经过的路径长为( )图A ．3π B.3πC.32 3πD ．4π10. 2017·衢州运用图变化的方法研究下列问题：如图AB 是⊙O 的直径，CD ，EF 是⊙O 的弦，且AB ∥CD ∥EF ，AB ＝10，CD ＝6，EF ＝8，则图阴影部分的面积是( )图A.252π B ．10π C ．24＋4πD ．24＋5π二、填空题（本大题共7道小题）11. 如图所示，在△ABC 中，AB ＝BC ＝2，∠ABC ＝90°，则图中阴影部分的面积是________．12. 如图，把一个圆锥沿母线OA 剪开，展开后得到扇形OAC .已知圆锥的高h 为12 cm ，OA ＝13 cm ，则扇形OAC 中AC ︵的长是________ cm.(结果保留π)13.若一个圆锥的底面圆半径为3cm ，其侧面展开图的圆心角为120°，则圆锥的母线长是________cm .14. 如图，已知扇形OAB 的圆心角为60°，扇形的面积为6π，则该扇形的弧长为________．15. (2019•贺州)已知圆锥的底面半径是1，高是，则该圆锥的侧面展开图的圆心角是__________度．16. 如图中的小方格都是边长为1的正方形，则以格点为圆心，半径为1和2的两种弧围成的“叶状”(阴影部分)图案的面积为________．17.如图在边长为3的正方形ABCD 中，以点A 为圆心，2为半径作圆弧EF ，以点D 为圆心，3为半径作圆弧AC.若图阴影部分的面积分别为S 1，S 2，则S 1－S 2＝________．三、解答题（本大题共4道小题）18.如图，在△ABC 中，以AB 为直径的⊙O 分别与BC ，AC 相交于点D ，E ，BD ＝C D ，过点D 作⊙O 的切线交边AC 于点F. (1)求证：DF ⊥AC ；(2)若⊙O 的半径为5，∠CDF ＝30°，求BD ︵的长．(结果保留π)19.如图，AB为⊙O的直径，C，D是半圆O的三等分点，过点C作AD延长线的垂线CE，垂足为E.(1)求证：CE是⊙O的切线；(2)若⊙O的半径为2，求图中阴影部分的面积．20. 如图，以△ABC的边BC为直径作⊙O，点A在⊙O上，点D在线段BC的延长线上，AD＝AB，∠D＝30°，(1)求证：直线AD是⊙O的切线；(2)若直径BC＝4，求图中阴影部分的面积．21. (2019•辽阳)如图，是⊙的直径，点和点是⊙上的两点，连接，，，过点作射线交的延长线于点，使．(1)求证：是⊙的切线；(2)若，求阴影部分的面积．人教版九年级数学24.4 弧长和扇形面积同步训练-答案一、选择题（本大题共10道小题）1. 【答案】C[解析]扇形的圆心角为90°，它的半径为6，即n=90°，r=6，根据弧长公式l=，得l==3π.故选C.2. 【答案】C[解析]在边长为4的正方形ABCD中，BD是对角线，∴AD=AB=4，∠BAD=90°，∠ABE=45°，∴S△ABD=·AD·AB=8，S扇形ABE==2π，∴S阴影=S△ABD-S扇形ABE=8-2π.故选C.3. 【答案】C[解析] 在边长为4的正方形ABCD中，BD是对角线，∴AD＝AB＝4，∠BAD＝90°，∠ABE＝45°，∴S△ABD＝12AD·AB＝8，S扇形BAE＝45·π·42360＝2π，∴S阴影＝S△ABD－S扇形BAE＝8－2π.故选C.4. 【答案】A5. 【答案】A[解析] ∵圆锥的底面圆直径为60 cm，∴圆锥的底面圆周长为60πcm，∴扇形的弧长为60π cm.设扇形的半径为r，则270πr180＝60π，解得r＝40 cm.6. 【答案】C【解析】该扇形的弧长=．故选C ．7. 【答案】B[解析] 如图，AC 边在旋转过程中所扫过的图形的面积即阴影部分的面积．S 阴影＝S △OCA ＋S 扇形OAB －S 扇形OCD －S △ODB.由旋转知△OCA ≌△ODB ，∴S △OCA ＝S △ODB ，∴S 阴影＝S 扇形OAB －S 扇形OCD ＝90π×32360－90π×12360＝2π(cm2)．故选B.8. 【答案】D9. 【答案】C[解析] 如图∵D 为AC 的中点，AC ＝AO ＝6，∴OD ⊥AC ，∴AD ＝12AC ＝12AO ， ∴∠AOD ＝30°，OD ＝3 3. 作BF ＝AC ，E 为BF 的中点．同理可得∠BOE ＝30°， ∴∠DOE ＝150°－60°＝90°，∴点D 所经过的路径长为nπR 180＝90π×3 3180＝3 32π.10. 【答案】A[解析] 如图作直径CG ，连接OD ，OE ，OF ，DG .∵CG 是⊙O 的直径，∴∠CDG ＝90°，则DG ＝CG2－CD2＝8.又∵EF ＝8，∴DG ＝EF ，∴DG ︵＝EF ︵， ∴S 扇形ODG ＝S 扇形OEF .∵AB ∥CD ∥EF ，∴S △OCD ＝S △ACD ，S △OEF ＝S △AEF ，∴S 阴影＝S 扇形OCD ＋S 扇形OEF ＝S 扇形OCD ＋S 扇形ODG ＝S 半圆＝12π×52＝252π.二、填空题（本大题共7道小题）11. 【答案】π－2[解析] ∵在△ABC 中，AB ＝BC ＝2，∠ABC ＝90°，∴△ABC 是等腰直角三角形，∴S 阴影＝S 半圆AB ＋S 半圆BC －S △ABC ＝12π×(22)2＋12π×(22)2－12×2×2 ＝π－2.12. 【答案】10π[解析] 由勾股定理，得圆锥的底面圆半径为132－122＝5(cm)，∴扇形的弧长＝圆锥的底面圆周长＝2π×5＝10π(cm)．13. 【答案】 9【解析】由n ＝360r l 得120＝360×3l ，解得l ＝9.14. 【答案】2π[解析] 设扇形的半径是R ，则60·π·R2360＝6π，解得R ＝6(负值已舍去)．设扇形的弧长是l ，则12lR ＝6π，即3l ＝6π，解得l ＝2π.故答案为2π.15. 【答案】90【解析】设圆锥的母线为a ，根据勾股定理得，a=4，设圆锥的侧面展开图的圆心角度数为，根据题意得，解得，即圆锥的侧面展开图的圆心角度数为．故答案为：90．16. 【答案】2π－4[解析] 如图所示，由题意，得阴影部分的面积＝2(S 扇形OAB－S △OAB)＝2(90π×22360－12×2×2)＝2π－4. 故答案为2π－4.17. 【答案】13π4－9 [解析] ∵S 正方形ABCD ＝3×3＝9，S 扇形DAC ＝9π4，S 扇形AEF ＝π，∴S 1－S 2＝S 扇形AEF －(S 正方形ABCD －S 扇形DAC )＝π－⎝ ⎛⎭⎪⎫9－9π4＝13π4－9.三、解答题（本大题共4道小题）18. 【答案】(1)证明：如解图，连接OD ，(1分) ∵DF 是⊙O 的切线，D 为切点，解图∴OD ⊥DF ， ∴∠ODF ＝90°，(2分) ∵BD ＝CD ，OA ＝OB ，∴OD 是△ABC 的中位线，(3分) ∴OD ∥AC ，∴∠CFD ＝∠ODF ＝90°， ∴DF ⊥AC.(4分)(2)解：∵∠CDF ＝30°，由(1)得∠ODF ＝90°， ∴∠ODB ＝180°－∠CDF －∠ODF ＝60°， ∵OB ＝OD ，∴△OBD 是等边三角形，(7分) ∴∠BOD ＝60°，∴lBD ︵＝nπR 180＝60π×5180＝53π.(8分)19. 【答案】解：(1)证明：连接OC . ∵C ，D 为半圆O 的三等分点，∴AD ︵＝CD ︵＝BC ︵， ∴∠DAC ＝∠BAC . ∵OA ＝OC ， ∴∠BAC ＝∠ACO ， ∴∠DAC ＝∠ACO ， ∴OC ∥AD . ∵CE ⊥AD ，∴CE ⊥OC ，∴CE 为⊙O 的切线． (2)连接OD . ∵AD ︵＝CD ︵＝BC ︵，∴∠AOD ＝∠COD ＝∠BOC ＝13×180°＝60°. 又∵OC ＝OD ，∴△COD 为等边三角形， ∴∠CDO ＝60°＝∠AOD ， ∴CD ∥AB ， ∴S △ACD ＝S △COD ，∴图中阴影部分的面积＝S 扇形COD ＝60×π×22360＝2π3.20. 【答案】解：(1)证明：如图，连接OA.∵AD ＝AB ，∠D ＝30°， ∴∠B ＝∠D ＝30°， ∴∠DAB ＝120°. ∵BC 是⊙O 的直径， ∴∠BAC ＝90°， ∴∠DAC ＝30°，∴∠BCA ＝60°.∵AO ＝CO ，∴△ACO 是等边三角形，∴∠CAO ＝60°，∴∠DAO ＝∠CAO ＋∠DAC ＝90°，即AD ⊥AO.又∵AO 是⊙O 的半径，∴直线AD 是⊙O 的切线．(2)由(1)知Rt △ADO 中，AO ＝2，∠D ＝30°，∴OD ＝2AO ＝4，∴AD ＝2 3，∴SRt △ADO ＝12×2 3×2＝2 3.∵△ACO 是等边三角形，∴∠AOD ＝60°，∴S 扇形OAC ＝60π×22360＝2π3，∴S 阴影＝SRt △ADO －S 扇形OAC ＝2 3－2π3. 21. 【答案】 (1)如图，连接，过作于，∴， ∴， ∵， ∴， ∵， ∴，∵，∴，∴，∵，∴，∴，∴是⊙的切线．(2)∵，∴，∵，∴，∵，，∴，∵，∴，，∴是等边三角形，∴，，∴，∴，在中，，∴，∴阴影部分的面积．。

人教版九年级数学上册24.4 弧长和扇形面积同步练习带答案【优】

第24章 24.4《弧长和扇形面积》同步练习及答案(2)第1题. 一条弧所对的圆心角是90o，半径是R ，则这条弧的长是．答案：12R π 第2题. 若»AB 的长为所对的圆的直径长，则»AB 所对的圆周角的度数为．答案：180πo第3题. 如图，AB 是半圆O 的直径，以O 为圆心，OE 为半径的半圆交AB 于E ，F 两点，弦AC 是小半圆的切线，D 为切点，若4OA =，2OE =，则图中阴影部分的面积为．答案：43π+第4题. 如果一条弧长等于l ，它的半径等于R ，这条弧所对的圆心角增加1o，则它的弧长增加（）Ａ．lnＢ．180R π Ｃ．180lRπ Ｄ．360l答案：Ｂ第5题. 在半径为3的O e 中，弦3AB =，则»AB 的长为（）Ａ．π2Ｂ．πＣ．32π Ｄ．2π答案：Ｂ第6题. 扇形的周长为16，圆心角为360πo，则扇形的面积是（）Ａ．16 Ｂ．32 Ｃ．64 Ｄ．16π答案：Ａ第7题. 如图，扇形OAB 的圆心角为90o，且半径为R ，分别以OA ，OB 为直径在扇形内作半圆，P 和Q 分别表示两个阴影部分的面积，那么P 和Q 的大小关系是（）Ａ．P Q =Ｂ．P Q >Ｃ．P Q <Ｄ．无法确定答案：Ａ第8题. 如图，矩形ABCD 中，1AB =，BC =，以BC 的中点E 为圆心的¼MPN与AD 相切，则图中的阴影部分的面积为（）Ａ．23π Ｂ．34πＤ．π3答案：Ｄ第9题. 如图所示，正方形ABCD 是以金属丝围成的，其边长1AB =，把此正方形的金属丝重新围成扇形的ADC ，使AD AD =，DC DC =不变，问正方形面积与扇形面积谁大？大多少？由计算得出结果．答案：1S =正方形，121122ADC S lR 1==⨯⨯=扇形，∴面积没有变化．第10题. 如图，O e 的半径为1，C 为O e 上一点，以C 为圆心，以1为半径作弧与O e 相交于A ，B 两点，则图中阴影部分的面积为．答案：2π3第11题. 如图，△ABC 中，105A ∠=o ，45B ∠=o，AB =AD BC ⊥，D 为垂足，以A为圆心，以AD 为半径画弧»EF，则图中阴影部分的面积为（）ＭＣＡＤＡ．76πＢ．76-π+2Ｃ．56πＤ．56-π+2答案：Ｂ第12题. 如图，半径为r 的1O e 与半径为3r 的2O e 外切于P 点，AB 是两圆的外公切线，切点分别为A ，B ，求AB 和»PA，»PB 所围成的阴影部分的面积．答案：连结2O B ，1O A ，过1O 作12O H O B ⊥，垂足为H ，则得矩形1ABHO ， 1BH O A r ∴==，1AB O H =．在Rt △21O HO 中，2232O H O B BH r r r =-=-=，122134O O O P O P r r r =+=+=，1O H ==，2211221cos 42O H r HO O O O r ∠===，2160HO O ∴∠=o ，1120AO P ∠=o ．21212111()(3)22ABO O S O A O B O H r r =+=+=g 梯形，26033606BO P O B r r S 222π()π(3)π===2g 2扇形，122120AO P O A S r π()π==3603扇形、，212122223ABO O BO P AO P S S S S r r ππ=--=--=23阴影梯形扇形扇形．第13题. 圆周角是90o，占整个周角的90360，因此它所对的弧长是圆周长的．答案：14第14题. 圆心角是45o，占整个周角的，因此它所对的弧长是圆周长的．答案：45360，18第15题. 圆心角是1o，占整个周角的，因此它所对的弧长是圆周长的．ＣＤＢＥＡＦ答案：1360，1360第16题. 扇形的圆心角为210o，弧长是28π，求扇形的面积．答案：336π第17题. 一个扇形的半径等于一个圆的半径的2倍，且面积相等．求这个扇形的圆心角．答案：90o第18题. 一服装厂里有大量形状为等腰直角三角形的边角布料（如图），现找出其中的一种，测得90C ∠=o ，4AC BC ==．今要从这种三角形中剪出一种扇形，做成不同形状的玩具，使扇形的边缘半径恰好都在ABC △的边上，且扇形的弧与ABC △的其他边相切，请设计出所有可能符合题意的方案示意图，并求出扇形的半径（只要求画出图形，并直接写出扇形半径）．答案：第19题.90o，半径为R Ａ．2R πＢ．3R πＣ．4R πＤ．6R答案：Ａ第20题. 已知一条弧长为l ，它所对圆心角的度数为n o，则这条弦所在圆的半径为（）．Ａ．180n lπ Ｂ．180ln πＣ．360ln πＤ．180lnπ答案：Ｂ第21题. 半径为6cm 的圆中，60o的圆周角所对的弧的弧长为．答案：4cm π第22题. 半径为9cm 的圆中，长为12cm π的一条弧所对的圆心角的度数为．答案：240o第23题. 已知圆的面积为281cm π，若其圆周上一段弧长为3cm π，则这段弧所对的圆心角的度42r =24r =1r =数为．答案：60o第24题. 若扇形的圆心角为120o，弧长为6cm π，则这个扇形的面积为．答案：227cm π第25题. 弯制管道时，先按中心线计算其“展直长度”，再下料．根据如图所示的图形可算得管道的展直长度为．（单位：mm ，精确到1mm ）答案：389mm第26题. 如图，在Rt △ABC 中，90C ∠=o，60A ∠=o，3cm AC =，将△ABC 绕点B 旋转至△A BC ''的位置，且使点A ，B ，C '三点在同一直线上，则点A 经过的最短路线长是cm ．答案：53π第27题. 一块等边三角形的木板，边长为１，若将木板沿水平线翻滚（如图），则点B 从开始至结束走过的路径长度为（）．Ａ．3π2Ｂ．4π3Ｃ．4Ｄ．322+π答案：Ｂ第28题. 如图，扇形AOB 的圆心角为60o，半径为6cm ，C ，D 是»AB 的三等分点，则图中阴影部分的面积和是．A ' C ' ＢＣＡＢＣ答案：22cm π第29题. 如图，已知在扇形AOB 中，若45AOB ∠=o，4cm AD =，3cm CD =π，则图中阴影部分的面积是．答案：214cm π第30题. 如图4，在两个同心圆中，三条直径把大圆分成相等的六部分，若大圆的半径为2，则图中阴影部分的面积为．答案：14.2π．图4。

人教版九年级数学上册《24.4弧长及扇形的面积》同步练习题(附答案)

人教版九年级数学上册《24.4弧长及扇形的面积》同步练习题(附答案）姓名班级学号成绩一、选择题：（本题共8小题，每小题5分，共40分．）1．若扇形的弧长是16cm，面积是56cm2，则它的半径是（）A．2.8cm B．3.5cm C．7cm D．14cm2．已知一个扇形的半径为R，圆心角为n°，当这个扇形的面积与一个直径为R的圆面积相等时，则n等于（）A．180 B．120 C．90 D．603．如图，放置在直线l上的扇形OAB．由图①滚动（无滑动）到图②，再由图②滚动到图③．若半径OA＝2，∠AOB＝45°，则点O所经过的最短路径的长是（）A．2π+2 B．3πC．D． +24．如图，一块直角三角板的60°角的顶点A落在⊙O上，两边分别交⊙O于B，C两点，若⊙O的半径是1，则的长是（）A．B．C．D．5．如图，AB为半圆的直径，且AB=4，半圆绕点B顺时针旋转45°，点A旋转到A′的位置，则图中阴影部分的面积为（）A．B．πC．2πD．4π6．如图，在△ABC中，∠A=40°，BC=3，分别以点B，C为圆心，BC长为半径在BC右侧画弧，两弧交于点D，与AB，AC的延长线分别交于点E，F，则弧DE和弧DF的长度和为（）A．B．C．D．2π7．如图，是的直径，且，是上一点，将沿直线翻折，若翻折后的圆弧恰好经过点，则图中阴影部分的面积为（）.A．B．C．D．8．如图，半径为2的两个等圆⊙O1与⊙O2外切于点P，过O1作⊙O2的两条切线，切点分别为A，B，与⊙O1分别交于C，D，则与的弧长之和为（）A．B．C．D．二、填空题：（本题共5小题，每小题3分，共15分．）9．扇形弧长为5πcm，面积为60πcm2，则扇形半径为．10．如图，的外接圆O的半径为3，则劣弧的长是.11．如图，以AB为直径，点O为圆心的半圆经过点C，若AC=BC= ，则图中阴影部分的面积是12．如图①，A，B表示某游乐场摩天轮上的两个轿厢．图②是其示意图，点O是圆心，半径r为，点A，B是圆上的两点，圆心角，则的长为．（结果保留）13．如图，菱形ABCD的边长为2，∠A=60°，以点B为圆心的圆与AD、DC相切，与AB、CB的延长线分别相交于点E，F，则图中阴影部分的面积为．三、解答题：（本题共5题，共45分）14．如图，在Rt△ABC中，∠C=90°，∠BAC=30°，BC=1，以B为圆心，BA为半径画弧交CB的延长线于点D，求弧AD的长15．如图1是某公园一块草坪上的自动旋转喷水装置，这种旋转喷水装置的旋转角度为240°，它的喷灌区是一个扇形．小涛同学想了解这种装置能够喷灌的草坪面积，他测量出了相关数据，并画出了示意图．如图2，A，B两点的距离为18米，求这种装置能够喷灌的草坪面积．16．如图，在△ABC中，AB＝AC，以AB为直径作⊙O，⊙O交BC于点D，交CA的延长线于点E.过点D作DF ⊥AC，垂足为F.（1）求证：DF为⊙O的切线；（2）若AB＝4，∠C＝30°，求劣弧的长.17．如图，已知过菱形的三个顶点A，B，D，连接，过点A作交的延长线于点E.（1）求证：为的切线；（2）若的半径为2，求图中阴影部分的面积.18．如图，在中，以边为直径作分别交，于点D，E，点D是中点，连接OE，OD.（1）求证：是等腰三角形.（2）若，求的长和扇形的面积.参考答案：1．C 2．C 3．C 4．C 5．C 6．B 7．D 8．A 9．24cm10．11．12．13．14．解：∵在Rt△ABC中，∠C=90°，∠BAC=30°，BC=1 ∴AB=2BC=2，∠ABC=90°-∠BAC=60°∴∠ABD=180°-∠ABC=120°∴弧AD=故答案为.15．解：过点O作OC⊥AB于C点．∵OC⊥AB，AB=18∴∵OA=OB，∠AOB=360°﹣240°=120°∴°．在Rt△OAC中，OA2=OC2+AC2又∵∴．∴πr2=72π（m2）16．（1）证明：如图，连接OD∵AB=AC∴∠B=∠C∵OB=OD∴∠B=∠ODB∴∠C=∠ODB∴OD// AC∵DF⊥AC∴DF⊥ODDF为⊙O的切线（2）解：如图，连接OE∵∠B=∠C=30°∴∠EAB=∠B+∠C=60°∴∠EOB=2∠EAB=120°∴的长=. 17．（1）证明：连接交于点P∵四边形是菱形∴∴∵∴∴∵为的半径∴为的切线；（2）解：∵四边形是菱形∴∵∴∴是等边三角形∴∵∴∴∴∴. 18．（1）证明：连接∵为直径∴，即又∵D是中点∴是线段的中垂线∴∴是等腰三角形（2）解：∵∴∴∵∴∴∵∴∴∴∴。

人教版数学九年级上册24.4弧长和扇形的面积同步练习含答案

人教版数学九年级上册24.4《弧长和扇形的面积》一、选择题1、如图，扇形纸扇完全打开后，外侧两竹条夹角为，的长为，贴纸部分的长为，则贴纸部分的面积为（）A． B．C． D．2、如图所示，⊙O是以坐标原点O为圆心，4为半径的圆，点P的坐标为（，），弦AB经过点P，则图中阴影部分面积的最小值等于（）A．2π﹣4 B．4π﹣8 C． D．3、如图所示，在扇形BAD中，点C在上，且∠BDC=30°，AB=2，∠BAD=105°，过点C作CE⊥AD，则图中阴影部分的面积为（）A．π﹣2 B．π﹣1 C．2π﹣2 D．2π+14、如图，在▱ABCD中，AD=2，AB=4，∠A=30°，以点A为圆心，AD的长为半径画弧交AB于点E，连接CE，则阴影部分的面积是（）A． B． C． D．5、如图，在△ABC 中，AB=5，AC=3，BC=4，将△ABC 绕点A 逆时针旋转30°后得到△ADE ，点B 经过的路径为，则图中阴影部分的面积为（）A ．πB ．πC ．πD ．π6、如图,把直角△ABC 的斜边AC 放在定直线l 上，按顺时针的方向在直线l 上转动两次，使它转到△A 2B 2C 2的位置，设AB=，BC=1，则顶点A 运动到点A 2的位置时，点A 所经过的路线为 ( )sA 、（ +）πB 、（ +）π/C 、2πD 、π27、一圆锥的底面直径为4cm ，高为cm ，则此圆锥的侧面积为（）A ．20πcm 2B ．10πcm 2C ．4πcm 2D ．4πcm 28、圆锥底面圆的半径为3cm ，其侧面展开图是半圆，则圆锥母线长为（） A ．3cm B ．6cm C ．9cm D ．12cm二、填空题9、半径为3，弧长为4的扇形面积为．10、.如果一个扇形的弧长等于它的半径，那么此扇形称为“等边扇形”.则半径为2的“等边扇形”的面积为 .11、如果圆锥的底面周长是20π，侧面展开后所得的扇形的圆心角为120°，则圆锥的母线长是．12、小丽在手工制作课上，想用扇形卡纸制作一个圣诞帽，卡纸的半径为30cm，面积为300πcm2，则这个圣诞帽的底面半径为cm．13、如图，AB⊥BC，AB＝BC＝2 cm，弧OA与弧OC关于点O成中心对称，则AB、BC、弧OC、弧OA所围成的面积是_______cm2．14、如图，在Rt△ABC中，∠C＝90°，∠BAC＝60°，将△ABC绕点A逆时针旋转60°后得到△ADE，若AC＝1，则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是___(结果保留π)．15、如图，正方形ABCD的边长为1cm，以CD为直径在正方形内画半圆，再以C为圆心，1cm长为半径画弧BD，则图中阴影部分的面积为．16、如图，某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心，AB为半径的扇形（忽略铁丝的粗细），则所得的扇形DAB的面积为．17、如图，在扇形OAB中，∠AOB=110°，半径OA=18，将扇形OAB沿过点B的直线折叠，点O恰好落在上的点D处，折痕交OA于点C，则的长为．18、如图，在Rt△ABC中，∠ACB=90°，AC=BC=2，以点A为圆心，AC的长为半径作交AB于点E，以点B为圆心，BC的长为半径作交AB于点D，则阴影部分的面积为．三、简答题19、如图，AB是⊙O的直径，C是⊙O上一点，OD⊥BC于点D，过点C作⊙O的切线，交OD的延长线于点E，连接BE．(1)求证：BE与⊙O相切；(2)设OE交⊙O于点F，若DF=1，BC=，求阴影部分的面积．20、如图，已知AB是⊙O的直径，点C、D在⊙O上，点E在⊙O外，∠EAC=∠D=60°．（1）求∠ABC的度数；（2）求证：AE是⊙O的切线；（3）当BC=4时，求劣弧AC的长．21、如图，AB是⊙O的直径，弦DE垂直平分半径OB，垂足为M，DE=4，连接AD，过E作AD平行线交AB延长线于点C．（1）求⊙O的半径；（2）求证：CE是⊙O的切线；（3）若弦DF与直径AB交于点N，当∠DNB=30°时，求图中阴影部分的面积．22、某班课题学习小组对无盖的纸杯进行制作与探究，所要制作的纸杯如图1所示，规格要求是：杯口直径AB=6cm，杯底直径CD=4cm，杯壁母线AC=BD=6cm．请你和他们一起解决下列问题：（1）小顾同学先画出了纸杯的侧面展开示意图（如图2，忽略拼接部分），得到图形是圆环的一部分．①图2中弧EF的长为cm，弧MN的长为cm；②要想准确画出纸杯侧面的设计图，需要确定弧MN所在圆的圆心O，如图3所示．小顾同学发现有=，请你帮她证明这一结论．③根据②中的结论，求弧MN所在圆的半径r及它所对的圆心角的度数n．（2）小顾同学计划利用正方形纸片一张，按如图甲所示的方式剪出这个纸杯的侧面，求正方形纸片的边长．参考答案一、选择题1、D2、D．3、A【考点】MO：扇形面积的计算．【分析】阴影部分的面积=S扇形ACD﹣S△ACE，根据面积公式计算即可．【解答】解：∵∠BDC=30°，∴∠BAC=60°，∵AC=AB，∴△ABC是等边三角形，∵∠BAD=105°，∴∠CAE=105°﹣60°=45°，∵CE⊥AD，AC=AB=2，∴AE=CE=2，∴S△ACE=2，S扇形ACD==π，∴阴影部分的面积为S扇形ACD﹣S△ACE=π﹣2，故选A．【点评】本题考查了三角形和扇形的面积公式及三角函数值，得到阴影部分的面积=S扇形ACD﹣S△ACE是解题的关键．4、A【考点】MO：扇形面积的计算；L5：平行四边形的性质．【分析】根据题意可以得到平行四边形底边AB上的高，由图可知图中阴影部分的面积是平行四边形的面积减去扇形的面积和△EBC的面积．【解答】解：作DF⊥AB于点F，∵AD=2，∠A=30°，∠DFA=90°，∴DF=1，∵AD=AE=2，AB=4，∴BE=2，∴阴影部分的面积是：4×1﹣=3﹣，故选A．5、A 【考点】MO ：扇形面积的计算；KS ：勾股定理的逆定理；R2：旋转的性质．【分析】根据AB=5，AC=3，BC=4和勾股定理的逆定理判断三角形的形状，根据旋转的性质得到△AED 的面积=△ABC 的面积，得到阴影部分的面积=扇形ADB 的面积，根据扇形面积公式计算即可．【解答】解：∵AB=5，AC=3，BC=4， ∴△ABC 为直角三角形，由题意得，△AED 的面积=△ABC 的面积，由图形可知，阴影部分的面积=△AED 的面积+扇形ADB 的面积﹣△ABC 的面积，∴阴影部分的面积=扇形ADB 的面积==，故选：A ．6、B7、B 【考点】MP ：圆锥的计算．【分析】利用勾股定理易得圆锥母线长，那么圆锥的侧面积=底面周长×母线长÷2．【解答】解：圆锥的底面直径为4cm ，高为cm ，则底面半径=2cm ，底面周长=4πcm ，由勾股定理得，母线长=5cm ，侧面面积=×4π×5=10πcm 2．故选B ．8、B二、填空题9、 6 ．【考点】扇形面积的计算．【分析】由扇形面积公式S=lR 进行计算．【解答】解：由题意得：S=×4×3=6．故答案是：6．10、；11、；12、10分析：由圆锥的几何特征，我们可得用半径为30cm，面积为300πcm2的扇形卡纸制作一个圣诞帽，则圆锥的底面周长等于扇形的弧长，据此求得圆锥的底面圆的半径．解：设卡纸扇形的半径和弧长分别为R、l，圣诞帽底面半径为r，则由题意得R=30，由Rl=300π得l=20π；由2πr=l得r=10cm．故答案是：10．13、214、_解析：∵∠C＝90°，∠BAC＝60°，AC＝1，∴AB＝2，扇形BAD的面积为：＝，在直角△ABC中，BC＝AB·sin60°＝2×＝，AC＝1，∴S△ABC＝S△ADE＝AC·BC＝×1×＝，扇形CAE的面积是：＝，∵S△ADE＝S△ABC，则阴影部分的面积是：S扇形DAB＋S△ABC－S△ADE－S扇形ACE＝－＝15、cm2．【考点】扇形面积的计算；正方形的性质．【分析】根据题意有S阴影部分=S扇形BCD﹣S半圆CD，然后根据扇形的面积公式：S=和圆的面积公式分别计算扇形和半圆的面积即可．【解答】解：根据题意得，S阴影部分=S扇形BAD﹣S半圆BA，∵S扇形BCD=，S半圆CD=π（）2=，∴S阴影部分=﹣=．故答案为：cm216、9 ．【考点】扇形面积的计算．【分析】由正方形的边长为3，可得弧BD的弧长为6，然后利用扇形的面积公式：S扇形DAB=lr，计算即可．【解答】解：∵正方形的边长为3，∴弧BD的弧长=6，∴S扇形DAB=lr=×6×3=9．故答案为：9．【点评】此题考查了扇形的面积公式，解题的关键是：熟记扇形的面积公式S扇形DAB=lr．17、5π．【考点】MN：弧长的计算；PB：翻折变换（折叠问题）．【分析】如图，连接OD．根据折叠的性质、圆的性质推知△ODB是等边三角形，则易求∠AOD=110°﹣∠DOB=50°；然后由弧长公式弧长的公式l=来求的长．【解答】解：如图，连接OD．根据折叠的性质知，OB=DB．又∵OD=OB，∴OD=OB=DB，即△ODB是等边三角形，∴∠DOB=60°．∵∠AOB=110°，∴∠AOD=∠AOB﹣∠DOB=50°，∴的长为=5π．故答案是：5π．18、π﹣2 ．【考点】MO：扇形面积的计算；KW：等腰直角三角形．【分析】空白处的面积等于△ABC的面积减去扇形BCD的面积的2倍，阴影部分的面积等于△ABC的面积减去空白处的面积即可得出答案．【解答】解：∵∠ACB=90°，AC=BC=2，∴S△ABC=×2×2=2，S扇形BCD==π，S空白=2×（2﹣π）=4﹣π，S阴影=S△ABC﹣S空白=2﹣4+π=π﹣2，故答案为π﹣2．三、简答题19、（1）证明：连接OC，如图，………1分∵CE为切线，∴OC⊥CE，∴∠OCE=90°，∵OD⊥BC，∴CD=BD，即OD垂直平分BC，∴EC=EB，在△OCE和△OBE中，∴△OCE≌△OBE，∴∠OBE=∠OCE=90°，∴OB⊥BE，∴BE与⊙O相切；………5分（2）解：设⊙O的半径为r，则OD=r﹣1，在Rt△OBD中，BD=CD=BC=，∴（r﹣1）2+（）2=r2，解得r=2，………7分∵BF=，∴∠BOD=60°，∴∠BOC=2∠BOD=120°，………8分在Rt△OBE中，BE=OB=2，∴阴影部分的面积=S四边形OBEC﹣S扇形BOC=2S△OBE﹣S扇形BOC=2××2×2﹣=4﹣π．………10分20、解：（1）∵∠ABC与∠D都是弧AC所对的圆周角，∴∠B=∠D=60°.（2）∵AB是⊙O的直径，∴∠ACB=90°．又∠B=60°∴∠BAC=30°. ∴∠BAE=∠BAC+∠EAC=30°+60°=90°，即BA⊥AE.∴AE是⊙O的切线.（3）如图，连接OC，∵∠ABC=60°，∴∠AOC=120°.∴劣弧AC的长为＝π．21、22、【考点】圆的综合题．【专题】综合题．【分析】（1）①直接根据圆的周长公式计算；②设它所对的圆心角的度数为n ，根据弧长公式得到的长=，的长=，然后把它们相比即可得到=；③由（2）中的结论得到得==，加上OF=ON+6，可求得ON=12，再利用弧长公式得到=4π，于是可求出n=60°；（2）如图4，连结EF ，OB ，它们相交于点P ，先证明△OEF 为等边三角形得到EF=OF=18，再证明Rt △AOE ≌Rt △COF 得到AE=CF ，则BE=BF ，于是可判断OB 垂直平分EF ，所以PF=EF=9，由勾股定理计算出OP==9，由△PFB 为等腰直角三角形和得到PB=PF=9，则OB=9+9，然后根据正方形的性质得OC=OB=．【解答】（1）解：①如图2，弧EF 的长为6πcm ，弧MN 的长为4πcm ；故答案为6π，4π；②证明：如图3，设它所对的圆心角的度数为n ，的长=，的长=，所以=；③由（2）得==，而OF=ON+6，解得ON=12，即r=12，因为=4π，解得n=60°；（2）解：如图4，连结EF，OB，它们相交于点P，∵四边形ABCD为正方形，∴OA=OC，∠OBC=45°，∵∠OEF=60°，OE=OF，∴△OEF为等边三角形，∴EF=OF=18，在Rt△AOE和Rt△COF中，，∴Rt△AOE≌Rt△COF，∴AE=CF，∴BE=BF，∴OB垂直平分EF，∴PF=EF=9，∴OP==9，∵△PFB为等腰直角三角形，∴PB=PF=9，∴OB=9+9，∴OC=OB=，即正方形纸片的边长为cm．【点评】本题考查了圆的综合题：熟练掌握圆的有关性质和正方形的性质；记住弧长公式；学会把几何题展开成平面图形的方法解决几何体的问题．。

人教版九年级数学上册《24.4弧长和扇形面积》同步测试题及答案

人教版九年级数学上册《24.4弧长和扇形面积》同步测试题及答案学校:___________姓名：___________班级：___________考号：___________一、单选题1．在半径为1的⊙O 中，120°的圆心角所对的弧长是（） A ．3π B ．23π C ．πD ．32π 2．用一个圆心角为150°，半径为12的扇形作一个圆锥的侧面，则这个圆锥的底面半径为（） A ．2.5B ．5C ．6D ．103．将一半径为6的圆形纸片，沿着两条半径剪开形成两个扇形．若其中一个扇形的弧长为5π，则另一个扇形的圆心角度数是多少？（） A ．30B ．60C ．105D ．2104．若圆锥的底面直径为6cm ，侧面展开图的面积为215πcm ，则圆锥的母线长为（） A ．5cm 2B ．2cm 5C ．3cmD ．5cm5．如图，在⊙ABC 中，AB=AC=，BC=2，以A 为圆心作圆弧切BC 于点D ，且分别交边AB 、AC 于E 、F ，则扇形AEF 的面积是（）A ．B ．C ．D ．6．用一个圆心角为120°，半径为4的扇形，做一个圆锥的侧面，则这个圆锥的全面积（侧面与底面面积的和）为（） A ．563πB ．643πC ．569πD ．649π二、填空题7．已知扇形的弧长为6π，它的圆心角为120，则该扇形的半径为． 8．圆锥底面圆的半径2cm r =，母线长为6cm ，则圆锥全面积为．9．如图，扇形OAB 的圆心角为30︒，半径为1，将它在水平直线上向右无滑动滚动到'''O A B 的位置时，则点O 到点'O 所经过的路径长为．10．如图，O 的直径6AB =，圆内接ACD 中，AC=CD ，30CAD ∠=︒则阴影部分的面积为．三、解答题11．（本小题满分10分）如图，已知扇形的半径为15cm ，⊙AOB=120°．（1）求扇形的面积；（2）用这扇形围成圆锥的侧面，求该圆锥的高和底面半径．12．如图，AB 是⊙O 的直径，BC 切⊙O 于点B ，OC 交⊙O 于点D 的半径为3 20C ∠=︒.（1）求A ∠的度数；（2）求AD 的长．(结果保留π)参考答案题号 1 2 3 4 5 6 答案BBDDB D1．【答案】B【分析】根据弧长公式可知弧长．【详解】解： l =120121803ππ⨯=. 故选B ． 2．【答案】B【分析】根据弧长公式先计算出扇形的弧长，再根据圆锥的底面周长等于这个扇形的弧长即可求解．【详解】解：由题意知：扇形的弧长＝1501210180ππ⨯= 设圆锥的底面半径为R ，圆锥的底面周长等于扇形的弧长 ⊙2πR ＝10π ∴R ＝5 故选：B ．【点睛】本题考查了扇形的弧长公式及圆锥的展开图，属于基础题，熟练掌握扇形弧长的计算公式是解题的关键． 3．【答案】D【分析】根据题意可知两个扇形的弧长之和就是圆的周长，则可以求得另一个扇形的弧长，再根据弧长公式求解即可．【详解】解：由题意可求得圆的周长2612C ⨯＝＝ππ 其中一个扇形的弧长15L ＝π，则另一个扇形的弧长21257L -＝＝πππ 设另一个扇形的圆心角度数为n ︒ 根据弧长公式：180n rL ＝π，有： 67180n ⨯＝ππ，解得210n ＝故选：D ．【点睛】本题考查弧长的计算，解题关键是理解题意，正确应用弧长公式进行计算．【分析】已知圆锥底面圆的半径可求出侧面展开图的弧长，根据侧面展开图的面积即可求解．【详解】如图所示⊙圆锥的底面直径为6cm ⊙圆锥的底面半径为3cm⊙圆锥的底面圆周长是2π6πC r == ⊙侧面展开图的面积为215πcm⊙侧面展开图的面积116π15π22S l C l ==⨯=⊙圆锥的母线长为5l = 故选：D ．【点睛】本题主要考查圆锥侧面展开图的面积，理解掌握面积公式的计算方法是解题的关键． 5．【答案】B【详解】试题分析：先判断出⊙ABC 是等腰直角三角形，从而连接AD ，可得出AD=1，直接代入扇形的面积公式进行运算即可． ⊙AB=AC=，BC=2⊙AB 2+AC 2=BC 2⊙⊙ABC 是等腰直角三角形连接AD ，则AD=BC=1则S 扇形AEF =故选B ．考点：1.扇形面积的计算；2.等腰直角三角形．【分析】先求出圆锥的侧面积和底面半径，再求圆锥的表面积，由此即可求出这个圆锥的表面积．【详解】解：圆锥的侧面积＝π×42×120?360?＝163π圆锥的底面半径＝2π×4×120?360?÷2π＝43圆锥的底面积＝π×(43)2＝169π圆锥的表面积＝侧面积＋底面积＝1616=39649πππ+．故选：D ．【点睛】本题考查圆锥的表面积，解题时要认真审题，掌握扇形面积、圆锥底面半径的计算方法是解题的关键． 7．【答案】9【分析】知道弧长，圆心角，直接代入弧长公式L=180n rπ即可求得扇形的半径．【详解】解：⊙扇形的圆心角为120°，它所对应的弧长6π ⊙6π=120180rπ 解得：r=9．故答案为9．【点睛】此题主要考查了扇形弧长的应用，要掌握弧长公式：L=180n rπ才能准确的解题． 8．【答案】216πcm【分析】圆锥的全面积是底面圆的面积与侧面扇形的面积，由此即可求解．【详解】解：如图所示，圆锥底面圆的半径2cm r =，母线长为6cm⊙底面圆的周长为2π2π24πcm r =⨯=，底面圆的面积为222ππ24πcm r ==，侧面扇形的面积为214π612πcm 2⨯= ⊙圆锥的全面积为24π12π16πcm +=故答案为：216πcm ．【点睛】本题主要考查立体几何图形的面积，掌握圆锥面积是底面圆面积与侧面扇形的面积之和是解题的关键． 9．【答案】76π【分析】点O 到点O ′所经过的路径长分三段，先以A 为圆心，1为半径，圆心角为90度的弧长，再平移了AB 弧的长，最后以B 为圆心，1为半径，圆心角为90度的弧长．根据弧长公式计算即可．【详解】解：⊙扇形OAB 的圆心角为30°，半径为1 ⊙AB 弧长＝301180π⨯⨯＝6π⊙点O 到点O ′所经过的路径长＝90172=18066πππ⨯⨯⨯+ 故答案为：76π. 【点睛】本题考查了弧长公式，旋转的性质和圆的性质，理解点O 到点O ′所经过的路径长分三段是解题的关键．10．【答案】9332π 【分析】连接OC 、OD ，交AD 与点K ，根据AC CD =，30CAD ∠=︒得到1230∠=∠=︒ AOC ∆ COD ∆为等边三角形，证明出四边形ACDO 为菱形，，进而求出阴影部分的面积．【详解】解：连接OC 、OD ，交AD 与点K ，如图所示：⊙AC CD = 30CAD ∠=︒ ⊙1230∠=∠=︒⊙32260∠=∠=︒ 42160∠=∠=︒ ⊙AO OC OD ==⊙AOC ∆，COD ∆为等边三角形 ⊙OA OD OC AC CD ==== ⊙四边形ACDO 为菱形⊙CO AD ⊥ ⊙360∠=︒ ⊙530∠=︒⊙AB 为圆O 直径为6 ⊙3AO = ⊙1322OK AO == ∴22333()322AK =-= 23CO KO ==∴233AD AK ==⊙19322ACDO S AD CO =⋅=菱形312033360AOD S ππ=⨯⨯=扇形 ⊙9332S π=阴【点睛】本题考查了求扇形阴影部分的面积，正确作出辅助线是解题的关键． 11．【答案】（1）150π平方厘米（2）r=10cm ；5cm 【分析】（1）根据扇形的面积公式S=2360n r π，代值计算即可（2）利用弧长公式可求得扇形的弧长，除以2π即为圆锥的底面半径，再利用勾股定理求得高即可.【详解】解：（1）⊙S=2360n r π ⊙S=224015360π⨯=150πcm 2（2）⊙弧长=24015180π⨯=20π ⊙2πr=20π，r=10cm⊙圆锥的高221510-55cm ）【点睛】本题考查了扇形的面积公式以及圆锥有关计算，解本题的关键是掌握圆锥的侧面展开图的弧长等于圆锥的底面周长.12．【答案】（1） 35A ∠=︒；（2）弧AD 的长为116π. 【分析】（1）由切线性质结合已知得70BOD ∠=︒，根据⊙OAD 是等腰三角形即可计算出⊙A =35°.（2）由（1）可知⊙AOC =110°，根据弧长公式即可计算. 【详解】解：（1）BC 是⊙O 的切线90B ∴∠=︒.又⊙⊙C =20°.902070BOC ∴∠=︒-︒=︒⊙OA =OD ⊙⊙A =⊙ADO1 352A BOC ∴∠=∠=︒（2）180AOC BOC ∠=︒-∠18070110AOC ∴∠=︒-︒=︒∴弧AD 的长为110111806ππ=. 【点睛】本题考查了切线的性质，等腰三角形的性质，弧长的计算等知识点，能求出⊙BOC 的度数是解此题的关键，注意：圆的切线垂直于过切点的半径．。

人教版九年级上数学册24.4弧长和扇形面积同步练习含答案

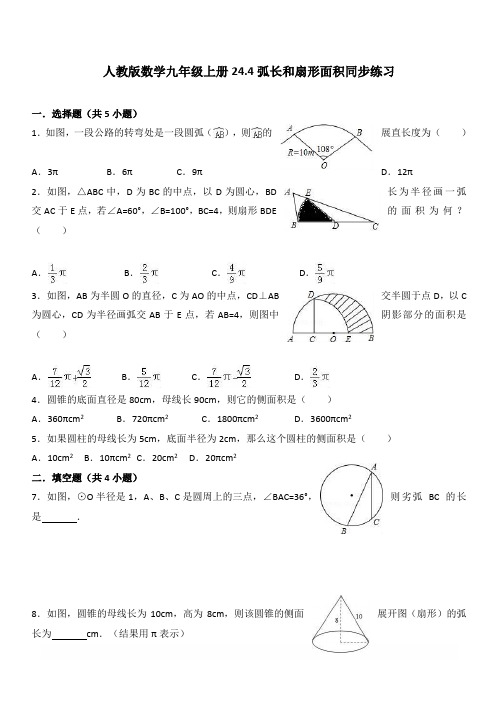
人教版数学九年级上册24.4弧长和扇形面积同步练习一．选择题（共5小题）1．如图，一段公路的转弯处是一段圆弧（），则的展直长度为（）A．3πB．6πC．9πD．12π2．如图，△ABC中，D为BC的中点，以D为圆心，BD长为半径画一弧交AC于E点，若∠A=60°，∠B=100°，BC=4，则扇形BDE的面积为何？（）A．B．C．D．3．如图，AB为半圆O的直径，C为AO的中点，CD⊥AB交半圆于点D，以C为圆心，CD为半径画弧交AB于E点，若AB=4，则图中阴影部分的面积是（）A．B．C．D．4．圆锥的底面直径是80cm，母线长90cm，则它的侧面积是（）A．360πcm2 B．720πcm2C．1800πcm2D．3600πcm25．如果圆柱的母线长为5cm，底面半径为2cm，那么这个圆柱的侧面积是（）A．10cm2B．10πcm2C．20cm2D．20πcm2二．填空题（共4小题）7．如图，⊙O半径是1，A、B、C是圆周上的三点，∠BAC=36°，则劣弧BC的长是．8．如图，圆锥的母线长为10cm，高为8cm，则该圆锥的侧面展开图（扇形）的弧长为cm．（结果用π表示）9．用一块圆心角为216°的扇形铁皮，做一个高为40cm的圆锥形工件（接缝忽略不计），那么这个扇形铁皮的半径是cm．10．如图，两圆半径均为1，且图中两块阴影部分的面积相等，那OO1的长度是．三．解答题（共4小题）11．如图所示，将直角△ABC向下旋转90°，已知BC=5厘米，AB=4厘米，AC=3厘米，求△ABC扫过的面积．12．如图，在矩形ABCD中，点F在边BC上，且AF=AD，过点D作DE⊥AF，垂足为点E．（1）求证：DE=AB；（2）以D为圆心，DE为半径作圆弧交AD于点G，若BF=FC=1，试求的长．13．如图，锚标浮筒是打捞作业中用来标记锚或沉船位置的，它的上下两部分是圆柱，中间是一个圆柱（如图，单位：mm）．电镀时，如果每平方米用锌0.11kg，要电镀1000个这样的锚标浮筒需要用多少锌？（精确到1kg）14．已知如图，在直角坐标系xOy中，点A，点B坐标分别为（﹣1，0），（0，），连结AB，OD由△AOB绕O点顺时针旋转60°而得．（1）求点C的坐标；（2）△AOB绕点O顺时针旋转60°所扫过的面积；（3）线段AB绕点O顺时针旋转60°所扫过的面积．参考答案一．选择题 1．B ． 2．C ． 3．A ． 4．D ． 5．D ．二．填空题7．=π．8．12π． 9．50．10．．三．解答题 11．解：∵将此三角形绕点A 顺时针旋转90°到直角△AB′C′的位置， ∴∠BAB′=90°，∴直角△ABC 扫过的面积是：S 扇形BAB′+S △ACB′=+×3×4=+6．12．（1）证明：∵四边形ABCD 是矩形， ∴∠B=∠C=90°，AB=DC ，BC=AD ，AD ∥BC ， ∴∠EAD=∠AFB ， ∵DE ⊥AF ， ∴∠AED=90°，在△ADE 和△FAB 中，，∴△ADE ≌△FAB （AAS ），∴DE=AB；（2）连接DF，如图所示：在△DCF和△ABF中，，∴△DCF≌△ABF（SAS），∴DF=AF，∵AF=AD，∴DF=AF=AD，∴△ADF是等边三角形，∴∠DAE=60°，∵DE⊥AF，∴∠AED=90°，∴∠ADE=30°，∵△ADE≌△FAB，∴AE=BF=1，∴DE=AE=，∴的长=．13．解：由图形可知圆锥的底面圆的半径为0.4m，圆锥的高为0.3m，则圆锥的母线长为：=0.5m．∴圆锥的侧面积S1=π×0.4×0.5=0.2π（m2），∵圆柱的高为0.8m．圆柱的侧面积S2=2π×0.4×0.8=0.64π（m2），∴浮筒的表面积=2S1+S2=1.04π（m2），∵每平方米用锌0.11kg，∴一个浮筒需用锌：1.04π×0.11kg，∴1000个这样的锚标浮筒需用锌：1000×1.04π×0.11=11.44π≈359（kg）．答：1000个这样的锚标浮筒需用锌359kg．14．解：（1）如图1，过C作CE⊥OA于E，∵点A，点B坐标分别为（﹣1，0），（0，），∴OA=1，OB=，∵△AOB绕点O顺时针旋转60°得到△COD，∴∠AOC=∠BOD=60°，AO=OC=1，∴OE=OC=，CE=OC=，∴C（﹣，）；（2）△AOB绕点O顺时针旋转60°所扫过的面积=++×=π+；（3）如图2，线段AB绕点O顺时针旋转60°所扫过的面积═（﹣1×）+（﹣）+（﹣）=π﹣．。

人教版九年级数学上册《24.4 弧长和扇形面积》同步测试题及答案

人教版九年级数学上册《24.4 弧长和扇形面积》同步测试题及答案学校:___________班级：___________姓名：___________考号：___________一、选择题：1.若用半径为6，圆心角为120°的扇形纸片围成一个圆锥的侧面，则这个圆锥的底面圆半径为( )A. 1B. 2C. 3D. 42.如图，圆锥的底面半径为2，母线长为6，则侧面积为( )A. 4πB. 6πC. 12πD. 16π3.若将半径为10cm的半圆形纸片围成一个圆锥的侧面，则这个圆锥的底面圆半径为( )A. 5cmB. 4cmC. 3cmD. 2cm4.一个圆锥的侧面积是底面积的2倍，则该圆锥侧面展开图的圆心角的度数是( )A. 120∘B. 180∘C. 240∘D. 300∘5.在半径为1的⊙O中，120°的圆心角所对的弧长是( )A. π3B. 2π3C. πD. 3π26.如图，在扇形AOB中，AC为弦∠AOB=140°，∠CAO=60°，OA=6，则BC⏜的长为( )A. 4π3B. 8π3C. 2√ 3πD. 2π7.如图，△ABC内接于⊙O，∠B=65°，∠C=70°.若BC=2√ 2，则BC⏜的长为( )A. πB. √ 2πC. 2πD. 2√ 2π8.如图，长方形的长为3cm、宽为2cm，分别以该长方形的长、宽所在直线为轴，将其旋转1周，形成甲、乙两个圆柱，其体积分别记作V甲、V乙，侧面积分别记作S甲、S乙，则下列说法正确的是 ( )A. V甲<V乙，S甲=S乙B. V甲>V乙，S甲>S乙C. V甲=V乙，S甲=S乙D. V甲>V乙，S甲<S乙9.如图，从一块直径为2m的圆形铁皮上剪出一个圆心角为90°的扇形，则此扇形的面积为( )A. π2m2 B. √ 32πm2 C. πm2 D. 2πm2二、填空题：10.扇形的半径为3cm，弧长为2πcm，则该扇形的面积为______cm2．11.已知一个圆锥的底面直径为20cm，母线长30cm，则这个圆锥的表面积是(结果保留π)12.如图，△ABC的外接圆O的半径为3，∠C=55°，则劣弧AB⏜的长是______.(结果保留π)13.一个扇形的圆心角为135°，弧长为3πcm，则此扇形的面积是cm2．14.在Rt△ABC中∠C=90°，AC=3，BC=4，把它沿斜边AB所在直线旋转一周，所得几何体的侧面积是______.(结果保留π)三、解答题：15.如图，AB是⊙O的直径，点C、D均在⊙O上∠ACD=30°，弦AD=4cm．(1)求⊙O的直径．(2)求AD⏜的长．16.如图，AB是⊙O的直径，BC是⊙O的弦，半径OD⊥BC，垂足为E，若BC=6√ 3，DE=3.求：(1)⊙O的半径；(2)弦AC的长；(3)阴影部分的面积．17.图 ①是一个长为4cm，宽为3cm的长方形纸片．(1)若将此长方形纸片绕长边或短边所在直线旋转一周，形成的几何体是，这能说明的事实是;(2)当此长方形纸片绕长边所在直线旋转一周时(如图 ②)，求所形成的几何体的体积;(3)当此长方形纸片绕短边所在直线旋转一周时(如图 ③)，求所形成的几何体的体积．18.如图，在等腰△ABC中∠BAC=120°，AD是∠BAC的角平分线，且AD=6，以点A为圆心，AD长为半径画弧EF，交AB于点E，交AC于点F．(1)求由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积；(2)将阴影部分剪掉，余下扇形AEF，将扇形AEF围成一个圆锥的侧面，AE与AF正好重合，圆锥侧面无重叠，求这个圆锥的高ℎ．19.如图，已知△ABC是⊙O的内接三角形，AD是⊙O的直径，连结BD，BC平分∠ABD．(1)求证：∠CAD=∠ABC；(2)若AD=6，求CD⏜的长．参考答案和解析1.【答案】B【解析】【分析】根据弧长公式求出扇形弧长，根据圆的周长公式计算，得到答案．本题考查的是圆锥的计算，正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键．【解答】=4π解：扇形的弧长=120π×6180∴圆锥的底面圆的周长=4π∴圆锥的底面圆半径=4π=22π故选：B．2.【答案】C【解析】解：根据圆锥的侧面积公式可得πrl =π×2×6=12π．故选C ．本题主要考查圆锥侧面积的计算．根据圆锥的底面半径为2，母线长为6，直接利用圆锥的侧面积公式即可求出它的侧面积．3.【答案】A【解析】【分析】本题考查了圆锥的计算．用到的知识点为：圆锥的弧长等于底面周长．易得圆锥的母线长为10cm ，以及圆锥的侧面展开图的弧长，也就是圆锥的底面周长，除以2π即为圆锥的底面半径．【解答】解：圆锥的侧面展开图的弧长为2π×10÷2=10π(cm)∴圆锥的底面半径为10π÷2π=5(cm)故选A ．4.【答案】B【解析】【分析】本题考查的是圆锥的计算，正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键，圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长．根据圆锥的侧面积是底面积的2倍可得到圆锥底面半径和母线长的关系，利用圆锥侧面展开图的弧长=底面周长即可得到该圆锥的侧面展开图扇形的圆心角度数．【解答】解：设该圆锥底面圆的半径为r ，母线长为l ，圆锥侧面展开图的圆心角的度数为n ∘由圆锥的侧面积是底面积的2倍，得nπl 2360=12⋅2πr ⋅l =2πr 2,∴l =2r,n =180．故选B ．5.【答案】B【解析】【分析】本题主要考查了扇形的弧长公式，这个公式要牢记，弧长公式为：l =nπr 180根据弧长公式可知弧长．【解答】解：∵⊙O 的半径为1，圆心角是120°∴所对的弧长l =120π⋅1180=2π3．故选B ． 6.【答案】B本题考查的是弧长的计算，等边三角形的判定和性质，属于基础题．连接OC，根据等边三角形的性质得到∠BOC=80°，根据弧长公式计算即可．【解答】解：连接OC∵OA=OC∴△AOC为等边三角形∴∠AOC=60°∴∠BOC=∠AOB−∠AOC=140°−60°=80°则BC⏜的长=80π×6180=8π3故选：B．7.【答案】A【解析】【分析】本题考查圆周角定理，弧长公式，等腰直角三角形的性质的等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．连接OB,OC.首先证明△OBC是等腰直角三角形，求出OB即可解决问题．【解答】解：连接OB,OC．∵∠A=180°−∠ABC−∠ACB=180°−65°−70°=45°∴∠BOC=90°∵BC=2√ 2∴OB=OC=2∴BC⏜的长为90×π×2180=π故选：A．8.【答案】A根据圆柱体的体积=底面积×高求解，再利用圆柱体侧面积求法得出答案．此题主要考查了面动成体，关键是掌握圆柱体的体积和侧面积计算公式．【解答】解：由题可得V甲=π⋅22×3=12πV乙=π⋅32×2=18π∵12π<18π∴V甲<V乙；∵S甲=2π×2×3=12πS乙=2π×3×2=12π∴S甲=S乙故选：A．9.【答案】A【解析】解：如图所示，连接AC∵从一块直径为2m的圆形铁皮上剪出一个圆心角为90°的扇形，即∠ABC=90°∴AC为⊙O直径，即AC=2m,AB=BC(扇形的半径相等)∵AB2+BC2=AC2=22∴AB=BC=√ 2m∴阴影部分的面积是90π×(√ 2)2360=π2m2．故选A．本题考查圆周角定理和扇形面积的计算．连接AC，根据圆周角定理得出AC为圆的直径，解直角三角形求出AB，根据扇形面积公式即可求出．10.【答案】3π【解析】解：S 扇形=12×3×2π=3πcm 2．故答案为3π．本题考查的是扇形面积的计算，直接利用扇形面积公式计算即可． 11.【答案】400πcm 2【解析】【分析】根据圆锥表面积=侧面积+底面积=12底面周长×母线长+底面积，计算即可．本题考查了圆锥的计算，解决本题的关键记准圆锥的侧面面积和底面面积公式．【解答】解：圆锥的表面积=12×20π×30+100π=400πcm 2．故答案为：400πcm 2． 12.【答案】11π6【解析】【分析】本题考查了同弧所对的圆心角是圆周角的2倍，弧长公式，关键是熟练运用弧长公式解决问题．根据同弧所对的圆心角是圆周角的2倍，可求∠AOB =110°，根据弧长公式可求劣弧AB⏜的长．【解答】解：∵∠AOB =2∠C 且∠C =55°∴∠AOB =110°根据弧长公式AB⏜的长=3×110×π180=11π6 故答案为11π6． 13.【答案】6π【解析】【分析】本题考查了扇形的面积计算和弧长的计算，能熟记扇形的面积公式和弧长公式是解此题的关键．先求出扇形对应的圆的半径，再根据扇形的面积公式求出面积即可．【解答】解：设扇形的半径为Rcm∵扇形的圆心角为135°，弧长为3πcm∴135π×R 180=3π 解得：R =4所以此扇形的面积为135π×42360=6π(cm 2)故答案为6π．14.【答案】845π【解析】解：作CD⊥AB于D，如图∵∠ACB=90°,AC=3∴AB=√ 32+42=5∵12×CD×AB=12×AC×BC ∴CD=3×45=125把Rt△ABC沿斜边AB所在直线旋转一周，所得几何体为两个圆锥，它们的底面为以D点为圆心，DC为半径的圆∴这个几何体的侧面积=12×2π×125×3+12×2π×125×4=845π.故答案为845π.作CD⊥AB于D，如图，利用勾股定理计算出AB=5，再根据面积法计算出CD=125，由于把Rt△ABC沿斜边AB所在直线旋转一周，所得几何体为两个圆锥，它们的底面为以D点为圆心，DC为半径的圆，所以利用扇形的面积公式计算两个圆锥的侧面积即可．本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．15.【答案】解：(1)∵AB是⊙O的直径∴∠ADB=90°．∵同弧所对的圆周角相等∴∠ABD=∠ACD=30°．∵AD=4∴AB=8．∴⊙O的直径为8cm．(2)连结OD，则∠AOD=2∠ACD=60°．∴AD⏜的长为60π×4180=4π3．【解析】(1)利用30度的角所对的边是斜边的一半进行计算；(2)连结OD，则∠AOD=2∠ACD=60°，然后利用面积公式计算．本题考查的是圆周角定理、弧长公式，掌握周角定理、弧长公式是解题的关键．16.【答案】解：(1)∵半径OD⊥BC∴CE=BE∵BC=6√ 3∴CE=3√ 3设OC=x，在直角三角形OCE中∴x2=(3√ 3)2+(x−3)2∴x=6即半径OC=6；(2)∵AB为直径∴∠ACB=90°又∵BC=6√ 3∴AC2=AB2−BC2=36∴AC=6；(3)∵OA=OC=AC=6∴∠AOC=60°∴S阴=S扇−S△OAC=60×π×62360−12×6×√ 62−32=6π−9√ 3．【解析】此题考查扇形面积的计算，阴影部分的面积可以看作是扇形的面积减去三角形的面积，求不规则的图形的面积，可以转化为几个规则图形的面积的和或差来求．(1)半径OD⊥BC，所以由垂径定理知：CE=BE，在直角△OCE中，根据勾股定理就可以求出OC的值；(2)根据AB是⊙O的直径，得到∠ACB=90°，因而在直角三角形ABC中根据勾股定理得到AC的长；(3)阴影部分的面积就是扇形OCA的面积减去△OAC的面积．17.【答案】解：(1)圆柱；面动成体；(2)绕长边所在直线旋转一周得到的圆柱的底面半径为3cm，高为4cm体积=π×32×4=36π(cm3)；(3)绕短边所在直线旋转一周得到的圆柱的底面半径为4cm，高为3cm体积=π×42×3=48π(cm3).【解析】【分析】本题考查了点、线、面、体的知识，熟记常见平面图形旋转可得到什么立体图形是解决本题的关键，另外要掌握圆柱的体积计算公式．(1)矩形旋转一周得到圆柱；(2)绕长边旋转得到的圆柱的底面半径为3cm，高为4cm，从而计算体积即可；(3)绕短边旋转得到的圆柱底面半径为4cm，高为3cm，从而计算体积即可．18.【答案】解：∵在等腰△ABC中∴∠B=30°∵AD是∠BAC的角平分线∴AD⊥BC∴BD=√ 3AD=6√ 3∴BC=2BD=12√ 3∴由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积=S△ABC−S扇形EAF =12×6×12√ 3−120⋅π⋅62360=36√ 3−12π；(2)设圆锥的底面圆的半径为r根据题意得2πr=120⋅π⋅6180，解得r=2这个圆锥的高ℎ=√ 62−22=4√ 2．【解析】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．也考查了等腰三角形的性质和扇形的面积公式．(1)利用等腰三角形的性质得到AD⊥BC，BD=CD，则可计算出BD=6√ 3，然后利用扇形的面积公式，利用由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积=S△ABC−S扇形EAF进行计算；(2)设圆锥的底面圆的半径为r，利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和弧长公式得到2πr=120⋅π⋅6180，解得r=2，然后利用勾股定理计算这个圆锥的高ℎ．19.【答案】解：(1)证明：∵BC平分∠ABD∴∠DBC=∠ABC∵∠CAD=∠DBC∴∠CAD=∠ABC；(2)∵∠CAD=∠ABC∴CD⏜=AC⏜∵AD是⊙O的直径∴CD⏜的长=12×12×π×6=32π.【解析】本题考查了三角形的外接圆和外心，圆周角定理，弧长公式等知识，灵活运用这些性质解决问题是本题的关键．(1)由角平分线的定义和圆周角定理可得∠DBC=∠ABC=∠CAD；(2)由圆周角定理可得CD⏜=AC⏜，由弧长公式可求解．。

人教版九年级上册数学弧长和扇形面积同步训练(含答案)

人教版九年级上册数学24.4 弧长和扇形面积同步训练一、单选题1．已知扇形的圆心角为120°，半径为3，则这个扇形的面积是（） A ．π B ．3π C ．4π D ．6π． 2．如图，一扇形纸扇完全打开后，外侧两条竹条AB 、AC 的夹角为120°，AB 长为30cm ，AD ＝10cm ，贴纸部分的面积为（）A ．8003πcm 2B ．5003πcm 2C ．800πcm 2D ．500πcm 2 3．如图，在ABC 中，,30,4AB AC C AC =∠=︒=，以AB 为直径的O 交BC 于点D ，则图中阴影部分的面积为（）A ．π3 B ．2π3 C ．4π3 D ．2π 4．如图，在Rt ABC 中，90C ∠=︒，30A ∠=︒，2BC =．以点C 为圆心，CB 长为半径画弧，分别交AC ，AB 于点D ，E ，则图中阴影部分的面积为（）A ．23πB ．34π-C 13π D 12π 5．如图，O 是ABC 的外接圆，22.5,8ABO ACO BC ∠=∠=︒=，若扇形OBC （图中阴影部分）正好是一个圆锥的侧面展开图，则该圆锥的高为（）AB．C D6．一装有某种液体的圆柱形容器，半径为6cm，高为18cm．小强不小心碰倒，容器水平静置时其截面如图所示，其中圆心O到液面AB的距离为3cm，若把该容器扶正竖直，则容器中液体的高度为（）A BC D7．如图，正六边形ABCDEF的边长为6，以顶点A为圆心，AB长为半径画圆．若图中阴影部分恰好是一个圆锥的侧面展开图，则这个圆锥的底面圆的周长是（）A．2πB．4πC．6πD．16π8．如图，C是O劣弧AB上一点，2OA=，120ACB∠=︒．则劣弧AB的长度为（）A．13πB．23πC．43πD．83π二、填空题9．一个扇形的圆心角为60°，它所对的弧长为2πcm ，则这个扇形所在圆的周长为____________cm ．10．如图，AB OB ⊥，2AB =，4OB =，把ABO ∠绕点O 顺时针旋转60°得CDO ∠，则AB 扫过的面积（图中阴影部分）为________．11．如图，点P 为⊙O 外一点，P A ，PB 分别与⊙O 相切于点A ，B ，90APB ∠=︒，若⊙O 半径为3，则图中阴影部分的面积为__________（结果保留π）12．如图，点A 、B 在半径为3的⊙O 上，劣弧AB 长为π2，则⊙AOB ＝____．13．如图，AB 是⊙O 的直径，BT 是⊙O 的切线，若⊙ATB ＝45°，AB ＝4cm ，则阴影部分的面积是 _________cm 214．如图，在⊙ABC 中，⊙ABC ＝90°，AB ＝BC ＝4，以点C 为圆心，线段CA 长为半径作AD ，交CB 的延长线于点D ，则阴影部分的面积为________（结果保留π）．15．如图，扇形OAB 中，90AOB ∠=︒，以AO 为直径作半圆．若2AO =，则阴影部分图形的周长为_______．16．如图所示，分别以n 边形的顶点为圆心，以3cm 为半径画圆，则图中阴影部分的面积之和为____．三、解答题17．如图，点B C D 、、都在O 上，过点C 作AC //BD 交OB 延长线于点A ，连接CD CO 、，且30,CDB OBD BD ∠=∠=︒=．(1)求证：AC 是O 的切线．(2)求O 的半径长．(3)求由弦CD BD 、与弧BC 所围成的阴影部分的面积（结果保留π）．18．如图，在Rt△ABC中，⊙C=90°，⊙B=30°，点D为边AB的中点，点O在边BC 上，以点O为圆心的圆过顶点C，与边AB交于点D．(1)求证：直线AB是⊙O的切线；(2)若AC19．如图，AB是⊙O的直径，C是⊙O上一点，D是AB延长线上一点，⊙BCD＝⊙A，CA＝CD.(1)求证：CD是⊙O的切线；(2)若BD=2，求图中阴影部分面积.20．如图，C是圆O被直径AB分成的半圆上一点，过点C的圆O的切线交AB的延长线于点P，连接CA，CO，CB．(1)求证：⊙ACO＝⊙BCP；(2)若⊙ABC＝2⊙BCP，求⊙P的度数；(3)在（2）的条件下，若AB＝4，求图中阴影部分的面积（结果保留π和根号）．参考答案：1．B2．A3．B4．A5．D6．B7．B8．C9．12π10．2 3π11．9 94π-12．30°13．414．4π-815．22π+16．29cmπ17．(2)⊙O的半径长为6cm (3)阴影部分的面积为6πcm218．6π19．(2)23 Sπ=阴影20．(2)30°(3)2π﹣答案第1页，共1页。

人教版九年级数学上册24.4弧长和扇形面积同步测试及答案【优】

弧长和扇形面积第1课时弧长和扇形面积 [见B 本P48]1.若扇形的半径为6，圆心角为120°，则此扇形的弧长是( B )A ．3πB ．4πC ．5πD ．6π2．按图24－4－1(1)的方法把圆锥的侧面展开，得到图24－4－1(2)所示的扇形，其半径OA ＝3，120°，则AB ︵的长为( B )(1) 图24－4－1A ．πB ．2πC ．3πD ．4π3．如果一个扇形的半径是1，弧长是π3，那么此扇形的圆心角的大小为( C ) A ．30° B ．45° C ．60° D ．90°4．[2012·兰州]如果一个扇形的弧长等于它的半径，那么此扇形称为“等边扇形”，则半径为2的“等边扇形”的面积为( C )A ．πB ．1C ．2 D.23π 【解析】设扇形的半径为r ，弧长为l ，根据扇形的面积公式得S ＝12lr ＝12r 2＝2. 5．钟面上的分针的长为1，从9点到9点30分，分针在钟面上扫过的面积是( A ) A.12π B.14π C.18π D ．π 【解析】从9点到9点30分分针扫过的扇形的圆心角是180°，则分针在钟面上扫过的面积是：180π×12360＝12π. 6．如图24－4－2，AB 与⊙O 相切于点B ，AO 的延长线交⊙O 于点C ，连接BC ，若∠ABC ＝120°，OC ＝3，则BC ︵的长为( B )3π D ．5π第6【解析】如图，连接OB ，∵AB 与⊙O 相切于点B ，∴∠ABO ＝90°.∵∠ABC ＝120°，∴∠OBC ＝30°.∵OB ＝OC ，∴∠OCB ＝30°，∴∠BOC ＝120°，∴BC ︵的长为n πr 180＝120π×3180＝2π. 7．如图24－4－3，水平地面上有一面积为30π cm 2的扇形OAB ，半径OA ＝6 cm ，且OA 与地面垂直．在没有滑动的情况下，将扇形向右滚动至OB 与地面垂直为止，则O 点移动的距离为( C )图24－4－3A ．20 cmB ．24 cmC ．10π cmD ．30π cm 【解析】点O 移动的距离就是扇形的弧长，设扇形弧长为l ，根据题意可得12l ×6＝30π，解得l ＝10π cm.8．在半径为6 cm 的圆中，60°的圆心角所对的弧长等于__2π__cm(结果保留π)．【解析】弧长为60π×6180＝2π(cm)． 9．一个扇形的圆心角为120°，半径为3，则这个扇形的面积为__3π__(结果保留π)．【解析】由题意得n ＝120°，R ＝3，故S 扇形＝n πR 2360＝120π×32360＝3π.图24－4－4 10．如图24－4－4，AB 切⊙O 于点B ，OA ＝2，∠OAB ＝30°，弦BC ∥OA ，劣弧BC ︵的弧长为__π3__.(结果保留π)11．如图24－4－5，在3×3的方格中(共有9个小格)，每个小方格都是边长为1的正方形，O ，B ，C 是格点，则扇形OBC 的面积等于__54π__(结果保留π)．12. 如图24－4－6，在边长为1的小正方形组成的方格纸上，将△ABC 绕着点A 顺时针旋转90°.(1)画出旋转后的△AB ′C ′；(2)求线段AC 在旋转过程中所扫过的扇形的面积．图24－4－6解：(1)如图；(2)线段AC 在旋转过程中所扫过的扇形的面积＝S 扇形ACC ′＝90π·22360＝π. 13．如图24－4－7，一根5 m 长的绳子，一端拴在围墙墙角的柱子上，另一端拴着一只小羊A (羊)，那么小羊A 在草地上的最大活动区域面积是( D )图24－4－7A.1712π m 2B.176π m 2 C.254π m 2 D.7712π m 2 14．如图24－4－8，△ABC 是正三角形，曲线CDEF 叫做正三角形的渐开线，其中弧CD ，弧DE ，弧EF 的圆心依次是A ，B ，C ，如果AB ＝1，那么曲线CDEF 的长是__4π__．图24－4－815．如图24－4－9，在矩形ABCD 中，AB ＝2DA ，以点A 为圆心，AB 为半径的圆弧交DC 于点E ，交AD 的延长线于点F ，设DA ＝2.(1)求线段EC 的长；(2)求图中阴影部分的面积．图24－4－9解：(1)∵在矩形ABCD 中，AB ＝2DA ，∴AE ＝2AD ，且∠ADE ＝90°.又DA ＝2，∴AE ＝AB ＝4，∴DE ＝AE 2－AD 2＝16－4＝23，∴EC ＝DC －DE ＝4－2 3.(2)S 阴影＝S 扇形AEF －S △ADE ＝60°×π×42360°－12×2×23＝83π－2 3. 16．如图24－4－10，已知AB 是⊙O 的直径，弦CD ⊥AB ，垂足为E ，∠AOC ＝60°，OC ＝2.(1)求OE 和CD 的长；【解析】 ∵∠CAD ，∠DBE ，∠ECF 是等边三角形的外角，∴∠CAD ＝∠DBE ＝∠ECF ＝120°，又∵AC ＝1，∴BD ＝2，CE ＝3，∴弧CD 的长＝13×2π×1，弧DE 的长＝13×2π×2，弧EF 的长＝13×2π×3， ∴曲线CDEF 的长＝13×2π×1＋13×2π×2＋13×2π×3＝4π. 解：(1)在△OCE 中，∵∠CEO ＝90°，∠EOC ＝60°，∴∠OCE ＝30°.∵OC ＝2，∴OE ＝12OC ＝1， ∴CE ＝OC 2－OE 2＝ 3.∵OA ⊥CD ，∴CE ＝DE ，∴CD ＝2CE ＝2 3.(2)∵S △ABC ＝12AB ·CE ＝12×4×3＝23， ∴S 阴影＝S 半圆－S △ABC ＝12π×22－23＝2π－2 3. 17．如图24－4－11，AB 是⊙O 的直径，C 是半圆O 上的一点，AC 平分∠DAB ，AD ⊥CD ，垂足为D ，AD 交⊙O 于E ，连接CE .(1)判断CD 与⊙O 的位置关系，并证明你的结论；(2)若E 是AC ︵的中点，⊙O 的半径为1，求图中阴影部分的面积．图24－4－11解：(1)CD 与圆O 相切，理由为：∵AC 为∠DAB 的平分线，∴∠DAC ＝∠BAC ，∵OA ＝OC ，∴∠OAC ＝∠OCA ，∴∠DAC ＝∠OCA ，∴OC ∥AD ，∵AD ⊥CD ，∴OC ⊥CD ，∴CD 与圆O 相切；(2)连接EB ，由AB 为直径，得到∠AEB ＝90°，∴EB ∥CD ，F 为EB 的中点，∴OF 为△ABE 的中位线，∴OF ＝12AE ＝12，即CF ＝DE ＝12，在Rt △OBF 中，根据勾股定理得：EF ＝FB ＝DC ＝32，则S 阴影＝S △DEC ＝12×12×32＝38.。

人教版九年级数学上册第24章 24.4弧长和扇形面积专题练习(含答案)

人教版九年级数学上册第24章 24.4弧长和扇形面积专题练习（含答案）基础巩固1.⊙的内接多边形周长为3 ，⊙的外切多边形周长为3.4，则下列各数中与此圆的周长最接近的是（）AB． D2.如图已知扇形的半径为6cm ，圆心角的度数为，若将此扇形围成一个圆锥，则围成的圆锥的侧面积为（）A ．B ．C ．D ．3.若一个圆锥的底面圆的周长是4πcm ，母线长是6cm ，则该圆锥的侧面展开图的圆心角的度数是A ．40°B ．80°C ．120°D ．150°4.艳军中学学术报告厅门的上沿是圆弧形，这条弧所在圆的半径为1.8 米，所对的圆心角为100°，则弧长是米．(π≈3) 【参考答案】 1. C 2. D 3. C 4. 3O O 10AOB 120°24πcm 26πcm 29πcm 212πcm 120 BOA6cm能力提高一、选择题1.如图，已知的半径，，则所对的弧的长为（） A ．B ．C ．D ．2.将直径为60cm 的圆形铁皮，做成三个相同的圆锥容器的侧面（不浪费材料，不计接缝处的材料损耗），那么每个圆锥容器的底面半径为 ( )A ．10cmB ．30cmC ．40cmD ．300cm3.若用半径为9，圆心角为120°的扇形围成一个圆锥的侧面（接缝忽略不计），则这个圆锥的底面半径是（） A ．1.5B ．2C ．3D ．64.有30％圆周的一个扇形彩纸片，该扇形的半径为40cm ，小红同学为了在“六一”儿童节联欢晚会上表演节目，她打算剪去部分扇形纸片后，利用剩下的纸片制作成一个底面半径为10cm 的圆锥形纸帽(接缝处不重叠)，那么剪去的扇形纸片的圆心角为（）．A.9°B.18°C.63°D.72°5.已知圆锥的底面半径为5cm ，侧面积为65πcm 2，设圆锥的母线与高的夹角为θ（如图所示），则sin θ的值为（）A.B. C. D. O ⊙6OA =90AOB ∠=°AOB ∠AB 2π3π6π12π125135131013126.在综合实践活动课上，小明同学用纸板制作了一个圆锥形漏斗模型．如图所示，它的底面半径高则这个圆锥漏斗的侧面积是（） A ． B ． C ． D ．二、填空题1.，圆心角等于450的扇形AOB 内部作一个正方形CDEF ，使点C 在OA上，点D .E 在OB 上，点F 在上，则阴影部分的面积为（结果保留） .2.如图，方格纸中4个小正方形的边长均为1，则图中阴影部分三个小扇形的面积和为（结果保留）．3.将一块含30°角的三角尺绕较长直角边旋转一周得一圆锥，这个圆锥的高是3，则圆锥的侧面积是____.4.如图，三角板中，，，．三角板绕直角顶点逆时针旋转，当点的对应点落在边的起始位置上时即停止转动，则点转过的路径长为．6cm OB =，8cm OC =．230cm 230cm π260cm π2120cm AB ππABC ︒=∠90ACB ︒=∠30B 6=BC C A 'A AB B 第2题图5.已知正六边形的边长为1cm ，分别以它的三个不相邻的顶点为圆心，1cm 长为半径画弧（如图），则所得到的三条弧的长度之和为 cm （结果保留）．6.矩形ABCD的边AB =8，AD =6，现将矩形ABCD 放在直线l 上且沿着l 向右作无滑动地翻滚，当它翻滚至类似开始的位置时（如图所示），则顶点A 所经过的路线长是_________．7.已知在△ABC 中，AB=6，AC=8，∠A=90°，把Rt△ABC 绕直线AC 旋转一周得到一个圆锥，其表面积为,把Rt△ABC 绕直线AB 旋转一周得到另一个圆锥，其表面积为，则：等于_________ 三、解答题1.如图，有一个圆O 和两个正六边形，．的6个顶点都在圆周上，的6条边都和圆O 相切（我们称，分别为圆O 的内接正六边形和外切正六边形）．（1）设，的边长分别为，，圆O 的半径为，求及的值；（2）求正六边形，的面积比的值．π1111A B C D 1S 2S 1S 2S 1T 2T 1T 2T 1T 2T 1T 2T a b r a r :b r :1T 2T 21:S SB 'A CAB 第4题2.如图，圆心角都是90º的扇形OAB 与扇形OCD 叠放在一起，连结AC ，BD ．（1）求证：AC=BD ；（2）若图中阴影部分的面积是，OA=2cm ，求OC 的长．3.如图，已知菱形的边长为，两点在扇形的上，求的长度及扇形的面积．2 43cm ABCD 1.5cm B C ，AEF ABCBCD AEF【参考答案】选择题 1. B 2. A3. C4. B5. A6. C 填空题 1.2. 3. 18π 4. 5. 6. 7. 2∶3 解答题1.解：（1）连接圆心O 和T 的6个顶点可得6个全等的正三角形 .所以r∶a=1∶1;连接圆心O 和T 相邻的两个顶点，得以圆O 半径为高的正三角形，所以r∶b=∶2;（2） T ∶T 的连长比是∶2，所以S ∶S = . 2. （1）证明：2385-π∏83π22ππ24123123124:3):(2=b a（2）根据题意得：；∴ 解得：OC ＝1cm ．3. 解：四边形是菱形且边长为1.5，．又两点在扇形的上，，是等边三角形．．的长（cm ）BDAC BOD AOC DO CO BO AB BOD AOC AODBOD AOD AOC COD AOB =⇒∆≅∆⇒⎪⎭⎪⎬⎫==∠=∠⇒∠+∠=∠+∠⇒∠∠ 900＝＝360)(9036090360902222OC OA OC OA S -=-=πππ阴影360)2(904322OC -=ππABCD 1.5AB BC ∴==B C 、AEF 1.5AB BC AC ∴===ABC ∴△60BAC ∴∠=°21805.160ππ=∙=ππ835.122121=∙∙==lR S ABC 扇形)(2cm。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第24章 24.4《弧长和扇形面积》同步练习及答案(2)
第1题. 一条弧所对的圆心角是90o
，半径是R ，则这条弧的长是．
答案：
12
R π 第2题. 若»
AB 的长为所对的圆的直径长，则»AB 所对的圆周角的度数为．
答案：180π
o
第3题. 如图，AB 是半圆O 的直径，以O 为圆心，OE 为半径的半圆交AB 于E ，F 两点，弦AC 是小半圆的切线，D 为切点，若4OA =，2OE =，则图中阴影部分的面积为．
答案：
4
3
π+
第4题. 如果一条弧长等于l ，它的半径等于R ，这条弧所对的圆心角增加1o
，则它的弧长增加（）Ａ．
l
n
Ｂ．
180
R π Ｃ．
180l
R
π Ｄ．
360
l
答案：Ｂ
第5题. 在半径为3的O e 中，弦3AB =，则»
AB 的长为（）
Ａ．
π
2
Ｂ．π
Ｃ．
32
π Ｄ．2π
答案：Ｂ
第6题. 扇形的周长为16，圆心角为360π
o
，则扇形的面积是（
）
Ａ．16 Ｂ．32 Ｃ．64 Ｄ．16π
答案：Ａ
第7题. 如图，扇形OAB 的圆心角为90o
，且半径为R ，分别以OA ，OB 为直径在扇形内作半圆，
P 和Q 分别表示两个阴影部分的面积，那么P 和Q 的大小关系是（）Ａ．P Q =
Ｂ．P Q >
Ｃ．P Q <
Ｄ．无法确定
答案：Ａ
第8题. 如图，矩形ABCD 中，1AB =
，BC =，以BC 的中点E 为圆心的¼MPN
与AD 相切，则图中的阴影部分的面积为（）
Ａ．
2
3
π Ｂ．
34
π
Ｄ．
π3
答案：Ｄ
第9题. 如图所示，正方形ABCD 是以金属丝围成的，其边长1AB =，把此正方形的金属丝重新围成扇形的ADC ，使AD AD =，DC DC =不变，问正方形面积与扇形面积谁大？大多少？由计算得出结果．答案：1S =正方形，1
21122
ADC S lR 1=
=⨯⨯=扇形，∴面积没有变化．
第10题. 如图，O e 的半径为1，C 为O e 上一点，
以C 为圆心，以1为半径作弧与O e 相交于A ，B 两点，则图中阴影部分的面积为
．
答案：2π3
第11题. 如图，△ABC 中，105A ∠=o ，45B ∠=o
，AB =AD BC ⊥，D 为垂足，以A
为圆心，以AD 为半径画弧»EF
，则图中阴影部分的面积为（）
Ｍ
ＣＡＤ
Ａ．7
6π
Ｂ．7
6-
π+2
Ｃ．5
6
π
Ｄ．5
6
-π+2
答案：Ｂ
第12题. 如图，半径为r 的1O e 与半径为3r 的2O e 外切于P 点，AB 是两圆的外公切线，切点分
别为A ，B ，求AB 和»PA
，»PB 所围成的阴影部分的面积．
答案：连结2O B ，1O A ，过1O 作12O H O B ⊥，垂足为H ，则得矩形1ABHO ， 1BH O A r ∴==，1AB O H =．
在Rt △21O HO 中，2232O H O B BH r r r =-=-=，
122134O O O P O P r r r =+=+=
，1O H ==，
2211221
cos 42O H r HO O O O r ∠=
==，2160HO O ∴∠=o ，1120AO P ∠=o ．
21212111
()(3)22ABO O S O A O B O H r r =+=+=g 梯形，
2
6033606BO P O B r r S 222π()π(3)π===2
g 2扇形，
12
2120AO P O A S r π()π
==3603
扇形、，
21212222
3ABO O BO P AO P S S S S r r ππ=--=--=23阴影梯形扇形扇形．
第13题. 圆周角是90o
，占整个周角的90
360
，因此它所对的弧长是圆周长的．答案：
14
第14题. 圆心角是45o
，占整个周角的，因此它所对的弧长是圆周长的．答案：
45
360，18
第15题. 圆心角是1o
，占整个周角的，因此它所对的弧长是圆周长的．
ＣＤＢＥ
Ａ
Ｆ
答案：
1360，1360
第16题. 扇形的圆心角为210o
，弧长是28π，求扇形的面积．
答案：336π
第17题. 一个扇形的半径等于一个圆的半径的2倍，且面积相等．求这个扇形的圆心角．
答案：90o
第18题. 一服装厂里有大量形状为等腰直角三角形的边角布料（如图），现找出其中的一种，测得
90C ∠=o ，4AC BC ==．今要从这种三角形中剪出一种扇形，做成不同形状的玩具，使扇形的边缘半径恰好都在ABC △的边上，且扇形的弧与ABC △的其他边相切，请设计出所有可能符合
题意的方案示意图，并求出扇形的半径（只要求画出图形，并直接写出扇形半径）．
答案：
第19题.
90o
，半径为R Ａ．
2
R π
Ｂ．
3
R π
Ｃ．
4
R π
Ｄ．
6
R
答案：Ａ
第20题. 已知一条弧长为l ，它所对圆心角的度数为n o
，则这条弦所在圆的半径为（）．
Ａ．
180
n l
π Ｂ．
180l
n π
Ｃ．
360l
n π
Ｄ．
180l
n
π
答案：Ｂ
第21题. 半径为6cm 的圆中，60o
的圆周角所对的弧的弧长为．
答案：4cm π
第22题. 半径为9cm 的圆中，长为12cm π的一条弧所对的圆心角的度数为．
答案：240o
第23题. 已知圆的面积为2
81cm π，若其圆周上一段弧长为3cm π，则这段弧所对的圆心角的度
42r =24r =1r =
数为．
答案：
60o
第24题. 若扇形的圆心角为120o
，弧长为6cm π，则这个扇形的面积为．
答案：2
27cm π
第25题. 弯制管道时，先按中心线计算其“展直长度”，再下料．根据如图所示的图形可算得管道的展直长度为．（单位：mm ，精确到1mm ）
答案：389mm
第26题. 如图，在Rt △ABC 中，90C ∠=o
，60A ∠=o
，3cm AC =，将△ABC 绕点B 旋转至△A BC ''的位置，且使点A ，B ，C '三点在同一直线上，则点A 经过的最短路线长是
cm ．答案：
53
π
第27题. 一块等边三角形的木板，边长为１，若将木板沿水平线翻滚（如图），则点B 从开始至结束走过的路径长度为（）．Ａ．
3π
2
Ｂ．
4π3
Ｃ．4
Ｄ．322
+
π
答案：Ｂ
第28题. 如图，扇形AOB 的圆心角为60o
，半径为6cm ，C ，D 是»
AB 的三等分点，则图中阴影部分的面积和是．
A ' C ' ＢＣＡＢ
Ｃ
答案：2
2cm π
第29题. 如图，已知在扇形AOB 中，若45AOB ∠=o
，4cm AD =，3cm CD =π，则图中阴影部分的面积是．
答案：2
14cm π
第30题. 如图4，在两个同心圆中，三条直径把大圆分成相等的六部分，若
大圆的半径为2，则图中阴影部分的面积为．
答案：14.2π．
图4。