哈密顿回路python蛮力法代码,解析
Python与物理计算使用Python模拟和分析物理现象

Python与物理计算使用Python模拟和分析物理现象Python与物理计算:使用Python模拟和分析物理现象Python是一种功能强大且易于学习的编程语言,它在物理计算领域中应用广泛。
通过使用Python的模拟和分析功能,我们可以更好地理解和研究各种物理现象。
本文将介绍如何使用Python来模拟和分析物理现象,并探讨计算物理在科学研究和工程应用中的重要性。
一、Python在物理计算中的应用在物理学研究中,计算模拟是一种重要的工具。
通过计算模拟,我们可以模拟复杂的物理系统,并观察和分析它们的行为。
Python作为一种高级编程语言,具有丰富的库和工具,使得模拟和分析物理现象变得非常容易。
1.1 物理模拟Python的科学计算库NumPy和SciPy提供了丰富的函数和数据结构,用于解决物理模型的数值求解问题。
例如,我们可以使用NumPy库来创建和处理多维数组,使用SciPy库来解决微分方程和优化问题。
这些功能使我们能够建立物理模型,并通过数值方法模拟物理过程。
1.2 数据分析与可视化Python的数据分析库Pandas和可视化库Matplotlib可以帮助我们处理和分析实验数据,并将结果以清晰的图形形式展示出来。
这些库提供了各种统计分析和图表绘制的功能,可以帮助我们更好地理解实验结果和物理现象。
二、使用Python模拟和分析物理现象的例子接下来,我们将通过几个具体的例子来演示如何使用Python来模拟和分析物理现象。
2.1 简谐振子模拟简谐振子是物理学中一个重要的模型,它可以用于描述弹簧振子、摆钟等多种现象。
我们可以使用Python的数值计算库来模拟简谐振子的运动过程,并绘制振动图。
import numpy as npimport matplotlib.pyplot as plt# 定义模拟参数m = 1.0 # 振子质量k = 1.0 # 振子劲度系数t = np.linspace(0, 10, 1000) # 模拟时间# 求解简谐振子的位移x = np.cos(np.sqrt(k/m) * t)# 绘制位移-时间曲线plt.plot(t, x)plt.xlabel('Time')plt.ylabel('Displacement')plt.title('Harmonic Oscillator')plt.show()2.2 自由落体模拟自由落体是物理学中的经典问题,我们可以使用Python来模拟自由落体过程,并分析物体的位移、速度和加速度随时间的变化。
python解析算法例题

python解析算法例题摘要:1. Python解析算法概述2.示例题目一:判断质数3.示例题目二:汉诺塔问题4.示例题目三:斐波那契数列5.总结与拓展正文:**一、Python解析算法概述**Python作为一种广泛应用于各个领域的编程语言,其强大的解析能力使得解决各类算法问题变得轻松愉快。
解析算法通常包括两大类:数学方法和逻辑方法。
数学方法主要包括数论、组合数学等,而逻辑方法则包括递归、动态规划等。
本文将通过三个示例题目,简要介绍Python在解析算法中的应用。
**二、示例题目一:判断质数**题目描述:编写一个函数,判断一个给定的整数是否为质数。
解题思路:质数是指大于1的自然数中,除了1和它本身以外,不能被其他自然数整除的数。
我们可以通过遍历2到sqrt(n)之间的整数,判断是否存在能够整除n的数。
```pythondef is_prime(n):if n <= 1:return Falsefor i in range(2, int(sqrt(n)) + 1):if n % i == 0:return Falsereturn True```**三、示例题目二:汉诺塔问题**题目描述:有一个宽度为n的汉诺塔,初始状态为最底层有n个盘子,依次向上递减。
现规定:每次只能将最底层的盘子移到最顶层,每次移动一个盘子,请问有多少种不同的移动方法?解题思路:利用递归思想,自顶向下计算每一层的移动方法,并累计到总方法数中。
```pythondef hanoi(n, src, aux, dest):if n > 0:# 将n-1个盘子从src移动到auxhanoi(n-1, src, dest, aux)# 将第n个盘子从src移动到destprint(f"Move disk {n} from {src} to {dest}")# 将n-1个盘子从aux移动到desthanoi(n-1, aux, dest, src)# 测试= 3hanoi(n, "A", "B", "C")```**四、示例题目三:斐波那契数列**题目描述:编写一个函数,求解斐波那契数列的第n项。
15.2-3哈密顿图-dijkstra算法
1
2
3
p4=1 4
3
5 6 p6=3
7
2
6
4
p7=3
min {c23,c25,c47,c67}=min {2+6,2+5,1+2,3+4}=min {8,7,3,7}=3
X={1,2,4,6,7}, p7=3
X={1,2,4,6,7}
p1=0 p2=2 2 1 10 6 5 9
1
2
Hale Waihona Puke 3p4=1 4p5=6 5
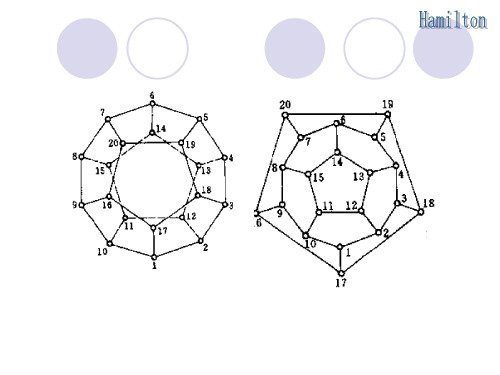
推论 n(n≥3)阶有向完全图为哈密尔顿 图.
思考:
一个售货员希望去访问n个城市的每 一个,开始和结束于v1城市。每两城市间 都有一条直接通路,我们记vi城市到vj城市 的距离为W(i,j),问题是去设计一个算法, 它将找出售货员能采取的最短路径。
数学问题:
用图论术语叙述就是:G=〈V,E,W〉是n个顶点 的无向完全图,其中W是从E到正实数集的一个函 数,对在V中任意三点 vi, vj, vk 满足 W(i,j)+W(j,k)≥W(i,k) 试求出赋权图上的最短哈密尔顿回路。
至今未找出有效的方法,但已找到了若干近似算 法. 最邻近算法,它为巡回售货员问题得出近似解。 选任意点作为始点,找出一个与始点最近的点,形成 一条边的初始路径。 设x表示最新加到这条路径上的点,从不在路径上的 所有点中,选一个与x最邻近的点,把连接x与此点的边 加到这条路径中。 重复这一步,直至G中所有顶点包含在路径中。 把始点和最后加入的顶点之间的边放入,这样就得出 一个回路。
T (v j ) min[ (v j ) , P(vi ) li j ] T
3.比较所有具有T标号的节点,把最小者改为P标号,即:
详解Python牛顿插值法

详解Python⽜顿插值法⽬录⼀、⽜顿多项式⼆、例题三、ACcode:⼀、⽜顿多项式拉格朗⽇多项式的公式不具备递推性,每个多项式需要单独构造。
但很多时候我们需要从若⼲个逼近多项式选择⼀个。
这个时候我们就需要⼀个具有递推关系的⽅法来构造——⽜顿多项式这⾥的的a0,a1…等可以通过逐⼀带⼊点的值来求得。
但是当项数多起来时,会发现式⼦变得很⼤,这个时候我们便要引⼊差商的概念(利⽤差分思想)具体见式⼦能更好理解这⾥在编程实现中我们可以推出相应的差商推导⽅程d(k,0)=y(k)d(k,j)=(d(k,j-1)-d(k-1,j-1)) / (x(k)-x(k-j))⼆、例题【问题描述】考虑[0,3]内的函数y=f(x)=cos(x)。
利⽤多个(最多为6个)节点构造⽜顿插值多项式。
【输⼊形式】在屏幕上依次输⼊在区间[0,3]内的⼀个值x*,构造插值多项式后求其P(x*)值,和多个节点的x坐标。
【输出形式】输出⽜顿插值多项式系数向量,差商矩阵,P(x*)值(保留6位有效数字),和与真实值的绝对误差(使⽤科学计数法,保留⼩数点后6位有数字)。
【样例1输⼊】0.80 0.5 1【样例1输出】-0.429726-0.029972111 0 00.877583 -0.244835 00.540302 -0.674561 -0.4297260.7009984.291237e-03【样例1说明】输⼊:x为0.8,3个节点为(k, cos(k)),其中k = 0, 0.5, 1。
输出:⽜顿插值多项式系数向量,表⽰P2(x)=-0.429726x^2 - 0.0299721x + 1;3⾏3列的差商矩阵;当x为0.8时,P2(0.8)值为0.700998与真实值的绝对误差为:4.291237*10^(-3)【评分标准】根据输⼊得到的输出准确三、ACcode:C++(后⾯还有python代码)/** @Author: csc* @Date: 2021-04-30 08:52:45* @LastEditTime: 2021-04-30 11:57:46* @LastEditors: Please set LastEditors* @Description: In User Settings Edit* @FilePath: \code_formal\course\cal\newton_quo.cpp*/#include <bits/stdc++.h>#define pr printf#define sc scanf#define for0(i, n) for (i = 0; i < n; i++)#define for1n(i, n) for (i = 1; i <= n; i++)#define forab(i, a, b) for (i = a; i <= b; i++)#define forba(i, a, b) for (i = b; i >= a; i--)#define pb push_back#define eb emplace_back#define fi first#define se second#define int long long#define pii pair<int, int>#define vi vector<int>#define vii vector<vector<int>>#define vt3 vector<tuple<int, int, int>>#define mem(ara, n) memset(ara, n, sizeof(ara))#define memb(ara) memset(ara, false, sizeof(ara))#define all(x) (x).begin(), (x).end()#define sq(x) ((x) * (x))#define sz(x) x.size()const int N = 2e5 + 100;const int mod = 1e9 + 7;namespace often{inline void input(int &res){char c = getchar();res = 0;int f = 1;while (!isdigit(c)){f ^= c == '-';c = getchar();}while (isdigit(c)){res = (res << 3) + (res << 1) + (c ^ 48);c = getchar();}res = f ? res : -res;}inline int qpow(int a, int b){int ans = 1, base = a;while (b){if (b & 1)ans = (ans * base % mod + mod) % mod;base = (base * base % mod + mod) % mod;b >>= 1;}return ans;}int fact(int n){int res = 1;for (int i = 1; i <= n; i++)res = res * 1ll * i % mod;return res;}int C(int n, int k){return fact(n) * 1ll * qpow(fact(k), mod - 2) % mod * 1ll * qpow(fact(n - k), mod - 2) % mod; }int exgcd(int a, int b, int &x, int &y){if (b == 0){x = 1, y = 0;return a;}int res = exgcd(b, a % b, x, y);int t = y;y = x - (a / b) * y;x = t;return res;}int invmod(int a, int mod){int x, y;exgcd(a, mod, x, y);x %= mod;if (x < 0)x += mod;return x;}}using namespace often;using namespace std;int n;signed main(){auto polymul = [&](vector<double> &v, double er) {v.emplace_back(0);vector<double> _ = v;int m = sz(v);for (int i = 1; i < m; i++)v[i] += er * _[i - 1];};auto polyval = [&](vector<double> const &c, double const &_x) -> double {double res = 0.0;int m = sz(c);for (int ii = 0; ii < m; ii++)res += c[ii] * pow(_x, (double)(m - ii - 1));return res;};int __ = 1;while (__--){double _x, temp;cin >> _x;vector<double> x, y;while (cin >> temp)x.emplace_back(temp), y.emplace_back(cos(temp));n = x.size();vector<vector<double>> a(n, vector<double>(n));int i, j;for0(i, n) a[i][0] = y[i];forab(j, 1, n - 1) forab(i, j, n - 1) a[i][j] = (a[i][j - 1] - a[i - 1][j - 1]) / (x[i] - x[i - j]); vector<double> v;v.emplace_back(a[n - 1][n - 1]);forba(i, 0, n - 2){polymul(v, -x[i]);int l = sz(v);v[l - 1] += a[i][i];}for0(i, n)pr("%g\n", v[i]);for0(i, n){for0(j, n)pr("%g ", a[i][j]);puts("");}double _y = polyval(v, _x);pr("%g\n", _y);pr("%.6e",fabs(_y-cos(_x)));}return 0;}python代码'''Author: cscDate: 2021-04-29 23:00:57LastEditTime: 2021-04-30 09:58:07LastEditors: Please set LastEditorsDescription: In User Settings EditFilePath: \code_py\newton_.py'''import numpy as npdef difference_quotient(x, y):n = len(x)a = np.zeros([n, n], dtype=float)for i in range(n):a[i][0] = y[i]for j in range(1, n):for i in range(j, n):a[i][j] = (a[i][j-1]-a[i-1][j-1])/(x[i]-x[i-j])return adef newton(x, y, _x):a = difference_quotient(x, y)n = len(x)s = a[n-1][n-1]j = n-2while j >= 0:s = np.polyadd(np.polymul(s, np.poly1d([x[j]], True)), np.poly1d([a[j][j]]))j -= 1for i in range(n):print('%g' % s[n-1-i])for i in range(n):for j in range(n):print('%g' % a[i][j], end=' ')_y = np.polyval(s, _x)print('%g' % _y)# re_errreal_y = np.cos(_x)err = abs(_y-real_y)print('%.6e' % err)def main():_x = float(input())x = list(map(float, input().split()))y = np.cos(x)newton(x, y, _x)if __name__ == '__main__':main()到此这篇关于详解Python⽜顿插值法的⽂章就介绍到这了,更多相关Python⽜顿插值法内容请搜索以前的⽂章或继续浏览下⾯的相关⽂章希望⼤家以后多多⽀持!。
python刷力扣 技巧

python刷力扣技巧
在刷力扣(LeetCode)时,有一些技巧可以帮助你更高效地解决问题:
理解题目背景:在开始解题之前,先理解题目的背景和要求。
确保你明白题目所描述的问题,以及需要解决的问题是什么。
分解问题:将复杂的问题分解成更小的子问题,逐个解决。
这有助于你更好地理解问题,并找到解决方案。
画图辅助:对于一些需要理解数据结构或算法的问题,可以尝试画图来辅助理解。
通过画图,你可以更直观地看到数据结构的变化,从而更容易找到解决方案。
优化算法:在编写代码时,要尽可能优化算法,以提高代码的执行效率。
这有助于你更快地找到答案,并且在提交答案时获得更高的评价。
参考答案:在遇到困难时,可以参考其他人的答案来帮助你解决问题。
但是要注意,不要直接复制粘贴别人的代码,而是要理解他们的思路和方法,然后自己尝试写出解决方案。
多做练习:通过多做练习,你可以提高自己的编程能力和解题技巧。
可以尝试不同的题目类型和难度,以帮助你更好地掌握算法和数据结构。
总结经验:在刷题过程中,要及时总结经验,记录下自己的解题思路和方法。
这有助于你更好地掌握知识,并在以后遇到类似问题时更快地找到解决方案。
总之,刷力扣需要不断地练习和总结经验,通过不断地提高自己的编程能力和解题技巧,你可以更好地掌握算法和数据结构,并在力扣上取得更好的成绩。
python解析verilog代码

Python解析Verilog代码一、引言Verilog是一种硬件描述语言(Hardware Description Language, HDL),用于描述数字电路。
Verilog代码通常用于设计和验证集成电路和数字系统。
然而,对于较大的设计,手动分析Verilog代码变得非常困难。
许多工程师和研究人员倾向于使用自动化工具,如Python 解析Verilog代码,以提高效率和准确性。
二、Python解析Verilog代码的需求1. Verilog代码的结构复杂。
Verilog代码通常包含模块、端口、连接、内部信号、时序逻辑等,需要一个高效且灵活的工具来处理。
2. 需要快速获取和分析Verilog代码中的特定信息,如模块层次结构、信号连接、时序约束等。
3. 需要进行Verilog代码的静态分析,以检查语法错误、逻辑错误、仿真问题等。
4. 需要将Verilog代码转换为其他格式,如图形表示、仿真模型等。
三、Python解析Verilog代码的实现1. 使用工具库:Python拥有丰富的工具库,如ply、pyverilog等,可以用于解析Verilog代码的词法分析、语法分析、抽象语法树构建等。
2. 定义数据结构:在Python中定义适当的数据结构,如模块类、端口类、信号类等,以便于存储和处理Verilog代码中的各种信息。
3. 编写解析器:利用工具库和数据结构,编写Verilog代码的解析器程序,实现对Verilog代码的快速、准确解析和分析。
四、Python解析Verilog代码的应用1. 设计验证:通过Python解析Verilog代码,可以快速获取Verilog 代码中的模块和信号等信息,用于设计验证和仿真。
2. 时序分析:Python解析Verilog代码可以帮助工程师进行时序分析,包括时序约束的提取和分析,路径延迟的计算和优化等。
3. 自动化生成:利用Python解析Verilog代码,可以自动化生成Verilog代码的图形表示、仿真模型、文档等,提高工作效率和质量。
附:蛮力法

3.1 字符串匹配 3.2 矩阵相乘 3.3 子集和问题 3.4 冒泡排序 3.5 若干最优化问题
蛮力法
思想:穷尽所有可能的情况来寻找问题的解
优势:思路简单,设计难度低
缺点:运行效率低
适用范围: 1、一些问题只能采用蛮力法求解 2、蛮力法设计简单,用其求解一些小问题 也是可接受的
3.1 字符串匹配
let d = 0; foreach (eL) do
d d + w[e.a, e.b]; d d + w[L.tail, L.head]; if (d < d_best) then
d_best d; L_best L; return L_best; end
O((n+1)!)
课后作业:
1、习题3-15 2、习题3-17 3、习题3-19
[字符串匹配算法] Algorithm Brute_Match(T, P: string) begin let i = 0, n = |T|, m = |P|; while (i ≤ n−m) do
let j = 0; while (j < m) do if (T[i+j] ≠ P[j]) then break; j j + 1; if (j = m) then return i; //匹配成功 i i + 1; return −1; end
O(m(m−n)) 存在改进可能?
3.2 矩阵相乘
输入:m×n型矩阵A和n×p型矩阵B 输出:C = A×B
3.2 矩阵相乘
[矩阵相乘算法]
Algorithm MatrixMultiple(A, B: int[,])
begin
let (m,n) = |A|, (n,p)= |B|, C = new int[m,p];
python在数学建模中常见算法及代码

python在数学建模中常见算法及代码在数学建模中,Python 是一种流行的编程语言,有许多用于解决不同数学建模问题的库和算法。
以下是一些在数学建模中常见的算法及其对应的 Python 代码示例:1.线性规划:•使用scipy库中的linprog函数:pythonfrom scipy.optimize import linprog c = [-3, 5] # 目标函数的系数 A = [[-1, 2], [4, 3]] # 不等式约束的系数 b = [8, 15] # 不等式约束的右侧值result = linprog(c, A_ub=A, b_ub=b) print("最小值:", result.fun) print("优化变量:", result.x)2.整数规划:•使用PuLP库:pythonfrom pulp import LpMaximize, LpProblem, LpVariable # 创建问题model = LpProblem(name="integer_programming_example",sense=LpMaximize) # 创建变量 x = LpVariable(name="x", lowBound=0, cat="Integer") y = LpVariable(name="y", lowBound=0, cat="Integer") # 添加目标函数和约束model += (2 * x + 4 * y <= 8, "constraint_1") model+= (5 * x + 3 * y <= 15, "constraint_2") model += (3 * x + 2 * y <= 7, "constraint_3") model += (4 * x + 2 * y <= 8, "constraint_4") model += (x + y >= 3, "constraint_5") model += 4 * x + 6 * y # 目标函数 # 解决问题model.solve() print("最优值:", model.objective.value()) print("最优解:") for var in model.variables(): print(f"{}: {var.value()}")3.数值积分:•使用scipy库中的quad函数:pythonfrom scipy.integrate import quad def integrand(x): return x**2 result, error = quad(integrand, 0, 1) print("数值积分结果:", result)这只是数学建模中一些常见问题的示例,具体问题和应用场景可能需要不同的算法和工具。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
哈密顿回路python蛮力法代码,解析
哈密顿回路(Hamiltonian cycle)是指一个图中经过每个顶点恰好一次的回路。
蛮力法(Brute Force)是一种基本的解决问题的方法,它通过穷举所有可能的情况来寻找问题的解。
下面是一个简单的使用蛮力法解决哈密顿回路问题的Python 代码示例:
```python
def hamiltonian_cycle(graph, start):
n = len(graph)
path = [start]
def is_valid(v, pos):
if graph[path[pos-1]][v] == 0:
return False
if v in path:
return False
return True
def hamiltonian_util(pos):
if pos == n:
if graph[path[pos-1]][path[0]] == 1:
return True
else:
return False
for v in range(1, n):
if is_valid(v, pos):
path.append(v)
if hamiltonian_util(pos+1):
return True
path.pop()
return False
if not hamiltonian_util(1):
print("No Hamiltonian cycle exists")
return False
else:
print("Hamiltonian cycle found:", path)
return True
# 一个简单的图的邻接矩阵表示
# 0表示顶点不相邻,1表示相邻
graph = [[0, 1, 0, 1, 0],
[1, 0, 1, 1, 1],
[0, 1, 0, 0, 1],
[1, 1, 0, 0, 1],
[0, 1, 1, 1, 0]]
# 从顶点0开始搜索哈密顿回路
hamiltonian_cycle(graph, 0)
```
在这个示例中,`hamiltonian_cycle` 函数接受一个邻接矩阵表示的图和一个起始顶点作为输入。
它使用嵌套函数`hamiltonian_util` 来递归地搜索哈密顿回路。
`is_valid` 函数用于检查从当前位置到下一个顶点是否是有效的移动。
如果找到了哈密顿回路,函数会打印出回路的路径。
需要注意的是,蛮力法对于大型图的哈密顿回路问题并不是一个高效的解决方法,因为其时间复杂度为O(n!),随着顶点数量的增加,计算量呈指数级增长。
在实际应用中,通常会使用更高效的算法来解决哈密顿回路问题,比如回溯法、动态规划等。
希望这个简单的示例能够帮助您理解如何使用蛮力法来解决哈密顿回路问题。
