最小路法
(完整版)初中数学[最短路径问题]典型题型及解题技巧
![(完整版)初中数学[最短路径问题]典型题型及解题技巧](https://img.taocdn.com/s3/m/8a7bcc235acfa1c7aa00cc97.png)
初中数学[最短路径问题]典型题型及解题技巧最短路径问题中,关键在于,我们善于作定点关于动点所在直线的对称点,或利用平移和展开图来处理。
这对于我们解决此类问题有事半功倍的作用。
理论依据:“两点之间线段最短”,“垂线段最短”,“点关于线对称”,“线段的平移” “立体图形展开图”。
教材中的例题“饮马问题”,“造桥选址问题” “立体展开图”。
考的较多的还是“饮马问题”。
知识点:“两点之间线段最短”,“垂线段最短”,“点关于线对称”,“线段的平移”。
“饮马问题”,“造桥选址问题”。
考的较多的还是“饮马问题”,出题背景变式有角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等。
解题总思路:找点关于线的对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查。
一、两点在一条直线异侧例:已知:如图,A,B在直线L的两侧,在L上求一点P,使得PA+PB h 最小。
解:连接AB,线段AB与直线L的交点P,就是所求。
(根据:两点之间线段最短.)二、两点在一条直线同侧例:图所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短.■解:只有A、C、B在一直线上时,才能使AC+BC最小.作点A关于直线“街道”的对称点A ',然后连接A ' B,交“街道”于点C,则点C就是所求的点.、一点在两相交直线内部例:已知:如图A是锐角/ MON内部任意一点,在/ MON的两边OM,ON上各取一点B,C,组成三角形,使三角形周长最小.解:分别作点A 关于0M , ON 的对称点AAOM , ON 于点B 、点C ,则点B 、点C 即为所求 分析:当AB 、BC 和AC 三条边的长度恰好能够体现在一条直线上时,三角形的周长最小例:如图,A.B 两地在一条河的两岸,现要在河上建一座桥MN ,桥造在何 处才能使从A 到B 的路径AMNB 最短?(假设河的两岸是平行的直线,桥 要与河垂直) 解:1.将点B 沿垂直与河岸的方向平移一个河宽到 E ,2.连接AE 交河对岸与点M,则点M 为建桥的位置,MN 为所建的桥 证明:由平移的性质,得 BN // EM 且 BN=EM, MN=CD, BD // CE, BD=CE,所以 A.B 两地的距:AM+MN+BN=AM+MN+EM=AE+MN, 若桥的位置建在 CD 处,连接AC.CD.DB.CE, 则AB 两地的距离为:AC+CD+DB=AC+CD+CE=AC+CE+MN,在厶ACE 中AC+CE >AE,二 AC+CE+MN >AE+MN,即 AC+CD+DB >AM+MN+BN 所以桥的位置建在CD 处,AB 两地的路程最短。
最小带权路径长度计算公式

最小带权路径长度计算公式在我们探讨最小带权路径长度计算公式之前,我先给您讲一件我曾经遇到的事儿。
那是在一个阳光明媚的周末,我去公园散步。
走着走着,就看到一群小朋友在玩一个有趣的游戏。
他们在公园的小路上,用彩色的粉笔标记出了一些节点,然后试图找到从起点到终点的最佳路径。
我好奇地凑过去看,发现他们还在每个节点之间标上了数字,原来是在模拟一个带权的路径问题。
小朋友们争得面红耳赤,都想找出那个能让路径“代价”最小的走法。
这让我不禁想到了我们今天要说的最小带权路径长度计算公式。
最小带权路径长度的计算在很多领域都有着重要的应用。
比如说在交通运输中,要找到从一个城市到另一个城市的最短运输成本路径;在通信网络里,要确定数据传输的最优路线以减少延迟和成本。
常见的计算最小带权路径长度的算法有迪杰斯特拉(Dijkstra)算法和贝尔曼-福特(Bellman-Ford)算法。
先来说说迪杰斯特拉算法。
它的基本思路就像是我们在一堆水果里挑出最甜的那个。
一开始,我们标记起点的距离为 0 ,其他点的距离为无穷大。
然后,不断地从还没确定最短路径的点中,找出距离起点“最近”的点,更新它相邻点的距离。
这个过程一直持续,直到到达终点为止。
举个例子,假设我们有 5 个节点 A、B、C、D、E ,它们之间的权值如下:A - B: 5A - C: 3B - D: 2C - D: 1D - E: 4我们从 A 点出发,一开始,只有 A 的距离是 0 ,B 和 C 的距离分别是 5 和 3 ,D 和 E 是无穷大。
然后,我们发现距离 A 最近的是 C ,距离为 3 。
接着更新与 C 相邻的点 D 的距离,变成 4 。
这样一步步下去,最终就能找到从 A 到其他点的最短路径。
再说说贝尔曼-福特算法。
它就像是一个勇敢的探险家,不断地试探和修正路径。
它会对所有的边进行多次松弛操作,如果在经过多次操作后,还能更新路径长度,那就说明存在负权环。
比如说还是上面的例子,我们先初始化所有点的距离。
初中数学最短路径问题总结

初中数学最短路径问题总结一、十二个基本问题概述问题一:在直线l 上求一点P,使得PA + PB 值最小 .作法:连接AB,与直线l 的交点即为P 点 .原理:两点之间线段最短 . PA + PB 最小值为AB .问题二:(“将军饮马问题”)在直线l 上求一点P,使得PA + PB 值最小 .作法:作点B 关于直线l 的对称点B',连接AB' 与l 的交点即为点P.原理:两点之间线段最短.PA + PB 最小值为AB' .问题三:在直线l1、l2 上分别求点M、N,使得△PMN 的周长最小.作法:分别作点P 关于两条直线的对称点P' 和P'',连接P'P'',与两条直线的交点即为点M,N.原理:两点之间线段最短.PM + MN + PN 的最小值为线段P'P'' 的长.问题四:在直线l1、l2 上分别求点M、N,使四边形PQMN 的周长最小.作法:分别作点Q 、P 关于直线l1、l2 的对称点Q' 和P' 连接Q'P',与两直线交点即为点M,N.原理:两点之间线段最短.四边形PQMN 周长的最小值为线段Q'P' + PQ 的长.问题五:(“造桥选址问题”)直线m∥n,在m、n 上分别求点M、N,使MN⊥m,且AM + MN + BN 的值最小.作法:将点A 向下平移MN 的长度单位得A',连接A'B,交n 于点N,过N 作NM⊥m 于M .原理:两点之间线段最短 . AM + MN + BN 的最小值为A'B + MN .问题六:在直线l 上求两点M , N (M 在左),使MN = a , 并使AM + MN + NB 的值最小 .作法:将点A 向右平移a 个长度单位得A',作A' 关于直线l 的对称点A'',连接A''B 交直线l 于点N,将N 点向左平移a 个单位得M .原理:两点之间线段最短 . AM + MN + NB 的最小值为A''B + MN .问题七:在l1 上求点A,在l2 上求点B,使PA + AB 值最小 .作法:作点P 关于l1 的对称点P',作P'B⊥l2 于点B,交l1 于点A .原理:点到直线,垂线段的距离最短 . PA + AB 的最小值为线段P'B 的长 .问题八:A 为l1上一定点,B 为l2 上一定点,在l2 上求点M,在l1上求点N,使AM + MN + NB 的值最小 .作法:作点A 关于l2 的对称点A' , 点B 关于l1 的对称点B',连接A'B' 交l2 于点M,交l1 于点N.原理:两点之间线段最短.AM + MN + NB 的最小值为线段A'B' 的长.问题九:在直线l 上求一点P,使| PA - PB | 的值最小.作法:连接AB,作AB 的中垂线与直线l 的交点即为P 点.原理:垂直平分上的点到线段两端点的距离相等.| PA - PB | = 0 .问题十:在直线l 上求一点P,使| PA - PB | 的值最大.作法:作直线AB,与直线l 的交点即为P 点.原理:三角形任意两边之差小于第三边.| PA - PB | ≤AB ,| PA - PB | 的最大值= AB . 问题十一:在直线l 上求一点P,使| PA - PB | 的值最大.作法:作点B 关于直线l 的对称点B' 作直线AB',与直线l 的交点即为P 点.原理:三角形任意两边之差小于第三边.| PA - PB | ≤AB' ,| PA - PB | 的最大值= AB' . 问题十二:(“费马点”)△ABC 中每一内角都小于120°,在△ABC 内求一点P,使得PA + PB + PC 的值最小 .作法:所求点为“费马点”,即满足∠APB = ∠BPC = ∠APC = 120° .以AB 、AC 为边向外作等边△ABD、△ACE,连接CD、BE 相交于点P,点P 即为所求 .原理:两点之间线段最短 . PA + PB + PC 的最小值= CD .二、“费马点”——到三点距离之和最小的点费马点的构造方法:①所给三点的连线构成三角形(△ABC),并且这个三角形的每个内角都小于120°;②如下图所示:A , B , C 是给定的三点,以AC 为边向外作正三角形得到点D , 以BC 为边向外作正三角形得到点E ,连接BD 和AE 交于点O,我们断言点O 就是“费马点” .费马点的证明方法:先证△AEC ≌△DBC .△AEC 绕点C 顺时针旋转60°,可得到△DBC,从而△AEC ≌△DBC .于是∠OBC = ∠OEC,所以O、B、E、C 四点共圆 .拓展知识:四点共圆判定方法若线段同侧二点到线段两端点连线夹角相等,那么这二点和线段二端点四点共圆 .所以∠BOE = ∠BCE = 60°,∠COE = ∠CBE = 60°,于是∠BOC = ∠BOE + ∠COE = 120°,同理可证∠AOC = ∠AOB = 120°,所以∠BOC = ∠AOC = ∠AOB = 120° .将O 点看作是AE 上的点,随着△AEC 一起绕点C 顺时针旋转60°得到点O2 , 所以∠OCO2 = 60°,OC = O2C , OA = O2D ,所以△OCO2 是等边三角形,于是有OO2 = OC .所以BD = OA + OB + OC .。
最小路径和--动态规划

最⼩路径和--动态规划给定⼀个包含⾮负整数的m * n ⽹格,请找出⼀条从左上⾓到右下⾓的路径,使得路径上的数字总合为最⼩.说明: 每次只能向下或者向右移动⼀下.⽰例:输⼊:[[1,3,1],[1,5,1],[4,2,1]]输出: 7解释: 因为路径1→3→1→1→1的总和最⼩。
解法⼀: 动态规划思想因为最近在做动态规划的专题,所以⽤动态规划的思想来解决本题⽬:我们新建⼀个dp数组,⽤来保存每⾛⼀步的最短路径,但是最后⼀个数值也就是最后⼀个元素肯定是有的;我们利⽤递推的公式:dp(i,j)=grid(i,j)+min(dp(i+1,j),dp(i,j+1))即可,思想⽐较特殊,但是找到规律后还是很好理解的.代码public int minPathSum(int[][] grid) {int[][] dp = new int[grid.length][grid[0].length];for (int i = grid.length - 1; i >= 0; i--) {for (int j = grid[0].length - 1; j >= 0; j--) {if(i == grid.length - 1 && j != grid[0].length - 1) dp[i][j] = grid[i][j] + dp[i][j + 1];else if(j == grid[0].length - 1 && i != grid.length - 1) dp[i][j] = grid[i][j] + dp[i + 1][j];else if(j != grid[0].length - 1 && i != grid.length - 1) dp[i][j] = grid[i][j] + Math.min(dp[i + 1][j], dp[i][j + 1]);else dp[i][j] = grid[i][j];}}return dp[0][0];}运⾏结果以上就是动态规划的⽅式解决最短路径和,在⽇后开发过程中,当讲到⼀种算法思想时,可以⽤于改题⽬,会增加新解(因本⼈⽬前在做动态规划的专题), 希望对⼤家有所帮助!!!。
最短路径问题—Bellman-Ford算法
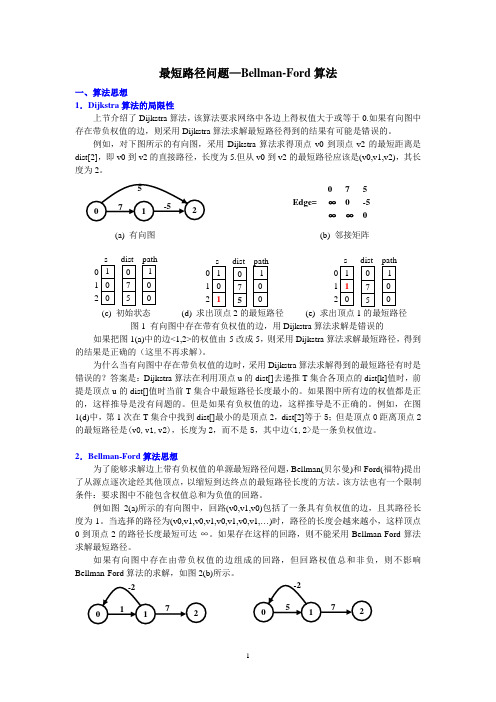
最短路径问题—Bellman-Ford 算法一、算法思想1.Dijkstra 算法的局限性上节介绍了Dijkstra 算法,该算法要求网络中各边上得权值大于或等于0.如果有向图中存在带负权值的边,则采用Dijkstra 算法求解最短路径得到的结果有可能是错误的。
例如,对下图所示的有向图,采用Dijkstra 算法求得顶点v0到顶点v2的最短距离是dist[2],即v0到v2的直接路径,长度为5.但从v0到v2的最短路径应该是(v0,v1,v2),其长度为2。
(a) 有向图 (b) 邻接矩阵(c) 初始状态(d) 求出顶点2的最短路径 (e) 求出顶点1的最短路径 图1 有向图中存在带有负权值的边,用Dijkstra算法求解是错误的如果把图1(a)中的边<1,2>的权值由-5改成5,则采用Dijkstra 算法求解最短路径,得到的结果是正确的(这里不再求解)。
为什么当有向图中存在带负权值的边时,采用Dijkstra 算法求解得到的最短路径有时是错误的?答案是:Dijkstra 算法在利用顶点u 的dist[]去递推T 集合各顶点的dist[k]值时,前提是顶点u的dist[]值时当前T 集合中最短路径长度最小的。
如果图中所有边的权值都是正的,这样推导是没有问题的。
但是如果有负权值的边,这样推导是不正确的。
例如,在图1(d)中,第1次在T 集合中找到dist[]最小的是顶点2,dist[2]等于5;但是顶点0距离顶点2的最短路径是(v0,v1,v2),长度为2,而不是5,其中边<1,2>是一条负权值边。
2.Bellman-Ford 算法思想为了能够求解边上带有负权值的单源最短路径问题,Bellman(贝尔曼)和Ford(福特)提出了从源点逐次途经其他顶点,以缩短到达终点的最短路径长度的方法。
该方法也有一个限制条件:要求图中不能包含权值总和为负值的回路。
例如图2(a)所示的有向图中,回路(v0,v1,v0)包括了一条具有负权值的边,且其路径长度为-1。
组合优化与算法分析之求解最小路径

组合优化与算法分析之求解最小路径Problem在赋权连通图G中寻找点到点的最短路径。
求解Single-source shortest paths(单源最短路径)给定了图G中起始点,我们要寻找从到其他点的最短路径。
1.Dijkstra’s AlgorithmDijkstra(迪杰斯特拉)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。
主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
算法描述1)算法思想:设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组,第一组为已求出最短路径的顶点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径, 就将加入到集合S中,直到全部顶点都加入到S中,算法就结束了),第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S中。
在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。
此外,每个顶点对应一个距离,S 中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点的距离,是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
2)算法步骤:a.初始时,S只包含源点,即S={v},v的距离为0。
U包含除v外的其他顶点,即:U={其余顶点},若v与U中顶点u有边,则<u,v>正常有权值,若u不是v的出边邻接点,则<u,v>权值为∞。
b.从U中选取一个距离v最小的顶点k,把k,加入S中(该选定的距离就是v到k 的最短路径长度)。
c.以k为新考虑的中间点,修改U中各顶点的距离;若从源点v到顶点u的距离(经过顶点k)比原来距离(不经过顶点k)短,则修改顶点u的距离值,修改后的距离值的顶点k的距离加上边上的权。
d.重复步骤b和c直到所有顶点都包含在S中。
2.Floyd-Warshall AlgorithmFloyd-Warshall算法(Floyd-Warshall algorithm)是解决任意两点间的最短路径的一种算法,可以正确处理有向图或负权的最短路径问题,同时也被用于计算有向图的传递闭包。
带分布式电源配电网的最小路可靠性分析方法
六年级下册奥数讲义-奥数方法:最短线路法 全国通用
思路剖析
直线AB上的点可以分 为两类,一类是 MN 的延长线与AB的交点,如图4所示,其余点是另 一类,这类点与M、N可以组成一个三角形,由前面的公理2可知,当P、 M、N三点可以组成三角形时,PM-PN<MN;当点P与Q点重合时,PM -PN=MN,因此Q点就是所求的P点位置。
[例3】 景泰蓝厂的工人师傅要给一个如图5所示的圆 柱型的制品嵌金钱,如果将金线的起点固定在A点,绕圆柱 一周之后终点为 B点,问沿什么线路嵌金线才能使金线用 量最少?
思路剖析 分别找出图17中三幅图中奇点的个数,然后就可以根据前面介绍的 知识作答。
说明:这就是历史上著名的“哥尼斯堡七桥问题”。当时有很多游客 尝试去走遍每一座桥,但没有一 个人能够不重复地一次走完这七座桥。 后来这个问题传到了瑞士著名数学家欧拉 (Euler)那里。经过周密的思 考,欧拉解决了这一问题,一笔画的问题也由此提出。
思路剖析
如果将圆柱型的制品的侧面沿A口剪开,就得到一个如图6所示的长 方形ABB'A’,从A起绕圆柱一周的金线在长方形中反映为从A到B’的一
条金线,使金线用量尽量少就要使得金线的长度尽量短,于是问题归结为 找从A到B’的最短距离。在前面的公理中知道连结两点的最 短线段是 直线段,因此从A到B’的最短距离为长方形的对角线AB’,如图7所示。
小学奥数系列:第四讲 最短路线问题
第四讲最短路线问题在日常工作、生活和娱乐中,经常会遇到有关行程路线的问题.在这一讲里,我们主要解决的问题是如何确定从某处到另一处最短路线的条数。
例1下图4—1中的线段表示的是汽车所能经过的所有马路,这辆汽车从A走到B处共有多少条最短路线?分析为了叙述方便,我们在各交叉点都标上字母.如图4—2.在这里,首先我们应该明确从A到B的最短路线到底有多长?从A点走到B点,不论怎样走,最短也要走长方形AHBD 的一个长与一个宽,即AD+DB.因此,在水平方向上,所有线段的长度和应等于AD;在竖直方向上,所有线段的长度和应等于DB.这样我们走的这条路线才是最短路线.为了保证这一点,我们就不应该走“回头路”,即在水平方向上不能向左走,在竖直方向上不能向上走.因此只能向右和向下走。
有些同学很快找出了从A到B的所有最短路线,即:A→C→D→G→B A→C→F→G→BA→C→F→I→B A→E→F→G→BA→E→F→I→B A→E→H→I→B通过验证,我们确信这六条路线都是从A到B的最短路线.如果按照上述方法找,它的缺点是不能保证找出所有的最短路线,即不能保证“不漏”.当然如果图形更复杂些,做到“不重”也是很困难的。
现在观察这种题是否有规律可循。
1.看C点:由A、由F和由D都可以到达C,而由F→C是由下向上走,由D→C是由右向左走,这两条路线不管以后怎样走都不可能是最短路线.因此,从A到C只有一条路线。
同样道理:从A到D、从A到E、从A到H也都只有一条路线。
我们把数字“1”分别标在C、D、E、H这四个点上,如图4—2。
2.看F点:从上向下走是C→F,从左向右走是E→F,那么从A点出发到F,可以是A →C→F,也可以是A→E→F,共有两种走法.我们在图4—2中的F点标上数字“2”.2=1+1.第一个“1”是从A→C的一种走法;第二个“1”是从A→E的一种走法。
3.看G点:从上向下走是D→G,从左向右走是F→G,那么从A→G我们在G点标上数字“3”.3=2+1,“2”是从A→F的两种走法,“1”是从A→D的一种走法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.研究目的在我国,配电网主要指110 kV 及以下系统。
配电网承担着给城市里各个配电站和各类用电负荷供给电源的任务,它直接和用户相连,因此对供电可靠性影响最大。
根据电力公司的统计,用户停电故障的80%以上是由电力系统中的配电环节引起的。
因而,对配电系统进行可靠性评估,提高配电系统的可靠性水平有着十分重要的意义。
进行可靠性评估的方法很多,有模拟法和解析法等,这里主要介绍解析法中的最小路法,基于最小路的配电系统可靠性评估算法考虑了分支线保护、隔离开关、分段断路器的影响,能够处理有无备用电源和有无备用变压器的情况,可以为不同接线方式的配电系统提供可靠性计算方法。
2.配电网主要可靠性指标配电系统基本的功能就是将电能从变电站传输给单个的用户负荷。
因此供电的连续性是衡量配电系统的一个很重要的指标,供电的连续性可以由三个基本的负荷点指标和一系列的系统指标来体现。
反映各负荷点可靠性的指标有:负荷点故障停运率λ(次/a);负荷点的年平均停运时间U(h/a);负荷点每次故障平均停运持续时间r(h/次)。
对N 个串联可修复元件,计算时采用以下公式: ()∑=+=n 1i '''i i λλλ (1)()()∑∑==++=ni i i i i i r r 1'''n 1i ''''''i r λλλλ (2) ∑=+=ni i i i i r r U 1''''''λλ (3)式中,λi ′为元件i 的故障停运率;λi "为元件i 的检修停运率;r i ′为元件i 的平均故障修复时间;r i " 为元件i 的平均检修持续时间。
对系统的可靠性评估指标采用IEEE 所提出的6个标准指标[4]:系统平均停电频率指标SAIFI 、系统平均停电持续时间SAIDI 、用户平均停电持续时间CAIDI 、平均供电可靠率ASAI 、平均供电不可靠率ASUI 、系统平均缺电指标AENS 。
3.最小路法[1,2]原理最小路法基本思想是:对每一负荷点求取其最小路,根据网络实际情况将非最小路上的元件故障对负荷点可靠性的影响,折算到相应的最小路节点上;仅对其最小路上元件与节点进行计算即可得到负荷点相应的可靠性指标。
该算法考虑了分支线保护、隔离开关、分段断路器及计划检修的影响,并且能够处理有无备用电源和有无备用变压器的情况;可以结合系统的实际配置,并能指出系统的最薄弱环节,但是对于由主馈线和分支线组成的相对复杂的系统,其最小路的求解和简化分析工作非常复杂。
此外,它对系统不着重关心的负荷节点的指标也做了大量的计算,耗费了不必要的时间。
下面用一个简单的辐射型系统见(见图1)介绍基于最小路的可靠性评估算法原理。
先求取每个负荷点到电源点的最小路,这样整个系统的元件便可分为最小路上的元件和非最小路上的元件2类。
例如,图1中对于负荷点2,它到电源点的最小路由主馈线1、2和分支线b 组成,这些线路上的元件为最小路上的元件,其他元件为非最小路上的元件。
对于最小路上元件处理原则如下:1)如果系统无备用电源,那么最小路上的每个元件发生故障或检修,均会引起负荷点的停运。
参与计算的是元件停运率()∑=+=n 1i '''i i λλλ和停运时间∑=+=ni i i i i r r U 1''''''λλ。
如图1所示,负荷2最小路上的主馈线1、2和分支线b 上的元件停运都会引起负荷点2的停运。
2)如果系统有备用电源,而且主馈线上装有分段装置(隔离开关、负荷开关或分段断路器),那么分段装置前的元件发生故障引起后段负荷点停运时间仅为max{t F ,t B }其中t F 为分段装置的操作时间,t B 为备用电源的倒闸操作时间; 而且认为前段元件的检修不会引起后段负荷点的停运。
以图1为例,主馈线1故障,负荷点2的停运时间仅为max{t F ,t B },如果主馈线1检修,则负荷点2不受影响。
除此之外,最小路的元件停运,均会引起负荷点的停运。
对于非最小路上的元件, 先根椐系统的结构,将其对负荷点可靠性指标的影响折算到相应的最小路节点上,然后按上述方法处理即可。
如图1所示,对于负荷点2,分支线a 的影响可以折算到节点A 上,主馈线3、4和分支线c 、d 的影响折算到节点B 上,这样非最小路上元件的影响便转化为最小路上的节点A 、B 的等效可靠性指标, 此时按照上面所讲的原则对A 、B 进行处理即可。
对于非最小路上的元件,根据系统的结构可分为以下几种情况处理。
对于分支线,如果其首端装有熔断器等分支线保护,那么分支线上的元件发生故障,熔断器熔断,故障不影响其他支线。
如图1中分支线c 故障,不影响负荷2和其他负荷的运行。
如果没有熔断器等分支线保护,则先求每个非最小路元件到电源的最短通路,并且找到通路上从元件出发的第一个开关或分段断路器,再判断开关或分段断路器是否位于负荷节点的最小路上。
如果通路上第一个开关或分段断路器不在负荷点的最小路上,则非最小路元件发生故障所引起的负荷点停运时间为开关或分段断路器的操作时间,并且检修不会引起前段负荷点的停运。
以图1为例,如主馈线3、4上元件故障,由于其到电源通路上的第一个开关或断路器QF2不在负荷点2的最小路上,则它们引起负荷2的停运时间仅为分段断路器的操作时间,并且检修时负荷2不停运。
如果通路上第一个开关或分段断路器在负荷点的最小路上,则开关不起作用,元件发生故障所引起的负荷点停运时间为元件停电时间。
如图1中馈线a 发生故障,由于其到电源的通路上的第一个隔离器件为QF1,并且在负荷点2的最小路上,则QF1不起作用,馈线a 故障或检修引起负荷2的停运时间就是馈线a的停运时间。
4.Dijkstra 算法利用最小路算法来解决可靠性问题,就必须求取网络的最小路径,Dijkstra算法是求取最小路径的经典算法,该算法包含了一个有权重的有向图G,以及G中的一个来源顶点V0。
我们以V表示G中所有顶点的集合。
每一个图中的边,都是两个顶点所形成的有序元素对。
4.1 基本思想:Dijkstra提出了按路径长度递增的顺序产生最短路径的方法,即:把图中所有顶点分成两组,第一组S 包括已经确定最短路径的顶点,初始时只含有源点;第二组V-S 中包括尚未包括最短路径的顶点,初始时含有图中除源点以外的所有其他顶点。
集合S每加入一个新的顶点i,都要修改顶点V0到集合V-S中剩余顶点的最短路径长度,按路径长度递增的顺序计算源点到各顶点的最短路径,逐个把第二组中的顶点加到第一组中去,直至S = V。
4.2 实现思路有向网用邻接矩阵cost [ ] [ ]表示,其中规定: (1) 两个顶点之间无直接路径,即< Vi ,Vj> 弧不存在的,矩阵中对应权值为无穷大; (2) 两个顶点之间有直接路径< Vi ,Vj > 的,矩阵中的权值就是< Vi ,Vj > 弧对应的公路长度; (3) < Vi ,Vi > 对应的值为0。
S 集合初始存放最短路径的源点,计算过程中将已经确定了最短路径的顶点加入到S 中去。
dist 数组最终存放源点到各顶点的最短路径结果。
Path 数组最终存放源点到各顶点的最短路径经过的顶点。
[3]图2 有权重的有向图G4.3 计算步骤(1) dist 初始存放源点到各顶点的权值。
(2) {dist (i) | Vi ∈(V - S) }中最小值对应的顶点就是从源点Vi 到其他顶点的最短路径中最短的一条所对应的顶点,即dist (j) = min{dist (i) | Vi∈(V - S) } 。
(3) 对于所有顶点Vk (Vk ∈(V - S) ) ,修改dist (k) 的值:dist (k) = min (dist [ k ] ,dist [ j ] + cost [ j ,k ])再在修改后的dist [ k ]中进行第二步,求得第二个j ,顶点Vj 加入S 集合中,第二条最短路径产生。
重复(2) (3) 步,直至求得从源点Vi 到各顶点的最短路径为止。
如图2所示,设a点为源点,b、c、d、e、f点为各个顶点,顶点分为两组,S组开始只有a点,V-S组开始有b、c、d、e、f点。
要求a点到这些顶点的最小路径。
步骤如下:(1)dist初始存放a点到其他顶点的权值(可理解为距离),如dist(b)=10km,dist(e)=5km,dist(c)=∞。
(2) {dist (i) | Vi ∈(V - S) }中最小值对应的顶点就是从源点a 到其他顶点的最短路径中最短的一条所对应的顶点,即dist (j) = min{dist (i) | Vi∈(V - S) } 。
由图可知min{dist (i) | Vi∈(V - S) }=5km,这里j=e,即最短路径的顶点为e,此时就把e点加入到集合S中。
(3)对V-S的所有顶点(现在包含b、c、d、f点)修改dist(k)的值:dist (k) = min (dist [ k ] ,dist [ j ] + cost [ j ,k ])如dist(b)= min (dist [ b ] ,dist [ b ] + cost [ e,b ])=min(10km, 10km+∞)=10kmdist(c)= min (dist [ c ] ,dist [ c ] + cost [ e,c ])= min (∞, ∞+∞)= ∞dist(d)= min (dist [ d ] ,dist [ e ] + cost [ e,d ])=min (8km,5km+2km)=7kmdist(f)= min (dist [ f ] ,dist [ e ] + cost [ e,f ])= min (∞,5km+4km)=9km在修改后的dist(k)中进行第二步,可以得到第二个j即d点,把d放入集合S中,即第二条最短路径产生,接着修改V-S中的dist(k),然后用第二个j进行(2)步,如此不断重复(2) (3) 步,直至求得从源点a 到各顶点的最短路径为止。
5.算例以某市输电系统下母线2的配电网为例,应用所提出等值法与最小路法相结合的方法对其进行可靠性评估计算。
该输电系统有43条35 kV线路,33个母线节点,5台发电机,总负荷220 MW。
取其母线2作为本文的算例。
母线2有1座35 kV变电所,4条出线,36条馈线,22个负荷点,12个断路器,2个联络开关,1 908户用户,总平均负荷12.291 MW。
配电系统各参数如表1、表2所示。
