改进型平行线法在非圆曲线插补中的应用
提高曲轴非圆磨削精度的插补方法

提高曲轴非圆磨削精度的插补方法
蔡晓敏;成超
【期刊名称】《机械制造》
【年(卷),期】2018(56)11
【摘要】为提高曲轴非圆磨削的精度,提出了一种分段多项式插补方法.这一插补方法引入中间参数P来构造函数,并根据磨削点的恒线速度确定插补参数步长△P.对这一插补方法的轮廓误差进行了分析与验证,确认这一插补方法的误差小,插补精度高.【总页数】4页(P71-73,95)
【作者】蔡晓敏;成超
【作者单位】南京邮电大学通达学院江苏扬州225000;扬州环锐科技有限公司江苏扬州 225000
【正文语种】中文
【中图分类】TH122
【相关文献】
1.一种计算曲轴非圆磨削中连杆颈受力变形的方法 [J], 吴晓健
2.曲轴磨削加工新方法与插补算法的研究 [J], 谢胜泉;朱国力;邓勇
3.曲轴非圆的恒当量磨削厚度磨削运动模型研究 [J], 吴钢华;何永义;田应仲
4.多面形非圆曲面数控磨削加工实时插补方法研究 [J], 邬义杰;项占琴
5.非圆磨削中曲轴角向定位方法及其误差分析 [J], 沈南燕;李静;方明伦;叶骏;汪学栋
因版权原因,仅展示原文概要,查看原文内容请购买。
非圆曲线数控插补的直接刀具半径补偿算法

非圆曲线数控插补的直接刀具半径补偿算法
马骏;宋颖慧
【期刊名称】《电加工》
【年(卷),期】1995(000)005
【摘要】本文通过对非圆二次曲线刀具补偿原理的分析,提出了一种新的刀补及算法,并给出了算法的计算机仿真,证明了其正确性与可行性。
最后,对算法进行了误差分析并提出了算法的改进方案,进一步提高了刀补的精度。
该方法同样适用于其它非圆曲线。
【总页数】5页(P13-16,24)
【作者】马骏;宋颖慧
【作者单位】不详;不详
【正文语种】中文
【中图分类】TG710.2
【相关文献】
1.基于NURBS曲线的非圆曲线数控插补算法研究 [J],
2.汽轮机叶片数控加工的直接插补算法研究 [J], 韩庆瑶;唐月夏;乐英
3.基于NURBS曲线直接插补算法的嵌入式数控系统设计与实现 [J], 过怡;刘凯
4.基于NURBS曲线直接插补算法的嵌入式数控系统设计与实现 [J], 寇明赟;
5.基于双圆弧步长伸缩数控插补非圆曲线算法的研究 [J], 陈明君;赵清亮;董申;李旦
因版权原因,仅展示原文概要,查看原文内容请购买。
非圆曲线的等误差直线逼近

曲线 的起点, 为 编程许 用
误差。现以 P 0 为圆心、 为
半径作 一 个误 差圆, 然 后 作
一条与误差圆、非圆曲线 y =
f ( x ) 均相切的直线, 即公切
线 m m , 切 点 分 别 为: PS
图 1 线性非 圆曲 线逼近图
( xS , yS ) 、PT ( xT , yT ) , 由此可得:
The lapping and cutting experiment of the diamond tools
Song Jian Wu Minjing
Abstract In this paper, four types material of diamond( natural singe crystal、DEBEERS MONODITE、PCD、CVD) are applied in the ex periment. Some basic data is gained and emphatically discusses the experimental conclusion. In the lapping experiment, the lapping meth od and efficiency and integrity of diamond tool are comprised, While the super precise cutting is done. Key words: PCD tools CVD tools Natural diamond tools Surface finish
PCD 聚晶金刚石刀具、PCBN( 聚晶立方氮化硼) 切 削工具以及 CVD 薄膜与厚膜金刚石切削工具、类金刚 石膜( DLC) 、金刚石膜和 CBN 膜涂层切削工具有广阔 的应用前景, 尤其是精密和超精密加工技术发展对切 削工具的需求, 促使这些切削工具迅猛发展。
数控编程非圆曲线数学的处理过程d

数控编程非圆曲线数学处理的基本过程数控系统一般只能作直线插补和圆弧插补的切削运动。
如果工件轮廓是非圆曲线,数控系统就无法直接实现插补,而需要通过一定的数学处理。
数学处理的方法是,用直线段或圆弧段去逼近非圆曲线,逼近线段与被加工曲线交点称为节点。
例如,对图1.42所示的曲线用直线逼近时,其交点A、B、C、D、E、F等即为节点。
图1.42零件轮廓的节点在编程时,首先要计算出节点的坐标,节点的计算一般都比较复杂,靠手工计算已很难胜任,必须借助计算机辅助处理。
求得各节点后,就可按相邻两节点间的直线来编写加工程序。
这种通过求得节点,再编写程序的方法,使得节点数目决定了程序段的数目。
如图1.42中有6个节点,即用五段直线逼近了曲线,因而就有五个直线插补程序段。
节点数目越多,由直线逼近曲线产生的误差δ越小,程序的长度则越长。
可见,节点数目的多少,决定了加工的精度和程序的长度。
因此,正确确定节点数目是个关键问题,也请参考本教程CAD/CAM 部分数控加工误差的组成图1. 43逼近误差数控加工误差△数加是由编程误差△编、机床误差△机、定位误差△定、对刀误差△刀等误差综合形成。
即:△数加=f(△编+△机+△定+△刀)其中:(1)编程误差△编由逼近误差δ、圆整误差组成。
逼近误差δ是在用直线段或圆弧段去逼近非圆曲线的过程中产生,如图1.43所示。
圆整误差是在数据处理时,将坐标值四舍五入圆整成整数脉冲当量值而产生的误差。
脉冲当量是指每个单位脉冲对应坐标轴的位移量。
普通精度级的数控机床,一般脉冲当量值为0.01mm;较精密数控机床的脉冲当量值为0.005mm 或0.001mm等。
(2)机床误差△机由数控系统误差、进给系统误差等原因产生。
(3)定位误差△定是当工件在夹具上定位、夹具在机床上定位时产生的。
(4)对刀误差△刀是在确定刀具与工件的相对位置时产生。
数控程序编制中的数值计算根据零件图样,按照已确定的加工路线和允许的编程误差,计算数控系统所需输入的数据,称为数控加工的数值计算。
浅谈非圆曲线在数控车床加工程序中的应用

X= U+S Y=V+T
后 Z值 1 G x 1Z 1F2 1 # 4 # 5 10
( 线 插 补进 给 , 直
① 取 △ 初值 , 取 01 x 一般 . 。 ②计算 (i i( 123 x, )i ,,…… ) y - 。 ③ 误 差验算 。 设 任一 逼 近直线 MN ,其 方程 为 : + y a b+ x c0则 与 M =, N平 行且 距离 为 8允 的直线 MN '
X ro01 = cs Y rn 1 =s 0 i 由0 =20 得: 10 — 可 X r s0 — ) =c ( 2 0 o Y ri 2 0 =s 0 — n 1)
X=X"o 0 Y i 0 c s + sn Y=Y i 一 c s sn0 X o O
X'ro0 =cs 2 Y =s 0 ' i 2 rn
N X5 2 3 ( X方 向退 出 ) M S 60 3 10 ( 主轴 正转 10r i) 60/ n m G0 12 7PQ ( 轮廓精 加 工循环 ) G x o Z0 M 9 0 l o 10 0 ( 刀 到 X0, 退 10 Z 0 , 闭切 削液 ) 10关 M 5 ( 主轴 停止 ) M3 0 ( 程序 结束 ) 结束 语 总之 ,数 控加 工工 艺 与编程 是一 门重 要 的专业课 程 , 论 和实 践性 强 , 对所 学 的专 理 是 图 2买 例 图 业 知识 的综合 应 用 。本 文 由理论 到 实例 较好 0 06 00 (0 6 主程序 ) 0o 号 地 解决 了非 圆 曲线 的旋转 问题 ,并 在实 践加 T 11 9 0 0G 8 ( 用 1 刀具 , 定 工 中得 到证 实 。研 究非 圆曲线 处理 方法 和过 调 号 确 进 给速度 单位 为 mr i) rm n d 程 , 于合 理选择 编程 方法 、 化编 程及 自动 对 优 M380 S0 ( 主轴 正转 80/i) 0r n 编程软件的二次开发,都有着积极 的指导意 a r G x 5 1 O 3z 0 ( 快速 定位 ) 义。 G 1O 20 0Z F 0M3 ( 进 给 到 Z向 参 考文献
非圆曲线类零件的优化加工路径

非圆曲线类零件的优化加工路径田杨【摘要】在对非圆曲线轴类零件进行加工程序编制时,对其加工区域以剩余切削面积最小为目标函数建立了数学模型,寻找了一种新型的加工方法,并且应用宏程序编制具体的零件程序,通过对仿形法和优化后编制的程序进行对比,优化后的加工路径比仿形法的加工路径节省了加工时间,提高了生产效率.【期刊名称】《制造业自动化》【年(卷),期】2012(034)005【总页数】2页(P52-53)【关键词】非圆曲线;宏程序;优化【作者】田杨【作者单位】辽宁工程职业学院,铁岭112000【正文语种】中文【中图分类】TH130 引言在数控车加工中,往往遇到非圆曲线轴类零件的加工,例如抛物线类零件、椭圆类零件和双曲线类零件。
加工这类零件大多数采用仿形后层层切削的方法,这种方法增加了走刀路线,增加了空运行时间。
这里的走刀路线是指刀具刀位点相对于工件运动的轨迹,也称为进给路线,走刀路线对零件的加工质量和加工效率有着直接的影响,所以要合理的选择加工路线,应尽量使加工路线最短,以减少加工路线的距离,减少空运行的时间,提高加工效率,而且应尽量简化数学处理时的数值计算量,以简化编程工作[1]。
1 优化模型的建立[2]1.1 抛物线类零件优化模型当抛物线方程确定后,直线方程在抛物线上方,设A点坐标为(x1,n),B点坐标为(0, x2)。
这样可以以A、B点坐标确定直线方程,使切削区域剩余面积最小,即图中阴影部分面积最小。
因为抛物线方程是确定的,所以由抛物线围成的面积设为SA,直线和x坐标上部分围成的面积为SB,剩余的面积为SC,则SC=m×n-SASB,其中三角形面积为SB=x1(n-x2)/2,当直线与抛物线方程联立后,因为不能产生过且的现象,所以要求Δ≤0即:其中:k=-m/xn,m/x1,b=x2。
优化目标函数:图1 抛物线类零件切削区域1.2 椭圆类零件优化模型设椭圆方程为:z2/a2+x2/b2=1,直线方程为:x=kz+w,在椭圆的上方,A点坐标为(x1,n),B点坐标为(m, x2)。
一种改进的NURBS插补算法

n
p( u)
∑ω d N i = 0 i i i, k =n
( u)
∑ωN j = 0 j j, k ( u )
n
=
∑d
i=0
i
R
i,
k
(
u)
(1)
R i, k ( u)
=
ωiN i, k ( u)
n
u∈[ 0, 1 ]
(2)
∑ωN j = 0 j j, k ( u)
其中 : R i, k ( u) ( i = 0, 1, …, n)称为 k次有理基函数 。
有考虑加减速过程中的速度变化要求 , 而且没有保证
插补精度 。
通过对文献 [ 2 ] 中算法的改进 , 本文提出一种 基于等弧长的可调步长插补算法 。该方法能够在运行
过程中 , 根据当前刀具位置 , 按照误差要求和加减速 状态 , 动态调整下一点的位置 。该算法能够保证较高 的插补速度 , 而且具有对机床冲击小 、速度平稳等优
( i = 3, 4, …, n)
(6)
将上式代入式 ( 1) 后 , 可以通过二分法求解 。 214 可调步长插补算法的实现方法
212 样条曲线总弧长计算
在上 面 的 计 算 中 ,
由式 (5) 、( 6) , 可以求得在第 i段上的参数增量 没有 考 虑 插 补 过 程 中 的
步长 d li:
( k3
d li )
(8)
∑ωN j = i - 3 j j, 3 ( k3 d li )
由式 ( 8) , 可以求得整段 NURBS曲线的弧长 :
L
n Mi
∑∑
i=3 k =1
n Mi
∑ ∑ds i = 3 k = 1 ik = ( X i, k - X i, k - 1 ) 2 + ( Yi, k - Yi, k - 1 ) 2 + ( Z i, k - Z i, k - 1 ) 2
GSK980TDc系统非圆曲线插补指令的应用
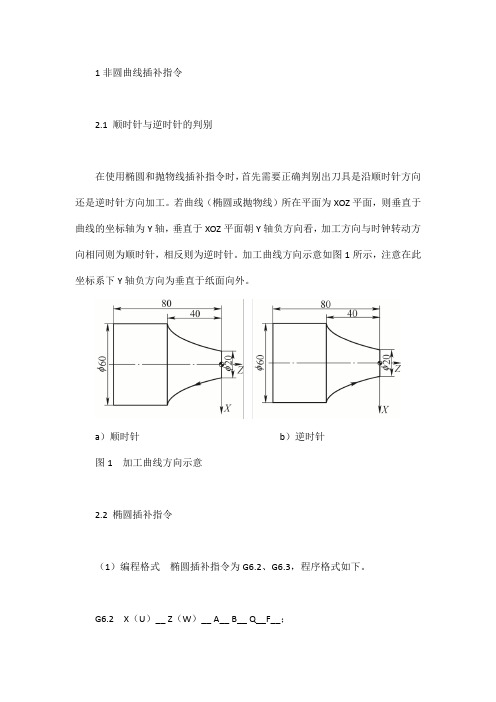
1非圆曲线插补指令2.1 顺时针与逆时针的判别在使用椭圆和抛物线插补指令时,首先需要正确判别出刀具是沿顺时针方向还是逆时针方向加工。
若曲线(椭圆或抛物线)所在平面为XOZ平面,则垂直于曲线的坐标轴为Y轴,垂直于XOZ平面朝Y轴负方向看,加工方向与时钟转动方向相同则为顺时针,相反则为逆时针。
加工曲线方向示意如图1所示,注意在此坐标系下Y轴负方向为垂直于纸面向外。
a)顺时针b)逆时针图1加工曲线方向示意2.2 椭圆插补指令(1)编程格式椭圆插补指令为G6.2、G6.3,程序格式如下。
G6.2 X(U)__ Z(W)__ A__ B__ Q__F__;G6.3 X(U)__ Z(W)__ A__ B__ Q__F__;其中,X、Z为椭圆终点的绝对坐标值;U、W为椭圆终点相对于椭圆起点的坐标增量;A为椭圆长半轴长(绝对值);B为椭圆短半轴长(绝对值);F为进给速度。
(2)Q参数的取值Q参数用于表征椭圆长轴与坐标系Z轴的夹角,其示意如图2所示。
其是指在右手直角笛卡尔坐标系中,顺着Y轴负方向看XOZ平面,Z轴正方向沿顺时针方向旋转到与椭圆长轴重合时所经过的角度。
在程序中,Q 参数的取值为该角度相对于0.001°的倍数,例如,若该夹角为180°,则程序中需输入“Q180000”。
a)前置刀架b)后置刀架图2Q参数示意(3)编程示例示例1如图3所示,椭圆加工程序如下。
G6.2 X55.0 Z-25.0 A25 B12.5 Q0 F80;或G6.2 U25.0 W-25.0 A25 B12.5 Q0 F80;图3示例1示例2如图4所示,椭圆长半轴长为48mm,短半轴长为25mm,椭圆长轴与坐标系Z轴的夹角为60°。
椭圆加工程序如下。
G6.2 X63.82 Z-50.0 A48 B25 Q60000 F80;或G6.2 U20.68 W-50.0 A48 B25 Q60000 F80;图4示例22.3 抛物线插补指令抛物线插补指令为G7.2、G7.3,程序格式如下。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
蔡慧林 ’ ,任恩恩 ,彭珍瑞 ’
CAI ii1 RE En e 2 PENG e -u’ .n , N — n , Hu 1 Zh n r i
(. 1 兰州交通大学 机 电工程学院 .兰州 7 0 7 ;2 兰州交通大学 电子与信息工程学院 ,兰州 7 0 7 ) 3 00 . 3 0 0
拟 合进行 节点计 算 。对测 量数据所 描述 的曲线,可 先采用最 小二乘法 、 小能量 法 、 UR 最 N BS曲面插 值 等方法[ 3 等先求得 曲线 方程, 用直线或 圆弧对 曲 再
标为S ( ) 终点坐标为 E (i ) 起点与终点 Y , ix , , + Y 均 在 曲线上 。
、 . 化 l 8
E (i 。 此方法需对 曲线进行坐标转换, i + o X 且在计 算 时,需 采用迭 代法 ,计算 比较麻 烦 。
Ng. L 的距离为 N i
一
l +()尼 厂 ) — f q 一(f k X+ i
() 5
D 图 1平行线法的节点坐标计算
Ax
补 时计算 比较方便 ,但 插补段数 较 多,且 当曲线 的
L,最后计 算直线 £与 曲线 y ) 的交点 巨 的坐标, 如图 1 示 。在 数值 计算过程 中, 由于要求取 误差 所 圆的 方程,计算 中必须求 解高 次方程组 ,曲线的次 数越 高,方程 组的次 数就越 高 ,计 算 比较 复杂 。 采用局部 坐标法 进行节 点坐标 计算时 ,首先 以 上一节 点 ( f 直线段 的起 点 ) 为原点 、X轴通 第 段 ’
例证明了该方法的有效性。 关键 词:非圆曲线 ; 补;平行线法;节点计算:等 误差 插 中图分类号:T I 5 H 6 文献标识码 :A 文章编号 :1 0- 1 4 2 1 )4 05 一 2 9 0 3 ( 00 0 — 常遇 到对非 圆 曲线轮 廓进 行数控
图 3 改 进 型平 行线 法 的 节 点 坐标 计 算
采用 平行线法 进行 节点计 算时,首 先以上一节
点 ( i 第 段直 线段的起 点 ) 为 圆心,以拟合误 差
为半 径作 误差 圆, 求取误 差 圆与 曲线的 公切线 L’ , 然后 ,求 取过误 差 圆圆心、且与 直线 £’ 的直线 平行
线 进行二次 拟合来 进行 节点计算 。直线拟 合可采 用 等 步长插补 与等误 差插补 两种方 法。采用 等步长插
r
1 等误差直线插补
设 非圆 曲线 段, 点坐标 为y ) 曲线 的终 点 起 ,
坐标 为 ( Y) X, ,曲线 在该范 围无 拐点,数 值拟合 时
允许 拟合误 差为 。设 第段拟 合直 线段 £ 的起点坐
是轮廓 曲线为 测量数据 所描述 的 曲线。对 轮廓 曲线 方程 已知 的 曲线,可直接 对其采 用直 线拟合 或圆弧
l 匐 m
改进型平行线法在非 圆曲线插补 中的应用
Ap l a i n o p o e a a l li e a s i h n e p a i n t on c r u a u v p i to fi r v d p r l n s me n t e it r olto o n - ic l r r e c m eI n c
过 欲求 的下一节 点E 建立 局部坐 标 系, 图2 示, 如 所
曲率变化较 大时 ,允许 的插 补误差 不能得 到有效 利
用 。等误 差插补 能充分 利用允许 插补误 差 ,插补 直 线段段 数 少,能 显著减小 编程工 作量 。在 等误差插
补节 点计算 中,目前常 用的方法 有平 行线法 和局部 坐标[。 两种 方法的数 值计算 量都 比较大 , 别是 7这 】 特
然 后 ,将坐 标 系 xy中的 曲线 ) ) o , 转换 到坐标 系 艘 中, 即获得 曲线在局部坐标系中的表达式
d’ v
X。
’ ) ,
在局部坐标系中利用条件 =0 求得 X g 叻的表 '’ (
达 式后 ,将 ( 入 ) g = 求取 ,从而求得 代 J ) f
加工 。由于 目前 大部分数 控 系统 只具 有直线插 补与 圆弧插补 功能 ,编 写数控加 工程序 时,需要采 用直 线段或 圆弧段对 非 圆曲线进行 拟合H 】非 圆曲线 轮 。 廓 有两种 情况,一种 是轮廓 曲线方 程 已知 ,另一种
误 差得 到充分 利用 的同时,降 低 了计 算过程 的复杂 度,具 有很好 的实用价 值 。
摘
要 :采用 直线插补对非圆曲线轮廓进行数控加工时,等误差插补的拟合直线段数最少,有利于数 控程序的输入与调试 。 以往采用的平行线法或局部坐标法 , 计算都 比较繁琐。 通过 对平行线法 和局 部坐标法进 行研究 , 提出了改进型平行线法。 该方法利用曲线 导数进行节点 计算 , 无需求 取误差圆 , 降低了等误差插补数值计算的复杂度, 对各种非圆曲线具有 良好的适应性 。 计算实
基盒项 目:兰州市科技专项资助(0 5 ) 2 7 0一基于网络与软 插件技术的 D NC集成制造技术及应用(0 71) 2 0 —o 作者简介 :蔡慧林 (9 5一) 16 ,男 ,教授 ,博士生 ,主要从事机械 制造 、数控技术及应用的科研与教学工作。 【2 第 3 5】 2卷 第 4 期 21- 00 4
曲线的次数较高时,计算非常麻烦。为简化等误差 拟合 中的计算工 作 ,本 文在对平 行线法 和局部 坐标 法进行研 究 的基 础上 ,提 出了一 种改进 型的等误 差
平行线插 补方法 。采用 该方法利 用 曲线方程 的导数 进行节 点计算 ,无需 求取误 差圆 ,在保 证允许插 补
收稿日期 : 0 90 —5 2 0 —6 1
