2018年江苏省镇江市中考数学试卷(含答案与解析)
专题3.13 江苏镇江(试题解读)-2018中考数学真题之名师立体解读高端精品

一、纵观全局,试卷评价(一)准确把握对数学知识与技能的考查从知识点上看,在命题方向上,没有太多的起伏;从内容上看,对这些知识点的考查并不放在对概念、性质的记忆上,而是对概念、性质的理解与运用上,通过现实生活来体验数学的妙趣。
(二)着重考查学生数学思想的理解及运用数学能力是学好数学的根本,主要表现为数学的思想方法。
其中数形结合思想、方程与函数思想、分类讨论思想等几乎是历年中考试卷考查的重点,必须引起足够重视。
1)分类讨论思想:当面临的问题不宜用统一方法处理时,就得把问题按照一定的原则或标准分为若干类,然后逐类进行讨论,再把结论汇总,得出问题的答案。
例如:今年中考数学题对分类讨论思想特别重视,如综合题第26题是圆与平行四边形的综合题,考查了圆的切线的性质、勾股定理、平行四边形性质和面积公式,第2问注意利用分类讨论的思想。
2)“化归”是转化和归结的简称。
总的指导思想是把未知问题转化为能够解决的问题,这就是化归思想。
例如第24题考查解直角三角形的应用﹣仰角俯角问题,解答本题的关键是明确题意,作出合适的辅助线转化为三角形问题,同时可以建立方程。
3)数形结合思想:指将数量与图形结合起来分析、研究、解决问题的一种思维策略,具有直观形象。
例如第28题二次函数背景的代数几何综合题,综合考查二次函数、一次函数、三角形相似的性质,应用数形结合的数学思想.。
(三)关注数学知识解决实际问题的考查数学来源于生活,同时也运用于生活,学数学就是为了解决生活中所碰到的问题。
(四)注重数学活动过程的考查这几年不仅关注对学生学习结果的评价,也关注对他们数学活动过程的评价;不仅关注数学思想方法的考查,还关注他们在一般性思维方法与创新思维能力的发展等方面的评价,尤其是注重对学生探索性思维能力和创新思维能力的考查;不仅关注知识的教学,更多的是要关注对学生数学思维潜力的开发与提高。
二、明晰试题,看明细表y=。
江苏省镇江市2018届数学中考一模试卷及参考答案

的度数等于( )
A . 55° B . 50° C . 45° D . 40°
4. 如图,一次函数
(
标为1,则关于 的不等式
)的图像与正比例函数 的解集为( )
(
)的图像相交于点 ,已知点 的横坐
A. B.
C.
D.
5. 阅读:设试验结果落在某个区域S中每一点的机会均等,用A表示事件“试验结果落在S中的一个小区域M中”,那么事
江苏省镇江市2018届数学中考一模试卷
一、单选题
1. 截止到2017年12月,全国移动互联网4G用户总数为947 000 000,这个数用科学记数法表示为( )
A.
B.
C.
D.
2. 如图是由6个大小相同的小正方体组成的几何体,它的俯视图是( )
A.
B.
C.
3. 有一张平行四边形纸片ABCD,已知
D. ,按如图所示的方法折叠两次,则
点构成正三角形,那么我们称这个抛物线为正三角抛物线.
(1) 抛物线
正三角抛物线;(填“是”或“不是”)
(2) 如图,已知二次函数
(m > 0)的图像是正三角抛物线,它与x轴交于A、B两点(点A在点B
的左侧),点E在y轴上,当∠AEB=2∠ABE时,求出点E的坐标.
参考答案
1.
2.
3.
4.
5.
6.
7.
(1) 证明:△ADE≌△CBF ;
(2) 连接AF、CE,四边形AECF是菱形吗?说明理由.
23. 如图,一次函数
与反比例函数
的图像交于点
和点
交于点A、B.
,与x轴、y轴
(1) , ;
(2) 将线段AB沿x轴的正方向平移,使得点B的对应点恰好落在反比例函数
2018年江苏省镇江市中考数学二模试卷(解析版)
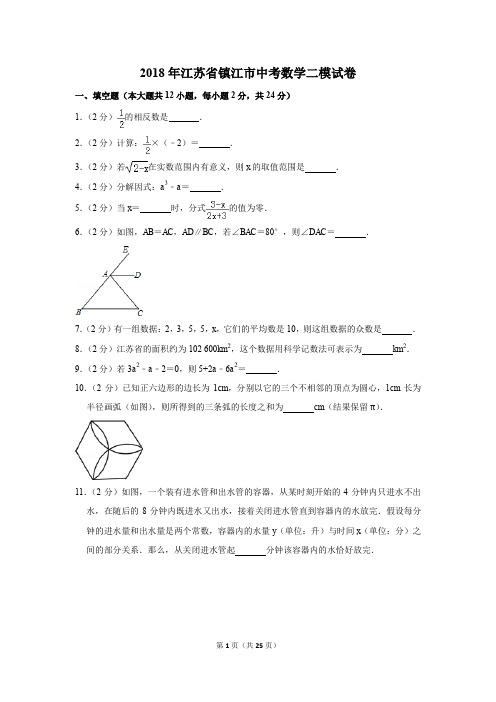
2018年江苏省镇江市中考数学二模试卷一、填空题(本大题共12小题,每小题2分,共24分)1.(2分)的相反数是.2.(2分)计算:×(﹣2)=.3.(2分)若在实数范围内有意义,则x的取值范围是.4.(2分)分解因式:a3﹣a=.5.(2分)当x=时,分式的值为零.6.(2分)如图,AB=AC,AD∥BC,若∠BAC=80°,则∠DAC=.7.(2分)有一组数据:2,3,5,5,x,它们的平均数是10,则这组数据的众数是.8.(2分)江苏省的面积约为102 600km2,这个数据用科学记数法可表示为km2.9.(2分)若3a2﹣a﹣2=0,则5+2a﹣6a2=.10.(2分)已知正六边形的边长为1cm,分别以它的三个不相邻的顶点为圆心,1cm长为半径画弧(如图),则所得到的三条弧的长度之和为cm(结果保留π).11.(2分)如图,一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的部分关系.那么,从关闭进水管起分钟该容器内的水恰好放完.12.(2分)如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME 的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为S3;…当AB=n时,△AME的面积记为S n.当n≥2时,S n﹣S n﹣1=.二、选择题(本小题共5小题,每小题3分,共15分)13.(3分)下列运算正确的是()A.a﹣3a=2a B.(ab2)0=ab2C.=D.×=9 14.(3分)下面四个几何体中,左视图是四边形的几何体共有()A.1个B.2个C.3个D.4个15.(3分)用半径为8的半圆围成一个圆锥的侧面,则圆锥的底面半径等于()A.4B.6C.16πD.816.(3分)二次函数y=﹣x2﹣4x+5的最大值是()A.﹣7B.5C.0D.917.(3分)如图,在Rt△ABC中,∠ABC=90°,BA=BC.点D是AB的中点,连结CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下四个结论:①=;②点F是GE的中点;③AF=AB;④S△ABC=5S△BDF,其中正确的结论序号是()A.4个B.3个C.2个D.1个三、解答题(本题共81分)18.(8分)(1)计算:(﹣2)﹣2+cos60°﹣(﹣2)0;(2)化简:(a﹣)÷.19.(9分)(1)解方程:﹣=0;(2)解不等式组,并把所得解集表示在数轴上.20.(6分)如图,AE∥FD,AE=FD,B、C在直线EF上,且BE=CF,(1)求证:△ABE≌△DCF;(2)试证明:以A、B、D、C为顶点的四边形是平行四边形.21.(6分)某中学开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的统计图,已知“查资料”的人数是40人.请你根据以上信息解答下列问题:(1)在扇形统计图中,“玩游戏”对应的圆心角度数是度;(2)补全条形统计图;(3)该校共有学生1200人,估计每周使用手机时间在2小时以上(不含2小时)的人数.22.(6分)小明和小刚玩“石头、剪刀、布”的游戏,每一局游戏双方各自随机做出“石头”、“剪刀”、“布”三种手势的一种,规定“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,相同的手势是和局.(1)用树形图或列表法计算在一局游戏中两人获胜的概率各是多少?(2)如果两人约定:只要谁率先胜两局,就成了游戏的赢家.用树形图或列表法求只进行两局游戏便能确定赢家的概率.23.(6分)如图,一枚运载火箭从距雷达站C处5km的地面O处发射,当火箭到达点A,B时,在雷达站C测得点A,B的仰角分别为34°,45°,其中点O,A,B在同一条直线上.(1)求A,B两点间的距离(结果精确到0.1km).(2)当运载火箭继续直线上升到D处,雷达站测得其仰角为56°,求此时雷达站C和运载火箭D两点间的距离(结果精确到0.1km).(参考数据:sin34°=0.56,cos34°=0.83,tan34°=0.67.)24.(6分)如图,一次函数y1=﹣x﹣1的图象与x轴交于点A,与y轴交于点B,与反比例函数y2=图象的一个交点为M(﹣2,m).(1)求反比例函数的解析式;(2)当y2>y1时,求x的取值范围;(3)求点B到直线OM的距离.25.(6分)如图,∠AOB=45°,点M,N在边OA上,点P是边OB上的点.(1)利用直尺和圆规在图1确定点P,使得PM=PN;(2)设OM=x,ON=x+4,①若x=0时,使P、M、N构成等腰三角形的点P有个;②若使P、M、N构成等腰三角形的点P恰好有三个,则x的值是.26.(8分)如图,△ABC内接于⊙O,CD是⊙O的直径,AB与CD交于点E,点P是CD 延长线上的一点,AP=AC,且∠B=2∠P.(1)求证:P A是⊙O的切线;(2)若PD=,求⊙O的直径;(3)在(2)的条件下,若点B等分半圆CD,求DE的长.27.(10分)阅读下列材料:题目:如图,在△ABC中,已知∠A(∠A<45°),∠C=90°,AB=1,请用sin A、cos A 表示sin2A.28.(10分)平面直角坐标系xOy(如图),抛物线y=﹣x2+2mx+3m2(m>0)与x轴交于点A、B(点A在点B左侧),与y轴交于点C,顶点为D,对称轴为直线l,过点C作直线l的垂线,垂足为点E,联结DC、BC.(1)当点C(0,3)时,①求这条抛物线的表达式和顶点坐标;②求证:∠DCE=∠BCE;(2)当CB平分∠DCO时,求m的值.2018年江苏省镇江市中考数学二模试卷参考答案与试题解析一、填空题(本大题共12小题,每小题2分,共24分)1.(2分)的相反数是﹣.【解答】解:的相反数是﹣.故答案为:﹣.2.(2分)计算:×(﹣2)=﹣1.【解答】解:×(﹣2)=﹣1,故答案为:﹣1.3.(2分)若在实数范围内有意义,则x的取值范围是x≤2.【解答】解:由题意得,2﹣x≥0,解得,x≤2,故答案为:x≤2.4.(2分)分解因式:a3﹣a=a(a+1)(a﹣1).【解答】解:a3﹣a,=a(a2﹣1),=a(a+1)(a﹣1).故答案为:a(a+1)(a﹣1).5.(2分)当x=3时,分式的值为零.【解答】解:依题意得:3﹣x=0且2x+3≠0.解得x=3,故答案是:3.6.(2分)如图,AB=AC,AD∥BC,若∠BAC=80°,则∠DAC=50°.【解答】解:∵AB=AC,∠BAC=80°,∴∠B=∠C=(180°﹣80°)÷2=50°;∵AD∥BC,∴∠DAC=∠C=50°,故答案为50°.7.(2分)有一组数据:2,3,5,5,x,它们的平均数是10,则这组数据的众数是5.【解答】解:由题意得,(2+3+5+5+x)=10,解得:x=35,这组数据中5出现的次数最多,则这组数据的众数为5.故答案为:5.8.(2分)江苏省的面积约为102 600km2,这个数据用科学记数法可表示为 1.026×105km2.【解答】解:102 600=1.026×105km2.9.(2分)若3a2﹣a﹣2=0,则5+2a﹣6a2=1.【解答】解;∵3a2﹣a﹣2=0,∴3a2﹣a=2,∴5+2a﹣6a2=5﹣2(3a2﹣a)=5﹣2×2=1.故答案为:1.10.(2分)已知正六边形的边长为1cm,分别以它的三个不相邻的顶点为圆心,1cm长为半径画弧(如图),则所得到的三条弧的长度之和为2πcm(结果保留π).【解答】解:方法一:先求出正六边形的每一个内角=,所得到的三条弧的长度之和=3×=2πcm;方法二:先求出正六边形的每一个外角为60°,得正六边形的每一个内角120°,每条弧的度数为120°,三条弧可拼成一整圆,其三条弧的长度之和为2πcm.故答案为:2π.11.(2分)如图,一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的部分关系.那么,从关闭进水管起8分钟该容器内的水恰好放完.【解答】解:由函数图象得:进水管每分钟的进水量为:20÷4=5升设出水管每分钟的出水量为a升,由函数图象,得20+8(5﹣a)=30,解得:a=,故关闭进水管后出水管放完水的时间为:30÷=8分钟.故答案为:8.12.(2分)如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME 的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为S3;…当AB=n时,△AME的面积记为S n.当n≥2时,S n﹣S n﹣1=.【解答】解:方法一:连接BE.∵在线段AC同侧作正方形ABMN及正方形BCEF,∴BE∥AM,∴△AME与△AMB同底等高,∴△AME的面积=△AMB的面积,∴当AB=n时,△AME的面积记为S n=n2,S n﹣1=(n﹣1)2=n2﹣n+,∴当n≥2时,S n﹣S n﹣1=.方法二:如图所示:延长CE与NM,交于点Q,∵线段AC=n+1(其中n为正整数),∴当AB=n时,BC=1,∴当△AME的面积记为:S n=S矩形ACQN﹣S△ACE﹣S△MQE﹣S△ANM,=n(n+1)﹣×1×(n+1)﹣×1×(n﹣1)﹣×n×n,=n2,当AB=n﹣1时,BC=2,∴此时△AME的面积记为:S n﹣1=S矩形ACQN﹣S△ACE﹣S△MQE﹣S△ANM,=(n+1)(n﹣1)﹣×2×(n+1)﹣×2×(n﹣3)﹣×(n﹣1)(n﹣1),=n2﹣n+,∴当n≥2时,S n﹣S n﹣1=n2﹣(n2﹣n+)=n﹣=.故答案为:.二、选择题(本小题共5小题,每小题3分,共15分)13.(3分)下列运算正确的是()A.a﹣3a=2a B.(ab2)0=ab2C.=D.×=9【解答】解:A、a﹣3a=﹣2a,故此选项错误;B、(ab2)0=1,故此选项错误;C、=2,故此选项错误;D、×=9,正确.故选:D.14.(3分)下面四个几何体中,左视图是四边形的几何体共有()A.1个B.2个C.3个D.4个【解答】解:因为圆柱的左视图是矩形,圆锥的左视图是等腰三角形,球的左视图是圆,正方体的左视图是正方形,所以,左视图是四边形的几何体是圆柱和正方体,故选:B.15.(3分)用半径为8的半圆围成一个圆锥的侧面,则圆锥的底面半径等于()A.4B.6C.16πD.8【解答】解:由题意知:底面周长=8π,∴底面半径=8π÷2π=4.故选:A.16.(3分)二次函数y=﹣x2﹣4x+5的最大值是()A.﹣7B.5C.0D.9【解答】解:y=﹣x2﹣4x+5=﹣(x+2)2+9,即二次函数y=﹣x2﹣4x+5的最大值是9,故选:D.17.(3分)如图,在Rt△ABC中,∠ABC=90°,BA=BC.点D是AB的中点,连结CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下四个结论:①=;②点F是GE的中点;③AF=AB;④S△ABC=5S△BDF,其中正确的结论序号是()A.4个B.3个C.2个D.1个【解答】解:∵∠ABC=90°,BG⊥CD,∴∠ABG+∠CBG=90°,∠BCD+∠CBG=90°,∴∠ABG=∠BCD,在△ABC和△BCD中,,∴△ABG≌和△BCD(ASA),∴AG=BD,∵点D是AB的中点,∴BD=AB,∴AG=BC,在Rt△ABC中,∠ABC=90°,∴AB⊥BC,∵AG⊥AB,∴AG∥BC,∴△AFG∽△CFB,∴=,∵BA=BC,∴=,故①正确;∵△AFG∽△CFB,∴==,∴FG=FB,∵FE≠BE,∴点F是GE的中点不成立,故②错误;∵△AFG∽△CFB,∴==,∴AF=AC,∵AC=AB,∴AF=AB,故③正确;过点F作MF⊥AB于M,则FM∥CB,∴==,∵=,∴==•=•=,故④错误.综上所述,正确的结论有①③共2个.故选:C.三、解答题(本题共81分)18.(8分)(1)计算:(﹣2)﹣2+cos60°﹣(﹣2)0;(2)化简:(a﹣)÷.【解答】解:(1)(﹣2)﹣2+cos60°﹣(﹣2)0=﹣1=﹣1=;(2)(a﹣)÷===.19.(9分)(1)解方程:﹣=0;(2)解不等式组,并把所得解集表示在数轴上.【解答】解:(1)方程两边都乘以(1﹣2x)(x+2)得:x+2﹣(1﹣2x)=0,解得:x=﹣,检验:当x=﹣时,(1﹣2x)(x+2)≠0,所以x=﹣是原方程的解,所以原方程的解是x=﹣;(2),∵解不等式①得:x>1,解不等式②得:x>3,∴不等式组的解集为x>3,在数轴上表示为:.20.(6分)如图,AE∥FD,AE=FD,B、C在直线EF上,且BE=CF,(1)求证:△ABE≌△DCF;(2)试证明:以A、B、D、C为顶点的四边形是平行四边形.【解答】(1)证明:∵AE∥DF,∴∠AEF=∠DFE,∴∠AEB=∠DFC,∵AE=FD,BE=CF,∴△AEB≌△DFC.(2)解:连接AC、BD.∵△AEB≌△DFC,∴AB=CD,∠ABE=∠DCF,∴AB∥DC,∴四边形ABDC是平行四边形.21.(6分)某中学开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的统计图,已知“查资料”的人数是40人.请你根据以上信息解答下列问题:(1)在扇形统计图中,“玩游戏”对应的圆心角度数是126度;(2)补全条形统计图;(3)该校共有学生1200人,估计每周使用手机时间在2小时以上(不含2小时)的人数.【解答】解:(1)根据题意得:1﹣(40%+18%+7%)=35%,则“玩游戏”对应的圆心角度数是360°×35%=126°;故答案为:126;(2)根据题意得:40÷40%=100(人),∴3小时以上的人数为100﹣(2+16+18+32)=32(人),补全条形统计图,如图所示:(3)根据题意得:1200×64%=768(人),则每周使用手机时间在2小时以上(不含2小时)的人数约有768人.22.(6分)小明和小刚玩“石头、剪刀、布”的游戏,每一局游戏双方各自随机做出“石头”、“剪刀”、“布”三种手势的一种,规定“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,相同的手势是和局.(1)用树形图或列表法计算在一局游戏中两人获胜的概率各是多少?(2)如果两人约定:只要谁率先胜两局,就成了游戏的赢家.用树形图或列表法求只进行两局游戏便能确定赢家的概率.【解答】解:(1)画树状图得:∵总共有9种情况,每一种出现的机会均等,每人获胜的情形都是3种,∴两人获胜的概率都是.(2)由(1)可知,一局游戏每人胜、负、和的机会均等,都为.任选其中一人的情形可画树状图得:∵总共有9种情况,每一种出现的机会均等,当出现(胜,胜)或(负,负)这两种情形时,赢家产生,∴两局游戏能确定赢家的概率为:.23.(6分)如图,一枚运载火箭从距雷达站C处5km的地面O处发射,当火箭到达点A,B时,在雷达站C测得点A,B的仰角分别为34°,45°,其中点O,A,B在同一条直线上.(1)求A,B两点间的距离(结果精确到0.1km).(2)当运载火箭继续直线上升到D处,雷达站测得其仰角为56°,求此时雷达站C和运载火箭D两点间的距离(结果精确到0.1km).(参考数据:sin34°=0.56,cos34°=0.83,tan34°=0.67.)【解答】解:(1)由题意可得,∠BOC=∠AOC=90°,∠ACO=34°,∠BCO=45°,OC=5km,∴AO=OC•tan34°,BO=OC•tan45°,∴AB=OB﹣OA=OC•tan45°﹣OC•tan34°=OC(tan45°﹣tan34°)=5×(1﹣0.67)≈1.7km,即A,B两点间的距离是1.7km;(2)由已知可得,∠DOC=90°,OC=5km,∠DCO=56°,∴cos∠DCO=,即cos56°=,∵sin34°=cos56°,∴0.56=,解得,CD≈8.9答:此时雷达站C和运载火箭D两点间的距离是8.9km.24.(6分)如图,一次函数y1=﹣x﹣1的图象与x轴交于点A,与y轴交于点B,与反比例函数y2=图象的一个交点为M(﹣2,m).(1)求反比例函数的解析式;(2)当y2>y1时,求x的取值范围;(3)求点B到直线OM的距离.【解答】解:(1)把M(﹣2,m)代入y=﹣x﹣1得m=2﹣1=1,则M(﹣2,1),把M(﹣2,1)代入y=得k=﹣2×1=﹣2,所以反比例函数解析式为y=﹣;(2)解方程组得或,则反比例函数与一次函数的另一个交点坐标为(1,﹣2),当﹣2<x<0或x>1时,y2>y1;(3)OM==,S△OMB=×1×2=1,设点B到直线OM的距离为h,••h=1,解得h=,即点B到直线OM的距离为.25.(6分)如图,∠AOB=45°,点M,N在边OA上,点P是边OB上的点.(1)利用直尺和圆规在图1确定点P,使得PM=PN;(2)设OM=x,ON=x+4,①若x=0时,使P、M、N构成等腰三角形的点P有3个;②若使P、M、N构成等腰三角形的点P恰好有三个,则x的值是x=0或x=4﹣4或4<x<4.【解答】解:(1)如图所示:(2)①如图所示:故答案为:3.②如图3,以M为圆心,以4为半径画圆,当⊙M与OB相切时,设切点为C,⊙M与OA交于D,∴MC⊥OB,∵∠AOB=45°,∴△MCO是等腰直角三角形,∴MC=OC=4,∴OM=4,当M与D重合时,即x=OM﹣DM=4﹣4时,同理可知:点P恰好有三个;如图4,取OM=4,以M为圆心,以OM为半径画圆.则⊙M与OB除了O外只有一个交点,此时x=4,即以∠PMN为顶角,MN为腰,符合条件的点P有一个,以N圆心,以MN为半径画圆,与直线OB相离,说明此时以∠PNM 为顶角,以MN为腰,符合条件的点P不存在,还有一个是以NM为底边的符合条件的点P;点M沿OA运动,到M1时,发现⊙M1与直线OB有一个交点;∴当4<x<4时,圆M在移动过程中,则会与OB除了O外有两个交点,满足点P恰好有三个;综上所述,若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是:x=0或x=4﹣4或4<x<4.故答案为:x=0或x=4﹣4或4<x<4.26.(8分)如图,△ABC内接于⊙O,CD是⊙O的直径,AB与CD交于点E,点P是CD 延长线上的一点,AP=AC,且∠B=2∠P.(1)求证:P A是⊙O的切线;(2)若PD=,求⊙O的直径;(3)在(2)的条件下,若点B等分半圆CD,求DE的长.【解答】(1)证明:连接OA、AD,如图,∵∠B=2∠P,∠B=∠ADC,∴∠ADC=2∠P,∵AP=AC,∴∠P=∠ACP,∴∠ADC=2∠ACP,∵CD为直径,∴∠DAC=90°,∴∠ADC=60°,∠C=30°,∴△ADO为等边三角形,∴∠AOP=60°,而∠P=∠ACP=30°,∴∠OAP=90°,∴OA⊥P A,∴P A是⊙O的切线;(2)解:在Rt△OAP中,∵∠P=30°,∴OP=2OA,∴PD=OD=,∴⊙O的直径为2;(3)解:作EH⊥AD于H,如图,∵点B等分半圆CD,∴∠BAC=45°,∴∠DAE=45°,设DH=x,在Rt△DHE中,DE=2x,HE=x,在Rt△AHE中,AH=HE=x,∴AD=x+x=(+1)x,即(+1)x=,解得x=,∴DE=2x=3﹣.27.(10分)阅读下列材料:题目:如图,在△ABC中,已知∠A(∠A<45°),∠C=90°,AB=1,请用sin A、cos A 表示sin2A.【解答】解:如图,作Rt△ABC的斜边AB上的中线CE,则CE=AB==AE,∴∠CED=2∠A,过点C作CD⊥AB于D,在Rt△ACD中,CD=AC sin A,在Rt△ABC中,AC=AB cos A=cos A在Rt△CED中,sin2A=sin∠CED==2AC sin A=2cos A sin A28.(10分)平面直角坐标系xOy(如图),抛物线y=﹣x2+2mx+3m2(m>0)与x轴交于点A、B(点A在点B左侧),与y轴交于点C,顶点为D,对称轴为直线l,过点C作直线l的垂线,垂足为点E,联结DC、BC.(1)当点C(0,3)时,①求这条抛物线的表达式和顶点坐标;②求证:∠DCE=∠BCE;(2)当CB平分∠DCO时,求m的值.【解答】(1)解:①把C(0,3)代入y=﹣x2+2mx+3m2得3m2=3,解得m1=1,m2=﹣1(舍去),∴抛物线解析式为y=﹣x2+2x+3;∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点D为(1,4);②证明:如图1,当y=0时,﹣x2+2x+3=0,解得x1=﹣1,x2=3,则B(3,0),∵OC=OB,∴△OCB为等腰直角三角形,∴∠OBC=45°,∵CE⊥直线x=1,∴∠BCE=45°,∵DE=1,CE=1,∴△CDE为等腰直角三角形,∴∠DCE=45°,∴∠DCE=∠BCE;(2)解:抛物线的对称轴交x轴于F点,交直线BC于G点,如图2,y=﹣x2+2mx+3m2=﹣(x﹣m)2+4m2,∴抛物线的对称轴为直线x=m,顶点D的坐标为(m,4m2),当y=0时,﹣x2+2mx+3m2=0,解得x1=﹣m,x2=3m,则B(3m,0),当x=0时,y=﹣x2+2mx+3m2=3m2,则C(0,3m2),∵GF∥OC,∴=,即=,解得GF=2m2,∴DG=4m2﹣2m2=2m2,∵CB平分∠DCO,∴∠DCB=∠OCB,∵∠OCB=∠DGC,∴∠DCG=∠DGC,∴DC=DG,即m2+(4m2﹣3m2)2=4m4,∴m2=,而m>0,∴m=.。
2018镇江市中考必备数学模拟试卷(3)附详细试题答案
矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学试卷 第1页(共24页) 数学试卷 第2页(共24页)绝密★启用前江苏省镇江市2018年初中学业水平考试数 学(满分:120分,考试时间:120分钟)一、填空题(本大题共有12小题,每小题2分,共计24分) 1.8-的绝对值是 .2.一组数据2,3,3,1,5的众数是 .3.计算:23()a = .4.分解因式:21x -= .5.若分式5有意义,则实数x 的取值范围是 . 6.= .7.圆锥底面圆的半径为1,侧面积等于3π,则它的母线长为 .8.反比例函数(0)ky k x=≠的图像经过点(2,4)A -,则在每一个像限内,y 随x 的增大而 .(填“增大”或“减小”)9.如图,AD 为ABC △的外接圆O 的直径,若50BAD ∠=︒,则ACB ∠= .(第9题) (第11题) (第12题)10.已知二次函数24y x x k -=+的图像的顶点在x 轴下方,则实数k 的取值范围是 .11.如图,ABC △中,90BAC ∠︒>,5BC =,将ABC △绕点C 按顺时针方向旋转90︒,点B 对应点B '落在BA 的延长线上,若9sin 10B AC ∠'=,则AC = . 12.如图,点E 、F 、G 分别在菱形ABCD 的边AB 、BC 、AD 上,13AE AB =,13CF CB =,13AG AD =.已知EFG △的面积等于6,则菱形ABCD 的面积等于 .二、选择题(本大题共有5小题,每小题3分,共计15分.在每小题所给出的四个选项中,只有一项符合题目要求.) 13.0.000 182用科学记数法表示应为( )A .30.18210-⨯B .41.8210-⨯C .51.8210-⨯D .418.210-⨯ 14.如图是由3个大小相同的小正方体组成的几何体,它的左视图是( )ABCD15.小明将如图所示的转盘分成n (n 是正整数)个扇形,并使得各个扇形的面积都相等,然后他在这些扇形区域内分别标连接偶数数字2,4,6,…,2n (每个区域内标注1个数字,且各区域内标注的数字互不相同),转动转盘1次,当转盘停止转动时,若事件“指针所落区域标注的数字大于8”的概率是56,则n 的取值为 ( )A .36B .30C .24D .18(第15题)(第16题)(第17题)16.甲、乙两地相距80 km ,一辆汽车上午900:从甲地出发驶往乙地,匀速行驶了一半的路程后将速度提高了20 km/h ,并继续匀速行驶至乙地,汽车行驶的路程) (km y 与时间) (h x 之间的函数关系如图所示,该车到达乙地的时间是当天上午( )A .1035:B .1040:C .1045:D .1050:17.如图,一次函数2y x =与反比例函数(0)ky k x=>的图像交于A 、B 两点,点P 在以(2,0)C -为圆心,1为半径的C 上,Q 是AP 的中点,已知OQ 长的最大值为32,则k的值为( )A .4932B.2518C.3225D .98毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第3页(共24页)数学试卷 第4页(共24页)三、解答题(本大题共11小题,共计81分.解答应写出必要的文字说明、证明过程或演算步骤)18.(本小题满分8分)(1)计算:102(2018π)sin30--+-︒.(2)化简:2()111()a a a +--+.19.(本小题满分10分)(1)解方程:2121x x x =++-.(2)解不等式组:24014(2)x x x -⎧⎨+-⎩>≤.20.(本小题满分6分)如图,数轴上的点A 、B 、C 、D 表示的数分别为3-,1-,1,2,从A 、B 、C 、D 四点中任意取两点,求所取两点之间的距离为2的概率.21.(本小题满分6分)小李读一本名著,星期六读了36页,第二天读了剩余部分的14,这两天共读了整本书的38,这本名著共有多少页?22.(本小题满分6分)如图,ABC △中,AB AC =,点E ,F 在边BC 上,BE CF =,点D 在AF 的延长线上,AD AC =.(1)求证:ABE ACF △≌△;(2)若30BAE ∠=︒,则ADC ∠= ︒.23.(本小题满分6分)某班50名学生的身高如下(单位:cm ): 160 163 152 161 167 154 158 171 156 168 178 151 156 158 165 160 148 155 162 175 158 167 157 153 164 172 153 159 154 155 169 163 158 150 177 155 166 161 159 164 171 154 157 165 152 167 157 162 155 160(1)小丽用简单随机抽样的方法从这50个数据中抽取一个容量为5的样本:161,155,174,163,152,请你计算小丽所抽取的这个样本的平均数;数学试卷 第5页(共24页) 数学试卷 第6页(共24页)(2)①m = ,n = ;②这50名学生身高的中位数落在哪个身高段内?身高在哪一段的学生数最多? 24.(本小题满分6分)如图,校园内有两幢高度相同的教学楼AB 、CD ,大楼的底部B 、D 在同一平面上,两幢楼之间的距离BD 长为24米,小明在点E (B 、E 、D 在一条直线上)处测得教学楼AB 顶部的仰角为45︒,然后沿EB 方向前进8米到达点G 处,测得教学楼CD 顶部的仰角为30︒,已知小明的两个观测点F 、H 距离地面的高度均为1.6米,求教学楼AB 的高度AB 长.(精确到0.1米) 1.41≈, 1.73≈.25.(本小题满分6分)如图,一次函数()0y kx b k =+≠的图像与x 轴,y轴分别交于(9,0)A -,(0,6)B 两点,过点(2,0)C 作直线l 与BC 垂直,点E 在直线l 位于x 轴上方的部分. (1)求一次函数()0y kx b k =+≠的表达式; (2)若ACE △的面积为11,求点E 的坐标; (3)当CBE ABO ∠=∠时,点E 的坐标为 .26.(本小题满分8分)如图1,平行四边形ABCD 中,AB AC ⊥,6AB =,10AD =,点P 在边AD 上运动,以P 为圆心,PA 为半径的P 与对角线AC 交于A 、E 两点. (1)如图2,当P 与边CD 相切于点F 时,求AP 的长;(2)不难发现:当P 与边CD 相切时,P 与平行四边形ABCD 的边有三个公共点,随着AP 的变化,P 与平行四边形ABCD 的边的公共点的个数也在变化,若公共点的个数为4,直接写出相对应的AP 的值的取值范围 .图1图2-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________数学试卷 第7页(共24页) 数学试卷 第8页(共24页)27.(本小题满分9分)(1)如图1,将矩形ABCD 折叠,使BC 落在对角线BD 上,折痕为BE ,点C 落在点C '处,若46ADB ∠=︒,则DBE ∠的度数为 ︒. (2)小明手中有一张矩形纸片ABCD ,4AB =,9AD =. 【画一画】如图2,点E 在这张矩形纸片的边AD 上,将纸片折叠,使AB 落在CE 所在直线上,折痕设为MN (点M ,N 分别在边AD ,BC 上),利用直尺和圆规画出折痕MN (不写作法,保留作图痕迹,并用黑色水笔把线段描清楚); 【算一算】如图3,点F 在这张矩形纸片的边BC 上,将纸片折叠,使FB 落在射线FD 上,折痕为GF ,点A ,B 分别落在点A ',B '处,若73AG =,求B D '的长; 【验一验】如图4,点K 在这张矩形纸片的边AD 上,3DK =,将纸片折叠,使AB 落在CK 所在直线上,折痕为HI ,点A ,B 分别落在点A ',B '处,小明认为B I '所在直线恰好经过点D ,他的判断是否正确,请说明理由.图1图2图3图428.(本小题满分10分)如图,二次函数23y x x =-的图像经过(0,0)O ,()4,4A ,(3,0)B 三点,以点O 为位似中心,在y 轴的右侧将OAB △按相似比2:1放大,得到OA B ''△,二次函数2()0y ax bx c a =++≠的图像经过O 、A '、B '三点.(1)画出OA B ''△,试求二次函数2()0y ax bx c a =++≠的表达式;(2)点(,)P m n 在二次函数23y x x =-的图像上,0m ≠,直线OP 与二次函数2()0y ax bx c a =++≠的图像交于点Q (异于点O ). ①求点Q 的坐标(横、纵坐标均用含m 的代数式表示) ②连接AP ,若2AP OQ >,求m 的取值范围;③当点Q 在第一像限内,过点Q 作QQ '平行于x 轴,与二次函数2()0y ax bx c a =++≠的图像交于另一点Q ',与二次函数23y x x =-的图像交于点M 、N (M 在N 的左侧),直线OQ '与二次函数23y x x =-的图像交于点P '.Q P M QB N '''△∽△,则线段NQ 的长度等于 .数学试卷 第9页(共24页) 数学试卷 第10页(共24页)江苏省镇江市2018年初中学业水平考试数学答案解析1.【答案】8【解析】解:8-的绝对值是8. 【考点】绝对值. 2.【答案】3【解析】解:数据2,3,3,1,5的众数为3. 故答案为3. 【考点】众数. 3.【答案】6a【解析】解:236()a a =.故答案为:6a . 【考点】幂的乘方与积的乘方. 4.【答案】()(11)x x +-【解析】解:2()(1)11x x x =+--. 故答案为:()(11)x x +-. 【考点】因式分解—运用公式法. 5.【答案】3x ≠【解析】解:由题意,得30x -≠,解得3x ≠,故答案为:3x ≠. 【考点】分式有意义的条件. 6.【答案】2【解析】解:原式=2=.故答案为:2【考点】二次根式的乘除法. 7.【答案】3【解析】解:设它的母线长为l ,根据题意得12π13π2l ⨯⨯⨯=, 解得3l =,即它的母线长为3. 故答案为3.【考点】圆锥的计算. 8.【答案】增大【解析】解:∵反比例函数(0ky k x=≠)的图象经过点(2,4)-, 42k∴=-,解得80k =-<, ∴函数图象在每个象限内y 随x 的增大而增大.故答案为:增大.【考点】反比例函数的性质,反比例函数图象上点的坐标特征. 9.【答案】40【解析】解:连接BD ,如图,AD 为ABC △的外接圆O 的直径,90ABD ∴∠=︒,90905040D BAD ∴∠=︒-∠=︒-︒=︒, 40ACB D ∴∠=∠=︒.故答案为40.【考点】三角形的外接圆与外心. 10.【答案】4k <【解析】解:二次函数24y x x k -=+中10a =>,图象的开口向上,又二次函数24y x x k -=+的图象的顶点在x 轴下方,210(44)k --∴∆=⨯⨯>,解得:4k <,故答案为:4k <.【考点】二次函数图象与系数的关系,抛物线与x 轴的交点.数学试卷 第11页(共24页) 数学试卷 第12页(共24页)11.【答案】1:9【解析】解:作CD BB ⊥'于D ,如图,ABC △绕点C 按顺时针方向旋转90︒,点B 对应点B '落在BA 的延长线上,5CB CB ∴='=,90BCB ∠'=︒, BCB ∴'△为等腰直角三角形,BB ∴'=122CD BB ∴='=,在Rt ACD △中,9sin 10CD DAC AC ∠==,1029AC ∴=⨯=.故答案为9【考点】旋转的性质,解直角三角形. 12.【答案】27【解析】解:在CD 上截取一点H ,使得13CH CD =.连接AC 交BD 于O ,BD 交EF 于Q ,EG 交AC 于P .AE AGAB AD=, EG BD ∴∥,同法可证:FH BD ∥, EG FH ∴∥,同法可证EF GF ∥,∴四边形EFGH 是平行四边形, 四边形ABCD 是菱形,AC BD ∴⊥,EF EG ∴⊥,∴四边形EFGH 是矩形,易证点O 在线段FG 上,四边形EQOP 是矩形,6EFG S =△,3EQOP S ∴=矩形,即 3OP OQ =,::2:3OP OA BE AB ==,32OA OP ∴=,同法可证3OB OQ =,113692722ABCD S AC BD OP OQ OP OQ ∴==⨯⨯=⨯=菱形.故答案为27. 【考点】菱形的性质. 13.【答案】B【解析】解:40.000182210-=⨯.故选:B . 【考点】科学记数法—表示较小的数. 14.【答案】D【解析】解:如图所示:它的左视图是:,故选:D .【考点】简单组合体的三视图. 15.【答案】C【解析】解:∵“指针所落区域标注的数字大于8”的概率是56, 456n n -∴=, 解得:24n=,故选:C .【考点】几何概率. 16.【答案】B【解析】解:因为匀速行驶了一半的路程后将速度提高了20km/h , 所以1小时后的路程为40 km ,速度为40 km/h ,数学试卷 第13页(共24页) 数学试卷 第14页(共24页)所以以后的速度为204060 km/h +=,时间为40604060⨯=分钟, 故该车到达乙地的时间是当天上午1040:;故选:B . 【考点】函数的图象. 17.【答案】C【解析】解:连接BP ,由对称性得:OA OB =,Q 是AP 的中点,∴12OQ BP =,12OQ BP ∴=,OQ 长的最大值为32,BP ∴长的最大值为3232⨯=,如图,当BP 过圆心C 时,BP 最长,过B 作BD x ⊥轴于D ,1CP =,2BC ∴=,B 在直线2y x =上,设2(),B t t ,则()22CD t t -=-=+,2BD t =-, 在Rt BCD △中,由勾股定理得:222BC CD BD =+,222()(222)t t +-∴=+,0t =(舍)或45-,49,55B ⎛⎫-- ⎪⎝⎭∴,点B 在反比例函数(0)ky k x=>的图象上, 49325525k ⎛⎫∴=-⨯-= ⎪⎝⎭;故选:C .【考点】反比例函数与一次函数的交点问题.18.【答案】解:(1)原式111122=+-=. (2)原式22211a a a a a =++--=-.【考点】实数的运算,单项式乘多项式,完全平方公式,零指数幂,负整数指数幂,特殊角的三角函数值.19.【答案】(1)解:两边都乘以()(12)x x -+, 得:()()(122)()12x x x x x -=++-+, 解得:12x =-, 当12x =-时,2)10()(x x -+≠, ∴分式方程的解为12x =-;(2)解不等式240x ->,得:2x >, 解不等式(12)4x x +-≤,得:3x ≥, 则不等式组的解集为3x ≥.【考点】解分式方程,解一元一次不等式组.20.【答案】解:画树状图为:共有12种等可能的结果数,其中所取两点之间的距离为2的结果数为4, 所以所取两点之间的距离为2的概率41123==. 【考点】列表法与树状图法.21.【答案】解:设这本名著共有x 页, 根据题意得:()13363648x x +-=, 解得:216x =.答:这本名著共有216页. 【考点】一元一次方程的应用. 22.【答案】(1)证明:AB AC =,B ACF ∴∠=∠,数学试卷 第15页(共24页) 数学试卷 第16页(共24页)在ABE △和ACF △中,AB AC B ACF BE CF =⎧⎪∠=∠⎨⎪=⎩, ()ABE ACF SAS ∴△≌△;(2)ABE ACF △≌△,30BAE ∠=︒,30BAE CAF ∴∠=∠=︒, AD AC =,ADC ACD ∴∠=∠,18030752ADC ︒-︒∴∠==︒,故答案为:75.【考点】全等三角形的判定与性质.23.【答案】解:(1)16115517416315216()1x =++++=; (2)①如表可知,0m =,22,3n = 故答案为:0.22;3;②这50名学生身高的中位数落在159.5~163.5, 身高在151.5~155.5的学生数最多.【考点】总体、个体、样本、样本容量;频数(率)分布表;加权平均数;中位数. 24.【答案】解:延长HF 交CD 于点N ,延长FH 交AB 于点M ,如右图所示,由题意可得, 1.6m MB HG FE ND ====,8m HF GE ==,MF BE =,HN GD =,24m MN BD ==,设m AM x =,则m CN x =,在Rt AFM △中,AM tan451xMF x ===︒,在Rt CNH △中,CN tan30HN ===︒,24HF MF HN MN x ∴=+-=+-,即824x =+-, 解得,11.7x ≈,11.7 1.613.3m AB ∴=+=,答:教学楼AB 的高度长13.3 m .【考点】解直角三角形的应用﹣仰角俯角问题.25.【答案】(1)解:一次函数()0y kx b k =+≠的图象与x 轴,y 轴分别交于0()9,A -,()0,6B 两点,906k b b -+=⎧∴⎨=⎩,236k b ⎧=⎪∴⎨⎪=⎩, ∴一次函数y kx b =+的表达式为263y x =+; (2)如图,记直线l 与y 轴的交点为D ,BC l ⊥,90BCD BOC ∴∠=︒=∠, OBC OCB OCD OCB ∴∠+∠=∠+∠, OBC OCD ∴∠=∠,BOC COD ∠=∠, OBC OCD ∴△∽△, OB OCOC OD=∴, (0,6)B ,(2,)0C ,6OB ∴=,2OC =, 622OD ∴=,23OD ∴=, 20,(3)D ∴-,)0(2,C ,∴直线l 的解析式为1233y x =-, 设12,33E t t ⎛⎫- ⎪⎝⎭,),(90A -,(2,)0C , 112111122)31(3E ACE S AC y t ∴=⨯=⨯⨯-=△,8t ∴=,)2(8,E ∴;数学试卷 第17页(共24页) 数学试卷 第18页(共24页)(3)如图,过点E 作EF x ⊥轴于F ,ABO CBE ∠=∠,90AOB BCE ∠=∠=︒ ABO EBC ∴△∽△, 23BC BO CE AO ∴==, 90BCE BOC ∠=︒=∠,BCO CBO BCO ECF ∴∠+∠=∠+∠, CBO ECF ∴∠=∠, 90BOC EFC ∠=∠=︒, BOC CFE ∴△∽△, 23BO OC BC CF EF CE ==∴= 6223CF EF ∴==, 9CF ∴=,3EF =,11OF ∴=,)3(11,E ∴.故答案为(11,3).【考点】一次函数综合题.26.【答案】(1)解:如图2所示,连接PF ,在Rt ABC △中,由勾股定理得:8AC ==, 设AP x =,则10DP x =-,PF x =,P 与边CD 相切于点F ,PF CD ∴⊥,四边形ABCD 是平行四边形,AB CD ∴∥,AB AC ⊥,AC CD ∴⊥,AC PF ∴∥,DPF DAC ∴△∽△, PF PDAC AD ∴=, 10810x x-∴=, 409x ∴=,409AP =; (2)当P 与BC 相切时,设切点为G ,如图3,1682102S ABCD PG =⨯⨯⨯=,245PG =, ①当P 与边AD 、CD 分别有两个公共点时,402495AP <<,即此时P 与平行四边形ABCD 的边的公共点的个数为4,②P 过点A 、C 、D 三点.,如图4,P 与平行四边形ABCD 的边的公共点的个数为4,此时5AP =,综上所述,AP 的值的取值范围是:402495AP <<或5AP =. 故答案为:402495AP <<或5AP =. 【考点】平行四边形的性质,直线与圆的位置关系,切线的判定与性质,相似三角形的判定与性质.27.【答案】解:(1)如图1中,数学试卷 第19页(共24页)数学试卷第20页(共24页)∵四边形ABCD 是矩形, ∴AD BC ∥,∴46ADB DBC ∠=∠=︒,由翻折不变性可知, 1232DBE EBC DBC ∠=∠=∠=︒ 故答案为23.(2)【画一画】,如图2中,【算一算】如图3中,73AG =,9AD =,720933GD ∴=-=, 四边形ABCD 是矩形,AD BC ∴∥,DGF BFG ∴∠=∠,由翻折不变性可知,BFG DFG ∠=∠,DFG DGF ∴∠=∠,203DF DG ∴==, 4CD AB ==,90C ∠=︒,∴在Rt CDF △中,163CF =, 113BF BC CF ∴=-=, 由翻折不变性可知,113FB FB ='=, 2011333DB DF FB ∴'=-'=-=. 【验一验】如图4中,小明的判断不正确.理由:连接ID ,在Rt CDK △中,3DK =,4CD =,5CK ∴=, AD BC ∥,DKC ICK ∴∠=∠,由折叠可知,90A B I B ∠''=∠=︒,90IB C D ∴∠'=︒=∠,CDK IB C ∴'△∽△,''CD DK CK IB BC IC ∴==,即435''IB BC IC==, 设3CB k '=,4IB k '=,5IC k =, 由折叠可知,4IB IB k ='=,459BC BI IC k k ∴=+=+=,1k ∴=,5IC ∴=,4IB '=,3B C '=,在Rt ICB '△中,'3tan '4CB B IC IB ∠'==,连接ID ,在Rt ICD △中,4tan 5DC DIC IC ∠==,tan tan B IC DIC ∴∠'≠∠,B I ∴'所在的直线不经过点D .【考点】四边形综合题.数学试卷 第21页(共24页) 数学试卷 第22页(共24页)28.【答案】解:(1)由以点O 为位似中心,在y 轴的右侧将OAB △按相似比2:1放大, 得'O '12OA B OA OB === )4(4,A ,(3,)0B 8(8,)A ∴',0()6,B '将()0,0O ,8(8,)A ',0(6,)B '代入2y ax bx c =++得036606480c a b a b =⎧⎪+=⎨⎪+=⎩;解得:1230a b c ⎧=⎪⎪=-⎨⎪=⎪⎩∴二次函数的解析式为2132y x x -=;(2)①点P 在23y x x =-的图象上,23n m m ∴=-,23(),P m m m -∴,设直线OP 的解析式为y kx =将点P 代入,得23mk m m =-,解得3k m =-,(3)OP y m x ∴=-:直线OP 与2132y x x -=交于点Q2(132)3x x m x ∴=--,解得10x =(舍),22x m =, 22,2()6Q m m ∴-②(m,)P n 在二次函数23y x x =-的图象上23n m m ∴=-,23(m,)P m m -∴设直线OP 的解析式为y kx =,将点23(m,)P m m -代入函数解析式, 得23mk m m =-,3k m ∴=-,OP ∴的解析是为3()y m x =-,OP 与2132y x x -=交于Q 点,()23132y m x y x x⎧=-⎪∴⎨=-⎪⎩, 解得00x y =⎧⎨=⎩(不符合题意舍去)2226x m y m m =⎧⎨=-⎩, 22,26()Q m m m -∴过点P 作PC x ⊥轴于点C ,过点Q 作QD x ⊥轴于点D ,则||OC m =,23||PC m m -=,|2|OD m =,26||2QD m -=,2OQ OD OC OP==, OCP ODQ ∴△∽△,2OQ OP ∴=,2AP OQ >,22AP OP ∴>,即AP OP>,化简,得2240m m --<,解得11m <且0m ≠; ③2(),3P m m m -,22,)26(Q m m m -, 点Q 在第一象限,22m 02m 6m 0⎧∴⎨-⎩>>,解得3m >, 由22,)26(Q m m m -,得QQ '的表达式是226y m m =-,QQ '交2132y x x -=交于点Q ', 2213226y x x y m m ⎧=⎪⎨⎪=-⎩-;解得2226x m y m =-=⎧⎨⎩(不符合题意,舍), 26226x m y m m=-⎧⎨=-⎩,262,()26Q m m m ∴-'-, 设OQ '的解析是为y kx =,2622()6m k m m -=-, 解得k m =-,OQ '的解析式为y m =-,OQ '与23y x x =-交于点P ', 23mx x x ∴=--,解得10x =(舍),23x m =-,23,()3P m m m ∴-'-,QQ '与23y x x =-交于点P ', 23mx x x ∴=--,解得10x =(舍去),23x m =-,数学试卷 第23页(共24页) 数学试卷 第24页(共24页)23,()3P m m m ∴-'-,QQ '与23y x x =-交于点M 、N , 22326x x m m ∴=--,解得1x =2xM 在N 左侧,226)M m m ∴-,226N m m ⎫⎝-⎪⎪⎭, Q P M QB N '''△∽△, P Q QM QB QN''∴=', 2222222(3)(3)1()(26)(26)4P Q m m m QB m m m '-+-==-+-, 12=, 化简得:212270m m +=-, 解得:13m =(舍),29m =,12,(8)10N ∴,18,()108Q ,6QN ∴=,故答案为:6.【考点】二次函数综合题.。
