初中数学一题多解(无答案)
人教版数学八年级上册代数经典集锦---一题多解(含答案)

2019--2020人教版数学八年级代数经典集锦---一题多解在初中几何的证明和求解中,需要培养学生严密推理论证能力、灵动转化变换思维等方面素养,而在初中代数的计算过程中,需要培养学生多角度、多维度思考问题,掌握整体与局部、特例分析等全方位能力,从而寻求结果,下面以一道经典例题的不同解法,展开思维训练。
1、已知:x y = - 2,则x 2-2xy-3y 2x 2-6xy-7y 2 = .解法一:令x=2,y=-1,则x 2-2xy-3y 2=22-2*2*(-1)-3*(-1)2=4+4-3=5,X 2-6xy-7y 2=22-6*2*(-1)-7*(-1)2=4+12-7=9,所以,原式=59 .李老师点评:本解法是最简单却学生最不容易想到的解法。
原式看起来很复杂,x,y 只给出了比例关系,没有给出具体数值,那么取特例也是满足题设要求的,所以,当没有寻找到更好的解决办法时,可以取特殊值进行计算。
解法二:由已知比例x y = - 2变形有:x=-2y ┅┅①将①带入原式有:x 2-2xy-3y 2=(-2y)2-2*(-2y)*y-3y 2=5y 2,X 2-6xy-7y 2=(-2y)2-6*(-2y)*y-7y 2=9y 2,x 2-2xy-3y 2x 2-6xy-7y 2 =59 .李老师点评:本解法使用了带入消元法进行解题,带入消元法是解决含有未知数类求值问题最基本的解题方法之一。
解法三:∵x y = - 2,∴x ≠0,y ≠0则将原式分子和分母同时除以y 2得到:x 2-2xy-3y 2x 2-6xy-7y 2 = = 59=李老师点评:本解法是一种技巧型解法,首先通过观察x,y 的取值情况以及原式中分子分母所含式子,我们会发现:x,y 都不等于0,同时分子分母其实每一项都是二次项(将x,y 都看作未知数),所以分子分母同时除以y2,便可以轻松的将原式化成已知条件中的样子,从而得解。
数学人教版八年级上册专题学习“一题多解”

方法1:延长AD到点E,使 DE=AD,连结CE. 方法2:取AC的中点E,连 结DE.
B
D
.
E C
E
谢谢! 再见!
专题学习
----几何证明中常见 “一题多解”方法
乐加初中 王刚
典例: 如图,四边形ABCD中, ∠A= ∠D =90o, BE、CE均是角平分线, 求证:BC=AB+CD.
证明:在BC上截取BF=AB,连接E,F ∵ BE、CE均是角平分线 ∴ ∠ABE= ∠FBE ∠BCE= ∠DCE 解法 1.在BC上截取BF=AB 在△ABE与△FBE中 AB=BF : 构造了 ∠ABE= ∠FBE 全等的三角形 BE=BE ∴ △ABE ≌ △FBE ∴ ∠A= ∠BFE BF=AB CF=CD 从而证得: ∵ ∠A= ∠D =90o 进而得证: BC=AB+CD. ∴ ∠A= ∠BFE = ∠CFE= ∠D =90o 在△FCE与△DCE中 ∠FCE= ∠DCE ∠CFE= ∠D CE=CE ∴ △FCE ≌ △DCE ∴CF=CD ∵ BC=BF+ CF BF=AB CF=CD ∴ BC=AB+CD
如图,四边形ABCD中, ∠A= ∠D =90o, BE、CE均是角平分线, 求证:BC=AB+CD.
练习:如图,△ABC中, ∠C =90o,AC=BC, AD平分∠BAC,求证:AB=AC+DC. 解法1:在AB上截取AE=AC,连接E,D 构造了: 解法2:过点E作DE⊥AB,垂足为E. 全等的直角三角形 从而证得: DC=DE =BE 构造了 : 解法3:延长AC至E使CE=DC,连接E,D E 进而得证:AB=AC+DC 全等的直角三角形 从而证得: AC=AE DC=BE 构造了: B 进而得证: AB=AC+DC 全等的三角形 从而证得:AB=AE 进而得证:AB=AC+DC
一题多解
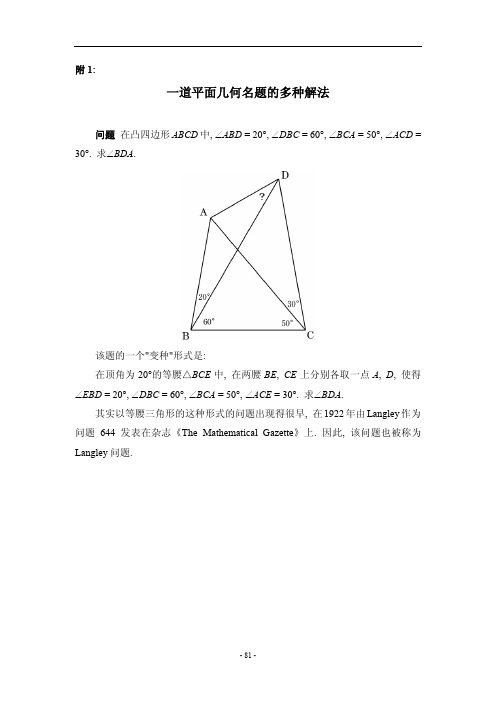
附1:一道平面几何名题的多种解法问题在凸四边形ABCD中, ∠ABD = 20°, ∠DBC = 60°, ∠BCA = 50°, ∠ACD = 30°. 求∠BDA.该题的一个"变种"形式是:在顶角为20°的等腰△BCE中, 在两腰BE, CE上分别各取一点A, D, 使得∠EBD = 20°, ∠DBC = 60°, ∠BCA = 50°, ∠ACE = 30°. 求∠BDA.其实以等腰三角形的这种形式的问题出现得很早, 在1922年由Langley作为问题644发表在杂志《The Mathematical Gazette》上. 因此, 该问题也被称为Langley问题.解法1在CD上取一点E, 使得∠EBC = 20°, 则∠BCE = ∠CEB = 80°, BC = BE. 又∠BCA = ∠BAC = 50°, BC = BA. 故BA = BE.因∠ABE = 60°, 故△ABE为正三角形.因∠DBE = ∠EDB = 40°, 故DE = BE = AE, 即E为△ABD的外心.所以, ∠BDA = ∠BEA/2 = 30°.解法2设∠ABC的角平分线与CD相交于点E, 在BE延长线上取一点X, 在BA延长线上取一点Y.易知, ∠CAB = 50° = ∠BCA, 故BC = BA, 点A与C关于直线BE对称.故∠CEB = 60°, ∠BEA = 60°, ∠AED = 60°, ∠DEX = 60°, 即DE为∠AEX的角平分线.因∠ABE = ∠ABC/2 = 40° = 2∠ABD, 故BD为∠ABE的角平分线.因此, 点D为△ABE与顶点B对应的旁心, 从而AD为∠YAE的角平分线.而∠YAE = ∠ABE + ∠BEA = 100°, 故∠YAD = ∠YAE/2 = 50°.所以, ∠BDA = ∠YAD – ∠ABD = 30°.解法3以AC为一边作正三角形△ACE, 且点E和B位于AC的两侧.因∠BCA = ∠CAB = 50°, 故BC = BA, 四边形ABCE为关于BE对称的筝形, ∠ABE = ∠ABC/2 = 40°, ∠BEA = ∠CEA/2 = 30°.因∠ACD = 30°, 故CD垂直平分AE.设CD与△ABE外接圆上的劣弧AE相交于点D', 由对称性, 弧AD' = 弧D'E, 故∠ABD' = ∠D'BE = ∠ABE/2 = 20° = ∠ABD. 因此, D'与D重合.所以, ∠BDA = ∠BEA = 30°.解法4以CD为一边作正三角形DCE, 且点E与B分别在CD的两侧. 过点D作CE的垂线, 交直线BC于点F. 在FE的延长线上取一点G, 使得EG = EC. 设直线DG与△GCF的外接圆再次相交于点A' (A'≠G).由图形的对称性, ∠FEC = ∠ECF = 180° – 50° – 30° – 60° = 40°. 因EG = EC,故∠EGC = ∠GCE = ∠FEC/2 = 20°.因EG = EC = ED, 故∠EGD = ∠GDE = ∠FED/2 = (60° + 40°)/2 = 50°.因A', C, F, G四点共圆, 故∠BCA' = ∠FGA' = 50°, ∠GA'F = ∠GCF = ∠GCE + ∠ECF = 20° + 40° = 60°.因∠DA'F = 60° = ∠DBF, 故A', B, F, D四点共圆, ∠A'BF = ∠GDF = ∠GDE + ∠EDF = 50° + 30° = 80°.故∠A'BC = 80° = ∠ABC, 且∠BCA '= 50° = ∠BCA, 所以A'与A重合.由A, C, F, G四点共圆, 有∠CGA = ∠EGD – ∠EGC = 30°, ∠BF A = ∠CF A = ∠CGA = 30°.再由A, B, F, D四点共圆, 便有∠BDA = ∠BF A = 30°.解法5设直线BA与CD的交点为E, 则∠ABC = ∠BCD = 80°, EB = EC, ∠CEB = 20° = ∠ABD, BD = ED.易知, ∠CAB = 50° = ∠BCA, 故BA = BC.在EB上取一点F, 使得BF = BD. 在DF延长线上取一点G, 使得FG = CB. 连GE.因BF = BD, ∠DBA = 20°, 故∠DFB = ∠BDF = 80°, ∠GDE = ∠DFB – ∠DEF = 60°.因∠GFE = ∠DFB = 80° = ∠BCD, EF = EB – BF = EB – BD = EC – ED = DC, 且FG = CB, 故△EGF≌△DBC, ∠EGD = ∠DBC = 60°.所以, △EGD为正三角形.故F A = BF – BA = BD – BC = ED –FG = GD – FG = FD, ∠ADF = ∠F AD = 50°.所以, ∠BDA = ∠BDF – ∠ADF = 30°.解法6易知, ∠CDB = 40°, ∠CAB = 50° = ∠BCA, BC = BA.在线段BD上取一点E, 使得BE= BC. 因∠EBC= 60°, 故△EBC为正三角形.设△DBC的内心为F, 则∠DBF = ∠FBC = 30°, ∠BCF = ∠FCD = 40°, ∠CDF = ∠FDB = 20°.因∠DCE = 20° = ∠CDF, ∠EDC = 40° = ∠FCD, 故△EDC≌△FCD, FD = EC = BC = BA.又∠FDB = 20° = ∠ABD, 故FD // BA, 四边形ABFD为平行四边形.所以, ∠BDA = ∠DBF = 30°.解法7过点A作BC的平行线, 交直线CD于点E. 过点B作CD的平行线, 交直线AE于点F. 过点C作BA的平行线, 交直线AE于点G.设直线BF与CA的交点为H. 连HG.易知, ∠CAB = 50° = ∠BCA, 故平行四边形ABCG为菱形.因∠ABC = ∠BCE = 80°, 故ABCE为等腰梯形, 且AB = EC.因此, 平行四边形ECBF与ABCG全等, 即FBCE也为菱形. 故∠GBC= ∠ABG = ∠ABC/2 = 40°.又∠FBC = 180° – ∠BCE = 100°, 故∠FBG = 60° = ∠CBD.由菱形FBCE图形的对称性可知, 直线BF与BC关于BE对称, 直线FE与CE也关于BE对称. 又因∠FBG = ∠CBD, 故直线BG与BD也关于BE对称. 而BG与FE的交点为G, BD与CE的交点为D, 故点G与D也关于BE对称. 所以, BG = BD.在菱形ABCG中, 有点B和G关于CA对称, 故∠HGB = ∠HBG = 60°, 即△HBG为正三角形, ∠BHA = ∠GHA = 30°, BH = BG.因BH = BG = BD, 且∠ABH = ∠FBC – ∠ABC = 20° = ∠ABD, 有△HBA≌△DBA.所以, ∠BDA = ∠BHA = 30°.解法8过点D作直线BC的平行线, 交直线BA于点E. 设BD与CE的交点为F.因∠EBC = ∠BCD = 80°, 故四边形EBCD为等腰梯形, 且EB = DC. 故∠BCE = ∠DBC = 60°, △FBC及△FDE均为正三角形.易知, ∠CAB = 50° = ∠BCA, 故BA = BC = BF, ∠BF A = ∠F AB = 80°.易知, ∠FEA = ∠CDB = 40°, 而∠AFE = 180° – ∠CFB – ∠BF A = 40° = ∠FEA, 故AE = AF. 四边形EAFD是一个以AD为对称轴的筝形.所以, ∠BDA = ∠FDE/2 = 30°.解法9以BC与CD为相邻两边, 作平行四边形EBCD, 则∠EBC = 100°.在BD上取一点F, 使得BF = BC. 又因∠FBC = 60°, 故△FBC为正三角形, BC = CF.易知, ∠ABC = ∠BCD = 80°, 故∠FCD = ∠BCD – 60° = 20°, ∠ABE = ∠EBC – ∠ABC = 100° – 80° = 20°.易知, ∠CAB = 50° = ∠BCA, 故BA = BC = CF.又因EBCD是平行四边形, 有EB= DC, 故△EBA≌△DCF, ∠AEB= ∠CDF = 180° – ∠DBC – ∠BCD = 180° – 60° – 80° = 40°.因∠DEB = ∠BCD = 80°, 故∠DEA = ∠DEB – ∠AEB = 40° = ∠AEB, 而∠EBA = ∠ABD = 20°, 故A为△EBD的内心.因ED // BC, 故∠BDE = ∠DBC = 60°.所以, ∠BDA = ∠BDE/2 = 30°.解法10易知, ∠BDC = 40°.设直线BA与CD的交点为E. 因∠ABC = ∠BCD = 80°, 故EB = EC, ∠CEB = 20° = ∠ABD, DB = DE.设点B关于EC的对称点为F, 由对称性可知, EF= EB, DF= DB= DE,∠EDF = ∠BDE = 180° – 40° = 140°, ∠FEC = ∠CEB = 20°.设点C关于EB的对称点为G, 同样由对称性, EG = EC, ∠EGA = ∠ACE = 30°, ∠BEG = ∠CEB = 20°.由EG = EC = EB = EF, 且∠GEF = ∠BEG + ∠CEB + ∠FEC = 20° + 20° + 20° = 60°, 故△EGF为正三角形.因∠EGA = 30°, 故直线GA是EF的垂直平分线. 又因DF = DE, 故点D也位于EF的垂直平分线上, 所以G, A, D三点共线.故∠GDE = ∠GDF = (360° – ∠EDF)/2 = 110°.所以, ∠BDA = 180° – ∠CDB – ∠GDE = 180° – 40° – 110° = 30°.解法11设直线BA与CD的交点为E, 则∠CEB = 20° = ∠ABD, 故DB = DE.易知, ∠CAB = 50° = ∠BCA, 故BA = BC.设∠BDE的角平分线与∠ABC的角平分线相交于点F, BF与DC交于点G.因BA= BC, 故点A与C关于BF对称; 因DE= DB, 故点E与B关于DF 对称, 且DF⊥BE.因此, ∠ABG = ∠GBC = ∠ABC/2 = 40°, ∠DBF = ∠ABG – ∠ABD = 20°, ∠FED = ∠DBF = 20°.∠BGA = ∠CGB = 180° – 40° – 50° – 30° = 60°, ∠AGE = 180° – 60° – 60° = 60°, ∠EGF = ∠CGB = 60°.因∠FEG = ∠GEA = 20°, ∠EGF = ∠AGE = 60°, 故△EAG≌△EFG, 点A 与F关于直线EG对称.∠BFD = 90° – ∠EBF = 50°, ∠DAG = ∠GFD = 50°.∠GDA = 180°– ∠DAG – ∠AGE = 70°.所以, ∠BDA = ∠GDA – ∠CDB = 70° – 40° = 30°.解法12设直线BA与CD的交点为E, 则由∠ABC = ∠BCD = 80°, 有EB = EC, ∠CEB = 20° = ∠ABD, 故DB = DE.又易知, ∠CAB = 50° = ∠BCA, 故BA = BC.设点E在BC上的垂足为F, 点D在BC上的垂足为G. 设EB = EC = 1, BA = BC = a, DB = DE = b.则因EB = EC , 故BF = FC = 2a . 且∠DBC = 60°, BG =2DB =2b , 有FG = BG – BF = 2a b -.又因1b EC ED FC FG ==, 有 FG = b ·FC =2ab .故22ab a b =-, aa b -=1. 因ECEA a b a BD BA =-==11, 且∠ABD = ∠AEC = 20°, 故△ABD ≌ △AEC . 所以, ∠BDA = ∠ECA = 30°.解法13设∠BDA = θ. 则∠DAB = 160° –θ, ∠BCD = 80°, ∠CDB = 40°.由正弦定理,)20sin()160sin(sin θθθ+︒=-︒=BD BD AB , ︒=︒80sin 40sin BD BC .因∠CAB = 50° = ∠BCA , 故BC = AB . 所以︒︒===+︒80sin 40sin )20sin(sin BD BC BD AB θθ.︒⋅+︒=⋅︒40sin )20sin(sin 80sin θθ︒⋅⋅︒+⋅︒=40sin )sin 20cos cos 20(sin θθθθsin 40sin 20cos cos 40sin 20sin ⋅︒⋅︒+⋅︒⋅︒=.故︒⋅︒-︒︒⋅︒==40sin 20cos 80sin 40sin 20sin cos sin tan θθθ︒⋅︒-︒⋅︒︒⋅︒=40sin 20cos 40cos 40sin 240sin 20sin ︒-︒︒=20cos 40cos 220sin . 而︒-︒=︒-︒=︒40sin 2140cos 23)4060sin(20sin , ︒+︒=︒-︒=︒40sin 2340cos 21)4060cos(20cos . 故︒=︒-︒=︒-︒20sin 340sin 2340cos 2320cos 40cos 2. 所以, 31tan =θ, 即 θ = 30°.附2:一道等腰三角形问题的多种解法问题在△ABC中, AB= AC, ∠BAC= 20°. 点D, E分别在边AC, AB上, 且∠DBC = 70°, ∠ECB = 60°. 求∠EDB.解法1在边AC上取一点F, 使得∠FBC = 60°. 设EC与FB相交于点O. 连EF.则由图形对称性, 有EF // BC, ∠FBC = ∠ECB = ∠FEO = ∠EFO, 故△OBC 及△EOF均为正三角形.∠ABO = 80° – 60° = 20°, ∠DBA = 10°, ∠DBF = 10°.连接AO, 则AO为∠BAC的角平分线, ∠OAC = 10°.又AB = AC, ∠ACO = ∠BAD, 故△AOC≌△BDA, AO = BD, OC = AD = BC.又因∠BDF = ∠ABD + ∠BAD = 10° + 20° = 30°, ∠AOF = ∠EOF/2 = 30°, 故△AOF≌△BDF.这样, 有DF = FO = EF, 而因EF // BC, 有∠DFE = ∠ACB = 80°, 从而∠EDF = 50°.所以, ∠EDB = ∠EDF – ∠BDF = 50° – 30° = 20°.解法2辅助线做法同解法1, 在边AC上取一点F, 使得∠FBC= 60°. 设EC与FB 相交于点O. 连EF.同样证得△AOC≌△BDA, AO = BD, OC = AD = BC.与解法1不同的是, 在证明DF = EF时采用了角平分线定理.因∠DBA = ∠DBF = 10°, 知BD为△ABF的内角平分线. 所以而∠ACE = ∠CAE = 20°, 故AE = CE = BF. 故即得DF = EF.以下步骤同解法1, 求得∠EDF = 50°, ∠EDB = ∠EDF – ∠BDF = 20°.解法3以AC为一边作正三角形△ACF, 且点F与B位于AC的同侧. 连FE, FB.因AF= AC= AB, 故点A为△BCF的外心, ∠BFC= ∠BAC/2 = 10° = ∠DBA.又∠BCF = ∠BCA – ∠FCA = 80° – 60° = 20° = ∠DAB, 且FC = AC = AB, 故△BAD≌△FCB, FB = BD.因∠EAC = ∠ECA = 20°, 故AE = EC. 结合FA = FC, 知点A与C关于直线EF对称, ∠CFE = 30°.∠BFE = ∠BFC +∠CFE = 10° + 30° = 40°, ∠BAF = ∠CAF –∠CAB = 60° – 20° = 40°, 故∠BFE = ∠BAF.所以△BFE∽△BAF, BF2 = BE⋅BA.而由FB = BD, 知BD2 = BE⋅BA. 即△BDE∽△BAD.所以, ∠BDE = ∠BAD = 20°.解法4在BD上取一点F, 使得∠BCF = 40°. 连EF. 在EC上取一点O, 使得AO平分∠BAC.由∠FBC = 70°, ∠BCF = 40°, 可得∠BFC = 70° = ∠FBC, BC = FC.∠FCE = ∠BCE – ∠BCF = 60° – 40° = 20°.因AO平分∠BAC, 故点B与C关于直线对称, ∠OBC = ∠OCB = 60°, △BOC为正三角形.∠ABO = ∠ABC – ∠OBC = 80° – 60° = 20° = ∠BAD, ∠BAO = 10° = ∠ABD, 故△BOA≌△ADB, AD = OB = BC = FC.又∠EAC = ∠ECA = 20°, 故AE = EC, 且∠FCE = 20° = ∠DAE, 得△FEC≌△DEA, ED = EF.故∠FED = ∠AEC = ∠ABC+ ∠ECB = 80° + 60° = 140°.所以, ∠EDB = ∠EDF = (180° – 140°)/2 = 20°.接下来, 为了叙述方便, 把后面几个证明中常用的两个结论作为引理列举如下.引理1在△ABC中, AB= AC, ∠BAC= 20°. 点D边AC上, 且∠DBC= 70°. 则AD = BC.引理1的证明方法较多, 其中之一可参见解法1中相应内容. 这里不再赘述.引理2在△ABC中, AB = AC, ∠BAC = 20°. 点D, E分别在边AC, AB上, 且∠DBC = 60°, ∠ECB = 50°. 则∠EDB = 30°.其实, 引理2就是附1所讨论的问题的变种形式. 故这里就不再重复给出证明了.解法5在AC上取一点F, 使得∠FBC = 50°. 连EF, BF.因∠BFC = 180° – ∠FBC – ∠FCB = 180° – 50° – 80° = 50° = ∠FBC, 故BC = FC.而由引题1, AD = BC , 故AD = FC .又∠ECF = ∠EAD = 20°, EC = EA , 故△AED ≌ △CEF , ED = EF .由引题2, 有∠CEF = 30°, 故∠AED = 30°, ∠EDF = ∠EAD + ∠AED = 20° + 30° = 50°.而∠BDC = ∠ABD + ∠BAD = 10° + 20° = 30°.所以, ∠EDB = ∠EDF – ∠BDC = 50° – 30° = 20°.解法6在AC 上取一点F , 使得∠FBC = 50°. 连EF , BF .由引题2, 有∠CEF = 30°, 故∠EFD = ∠CEF + ∠ECF = 30° + 20° = 50°.因∠DBF = ∠DBC – ∠FBC = 70° – 50° = 20° = ∠ECF , ∠BDF = ∠ABD + ∠BAD = 10° + 20° = 30° = ∠CEF , 故△DFB ∽ △EFC , 故FCFB EF DF =. 再由∠BFC = 180° – ∠FBC – ∠BCF = 180° – 50° – 80° = 50° = ∠EFD , 知△DFE ∽ △BFC , ∠EDF = ∠CBF = 50°.所以, ∠EDB = ∠EDF – ∠BDF = 50° – 30° = 20°.解法7在AC上取一点F, 使得∠FBC = 50°. 连EF, BF. 设EC与BD相交于点O.由引题2, 知∠OEF= ∠CEF= 30°, 而∠ODF= ∠BDF= ∠ABD+ ∠BAD= 10° + 20° = 30°, 故E, O, D, F四点共圆.又因∠OBF = ∠DBC – ∠FBC = 70° – 50° = 20° = ∠OCF, 故O, F, C, B也四点共圆.因∠BFC = 180° – ∠FBC – ∠BCF = 180° – 50° – 80° = 50°, ∠DFE = ∠DOE = ∠BOC = 180° – ∠OBC – ∠OCB = 180° – 70° – 60° = 50°. 故∠EFB = 180° – ∠DFE –∠BFC = 180° – 50° – 50° = 80°.所以, ∠EDB = ∠EDO = ∠EFO = ∠EFB – ∠OFB = ∠EFB – ∠ECB = 80° – 60° =20°.解法8在AB上取一点F, 使得AD = DF. 作△BCD的外心G.连FD, GD, GB, GC.因AD = DF, ∠AFD = ∠F AD = 20°. 而∠ABD = 10°, 故∠FDB = 10°, DF = BF.由引题1, AD = BC, 故AD = DF = BF = BC.因∠BDC= ∠ABD+ ∠BAD= 10° + 20° = 30°, 而G为△BCD的外心, 故-101 - ∠BGC = 60°, 且BG = CG = DG , 即△BGC 为正三角形, BC = BG.所以, BF = BC = BG , 点B 为△GFC 的外心, ∠GCF = ∠GBF /2 = (∠CBA – ∠CBG )/2 = (80° – 60°)/2 = 10°.而且, 因∠BCG = 60° = ∠BCE , 故E , G , C 三点共线, ∠ECF = ∠GCF = 10°. 因∠FEC = ∠BEC = ∠EAC + ∠ACE = 20° + 20° = 40°, ∠FDC = ∠AFD + ∠F AD = 20° + 20° = 40°, 故点E , D , C , F 四点共圆, ∠EDF = ∠ECF =10°.所以, ∠EDB = ∠EDF + ∠FDB =10° + 10° = 20°.。
初中数学一题多解

初中数学一题多解——初二三班蔡晨晖摘要:“一题多解”有利于调动学生的学习积极性,在教师的启发、引导下,对一道题学生可能提出两种、三种甚至更多种解法,课堂成为同学们合作、争辩、探究、交流的场所,它能极大提高学生的学习兴趣。
“一题多解”有利于锻炼学生思维的灵活性,活跃思路,让学生能根据题目给出的已知条件,并结合自身情况,灵活地选择解题的切入点。
“一题多解”有利于培养学生的创新思维,使学生不满足仅仅得出一道习题的答案,而去追求更独特、更快捷的其他的解题方法。
“一题多解”有利于学生积累解题经验和丰富解题方法,学会如何综合运用已有的知识不断提高解题能力。
对于"一题多解",我是从两个方面来认识和解释的:第一,同一个问题,用不同的方法和途径来解决;其二,同一个问题,其结论是多种的,就是结论开放性问题。
一题多解,有利于沟通各知识的内涵和外延,深化知识,培养发散性思维;一题多解有利于分析问题和解决问题的思路和方法,解题后从中择优,培养创新思维。
总而言之“一题多解”有利于学生解题思维能力的提高和发展。
图1图2如图1,Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F。
(1)求证:CE=CF;(2)将图1中的△ADE沿AB向右平移到△A′D'E′的位置,使点E′落在BC边上,其它条件不变,如图2所示,试猜想:BE′与CF有怎样的数量关系?请证明你的结论。
解:方法一:(1)∵∠ACB=90°∴∠CAB+∠B=180°-90°=90°∵CD⊥AB∴∠CDA=90°∴∠CAB+∠ACD=180°-90°=90°∴∠B=∠ACD∵∠CEF=∠ACD+∠CAF , ∠CFE=∠B+∠FAB又∵AF平分∠CAB∴∠CAF=∠FAB∴∠CEF=∠CFE∴CE=CF方法二:∵∠ACB =90°∴∠CFA=180°-∠ACB-∠CAF=180°-90°-∠CAF=90°-∠CAF∵CD⊥AB∴∠CDA= 90°∵∠CEF=∠ACD= 180°-∠CDA-∠FAB= 180°-90°-∠FAB= 90°-∠FAB∵AF平分∠CAB∴∠CAF=∠BAF∴∠CEF=∠CFA∴CE=CF(2)解:BE ′=CF 方法一: ∵△A ′D ′E ′为△ADE ∴△A ′D ′E ′≌△ADE∴∠E ′A ′B=∠EAB , A ′E ′=AE ∵AF 平分∠CAB∴∠CAF=∠BAE=∠BA ′E ′ 在△CAE 和△BA ′E ′中CAE=∠E ′A ′B ′∴△CAE ≌△BA ′E ′∴CE=BE ′∵CE=CF∴BE ′=CF方法二:作EG ⊥AC∵∠ACB=90°,∠CEF=∠CFA ∴∠CAE=∠ACE在△ ∠ACD=∠BA ′E ′AE=A ′E ′。
八年级一道几何题的一题多解发散思维

题目:如图,四边形ABCD是正方形,点E是边BC上一点,∠AEF=90°,EF交正方形外角的均分线CF于F.求证:AE=EF.【方法一】在AB上取一点G使得AG=CE,易得△BGE为等腰直角三角形,再证明△AGE≌△ECF(ASA)即可.【方法二】过点E作EG⊥BC交FC的延伸线于点G,证明△AEC≌△FEG(ASA)即可.【方法三】延伸AC至点G使得CG=CF并连结EG,证明△ECF≌△ECG(SAS),再得∠ECA=∠G(提示:外角的性质)即可.【方法四】分别延伸AB,FC交于点G,并连结EG,证明△ABE≌△GBE(SAS),再证∠EGC=∠F(提示:外角的性质)即可.【方法五】延伸AB至点G,使得BG=BE,并连结EG,CG,证明△ABE≌△CBG (SAS),再证明四边形EGCF为平行四边形即可(两组对边分别平行).【方法六】连结AC,过点E作EG⊥BC,交AC于点G,证明△AEG≌△FEC(ASA)即可.【方法七】如图,分别过点E,F作EG∥CF,FG∥CD和FH∥BC,EG分别与FG,FH交于点G,H,易得四边形ECFH为平行四边形,再证明△ACE≌△EGF(ASA)即可.【方法八】过点F作FG⊥BC于点G,分别设AB=a,EC=x,FG=CG=y,则BE=a-x,依据△ABE∽△EGF得AB:BE=EG:GF,即a:(a-x)=(x+y):y,得ay=ax+ay-x2-xy,得x(a-x-y)=0,即a=x+y,因此AB=EG,BE=FG因此AE=EF.【总结】此题还有很多其余结构协助线的方法来证明,有的是同种种类的不一样构法,异曲同工。
欢迎大家议论!自然,除了一题多解以外,大家也能够考虑把条件和结论对换进行证明,要不试一试看?题目:如图,四边形ABCD是正方形,点E是边BC上一点,在正方形外角的均分线CF上取一点F使得AE=EF.求证:∠AEF=90°.。
初中数学 一题多解

初中数学一题多解
最近,有很多人在讨论一题多解这个话题,这个话题在初中数学课堂上引起了特别大的兴趣。
一题多解指的是一道数学题可以用多种方式解决的问题。
一题多解的好处是可以让学生更加深入地思考,更加灵活地解决问题,并能让学生从多角度理解问题,从而更加深刻的理解数学。
首先,一题多解可以提高学生的数学思维能力。
学生在解决一题多解的问题时,可以使用不同的思维方式,形成更多的解决思路。
在这种情况下,学生可以从不同的角度思考问题,更加深刻地理解课堂上讲授的知识。
其次,一题多解还可以培养学生的灵活性。
学生研究一题多解后,可以用不同的方法解决问题,有一定的可操作性。
学生可以学会用多种不同的方法解决同一个问题,这样就可以培养学生的灵活性,使学生应对不同的数学问题有更强的适应能力。
最后,一题多解可以提高学生的创新能力。
学生在解决一题多解的问题时,可以根据自己的特点创造新的思路,也可以利用自己所掌握的知识,用不同的方法解决问题,从而提高学生的创新能力。
总之,一题多解可以使学生更加深入地思考,更加灵活地解决问题,并能让学生从多角度理解问题,从而更加深刻的理
解数学,提高学生的数学思维能力、灵活性和创新能力,也能提高学生的研究兴趣。
为此,在数学课堂上更多地引入一题多解的教学方式,有助于学生更好地掌握数学知识。
初中数学,有理数的一题多解
初中数学,有理数的一题多解
一个可以真正学习的平台!
有理数是学生进入初中阶段接触的第一块系统学习的代数知识,它不仅在知识体系上让学生第一次领略了系统性、层次性,而且也渗透了“分类”、“一题多解”等好的数学思想。
所谓“一题多解”,是指答案的多样性或方法的多样性。
本文试就本章出现的一题多解问题作一归类说明。
1、绝对值方程中的一题多解
一个数的绝对值表示点到原点的距离,而互为相反数的两数到原点的距离相同,故方程|x|=a(a>0) 的解有两个:x1=a或x2=—a,他们是一对互为相反数。
2、最值问题中的一题多解
所谓最值,即指最大值或最小值,在本章中涉及的最值问题主要是与绝对值相关的距离的最值,在竞赛中会有所涉及。
3、四则运算中的一题多解 此处的“一题多解”取多种解法的意思。
我们知道,四则运算中,运算律或运算技巧的使用可以让我们充分领略“条条大路通罗马”的数学思想方法。
当我们熟悉多种方法后,可以选择一种最好的。
本章中的一题多解问题只是为我们提供了一个领略数学思想方法的窗口,在后继课程中我们还要学习更多的一题多解问题,同学们要能养成及时总结、归纳的习惯,形成自己的学习方法,从而更高效地学习数学知识。
愿我的分享能够帮助到你!。
初中数学一题多解
浅谈初中数学一题多解王仲学一题多解是指运用不同的思维途径,用两种或两种以上的方法求解同一个问题。
多元化的思维训练,可以通过“一题多解”得到实现。
对于一个数学问题,若能根据已知与要求之间的关系,发散思维,善于联系,多角度深入地思考,可以得到多种不同的解法。
而采用一题多解的形式进行教学,能唤起学生学习数学的兴趣,在揭示知识的过程中,逐步把学生引入胜境,启发学生主动分析、思考问题,有助于学生大胆尝试,主动愉快地获取知识,从而训练思维的广阔性、灵活性、深刻性。
同时还可以帮助学生对知识系统性、特殊性、广泛性的深刻理解。
下面结合本人多年初中数学教学工作实践,谈谈我在教学中一题多解的做法。
【关键词】 一题多解 数学 初中 发散思维 解法 知识平行线中的一题多解例题一、如图1,已知AB//CD ,试找出B ∠、BED ∠和D ∠的关系并证明。
我们找出他们的关系是:D B BED ∠+∠=∠。
证明如下:方法一:如图2,过点E 作EF//AB 。
因为EF AB //,所以B BEF ∠=∠;因为CD AB //,EF AB //,所以CD EF //,所以D FED ∠=∠,所以D B FED BEF BED ∠+∠=∠+∠=∠。
方法二:如图3,过点E 作EF//AB 。
因为EF AB //,所以 180=∠+∠B BEF ,即B BEF ∠-=∠ 180;因为CD AB //,EF AB //,所以CD EF //,所以 180=∠+∠D FED ,即D FED ∠-=∠ 180;因为︒=∠+∠+∠360FED BED BEF ,所以)180180(360)(360D B FED BEF BED ∠-+∠--=∠+∠-=∠︒︒ D B ∠+∠=。
方法三:如图4,连接BD 。
因为CD AB //,所以 180=∠+∠BDC ABD ,即)(180EDB EBD EDC ABE ∠+∠-=∠+∠ ;在ΔBED 中,)(180EDB EBD BED ∠+∠-=∠ ,所以EDC ABE BED ∠+∠=∠。
2020年中考数学 一题多解 开拓思路
C B一题多解 开拓思路题目:如图,△ABC 中,AB=AC ,BD ⊥AC 于D . 求证:BC 2=2AC ·CD .B一道题由不同的思路,可以得出多种解法.等积式的证明,基本思路是化为比例式,解此题的关键之一,是如何处理系数的问题.思路一:将BC 2=2AC ·CD 化为比例式2AC/BC=BC/CD,或AC/BC=BC/2CD ,设法取一条线段,使它等于2AC 或2CD ,构造相似三角形进行证明. 证法一:延长CA 至E ,使AE=AC ,连结BE ,则CE=2AC . ∵AB=AE=AC ,∴∠EBC=90°=∠BDC . ∵∠C=∠C ,∴△ECB ∽△BCD .∴EC/BC=BC/CD . ∴2AC/BC=BC/CD .即BC 2=2AC ·CD .证法二:在DA 上截取DE=CD ,连结BE,则CE=2CD . ∵BD ⊥AD , ∴BE=BC .∴∠BEC=∠C .∵AB=AC ,∴∠ABC=∠C . ∴∠ABC=∠BEC . ∵∠C=∠C ,∴△ABC ∽△BEC . ∴AC/BC=BC/CE . ∴AC/BC=BC/2CD . 即BC 2=2AC ·CD .BE思路二:将BC 2=2AC ·CD 化为21BC 2=AC ·CD ,即AC/21BC=BC/CD 或 AC/BC=21BC /CD ,仿上,可得证法三、证法四. 证法三:取B C 中点E ,连结DE ,则CE=21BC .在Rt △BCD 中,DE=21BC=CE ,∴∠EDC=∠C . ∵AB=AC , ∴∠ABC=∠C . ∴∠ABC=∠EDC . ∵∠C=∠C , ∴△ABC ∽△EDC . ∴AC/EC=BC/CD . ∴AC/21BC=BC/CD . ∴21BC 2=AC ·CD . 即BC 2=2AC ·CD .证法四:取BC 中点E ,连结AE ,则CE=21BC . ∵AB=AC ,∴∠AEC=90°=∠BCD . ∵∠C=∠C ,∴△ACE ∽△BCD . ∴AC/BC=CE/CD . ∴AC/BC=21BC/CD . ∴21BC 2=AC ·CD . 即BC 2=2AC ·CD .思路三:BC2=2AC ·CD 还可化为(21BC )2 =21AC ·CD 或(21BC )2=AC ·21CD ,这时只需取BC 的一半,再取AC 的一半或CD 的一半即可得证法五、证法六.证法五:取BC 的中点E ,AC 的中点F ,连结DE 、EF 及AE .BECB ∵AB=AC , ∴AE ⊥BC . ∴FE=FC . ∴∠FEC=∠C . 同理∠EDC=∠C . ∴∠FEC=∠EDC . 又∠C=∠C ,∴△FEC ∽△EDC . ∴FC/EC=EC/CD . ∴CE 2=FC ·CD . 即(21BC )2 =21AC ·CD . ∴BC 2=2AC ·CD .证法六:取BC 的中点E ,CD 的中点F ,连结AE 、EF . 则AE ⊥BC ,EF ∥BD .又∵BD ⊥AC , ∴EF ⊥AC .故EC 2=CF ·CA .即(21BC )2 =21CD ·AC . ∴BC 2=2AC ·CD .思路四:由BD ⊥AC ,BC2=2AC ·CD 想到射影定理,只需要BC 成为以BD 为斜边上的高的直角三角形的一直角边即可,这不难做到.证法七:过点B 作BE ⊥AC 交CA 的延长线于E ,垂足为B . ∵ BD ⊥CE , ∴BC 2=CD ·CE . ∵AB=AC , ∴∠ABC=∠C . ∵∠ABC+∠EBA=90°,∠C+∠E=90°. ∴∠EBA=∠E .∴AE=AB=AC 即CE=2AC .即BC 2=2AC ·CD .思路五:由直角三角形及左边平方式,联想到应用勾股定理.证法八:在Rt △BDC 中,BC 2=BD 2+CD 2在Rt △ABD 中,BD 2=AB 2-AD 2BC2=AB2-AD2+CD2=AC2-AD2+CD2=(AD+CD)2 - AD2+CD2 =2AD·CD+2CD2=2CD(AD+CD)=2AC·CD.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学一题多解
1、若()16x 3-m 2x 2++ 是关于x 的完全平方公式(或完全平方数),则m=
2、4的平方根为 ,
16的平方根为 3、若2a =时, a 为 。
在数轴上,到原点的距离为3个单位的数
有 。
4、若64x 1x 2=⎪⎭⎫ ⎝
⎛+ ,则代数式=+x 1x 5、若关于x 的方程16
-x 3m 4x m 4-x 12+=++无解,则m 的值为 6、在平面直角坐标系xoy 中,已知点A (3,4),点P 在x 轴上,若△AOP 为等腰三角形,则点P 的坐标是
7、在一个等腰三角形中,有一个角为70°,则另两个角分别为
8、已知直角三角形的两边长分别为5和12,那么以这个直角三角形的斜边为边长的正方形的面积为
9、 在△ABC 中,AB=15,AC=13,BC 边上的高为12,求BC 边的边长为
10、在平行四边形ABCD 中,∠A 的角平分线把BC 边分为3和4的两条线段,则此平行四边形ABCD 的周长为
11、若⊙O 的半径为5cm ,某个点A 到圆上的距离为2cm ,则圆心到点A 的距离为
12、 若⊙O 中的某条弦AB 所对的圆心角为120°,则弦AB 所对的圆周角
为
13、已知x满足62
x
1
x
2
2=
+,则
x
1
x+的值是
14、当-2≤x≤1时,二次函数
()1
m
m
-x
-
y2
2+
+
=有最大值4,则实数m 的值为
15、在平面直角坐标系中有一点M,点M到x轴的距离为3,到y轴的距离为4,则点M的坐标为
16、若某条线段AB长为2,则该线段AB的黄金分割点离A点的距离为
17、若△OAB与△OCD是以坐标原点O为位似中心的位似图形,相似比为3:4,∠OCD=90°,∠AOB=60°,若点B的坐标为(6,0),则点A的对应点C的坐标为
18、如下图在△ABC中,AB=5,AC=4,点Q从点A出发向点B以2个单位/s的速度出发,点P从点C向点A以1个单位/s的速度出发,若要使△ABC 与△AQP相似,则运动的时间为s。
19、一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原来多边形的边数可能为
20、在平面直角坐标系中,点P(m-3,4-2m)可能在第象限
21、若⊙O与⊙P相切,且⊙O的半径为5cm,⊙P的半径为2cm,则OP的距离为。
