电磁场理论中的静磁场边界条件研究
谢处方《电磁场与电磁波》(第4版)课后习题-第3章 静态电磁场及其边值问题的解【圣才出品】

第3章 静态电磁场及其边值问题的解(一)思考题3.1 电位是如何定义的?中的负号的意义是什么?答:由静电场基本方程▽×E=0和矢量恒等式可知,电场强度E 可表示为标量函数φ的梯度,即式中的标量函数φ称为静电场的电位函数,简称电位;式中负号表示场强方向与该点电位梯度的方向相反。
3.2“如果空间某一点的电位为零,则该点的电场强度也为零”,这种说法正确吗?为什么?答:不正确。
因为电场强度大小是该点电位的变化率。
3.3“如果空间某一点的电场强度为零,则该点的电位为零”,这种说法正确吗?为什么?答:不正确。
此时该点电位可能是任一个不为零的常数。
3.4 求解电位函数的泊松方程或拉普拉斯方程时,边界条件有何意义?答:边界条件起到给方程定解的作用。
3.5 电容是如何定义的?写出计算电容的基本步骤。
答:两导体系统的电容为任一导体上的总电荷与两导体之间的电位差之比,即其基本计算步骤:①根据导体的几何形状,选取合适坐标系;②假定两导体上分别带电荷+q和-q;③根据假定电荷求出E;④由求得电位差;⑤求出比值3.6 多导体系统的部分电容是如何定义的?试以考虑地面影响时的平行双导线为例,说明部分电容与等效电容的含义。
答:多导体系统的部分电容是指多导体系统中一个导体在其余导体的影响下,与另一个导体构成的电容。
计及大地影响的平行双线传输线,如图3-1-1所示,它有三个部分电容C11、C12和C22,导线1、2间的等效电容为;导线1和大地间的等效电容为;导线2和大地间的等效电容为图3-1-13.7 计算静电场能量的公式和之间有何联系?在什么条件下二者是一致的?答:表示连续分布电荷系统的静电能量计算公式,虽然只有ρ≠0的区域才对积分有贡献,但不能认为静电场能量只存在于有电荷区域,它只适用静电场。
表示静电场能量存在于整个电场区域,所有E≠0区域对积分都有贡献,既适用于静电场,也用于时变电磁场,当电荷分布在有限区域内,闭合面S无限扩大时,有限区内的电荷可近似为点电荷时,二者是一致的。
《电磁场与电磁波》课程教学大纲

《电磁场与电磁波》课程教学大纲一、课程基本信息课程编码:07S2117B中文名称:电磁场与电磁波英文名称:E1ectromagneticFie1dandE1ectromagneticWave课程类别:专业核心课总学时:48总学分:3适用专业:电子科学与技术专业先修课程:高等数学、大学物理、场论、数学物理方程二、课程性质及目标教学性质:电磁场与电磁波是电子科学与技术专业学生的一门专业核心课程。
通过本课程的学习,要求学生系统地理解电磁场与电磁波的基本概念、基本性质和基本规律,掌握求解电磁场问题的基本方法,为进一步学习其他课程特别是专业课打下基础。
课程目标:1.通过本课程知识的学习,使学生了解电磁场论的发展历程,掌握电磁场论的基本概念、基本性质和基本规律,掌握求解电磁场问题的基本方法,为后续专业课程奠定基础。
引导学生学习科技发展史,树立科技强国意识,感受中国在电子领域的先进成果,激励学生自觉融入到实现中华民族伟大复兴的中国梦进程中。
2.通过本课程知识的学习,使学生掌握电磁场论计算理论的基本方法,并能在具体电子科学与技术专业的具体问题中加以应用。
培养学生解决问题方法的多样性,提高学生数学分析的能力。
3.通过本课程知识的学习,使学生掌握电磁场论分析问题的基本方法,并能在复杂的实际情况中加以应用。
培养学生逻辑思维和创新能力,提高学生设计、开发系统的能力。
不同介质和边界条件对应的场方程形式不同,引导学生用发展的眼光看问题,终身学习,与时俱进,始终拥有先进的理念和较高的职业素养。
I.采用启发式、案例式教学,激发学生主动学习的兴趣,培养学生独立思考、分析问题和解决问题的能力。
2.结合科研生产中的实际例子对课程进行讲解,通过课堂讲解,加强学生对基础知识及基本理论的理解。
3.教学以课堂讲授为主,多媒体辅助教学,提高课堂教学信息量,增强教学的直观性、形象性。
4.通过课内讨论与课外答疑、线下辅导与线上交流相结合的方式,调动学生学习的主观能动性,培养学生的自学能力。
【精品】第八讲:麦克斯韦方程组、电磁场的边界条件
第八讲:麦克斯韦方程组、电磁场的边界条件2.6麦克斯韦方程组2.7电磁场的边值关系1、了解麦克斯韦方程组的建立过程,掌握它的基本性质;2、了解边界上场不连续的原因,能导出电磁场的边值关系;3、掌握电磁场方程微分形式和边界形式的联系与区别。
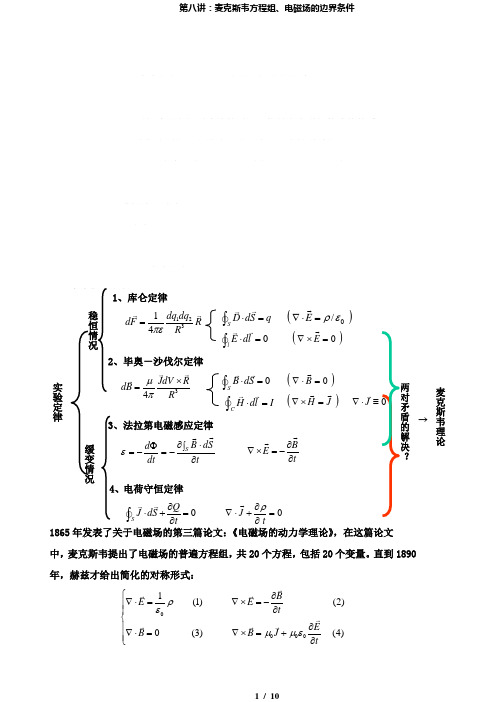
重点:1)麦克斯韦方程组的基本性质;2)电磁场的边值关系 难点:电磁场切向边值关系的推导 讲授法、讨论 2学时2.6麦克斯韦方程组(Maxwell ’sEquations )一、麦克斯韦方程1865年发表了关于电磁场的第三篇论文:《电磁场的动力学理论》,在这篇论文中,麦克斯韦提出了电磁场的普遍方程组,共20个方程,包括20个变量。
直到1890 年,赫兹才给出简化的对称形式:00001(1)(2)0(3)(4)BE E tE B B J tρεμμε⎧∂∇⋅=∇⨯=-⎪∂⎪⎨∂⎪∇⋅=∇⨯=+⎪∂⎩实验定律3、法拉第电磁感应定律4、电荷守恒定律12314dq dq dF RR πε=S D dS q ⋅=⎰0l E dl ⋅=⎰34JdV R dB R μπ⨯=0SB dS ⋅=⎰()0=⋅∇B CH dl I ⋅=⎰()JH =⨯∇tB E ∂∂-=⨯∇ 0=∂∂+⋅∇tJ ρ 0J ∇⋅≡对矛盾的解决麦克斯韦理论稳恒况缓变情况2、毕奥-沙伐尔定律1、库仑定律()/ερ=⋅∇E()=⨯∇E t S d B dt d S ∂⎰⋅∂-=Φ-= ε0S QJ dS t ∂⋅+=∂⎰→上式即为真空中的麦克斯韦方程组,其中(2)(4)含有对时间的偏导数,对应 运动方程,(1)(3)为约束方程。
二、麦克斯韦方程组的基本性质 1、线性性麦克斯韦方程组是一组线性方程,表明场服从迭加原理。
2、自洽性方程组各个方程彼此协调,且与电荷守恒定律协调。
如(2)式和(3)式一致:由(2)式有:()0=∂⋅∂∇-=⨯∇⋅∇tBE⇒C B =⋅∇ ,考虑到静磁时0=⋅∇B,所以取0=C 。
《电磁场》第三版思考题目答案-(1)

二章:2.1点电荷的严格定义是什么?点电荷是电荷分布的一种极限情况,可将它看做一个体积很小而电荷密度很大的带电小球的极限。
当带电体的尺寸远小于观察点至带电体的距离时,带电体的形状及其在的电荷分布已无关紧要。
就可将带电体所带电荷看成集中在带电体的中心上。
即将带电体抽离为一个几何点模型,称为点电荷。
2.2 研究宏观电磁场时,常用到哪几种电荷的分布模型?有哪几种电流分布模型?他们是如何定义的?常用的电荷分布模型有 体电荷,,面电荷,线电荷和点电荷常用的电流分布模型有体电流模型,面电流模型和线电流模型他们是根据电荷和电流的密度分布来定义的2,3点电荷的电场强度随距离变化的规律是什么?电偶极子的电场强度又如何呢?点电荷的电场强度与距离r 的平方成反比。
电偶极子的电场强度与距离r 的立方成反比2.4 简述ερ=•∇E 和0E =⨯∇所表征的静电场特性ερ0=•∇E 表明空间任意一点电场强度的散度与该处的电荷密度有关,静电荷是静电场的通量源。
0 =⨯∇E 表明静电场是无旋场。
2.5 表述高斯定律,并说明在什么条件下可应用高斯定律求解给定电荷分布的电场强度。
高斯定律:通过一个任意闭合曲面的电通量等于该面所包围的所有电量的代数和除以0ε与闭合面外的电荷无关,即dV dS E V S ρε⎰⎰=⋅01在电场(电荷)分布具有某些对称性时,可应用高斯定律求解给定电荷分布的电场强度。
2.6 简述0=•∇B 和J B 0μ=⨯∇所表征的静磁场特性0=⋅∇B 表明穿过任意闭合面的磁感应强度的通量等于0,磁力线是无关尾的闭合线,J B 0μ=⨯∇表明恒定磁场是有旋场,恒定电流是产生恒定磁场的漩涡源2.7 表述安培环路定理,并说明在什么条件下可用该定律求解给定的电流分布的磁感应强度。
安培环路定理:磁感应强度沿任何闭合回路的线积分等于穿过这个环路所有电流的代数和0μ倍,即I dl B C0μ=⋅⎰如果电路分布存在某种对称性,则可用该定理求解给定电流分布的磁感应强度。
第四章准静态电磁场

第四章 准静态电磁场4.1 准静态电磁场1.电准静态场由麦克斯韦方程组知,时变电场由时变电荷和时变磁场产生的感应电压产生。
时变电荷产生库仑电场,时变磁场产生感应电场。
在低频情况下,一般时变磁场产生的感应电场远小于时变电荷产生的库仑电场,可以忽略。
此时,时变电场满足ρ=∙∇≈⨯∇D 0E 称为电准静态场。
可见,电准静态场与静电场类似,可以定义时变电位函数ϕ ,即ϕ-∇=E且满足泊松方程ερϕ-=∇2 与电准静态场对应的时变磁场满足 0t =∙∇∂∂+=⨯∇B DE H γ 2.磁准静态场由麦克斯韦方程组知,时变磁场由时变传导电流和时变电场产生的位移电流产生。
在低频情况下,一般位移电流密度远小于时变传导电流密度,可以忽略。
此时,时变磁场满足0=∙∇≈⨯∇B J H c称为磁准静态场。
可见,磁准静态场与恒定磁场类似,可以定义时变矢量位函数A ,即A B ⨯∇=且满足矢量泊松方程c J A μ-=∇2与磁准静态场对应的时变电场满足ρ=∙∇∂∂-=⨯∇D B E t例1:图示圆形平板电容器,极板间距d = 0.5 cm ,电容器填充εr =5.4的云母介质。
忽略边缘效应,极板间外施电压t t u 314cos 2110)(=V ,求极板间的电场与磁场。
[解]:极板间的电场由极板上的电荷和时变磁场产生。
在工频情况下,忽略时变磁场的影响,即极板间的电场为电准静态场。
在如示坐标系下,得()()()V/m t 31410113t 31410501102d u z 4z 2z e e e E -⨯=-⨯⨯=-=-cos .cos . 由全电流定律得出,即由()z z 20r 4Sl t 31431410113d t H 2d e e S D l H ∙-π⨯⨯-=∙∂∂=π=∙⎰⎰ρεερφsin . 极板间磁场为φφφρe e H t 314103352H 4sin .-⨯== A/m也可以由麦克斯韦方程直接求解磁场强度,如下tt 0r ∂∂=∂∂=⨯∇E D H εε 展开,得t 314106694H 14sin .)(-⨯=∂∂φρρρ 解得φφφρe e H t 314103352H 4sin .-⨯== A/m 讨论:若考虑时变磁场产生的感应电场,则有tt ∂∂-=∂∂-=⨯∇H B E 0μ 展开,得t E z 314cos 103.231440ρμρ-⨯⨯-=∂∂- 解得 t E z 314cos 10537.428ρ-⨯= V/m可见,在工频情况下,由时变磁场产生的感应电场远小于库仑电场。
电磁场理论课件-6.1 法拉第电磁感应定律

静态场:场的大小不随时间发生改变(静电场、恒定 电场、恒定磁场)
特性:电场和磁场相互独立,互不影响。
时变场:场的大小随时间发生改变。
特性:电场和磁场相互激励,从而形成不可分隔的统 一的整体,称为电磁场。
本章主要内容:
电磁场的基本方程——麦克斯韦方程组
电磁场的边界条件
电磁场的能流和能流定律
d dt
上式对磁场中的任意回路都成立。
1.磁通变化的三种方式:
a)闭合回路与恒定磁场之间存在相对运动,即磁场与时 间无关,磁通量随时间变化,这时回路中的感应电 动势称为动生电动势。
i
t
B dS
S
07:24:37
4
6.1 法拉第电磁感应定律
b) 闭合回路是静止的,但与之交链的磁场是随时间变化
生电场(对电荷有作用力是电场的本质,因此它与静电场
在这一点上无本质差别)。
07电:26:4磁6 感应现象的实质:变化磁场激发电场
5
6.1 法拉第电磁感应定律
三、总电场的方程
设空间还存在静止电荷产生的静电场Ec,则总电场为
E Ein Ec
沿任意闭合路径的积分
(静电场Ec沿任意闭 合路径的积分为零)
的,这时回路中产生的感应电动势称为感生电动势。
i
S
B t
dS
c)既存在时变磁场又存在回路的相对运动,则总的感应
电动势为:
i
t
B dS
S
2.物理机制
动生可以认为电荷受到磁场的洛伦兹力,因此产生电
动势;感生情况回路不动,应该是受到电场力的作用。因
为无外电动势,该电场不是由静止电荷产生,因此称为感
in t
电磁场与电磁波 第4章 静态场的边值问题

设 q’ 距球心为b,则 q 和 q’ 在球外 任一点(r,,)处产生的电位为
第四章 静态场的边值问题
1 ( q q) 4π 0 R R
1(
q
4π 0 r 2 d 2 2rd cos
q
)
r 2 b2 2rb cos
径为a 的圆的反演点。
第四章 静态场的边值问题
将式(4-2-3)代入(4-2-2),可得球外任意点(r,,)的电位
q (
1
a
)
4π 0 r 2 d 2 2rd cos d r 2 b2 2rb cos
(4-2-5)
若导体球不接地且不带电,则当球外放置点电荷 q 后,它的
电位不为零,球面上净电荷为零。此情形下,为满足边界条件,
第四章 静态场的边值问题
第四章 静态场的边值问题
在给定的边界条件下求解泊松方程或拉普拉斯方程称为边 值问题。根据场域边界面上所给定的边界条件的不同,边值问 题通常分为 3 类:
第一类边值问题,给定位函数在场域边界面上的值; 第二类边值问题,给定位函数在场域边界面上的法向导数值; 第三类边值问题又称混合边值问题,一部分边界面上给定的 是位函数值,另一部分边界面上给定的是位函数的法向导数 值。
4.3.1 直角坐标系中的分离变量
直角坐标系中,标量拉普拉斯方程为
2 2 2
0 x2 y2 z2
(4-3-1)
第四章 静态场的边值问题
设 (x,y,z) = X (x)Y(y)Z(z),代入方程(4-3-1),整理可得
1 X
d2 X dx2
1 Y
d 2Y dy2
1 Z
d2Z dz2
电磁场与电磁感应静电场静磁场电磁感应定律等

电磁场与电磁感应静电场静磁场电磁感应定律等电磁场与电磁感应是物理学中重要的概念和理论,对电磁学的研究和应用有着重要的意义。
本文将介绍关于电磁场和电磁感应的一些基本概念和定律,以及它们的应用。
一、电磁场电磁场是由电荷和电流产生的相互作用结果,它可以分为静电场和静磁场两种。
静电场是由静止电荷所产生的力场,其力的作用是直接的、距离的平方反比的。
静磁场是由静止电流所产生的磁场,其力的作用是间接的,与距离成反比。
静电场遵循库仑定律,即两个点电荷之间的作用力等于它们电荷的乘积与它们之间距离的平方成反比。
静磁场遵循安培定律,即电流元产生的磁场与电流元的乘积成正比,并与它们之间的距离成反比。
二、电磁感应电磁感应是指导体中的电场或磁场的变化所引起的感应电流和感应电动势的现象。
根据法拉第电磁感应定律,当导体中的磁通量发生变化时,将会在导体中产生感应电动势,并且导体两端将产生感应电流。
电磁感应定律是物理学中的一个重要定律,它描述了磁场和电场的相互关系。
根据这个定律,磁场的变化会引起感应电动势,并且感应电动势的方向与磁场变化的速率成正比。
这个定律对于电磁波的产生和电动机的工作原理有着重要的意义。
三、电磁感应定律的应用电磁感应定律在生活和科学研究中有着广泛的应用。
下面介绍其中的几个重要应用:1. 电磁感应产生电流:电磁感应定律的最重要应用是发电机,它将机械能转化为电能。
发电机的工作原理就是利用磁场的变化来产生感应电流,从而产生电能。
2. 电磁感应制动:利用电磁感应的原理可以实现制动装置,例如电磁制动器、电磁刹车等。
这些装置利用磁场的变化来产生感应电流,通过感应电流的作用来达到制动的效果。
3. 电磁感应传感器:电磁感应定律在传感器技术中也有着广泛的应用。
例如,磁力计利用电磁感应原理来测量磁场的大小和方向;感应电动机利用电磁感应原理来测量电动机的转速和转向等。
4. 变压器:变压器是利用电磁感应原理来实现电压的变换。
通常,它由两个或多个线圈组成,当一个线圈中的电流发生变化时,将在其他线圈中感应出电动势,从而实现电压的变换。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电磁场理论中的静磁场边界条件研究引言:
电磁场理论是物理学中的重要分支之一,研究电场和磁场的相互作用及其规律。
在电磁场理论中,边界条件是一个关键概念,它描述了电磁场在不同介质之间的传播和相互作用。
本文将重点讨论静磁场的边界条件,并探讨其在实际应用中的意义。
一、静磁场边界条件的基本原理
静磁场边界条件是指在两个不同介质之间,磁场在边界上的行为和性质。
根据
麦克斯韦方程组的推导,我们可以得到静磁场边界条件的基本原理。
首先,根据安培环路定理,磁场的环路积分等于通过该环路的电流。
在两个不
同介质的边界上,磁场的环路积分应该是连续的,即磁场沿着边界的环路积分相等。
其次,根据磁感应强度的定义,磁感应强度是由磁场和介质磁导率的乘积决定的。
在两个不同介质的边界上,磁感应强度的法向分量应该是连续的,即磁感应强度的法向分量在边界上保持一致。
基于以上原理,我们可以得到静磁场边界条件的数学表达式。
对于平行于边界
的磁场,边界上的磁场强度和法向分量的变化满足以下关系:
H1t = H2t
B1n/μ1 = B2n/μ2
其中,H1t和H2t分别表示边界两侧的磁场强度的切向分量,B1n和B2n分别
表示边界两侧的磁感应强度的法向分量,μ1和μ2分别表示边界两侧的介质磁导率。
二、静磁场边界条件的应用
静磁场边界条件在实际应用中具有广泛的意义。
以下将从几个方面讨论其应用。
1. 电磁感应现象
根据法拉第电磁感应定律,磁场的变化可以引起电场的产生。
而电场的产生又会导致电流的产生。
在电磁感应现象中,静磁场边界条件起到了关键的作用。
当磁场通过一个闭合回路时,根据静磁场边界条件,磁场的环路积分为零。
这意味着在闭合回路内部,电场的环路积分也为零,从而保证了电场的闭合性。
2. 磁屏蔽技术
静磁场边界条件在磁屏蔽技术中也起到了重要的作用。
磁屏蔽技术是指利用特定材料或结构来抵消或减弱外部磁场的影响。
在磁屏蔽技术中,静磁场边界条件可以帮助我们设计合适的磁屏蔽结构,使得磁场在屏蔽材料内部得到有效的衰减。
3. 电磁波传播
静磁场边界条件在电磁波传播中也起到了重要的作用。
根据麦克斯韦方程组的推导,电磁波的传播是由电场和磁场相互耦合而形成的。
在介质边界上,电场和磁场的连续性要求使得电磁波能够正常传播,而静磁场边界条件则提供了关键的数学表达式,帮助我们分析和计算电磁波在不同介质中的传播规律。
结论:
静磁场边界条件是电磁场理论中的重要概念,它描述了磁场在不同介质之间的传播和相互作用。
本文从静磁场边界条件的基本原理出发,探讨了其在实际应用中的意义。
静磁场边界条件在电磁感应现象、磁屏蔽技术和电磁波传播等方面都具有重要的应用价值。
通过深入研究和理解静磁场边界条件,我们可以更好地理解和应用电磁场理论,推动科学技术的发展。
