电介质和磁介质的边界条件
合集下载
电磁场与电磁波第三章媒质的电磁性质和边界条件
6.介质的击穿 介质的击穿：当电介质上的外加电场足够大时 ，束缚电荷有可能克服原子结构的吸引力，成 为自由电荷。此时，介质呈现导体特性。
击穿场强：介质所能承受的最大电场强度。它 在高压技术中是一个表征材料性能的重要参数。
三、磁介质
1.磁介质的磁化 磁偶极矩
pm IdS
I —分子电流
电子轨道磁矩
2.各项异性媒质 本构方程为：
D E B H
D B 0
0 E
H
这种媒质中P的方向不一定与E相同，M的方向 不一定与B相同。进而D不一定平行于E，B不一定 平行于H。 当ε为张量而μ为标量时，称为电各项异性媒 质；当μ为张量而ε为标量时，称为磁各项异性 媒质。
Am2
磁偶极子
主要考虑
原子磁矩 电子自旋磁矩 原子核自旋磁矩
在没有外磁场作用时
p
m
0
在外磁场的作用下，发生磁化现象。
在外磁场作用下，物质中的 原子磁矩都将受到一个扭矩作 用，所有原子磁矩都趋于和外 磁场方向一致排列，结果对外 产生磁效应，这种现象称为物 质的磁化。
磁偶极子受 磁场力而转动
p
5. 电介质的物态方程
D 0 E P
D (1 e ) 0 E
D r 0 E E
P e 0 E 已知：
令： r 1 e
电介质的物态方程
r 称为相对介电常数。 其中：
r 0 材料的介电常数表示为： 各向同性：媒质的特性不随电场的方向而改变 , 反之称为各向异性； 线性：媒质的参数不随电场的值而变化； 均匀：媒质参数不随空间坐标（x,y,z）而变化。
（2）导体内部电场为零； （1）导体为等位体；
电磁场与电磁波媒质的电磁性质和边界条件
6.介质的击穿
介质的击穿： 当电介质上的外加电场足够大时 ，束缚电荷有可能克服原子结构的吸引力，成 为自由电荷。此时，介质呈现导体特性。
击穿场强： 介质所能承受的最大电场强度。它 在高压技术中是一个表征材料性能的重要参数。
三、磁介质
1.磁介质的磁化
? 磁偶极矩
r pm
?
r IdS
I —分子电流
Am 2
3. 极化电荷（束缚电荷）
由于电场作用产生极化 ,从而使介质内部出
现极化体电荷 ,介质表面出现极化面电荷 .我们
定义:
极化体电荷密度 极化面电荷密度
r
?P ? ??? P
? Ps
?
r P
?
r a
n
若电介质中还存在自由电荷分布时，电介质中 一点总的电位为：
? ? ?A
?
1
4π?0
?V ? ? P dV?? 1
? 磁介质的磁化现象：
还有一些材料对磁场较敏感，例如螺丝刀在 磁铁上放一会儿，螺丝刀就具有一定的磁性， 能吸起小螺钉。这种现象称为 磁化现象。能产 生磁化现象的材料称为 磁介质。
一、导体
1. 导体的定义： 含有大量可以自由移动的带电粒子 的物质。
导体分为两种 金属导体：由自由电子导电 电解质导体：由带电离子导电
2. 极化强度
为了描述介质极化的状态， 引入极化强度 矢量.定义单位体积内的电偶极矩为 极化强度 矢量(Polarization Intensity Vector), 即
ur
r P?
lim ?
p
?V? 0 ? V
C / m2
式中 ?为p体积元 内?电V偶极矩的矢量和，
pr的方向从负极化电荷指向正极化电荷。
3.5-3.6 磁介质的边界条件、电感
单位长度的“电容” C ?
C
0
ln(b a )
o
b
L C ? 进行对比： L / C ?
电磁场与电磁波
L C L / C Z (特征阻抗)
24
意义：传输线、双绞线、高速电路
例2. 单位长度上直导线的内自感
已知: 半径为a的长直导线在单位长度上的内自感 a Ir 按常用套路求解—— H 由§3.1例3可知导线内磁场强度是—— 2a 2 如图, 微元(阴影)区域上的磁通是—— 0 Ir dΦ B dS dr 1 2 2a 这部分磁通所交链的电流是——？？
C
d a
c b
B
管内是均匀磁场, 大小与……有关。 I
I
10
法二：上题“联想”——“地球赤道”
B
"掰开"
r
B
I
b
I I
I
a b
b 且 r ， r b
N 0 NI B 0 I ( ) 0 I n 2b 2b
电磁场与电磁波
“地球赤道”——“环”——“平地” 0 NI (b a ) r (b a) B环 2 r
互感Mutual‐Inductance: 某电流产生的磁场与 其他回路相交的磁链/该电流
一回路通单位电流时，另一回路所交链的磁链数
M 12 1施加到2 I1
电磁场与电磁波
18
z
1‐2 C2 1
y
C1
电磁场与电磁波
19
如何求“自感”？
思路一（常用套路）： 1. 根据给定的几何形状选择合适的坐标系 2. 假设导线中电流为I 3. 如何求B——(A‐C定理、B‐S定理) 什么时候用 4. 由B求磁通(1圈) 5. 由磁通求磁链(“交链”) ‐‐‐‐‐‐‐ 难点 6. 用定义式求自感
C
0
ln(b a )
o
b
L C ? 进行对比： L / C ?
电磁场与电磁波
L C L / C Z (特征阻抗)
24
意义：传输线、双绞线、高速电路
例2. 单位长度上直导线的内自感
已知: 半径为a的长直导线在单位长度上的内自感 a Ir 按常用套路求解—— H 由§3.1例3可知导线内磁场强度是—— 2a 2 如图, 微元(阴影)区域上的磁通是—— 0 Ir dΦ B dS dr 1 2 2a 这部分磁通所交链的电流是——？？
C
d a
c b
B
管内是均匀磁场, 大小与……有关。 I
I
10
法二：上题“联想”——“地球赤道”
B
"掰开"
r
B
I
b
I I
I
a b
b 且 r ， r b
N 0 NI B 0 I ( ) 0 I n 2b 2b
电磁场与电磁波
“地球赤道”——“环”——“平地” 0 NI (b a ) r (b a) B环 2 r
互感Mutual‐Inductance: 某电流产生的磁场与 其他回路相交的磁链/该电流
一回路通单位电流时，另一回路所交链的磁链数
M 12 1施加到2 I1
电磁场与电磁波
18
z
1‐2 C2 1
y
C1
电磁场与电磁波
19
如何求“自感”？
思路一（常用套路）： 1. 根据给定的几何形状选择合适的坐标系 2. 假设导线中电流为I 3. 如何求B——(A‐C定理、B‐S定理) 什么时候用 4. 由B求磁通(1圈) 5. 由磁通求磁链(“交链”) ‐‐‐‐‐‐‐ 难点 6. 用定义式求自感
第3章 媒质的电磁性质和边界条件
可得： (0E P) V
定义一个新矢量，称为电位移矢量或电通量密度：
D 0E P
已知：P e0E
D (1 e )0E
令： r 1 e
D r0E
电介质的物态方程
其中： r 称为相对介电常数。材料的介电常数表示为： r0
电磁场与电磁波
形成电流。这种现象称为传导。能发生传导现象的材料称 为导体。
☺电介质的极化现象： 这种在外加电场作用下，分子的电偶极矩将增大或发
生转向的现象称为电介质的极化现象。
☺磁介质的磁化现象： 还有一些材料对磁场较敏感，例如螺丝刀在磁铁上放
一会儿，螺丝刀就具有一定的磁性，能吸起小螺钉。这种 现象称为磁化现象。能产生磁化现象的材料称为磁介质。
第3章 媒质的电磁性质和边界条件
高斯定律： D V
积分形式： S D dS V V dV
结论：穿过任意封闭曲面的电通量，只与曲面中包围的自由 电荷有关，而与介质的极化状况无关。
常见电介质的相对介电常数见教材上的表3-2 。
6. 介质的击穿
介质的击穿：当电介质上的外加电场足够大时，束缚电荷有 可能克服原子结构的吸引力，成为自由电荷。 此时，介质呈现导体特性。
电磁场与电磁波
第3章 媒质的电磁性质和边界条件
2、电介质的极化
定义：这种在外电场作用下，电介质中出 现有序排列的电偶极子，表面上出现束缚 电荷的现象，称为电介质的极化。
(1)无极分子的极化：位移极化演示
在外电场作用下，由无极分子组成的电介质中，分子的正 负电荷“重心”将发生相对位移，形成等效电偶极子。
积分形式
H dl l
S
(
J
C
定义一个新矢量，称为电位移矢量或电通量密度：
D 0E P
已知：P e0E
D (1 e )0E
令： r 1 e
D r0E
电介质的物态方程
其中： r 称为相对介电常数。材料的介电常数表示为： r0
电磁场与电磁波
形成电流。这种现象称为传导。能发生传导现象的材料称 为导体。
☺电介质的极化现象： 这种在外加电场作用下，分子的电偶极矩将增大或发
生转向的现象称为电介质的极化现象。
☺磁介质的磁化现象： 还有一些材料对磁场较敏感，例如螺丝刀在磁铁上放
一会儿，螺丝刀就具有一定的磁性，能吸起小螺钉。这种 现象称为磁化现象。能产生磁化现象的材料称为磁介质。
第3章 媒质的电磁性质和边界条件
高斯定律： D V
积分形式： S D dS V V dV
结论：穿过任意封闭曲面的电通量，只与曲面中包围的自由 电荷有关，而与介质的极化状况无关。
常见电介质的相对介电常数见教材上的表3-2 。
6. 介质的击穿
介质的击穿：当电介质上的外加电场足够大时，束缚电荷有 可能克服原子结构的吸引力，成为自由电荷。 此时，介质呈现导体特性。
电磁场与电磁波
第3章 媒质的电磁性质和边界条件
2、电介质的极化
定义：这种在外电场作用下，电介质中出 现有序排列的电偶极子，表面上出现束缚 电荷的现象，称为电介质的极化。
(1)无极分子的极化：位移极化演示
在外电场作用下，由无极分子组成的电介质中，分子的正 负电荷“重心”将发生相对位移，形成等效电偶极子。
积分形式
H dl l
S
(
J
C
边界条件 磁路
S
电流线
规定：曲线上每一点的切线方向与该点的电流密度方向相同； 规定：曲线上每一点的切线方向与该点的电流密度方向相同； 而任一点的曲线数密度与该点的电流密度的大小成正比
三、电流的连续性方程 恒定电流条件 电流的连续性方程
1、电流的连续性方程 、电流的连续性方程
在单位时间内从闭合曲面向外流出的电荷， 在单位时间内从闭合曲面向外流出的电荷，即通过闭合 曲面向外的总电流为
4、 欧姆定律的微分形式 、
在导体中取一长为dl、横截面积为 的小圆柱体 的小圆柱体， 在导体中取一长为 、横截面积为dS的小圆柱体，圆柱体的轴线 与电流流向平行。设小圆柱体两端面上的电势为U和 与电流流向平行。设小圆柱体两端面上的电势为 和U+dU。根据 。 欧姆定律，通过截面dS的电流为 欧姆定律，通过截面 的电流为
2、 电流 、
电流方向 ：正电荷运动的方向 单位时间内通过任一截面的电量，叫做电流 单位时间内通过任一截面的电量， 是表示电流强弱的物理量，是标量， 表示。 是表示电流强弱的物理量，是标量，用 I 表示。
dq I= dt
用载流子定向运动的速率表示
I
I = nqus
3、 电流密度矢量 、 电流密度矢量 定义：电流密度矢量的方向代表 定义：电流密度矢量的方向代表
=0
v v v n ⋅ (J2 − J1) = 0 或J1n = J2n
同理
v v ∫∫ B ⋅ dS = 0
S
→ →
v v v n ⋅ (B2 − B ) = 0 1
v v v n ⋅ (D2 − D ) = 0 1
若电介质界面上无自由电荷: 若电介质界面上无自由电荷
v v ∫∫ D ⋅ dS = 0
超导现象的几个概念： 超导现象的几个概念：
电流线
规定：曲线上每一点的切线方向与该点的电流密度方向相同； 规定：曲线上每一点的切线方向与该点的电流密度方向相同； 而任一点的曲线数密度与该点的电流密度的大小成正比
三、电流的连续性方程 恒定电流条件 电流的连续性方程
1、电流的连续性方程 、电流的连续性方程
在单位时间内从闭合曲面向外流出的电荷， 在单位时间内从闭合曲面向外流出的电荷，即通过闭合 曲面向外的总电流为
4、 欧姆定律的微分形式 、
在导体中取一长为dl、横截面积为 的小圆柱体 的小圆柱体， 在导体中取一长为 、横截面积为dS的小圆柱体，圆柱体的轴线 与电流流向平行。设小圆柱体两端面上的电势为U和 与电流流向平行。设小圆柱体两端面上的电势为 和U+dU。根据 。 欧姆定律，通过截面dS的电流为 欧姆定律，通过截面 的电流为
2、 电流 、
电流方向 ：正电荷运动的方向 单位时间内通过任一截面的电量，叫做电流 单位时间内通过任一截面的电量， 是表示电流强弱的物理量，是标量， 表示。 是表示电流强弱的物理量，是标量，用 I 表示。
dq I= dt
用载流子定向运动的速率表示
I
I = nqus
3、 电流密度矢量 、 电流密度矢量 定义：电流密度矢量的方向代表 定义：电流密度矢量的方向代表
=0
v v v n ⋅ (J2 − J1) = 0 或J1n = J2n
同理
v v ∫∫ B ⋅ dS = 0
S
→ →
v v v n ⋅ (B2 − B ) = 0 1
v v v n ⋅ (D2 − D ) = 0 1
若电介质界面上无自由电荷: 若电介质界面上无自由电荷
v v ∫∫ D ⋅ dS = 0
超导现象的几个概念： 超导现象的几个概念：
第三章媒质的电磁性质和边界条件
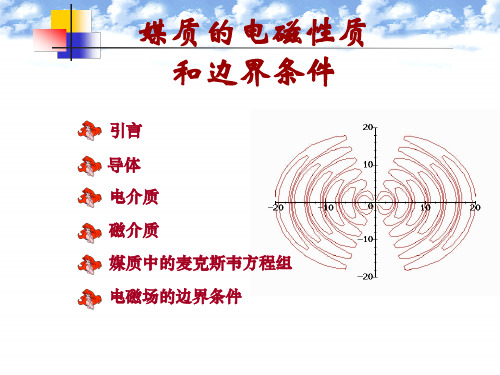
χ m >> 0
µr >> 1
µ >> µ0
如铁、镍和钴等属于铁磁质。 如铁、镍和钴等属于铁磁质。
在铁磁性材料中，有许多小天然磁化区，称为磁畴。 在铁磁性材料中，有许多小天然磁化区，称为磁畴。 磁畴 铁磁性物质被磁化后， 铁磁性物质被磁化后，撤去外磁 部分磁畴的取向仍保持一致， 场，部分磁畴的取向仍保持一致， 对外仍然呈现磁性。称为剩余磁化 剩余磁化。 对外仍然呈现磁性。称为剩余磁化。 铁磁材料的磁性和温度也有很大关 超过某一温度值后， 系，超过某一温度值后，铁磁材料会 失去磁性，这个温度称为居里点 居里点。 失去磁性，这个温度称为居里点。
r ρP =−∇• P r r ρPs = P•an
若电介质中还存在自由电荷分布时， 若电介质中还存在自由电荷分布时，电介质 中一点总的电位为： 中一点总的电位为：
1 φA = 4πε 0
∫
ρV + ρ P
R
V′
dV ′ +
1 4πε 0
∫
ρ PS
S′
R
dS ′
4. 电介质中的高斯定理 r r ρv ρ ρv −∇• P vb ∇• E = + =
媒质的电磁性质 和边界条件
引言 导体 电介质 磁介质 媒质中的麦克斯韦方程组 电磁场的边界条件
引言
媒质在电磁场作用下可发生现象： 媒质在电磁场作用下可发生现象： ☺导体的传导现象： 导体的传导现象： 在外电场的作用下， 在外电场的作用下，这些带电粒子将发生定 向运动，形成电流。这种现象称为传导 传导。 向运动，形成电流。这种现象称为传导。能发生 传导现象的材料称为导体 导体。 传导现象的材料称为导体。 ☺电介质的极化现象： 电介质的极化现象： 这种在外加电场作用下， 这种在外加电场作用下，分子的电偶极矩将 增大或发生转向的现象称为电介质的极化现象。 极化现象 增大或发生转向的现象称为电介质的极化现象。
电磁场的边界条件
1)理想介质是指电导率为无穷大的导体，2)电场强度和磁感应强度均为零。
3)表面上，一般存在自由电荷和自由电流。
设区域2为理想导体，区域1为介质，有 ,,均为零，得nD 2tE 2n B 2t H 2注意：理想介质和理想导体只是理论上存在。
在实际应用中，某些媒质的电导率极小或极大，则可视作理想介质或理想导体进行处理。
电磁场的边界条件可总结归纳如下：1)在两种媒质分界面上，如果存在面电流，使 H 切向分量不连续，其不连续量由式 确定若分界面上不存在面电流，则 H 的切向分量是连续的。
2)在两种媒质的分界面上，E 的切向分量是连续的。
3)在两种媒质的分界面上，B 的法向分量是连续的。
4)在两种媒质的分界面上，如果存在面电荷，使 D 的法向分量不连续，其不连续量由 确定。
若分界面上不存在面电荷，则D 的法向分量是连续的。
n B ⋅= 1Sn H J ⨯= t SH J =0n B =⇒1Sn D σ⋅=0t E =⇒⇒10n E ⨯=⇒n SD σ= 12()Sn H H J ⨯-=12()n D D σ⋅-=：积分形式：积分形式微分形式：微分形式：电磁场的基本方程和边界条件12()0n B B ⋅-=B ∇⋅= 积分形式：微分形式：积分形式：12()0n B B ⋅-=D ρ∇⋅= 0SB d S ⋅=⎰A SD d S q⋅=⎰A 微分形式：基本方程10n B ⋅= 12()n D D σ⋅-=12()0n D D ⋅-=10n D ⋅= 边界条件积分形式。
第3章媒质的电磁性质和边界条件
r = 1 + χ m < 1
且
r ≈ 1
如金,银和铜等属于抗磁质. (2)顺磁质:磁化率为正,相对磁导率略大于1,即 = 1+ χ > 1 且 r ≈ 1 r m 如镁,锂和钨等属于顺磁质. (3)铁磁质:其磁化率非常大,其相对磁导率远大于1,即
r >> 1
如铁,镍和钴等属于铁磁质.
在铁磁性材料中,有许多小天然磁化区,称为磁畴.
电磁场与电磁波
第3章 媒质的电磁性质和边界条件 章
电介质的物态方程 5. 电介质的物态方程 电介质极化后,场域中除了自由电荷之外,又多了束缚电荷, 根据高斯定律: (ε 0 E ) = ρV + ρ P = ρV + ( P ) 可得: (ε 0 E + P ) = ρV 定义一个新矢量: D = ε 0 E + P
电磁场与电磁波
第3章 媒质的电磁性质和边界条件 章
四,媒质中的麦克斯韦方程组
积分形式 微分形式
D ) dS t
∫ ∫
l
H dl = ∫ ( J C +
S
l
E dl = ∫
S
B dS S t
D × H = JC + t B ×E = t
D = ρV
B = 0
∫
D dS = ∫ ρV dV
电磁场与电磁波
第3章 媒质的电磁性质和边界条件 章
3. 磁化强度 磁化强度的定义:单位体积内,所有磁矩的矢量和.
(A/m) V 磁介质被磁化后,磁介质中出现束缚电流. 束缚电流面密度: J mS = M × an′
V → 0
∑m M = lim
i
束缚电流体密度: J m = ′ × M 介质磁化后束缚电流在空间产生的矢量磁位:
且
r ≈ 1
如金,银和铜等属于抗磁质. (2)顺磁质:磁化率为正,相对磁导率略大于1,即 = 1+ χ > 1 且 r ≈ 1 r m 如镁,锂和钨等属于顺磁质. (3)铁磁质:其磁化率非常大,其相对磁导率远大于1,即
r >> 1
如铁,镍和钴等属于铁磁质.
在铁磁性材料中,有许多小天然磁化区,称为磁畴.
电磁场与电磁波
第3章 媒质的电磁性质和边界条件 章
电介质的物态方程 5. 电介质的物态方程 电介质极化后,场域中除了自由电荷之外,又多了束缚电荷, 根据高斯定律: (ε 0 E ) = ρV + ρ P = ρV + ( P ) 可得: (ε 0 E + P ) = ρV 定义一个新矢量: D = ε 0 E + P
电磁场与电磁波
第3章 媒质的电磁性质和边界条件 章
四,媒质中的麦克斯韦方程组
积分形式 微分形式
D ) dS t
∫ ∫
l
H dl = ∫ ( J C +
S
l
E dl = ∫
S
B dS S t
D × H = JC + t B ×E = t
D = ρV
B = 0
∫
D dS = ∫ ρV dV
电磁场与电磁波
第3章 媒质的电磁性质和边界条件 章
3. 磁化强度 磁化强度的定义:单位体积内,所有磁矩的矢量和.
(A/m) V 磁介质被磁化后,磁介质中出现束缚电流. 束缚电流面密度: J mS = M × an′
V → 0
∑m M = lim
i
束缚电流体密度: J m = ′ × M 介质磁化后束缚电流在空间产生的矢量磁位:
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
电介质和磁介质的边界条件
在电磁学中，边界条件是指在两个不同介质之间的边界上，电场和磁场需要满
足的特定条件。
这些条件确保了电磁场的连续性和相容性。
对于电介质和磁介质的边界条件，下面将分别进行描述。
电介质的边界条件：
1. 边界面上的法向电场分量相等：
在电介质的边界上，两个相邻介质的法向电场分量相等。
这意味着电场线在两
个介质之间的边界上是连续的。
2. 边界面上的切向电场分量满足电场平行条件：
切向电场分量在边界上不连续。
而是满足电场平行条件，即两个介质中的切向
电场分量与介质的电导率和电场强度成正比。
磁介质的边界条件：
1. 边界面上的法向磁场分量相等：
在磁介质的边界上，两个相邻介质的法向磁场分量相等。
这确保了磁场线在两
个介质之间的边界上是连续的。
2. 边界面上的切向磁场分量满足磁场平行条件：
切向磁场分量在边界上不连续。
与电介质不同，切向磁场分量满足磁场平行条件，即两个介质中的切向磁场分量与介质的磁导率和磁场强度成正比。
总结起来，电介质和磁介质的边界条件要求法向分量连续，而切向分量则满足
平行条件。
这些条件保证了电场和磁场在不同介质之间的边界上的相容性和连续性。
对于电磁问题的求解和分析，理解和应用这些边界条件是非常重要的。