八年级下册数学- 一次函数与几何大综合
湘教版初中数学八年级下册23.一次函数与几何图形的结合PPT课件

x
D
课堂小结
一次函数 一次函数 与三角形 与四边形 结合 结合
优翼微课
初中数学知识点精讲课程
一次函数与几何图形的结合
解题步骤归纳
根据条件
求出解析式
结合三角形全等求出线段长
根据解析式和正方形性质求出点的坐标
待定系数法求解析式
典例精讲 类型一:一次函数与三角形结合
如图①所示,直线l:y=mx+5m与x轴负半轴、y轴 正半轴分别交于A、B两点。 (1)当OA=OB时,试确定直线l的解析式; (2)在(1)的条件下,如图②所示,设Q为AB延长线 上一点,作直线OQ,过A、B两点分别作AM⊥OQ 于M,BN⊥OQ于N,若AM=4,BN=3,求MN的 长.
典例精讲
类型二:一次函数与四边形的结合
如图,一次函数y=2x+4的图象与x、y轴分别 相交于点A、B,四边形ABCD是正方形。 (1)求点A、B、D的坐标; (2)求直线BD的表达式.
y
B
C
AO
x
E
D
典例精讲
解:(1)∵当y=0时,2x+4=0,x=-2 ∴点A(-2,0), ∵当xቤተ መጻሕፍቲ ባይዱ0时,y=4,∴点B(0,4), 过D作DH⊥x轴于H点, ∵四边形ABCD是正方形, ∴∠BAD=∠AOB=∠AHD=90°, AB=AD
∴∠BAO+∠ABO=∠BAO+∠DAH,
∴∠ABO=∠DAH.
∴△ABO≌△DAH。
y
∴DH=AO=2,AH=BO=4,
∴OH=AH-AO=2,
B
∴点D(2,-2)。 A O H C
E
x
D
典例精讲
(2)设直线BD的表达式为y=kx+b ∴
一次函数与几何综合题目

∴OH=EG= ,DH=
∴点 D 的坐标为( , )
方法(二) 易得∠AEB=∠BGD=90°,∠ABE=∠BDG,∴△ABE∽△BDG,
∴
;而 AE=2,BD=OP= ,BE=2 ,AB=4,
则有
,解得 BG= ,DG= ;
∴OH= ,DH= ;
∴点 D 的坐标为( , ).
(3)假设存在点 P,在它的运动过程中,使△ OPD 的面积等于 . 设点 P 为(t,0),下面分三种情况讨论: ①当 t>0 时,如图,BD=OP=t,DG= t,
(3)是否存在点 P,使△ OPD 的面积等于 ?若存在,请求出符合条件的点 P 的坐标;若不存在,请说明理由.
考点: 一次函数综合题. 菁优网版权所有
专题: 压轴题. 分析: (1)过点 B 作 BE⊥y 轴于点 E,作 BF⊥x 轴于点 F.依题意得 BF=OE=2,利用勾股定理求出 OF,然后可
人教版数学八年级下册一次函数综合大题练习参考答案

20232024学年人教版数学八年级下册一次函数综合大题练习参考答案1、解:(1)将B(﹣1,m)代入一次函数y=x+2,得m=﹣1+2=1∴B(﹣1,1)将B(﹣1,1)代入y=kx,得﹣k=1∴k=﹣1∴y=﹣x(2)令y=x+2=0,得x=﹣2∴C(﹣2,0)∴OC=2设D(x,y)==4则S△OCD∴|y|=4当y=4时,x=4﹣2=2∴D(2,4)当y=﹣4时,x=﹣4﹣2=﹣6∴D(﹣6,﹣4)综上所述,D为(2,4)或(﹣6,﹣4)(3)C(﹣2,0)关于y轴对称C′(2,0)设直线BC′解析式为y=k1x+b(k≠0)将B(﹣1,1)C′(2,0)代入上式,得解得∴y=﹣x对于,y=﹣x当x=0时,y=﹣x=∴P(0,)2、解:(1)当x=0时,y=﹣x+3=3∴B(0,3)令y=﹣x+3=0,得x=6∴A(6,0)(2)联立方程y=x,y=﹣x+3 解得x=2∴C(2,2)=OB•x C=×3×2=3∴S△COB(3)存在.∵点C(2,2)∴OC==2,∠AOC=45°设P(x,0),分三种情况:①如图,过C作CP垂直x轴∵∠AOC=45°∴CP=OP=2∴P(2,0)②当OC=OP=2时点P(2,0)或(﹣2,0)③当PC=OC=2时∵点C(2,2)∴22+(x﹣2)2=(2)2∴x=0或4∴P(4,0)综上,P为(2,0)或(﹣2,0)或(2,0)或(4,0)3、解:(1)∵x+y=8∴y=8﹣x∵点P(x,y)在第一象限∴x>0,y>0如图,AO=6 ,点P(x,y)∴S=×6×y=3y∴S=3(8﹣x)=24﹣3x∵S=﹣3x+24>0∴x<8∴0<x<8(2)当x=5时,S=﹣3×5+24=﹣15+24=9(3)不能若﹣3x+24>24,则x<0∵0<x<8∴△OP A的面积不能大于244、解:(1)将A(3,0)、B(0,4)代入y=kx+b得解得∴y=﹣x+4(2)由折叠性质,得AC=AB=5,BD=CD∴C(8,0)设D(0,m)∴=4﹣m解得m=﹣6∴D(0,﹣6)(2)设点P(0,a)由题意,得CO=6,OD=8,OA=3,BP=|4﹣a| =××6×8=6∴S△OCD∴S=|4﹣a|×3=6△ABP解得:a=8或0∴P(0,8)5、解:(1)令y=﹣2x=4,得x=﹣2∴C(﹣2,4)将(﹣2,4)代入y=x+b,得﹣2+b=4 解得b=6∴y=x+6当x=0时,y=x+6=6∴A(0,6)令y=x+6=0,得x=﹣6∴B(﹣6,0)(2)设P(t,t+6)∵A(0,6),B(﹣6,0),C(﹣2,4)∴OA=6,OB=6,y C=4∴S△OBC=×6×4=12∵S△OAP =S△OBC∴×6×|t|=×12解得t=﹣或∵P在射线CA上运动∴t≥﹣2∴P或(3)﹣4<m<﹣16、解:(1)∵点B的横坐标为3∴∴B(3,4)将点A(0,6)、B(3,4)代入y=kx+b,得解得,b=6∴(2)设Q(t,﹣t+6)∵A(0,6)∴OA=6=×OA×|x Q﹣x B|∴S△OBQ=×6×|t﹣3|=解得t=4.5或1.5,此时点Q(4.5,3)或(1.5,5)(3)P为或或或(0,2)理由如下:设点P(0,t)∵A(0,6)、B(3,4)∴AB2=13,AP2=(t﹣6)2,BP2=(t﹣4)2+9若AP=AB,则(t﹣6)2=13解得t=或若AP=BP,则(t﹣6)2=(t﹣4)2+9解得t=若AB=BP,则(t﹣4)2+9=13解得t=2综上,P为或或或(0,2)7、解:(1)当x=1时,y=3x=3∴C(1,3)当x=0时,得y=﹣x+=∴B(0,)令y=﹣x+=0,得x=3∴A(3,0)(2)存在.理由如下:如图1,过C作CF⊥x,则F(1,0)∴AF=3﹣1=2,CF=3∴AC==当AE=AC=时,OE=3+或﹣3∴E(3+,0)或(3﹣,0)当CA=CE时,则AF=EF=2∴OE=2﹣1=1∴E(﹣1,0)(3)如图,设M(t,﹣t+),则N(t,3t),D(t,0)∴MN=﹣t+﹣3t=2或3t﹣(﹣t+)=2解得t=或∴D(,0)或(,0)8、解:(1)当x=0,=4∴A(0,4)将A(0,4),B(﹣5,0)代入y=kx+b ,得解得∴直线AB的函数表达式为(2)设点P坐标为(t,t+4)令y=﹣x+4y=0得x=3∴C(3,0)又∵A(0,4),B(﹣5,0)∴OA=4,OB=5,BC=8当P在线段BA上时,S=×8×4﹣×8×(t+4)=×5×4△ACP解得t=﹣∴P(﹣,)当P'在线段BA延长线上时,S=×8×(t+4)﹣×8×4=×5×4△ACP解得p=∴P(,)综上,P为(﹣,)或(,)(3)存在Q(﹣2,﹣4),使四边形ABQC为平行四边形,理由如下:设Q(m,n)由中点坐标公式,得解得∴Q(﹣2,﹣4)。
人教版-数学-八年级下册一次函数综合题型归纳 讲义

一次函数综合题型归纳类型一:一次函数与最值问题例题1.如图,平面直角坐标系中,直线y=2x+my轴交于点A,与直线y=−x+5交于点B(4,n),P为直线y=−x+5上一点.(1)求m,n的值;(2)求线段AP的最小值,并求此时点P的坐标.例题2.如图,直线l1:y=−x+3与x轴相交于点A,直线l2:y=kx+b经过点(3,−1),与x轴交于点B(6,0),与y轴交于点C,与直线l1相交于点D.(1)求直线l2的函数关系式;(2)点P是l2上的一点,若△ABP的面积等于△ABD的面积的2倍,求点P的坐标;(3)设点Q的坐标为(m,3),是否存在m的值使得QA+QB最小?若存在,请求出点Q的坐标;若不存在,请说明理由.例题3.如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.(Ⅰ)直接写出点E.F的坐标;(Ⅱ)若M为x轴上的动点,N为y轴上的动点,当四边形MNFE的周长最小时,求出点M、N 的坐标,并求出周长的最小值.变式练习:1.如图,正方形ABOD的边长为2,OB在x轴上,OD在y轴上,且AD//OB,AB//OD,点C为AB的中点,直线CD交x轴于点F.(1)求直线CD的函数关系式;(2)过点C作CE⊥DF且交于点E,求证:∠ADC=∠EDC;(3)求点E坐标;(4)点P是直线CE上的一个动点,求PB+PF的最小值.类型二一次函数与几何问题例题1.如图,平面直角坐标系中,直线l分别交x轴、y轴于A.B两点(OA<OB)且OA.OB的长分别是一元二次方程x2−(√3+1)x+√3=0的两个根,点C在x轴负半轴上,且AB:AC=1:2(1)求A.C两点的坐标;(2)若点M从C点出发,以每秒1个单位的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,写出S关于t的函数关系式,并写出自变量的取值范围;(3)点P是y轴上的点,在坐标平面内是否存在点Q,使以A.B.P、Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,请说明理由.例题2.如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA.OB的长分别是一元二次方程x2−7x+12=0的两个根(OA>OB).(1)求点D的坐标.(2)求直线BC的解析式.(3)在直线BC上是否存在点P,使△PCD为等腰三角形?若存在,请直接写出点P的坐标;若不存在,说明理由.例题3.如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,−1),与x轴以及y=x+1的图象分别交于点C.D,且点D的坐标为(1,n),(1)则n=______ ,k=______ ,b=______ ;(2)函数y=kx+b的函数值大于函数y=x+1的函数值,则x的取值范围是______(3)求四边形AOCD的面积;(4)在x轴上是否存在点P,使得以点P,C,D为顶点的三角形是直角三角形?若存在求出点P的坐标;若不存在,请说明理由.变式练习:1.如图,在平面直角坐标系中,直线AB与x轴、y轴的正半轴分别交于点A,B,直线CD与x轴正半轴、y轴负半轴分别交于点D,C,AB与CD相交于点E,点A,B,C,D的坐标分别为(8,0)、(0,6)、(0,−3)、(4,0),点M是OB的中点,点P在直线AB上,过点P作PQ//y轴,交直线CD于点Q,设点P的横坐标为m.(1)求直线AB,CD对应的函数关系式;(2)用含m的代数式表示PQ的长;(3)若以点M,O,P,Q为顶点的四边形是矩形,请直接写出相应的m的值.2.已知一次函数y=kx+b的图象经过点M(−1,3)、N(1,5).直线MN与坐标轴相交于点A.B两点.(1)求一次函数的解析式.(2)如图1,点C与点B关于x轴对称,点D在线段OA上,连结BD,把线段BD顺时针方向的值.旋转90∘得到线段DE,作直线CE交x轴于点F,求DF−DAEF(3)如图2,点P是直线AB上一动点,以OP为边作正方形OPNM,连接ON、PM交于点Q,连BQ,当点P在直线AB上运动时,BQ的值是否会发生变化?若不变,请求出其值;若变化,OP请说明理由.类型三一次函数与面积问题例题1.如图,在平面直角坐标系中,直线AC:y=−x+2.5与x轴交于C点,与y轴交于A点,直线AB与x轴交于C点,与y轴交于A点,已知B(−3,0).(1)求直线AB的解析式.(2)直线AD过点A,交线段BC于点D,把s△ABC的面积分为1:2两部分;求出此时的点D的坐标.x+2与x轴、y轴交于A.B两点,在y轴上有一个点C(0,4),例题2.已知直线L:y=−12动点M从A点出发,以每秒1个单位的速度沿x轴向左移动.(1)求A.B两点的坐标.(2)求△COM的面积S与点M移动的时间t之间的函数关系式.(3)当t=6时,①求直线CM所对应的解析式.②问直线CM与直线L有怎样的位置关系?为什么?变式练习:平面直角坐标系xOy中,点P的坐标为(m+1,m−1).(1)试判断点P是否在一次函数y=x−2的图象上,并说明理由;(2)如图,一次函数y=−1x+3的图象与x轴、y轴分别相交于点A.B,若点2P在△AOB的内部,求m的取值范围.x+m的图象交于P(n,−2).如图,函数y=−2x+3与y=−12(1)求出m、n的值;(2)求出△ABP的面积.类型四、一次函数与方程不等式例题1.如图,已知函数y1=2x+b和y2=ax−3的图象交于点P (−2,−5),这两个函数的图象与x轴分别交于点A.B.(1)分别求出这两个函数的解析式;(2)求△ABP的面积;(3)根据图象直接写出不等式2x+b<ax−3的解集.例题2.如图,函数y=−2x+3与y=−12x+m的图象交于P(n,−2).(1)求出m、n的值;(2)直接写出不等式−12x+m>−2x+3的解集;(3)求出△ABP的面积.变式练习:1.在同一坐标系中画出了三个一次函数的图象:y=1−x,y=x+1和y=3x−1(1)求y=1−x和y=3x−1的交点A的坐标;(2)根据图象填空:①当x______ 时3x−1>x+1;②当x______ 时1−x>x+1;(3)对于三个实数a,b,c,用max{a,b,c}表示这三个数中最大的数,如max{−1,2,3}=3,max{−1,2,a}={2(当a≤2时)a(当a>2时),请观察三个函数的图象,直接写出max{1−x,x+1,3x−1}的最小值.。
初中数学一次函数与几何综合练习题

一次函數與幾何1. 如圖,直線l1の函數解析式為y=-3x+3,且l1與x軸交於點D,直線l2經過點A,B,直線l1,l2交於點C.(1)求點Dの座標;(2)求直線l2の函數解析式;(3)求△ADCの面積;(4)在直線l2上存在異於點Cの另一點P,使得△ADP與△ADCの面積相等,請直接寫出點P の座標.2. 如圖,直線y=2x+6與x軸交於點A,與y軸交於點B,直線y=-12x+1與x軸交於點C,與y軸交於點D,兩直線交於點E,求S△BDE和S四邊形AODE.3.如圖,直線y=-43x+8分別交x軸、y軸於A,B兩點,線段ABの垂直平分線分別交x軸、y軸於C,D兩點.(1)求點Cの座標;(2)求直線CEの解析式;(3)求△BCDの面積.4. 如圖,在平面直角坐標系中,點A(-1,0),B(0,3),直線BC交坐標軸於B,C兩點,且∠CBA=45°.求直線BCの解析式.5. 如圖,A(0,4),B(-4,0),D(-2,0),OE⊥AD 於點F ,交AB 於點E ,BM⊥OB 交OE の延長線於點M.(1)求直線AB 和直線AD の解析式;(2)求點M の座標;(3)求點E ,F の座標.6. 如圖,正方形OBAC 中,O(0,0),A(-2,2),B ,C 分別在x 軸、y 軸上,D(0,1),CE⊥BD 交BD 延長線於點E ,求點E の座標.7. 如圖,在平面直角坐標系中,A(0,1),B(3,12),P 為x 軸上一動點,則PA +PB 最小時點P の座標為________.8. 如圖,直線y=x+4與坐標軸交於點A,B,點C(-3,m)在直線AB上,在y軸上找一點P,使PA+PCの值最小,求這個最小值及點Pの座標.答案:1. (1) D(1,0) (2)y=32x-6 (3) S△ADC=92(4)P(6,3)2. A(-3,0)B(0,6)C(2,0)D(0,1)E(-2,2)S △BDE =5,S 四邊形AODE =S △AOB -S △BDE =9-5=43. (1) A(6,0),B(0,8),中點得E (3,4), k1*k2=-1帶入E 座標或畢氏定理AC ²=BC ² (6-n )²=n ²+64 得C(-73,0) (2) y =34x +74 (3)D (0,74),S △BCD =12×(8-74)×73=175244. 過點A 作AD⊥AB, AD =AB=√10,過點D 作DE⊥x 軸,△DEA≌△AOB,∴DE=OA =1,EA =OB =3,∴D(-4,1),直線BC :y =12x +35. (1)AB :y =x +4,AD :y =2x +4(2)由△OBM≌△AOD 得BM =OD ,∴M(-4,2)(3) OM :y =-12x ,聯立⎩⎨⎧y =-12x ,y =x +4,得E(-83,43);聯立⎩⎨⎧y =2x +4,y =-12x ,得F(-85,45)6. 延長CE 交x 軸於點F ,△BOD≌△COF,OD =OF =1,F(1,0),∵C(0,2),∴CF:y =-2x +2,∵B(-2,0),D(0,1),∴BD:y =12x +1,由⎩⎨⎧y =12x +1,y =-2x +2,得E(25,65)7. P (2,0) s=3√5/2 作出點A 關於x 軸の對稱點A′,直線A′B の解析式為y=0.5x-18. C(-3,1),作點A 關於y 軸の對稱點A′,連接CA′交y 軸於P ,此時PA +PC 最小值為CA′,∵A′(4,0),∴CA′:y =-17x +47,∴P(0,47),作CE⊥x 軸於E ,∴CA′=CE 2+A′E 2=5 2。
初中数学一次函数与几何综合练习题

一次函数与几何1. 如图,直线l1的函数解析式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.(1)求点D的坐标;(2)求直线l2的函数解析式;(3)求△ADC的面积;(4)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.2. 如图,直线y=2x+6与x轴交于点A,与y轴交于点B,直线y=-12x+1与x轴交于点C,与y轴交于点D,两直线交于点E,求S△BDE和S四边形AODE.3.如图,直线y=-43x+8分别交x轴、y轴于A,B两点,线段AB的垂直平分线分别交x轴、y轴于C,D两点.(1)求点C的坐标;(2)求直线CE的解析式;(3)求△BCD的面积.4. 如图,在平面直角坐标系中,点A(-1,0),B(0,3),直线BC交坐标轴于B,C两点,且∠CBA=45°.求直线BC的解析式.5. 如图,A(0,4),B(-4,0),D(-2,0),OE⊥AD于点F,交AB于点E,BM⊥OB 交OE的延长线于点M.(1)求直线AB和直线AD的解析式;(2)求点M的坐标;(3)求点E,F的坐标.6. 如图,正方形OBAC中,O(0,0),A(-2,2),B,C分别在x轴、y轴上,D(0,1),CE⊥BD交BD延长线于点E,求点E的坐标.7. 如图,在平面直角坐标系中,A(0,1),B(3,12),P为x轴上一动点,则PA+PB最小时点P的坐标为________.8. 如图,直线y=x+4与坐标轴交于点A,B,点C(-3,m)在直线AB上,在y 轴上找一点P,使PA+PC的值最小,求这个最小值及点P的坐标.答案:1. (1) D(1,0) (2)y=32x-6 (3) S△ADC=92(4)P(6,3)2. A(-3,0)B(0,6)C(2,0)D(0,1)E(-2,2)S△BDE=5,S四边形AODE=S△AOB-S△BDE=9-5=43. (1) A(6,0),B(0,8),中点得E (3,4), k1*k2=-1带入E坐标或勾股定理AC²=BC²(6-n)²=n²+64 得C(-73,0)(2) y=34x+74(3)D (0,74),S△BCD=12×(8-74)×73=175244. 过点A作AD⊥AB, AD=AB=√10,过点D作DE⊥x轴,△DEA≌△AOB,∴DE=OA=1,EA=OB=3,∴D(-4,1),直线BC:y=12x+35. (1)AB:y=x+4,AD:y=2x+4(2)由△OBM≌△AOD得BM=OD,∴M(-4,2)(3) OM:y=-12x,联立⎩⎨⎧y=-12x,y=x+4,得E(-83,43);联立⎩⎨⎧y=2x+4,y=-12x,得F(-85,45)6. 延长CE交x轴于点F,△BOD≌△COF,OD=OF=1,F(1,0),∵C(0,2),∴CF:y=-2x+2,∵B(-2,0),D(0,1),∴BD:y=12x+1,由⎩⎨⎧y=12x+1,y=-2x+2,得E(25,65)7. P (2,0) s=3√5/2 作出点A关于x轴的对称点A′,直线A′B的解析式为y=0.5x-18. C(-3,1),作点A关于y轴的对称点A′,连接CA′交y轴于P,此时PA+PC最小值为CA′,∵A′(4,0),∴CA′:y=-17x+47,∴P(0,47),作CE⊥x轴于E,∴CA′=CE2+A′E2=52。
初中数学解题技巧专题---一次函数与几何图形的综合问题
第2页共3页
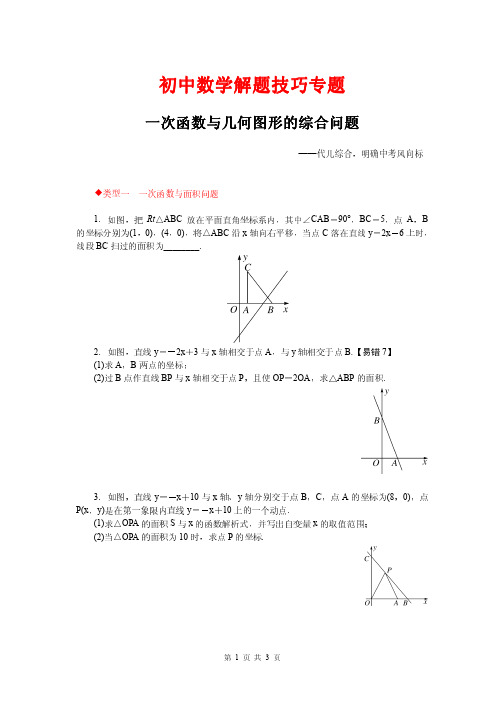
参考答案与解析 .1 16 解析:如图,∵点 ,A B 的坐标分别为(1,0),(4,0),∴AB=3.∵∠CAB=90°,
==BC24=x×-54,6=上∴16,在.即∴R线2t△x段-AB6B=CC扫4中,过,解的由得面勾x积股=为定5.即理16得O. AA′=C=5,∴BCC2C-′=AABA2=′=45,-∴1=A′C4.′=∴4S.▱∵BCC点′B′C=′在C直C′线·CAy
9
Hale Waihona Puke AP OP OA 2 AP OP OA 2
S△ABP
1 2AP·OB
1 2
9 2
3
27 4
S△ABP
1 2AP·OB
=12×32×3=94.综上所述,△ABP 的面积为247或94. 3.解:(1)∵点 P 在直线 y=-x+10 上,且点 P 在第一象限内,∴x>0 且 y>0,即-x
+10>0,解得 ∵点 0<x<10. A(8,0),∴OA=8,∴S=12OA·|yP|=12×8×(-x+10)=-4x+ . 40(0<x<10)
= ,∴ , , , , , … ∵ = - , = - , = - ,…∴ B2B3 8 B1(2 0) B2(6 0) B3(14 0) . 2 22 2 6 23 2 14 24 2
Bn
的横坐标为 - 故答案为 - 2n+1 2.
2n+1 2.
B直∴形3(线点2A217,ByB.=212C的(3x21--On坐-111是标),,上正为2…,n-方(2∴,,1形)点∴3,)点A,解∴2同B析的An1理:坐的B1∵可标坐=y得为标O=A点为(x21=-,(B21113n-,)的与.1,∴坐∵x2点标四轴n-为边交B11()形于4的.,点坐A72)B标A.21C,为∵2∴C(B11,1点是(210正A),.1方的2∵1形-坐C,1标1A)∴,为2∥AB(2x12B(,2轴21=0,,).A2点22∵C-1A四=12)边在2,,
部编数学八年级下册专题38一次函数的应用之几何问题(解析版)含答案

专题38一次函数的应用之几何问题1.如图,在平面坐标系中,直线:l y kx b =+分别与x 轴,y 轴交于点3,02A æö-ç÷èø,点()0,3B .(1)求直线l 的解析式;(2)若点C 是y 轴上一点,且ABC V 的面积是154,求点C 的坐标;(3)在(2)的条件下,当点C 在y 轴负半轴时,在平面内是否存在点D ,使以A ,B ,C ,D 为顶点的四边形是平行四边形?若存在,直接写出点D 的坐标;若不存在,请说明理由.2.如图①,在矩形OACB 中,点A 、B 分别在x 轴、y 轴正半轴上,点C 在第一象限,8OA =,6OB =.(1)请直接写出点C 的坐标;(2)如图②,点F 在BC 上,连接AF ,把ACF V 沿着AF 折叠,点C 刚好与线段AB 上一点C ¢重合,求线段CF 的长度;(3)如图③,点(,)P x y 为直线26y x =-在第一象限内的图象上的个动点,点D 在线段AC 上(不与点A 、C 重合),是否存在直角顶点为P 的等腰直角BDP △,若存在,请求出点P 的坐标:若不存在,请说明理由.Q BPD D 是等腰三角形,\ BP PD =,90BPD Ð=°,\EF BC ∥,\BEP Ð=90PFD Ð=°,\BPE DPF DPF PDF Ð+Ð=Ð+Ð,\BPE PDF Ð=Ð,\()BPE PDF AAS D D ≌,\6(26)122PF BE a a ==--=-,EP DF =,Q 1228EF EP PF a a =+=+-=,\4a =,\点(4,2)P ,点D 为(8,6)在端点上,点(4,2)P 不符合题意,舍去;②当点P 在BC 的上方时,如图④,过点P 作EF BC ∥,交y 轴于E ,交AC 的延长线于F ,同理可证BPE PDF D D ≌,\266212BE PF a a ==--=-,3.如图,在平面直角坐标系中,正方形OABC的边OA,OC分别在x轴,y轴的正半轴上,直线y =2x-6经过线段OA的中点D,与y轴交于点G,E是线段CG上一点,作点E关于直线DG的对称点F,连接BE,BF,FG.设点E的坐标为(0,m).(1)写出点B的坐标是( , );(2)当43OABCBEGFS S=正方形四边形时,求点E的坐标;(3)在点E的整个运动过程中,①当四边形BEGF为菱形时,求点E的坐标;②若N为平面内一点,当以B,E,F,N为顶点的四边形为矩形时,m的值为 .(请直接写出答案)4.如图,在平面直角坐标系中,过点B(4,0)的直线AB与直线OA相交于点A(3,1),动点M 在线段OA和射线AC上运动.(1)求直线AB的解析式;(2)直线AB交y轴于点C,求△OAC的面积;(3)当△OAC的面积是△OMC面积的3倍时,求出这时点M的坐标.5.如图1,在平面直角坐标系中,直线AB 分别交x 轴、y 轴于A(a ,0)、B(0,b)两点,且a ,b 满足(a ﹣b )2+|a ﹣4t|=0,且t >0,t 是常数.直线BD 平分∠OBA ,交x 轴于D 点.(1)若AB 的中点为M ,连接OM 交BD 于N ,求证:ON =OD ;(2)如图2,过点A 作AE ⊥BD ,垂足为E ,猜想AE 与BD 间的数量关系,并证明你的猜想;(3)如图3,在x 轴上有一个动点P (在A 点的右侧),连接PB ,并作等腰Rt △BPF ,其中∠BPF =90°,连接FA 并延长交y 轴于G 点,当P 点在运动时,OG 的长是否发生改变?若改变,请求出它的变化范围;若不变,求出它的长度.【答案】(1)见解析;(2)BD =2AE ,证明见解析;(3)OG 的长不变,OG =4t【分析】(1)根据直线解析式求出点A 、B 的坐标,然后得出AOB D 是等腰直角三角形,再根据角平分线的定义求出22.5ABD Ð=°,根据等腰三角形三线合一的性质OM AB ^,然后根据直角三角形两锐角互余的性质与三角形的一个外角等于与它不相邻的两个内角的和求出67.5OND Ð=°,67.5ODB Ð=°,利用等角对等边得到ON OD =;(2)延长AE 交BO 于C ,得ABE CBE D @D ,得到2AC AE =,再证OAC OBD D @D 得到BD AE =,从而得到2BD AE =;()ABE CBE ASA \D @D ,AE CE \=,2AC AE \=,AE BD ^Q ,90OAC ADE \Ð+Ð=°,又90OBD BDO Ð+Ð=°,ADE BDO Ð=Ð(对顶角相等),OAC OBD \Ð=Ð,在OAC D 与OBD D 中,OAC OBD OA OB BOD AOCìÐ=Ðïïïï=íïïïÐ=Ðïî,()OAC OBD ASA \D @D ,BD AC \=,2BD AE \=;(3)OG 的长不变,且4OG t =.过F 作FH OP ^,垂足为H ,90FPH PFH \Ð+Ð=°,90BPF Ð=°Q ,90BPO FPH \Ð+Ð=°,FPH BPO \Ð=Ð,BPF D Q 是等腰直角三角形,BP FP \=,在OBP D 与HPF D 中,90FPH BPO BOP FHP BP FPìÐ=ÐïïïïÐ=Ð=°íïïï=ïî,()OBP HPF AAS \D @D ,FH OP \=,4PH OB t ==,=,Q,OA OB=+=+AH PH AP OB AP\=+=,AH OA OP OP\=,FH AH\Ð=Ð=°,45GAO FAH\D是等腰直角三角形,AOG\==.OG OA t4【点睛】本题综合考查了一次函数,全等三角形的判定与全等三角形的性质,以及等腰直角三角形的性质,角平分线的定义,等腰三角形三线合一的性质等等知识点,熟悉相关性质是解题的关键.6.如图,在平面直角坐标系中,边长为3的正方形ABCD在第一象限内,AB∥x轴,点A的坐标为(5,4)经过点O、点C作直线l,将直线l沿y轴上下平移.(1)当直线l与正方形ABCD只有一个公共点时,求直线l的解析式;(2)当直线l在平移过程中恰好平分正方形ABCD的面积时,直线l分别与x轴、y轴相交于点E、点F,连接BE、BF,求△BEF的面积.【点睛】本题主要考查一次函数的图象的平移和正方形的性质的综合,掌握待定系数法和求直线和坐标轴的交点坐标是解题的关键.7.已知,一次函数364y x =-+的图像与x 轴、y 轴分别交于点A 、点B ,与直线54y x = 相交于点C ,过点B 作x 轴的平行线l .点P 是直线l 上的一个动点.(1)求点A ,点B 的坐标.(2)若AOC BCP S S =△△,求点P 的坐标.(3)若点E 是直线54y x =上的一个动点,当△APE 是以AP 为直角边的等腰直角三角形时,求点E 的坐标.8.如图,将一矩形纸片OABC 放在平面直角坐标系中,()0,0O ,()6,0A ,()0,3C .动点F 从点O 出发以每秒1个单位长度的速度沿OC 向终点C 运动,运动23秒时,动点E 从点A 出发以相同的速度沿AO 向终点O 运动,当点E 、F 其中一点到达终点时,另一点也停止运动.设点E 的运动时间为t (秒).(Ⅰ)OE =_____________,OF =_____________;(用含t 的代数式表示)(Ⅱ)当1t =时,将OEF V 沿EF 翻折,点O 恰好落在CB 边上的点D 处.①求点D 的坐标及直线DE 的解析式;②点M 是射线DB 上的任意一点,过点M 作直线DE 的平行线,与x 轴交于N 点,设直线MN 的解析式为y kx b =+,当点M 与点B 不重合时,S 为MBN △的面积,当点M 与点B 重合时,0S =.求S 与b 之间的函数关系式,并求出自变量b 的取值范围.∵OEF V 沿EF 翻折得到DEF V ,∴53FD OF ==.∴1410BM b=-+.9.已知,直线y=2x-2与x轴交于点A,与y轴交于点B.(1)如图①,点A的坐标为_______,点B的坐标为_______;(2)如图②,点C是直线AB上不同于点B的点,且CA=AB.①求点C的坐标;②过动点P(m,0)且垂直与x轴的直线与直线AB交于点E,若点E不在线段BC上,则m的取值范围是_______;(3)若∠ABN=45º,求直线BN的解析式.令y=0,则2x-2=0,即x=1过点C 作CD⊥x 轴,垂足是D,∵∠BOA=∠ADC=90°,∠BAO=∠CAD,CA=AB,∴△BOA≌△CAD(AAS),∴CD=OB=2,AD=OA=1,∴C(2,2);②由①可知D(2,0),观察图②,可知m的取值范围是:m<0或m>2.故答案是:m<0或m>2;(3)如图③,作AN⊥AB,使得AN=AB,作NH⊥x轴于H,则△ABN是等腰直角三角形,∠ABN=45°.∵∠AOB=∠BAN=∠AHN=90°,∴∠OAB+∠ABO=90°,∠OAB+∠HAN=90°,∴∠ABO=∠HAN,∵AB=AN,∴△ABO≌△NAH(AAS),∴AH=OB=2,NH=OA=1,∴N(3,-1),设直线BN的解析式为y=kx+b,则有:312k bb+=-ìí=-î,解得132kbì=ïíï=-î,∴直线BN的解析式为y=13x-2,当直线BN′⊥直线BN时,直线BN′也满足条件,直线BN′的解析式为:y3x2=--.∴满足条件的直线BN的解析式为y=13x-2或y=-3x-2.【点睛】本题考查一次函数的性质、全等三角形的判定和性质、等腰直角三角形的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.10.如图,将一矩形纸片OABC放在平面直角坐标系中,O(0,0),A(6,0),C(0,3),动点F从点O出发以每秒1个单位长度的速度沿OC向终点C运动,运动23秒时,动点E从点A出发以相同的速度沿AO向终点O运动,当点E、F其中一点到达终点时,另一点也停止运动设点E的运动时间为t:(秒)(1)OE= ,OF= (用含t的代数式表示)(2)当t=1时,将△OEF沿EF翻折,点O恰好落在CB边上的点D处①求点D的坐标及直线DE的解析式;②点M是射线DB上的任意一点,过点M作直线DE的平行线,与x轴交于N点,设直线MN的解析式为y=kx+b,当点M与点B不重合时,S为△MBN的面积,当点M与点B重合时,S=0.求S 与b之间的函数关系式,并求出自变量b的取值范围.11.如图,一次函数y=kx+b的图象为直线l1,经过A(0,4)和D(4,0)两点;一次函数y=x+1的图象为直线l2,与x轴交于点C;两直线l1,l2相交于点B.(1)求k、b的值;(2)求点B的坐标;(3)求△ABC的面积.12.已知11y kx =+过点(2,-1),与x 轴交于点A,F 点为(1,2).(Ⅰ)求k 的值及A 点的坐标;(Ⅱ)将函数1y 的图象沿y 轴方向向上平移得到函数2y ,其图象与y 轴交于点Q,且OQ=QF,求平移后的函数2y 的解析式;(Ⅲ)若点A 关于2y 的对称点为K,请求出直线FK 与x 轴的交点坐标.13.在平面直角坐标系中,直线1l:142y x=-+分别与x轴、y轴交于点A、点B,且与直线2l:y x=于点C.(Ⅰ)如图①,求出B、C两点的坐标;(Ⅱ)若D是线段OC上的点,且BODV的面积为4,求直线BD的函数解析式.(Ⅲ)如图②,在(Ⅱ)的条件下,设P是射线BD上的点,在平面内是否存在点Q,使以O、B、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.14.如图1,直线AB交x轴于点A(4 ,0),交y轴于点B(0 ,-4),(1)如图,若C的坐标为(-1, ,0),且AH⊥BC于点H,AH交OB于点P,试求点P的坐标;(2)在(1)的条件下,如图2,连接OH ,求证:∠OHP=45°;(3)如图3,若点D 为AB 的中点,点M 为y 轴正半轴上一动点,连结MD ,过点D 作DN ⊥DM 交x 轴于N 点,当M 点在y 轴正半轴上运动的过程中,式子BDM ADN S S -V V 的值是否发生改变?如发生改变,求出该式子的值的变化范围;若不改变,求该式子的值.【答案】(1)P (0 ,-1);(2)证明见解析;(3)不变;4.【分析】(1)利用坐标的特点,得出△OAP ≌△OB ,得出OP=OC=1,得出结论;(2)过O 分别做OM ⊥CB 于M 点,ON ⊥HA 于N 点,证出△COM ≌△PON ,得出OM=ON ,HO 平分∠CHA ,求得结论;(3)连接OD ,则OD ⊥AB ,证得△ODM ≌△ADN ,利用三角形的面积进一步解决问题.试题解析:(1)由题得,OA=OB=4.【详解】解:∵AH ⊥BC 于H ,∴∠OAP +∠OPA=∠BPH +∠OBC=90°,∴∠OAP=∠OBC在△OAP 和△OBC 中,90COB POA OA OB OAP OBC Ð=Ð=°ìï=íïÐ=Ðî∴△OAP ≌△OBC (ASA ),∴OP=OC=1,则点P (0 ,-1)(2)过点O 分别作OM ⊥CB 于M 点,ON ⊥HA 于N 点,15.如图,直线12y x b=-+与x轴,y轴分别交于点A,点B,与函数y=kx的图象交于点M(1,2).(1)直接写出k,b的值和不等式012x b kx£-+£的解集;(2)在x轴上有一点P,过点P作x轴的垂线,分别交函数y=﹣12x+b和y=kx的图象于点C,点D.若2CD=OB,求点P的坐标.16.无刻度直尺作图:图1 图2(1)直接写出四边形ABCD的形状.(2)在图1中,先过E点画一条直线平分四边形ABCD的面积,再在AB上画点F,使得AF=AE.(3)在图2中,先在AD上画一点G,使得∠DCG=45°;连接AC,再在AC上画点H,使得GH=GA.【答案】(1)四边形ABCD是菱形,理由见解析(2)见解析(3)见解析【分析】(1)只需要证明AB=CD=AD=BC即可得到结论;(2)如图连接AC,BD交于点T,作直线ET交BC于G,连接AG交BD于H,连接CH并延长交AB于F,则直线EG,点F即为所求;(3)如图所示,取格点T,连接CT交AD于G,取格点M、N,连接MN交BC于P,连接GP交AC于H,则点G、H即为所求;(1)求直线AB 的解折式;(2)如图2,已知P 为直线l :152y x =-+上一点,且512ABI ABCO S S =四边形△,求点P 的坐标;(3)若点D 为第一象限内一动点,且45ODC Ð=°,求BD 的最小值.∴∠BDA =90°,∵BC ∥OA ,BC =2,OA =6,∴AD =6−2=4,在Rt △ABD 中,BD =(22213AB AD -=∴PQ=|yQ−yP|=31922m m -++∵xA−xB=6−2=4,∴S△ABP=12PQ•(xA−xB)=12×4×|4−S四边形ABCO=12×(2+6)×6=24,∵∠ODC=45°,∠MOD=90°,18.如图,直线y =x +9与直线y =-2x -3交于点C ,它们与y 轴分别交于A 、B 两点.(1)求A 、B 、C 三点的坐标;(2)点F 在x 轴上,使10BFC S =△,求点F 的坐标;(3)点P 在x 轴上,使∠PBO +∠PAO =90°,直接写出点P 的坐标.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第23讲一次函数与几何大综合
【板块一】探求点的坐标或坐标关系
题型一 求点的坐标
【例1】已知一次函数y =2kx -3k +
1
2
(k ≠0). (1)不论k 为何值,函数图象必过一定点,求定点的坐标;
(2)如图1,设(1)中的定点为P ,C 为y 轴正半轴上一点,∠CPO =45°,求S △CPC ; (3)如图2,若k =1
4
-
,函数图象与x 轴,y 轴分别交于A ,B 两点,在直线AB 上是否存在点Q ,使
25QA QB =?若存在,求点Q 的坐标;若不存在,说明理由.
图1
针对练习1
1.如图1,在平面直角坐标系xOy 中,正方形ABCD 的边AB 在x 轴上,点O 是AB 的中点,直线l :y =kx -2k +4过定点C ,交x 轴于点E . (1)求正方形ABCD 的边长;
(2)如图2,在直线l 上有一点N ,CN =1
2
AB ,连接AN ,点M 为AN 的中点,连接BM ,求线段BM 的长度的最小值,并求出此时点N 的坐标.
图1
图2
2.已知一次函数y =-3x +3的图象与x 轴、y 轴交于点A ,B ,点C (3,0). ⑴求线段AB 的长度;
(2)点G 和点B 关于x 轴对称,点P 在直线CG 上,若△ABP 是等腰三角形,求点P 的坐标.
图2
图1
【板块二】 字母系数求解析式或解析式中的的值
题型二
求解析式或字母系数的值
【例2】在平面直角坐标系中,已知点A (a ,0),C (0,b )且a ,b 满足(a +1)2
=0.
⑴直接写出:a =_______,b =_______;
(2)如图1,点B 为x 轴正半轴上的一点:BE ⊥AC 于点E ,交y 轴于点D 连接OE ,若OE 平分∠AEB ,求直线BE 的解析式;
(3)如图2,在(2)的条件下,点M 为直线BE 上的一动点:连接OM ,将线段OM 绕点M 逆时针旋转90°,点O 的对应点为N ,当点M 运动时,判断点N 的运动路线是什么图形,并说明理由.
图2
图1
针对练习2
1.在平直角坐标系中,直线y =ax +b 与x 轴,y 轴分别交于点B ,C ,且a ,b 满足a +3,不论k 为何值,直线l :y =kx -2k 都经过x 轴上一定点A .
⑴a =____,b =_____;点A 的坐标为________.
(2)如图1,当k =1时,将线段BC 沿某个方向平移,使点B ,C 对应的点M ,N 恰好分别在直线l 和直线y =2x -4上,请你判断四边形BMNC 的形状,并说明理由;
⑶图2,当k 的取值发生变化时,直线l :y =kx -2k 绕着点A 旋转,当它与直线y =ax +b 相交的夹角为45°时,求出相应的k 的值.
图2
2.如图,直线l 1:y =2kx +4k +4交x 轴正半轴于点A ,交y 轴正半轴于点B ,经过点B 的直线l 2:y =x +4k +4交x 轴于点C .
⑴若A (4,0),求两直线的解析式;
⑵直线 y =-2x 交直线l 1于点M ,,交直线l 2于点N ,若S △MNB =S △NCO 求BM
AB
的值; ⑶直线x =k 交l 1于点D ,交l 2于点E ,若2DE -kAC =5,求k 的值.
图2
图1
针对练习2
1.在平面直角坐标系中,直线y =ax +b 与x 轴,y 轴分别交于点B ,C ,且a ,b 满足a +3,不论k 为何值,直线l :y =kx 一2k 都经过x 轴上一定点A . (1)a = ,b = ;点A 的坐标为 ;
(2)如图1,当k=1时,将线段BC沿某个方向平移,使点B,C对应的点M,N恰好分别在直线l和直线y=2x -4上,请你判断四边形BMNC的形状,并说明理由;
(3)如图2,当k的取值发生变化时,直线l:y=kx-2k绕着点A旋转,当它与直线y=ax+b相交的夹角为45°时,求出相应的k的值.
图1 图2
2.如图,直线l1:y=2kx+4k+4交x轴正半轴于点A,交y轴正半轴于点B,经过点B的直线l2:y=x+4k+4交x轴于点C.
(1)若A(4,0),求两直线的解析式;
(2)直线y=-2x交直线l1于点M,交直线l2于点N,若S△MNB=S△NCO,求BM
AB
的值;
(3)直线x=k交l1于点D,交l2于点E,若2DE一kAC=5,求k的值.
【板块三】探求点的轨迹
模型三探求点的轨迹
【例3】在平面直角坐标系中,点A(0,8)、C(8,0),四边形AOCB是正方形,点D(a,0)是x轴正半轴上的一动点,∠ADE=90°,DE交正方形AOCB的外角的平分线CE于点E.
(1)点D(a,0)在x轴正半轴上运动,点P在y轴上,若四边形PDEB为菱形,求直线PB的解析式;(2)连接AE,点F是AE的中点,当点D在x轴正半轴上运动时,点F到CE的距离是否为定值?若为定值,求出这个值;若不是定值,请说明理由.
针对练习3
2.已知直线l 1:y =mx -4m 交x 轴于点A ,交y 轴于点B ,直线l 2:y =nx -12m ,交x 轴于点C ,交y 轴于点D ,交l 1于点E (1)求点A 坐标;
(2)如图1,若B 为线段AE 中点,求证:EC =EA ;
(3)如图2,P (0,t ),将线段P A 绕点P 逆时针方向旋转90°至PF ,连接AF ,OF ,求OF +AF 的最小值.
【板块四】 探求线段关系
题型四 探求线段关系
【例4】 直线y =kx -2k 交x 轴于点B ,交y 轴于点A
(1)当k =-2时,①点P 为直线AB 上的一动点,求OP 的最小值;②若点Q 为x 轴上的一点,∠QAB =45°,求点Q 坐标;
(2)若直线CD :Y =2
2
k
k x -交AB 于点D ,点C 的横坐标为-1,求
AD AC
BD
-
针对练习4
1.已知点C (0,-2),直线l :y =kx -2k ,无论k 取何值,直线总经过点B . (1)求定点B 的坐标;
(2)若直线BC 关于x 轴对称后再向上平移5个单位得到直线B 1C 1,如图,点G (1,a )和H (6,b )是直线B 1C 1上的两点,点P (m ,n )为第一象限内(G ,H 两点除外)的一点,且mn =6,直线PG 和PH 分别交y 轴M ,N 两点,问线段OM ,ON 有什么数量关系?请证明.
2.如图1,直线AB 交x 轴正半轴于点A ,交y 轴正半轴于点B ,OA =OB . (1)当AB
=AB 的解析式;
(2)如图2,直线y =kx 交直线AB 于点C ,点D 是AB 上的一点,过点D 分别作x 轴,y 轴的垂线交直线y =kx 于点E ,F ,若CF =2CE ,求k 的值;
图1 图2。
