角的比较和运算
+6.3.2+角的比较与运算-教案2024-2025学年人教版(2024)数学七年级上册

《6.3.2 角的比较与运算》教学设计教学内容分析本节课主要学习角的比较,角的和差计算.角的比较,角的和差计算是重要的基础知识,也是后续学习图形与几何必备的知识基础。
学习者分析学生在学习本节课之前,已经了解了线段的比较、线段的和差等知识,为本节课的进行,在学习方法上做好了类比铺垫,同时,这些已有的知识经验也是学生学好这节课的基础和关键。
教学目标 1.通过类比线段的比较与运算的研究过程,构建角的比较与运算的研究思路,体会不同学习内容之间数学研究方法的一致性和可迁移性,体会类比思想。
2.能比较角的大小,会计算角的和与差,并会用文字、图形和符号语言进行描述,体会数形结合思想,发展几何直观、推理能力。
教学重点角的大小比较方法。
教学难点角的和差关系。
学习活动设计教师活动学生活动环节一:学习目标教师活动1:师出示学习目标:1.通过类比线段的比较与运算的研究过程,构建角的比较与运算的研究思路,体会不同学习内容之间数学研究方法的一致性和可迁移性,体会类比思想。
2.能比较角的大小,会计算角的和与差,并会用文字、图形和符号语言进行描述,体会数形结合思想,发展几何直观、推理能力。
学生活动1:学生齐声读本课的学习目标活动意图说明:明确本节课的学习目标,使教师的教和学生的学有效结合在一起,激发学生的学习动力,提高学生课堂参与的兴趣与积极性。
环节二:新知导入教师活动2:1.角的定义:静态定义:有___________的___________组成的图形叫做角,这个公共端点是角的_______,这两条射线是角的_________.动态定义:角也可以看作由___________绕着它的___________而形成的图形.答案:公共端点,两条射线,顶点,两条边,一条射线,端点旋转2.角度制:以________为单位的角的度量制,叫做角度制.1周角=______°,1平角=______°,1直角=______°,1°=______′,1′=______″.答案:度、分、秒,360,180,90,60,60 3.如何比较两条线段的大小?预设:度量法,叠合法学生活动2:学生快速回答老师提出的问题活动意图说明:通过复习角的概念、角的单位及换算,为角的比较与和、差运算做好准备。
初一数学上册角的比较和运算典型例题解析与练习

4.角的比较和运算◆典例分析例:如图,(1)已知∠AOB 是直角,∠BOC=30°,OM 平分∠AOC ,ON 平分∠BOC ,求∠MON 的度数。
(2)如果(1)中∠AOB=α,其他条件不变,求∠MON 的度数。
(3)你从(1)、(2)的结果中能发现什么规律? 解:(1)∵ OM 平分∠AOC ,ON 平分∠BOC ,∴ ∠MOC=21∠AOC ,∠NOC=21∠BOC ∴ ∠MON=∠MOC-∠NOC=21∠AOC-21∠BOC=21∠AOB∵ ∠AOB=90°, ∴ ∠MON=45°(2)当∠AOB=α时,其他条件不变。
总有∠MON=21∠AOB=2(3)由(1)(2)的结果,可得出结论:∠MON 的大小总等于∠AOB 的一半。
评析:本例主要是利用角平分线的定义及角和差的意义来解。
由特殊从而推断出一般性的规律。
●拓展提高1、平面内两个角∠AOB=60°,∠AOC=20°,OA 为两角的公共边,则∠BOC 为( ) A 、40° B、80° C、40°或80° D、无法确定2、下面一些角中,可以只用一副三角尺(不用量角器)画出来的角是( ) (1)150的角 (2)650的角 (3)750的角 (4)1350的角 (5)1450的角 A 、(1)(3)(4) B 、(1)(3)(5) C 、(1)(2)(4) D 、(2)(4)(5) 3、已知:∠A=50º24’,∠B=50.24º,∠C =50º14’24”,那么下列各式正确的是( ) A 、∠A>∠B >∠C B 、∠A>∠B=∠C C 、∠B>∠C>∠A D 、∠B=∠C>∠A 4、如图,BO 、CO 分别平分∠ABC 和∠ACB ,已知任意三角形的3个内角的和都是180°,若∠A =80°,你能求出∠BOC 的度数吗?试试看。
角的比较和运算 课件(湘教版七年级上)

C
E
A
O
D
(3)如果AE落在∠BOD的外部,那么 ∠AEC大于∠ BOD,记作∠AEC> ∠BOD
B C
O
D
E
A
例1 根据右图,求解下列问题: (1)比较∠AOB,∠AOC,∠AOD, ∠AOE的大小,并指出其中的锐 角、直角、钝角、平角。
A
B C
O
D E
(2)写出∠AOB 、∠AOC、 ∠BOC、 ∠AOE中某些角之间的两个等量关系。
n条射线 (n+1)+n+(n-1)+…+2+1=? 个角
(1)若时钟由2点30分 走到2点55分,问时针、 分针各转过多大的角度?
(2)钟表上2时15分时,
时针与分针所成的锐角是 多少度?
1. 角的大小比较的方法 (1) 度量法 (2) 叠合法
2.角的平分线的定义及用法
3.角的简单运算 4.画一个角,使它等于已知角
例1.如图, ∠AOB是已知角,用圆规 和直尺画一个角等于∠AOB.
B
A
如图,∠AOC和∠BOD都是直角。
①估测∠COB的度数;
②若∠DOC=28°,说出∠AOB的度数。
D A B O C
从一个角的顶点引出的一条射线, 把这个角分成两个相等的角,这条 射线叫做这个角的平分线
例3.已知∠BAC,画一条射线,使 它平分∠BAC 。
把∠ AEC移动,使它的顶点E移到和∠ BOD的 顶点O重合,一边EA和DO重合,另一边OB和CE落 在OD的同旁。
B
C
E
A
O
D
(1)如果AE与OB重合,那么∠AEC就等于
∠ BOD,记作∠AEC= ∠BOD
教案角的比较和运算

角的比较和运算一、教学目标:1. 让学生理解角的概念,能够识别和比较不同类型的角。
2. 培养学生运用角度知识解决实际问题的能力。
3. 引导学生掌握角的运算方法,提高学生的逻辑思维能力。
二、教学内容:1. 角的概念及分类2. 角的比较方法3. 角的运算方法4. 实际问题解答5. 练习与巩固三、教学重点与难点:1. 教学重点:角的概念,角的分类,角的比较方法,角的运算方法。
2. 教学难点:角的运算方法在实际问题中的应用。
四、教学方法:1. 采用问题驱动法,引导学生主动探索和学习角的知识。
2. 运用实例分析法,让学生通过解决实际问题来掌握角的运算方法。
3. 采用小组合作学习法,培养学生的团队协作能力。
五、教学准备:1. 教学课件:角的图片、实例分析、练习题等。
2. 教学工具:直尺、量角器等。
3. 练习题:选择题、填空题、解答题等。
教案一角的概念及分类:教学时间:40分钟教学过程:1. 导入:引导学生回顾已学过的几何知识,为新课的学习做好铺垫。
2. 讲解:介绍角的概念,讲解角的分类,包括锐角、直角、钝角、平角、周角等。
3. 实例演示:展示各种角的图片,让学生直观地感受不同类型的角。
4. 课堂互动:让学生举例说明生活中常见的各种角,加深对角的理解。
5. 练习:布置练习题,让学生区分和识别不同类型的角。
六、角的比较方法教学时间:40分钟教学过程:1. 导入:复习上节课所学的内容,引导学生进入新课。
2. 讲解:介绍角的比较方法,包括度量法和图形比较法。
3. 演示:利用教具展示角的比较过程,让学生直观地理解比较方法。
4. 课堂互动:让学生互相比较角度大小,交流比较方法。
5. 练习:布置练习题,让学生运用比较方法判断角度大小。
七、角的运算方法教学时间:40分钟教学过程:1. 导入:复习上节课所学的内容,引导学生进入新课。
2. 讲解:介绍角的运算方法,包括加法、减法、乘法、除法等。
3. 演示:利用教具展示角的运算过程,让学生直观地理解运算方法。
第六课时角的比较和运算

B
冲 击
D
C B
E
1 2
A
图中∠1= ∠2, 试判断∠BAD和 ∠EAC的大小, 并说明理由.
解: ∠BAD= ∠2+ ∠DCA
∠EAC= ∠1+∠DCA
探究:
借助一个三角尺可以画 出哪些度数的角,用一副三 角尺你还能画出哪些度数的 角?上台来展示你的结果。
15° 75°
105 °
15°
120°
15°、 30°、45°、60°、 75°、 90°、 105°、120°、135°、150°、 180°
角平分线
将你手中的角对折,使其两边重合,折 痕把这个角分成的两部分是什么图形,你发 现它们的大小有什么关系?
折痕与这个角的两边组成两个角
它们的大小相等 ∠1 =∠2
从一个角的顶点出发, 把这个角分成相等的两 个角的射线,叫做这个 角的平分线
(1) 角的大小与角的两边画出的 结论: 长短没有关系。 (2)角张开的程度越小,角度 就越小
退出
返回 上一张下一张
角的运算
图中共有几个角,它们之间的大小有什么关系? C ∠AOC = ∠AOB + ∠BOC ∠AOB = ∠AOC-∠ BOC __
B
AOC-∠ __ AOB ∠BOC = ∠__
1、角的大小比较方法:
2、角的大小关系有哪些?
3、角的和差计算 4、三角板可拼出哪些角?
数一数:图中共有几个小于平角的 角,找出规律。 D
C
C
B
B
2 O
1
3 A
O
A
( 1)
( 2)
E
F
D C B
E
D
C B
……
最新2024人教版七年级数学上册6.3.2 角的比较与运算--教案
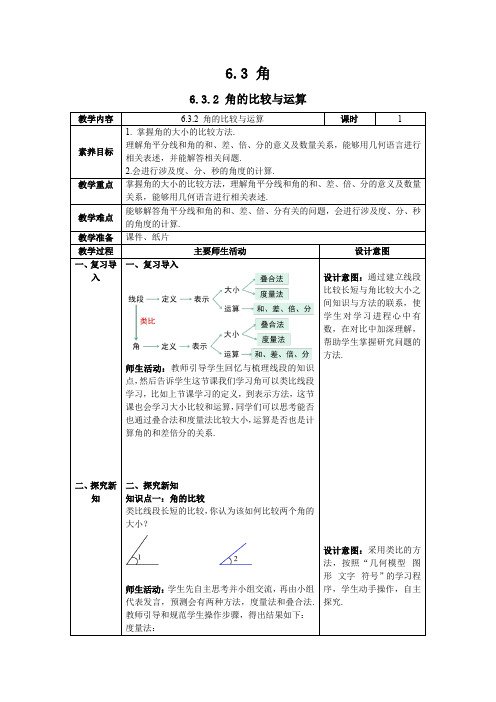
6.3 角6.3.2 角的比较与运算主要师生活动一、复习导入师生活动:教师引导学生回忆与梳理线段的知识点,然后告诉学生这节课我们学习角可以类比线段学习,比如上节课学习的定义,到表示方法,这节课也会学习大小比较和运算,同学们可以思考能否也通过叠合法和度量法比较大小,运算是否也是计算角的和差倍分的关系.二、探究新知知识点一:角的比较类比线段长短的比较,你认为该如何比较两个角的大小?师生活动:学生先自主思考并小组交流,再由小组代表发言,预测会有两种方法,度量法和叠合法.教师引导和规范学生操作步骤,得出结果如下:度量法:因为55°>40°,所以∠1>∠2.叠合法:想一想:你能用图形和几何语言说明两个角的大小关系吗(两个角分别记作∠AOB,∠A'O'B' )?师生活动:学生画出图形,并用符号表示,指出两个角的大小关系有且仅有三种情况.知识点二:角的运算探究1:如图,图中共有几个角?它们之间有什么关系?师生活动:预测学生能确定角的个数,明确角之间的和差关系如下:3个:∠AOB、∠AOC、∠BOC∠AOC =∠AOB +∠BOC∠AOB =∠AOC-∠BOC∠BOC =∠AOC -∠AOB教师关注学生是否能发现角的和差关系,教师可引导学生类比线段的和与差,发现角的和差关系.然后教师引导学生总结:共顶点的几个角,可进行加减.探究2 :如图,借助三角尺画出15°,75°的角.用一副三角尺,你还能画出哪些度数的角?试一试.师生活动:学生动手操作,小组合作探究,师生归纳,如下:用三角尺画特殊角,关键在于把它写成30°,45°,60°,90°角的和或差.凡是15的整数倍的角,都能用三角尺画出,而能用三角尺画出的,也只限于这样的角.例题精析:例1 如图,O是直线AB上一点,∠AOC = 53°17′,求∠BOC的度数.师生活动:学生独立思考,请学生代表发言,教师予以适当的评价并整理板书.解:由题意可知,∠AOB是平角,∠AOB =∠AOC +∠BOC所以∠BOC =∠AOB-∠AOC= 180° - 53°17′= 126°43′总结:∠同单位加减(度与度、分与分、秒与秒分别相加、减);∠度分秒是60进制(相加时逢60要进位,相减时要借1作60).师生活动:教师引导学生思考与总结解题思路与过程.知识点3:角平分线探究3:你能在∠AOC内找一条射线OB,使∠AOB =∠BOC吗?师生活动:教师提问,学生自主思考,教师巡堂指导,预测会有不同方法,教师可让这些学生代表分别展示,预测两种方法(如下):对折法:生巩固角的和与差概念外,也使学生对这些特殊角的大小有直观的认识,培养对角的大小的估计能力和动手操作能力,加深学生对角的认识.设计意图:通过题目锻炼学生运算能力,初步学习几何语言在解题中的运用,体会几何与代数之间的联系与不同,加深学生的数形结合思想.设计意图:从角的和差问题中,将射线OB的位置特殊化,并类比线段的中点,引出角的平分线的概念,不仅知识的产生、发展自然连续,也体现了由一般到特殊,由特殊到一般的研究方法,同时,也能建立知识间的联系,完善认知结构.度量法:教师追问:同学们知道图中三个角的数量关系吗?学生思考,学生代表回答,师生共同总结与填空.教师再以此引出角平分线的定义.定义总结:师生活动:教师讲解,再让学生朗读定义,加深印象.类比:仿照角平分线的结论,你能写出角的三等分线的结论吗?师生活动:学生独立思考,由学生代表发言,教师予以适当评价,帮助学生正确规范完成几何书写.例2 把一个周角7等分,每一份是多少度的角(精确到分)?师生活动:学生独立思考,由学生代表发言,教师与学生共同完成板书:解:360°÷7 = 51°+ 3°÷7= 51°+ 180′÷7≈51°26′答:每份是51°26′的角.教师引导学生总结:注意度、分、秒是60进制的,要把剩余的度数化成分.设计意图:进一步明晰角平分线的概念,为后续学习轴对称和研究有关图形的翻折问题打下基础.设计意图:通过类比让学生学会举一反三,体会几何知识的关联性,巩固几何语言的书写.设计意图:通过题目帮助学生巩固角平分线的知识与角的运算,提高学生的识图能力和运算能力.又通过思考题启发学生思考其他可能性,建立分类讨论思想,养成严谨思考的习惯.三、当堂练习例3 如图OC是∠AOB的平分线,OB是∠COD的三等平分线,∠BOD = 15°.则∠AOB等于( )A. 75B. 70C. 65D. 60师生活动:学生独立思考,学生代表发言,教师适时评价与引导.思考:除此题所给图片的情况,你还能想出其他情况与答案吗?师生活动:学生独立思考,学生代表上台展示,教师予以评价与指导,得出另一种结果,∠AOB = 15°.三、当堂练习1. 比较大小:60°25′60.25°(填“>”,“<”或“=”).2. 计算:(1) 180° - 98°24′30″(2) 62°24′17″×43. 如图,OB是∠AOC的平分线,OD是∠COE的平分线,若∠AOB = 50°,∠DOE = 30°,那么∠BOD是多少度?设计意图:通过练习巩固角的大小比较.设计意图:通过练习巩固角度的运算.设计意图:通过练习强化试图能力和运算能力.板书设计角的比较与运算一、角的概念二、角的表示三、角的度量和单位教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图.数形结合,培养识图能力。
人教版七年级数学上册角的比较和运算
O
A
那么OC 是_∠_D_O__B 的平分线;
则∠BOC = 1_∠_D__O_B_= 1 _∠_A_O__C_= 1 _∠_D__O_A_。
2
2
3
类似地:还有角的三等分线
D
C
B
32
1
O
A
OB、OC是∠AOD的三等分线
巩固练习:
O是直线AB上一点,∠AOC=53°,OD平分∠BOC,
求∠BOD的度数?
90° 90°
180°
1 2
2 1
O
C B
A
当 1 = 2 时,射线OB 把 AOC分成两个相等的角 ,这时OB叫做 AOC 的平 分线,也可以说OB平分∠AOC
定义:在角的内部,自顶点引一条射线把 这个角分成 两个相等的角,那么,这条射线叫做角的平分线。
思考:几何语言怎么描述?
几何语言:
C
∵OB平分∠AOC
图1 A 7)∠A0D-_∠__B_O_D_ =∠A0B
巩固练习2: 如图:O是直线AB上一点,∠AOC=53° 则∠BOC的度数=__1_2_7°__ C
∵O是直线AB上一点,
∴∠AOB是平角,
A
53° ?
O
B
∴∠AOB==1∠8A0O°C+∠BOC
∴∠BOC=∠AOB-∠AOC =180°-53° =127°
A
OHale Waihona Puke BA巩固练习1:
按图1填空:
D
1) ∠D0B___>___∠BOC 2) ∠C0B___<___∠AOC 3) ∠DOC+∠COB___=_____∠B0D
4)∠A0B+∠BOC=_∠__A_O_C___
角的比较重难点题型
角的比较--重难点题型【知识点1 角的比较与运算】【题型1 角的大小比较】∠COD=50°;小丽用叠合法比较,将两个角的顶点重合,边OB与OD重合,边OA 和OC置于重合边的同侧,则边OA.(填序号:①“在∠COD的内部”;②“在∠COD的外部”;③“与边OC重合”)【变式1-1】(2021春•呼和浩特期末)如图,∠AOB=∠COD,则∠AOC与∠DOB的大小关系是()A.∠AOC>∠DOBB.∠AOC<∠DOBC.∠AOC=∠DOBD.∠AOC与∠DOB无法比较大小【变式1-2】(2021秋•开封期末)如图所示,其中最大的角是,∠DOC,∠DOB,∠DOA的大小关系是.【变式1-3】(2021秋•门头沟区期末)如图所示的网格是正方形网格,点A,B,C,D,O 是网格线交点,那么∠AOB∠COD.(填“>”,“<”或“=”)【题型2 角的和差】【例2】(2021秋•安庆期末)如图,已知∠BOC=2∠AOC,OD平分∠AOB,且∠COD=20°,求∠AOB的度数.【变式2-1】(2021秋•五常市期末)用一副三角板不能画出的角是()A.75°B.105°C.110°D.135°【变式2-2】2021秋•北碚区期末)将一张长方形纸片按如图所示的方式折叠,BD、BE为折痕.若∠ABE=30°,则∠DBC为度.【变式2-3】(2021秋•荔湾区期末)把一副三角尺ABC与BDE按如图所示那样拼在一起,其中A、D、B三点在同一直线上,BM为∠ABC的平分线,BN为∠CBE的平分线,则∠MBN的度数是()A.30°B.45°C.55°D.60°【题型3 n等分线】【例3】(2021秋•罗湖区校级期末)如图,已知O为直线AB上一点,过点O向直线AB 上方引三条射线OC、OD、OE,且OC平分∠AOD,∠2=3∠1,∠COE=70°,求∠2的度数.【变式3-1】(2021秋•奉化区校级期末)OB是∠AOC内部一条射线,OM是∠AOB平分线,ON是∠AOC平分线,OP是∠NOA平分线,OQ是∠MOA平分线,则∠POQ:∠BOC=()A.1:2B.1:3C.2:5D.1:4【变式3-2】(2021秋•江汉区期末)如图,射线OB、OC在∠AOD内部,其中OB为∠AOC 的三等分线,OE、OF分别平分∠BOD和∠COD,若∠EOF=14°,请直接写出∠AOC 的大小.【变式3-3】(2021秋•越秀区校级月考)如图1,已知∠AOB=120°,∠COD=60°,OM在∠AOC内,ON在∠BOD内,∠AOM=13∠AOC,∠BON=13∠BOD.(本题中所有角均大于0°且小于等于180°)(1)∠COD从图1中的位置绕点O逆时针旋转到OC与OB重合时,如图2,则∠MON =°;(2)∠COD从图2中的位置绕点O逆时针旋转n°(0<n<120且n≠60),求∠MON 的度数;(3)∠COD从图2中的位置绕点O顺时针旋转n°(0<n<180且n≠60a,其中a为正整数),直接写出所有使∠MON=2∠BOC的n值.【题型4 角平分线】【例4】(2021秋•武都区期末)如图所示,点O是直线AB上一点,OE,OF分别平分∠AOC和∠BOC,若∠AOC=68°,则∠BOF和∠EOF是多少度?【变式4-1】(2021秋•南山区期末)已知三条不同的射线OA、OB、OC,有下列条件,其中能确定OC平分∠AOB的有()①∠AOC=∠BOC②∠AOB=2∠AOC③∠AOC+∠COB=∠AOB④∠BOC=12∠AOBA.1个B.2个C.3个D.4个【变式4-2】(2021秋•曲阳县期末)已知将一副三角板(直角三角板OAB和直角板OCD,∠AOB=90°,∠ABO=45°,∠CDO=90°,∠COD=30°)(1)如图1摆放,点O、A、C在一条直线上,∠BOD的度数是;(2)如图2,变化摆放位置将直角三角板COD绕点O逆时针方向转动,若要OB恰好平分∠COD,则∠AOC的度数是;(3)如图3,当三角板OCD摆放在∠AOB内部时,作射线OM平分∠AOC.射线ON 平分∠BOD,如果三角板OCD在∠AOB内绕点O任意转动,∠MON的度数是否发生变化?如果不变,求其值;如果变化,说明理由.【变式4-3】(2021秋•裕华区校级期中)如图1,∠AOB=40°,∠AOB的一边OB与射线OM重合,现将∠AOB绕着点O按顺时针方向旋转180°.在旋转过程中,当射线OA、OB或者直线MN是某一个角(小于180°)的平分线时,旋转角的度数为.【题型5 余角与补角的定义】【例5】(2021春•金山区期末)如果一个角的补角的2倍减去这个角的余角恰好等于这个角的4倍,求这个角的度数.【变式5-1】(2021•寻乌县模拟)已知∠A是锐角,∠A与∠B互补,∠A与∠C互余,则∠B﹣∠C的值等于()A.45°B.60°C.90°D.180°【变式5-2】(2020秋•麦积区期末)一个角的补角加上10°后,等于这个角的余角的3倍,求这个角以及它的余角和补角的度数.【变式5-3】(2021秋•沂水县期末)如图,已知∠AOB=130°,画∠AOB的平分线OC,画射线OD,使∠COD和∠AOC互余,并求∠BOD的度数.【题型6 利用余角或补角的性质得角相等】【例6】(2021秋•鹿邑县期末)如图,O为直线AB上一点,∠DOE=90°,OD是∠AOC 的角平分线,若∠AOC=70°.(1)求∠BOD的度数.(2)试判断OE是否平分∠BOC,并说明理由.【变式6-1】(2021秋•旌阳区期末)如图,两个直角∠AOC和∠BOD有公共顶点O,下列结论:①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠AOD+∠BOC=180°;④若OB平分∠AOC,则OC平分∠BOD;⑤∠AOD的平分线与∠BOC的平分线是同一条射线,其中正确的有.(填序号)【变式6-2】(2021秋•芮城县期末)综合与实践已知直线AB 经过点O ,∠COD =90°,OE 是∠BOC 的平分线.(1)如图1,若∠AOC =30°,求∠DOE ;(2)如图1,若∠AOC =α,求∠DOE ;(用含α的式子表示)(3)将图1中的∠COD 绕顶点O 顺时针旋转到图2的位置,其它条件不变,(2)中的结论是否还成立?试说明理由;(4)将图1中的∠COD 绕顶点O 逆时针旋转到图3的位置,其它条件不变,直接用含α的式子表示∠DOE .【变式6-3】(2019秋•东西湖区期末)如图1,平面内一定点A 在直线EF 的上方,点O 为直线EF 上一动点,作射线OA 、OP 、OA ',当点O 在直线EF 上运动时,始终保持∠EOP =90°、∠AOP =∠A 'OP ,将射线OA 绕点O 顺时针旋转60°得到射线OB .(1)如图1,当点O 运动到使点A 在射线OP 的左侧,若OA '平分∠POB ,求∠BOF 的度数;(2)当点O 运动到使点A 在射线OP 的左侧,且∠AOE =3∠A 'OB 时,求∠AOF ∠AOP 的值;(3)当点O 运动到某一时刻时,∠A 'OB =130°,请直接写出∠BOP = 度.【题型7 求几何图形中互余或互补角的个数】【例7】(2021•娄星区模拟)如图,C 是直线AB 上一点,CD 是∠ACB 的平分线. ② 图中互余的角有 ;②图中互补的角有 ;③图中相等的角有 .【变式7-1】(2021秋•南开区期末)如图所示,已知O 是直线AB 上一点,∠BOE =∠FOD =90°,OB 平分∠COD .(1)图中与∠DOE 相等的角有 ;(2)图中与∠DOE 互余的角有 ;(3)图中与∠DOE 互补的角有 .【变式7-2】(2021秋•成都期中)如图,O 是直线AB 上的一点,∠AOD =120°,∠AOC =90°,OE 平分∠BOD .写出图中所有互补的角和互余的角.【变式7-3】(2021春•吴中区月考)如果∠α和∠β互补,且∠α>∠β,则下列式子中:①90°﹣∠β;②∠α﹣90°;③12(∠α+∠β);④12(∠α﹣∠β).可以表示∠β的余角的有( )A .①②B .①②③C .①②④D .①②③④【题型8 数学思想方法与角】【例8】(2021秋•河东区期末)已知∠AOB=90°,OC为一射线,OM,ON分别平分∠BOC和∠AOC,则∠MON是()A.45°B.90°C.45°或135°D.90°或135°【变式8-1】(2021秋•成华区期中)(1)如图1,射线OC、OD在∠AOB的内部,射线OM、ON分别平分∠AOD、∠BOC、且∠BON=50°,∠AOM=40°,∠COD=30°,求∠AOB的度数;(2)如图2,射线OC、OD在∠AOB的内部,射线OM、ON分别平分∠AOD、∠BOC、且∠AOB=150°,∠COD=30°,求∠MON的度数【变式8-2】(2021秋•无锡期末)如图,∠AOB=150°,∠COD=40°,OE平分∠AOC,则2∠BOE﹣∠BOD=°.【变式8-3】(2021秋•镇海区期末)新定义问题如图①,已知∠AOB,在∠AOB内部画射线OC,得到三个角,分别为∠AOC、∠BOC、∠AOB.若这三个角中有一个角是另外一个角的2倍,则称射线OC为∠AOB的“幸运线”.(本题中所研究的角都是大于0°而小于180°的角.)【阅读理解】(1)角的平分线这个角的“幸运线”;(填“是”或“不是”)【初步应用】(2)如图①,∠AOB=45°,射线OC为∠AOB的“幸运线”,则∠AOC的度数为;【解决问题】(3)如图②,已知∠AOB=60°,射线OM从OA出发,以每秒20°的速度绕O点逆时针旋转,同时,射线ON从OB出发,以每秒15°的速度绕O点逆时针旋转,设运动的时间为t秒(0<t<9).若OM、ON、OA三条射线中,一条射线恰好是以另外两条射线为边的角的“幸运线”,求出所有可能的t值.。
角的度量及比较和运算
初一数学—角的度量及比较和运算一、知识要点1、角的定义:有公共端点的两条射线所组成的图形叫做角,角也可以看作由一条射线绕着它的端点,旋转而成的图形.2、角的度量:把一个周角360等分,每1份的角记作1°,1°=60分,1分=60秒.3、1周角=360°,1平角=180°, 1直角=90°.4、角的平分线:从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.如图,OC是∠AOB的平分线,则有以下写法:∵OC是∠AOB的平分线∴(1)∠AOC=∠BOC(2)或(3)∠AOB=2∠AOC或∠BOA=2∠BOC5、角的特殊关系(1)余角、补角的概念如果两个角的和等于90°(直角),那么就说这两个角互为余角,简称互余.如果两个角的和等于180°(平角),那么就说这两个角互为补角,简称互补.(2)余角、补角的性质:余角和补角的性质. 同角或等角的余角相等.同角或等角的补角相等.6、对顶角的性质:对顶角相等.三、典例剖析例1、57.32°是几度几分几秒?例2、计算:(1)39°48′+41°37′(2)48°2′÷5例3、画出表示下列方向的射线:(如图)(1)东南方向射线OA;(2)北偏东60°的射线OB;(3)南偏西30°的射线OC;(4)北偏西30°的射线OD.例4、如图,O为直线AB上一点,射线OD、OE分别平分∠AOC、∠BOC.求∠DOE的度数.例5、已知一个角的补角与一个直角的和比这个角的余角的5倍少44°,求这个角.一、选择题1、用一副三角板画角,不能画出的角的度数是()A.15°B.75° C.145°D.165°2、如果一个角是36°,那么()A.它的余角是64° B.它的补角是64° C.它的余角是144°D.它的补角是144°3、如图所示是一块手表,早上8时的时针、分针的位置如图所示,那么分针与时针所成的角的度数是()A.60°B.80° C.120°D.150°4、下列算式中,正确的是()A.①和②B.①和③ C.②和③D.②和④①33.33°=33°3′3″②33.33°=33°19′48″③50°40′33″=50.43°④50°40′33″=50.675°5、如图,射线OA表示的方向是()A.西北方向B.东南方向 C.西偏南30°D.南偏西30°6、∠1,∠2互为补角,且∠1>∠2,那么∠2的余角是()A.B. C.D.7、如图,已知∠ACB=90°,∠1=∠B,∠2=∠A,则下列说法错误的是()A.∠A与∠B不互为余角;B.∠1与∠2互为余角;C.∠2与∠B互为余角;D.∠1与∠A互为余角8、如图,射线OQ平分∠POR,OR平分∠QOS,以下结论:①∠POQ=∠QOR=∠ROS;②∠POR=∠QOS;③∠POR=2∠ROS;④∠POS=2∠POQ,其中正确的是()A.①、②和③B.①、②和④C.①、③和④D.①、②、③、④9、如图,AOB是直线,OD平分∠BOC,OE平分∠AOC,则下列说法中错误的是()A.∠DOE为直角 B.∠DOC和∠AOE互余C.∠AOE和∠BOC互补D.∠AOD和∠DOC互补10、∠1和∠2互余,∠2和∠3互补,∠1=63°,则∠3等于()A.117°B.27° C.153°D.37°11、如果一个角的补角是120°,那么这个角的余角为()A.30° B.60° C.90° D.120°12、两个角的比是7︰3,它们的差是72°,则这两个角的关系是()A.互为余角B.互为补角C.相等D.和为144°二、填空题1、如图,已知A、O、B在一条直线上,OE平分∠BOC,则∠BOE=_____度.2、如果一个角的补角是这个角的余角的4倍,则这个角为___________.3、若∠AOB=40°,∠BOC=60°,则∠AOC=________4、1点15分,时针与分针的夹角是_______度。
4.3.2角的比较与运算 课件人教版七年级数学上册
典型例题 例2 把一个周角7等分,每一份是多少度的角(精确到分)?
解:360º÷7=51º+3º÷7 =51º+180′÷7 ≈ 51º26′.
答:每份约是51º26′.
创设情境 探究新知 应用新知 巩固新知 课堂小结 布置作业
随堂练习
练习1 按图填空: (1)∠AOB+∠BOC=_∠__A__O_C____; (2)∠AOC+∠COD=_∠__A_O__D____; (3)∠BOD-∠COD=_∠__B_O__C____; (4)∠AOD-__∠__B_O_D____=∠AOB.
探究 怎么用符号语言表示角平分线呢?
C
O
B
A
∵OB平分∠AOC,
∴∠AOB =∠BOC = 1 ∠AOC
2
(或者∠AOC =2 ∠AOB = 2∠COB ).
创设情境 探究新知 应用新知 巩固新知 课堂小结 布置作业
探究 类似角平分线,如图射线OB、OC是∠AOD的三等分线.
D
α α α
O
C B
A
创设情境 探究新知 应用新知 巩固新知 课堂小结 布置作业
随堂练习
练习2 如图,OP是∠AOB的平分线,则下列说法错误的是( C )
A.∠AOB=2∠AOP
C.∠AOB= 1 ∠BOP 2
B.∠AOP= 1 ∠AOB 2
D.∠AOP=∠BOP
创设情境
探究新知
角
的
应用新知
比
较
巩固新知
与 运
算
课堂小结
创设情境 探究新知 应用新知 巩固新知 课堂小结 布置作业
典型例题 例1 如图,O是直线AB上一点,∠AOC=53º17′,求∠BOC的度数.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∠ BOC=( ∠ BOD) - (∠ COD )
=
( D∠
AOC
)- C
(∠ AOB
)
B
O
A
19
实践活动:
借助一副三角尺,大家都能画出哪些度 数的角?
75°
探究新知 ? 如何进行角的运算 类似的,用一副三角尺,你还能画出那些度数的 角呢? (0°~180°) 15°,30°,45°,60°,75°,90°,105°,120°,
C
( 1 ) DAB = DAC+ CAB
DБайду номын сангаас
( 2 ) ACB = DCB – DCA
A
B
A
( 1 ) ABC = ABD + ( 2 ) BDC = ADC –
CBD
B
BDA
D C
探究新知 如何进行角的运算
? 3.你能把 任90意°一的个角分成相等的两部分吗?
请大家拿出你手里的角,把它分成大小相等的两部分.
§4.3.2 角的比较与运算
? 探究新知 如何比较两角的大小 移动∠ ABC,使两角的顶点重合,一边BA和 E1D.请重拿合出,你另手一里边的B角C和与E同F桌落比在一重比合看边谁的的同角旁大. ? F
C
B
A
E
D
? 探究新知 如何比较两角的大小 (1)如果BC落在∠DEF的内部, 那么∠ABC 小于∠ DEF,记作∠ABC <∠DEF. F
O
O
A
角的和差
顶 点 与 一 边 重 合
O
C B
2 1
O
A
( AOC为 1 和 2 的和
记作 AOC = 1 + 2 )
B
B
2
C 1
O
A
( AOC为 1 和 2 的差
记作 AOC = 1 – 2 )
练习2, 如图:
∠ AOC = ( ∠ AOB ) + (∠ BOC )
= ( ∠ AOD ) - ( ∠ COD )
像OC这样,从一个角的顶点出发,把一个角分成两 个相等的角的射线,叫做这个角的角平分线.
B
C
α
O
α
A
∠AOC = ∠BOC ;
∠AOB =2 ∠AOC = 2 ∠BOC ; ∠AOC =∠BOC=1/2 ∠AOB.
练习:已知射线OB是∠AOC的角平分线, 你能写出图中各角的关系吗?
A
B
O
C
类似地:还有角的三等分线
DC
A
┓
O
X
H
29
比一比 看谁反应快:
3.(2008呼和浩特中考)将一副三角板按图示方法放置 (直角顶点重合)
则∠AOB+∠DOC= 180°. D C
A
┓
O
X
H
29
比一比 看谁反应快:
3.(2008呼和浩特中考)将一副三角板按图示方法放置 (直角顶点重合)
则∠AOB+∠DOC= 180°.
DC
知识海洋,追逐梦想.
快乐学习,快乐成长.
知识回顾
1.有公共端点的两条射线组成的图形
叫做 角
.
2.常用的度量角的工具是 量角器 .
3.常用的度量角的单位是 度、分、秒 .
它们之间的关系是 1°=60′,1′=60″ .
4.如果一个点把一条线段分成两条相等
的线段,那么这个点叫做线段的 中点 .
5.比较两条线段大小的方法 有 叠合法,测量法.
学.科.网
探究新知
? 如何比较两角的大小
3. 现在老师很想快速地找出我们全班同学 中哪个同学手里的角最大?谁能帮助老师想出 办法.
如
A
何
读数为45
比
较
角
45°
的 大
o DB
小?
60°
E
F
所以:∠AOB<∠DEF
二. 度量法 1、对“中”—角的顶点对量角器的中心 2、重合—角的一边与量角器的00刻度
• 两个角的大小关系有三种, A D 记作:
(1) ∠ABC > ∠DEF
B
(E)
(2)∠ABC< ∠DEF
C D (F)
A
B(E)
(3)∠ABC = ∠DEF
C (FA) (D)
B(E)
C(F)
用你手中的两个角,拼一拼看看还 能组成多少度的角?
角的和差
C BB
顶
2
点
1
与
OO
A
一
边
重
合
B
B
2
C 1
D
C
B
32 ⌒
1
O
A
OB、OC是∠AOD的三等分线
如图
D
C B
O
A
D
C B
O
A
应用新知解决问题
3. 如图,把一个蛋糕等分成7份,每份中的角
是多少度(精确到分)?
解:360°÷7 =51°+3°÷7 = 51°+180′÷7 ≈ 51°26′.
答:每份中的角约是51°26′.
51
7 360
35 10 7 3
∠EAC= ∠1+∠DCA
1.计算: (1)48°35′+17°45′ =66°20′
(2)15°20′×5 =76°40′
(3)48°18′-17°45′ =30°33′ (4)360°÷11
34
比一比 看谁反应快:
3.(2008呼和浩特中考)将一副三角板按图示方法放置 (直角顶点重合)
则∠AOB+∠DOC= 180°.
C
B
A
E
D
探究新知 如何比较两角的大小
(2)如果BC与EF重合,
?
那么∠ABC 等于∠ DEF,记作∠ABC ∠=DEF.
C
F
B
A
E
D
探究新知 ? 如何比较两角的大小 (3)如果BC落在∠DEF的外部, 那么∠ABC 大于∠ DEF,记作∠ABC >∠DEF. C
F
B
AE
D
一. 叠合法 注意:1.将两个角的顶点及一边重合 2. 两个角的另一边落在重合一边的同侧 3.由两个角的另一边的位置确定两个角 的大小
注意度、分、秒是60 进制的,要把剩余的 度数化成分.
小结: 1、角的大小比较方法: 2、角的大小关系有哪些? 3、角的和差计算 4、三角板可拼出哪些角?
30
比一比,我赢
C D
A A
B D
B
C
E
冲
D
击
1
C
2
B
A
图中∠1= ∠2, 试判断∠BAD和
∠EAC的大小, 并说明理由.
解: ∠BAD= ∠2+ ∠DCA
135°,150°,165°. 回顾刚才画角的过程,我们可以发现:
※ 角之间可以进行 加减 运算. ※ 一个角可以用其他角的 和或差 来表示.
例1 如图:O是直线AB上一点,∠AOC=53°17′
求∠BOC的度数
C
A
解:因为∠AOB是平角 ∠AOB=∠AOC+∠BOC
O
B
所以∠BOC=∠AOB-∠AOC =180°-53°17′ =126°43′
线重合
3、读数—读出角的另一边所对的度数
用量角器量出角的度数,角的大小按 其度数比较,度数大的角则大,度
数小的角则小.
注意:角的大小只与开口大小有关,而与所画 边的长短无关.
探究新知 如何比较两角的大小
两个角大小的比较方法:
?
(1)用度量法来比较;
(2)运用叠合法进行比较, (在书面很难做到).
A
解: ∠AOB+∠DOC
┓
= ∠BOD +∠DOA + ∠DOC O
= 90° +∠DOA + ∠DOC
