新人教版2014年八年级下册期中考试数学测试试题
2014春新人教版八年级下册数学期中考试测试卷

八年级数学期中考试测试卷一.选择题(共10小题,满分40分,每小题4分)1.使代数式有意义的自变量x的取值范围是()B..B..C. AC=BD二.填空题(共6小题,满分30分,每小题5分)11.计算:(+1)(﹣1)=_________.12.若最简二次根式与是同类二次根式,则a=_________.13.已知等腰△ABC的腰AB=AC=10cm,底边BC=12cm,则△ABC的角平分线AD的长是_________cm14.如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1、S2、S3,且S1=4,S2=8,则AB的长为_________.15.如图,四边形ABCD中,AB∥CD,要使四边形ABCD为平行四边形,则应添加的条件是__..16.如图,已知△ABC中,AB=5cm,BC=12cm,AC=13cm,那么AC边上的中线BD的长为____cm.三.解答题(本大题共3小题,每小题7分,共21分)17.计算:(π﹣1)0++﹣2.18.先化简,再求值:,其中x=.19.如图所示,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,CD=5cm,求AB的长.20.已知:如图,在四边形ABCD中,AB∥CD,对角线AC、BD相交于点O,BO=DO.求证:四边形ABCD是平行四边形.21.如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作▱ABDE,连接AD,EC.(1)求证:△ADC≌△ECD;(2)若BD=CD,求证:四边形ADCE是矩形.22.如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8,CD=3.(1)求DE的长;(2)求△ADB的面积.23.如图,在△ABC中,AB=AC,D是BC的中点,连接AD,在AD的延长线上取一点E,连接BE,CE.(1)求证:△ABE≌△ACE;(2)当AE与AD满足什么数量关系时,四边形ABEC是菱形?并说明理由.24.(9分)如图,南北方向PQ以东为我国领海,以西为公海,晚上10时28分,我边防反偷渡巡逻101号艇在A处发现其正西方向的C处有一艘可疑船只正向我沿海靠近,便立即通知下在PQ上B处巡逻的103号艇注意其动向,经检测,AC=10海里,AB=6海里,BC=8海里,若该船只的速度为12.8海里/小时,则可疑船只最早何时进入我领海?25.如图,在四边形ABCD中,AB⊥BC,AD⊥AB,AB=1,BC=CD=2.求:(1)AD的长;(2)四边形ABCD的周长;(3)四边形ABCD的面积。
14级初二下数学期中考试试题.docx

&对于任意整数斤, 多项式(n + 9)2-n2都能够(A.被2整除B.被9整除C.被"整除D.被S + 9)整除9.某单位向一所希望小学赠送1080件文具,现用型包装箱比A型包装箱多装15件文具,单独使用B型包装箱比单独使用A型包装箱可少用12 个,A、B两种不同的包装箱进行包装,已知每个BA.C. 设B型包装箱每个可以装x件文具,根据题意列方程为()1080 1080 “ - = +12x x-151080 1080 ’------ =------------ 121080 1080 一x x-151080 1080 一D- - = +12x x + 15成都七中育才学校初2014级八年级(下)期中考试卷命题人:贺莉鄢正清审题人:陈开文罗丹梅温馨提示:请将所有题目做在答题卷上。
A卷(100分)一、选择题(每题3分,共30分)1.在丄f出,出丄(兀-必丄@+小中,分式的个数有()x 3 x-y x-2 7t 4 )‘A. 6个B. 3个C. 4个D. 5个2.卞列等式从左到右的变形是因式分解的是()A. 6a2b2 = 3ab - 2abB. 2x2 + 8%-1 = 2x(x + 4)-1C. /_3°_4二@ + 1)(°一4)D. a2 -3 = (d + 2*0 -2)-13.已知£ = 2 = £工0,则£±2的值为()•2 3 4 cA. -B. -C. 2D.-5 4 24.下列各式:①4x2— y2;②2兀"+ 8兀》+ 8疋))2 ;③f十2ab_b?;④x2 —?⑤兀?+2兀+ 3其中不能分解因式的有()A. 1个B. 2个C. 3个D. 4个5.点C是线段AB的黄金分割点(AOBC),若AB=10cm,则AC等于()A. 6cmB. 5(75+l)cmC. 5(V^T)cmD. (sV5-l)cm6.若a>0, b<—2,则点(a, b+2)应在()A.笫一彖限B.第二彖限C.第三彖限D第四彖限7.若多项式—12/)』+]6兀3),2+4兀2),2的一个因式是—4/),2,则另一个因式是()B. 3j-4x-lC.3y-4x + lD. 3y - 4xA. 3y + 4x— 1io.如果不等式组r+5<4x_1有解,则加的取值范围是()x<mA N m<2B、m>2Cs m>2D^ m<2二、填空题(每题4分,共16分)11.___________________________________________________ 线段a = 2cm,b = 8cm ,则a、b的比例中项c = _____________________________________________ , a、b、c的第四比例项d = _______________ .i12.已知兀=1是分式方程——二丄的根,则实数£= ___________________ .x +1 x13.不等式8-3x>0的最大整数解是____________________ .14.在比例尺为1: 3000的我校规划图上,矩形运动场的图上尺寸是lcmx2cm,则运动场的实际面积_____________ 米2 o三、解答题(共38分)15.分解因式(每小题5分,共10分)(1) 5兀'—10兀'y + 5兀)‘(2) a'—2/—3d16.计算(每小题5分,共10分)(1)x24x 4-------------------- 1 --------x — 2 x — 2 x — 2(2)2m + 4■m +117.(每小题5分,共10分)x + 3 2 ⑴解方程2x-1 [ / 5x +1 (2)解不等式组,并在数轴上表示解集:—一3(x + l)>5x-l18. (8分)先化简,再求值:36 — / 6— Q a2 +10^ + 25 2a +10a+ 5cT + 6a其中,a = 2y[2四、解答题(共1 6分,其中19题6分,20题10分)19.科学研究表明,当人的下肢长与身高Z比为0.618时,看起来最美.某成年女士身高为153cm,下肢长为92cm,求该女士穿的高跟鞋鞋跟的最佳高度约为多少cm?(结果精确到0. 1cm)20.某项工程,若由甲、乙两建筑队合做,6个月可以完成,若由甲、乙两队独做,甲队比乙队少用5个刀的时间完成.(1)甲、乙两队单独完成这项工程各需几个月的时间?(2)已知甲队每月施工费用为15万元,比乙队多6万元,按要求该工程总费用不超过141万元,工程必须在一年内竣工(包括12个月).为了确保经费和工期,采取甲队做。
(完整word)2014人教版八年级数学下册期中试卷

八年级下册数学期中试卷总分150分, 时间120分钟一、单项选择题(本大题共10个小题;每小题5分, 共50分) 1. 下列式子中一定是二次根式的是( )a -2a 2a -3a 2. 若 是二次根式, 则x 应满足( )(A)x ≠2 (B )x <2 (C )x >2 (D )x ≥2 3. 若 , 则( )(A )b>3 (B )b<3 (C )b ≥3 (D )b ≤3 4. 下列根式中属最简二次根式的是( )21a + (B 12(C 8(D 275. 下列说法正确的是( ).(A )有两组对边分别平行的图形是平行四边形 (B )平行四边形的对角线相等(C )平行四边形的对角互补, 邻角相等 (D )平行四边形的对边平等且相等6.下列各组数中, 能构成直角三角形的是( )(A )4, 5, 6 (B )1, 1, (C )6, 8, 11 (D )5, 12, 23 7.如果等边三角形的边长为3, 那么连结各边中点所成的三角形的周长为( ).(A )9 (B )6 (C )3 (D )928, 在四边形ABCD 中, O 是对角线的交点, 能判定这个四边形是正方形的条件是( )(A )AC =BD, AB =CD, AB ∥CD (B )AD//BC, ∠A =∠C (C )AO =BO =CO =DO, AC ⊥BD (D )AO =CO, BO =DO, AB =BC9.一直角三角形的斜边长比一直角边长大 ,另一直角边长为 ,则斜边. .. ) (A ) 4 (B ) 8 (C ) 10 (D ) 12 10.已知三角形的面积一定, 则它底边a 上的高h 与底边a 之间的函数关系的图象大致是( )二、填空题(本大题共6个小题;每小题5分, 共30分) 11. 计算 = ; × = ; =12.将长为10米的梯子斜靠在墙上, 若梯子的上端到梯子的底端的距离为6米, 则梯子的底端到墙的底端的距离为 。
新人教版2014年八年级下册数学期中试卷

(新人教版)2014年八年级下册中期数学试卷(时间:120分钟,总分150分)命题人:吴诗彦 审核人:黄坤权一、选择题(每小题4分,共48分) ( )1、有意义的条件是二次根式3-xA .x ≥3 B. x >-3 C. x >3 D.x ≥-3 ( )2、化简二次根式16得A . 8B . 4C . 4±D . 8±( )3、如图字母B 所代表的正方形的面积是A. 12B. 13C. 144D. 194( )4、以下列线段a 、b 、c 的长为三边的三角形中,不是直角三角形的是A.2,3,1===c b aB.1,2,1===c b aC.2,2,1===c b aD.5,4,3===c b a( )5、①两组对边分别平行;②两组对边分别相等;③有一组对边平行且相等;④对角线相等。
以上四个条件中可判定四边形是平行四边形的有 A. 1个 B.2个 C.3个 D.4个( )6、已知矩形ABCD 两条对角线AC 与BD 相交于O , =∠C A B 40°,则AOD ∠的度数是 A.50° B.60° C.70° D .80° ( )7、下列运算正确的是( )A .523=+B .623=⨯C .13)13(2-=-D .353522-=-( )8、如图,菱形ABCD 中,对角线AC 、BD交于E 点,F 为AB 中点,若EF =3,则菱形ABCD 的周长是 A .12 B .16 C .20 D .24( )9、已知直角三角形两边的长分别为3和4,则此直角三角形的第三边为A .5 B.7 C .5或7 D.以上都不对( )10、如图,在□ABCD 中,已知AD =10cm , AB =6cm ,AE 平分∠BAD 交BC 边于 点E ,则EC 等于A.1cmB.2cmC.3cmD.4cm( )11、如图,正方形ABCD 中,AE =AB ,直线DE 交BC 于点F ,则∠BEF = A .45° B .30° C .60° D .55°( )12、如图,一只蚂蚁从长5、宽3,高4的长方体纸箱的A 点沿纸箱表面爬 到B 点,那么它所行的最短路线的长是( )A.12 B .10 C .54 D .74二B16925A B5 12题 3411题 FD B A C E6题8题二、填空题(每小题4分,共24分) 13、=÷28 .14、一个直角三角形两直角边为5和12,则斜边长为________.15、在矩形ABCD 中,对角线AC 与BD 相交于点O ,∠AOB =120o,且AD=4,则矩形ABCD 的面积为 .16、已知菱形的两条对角线长为8cm 和6cm,那么这个菱形的周长是 cm. 17、如图,有一块直角三角形纸片,两直角边AC =6cm ,BC =8cm ,先将直角边AC 沿AD 折叠,使它落在斜边AB 上,且与AE 重合,则CD = . 18、 观察下列各式:11111112,23,34, (334455)+=+=+=请你找出 其中规律,并将第n (n ≥1的整数)个等式写出来 .15题题17题CBADE(新人教版)2014年八年级下册中期数学答题卷命题人:吴诗彦 审核人:黄坤权一、选择题(每小题4分,共48分) 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案二、填空题(每小题4分,共24分)13. 14. 15. ; 16. 17. 18. . 三、解答题(共78分)19、计算题(每小题5分,共10分) ①)227(328--+ ②5232232⨯÷20、(6分)计算:284)23()21(01--+-⨯-21、(8分)已知32+=x ,32-=y ,求222y xy x +-的值.22、(10分) 已知:在□ABCD 中,点E 、F 分别在AD 、BC 上,且AE =CF . 求证:四边形BFDE 是平行四边形.23、(10分)如图,四边形ABCD 是菱形,菱形ABCD 的周长为20,对角线AC 与BD相交于O,AO=4. 求菱形ABCD 的面积.24、(10分)已知,如图,四边形ABCD 中,1AB BC ==,3CD =,1DA =,且090B ∠=,试求:(1)BAD ∠的度数;(2)四边形ABCD 的面积(结果保留根号);中期数学试卷 班级 考号 姓名 .A BCDEF BADC25、(12分)已知:如图,△ABC中,∠A CB=90°,点D、E分别是AC、AB的中点,点F在BC的延长线上,且∠CDF=∠A.求证BC=2FC 26、(12分)如图,正方形ABCD中,E为AB边上一动点,过点D作DF DE⊥,与BC延长线交于点F,连接EF,与CD边交于点G,与对角线BD交于点H.(1)若2BF BD==,求BE的长;(2)求证222HGGFEH=+.EDF BCA。
2013-2014年八年级下学期数学期中考试卷(新人教版)

2014学年度下学期八年级数学期中考试一、选择题:(每小题3分,共42分)1、下列各式中是二次根式的是()A.7- B.32m C. 12+x D.3ab2、(2+3)10与(2—3)9作乘积的结果是()A.2+3 B. 2—3 C.—2+3 D. —2—33、如果2)1()2()1(2++-=++xxxx,则x的取值范围是()A.x≥—1 B。
x≥—2 C.x≤—1 D.—2≤x≤—14、直角三角形的两直角边分别为5cm,12cm,其中斜边上的高为()A.6cm B.8.5cm C.30/13cm D.60/13 cm5、已知一个Rt△的两边长分别为3和4,则第三边长的平方是()(A)25 (B)14 (C)7 (D)7或256、如图,AB⊥CD于B,△ABD和△BCE都是等腰直角三角形,如果CD=17,BE=5,那么AC的长为().(A)12 (B)7 (C)5 (D)137、如图,数轴上的点A所表示的数为x,则x2—10的立方根为()A .2-10 B.-2-10 C.2 D.-28、△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为()A.42 B.32 C.42 或32 D.37 或339、如图,在平行四边形ABCD中,∠B=80°,AE平分∠BAD交BC于点E,CF∥AE交AE于点F,则∠1=()A.40°B.50°C.60°D.80°10、将一张平行四边形的纸片折一次,使得折痕平分这个平行四边形的面积.则这样的折纸方法共有()A、1种B、2种C、4种D、无数种11、菱形ABCD的周长是16,∠A=60°,则对角线BD的长度为()]A.2 B.23C.4 D.4312、如图,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=CD.下列结论:①EG⊥FH,②四边形EFGH是矩形,③HF平分∠EHG,④EG=错误!未找到引用源。
2014年新人教版八年级数学下册期中质量检测试卷
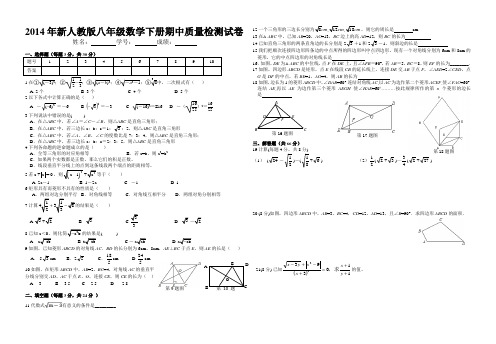
16.如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为________.
17.如图。四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点,若BE=1,AG=4,则AB的长为
2014年新人教版八年级数学下册期中质量检测试卷
姓名:学号:成绩:
一、选择题(每题3分,共30分)
题号
1
2
3
4
5
6
7
8
9
10
答案
1.在①;②;③;④;⑤中,二次根式有()
A.2个B. 3个C. 4个D. 5个
2.以下各式中计算正确的是()
A.- =-6B. =-3 C.=±16 D.-()2=
3.下列说法中错误的是( )
(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.
24.( 10分)已知 为实数,且y< + +3,化简:
25.( 10分)如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF= CD,求证:∠AEF=90°
26.(本题满分12分)如图,在四边形ABCD中,AD∥BC,B=90°,AB=8cm,AD=21cm,BC=22.5cm,点P从点A出发,以1cm/s的速度向点D运动,点Q从点C出发,以2cm/s的速度向点B运动。规定其中一个运动到终点时,另一个也随之停止运动。设运动的时间为 ,求
18.如图,边长为1的F,使∠FAC=60°.连结AE,再以AE为边作第三个菱形AEGH使∠HAE=60°………按此规律所作的第n个菱形的边长是.
人教版八年级下册数学期中考试试题含答案
人教版八年级下册数学期中考试试卷一、选择题(本大题共12个小题;每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.要使式子有意义,则x的取值范围是()A.x≤﹣2B.x≤2C.x≥2D.x≥﹣22.下列二次根式中,最简二次根式是()A.B.C.D.3.下列二次根式中,与之积为无理数的是()A.B.C.D.4.若(m﹣1)2+=0,则m+n的值是()A.﹣1B.0C.1D.25.以下列长度为三角形边长,不能构成直角三角形的是()A.5,12,13B.4,5,6C.1,,D.7,24,256.如图,在平行四边形ABCD中,下列结论中错误的是()A.∠1=∠2B.∠BAD=∠BCD C.AB=CD D.AC⊥BD7.如图,是由三个正方形组成的图形,则∠1+∠2+∠3等于()A.60°B.90°C.120°D.180°8.如图,在△ABC中,∠C=90°,AB=17cm,AC=8cm,若BE=3cm,则矩形CBEF 的面积是()A.9cm2B.24cm2C.45cm2D.51cm29.设n为正整数,且n<<n+1,则n的值为()A.5B.6C.7D.810.三角形的三边长a,b,c满足2ab=(a+b)2﹣c2,则此三角形是()A.钝角三角形B.锐角三角形C.直角三角形D.等边三角形11.如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD的面积的()A.B.C.D.12.如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的边长为()A.2B.4C.4D.8二、填空题(本大题共8个小题;每小题3分,共24分.把答案写在题中横线上)13.计算:=.14.相邻两边长分别是2+与2﹣的平行四边形的周长是.15.等腰三角形的腰为13cm,底边长为10cm,则它的面积为.16.已知▱ABCD中,∠A+∠C=240°,则∠B的度数是.17.若菱形的两条对角线长分别是6和8,则此菱形的周长是,面积是.18.如图所示,平行四边形ABCD中,顶点A、B、D在坐标轴上,AD=5,AB=9,点A的坐标为(﹣3,0),则点C的坐标为.19.如图,在平行四边形ABCD中,DE平分∠ADC,AD=8,BE=4,则平行四边形ABCD的周长是.20.如图所示的一块地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,这块地的面积为.三、解答下列各题(本题有7个小题,共60分)21.计算:(1)4+﹣+4(2)(﹣2)2÷(+3﹣)22.(1)先化简,再求值:÷(﹣),其中x=+,y=﹣.(2)在数轴上画出表示的点.(要求画出作图痕迹)(3)如图,左边是由两个边长为2的小正方形组成,沿着图中虚线剪开,可以拼成右边的大正方形,求大正方形的边长.23.如图,平行四边形ABCD,点E,F分别在BC,AD上,且BE=DF,求证:四边形AECF是平行四边形.24.如图,折叠矩形的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,求EC的长.25.观察下列等式:①==;②==;③==…回答下列问题:(1)利用你观察到的规律,化简:(2)计算:+++…+.26.如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.(1)求证:∠ADB=∠CDB;(2)若∠ADC=90°,求证:四边形MPND是正方形.27.如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.(1)求证:四边形AEBD是矩形;(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.参考答案与试题解析一、选择题(本大题共12个小题;每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.要使式子有意义,则x的取值范围是()A.x≤﹣2B.x≤2C.x≥2D.x≥﹣2【考点】二次根式有意义的条件.【分析】根据二次根式的性质,被开方数大于或等于0,列不等式,即可求出x的取值范围.【解答】解:由题意得:2+x≥0,解得:x≥﹣2,故选D.【点评】本题考查了二次根式有意义的条件,难度不大,解答本题的关键是掌握二次根式的被开方数为非负数.2.下列二次根式中,最简二次根式是()A.B.C.D.【考点】最简二次根式.【分析】根据最简二次根式的概念进行判断即可.【解答】解:=a,A错误;=,B错误;=3,C错误;是最简二次根式,D正确,故选:D.【点评】本题考查的是最简二次根式的概念,最简二次根式的概念:(1)被开方数不含分母;(2)被开方数中不含能开得尽方的因数或因式.3.下列二次根式中,与之积为无理数的是()A.B.C.D.【考点】二次根式的乘除法.【分析】根据二次根式的乘法进行计算逐一判断即可.【解答】解:A、,不是无理数,错误;B、,是无理数,正确;C、,不是无理数,错误;D、,不是无理数,错误;故选B.【点评】此题考查二次根式的乘法,关键是根据法则进行计算,再利用无理数的定义判断.4.若(m﹣1)2+=0,则m+n的值是()A.﹣1B.0C.1D.2【考点】非负数的性质:算术平方根;非负数的性质:偶次方.【分析】根据非负数的性质列式求出m、n的值,然后代入代数式进行计算即可得解.【解答】解:由题意得,m﹣1=0,n+2=0,解得m=1,n=﹣2,所以,m+n=1+(﹣2)=﹣1.故选A.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.5.以下列长度为三角形边长,不能构成直角三角形的是()A.5,12,13B.4,5,6C.1,,D.7,24,25【考点】勾股定理的逆定理.【分析】由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方即可.【解答】解:A、52+122=132,故是直角三角形,故正确;B、42+52≠62,故不是直角三角形,故错误;C、12+()2=()2,故是直角三角形,故正确;D、72+242=252,故是直角三角形,故正确.故选B.【点评】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.6.如图,在平行四边形ABCD中,下列结论中错误的是()A.∠1=∠2B.∠BAD=∠BCD C.AB=CD D.AC⊥BD【考点】平行四边形的性质.【分析】根据平行四边形的性质,平行四边形对边平行以及对边相等和对角相等分别判断得出即可.【解答】解:∵在平行四边形ABCD中,∴AB∥CD,∴∠1=∠2,(故A选项正确,不合题意);∵四边形ABCD是平行四边形,∴∠BAD=∠BCD,(故B选项正确,不合题意);AB=CD,(故C选项正确,不合题意);无法得出AC⊥BD,(故D选项错误,符合题意).故选:D.【点评】此题主要考查了平行四边形的性质,熟练掌握相关的性质是解题关键.7.如图,是由三个正方形组成的图形,则∠1+∠2+∠3等于()A.60°B.90°C.120°D.180°【考点】三角形内角和定理;正方形的性质.【分析】根据三角形内角和为180°,得到∠BAC+∠BCA+∠ABC=180°,又∠4=∠5=∠6=90°,根据平角为180°,即可解答.【解答】解:如图,∵图中是三个正方形,∴∠4=∠5=∠6=90°,∵△ABC的内角和为180°,∴∠BAC+∠BCA+∠ABC=180°,∵∠1+∠4+∠BAC=180°,∠2+∠6+∠ABC=180°,∠3+∠5+∠ACB=180°,∴∠1+∠4+∠BAC+∠2+∠6+∠ABC+∠3+∠5+∠ACB=540°,∴∠1+∠2+∠3=540°﹣(∠4+∠5+∠6+∠BAC+∠ABC+∠ACB)=540°﹣90°﹣90°﹣90°﹣180°=90°,故选:B.【点评】本题考查了三角形内角和定理,解决本题的关键是运用三角形内角和为180°,正方形的内角为90°以及平角为180°,即可解答.8.如图,在△ABC中,∠C=90°,AB=17cm,AC=8cm,若BE=3cm,则矩形CBEF 的面积是()A.9cm2B.24cm2C.45cm2D.51cm2【考点】勾股定理;矩形的性质.【专题】计算题.【分析】在直角三角形ABC中,由AB与AC的长,利用勾股定理求出BC的长,再由BE的长,求出矩形CBEF的面积即可.【解答】解:在Rt△ABC中,AB=17cm,AC=8cm,根据勾股定理得:BC==15cm,则矩形CBEF面积S=BC•BE=45cm2.故选C【点评】此题考查了勾股定理,以及矩形的性质,熟练掌握勾股定理是解本题的关键.9.设n为正整数,且n<<n+1,则n的值为()A.5B.6C.7D.8【考点】估算无理数的大小.【分析】首先得出<<,进而求出的取值范围,即可得出n的值.【解答】解:∵<<,∴8<<9,∵n<<n+1,∴n=8,故选;D.【点评】此题主要考查了估算无理数,得出<<是解题关键.10.三角形的三边长a,b,c满足2ab=(a+b)2﹣c2,则此三角形是()A.钝角三角形B.锐角三角形C.直角三角形D.等边三角形【考点】勾股定理的逆定理.【分析】对原式进行化简,发现三边的关系符合勾股定理的逆定理,从而可判定其形状.【解答】解:∵原式可化为a2+b2=c2,∴此三角形是直角三角形.故选:C.【点评】解答此题要用到勾股定理的逆定理:已知三角形ABC的三边满足a2+b2=c2,则三角形ABC是直角三角形.11.如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD的面积的()【考点】矩形的性质.【分析】本题主要根据矩形的性质,得△EBO ≌△FDO ,再由△AOB 与△OBC 同底等高,△AOB 与△ABC 同底且△AOB 的高是△ABC 高的得出结论.【解答】解:∵四边形为矩形,∴OB=OD=OA=OC ,在△EBO 与△FDO 中,∵,∴△EBO ≌△FDO (ASA ),∴阴影部分的面积=S △AEO +S △EBO =S △AOB ,∵△AOB 与△ABC 同底且△AOB 的高是△ABC 高的,∴S △AOB =S △OBC =S 矩形ABCD .故选:B .【点评】本题考查矩形的性质,矩形具有平行四边形的性质,又具有自己的特性,要注意运用矩形具备而一般平行四边形不具备的性质.12.如图,在平行四边形ABCD 中,AB=4,∠BAD 的平分线与BC 的延长线交于点E ,与DC 交于点F ,且点F 为边DC 的中点,DG ⊥AE ,垂足为G ,若DG=1,则AE 的边长为()【考点】平行四边形的性质;等腰三角形的判定与性质;含30度角的直角三角形;勾股定理.【专题】计算题;压轴题.【分析】由AE为角平分线,得到一对角相等,再由ABCD为平行四边形,得到AD与BE 平行,利用两直线平行内错角相等得到一对角相等,等量代换及等角对等边得到AD=DF,由F为DC中点,AB=CD,求出AD与DF的长,得出三角形ADF为等腰三角形,根据三线合一得到G为AF中点,在直角三角形ADG中,由AD与DG的长,利用勾股定理求出AG的长,进而求出AF的长,再由三角形ADF与三角形ECF全等,得出AF=EF,即可求出AE的长.【解答】解:∵AE为∠DAB的平分线,∴∠DAE=∠BAE,∵DC∥AB,∴∠BAE=∠DFA,∴∠DAE=∠DFA,∴AD=FD,又F为DC的中点,∴DF=CF,∴AD=DF=DC=AB=2,在Rt△ADG中,根据勾股定理得:AG=,则AF=2AG=2,∵平行四边形ABCD,∴AD∥BC,∴∠DAF=∠E,∠ADF=∠ECF,在△ADF和△ECF中,,∴△ADF≌△ECF(AAS),∴AF=EF,则AE=2AF=4.故选:B【点评】此题考查了平行四边形的性质,全等三角形的判定与性质,勾股定理,等腰三角形的判定与性质,熟练掌握平行四边形的判定与性质是解本题的关键.二、填空题(本大题共8个小题;每小题3分,共24分.把答案写在题中横线上)13.计算:=6.【考点】二次根式的混合运算.【专题】计算题.【分析】先把化简,然后把括号内合并后进行二次根式的乘法运算即可.【解答】解:原式=(+2)×=3×=6.故答案为6.【点评】本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.14.相邻两边长分别是2+与2﹣的平行四边形的周长是8.【考点】二次根式的应用.【分析】根据平行四边形的周长等于相邻两边的和的2倍进行计算即可.【解答】解:平行四边形的周长为:(2++2﹣)×2=8.故答案为:8.【点评】本题考查的是平行四边形的周长的计算和二次根式的加减,掌握平行四边形的周长公式和二次根式的加减运算法则是解题的关键.15.等腰三角形的腰为13cm,底边长为10cm,则它的面积为60cm2.【考点】勾股定理;等腰三角形的性质.【分析】根据题意画出图形,过点A作AD⊥BC于点D,根据BC=10cm可知BD=5cm.由勾股定理求出AD的长,再由三角形的面积公式即可得出结论.【解答】解:如图所示,过点A作AD⊥BC于点D,∵AB=AC=13cm,BC=10cm,∴BD=5cm,∴AD===12cm,∴S△ABC=BC•AD=×10×12=60(cm2).故答案为:60cm2.【点评】本题考查的是勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.16.已知▱ABCD中,∠A+∠C=240°,则∠B的度数是60°.【考点】平行四边形的性质.【分析】由平行四边形的性质得出∠A=∠C,∠A+∠B=180°,再由已知条件求出∠A,即可得出∠B.【解答】解:∵四边形ABCD是平行四边形,∴∠A=∠C,∠A+∠B=180°,∵∠A+∠C=240°,∴∠A=120°,∴∠B=60°;故答案为:60°.【点评】本题考查了平行四边形的性质;熟练掌握平行四边形的性质,并能进行推理计算是解决问题的关键.17.若菱形的两条对角线长分别是6和8,则此菱形的周长是20,面积是24.【考点】菱形的性质.【分析】首先根据题意画出图形,然后由菱形的两条对角线长分别是6和8,可求得OA=4,OB=3,再由勾股定理求得边长,继而求得此菱形的周长与面积.【解答】解:如图,菱形ABCD中,AC=8,BD=6,∴OA=AC=4,OB=BD=3,AC⊥BD,∴AB==5,∴此菱形的周长是:5×4=20,面积是:×6×8=24.故答案为:20,24.【点评】此题考查了菱形的性质以及勾股定理.注意菱形的面积等于对角线积的一半.18.如图所示,平行四边形ABCD中,顶点A、B、D在坐标轴上,AD=5,AB=9,点A的坐标为(﹣3,0),则点C的坐标为(9,4).【考点】平行四边形的性质;坐标与图形性质.【分析】由平行四边形的性质得出CD=AB=9,由勾股定理求出OD,即可得出点C的坐标.【解答】解:∵四边形ABCD是平行四边形,∴CD=AB=9,∵点A的坐标为(﹣3,0),∴OA=3,∴OD===4,∴点C的坐标为(9,4).故答案为:(9,4).【点评】本题考查了平行四边形的性质、坐标与图形性质、勾股定理;熟练掌握平行四边形的性质,由勾股定理求出OD是解决问题的关键.19.如图,在平行四边形ABCD中,DE平分∠ADC,AD=8,BE=4,则平行四边形ABCD的周长是24.【考点】平行四边形的性质.【分析】由在平行四边形ABCD中,DE平分∠ADC,易证得△CDE是等腰三角形,继而求得CD的长,则可求得答案.【解答】解:∵四边形ABCD是平行四边形,∴AD∥BC,BC=AD=8,∴∠ADE=∠DEC,∵DE平分∠ADC,∴∠ADE=∠CDE,∴∠CDE=∠DEC,∴CD=CE=BC﹣BE=8﹣4=4,∴AB=CD=4,∴平行四边形ABCD的周长是:AD+BC+CD+AB=24.故答案为:24.【点评】此题考查了平行四边形的性质以及等腰三角形的判定与性质.注意证得△CDE是等腰三角形是关键.20.如图所示的一块地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,这块地的面积为24m2.【考点】勾股定理的应用.【分析】连接AC,利用勾股定理可以得出三角形ACD和ABC是直角三角形,△ABC的面积减去△ACD的面积就是所求的面积.【解答】解:如图,连接AC由勾股定理可知AC===5,又AC2+BC2=52+122=132=AB2故三角形ABC是直角三角形故所求面积=△ABC的面积﹣△ACD的面积==24(m2).【点评】考查了直角三角形面积公式以及勾股定理的应用.三、解答下列各题(本题有7个小题,共60分)21.计算:(1)4+﹣+4(2)(﹣2)2÷(+3﹣)【考点】二次根式的混合运算.【专题】计算题.【分析】(1)先把各二次根式化为最简二次根式,然后合并即可;(2)先把各二次根式化为最简二次根式,然后把括号内合并后进行二次根式的除法运算.【解答】解:(1)原式=4+3﹣2+4=7+2;(2)原式=4×12÷(5+﹣4)=48÷(2)=8.【点评】本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.22.(1)先化简,再求值:÷(﹣),其中x=+,y=﹣.(2)在数轴上画出表示的点.(要求画出作图痕迹)(3)如图,左边是由两个边长为2的小正方形组成,沿着图中虚线剪开,可以拼成右边的大正方形,求大正方形的边长.【考点】图形的剪拼;实数与数轴;分式的化简求值;勾股定理.【分析】(1)首先将括号里面通分,进而利用分式的除法运算法则化简,进而将已知代入求出答案;(2)直接利用勾股定理结合数轴得出的位置;(3)直接利用勾股定理得出大正方形的边长即可.【解答】解:(1)原式=÷=×=,当x=+,y=﹣时,原式==;(2)因为30=25+5,则首先作出以5和为直角边的直角三角形,则其斜边的长即是.如图所示:;(3)如图所示:∵左边是由两个边长为2的小正方形组成,∴大正方形的边长为:=2.【点评】此题主要考查了分式的混合运算以及无理数的确定方法以及勾股定理、图形的剪拼,正确应用勾股定理是解题关键.23.如图,平行四边形ABCD,点E,F分别在BC,AD上,且BE=DF,求证:四边形AECF是平行四边形.【考点】平行四边形的判定与性质.【专题】证明题.【分析】根据平行四边形的性质得出AD∥BC,AD=BC,求出AF=CE,根据平行四边形的判定得出即可.【解答】证明:四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∵DF=BE,∴AF=CE,∴四边形AECF是平行四边形.【点评】本题考查了平行四边形的性质和判定的应用,能灵活运用定理进行推理是解此题的关键.24.如图,折叠矩形的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,求EC的长.【考点】翻折变换(折叠问题).【专题】计算题.【分析】根据矩形的性质得DC=AB=8,AD=BC=10,∠B=∠D=∠C=90°,再根据折叠的性质得AF=AD=10,DE=EF,在Rt△ABF中,利用勾股定理计算出BF=6,则FC=4,设EC=x,则DE=EF=8﹣x,在Rt△EFC中,根据勾股定理得x2+42=(8﹣x)2,然后解方程即可.【解答】解:∵四边形ABCD为矩形,∴DC=AB=8,AD=BC=10,∠B=∠D=∠C=90°,∵折叠矩形的一边AD,使点D落在BC边的点F处∴AF=AD=10,DE=EF,在Rt△ABF中,BF===6,∴FC=BC﹣BF=4,设EC=x,则DE=8﹣x,EF=8﹣x,在Rt△EFC中,∵EC2+FC2=EF2,∴x2+42=(8﹣x)2,解得x=3,∴EC的长为3cm.【点评】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了勾股定理.25.观察下列等式:①==;②==;③==…回答下列问题:(1)利用你观察到的规律,化简:(2)计算:+++…+.【考点】分母有理化.【专题】规律型.【分析】(1)根据观察,可发现规律;=,根据规律,可得答案;(2)根据二次根式的性质,分子分母都乘以分母两个数的差,可分母有理化.【解答】解:(1)原式==;(2)原式=+++…+=(﹣1).【点评】本题考查了分母有理化,分子分母都乘以分母两个数的差是分母有理化的关键.26.如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.(1)求证:∠ADB=∠CDB;(2)若∠ADC=90°,求证:四边形MPND是正方形.【考点】正方形的判定;全等三角形的判定与性质.【专题】证明题.【分析】(1)根据角平分线的性质和全等三角形的判定方法证明△ABD≌△CBD,由全等三角形的性质即可得到:∠ADB=∠CDB;(2)若∠ADC=90°,由(1)中的条件可得四边形MPND是矩形,再根据两边相等的四边形是正方形即可证明四边形MPND是正方形.【解答】证明:(1)∵对角线BD平分∠ABC,∴∠ABD=∠CBD,在△ABD和△CBD中,,∴△ABD≌△CBD(SAS),∴∠ADB=∠CDB;(2)∵PM⊥AD,PN⊥CD,∴∠PMD=∠PND=90°,∵∠ADC=90°,∴四边形MPND是矩形,∵∠ADB=∠CDB,∴∠ADB=45°∴PM=MD,∴四边形MPND是正方形.【点评】本题考查了全等三角形的判定和性质、角平分线的性质、矩形的判定和性质以及正方形的判定,解题的关键是熟记各种几何图形的性质和判定.27.如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.(1)求证:四边形AEBD是矩形;(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.【考点】矩形的判定;正方形的判定.【专题】压轴题.【分析】(1)利用平行四边形的判定首先得出四边形AEBD是平行四边形,进而由等腰三角形的性质得出∠ADB=90°,即可得出答案;(2)利用等腰直角三角形的性质得出AD=BD=CD,进而利用正方形的判定得出即可.【解答】(1)证明:∵点O为AB的中点,连接DO并延长到点E,使OE=OD,∴四边形AEBD是平行四边形,∵AB=AC,AD是∠BAC的角平分线,∴AD⊥BC,∴∠ADB=90°,∴平行四边形AEBD是矩形;(2)当∠BAC=90°时,理由:∵∠BAC=90°,AB=AC,AD是∠BAC的角平分线,∴AD=BD=CD,∵由(1)得四边形AEBD是矩形,∴矩形AEBD是正方形.【点评】此题主要考查了正方形的判定以及矩形的判定和等腰直角三角形的性质等知识,熟练掌握正方形和矩形的判定是解题关键.。
2014-2015学年八年级下学期期中考试数学试题
2014-2015学年八年级下学期期中考试数学试题八年级数学下学期期中联考试卷一、选择题(40分)1、下列各数中,没有平方根的是( )A 、()22- B 、64 C 、21 D 、22- 2、下列二次根式有意义的范围为x ≥2的是( )A 、21-x B 、2-x C 、21+x D 、2+x3、下列运算正确的是( )A 、235=- B 、312914= C 、()52522-=- D 、32321+=-4、由线段a 、b 、c 组成的三角形不是直角三角形的是( )A 、a=7,b=24,c=25;B 、a=13,b=14,c=15; C 、a=54,b=1,c=34; D 、b=4,c=5;5、若平行四边形中两个内角的度数比为1∶2,则其中较小的内角是( )A 、30°B 、45°C 、60°D 、75° 6、已知n12是整数,则满足条件的最小正整数n 为( )A 、2B 、3C 、4D 、5延长AF 与BC 的延长线交于点M 。
以下结论:①AB=CM ; ②AE=AB+CE ;③S △AEF =ABCFS31四边形;④∠AFE=90°,其中正确结论的个数有( )A 、1个B 、2个C 、3个D 、4个二、填空题(24分) 10题图11、计算⑴20= ; ⑵114= 。
12、平面直角坐标系中,已知点A(-1,-3)和点B(1,-2),则线段AB 的长为 。
13、如图,平行四边形ABCD 的顶点A 、B 、D 的坐标分别是(0,0)、(5,0)、(2,3),则顶点C 的坐标是 。
13题图 14题图 15题图 14、如图,若将四根木条钉成的矩形木框变成平行四边形ABCD 的形状,并使其面积为矩形面积的一半,则这个平行四边形的最大内角等于15、如图,在Rt ΔABC 中,∠ACB=90°,AC=4,BC=3,DABCEDCBAD为斜边AB上一点,以CD、CB为边作平行四边形CDEB,当AD= 时,平行四边形CDEB为菱形。
最新2014年人教版八年级下学期数学期中试卷
最新2014年人教版八年级下学期数学期中试卷2014.4.20班级 座号 姓名(时间120分钟, 总分150分)一、选择题(共40分):1、正方形的对称轴的条数( )A .2 B.3 C.4 D.无数条2、下列各式中,不是二次根式的是( )ABD3、下列根式中,最简二次根式是( )4、正方形的面积是4,则它的对角线长是( )A 、2B 、2C 、22D 、45、计算:3÷6的结果是 ( )A 、12B 、62C 、32D 、 2 6、如果a 2=-a ,那么a 一定是 ( )A 、负数B 、正数C 、正数或零D 、负数或零 7. 园丁住宅小区有一块草坪如图所示,已知3AB =米,4BC =米,12CD =米,13DA =米,且AB BC ⊥,这块草坪的面积是( )A.24米2 B.36米2 C.48米2 D.72米28、平行四边形ABCD 中,AD BC CD AB :::可以是 ( )A 5:4:3:2B 3:3:2:2C 3:2:3:2D 2:3:3:29. 如图,平行四边形ABCD 中,AE 平分DAB ∠, 100=∠B ,则DAE ∠等于( )(A ) 100 (B ) 80 (C ) 60 (D ) 4010. 如图,已知ABCD 是平行四边形,下列结论中,不一定正确的是 ( )(A )AB = CD (B )AC = BD(C )当AC ⊥BD 时,它是菱形 (D )当 90=∠ABC 时,它是矩形第9题 第10题 B.8X C.6X 3 D.X2+1C B第7题二、填空题(每题3分,共24分)11、2=_____;12、、对角线_____平行四边形是矩形13、、下列各式中,不是二次根式的有_________________________。
(填序号); ; ;14. 已知平行四边形ABCD 的面积为16,对角线AC , BD 相交于点O ,则COD ∆的面积为 。
15.已知一个直角三角形的两条直角边分别为6cm 、8cm ,那么这个直角三角形斜边上的高为_________________.16. 已知平行四边形ABCD 的周长为28,对角线AC ,BD 相交于一点O ,且AOB ∆的周长比BOC ∆的周长大4,则AB = ,BC = ;17. 已知:如图,把一张矩形纸片ABCD 沿BD 对折,使C 点落在E 处且BE 与AD 相交于点O .写出一组相等的线段 (不包括CD AB =和BC AD =).18.一直角三角形的三边分别为2、3、x ,那么以x 为边长的正方形的面积为三、解答题19、计算:(每题6分,共24分)(1)(2))32)(532(+-(3)2)3223(+ (4)(20、(10分)如图,要从电线杆离地面8m处向地面拉一条长10m的电缆,求地面电缆固定点A到电线杆底部B的距离.CA B21、(10分)如图:在□ABCD中,∠BAD的平分线AE交DC于E,若∠DAE=25o,求∠C、∠B的度数。
2014八年级数学下期期中考试(新人教)
学校 班级 考号 姓名_________________试场号______________ 装订线内不要答题 ◆◆◆◆◆◆◆◆◆◆◆◆◆◆装◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆订◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆线◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆2013——2014学年度下期期中考试八年级数学试题一、选择题(每小题3分,共27分)1.下列各式成立的是……………………………………………………………【 】2-, B.C.D. 2=3( 2.x 的取值范围是………………………… 【 】 A. x ≥52 B. x ≤52 C. x ≥52- D. x ≤52- 3.计算的结果是……………………………………【 】. A . 32 B. 16 C. 8 D. 44. 甲、乙两艘客轮同时离开港口,航行的速度都是40m/min ,甲客轮用15min 到达A ,乙客轮用20min 到达B 。
若A ,B 两点的直线距离为1000m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向可能是…………………………………………………………【 】 A, 北偏西30° B, 南偏西30° C, 南偏东60° D, 南偏西60° 5.如图所示:在四边形ABCD 中,AB=1,BC=1,CD=2,,且∠ABC=90°则四边形ABCD 的面积是……………………………………………………………………………【 】A .2 B.121 D.12+6.如图所示,大正方形中有两个小正方形,如果它们的面积分别为1S 、2S ,那么1S 与2S 的大小关系………………………………………………………………………………………【 】 A .1S >2S B. 1S =2S C. 1S <2S D. 无法确定7.在周长为20cm 的平行四边形ABCD 中,AB ≠AD ,AC 、BD 相交于点O ,OE ⊥BD 交AD 于E ,则△ABE 的周长为………………………………………………………………………【 】 A .4cm B.6cm C.8cm D.10cm 8.如图,下列命题中,属于假命题的是【 】①两条对角线相等的四边形是矩形 ②两条对角线互相垂直的四边形是矩形③两条对角线互相垂直且相等的四边形是正方形④两条对角线互相平分的四边形是平行四边形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014年春季八年级第二学期期中数学试卷(卷Ⅰ)
(时间:120分钟 满分:150分)
一、填空题(本大题共8个小题;每小题4分,共32分.)
1.若分式1
x
x --有意义,则x 的取值范围是。
2. 若关于x 的分式方程1
-+x x
m =1的解为x =2,则m 的值为 。
3. 某种感冒病毒的直径是0.00000012米,用科学记数法表示为 米
4.函数k
y x
=的图象经过点(1,一2),则k 的值为 .
5.由于受台风的影响,一棵树在离地面6m 处折断,树顶落在离树干底部8m 处(如图2)则这棵树在折断前(不包括树根)的长度是 。
6.反比例函数y =x
k
(k>0)在第一象限内的图象如图3所示,点M 是图象上一点,MP
垂直x 轴于点P ,如果△MOP 的面积为1,那么k = .
7.如图4,在一条公路CD 的同一侧有A 、B 两个村庄,A 、B 与公路的距离AC 、BD 分别为50m 、70m ,且C 、D 两地相距50m ,若要在公路旁(在CD 上)建一个集贸市场(看作一个点),则A 、B 两村庄到集贸市场的距离之和最短是 m.
8. 直角三角形纸片的两直角边长分别为6,8,现将△ABC 如图5那样折叠,使点A 与点B 重合,折痕为DE ,则AE 的长为________.
二、选择题(本大题共8个小题;每小题4分,共32分)
9.在1x 、12、212x +、3x y +、1
a m
+中分式有( ).
A 、2个
B 、3个
C 、4个
D 、5个 10.把分式方程
21-y -y
y --21=1的两边同乘y-2,约去分母,得 ( ) A 、 1-(1-y )=1
B 、 1+(1-y )=1
C 、 1-(1-y )=y-2
D 、 1+(1-y )=y-2
11.如果1
12
--x x 的值为0,则x 的值为 ( )
A 、 0
B 、 1
C 、 -1
D 、 ±1
12.下面的函数是反比例函数的是( )
A 、31y x =+
B 、22y x x =+
C 、2x y =
D 、2y x
= 13.已知函数y =
x
k
的图象经过点(2,3),则下列说法正确的是 ( ) A 、点(-2,-3)一定在此函数的图象上。
B 、此函数的图象只在第一象限。
C 、y 随x 增大而增大。
D 、此函数与x 轴的交点的纵坐标为0。
14.如图6,点A 所表示的数是( )
A 、1.5
B 、3
C 、2
D 、5
15.已知△ABC 的三边长分别为5,13,12,则△ABC 的面积为( )
A 、30
B 、60
C 、 78
D 、 不能确定
16.函数
(
)在同一直角坐标系中的图象可能是( )
______________中学 班级___________
姓名___________ 座号
___________ 图5
图6
A. B. C. D.
x y
O y
y y x x
x
O O O
2014春季八年级第二学期期中数学试卷(卷Ⅱ)
一、 填空题(每题4分,共32分)
1. 2. 3. 4.
5. 6. 7. 8. 二、单选题(每题4分,共32分)
9. 10. 11. 12. 13. 14. 15. 16. 三、用心答一答(共86分)
17.(8分)化简:(-b a 23)2
÷(-b a 2)3²(2
b )2
18.(8分)解分式方程:23+x x +2
2
-x =3
19 (8分)先化简,再求值:11-+a a -122+-a a a ÷a
1
,其中a =3
20. (8分)如果y 与x+2成反比例,且x =4时,y =1.○1求y 与x 之间的函数关系式; ○
2当y =3时,求x 的值。
.
21.(10分 )你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y (单位:m )是面条的粗细(横截面积)x (单位:mm 2)的反比例函数,其图象如图所示. (1)写出y 与x 的函数关系式;
(2)若当面条的粗细应不小于1.6mm 2,面条的总长度最长是多少? (3)若面条的长度为50m ,那么面条的粗细程度为多少mm 2?
21题图
______________中学 班级___________ 姓名_____
______ 座号
_____
____
__
22. (10分)如图,四边形ABCD 中,AB=3,BC=4,CD=12,AD=13,且∠B=90°.求四边形ABCD 的面积。
23.(10分)在“情系汶川”捐款活动中,小明对甲、乙两班捐款情况进行了统计:甲班人数比乙班人数多3人,甲班共捐款2400元,乙班共捐款1800元,乙班平均每人捐款的钱数是甲班平均每人捐款钱数的5
4倍,求甲、乙两班各有多少人?
24(10分)如图,将一张边长AB=4cm ,AD=8cm 的长方形纸片ABCD 折叠,使点C 与点A 重合,则EB 的长是多少?
P
25.(14分)已知反比例函数图象过第二象限内的点A (-2,m ),
AB ⊥x 轴于B ,Rt △AOB 面积为3, 若直线y=ax+b 经过点A ,
的图象上另一点C (n ,—23
), 并且经过反比例函数
(1) 反比例函数的解析式为 ,m= ,n= ; (2) 求直线y=ax+b 的解析式;
(3) 在y 轴上是否存在一点P ,使△PAO 为等腰三角形,若存在,请直接写出P 点坐标,若不存在,说明理由。
x k
y =x k
y =。
