麻省理工学院公开课《微分方程》学习笔记全
数学分析知识点总结(微分方程)

2.7.微分方程初步2.7.1 概说涉及到量的变化率满足的制约关系,通常是含有导数的方程——微分方程。
简单例子:(1)放射性物质,在每一时刻t ,衰变的速率dm dt -(由于是减少,因此0dm dt<,速率为标量,是正值)正比于该放射性物质尚存的质量,因此质量应满足一下微分方程。
dmkm dt-= (2)质量为m 的物体自由落体,取坐标轴沿竖直方向指向地心,下落距离()y y t =应该满足牛顿第二定律F ma =,即22d ymg m dt=(3)质量为m 的跳伞员下落,所受空气阻力正比下降的速度,取坐标轴沿竖直方向指向地心,则t 时刻下降距离()y y t =满足22dy d y mg k m dt dt-=(1)如下图所示,钢球在以水平光滑杆上,受到弹力而来回整栋,原点位置为O ,钢球在t 时刻的坐标()x x t =满足微分方程()22d x kx m dt-=如果钢球还受到一个与速度成正比,方向与速度相反的阻尼力的作用,那么它所满足的微分方程是22dx d xkx h m dt dt--=总结:最简单的一阶微分方程是()dxf t dt= 其中t 是自变量,上述方程的一般解应该是()x f t dt C =+⎰最简单的n 阶方程()n nd xf t dt = 它等价于说11n n d xdt--是()f t 的原函数,即11()n n d xf t dt C dt --=+⎰则再次积分,一直积分下去得到111()(1)!n n n t x f t dtdt C C t C n --=++++-⎰⎰2.7.2 一阶线性微分方程考察下面的方程()()dxa t xb t dt+= 方程中有未知函数的一阶导数,且其一阶导数的系数为常数,其余部分未知函数最高层次数为一次,称为线性,上述方程为一阶线性微分方程。
如果()0a t =,则称为一阶线性常微分方程。
试着求解上述方程,方程两端都乘以()a t dte ⎰,得到()()()()()a t dta t dt a t dt dxe a t e x b t e dt⎰⎰⎰+= 即为下面的形式()()()()a t dta t dta t dt d e dxe x b t e dt dt ⎛⎫⎰ ⎪⎝⎭⎰⎰+=即()()()a t dta t dt d xeb t e dt⎛⎫⎰ ⎪⎝⎭⎰=于是有()()()a t dta t dtxe b t e dt C ⎰⎰=+⎰那么有()()()a t dt a t dt x e b t e dt C -⎛⎫⎰⎰=+ ⎪⎝⎭⎰ 这就是一阶线性微分方程的一般解。
高数下册笔记精

第七萃微分方程§ 1微分方程的根木概念一•根木概念:1.微分方程;凡表示未知函数,未知函数的导数与自变址之间的关系式称为微分方程.2•常微分方程;如果微分方程中的未知函数是一元函数,那么称此类方程为常微分方程.3•偏微分方程;如果微分方程中的未知函数是多元函数,那么称此类方程为偏微分方程.4.微分方程的阶;微分方程中所出现的未知函数的最商阶导数的阶数.就称为此微分方程的阶.5.微分方程的解;将某个函数代入到微分方程的左右两边可使其成为恒等式,那么就称此函数为此微分方程的解.6.微分方程的通解:如果微分方程的解中含有任总常数.并且任意常数的个数与微分方程的阶数相等.那么这样的解就称为此微分方程的通解.7.微分方程的初始条件与特解.8.微分方程的积分曲线:微分方程的解的图象是一条平面曲线.称此曲线为微分方程的积分曲线.二•例题分析P263. 5.写出由以下条件所确定的曲线所满足的微分方程:例1.曲线在点处(兀的切线的斜率等于该点横坐标的平方.解:设该曲线的方程为y = f(x),那么由題总得:y* = x2. ------------- 这就是所需确定的曲线应满足的微分方程.例2.曲线上点P(x, y)处的法线与X轴的交点为Q,且线段PQ被y轴平分.解:设该曲线的方程为y = 且设曲线在点P处的法线记为L.那么其斜率为一1/才:设法线L与Y轴的交点为点A,再设法线L上任总:一点M的坐标为进而得法线L的方程为:Y — y = k(X—x)且&=一1/〉「即y-y = -(X-x)/y':那么易求得:X Q=x+y・y‘且Y A = y + x/y l ........................ ①由題意知点A为线段P0的中点知:X Q+X P=2X A且命+"=2齐........................ ②由上述①.②两式最终可得:2x=y・y‘-------------- 这就是所需确定的曲线应满足的微分方程.§2.可别离变址的一阶微分方程(注:它是一类最易求解的微分方程!〕一・一阶微分方程的一般形式和一阶微分方程的对称形式:一般形式:F(x,”y) = Ou>对称形式:P(x. y)dx + Q(x. y)dy = 0二•何为可别离变址的一阶微分方程?如果某一阶微分方程由对称式:P(x.y)dx + Q(x. y)dy = 0 >可等价地转化为f(x)dx + g(y)dy = 0的形式,那么称原方程为可别离变虽的微分方程.三.可别离变量的一阶微分方程的根木解法:(可由如下两步來完成求解过程)第一步:进展自变址兀,dx与因变虽dy的左右别离:第二步方程两边同时作不定积分即可求得原方程的隐式通解.§3. —阶齐次微分方程(注:它是一类经变虽代换之后.可转化为"变址左右别离的一阶微分方程!)一・一阶齐次微分方程的定义:在某个一阶微分方^ — = /(兀刃中,如果方程右边的函数/(%, V)可写成丄的函数式即/(俎刃=0(上)・dx x x ....................... 高数下册辅导材料……徐松林版...........................也即丿京方程形如:© = 0(上),那么称此微分方程为一阶齐次微分方程.dx X二. 一阶齐次微分方程的根本解法:转化求解法——即首先将原一阶齐次微分方程转化为变址别离方程:然后再按变虽别离方程的解法去求解即可!具体地说.第一步,作变虽:代换令"=—,那么y = ux,— = u + x—•代入原一阶齐次微分方程© =卩(丄)得:it + x— =(p(u): x ” dxdx dx x dx第二步•进展变駅"与x的左右别离得: ----------- =—:(p(u)-u X第三步•两边求不定积分即可得其解・・・・三・例题分析参见P271.例1・又如.P276. 1. (4).求方程(%3 + y3)dx-3xy2dy = 0的通解.八dy X s + y3x2 y y dy duM:原方程可转化为3—= ——=—4■->作变虽代换令u = -.那么y = ux.— = u + x—,dx xy* 厂兀x dx dx那么原方程转化为:3(M+X—) = -V+H (注意:齐次方程在进展变虽代换之后.一定是可以进展变虽别离的!) dx irf J w紧接着就进展自变址与因变量的左右别离=>x—= —-2M =>上■上=—・最后两边作不定积分即可・・・dx ir 1-2M x § 4・一阶线性微分方程一. 一阶线性微分方程的定义:dy称形如:—+ P(x) v = Q(x)的方程为一阶线性微分方程.dx(注:因为方程的左边对未知函数y及其导数來说是一次线性组合的形式,所以称上述方程为”线性”方程!)dy(i)・QM = 0时,那么称— + P(x)y = 0为一阶线性齐次微分方程.dxdy(ii)・•、勺0(x)HO时,那么称— + p(x)y = QM为一阶线性非齐次微分方程.dx二. 一阶线性微分方程的解法(常数变易法是求解线性非齐次方程的根木方法)1.所谓的”常数变易法":就是为了求解某一阶线性非齐次方程,可先去求解与其所对应的齐次方程:然后在所得齐次方程的通解中.将任总常数C代换成一个待定的未知函数u(x)來构造生成非齐次方程的解:最后再将由此法构造生成的解,代回原非齐次方程中去确定那个待定函数"(X)的表达式. --------- 整个这样的求解过程就称为非齐次方程的常数变易法・(可参考P278 ■例1 )2.一阶线性微分方程:半+ P(x)y = 0(x)的通解公式如下:y = eT"M・[jQ(x)』"M〃x + c] ------------------- 请牢记!三•伯努利方程(注:它是一类经变址代换之后可转化为可别离变虽的一阶微分方程!)1・伯努利方程的定义dy我们称形如:— + PMy = Q(x)^y n.... (* )的方程为”伯努利方程”(或称” 〃级伯努利方程”).dx2・伯發利方程的解法(变址代换转化法)只要令z = 严,那么虫= (l —〃)yj •空.将其代入原川级伯努利方程(*)可得dx dx=> —+ (1 —x)”(x)・z = (1 —戸)・Q(x)——这是一个一阶线性非齐次方程!dx进而可由一阶线性非齐次方程的通解公式求出其解,这样也就求出原伯纺利方程(*)的解!3・变虽代换法在求解微分方程中的运用利用变虽代换(包括自变虽的变址代换和因变址的变虽代换),把一个微分方程转化为可别离变虽方程,或转化为一个其求解步骤的方程,这是解微分方程的常用方法.例1・解方程.P282. 9. (1). — = (X+y)2dx解:可令u = x+y9那么原方程转化为© = —-l = zr => —= w2 + l=>-^ = ^两边积分就可得其解…… dx dx dx ir+1例2. P282.9. (3)解方程xyy = y(In x + In y)解:可令"=Inx + In y = In小=> 小=e u两边关于自变量X求导得=> y +小‘=”仁—代入原方程得: dxue ll x~] =e l<• —=> MX"1=— => — = —两边枳分就可得其解.......dx dx u x§ 6・可降阶的商阶微分方程(木节着重学握三种容易降阶的岛阶微分方程的解法)一・)")=/(“)型微分方程------------ 这类尚阶微分方程的解法很简也,只要两边枳分"次,就可得其通解・二y^ = f(x,y r)型微分方程首先此方程y M = 的类型是二阶显微分方程,且此这类二阶显微分方程的特征是”不显含I対变虽y ”・此类方程的解法:运用变量代换进展降阶求解.具体地.可令/? = —,那么«< =仝.dx dx" dx进而原方程转化为:—= ----------------- 这是一个一阶显微分方程.根据其具体形式,可按前几节所介绍的求解一阶方程的dx解法去求解.....得其通解设为p =(p(x、C\ )又/? = —.也即有—=(p(x.q ) => dy =(p{x,c} )dx .最后只耍两边再作dx dx一次积分,就可得原二阶显微分方程的解.三・* = /(”)')型微分方程首先方程)严=f(y.y r)的类型也是二阶显微分方程,且此这类二阶显微分方程的特征是”不显含自伏I变虽兀“・dy d2y dp dp dy dp此类方程的解法:也是运用变址代换进展降阶求解.具体地.可令p = ——,那么一六=斗=斗•十=P•斗,进而原dx dx^ dx dy dx dy方程转化为P-—= f(y.p)一一这也是一个一阶显微分方程•根据其具体形式,可按前几节所介绍的求解一阶方程的解法dy、dy z dy去求解… 设得其通解为p =(p(y.c{)又/? = —>也即有一= 0(”q)=>必=—:一•最后只要两边再作一次积分, dx dx0(” C|)就可得原二阶显微分方程的解.四・例題分析P292. 1. (5)求解方程:=从而原方程的参数方y = |ln(l + /j2) + c2解:第一步:判定此方程的类型是二阶显微分方程且不显含因变Sy >即)』= 型.dy d^y dp dp接着可令厂矿那么京二矿进而原方程转化为:莎刁-这是-阶线性非齐次方斤4-p = X. dx由一阶线性非齐次方程的通解公式知:p = e『欣• [j*x•丿皿dx + c] = e x-[J A^^Z V + C]=-X + e2x + ce x :进而知:p = — = -x + e1' +ce x =>dy = {e2x +ce x-x)dx .最后只要两边再作一次积得原方程的通解••… dx五.微分方程的参数方程形式的隐式通解及其在有关问題中的运用所谓”微分方程的参数方程形式的隐式通解”就是将微分方程的通解用参数方程形式來刻画. 即将微分方程的自变址x 与因变虽y都表达成某个参数p的函数式的形式.例如:P292. 1. (4)求解方程:= l +解:首先判定此方程的类型是二阶显微分方程且不显变址X和y.它同屈y” =与y M = 所以解法相对由自.以下我们來介绍微分方程的参数方程形式的隐式通解给大家!先设/? = —.那么2 =—.进而原方程转化为:—=1 + /< => -化 =tZx=> [ 〃、- = f dx .dx dx^ dx dx 1 + jr J 1 + /?" J=> x = arctan /? + q ------ 这就求得了自变址x关于参数p的函数式:以下再來求出因变址y关干参数p的函数式.进而就可得原方程的参数方程形式的隐式通解.由p = — =>dy = pdx = "'P、,所以y = L In(l + 〃')+dx 1 + /广 2 ・x = arctan p + q注:运用同样的方法.大家可以尝试一下去求解P292. 1・(8): (9): (10).§7・商阶线性微分方程(主婆的是学习二阶线性微分方程的有关理论!)一. 二阶线性微分方程的定义:称形如:y1•+ PWy t+Q(x)y = f(x)…… (*)的方程为二阶线性微分方程.(注:方程的左边对未知函数y及其导数这三者來说,是一次线性组合形式!)⑴•'勺/(x) = 0时,那么称y"+P(x)y'+Q(x)y = 0为二阶线性齐次微分方程.(ii).当/WHO时,那么称y"+P(x)y'+Q(x)y = /(x)为二阶线性非齐次微分方程.二. 二阶线性微分方程的解的构造1・二阶线性齐次微分方程“解的磴加原理••定理1 :设y}W与儿匕)都是二阶线性齐次微分方程y M+ PMy9+Q(x)y = 0的解,那么此两解的任意线性组合y = q •(x) + c2・y2(x)也是此二阶线性齐次微分方程的解.---- 定理1提醜r齐次方程的解所满足的一种性质.此性质常称为齐次方程••解的腔加原理”・2・藝个函数间的线性相关性与线性无关性的定义(参见教材P296从略) 特别地,两个函数y\W与北(X)在区间I上线性相关O丄山=常数.Vxe I・3.二阶线性齐次微分方程的通解的构造定理2 :设”(x)与y2(x)是二阶线性齐次微分方程y ” + P(x)・y 4 Q(x)・y = 0的解•且牙(x)与y2(x)线性无关,那么此两解的任总线性组合y = c t・才(兀)+彳・)‘2(羽就是原二阶线性齐次微分方程的通解.---- 定理2提程了如何用齐次方程的两个线性无关的特解去构造生成齐次方程的通解!4・二阶线性非齐次微分方程通解的构造定理3:设y\x)是二阶线性非齐次微分方程y M+ P(x)y'+ Q(x)y = f(x)... (* )的一个特解.且Y(x)是对应的二阶线性齐次方程y"+P(x)y'+O(x)y = 0的通解,那么y=r(x) + /(x)就是原二阶线性非齐次微分方程(*) 的通解.---- 定理3提駁了如何用齐次方程的通解去构造非齐次方程的通解!即:非齐次通解y =齐次通解Y +非齐次特解y *・ 5・二阶线性非齐次微分方程解的磴加原理(P297定理4)定理4:设有二阶线性非齐次微分方程y,'+P(x)y'+Q(x)y = f(x),(其中/(x) = /(x) + /2(x).)而 (%)是y"+ P(x)y'+ QWy = f x(x)的特解,且y2(x)是y"+ P(x)y'+ Q(x)y = f2(x)的持解那么Y{x) = x(x) + y2(x)就是原二阶线性非齐次方程y"+ P(x)y'+Q(x)y = f(x)的一个特解.---- 定埋4提醜了如何去求非齐次方程特解的一种方法.它通常又称为非齐次方程解的叠加原理!6.定理5:设比(X)与〉,2(x)是二阶线性非齐次微分方程y "+P(x)y'+Q(x)y = /(x)... (*)的两个不相等的特解,那么Y(x) = y2(x) - y,(x)是对应的二阶线性齐次方程y"+ P(x)y'+ Q(x)y = 0的一个非零特解.---- 此定理提程了如何用二阶线性非齐次方程的二个特解去构造生成对应的齐次方程的特解!7 •例题分析P326. 1・(4). y}=\.y2=x,y3=x2是某二阶线性非齐次微分方程的三个解•试求该方程的通解?分析与解答:设此二阶线性非齐次微分方程为y"+ P(A-)y'+ Q(x)y = /(A)....(*),那么由定理3知:非齐次通解y =齐次通解Y +非齐次持解y* ,现由题意知”非齐次特解y* ”可取X =1」2 =匕儿=疋之中的任总:一个,故以下只要求出”齐次通解孑”來即可・再由定理2知:”齐次通解丫 "是两个线性无关的齐次持解的任意线性组合即:Y(X)= C}Y{M+ C2'Y2(X)(其中Y}{X\Y2(X)是两个线性无关的齐次持解).而现在又应如何來求得两个线性无关的齐次特解呢?这可根据”定理5 ”來得到!由"定理5”知,可令:y;(x)仝儿(力一儿(兀)三x-i且冬(无)兰儿co一x(x)三戸一1・且显然两者线性无关,所以原非齐次方程的通解为y = y(X)+ X(X)= C]・Y}(x) + C2 Y2(x) +儿(x) = q・(x — 1) + —•(妒一1) +1・三. 二阶线性非齐次微分方程的求解过程中的常数变易法与二阶线性非齐次微分方程的通解公式1・二阶线性非齐次微分方程求解过程中的”常数变易法11・为了求解二阶线性非齐次微分方程y1•+ PMy'+Q(x)y = /(%)..・(1 ),可先求解与之对应的齐次方程:第一步:先求得对应的二阶线性齐次微分方程+ P(x)y9+Q(x)y = O..・(2)的两个线性无关特解”(x)与儿(切・那么由定理2知:y = q・比(0 + 02・儿(%)•…(3)就是原二阶线性齐次微分方程(2)的通解:第二步:对齐次方程的通解(3 [作常数变豺去构造生成非齐次微分方程(1 )的解为y = M(X)・” (x) + v(x)・儿(兀)…(4)(其中u(x\v(x)是两个待定的未知函数h第三步:接下來将(4 )式代入原非齐次方程(1 )并设法去求出这样也就求出了原非齐次方程(1 )的解G 这就是二阶线性非齐次微分方程求解过程中的常数变易法.2・二阶线性非齐次微分方程的通解公式定理6・设y}(x)与"(X)是二阶线性齐次方程y n+P(x)y'+Q(x)y = O・・・・・(1)的两个线性无关的特解,记必/=刃儿H0 ■那么与之对应的二阶线性非齐次方程+ P(x)y l+Q(x)y = f(x)•• (2)31 ”有通解公式:y =)订罟1厶一)订耳亠仪.§ 8・常系数齐次线性微分方程(重点是卑握二阶线性常系数微分方程的有关理论!)一. 二阶线性常系数微分方程的定义:在二阶线性微分方程:y M+P(x)y*+C(x)y = O.... (1 )之中.(i).如果y;y的系数p(x\Q(x)都是常数,即(1)式成为y n+py l+qy = O(其中为常数),那么称其为二阶线性常系数微分方程:(门)・如果不全为常数,那么称y^+py'+gy = 0为二阶线性变系数微分方程.二. 二阶常系数齐线性微分方程y ,f4- py'+qy = 0的解法:(如下方法通常称为"特征根公式法”)第一步,写出原微分方程的特征方程r + pr + q = 09并求出此方程的二个特征根第二步•根据特征根斤卡的不同情形,原方程y"+py+qy = 0的通解公式如下:(i).假设特征根GE不相等,那么原方程的通解为:y = c/1V+cZ2X:(ii)・假设持征根G 3为相等,那么原方程的通解为y = (q + C2x)e r'x :假设特征根斤上为一对共純复根r} 2=a + i/3,那么原方程的通解为:y = - (q cos px + c2 sin px).三. 二阶常系数齐次线性微分方程y^+py'+qy = 0的求解举例:参见教材P301-305例1;例2;例3等.6 / 126 §9.常系数非齐次线性微分方程(重点只需掌握如下关于二阶线性常系数非齐次微分方程的通解公式!)....................... 高数下册辅导材料……徐松林版...........................一. 关于二阶线性常系数非齐次微分方程y"+py9+gy = fM (其中为常数)有如下结论:定理6J设y^x)与比(X)是二阶线性常系数非齐次微分方程y v+py9+qy = O••… 门)的两个线性无关的特解.记W = N "工° .那么与之对应的二阶线性非齐次方程)严+ py9+qy = f(x)••…(2 )有通解公式:--------------------------------------- 请记牢!------- 注:此定理6’只不过是第七节中介绍的"定理6 ”的一个特例而已!二. 常系数二阶非齐次线性微分方程求解举例例如P313.例2・求方程y”一5y'+6y = 的通解.解:由定理5’应首先求对应的齐次方程y”一5>「+6y = 0的通解•再运用定理5’來求原非齐次方程的通解.易知齐次方程y"一5y'+ 6y = 0的持征方程为r2-5r + 6 = 0,特征根斤=2,“ = 3.于是,齐次方程的两个线性无关的特解为X =纟",儿==> IV =" 儿=芒:・X >1、:— dx-e2x | "_、:— dx 进而原非齐次方程的通解为:y = yA丄亠dx一yJ - dx = /T"_■J W J W J e J e=> y = e'x (~xe~x - e~x + c J _ e2x (^x2 +c2) = d}e2x + d2e yx - * (A2 + jv)e".三. 木草朵例P327. 7.设有可导函数0(x)满足(P(x)cosx + 2£l(p(t)sin tdt = x +1.求(p(x) = ?分析与解答:这是一个”积分方程”,求解”积分方程”的思路:首先我们把它转化为一个与其对应的微分方程,再來求解.现由(p{x)cos x + 2£ 0(/)sin tdt = x + l两边关于自变虽X求导数得:(p\x) cos x一(p{x) sin x + 2(p(x) sin x = 1 => (p\x} cos x +(p(x) sin x = 1现记y = 0(x),那么有y*cosx +ysinx = l <=> y*+y tanx = secx——这是H一阶线性非齐次微分方程H・-fp(x)dr r \p(x}dx - lanxdx f Itan.vdr ,由通解公式得:y = e J -[I Q(x)-e J dx + c] = y = e J -[I sec x-e J dx + c] =sinx+c cosx ・又由条件(p{x)cos x + 2£(p(t)sin tdt = x +1 >l1 x = 0时.那么y = 0(O) = l,所以c = l・综上得原方程的解为:y = sin x + cos x・四. 综述”求解微分方程的一般程序“如下:第一步,判定方程的类型,它是一阶微分方程还是二阶微分方程?(我们知道标准求解步骤的一阶方程类型包括:①可别离变量方程:②齐次方程:③一阶线性(非)齐次方程:④贝努利方程):第二步•根据我们在木章所讲的各种方程的标准解法去求解!补充说明:如果方程类型是我们很陌生的形式.那么就首先考虑运用“变虽代换法”将其转化为我们所熟悉的方程类型:然后再按上面的标准步骤去解决问題.第八草空间解析几何....................... 高数下册辅导材料-•-…徐松林版..........................§ 1向虽及其线性运算一. 一些根本概念①向虽与自由向址;②讥位向虽与零向址;③向虽的共线与共面;④向虽的模,方向角,以及投影等.二. 向虽的加法运算与数乘运算的定义三•向虽的线性运算在空间直角坐标系下的表达借助干空间直角坐标系.向量间的线性运算可以转化为它们坐标之间的线性运算.§ 2向虽的数址积向址枳混合积一•两个向量的数量积1.数虽积的定义a-b=\a\-\b\cos0.(其中8为向虽方/之间的夹角)2.数址积与投影之间的关系------ a b =1 a I Pr j ./? =1 b I Pr3・数址积的运算规律二•两个向虽:的向址积1.向址积的定义axb=\a\-\b\sin 0,(其中&为向虽0,乙之间的夹角)2.向址枳的模的几何总义:它表示以向:sN乙为邻边所成的平行四边形的面枳.三. 三个向虽的混合枳1・混合枳的定义[adc]仝(“xZ?)・c2・三个混合积的模的几何意义:它表示以向虽a.b.c为邻边所成的平行六面体的"有向体积11・即[a,b9c] = s V; (i)当N恥呈右手系时,£ = 1: (ii)当a.b.c呈左手系时,£ = -\.§ 3曲面及其方程一.曲面方程的概念1.如果某曲而s上的点的坐标= v与某个三元方程F(x,y,z) = 0的解之间能构成一一对应,那么称这个三元方程F(x, y, z) = 0为此曲面s的方程;2.建立曲面方程的一般方法:首先在所求曲倆上任取一点M.记其坐标为M(x, y, z),然后利用该曲面的特征并将其等价地表达为点M(x, >\ z)的坐标应满足的条件式即可!例如:试求球心在点MoCxdy。
超详细MIT线性代数公开课笔记 完整版
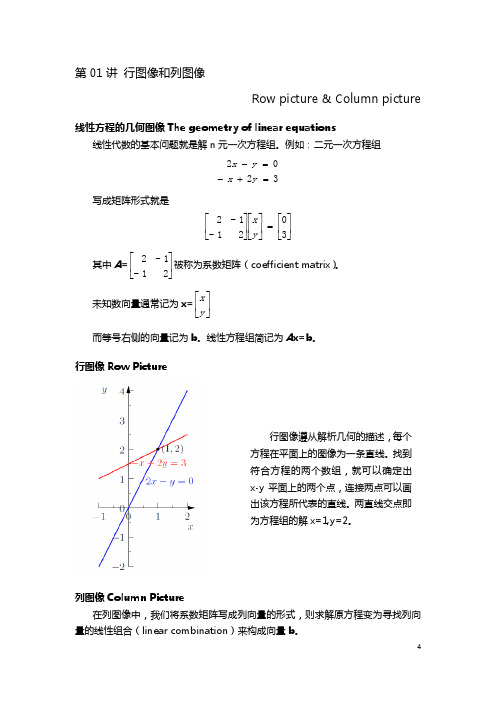
第三行: 0 0
1 2 关键第二行: -3 1 0 3 8 0 4
1 0 3 0 1 1 3 0 1 1 1
2 1 8 1 1 2 1 4 1 2 1 8 1 0 4 1 4 1 -3 [1 2 1] 1 [3 8 1] 0 2 2 0 [0 4 1] 1 2 1 1 0 2 0 4 1 E21A 1 2 1
1 2 1 1 2 1 1 2 1 (3,2) (2,1) A= 3 8 1 0 2 -2 U= 0 2 - 2 0 0 5 0 4 1 0 4 1
处在第二行第二列的主元二为 2,因此用第三行减去第二行的两倍进行消元, 得到第三个主元为 5。 , 矩阵 A 为可逆矩阵,消元结束后得到上三角阵 U(Uppertriangular matrix) 其左侧下半部分的元素均为 0,而主元 1,2,5 分列在 U 的对角线上。主元之积即行 列式的值。 需要说明的是, 主元不能为 0, 如果恰好消元至某行, 0 出现在了主元的位置上, 应当通过与下方一行进行“行交换”使得非零数字出现在主元位置上。如果 0 出现 在了主元位置上,并且下方没有对等位置为非 0 数字的行,则消元终止,并证明矩 阵 A 为不可逆矩阵,且线性方程组没有唯一解。
* * * 3 * * * 例如 * * * 4 3* 4 * 5* * * * 5 * * *
画图真不是 GS 的长项,在视频里画的就比较 shi,他自己也承认了。在课本里 他用两个面相交于一条直线画了一个图,然后让这条直线和第三个平面相交画了第 二个图。同样的事,y 一张图分分钟搞定。
mit一千多页的高等数学教材

mit一千多页的高等数学教材高等数学是大多数理工科学生必修的一门课程,也是培养学生数学思维和分析问题能力的重要课程。
而来自麻省理工学院(Massachusetts Institute of Technology,简称MIT)的一本高等数学教材,以其全面、深入的内容而闻名于世,被广大数学爱好者所喜爱和推崇。
这本教材共有一千多页,涉及了广泛的高等数学知识,为学习者提供了全面而丰富的学习资源。
这本高等数学教材从基础数学开始,包括了线性代数、微积分、常微分方程、偏微分方程等多个领域的知识。
它将这些知识分门别类地组织在一起,每个部分都有详细的讲解和丰富的例题,以帮助学生理解和掌握相关的数学概念和技巧。
在每个章节的开头,还会给出该章节的主要内容和学习目标,有助于学生了解自己的学习进度和方向。
这本教材的特点之一是其详细而准确的推导过程。
作者在书中给出了每个公式的推导和证明过程,这一特点使得学生能够更深入地理解数学原理,并且能够结合具体的例题进行实际应用。
此外,教材还提供了一些常用的数学工具和技巧,如积分表、微分方程的解法等,方便学生在解题过程中快速应用这些工具。
除了内容的深度和广度之外,教材还注重与实际应用的结合。
它将一些数学模型和问题与实际生活和科学领域相结合,展示了数学在各个领域的应用,激发了学生对数学的兴趣和学习的动力。
同时,教材中还会给出一些拓展的内容和练习题,以帮助学生深入理解和运用所学的数学知识。
在学习过程中,这本教材通常被视为一本参考书或者扩展阅读的资料。
学生可以根据自己的学习进度和兴趣,选择阅读相关章节和内容,进行系统的学习和实践。
教材的篇幅较长,但学生可以根据自己的需求来合理规划学习进度,有选择地学习教材中的部分内容。
总之,MIT出版的高等数学教材是一本权威且全面的学习资料,它具有丰富的内容和详细的讲解,为学习者提供了广泛的数学知识。
这本教材的出版不仅有利于学生打好数学基础,也为数学爱好者提供了一个系统学习高等数学的机会。
MIT公开课-线性代数笔记

目录方程组的几何解释 (2)矩阵消元 (3)乘法和逆矩阵 (4)A的LU分解 (6)转置-置换-向量空间R (8)求解AX=0:主变量,特解 (9)求解AX=b:可解性和解的解构 (10)线性相关性、基、维数 (11)四个基本子空间 (12)矩阵空间、秩1矩阵和小世界图 (13)图和网络 (14)正交向量与子空间 (15)子空间投影 (18)投影矩阵与最小二乘 (20)正交矩阵和Gram-Schmidt正交化 (21)特征值与特征向量 (27)对角化和A的幂 (28)微分方程和exp(At)(待处理) (29)对称矩阵与正定性 (29)正定矩阵与最小值 (31)相似矩阵和若尔当型(未完成) (32)奇异值分解(SVD) (33)线性变换及对应矩阵 (34)基变换和图像压缩 (36)NOTATIONp:projection vectorP:projection matrixe:error vectorP:permutation matrixT:transport signC(A):column spaceN(A):null spaceU:upper triangularL:lower triangularE:elimination matrixQ:orthogonal matrix, which means the column vectors are orthogonalE:elementary/elimination matrix, which always appears in the elimination of matrix N:null space matrix, the “solution matrix” of AX=0R:reduced matrix, which always appears in the triangular matrix, “IF00”I:identity matrixS:eigenvector matrixΛ:eigenvalue matrixC:cofactor matrix关于LINER ALGEBA名垂青史的分析方法:由具象到抽象,由二维到高维。
名校课堂——精选推荐

附录一VERYCD上目前已有的一些开放课程(1)麻省理工学院《麻省理工开放课程:微积分重点》(Highlights of Calculus)《麻省理工开放课程:单变量微积分》(Single Variable Calculus)《麻省理工开放课程:多变量微积分》(Multivariable Calculus)《麻省理工开放课程:微分方程》(Differential Equations,Spring,2004)《麻省理工开放课程:线性代数》(Linear Algebra)《麻省理工开放课程:经典力学》(Classical MEchanics)《麻省理工开放课程: 物理学I》(Physics I)《麻省理工开放课程:电磁学》(Electricity & Magnetism)《麻省理工开放课程: 振动与波》(Vibrations and Waves)《麻省理工开放课程:航天系统工程学》(Aircraft Systems Engineering)《麻省理工开放课程:算法导论》(Introduction to Algorithms)《麻省理工开放课程:计算机科学及编程导论》(MIT Introduction to Computer Science and Programming)《麻省理工开放课程:计算机程序设计与解释》(Structure and Interpretation of Comput er Programs)《麻省理工开放课程:固态化学导论》(Introduction to Solid State Chemistry)《麻省理工开放课程:生物学》(Biology)《麻省理工开放课程:生物学导论》(Introduction to Biology)《麻省理工开放课程:生物工程学导论》(Introduction to Bioengineering)《麻省理工开放课程:西方世界的爱情哲学》(Philosophy of Love in the Western World)《麻省理工开放课程:哥德尔,埃舍尔,巴赫:一次心灵太空漫游》(Gödel, Escher, Bac h: A Mental Space Odyssey)《麻省理工开放课程:建筑设计:地景中的建筑》(Architecture Studio : Building in Land scapes)《麻省理工开放课程:电影哲学》(Philosophy of Film)《麻省理工开放课程:艺术、科学和技术中的情感和想象》(Feeling and Imagination in Art, Science, and Technology)《麻省理工开放课程:心理学导论》(Introduction to Psychology)《麻省理工开放课程:西班牙语学习》(Learn Spanish)(2)斯坦福大学《斯坦福大学开放课程:编程范式》(Programming Paradigms )《斯坦福大学开放课程:抽象编程》(Programming Abstractions)《斯坦福大学开放课程:iPhone开发教程》(Phone Application Programming)《斯坦福大学开放课程:编程模式(C和C++)》(Introduction to Computer Science - Pro gramming Abstractions)《斯坦福大学开放课程:编程方法》(Programming Methodology)《斯坦福大学开放课程:人机交互研讨》(Human-Computer Interaction Seminar)《斯坦福大学开放课程:机器学习》(Engineering Everywhere - Machine Learning)《斯坦福大学开放课程:机器人学》(Introduction to robotics)《斯坦福大学开放课程:傅立叶变换及应用》(The Fourier Transform and Its Application s )《斯坦福大学开放课程:近现代物理专题课程-宇宙学》(Modern Physics - Cosmology)《斯坦福大学开放课程:近现代物理专题课程-经典力学》(Modern Physics - Classical Me chanics)《斯坦福大学开放课程:近现代物理专题课程-统计力学》(Modern Physics - Statistic Me chanics)[《斯坦福大学开放课程:近现代物理专题课程-量子力学》(Modern Physics - Quantum M echanics)《斯坦福大学开放课程:近现代物理专题课程-量子纠缠-part1》(Modern Physics - Quant um Entanglement, Part 1)《斯坦福大学开放课程:近现代物理专题课程-量子纠缠-part3》(Modern Physics - Quant um Entanglement, Part 3)《斯坦福大学开放课程:近现代物理专题课程-广义相对论》(Modern Physics - Einstein's Theory)《斯坦福大学开放课程:近现代物理专题课程-狭义相对论》(Modern Physics - Special Re lativ ity)《斯坦福大学开放课程:线性动力系统绪论》(Introduction to Linear Dynamical Systems)《斯坦福大学开放课程:经济学》(Economics)《斯坦福大学开放课程:商业领袖和企业家》(Business Leaders and Entrepreneurs)《斯坦福大学开放课程:法律学》(Law)《斯坦福大学开放课程:达尔文的遗产》(Darwin's Legacy)《斯坦福大学开放课程:人类健康的未来:七个颠覆你思想的演讲》(The Future of Huma n Health: 7 Very Short Talks That Will Blow Your Mind)《斯坦福大学开放课程:迷你医学课堂:医学、健康及科技前沿》(Mini Med School:Med icine, Human Health, and the Frontiers of Science)《斯坦福大学开放课程:迷你医学课堂:人类健康之动态》(Mini Med School : The Dyna mics of Human Health)(3)耶鲁大学《耶鲁大学开放课程:基础物理》(Fundamentals of Physics)《耶鲁大学开放课程:天体物理学之探索和争议》(Frontiers and Controversies in Astrop hysics)《耶鲁大学开放课程:新生有机化学》(Freshman Organic Chemistry )《耶鲁大学开放课程:生物医学工程探索》(Frontiers of Biomedical Engineering)《耶鲁大学开放课程:博弈论》(Game Theory)《耶鲁大学开放课程:金融市场》(Financial Markets )《耶鲁大学开放课程:文学理论导论》(Introduction to Theory of Literature )《耶鲁大学开放课程:现代诗歌》(Modern Poetry)《耶鲁大学开放课程:1945年后的美国小说》(The American Novel Since 1945)《耶鲁大学开放课程: 弥尔顿》(Milton)《耶鲁大学开放课程:欧洲文明》(European Civilization )《耶鲁大学开放课程:旧约全书导论》(Introduction to the Old Testament (Hebrew Bibl e) )《耶鲁大学开放课程:新约及其历史背景》(Introduction to New Testament History and Literature)《耶鲁大学开放课程:1871年后的法国》(France Since 1871)《耶鲁大学开放课程:古希腊历史简介》(Introduction to Ancient Greek History )《耶鲁大学开放课程:美国内战与重建,1845-1877》(The Civil War and Reconstruction Era,1845-1877)《耶鲁大学开放课程:全球人口增长问题》(Global Problems of Population Growth)《耶鲁大学开放课程:进化,生态和行为原理》(Principles of Evolution, Ecology, and Be havior )《耶鲁大学开放课程:哲学:死亡》(Philosophy:Death)《耶鲁大学开放课程:政治哲学导论》(Introduction to Political Philosophy)《耶鲁大学开放课程:有关食物的心理学,生物学和政治学》(The Psychology, Biology a nd Politics of Food)《耶鲁大学开放课程:心理学导论》(Introduction to Psychology)《耶鲁大学开放课程:罗马建筑》(Roman Architecture)《耶鲁大学开放课程:聆听音乐》(Listening to Music)(4)哈佛大学《哈佛大学开放课程:哈佛幸福课》(Positive Psychology at Harvard)《哈佛大学开放课程:公正:该如何做是好?》(Justice: What's the Right Thing to Do? )《哈佛大学开放课程:构设动态网站》(Building Dynamic Websites)(5)牛津大学《牛津大学开放课程:尼采的心灵与自然》(Nietzsche on Mind and Nature)《牛津大学开放课程:哲学概论》(General Philosophy)《牛津大学开放课程:哲学入门》(Philosophy for Beginners)《牛津大学开放课程:批判性推理入门》(Critical Reasoning for Beginners) (6)其它名校《普林斯顿大学开放课程:人性》(InnerCore)《普林斯顿大学开放课程:自由意志定理》(The Free Will Theorem)《剑桥大学开放课程:人类学》(Anthropology)《沃顿商学院开放课程:沃顿知识在线》(Knowledge@Wharton)《哥伦比亚大学开放课程:房地产金融学I》(Real Estate Finance I)附录二部分英美名校开放课程网站美国1. 麻省理工学院/index.htm2. 卡内基梅隆大学/openlearning/forstudents/freecourses3. 约翰霍普金斯大学彭博公共卫生学院/4. 斯坦福大学/5. 圣母大学/courselist6. 杜克大学法律中心的公共领域/cspd/lectures7. 哈佛医学院/public/8. 普林斯顿大学/main/index.php9. 耶鲁大学/10. 加州大学伯克利分校英国1. 牛津大学的文字资料馆2. Greshem学院/default.asp3. 格拉斯哥大学/downloads.html4. 萨里大学/Teaching/5. 诺丁汉大学/6. 剑桥大学播客/main/Podcasts.html 参考资料:/thread-42142-1-1.html。
MIT线性代数中文笔记
1.31
31. 线性变换及对应矩阵
1.32
32. 基变换和图像压缩
1.33
33. 复习三
1.34
34. 左右逆和伪逆
1.35
35. 期末复习
1.36
2
MIT 线性代数中文笔记
中文 Linear Algebra (线性代数) 笔记
ApacheCN 机器学习交流群 629470233 ApacheCN 学习资源
Contents (目录)
01. 方程组的几何解释 01.01 方程组的几何解释
02. 矩阵消元 02.01 矩阵消元
03. 乘法和逆矩阵 03.01 矩阵乘法和逆矩阵
04. A的LU分解 04.01 A的LU分解
05. 转置-置换-向量空间R
3
MIT 线性代数中文笔记
05.01 矩阵转置 05.02 置换 05.03 向量空间 R 06. 列空间和零空间 06.01 列空间 06.02 零空间 07. 求解Ax=0:主变量,特解 07.01 主变量 07.02 特解 08. 求解Ax=b:可解性和解的结构 08.01 可解性 08.02 解的结构 09. 线性相关性、基、维数 09.01 线性相关性 09.02 基 09.03 维数 10. 四个基本子空间 10.01 基本子空间 10.02 四个基本子空间 11. 矩阵空间、秩1矩阵和小世界图 11.01 矩阵空间 11.02 秩1矩阵 11.03 小世界图 12. 图和网络 12.01 图 12.02 网络 13. 复习一 13.01 复习一 14. 正交向量与子空间 14.01 正交向量 14.02 子空间 15. 子空间投影 15.01 子空间投影 16. 投影矩阵和最小二乘 16.01 投影矩阵 16.02 最小二乘 17. 正交矩阵和Gram-Schmidt正交化 17.01 正交矩阵 17.02 Gram-Schmidt正交化 18. 行列式及其性质
《微分方程 》课件
解法
通过迭代法、几何法、幂级数展开法等方法求 解。
应用
在解决实际问题时,很多情况下会遇到非线性微分方程,因此其应用非常广泛 。
一阶常系数线性微分方程
定义
形如y'=a*x+by' = a x + by′=a×x+by' = ax+b的一 阶微分方程称为一阶常系数线性微分方程。
解法
通过解特征方程、使用常数变易法和公式法等方法求 解。
形如 y'' = f(x, y, y') 的微分方程称为二阶非 线性微分方程。
解法
通常需要使用迭代法、分离变量法等技巧求 解。
性质
解的形式较为复杂,通常需要具体分析。
二阶常系数线性微分方程
定义
01
形如 y'' + py' + qy = 0 的微分方程称为二阶常系数线性微分
方程。
解法
02
通过求解对应的特征方程,得到通解。
性质
03
解的形式由方程的系数和初值条件决定,且具有特定的对称性
和周期性。方程
1 2 3
定义
高阶线性微分方程是形如y(n)=f(x)的方程,其中 y(n)表示y的n阶导数,f(x)是x的已知函数。
求解方法
通过变量代换和降阶法,将高阶线性微分方程转 化为较低阶的微分方程或常微分方程,然后求解 。
应用
在物理、工程等领域有广泛应用,如振动问题、电路 分析等。
03
二阶微分方程
二阶线性微分方程
定义
形如 y'' + p(x)y' + q(x)y = f(x) 的微分方程 称为二阶线性微分方程。
ode复习资料
ode复习资料ODE 复习资料ODE(Ordinary Differential Equations,常微分方程)是数学中的一个重要分支,研究的是描述自然界中变化现象的方程。
它在物理学、工程学、生物学等领域都有广泛的应用。
对于学习ODE的同学来说,复习资料是非常重要的辅助工具。
本文将介绍一些常见的ODE复习资料,并提供一些学习建议。
一、经典教材1. 《常微分方程教程》(作者:丁同仁):这是一本经典的ODE教材,内容全面、系统,适合初学者。
书中深入浅出地介绍了ODE的基本概念、解法和应用,配有大量的例题和习题,有助于读者理解和巩固知识。
2. 《常微分方程教程》(作者:谢金星):这本教材是国内外ODE教学的重要参考书之一。
作者结合自己多年的教学经验,将复杂的理论问题简化为易于理解的形式,让读者能够迅速掌握ODE的基本概念和解法。
3. 《Ordinary Differential Equations》(作者:Vladimir I. Arnold):这是一本经典的英文教材,被誉为ODE领域的圣经。
书中内容丰富,涵盖了ODE的各个方面,包括基本理论、解的存在唯一性、稳定性等。
虽然是英文教材,但对于有一定数学基础的同学来说,是一本不可多得的学习资料。
二、在线课程1. Coursera:Coursera是一个知名的在线教育平台,提供了许多优质的ODE课程。
例如,由加州大学洛杉矶分校(UCLA)开设的《Ordinary Differential Equations for Engineers》课程,介绍了ODE的基本概念和解法,并通过实例讲解了ODE在工程领域的应用。
2. MIT OpenCourseWare:麻省理工学院的开放课程平台提供了许多免费的ODE课程资料。
例如,他们的《Differential Equations》课程包括了从ODE的基本概念到高级应用的内容,让学习者能够全面掌握ODE的知识。
三、学习建议1. 理论与实践结合:ODE是一门理论与实践相结合的学科,理论只有通过实际问题的解析才能更好地理解。
MIT公开课:单变量微积分讲义unit1(1~7)
Lecture 1
18.01 Fall 2006
Unit 1: Derivatives
A. What is a derivative?
• Geometric interpretation • Physical interpretation • Important for any measurement (economics, political science, finance, physics, etc.)
Lecture 1: Derivatives, Slope, Velocity, and Rate of Change
Geometric Viewpoint on Derivatives
y
Q Secant line P f(x) x0 x0+∆x Tangent line
Figure 1: A function with secant and tangent lines The derivative is the slope of the line tangent to the graph of f (x). But what is a tangent line, exactly? 1
Δx→0
n times
lim
Δy = nxn−1 Δx
Therefore,
d n x = nxn−1 dx This result extends to polynomials. For example, d 2 (x + 3x10 ) = 2x + 30x9 dx
Physical Interpretation of Derivatives
Area = 1 1
(2y0 )(2x0 ) = 2x0 y0 = 2x0 ( ) = 2 (see Fig. 5) 2 x0
