十杆桁架结构优化设计
舞台桁架结构的优化设计分析

舞台桁架结构的优化设计分析摘要:随着市场经济的发展以及工业化进程的加快,剧场演出的数量越来越多,规模也越来越大。
为了保证演出的安全性,可以将桁架结构应用在演出舞台搭建当中,而桁架结构不仅能够提高舞台的质量,还具有跨度大、成本低等特点,因此需要对舞台搭建中桁架结构的应用进行深入研究。
本文将对舞台搭建中桁架结构的优化设计进行简析。
关键词:舞台搭建;桁架结构;优化设计桁架结构是当前常用的一种梁式结构,具有结构布置灵活、抗弯性强、抗剪性强、应用范围广泛等特点。
将桁架结构应用在舞台搭建当中能够有效增强舞台的抗剪性、抗压性,有利于提高舞台的质量。
但是当前舞台搭建企业在应用桁架结构时还存在一些问题,需要不断对桁架结构进行优化设计才能够充分发挥桁架结构的作用。
1 舞台搭建中的桁架结构桁架结构是一种梁式结构,其中桁架是指桁架梁,也被称为屋架,比較适用于跨度较大的展览馆、厂房等建筑当中。
桁架结构的布置比较灵活,无论是抗弯性能还是抗剪性能都比较强,因此适用于各种跨度的建筑。
按照桁架的外形,可将桁架结构分为平行弦桁架、折弦桁架以及三角形桁架;按照桁架的几何组成方式可将桁架结构分为简单桁架、联合桁架以及复杂桁架;按照所受水平推力的不同可将桁架结构分为无推力的梁式桁架以及有推力的拱式桁架[1]。
桁架的外形不同,对杆件内力分布的影响也不同,比如说平行弦桁架弦杆的内力是由中间向两端逐渐减少的,而三角形桁架弦杆的内力则是由中间向两端逐渐增加的。
当前在实际演出过程中,舞台搭建的内部空间较大,受临时场地环境的影响,结构复杂,由于演出对光线等情况的要求,所以在实际的舞台搭建桁架结构施工过程中,对施工技术的要求也比较高,舞台桁架主要是为了支撑舞台的(如下图),在经过专业力学测试的情况下,舞台承重结构满足实际需求,所搭建起来的舞台稳定性都很好,同时也可以搭建成后台影视墙和顶层支架,可以悬挂背景布、灯光和音响。
舞台桁架结构2 舞台搭建中桁架结构的优化设计2.1 根据工程情况进行优化工程建筑企业必须根据舞台搭建工程的具体情况对桁架结构进行优化设计,只有这样才能够让桁架结构更符合舞台搭建的实际需要。
桁架机构的优化设计

空间桁架结构是将杆件按一定规律布置,通过节点连接瓤成的一种抒系结构,具有经济、跨越能力大以及形式活泼新颖等优点n3.由于是空间超静定结构,力学分析和结构设计都较为复杂,采用计算机辕韵优化设计,对减轻结构重遗、降低缕构造徐有饕重要意义.在桁架结构中根据锫杆件的受力,合理选择杆件截丽尺寸,使其在满足多种约束条件的前提下最大限凌缝承受骜载,就可以达裂减轻结构重量、降低结构造价的目的桁架结构优化问题可以表述如下:以雄杆桁架结构系统蠹研究对象,该系统基本参数<包括弹性模量、材料密度、最大容许应力、最大允许位移等)已知;问题是在给定的荷载条件下,确定桁架的最优截瑟瑟积,使结搀夔量最轻。
设各杆截面积为设计变量:工=[x 1,x 2,...,X n ]T ,目标函数可写为:min ʃ(x)= ρn i =1x t L i ; 约束包括:σt ≤σt a (i 一1,2,⋯,刀)“μj ≤μj a “; (j=1,2,⋯,n)A min ≤x t ≤A max (i=1,2,⋯,n)式中:x t 为第i 杆件的截面面积,L t 为第i 杆件的长度,ρ为材料密度,σt 、σt a 分别为第i 杆的应力和允许应力,μj 、μj a ;分别为第J 节点的位移和位移限值,A min 、A max ;分别为杆件截面积的上、下限.桁架与框架同属于杆系结构,在结构工程、工民建等有着广泛的应用,是常见但又 重要的结构形式。
杆系结构的失效模式很多,其中有代表性的是结构的整体和局部届曲 失稳。
随着设计和施工水平的不断进步,杆系结构正向着大跨度、轻柔化的方向发展, 因此对结构稳定性的要求越来越高,需要准确的稳定性理论分析和数值计算方法。
桁架结构的稳定性理论已有两种:几何非线性特征值稳定性理论和几何非线性临界 点理论。
其中几何非线性特征值稳定性理论出现的最早。
国内外的许多学者们一直沿用 这个理论来解决整体稳定性问题。
但是,近些年来,人们发现,用这套稳定性理论时会 出现一些问题,比如应力过高,有时甚至会超过材料的许用应力.结构在整体失稳之前 已经局部欧拉失稳或发生材料屈服。
桁架杆机构的优化设计

OCCUPATION2013 08108案例CASES桁架杆机构的优化设计文/宋育红摘 要:桁架结构优化设计中普遍存在约束的作用,现有优化设计一般采用满应力法、遗传优化或直接实验法搜索等优化方法,但其时间周期长、优化复杂。
本文主要采用复合形法,建立了桁架结构优化设计的数学模型,利用Fortran优化程序对其进行优化并获得最优解。
关键词:桁架结构 优化设计 复合形法一、优化目标及设计原则1.优化目标在工程力学教学当中,笔者利用复合形法对桁架杆进行优化设计,以求得到其最优解。
桁架杆设计的优化可以选择多种目标,如尺寸最小、质量最轻、强度最高等,一般应根据不同的需要选定。
笔者以桁架杆为例,以其质量最小为优化目标。
2.设计原则在桁架杆设计时我们首先要求两杆同时满足强度条件,其次要满足几何条件约束,进而确定目标函数,并对其优化。
二、复合形法优化设计简述复合形法的基本思路是在n 维空间的可行域中选取K 个设计点(通常取n +1≤K ≤2n )作为初始复合形(多面体)的顶点。
然后比较复合形各顶点目标函数的大小,其中把目标函数值最大的点作为坏点,以坏点之外其余各点的中心为映射中心,寻找坏点的映射点。
一般说来,此映射点的目标函数值总是小于坏点的,也就是说映射点优于坏点。
这时,以映射点替换坏点与原复合形除坏点之外其余各点构成K 个顶点的新的复合形。
如此反复迭代计算,在可行域中不断以目标函数值低的新点代替目标函数值最大的坏点从而构成新复合形,使复合形不断向最优点移动和收缩,直至收缩到复合形的各顶点与其形心非常接近、满足迭代精度要求时为止。
最后输出复合形各顶点中的目标函数值最小的顶点作为近似最优点。
三、建立数学模型1.已知参数如桁架杆的结构,已知l =2m,x B =1m,载荷ρ=100kN桁架材料的密度 ρ=7.5×10-5N/mm 3,许用拉应力[σ+ ]=150MPa,许用压应力[σ- ]=100MPa,y B 的范围为:0.5m≤y B ≤1.5m,求桁架杆在满足强度的条件下,其质量的最小值。
桁架结构优化设计
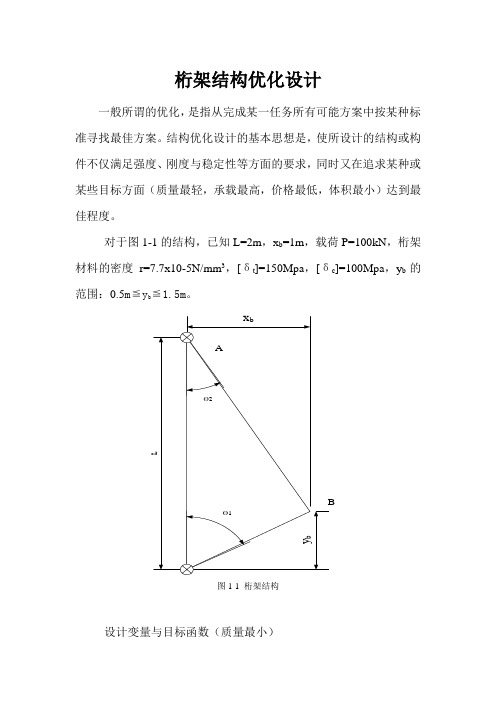
桁架结构优化设计一般所谓的优化,是指从完成某一任务所有可能方案中按某种标准寻找最佳方案。
结构优化设计的基本思想是,使所设计的结构或构件不仅满足强度、刚度与稳定性等方面的要求,同时又在追求某种或某些目标方面(质量最轻,承载最高,价格最低,体积最小)达到最佳程度。
对于图1-1的结构,已知L=2m,x b=1m,载荷P=100kN,桁架材料的密度r=7.7x10-5N/mm3,[δt]=150Mpa,[δc]=100Mpa,y b的范围:0.5m≦y b≦1.5m。
图1-1 桁架结构设计变量与目标函数(质量最小)预定参数(设计中已确定,设计者不能任意修改的量):L , x b ,P ,r ,[δt ] ,[δc ]设计变量(可由设计者调整的量)y b ,A 1,A 2 约束条件(对设计变量的约束条件) (1) 强度条件约束(截面、杆件的强度) (2) 几何条件约束(B 点的高度范围) 目标函数:桁架的质量W (最小)解:1. 应力分析0sin sin 02112=--=∑θθN N F x0cos cos 02112=---=∑P N N Fyθθ由此得:)sin(sin 2111θθθ+=p N )sin(sin 2122θθθ+-=p N由正弦定理得:ly l x pN B B 21)(2-+=ly x pN BB 222+=由此得杆1和2横截面上的正应力121)(2lA y l x pB B -+=σ2222lA y x pB B +=σ2.最轻质量设计目标函数(桁架的质量)))((222122B B y x A y l x A W B B ++-+=γ(1-1)约束条件[][]⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧≤+≤-+c B t B lA y x p lA y l x p B B σσ221222)( (1-2)0.5≦y b ≦1.5(m ) (1-3) (于是问题归结为:在满足上述约束条件下,确定设计变量y b ,A 1,A 2,使目标函数W 最小。
钢桁架桥的设计与优化

钢桁架桥的设计与优化钢桁架桥是一种常见且重要的桥梁结构形式,其以其高度的强度和耐久性而被广泛应用于现代交通建设。
设计和优化钢桁架桥的过程是一个综合性的工程,需要考虑多种因素并做出合理权衡。
本文将探讨钢桁架桥的设计和优化过程,并介绍一些相关的技术和方法。
首先,设计钢桁架桥时需要考虑的一个重要因素是桥梁的结构强度。
钢桁架桥需要能够承受车辆和行人的荷载,并保证桥梁的稳定和安全运行。
设计师通常会使用结构力学和有限元分析等方法来计算和评估桥梁的结构强度,并确保其满足工程要求。
同时,设计师还应考虑桥梁在不同环境条件下的稳定性和可靠性,如地震和风荷载等。
其次,钢桁架桥的设计过程还需要考虑到桥梁的美观性和可持续性。
作为城市交通建设的重要组成部分,钢桁架桥的外观设计应与周围环境相协调,并具备一定的艺术价值。
同时,设计师还应采用可持续材料和技术来减少桥梁的环境影响,如使用高强度钢材和节能设计等。
此外,钢桁架桥的优化也是设计过程中的一个重要环节。
通过优化设计,可以改善桥梁的结构性能、减少材料的使用量和降低工程成本。
一种常见的优化方法是拟合和调整钢桁架的形状和尺寸,以实现最佳的结构效果。
此外,优化还可以通过改进桥梁的抗震性能和减少桥梁的自重来提高桥梁的性能。
在设计和优化钢桁架桥时,还需要考虑到桥梁施工和维护的可行性。
设计师应该选择合适的施工方法和工艺,以确保桥梁能够按照设计要求安全、高效地建设。
此外,桥梁的维护和保养也是一个重要的方面,设计师应考虑到桥梁的维修和检查的便利性,并采用合理的方法和技术来延长桥梁的使用寿命。
总结来说,钢桁架桥的设计和优化是一个复杂且综合性的工程,需要考虑多个因素并做出合理的决策。
设计师应该熟悉相关的技术和方法,并具备一定的工程实践经验。
通过合理的设计和优化,可以创建出结构稳定、美观实用且具备可持续性的钢桁架桥,为城市交通建设提供有效的支持。
桁架结构形状与尺寸组合优化

截面均按满应力设计。由于上弦杆受压,局部稳定约
束引起上弦杆截面成倍增大,结构重量发生巨大变
化(&’+, )。
图" 桁架简支桥的初始设计
图* 简支桁架桥优化设计结果
表& 桁架简支桥优化设计结果
!!!!!!!!!!!!!!!!!!!!!
无局部稳定约束
节点
",&/ ),&+ +,&) /,&"
方法的有效性通过二个算例得到证实。
关键词:形状与尺寸优化;灵敏度分析;桁架结构优化设计
中图分类号:2#/);34#)#
!引 言
文献标识码: 5 计变量,然后再进行优化。文献[/]采用凸规划法同 时优化两类变量。本文提出一种渐进优化方法,按
设计变量的性质构造两个子空间,用满应力法确定
桁架结构形状与尺寸组合优化,即同时优化结 截面的最小尺寸,以满足单元应力和局部稳定约束
第 !" 卷 第 # 期
应用力学学报
$%&’!" (%’#
)**)年"月
!"#$%&%’()*$+,(-+..,#%/ 0%!"+$#!&
+,-’)**)
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
文章编号:!***./"#"()**))*#.**0).*1
两种情况:(&)不考虑局部稳定约束;(!)考虑局部 稳定约束。
桁架桥的优化 设 计 见 图 *,重 量 变 化 过 程 见 图 ),优化设计结果见表&。上弦近似抛物线,类似于简 支梁弯距分布。两种情况的结构重量分别为 )’(+%& 和 &’)(!%&。不考虑局部稳定约束时,结构重量稳步 减小;而考虑局部稳定约束时,结构重量振荡减小。
舞台桁架结构的优化设计分析

舞台桁架结构的优化设计分析舞台桁架结构是舞台搭建中的重要组成部分,它承载着舞台上的各种装置和设备,起到支撑和固定的作用。
在舞台设计中,桁架结构的优化设计是非常重要的,可以提高舞台的安全性和稳定性,同时也可以减少材料的使用量,降低成本。
本文将对舞台桁架结构的优化设计进行分析,探讨如何在保证舞台安全的前提下实现材料的节约和效益的最大化。
一、舞台桁架结构的构成和功能舞台桁架结构通常由立柱、横向梁和斜杆组成,它们共同构成了一个稳定的支撑系统,承载着舞台上的各种设备和装置。
立柱支撑着整个桁架结构的重量,横向梁则起到了连接和支撑的作用,而斜杆则增强了结构的稳定性和承载能力。
这些部件在舞台搭建过程中是紧密相连的,构成了一个整体的支撑系统。
二、舞台桁架结构的优化设计方法1. 选材优化在舞台桁架结构的设计中,选材是非常重要的一环。
选择合适的材料不仅可以达到承载要求,还可以降低材料成本和重量,提高结构的使用寿命。
在选材时,需要考虑材料的强度、刚度、耐腐蚀性、重量等因素,以及材料的可加工性和可维护性。
根据舞台桁架结构的实际需求和使用环境,选择合适的材料,如钢材、铝合金等,进行优化设计。
2. 结构优化舞台桁架结构的优化设计还包括对结构的优化布局和连接方式的设计。
通过合理的结构布局和连接方式,可以提高结构的承载能力和稳定性,减少结构的自重,增加整体结构的安全性和稳固性。
在设计中,可以采用一些新颖的设计理念和技术,如空间桁架结构、三维结构等,来实现结构的优化设计和目标的实现。
3. 节能减排在舞台桁架结构的设计中,还需要考虑节能减排和环保要求。
可以通过合理的设计和材料选择,减少结构的自重,降低能源消耗,减少二氧化碳的排放。
还可以考虑结构的再利用和循环利用,减少对自然资源的消耗,降低对环境的影响,实现舞台桁架结构设计的可持续发展。
以某大型室内演出场馆的舞台桁架结构为例,进行优化设计分析。
该场馆的舞台桁架结构由钢材组成,包括立柱、横向梁和斜杆,用于支撑舞台上的吊装设备和装置。
结合可靠性的桁架结构形状与尺寸组合优化设计

法, 并且优化结果满 足可靠度 的要 求。
2 . 1 统 一 设 计 变 量
0 前
言
本 文通 过设 计变 量 的数 学变 换 ,将两类 不 同量纲 的设 计变量转换 为同一性 质的无量纲设 计变量。具体方法如 下 :
结 构优化的 目的是得 到满 足结 构要求 ,并且 保证结 构 安 全的荷载较轻或 者费 用较 低 的结 构 。桁 架结 构最 优形状 受 到构件截面 尺寸 的影 响 ,同样 ,结 构最 优尺 寸也受 到桁
式中 ,x 为设计 变量 ;y为随 机变 量 ;W 为 目标 函数 ,
为e 单元的弹性矩阵和几何矩阵;n 为结构单元数量。
将公式 ( 1 0 ) 两 端对 设计 变量 A j 求导 ,可得单 元对第 i
个设计 变量的灵敏度为 :
它代表结构的质量 ;P 为密度 ;L为杆件 长度 ;A为截面 尺 寸; 、 、 r O , - 分别 为 i 号杆的应力 、 拉伸容许应力 、 压缩容许
构可靠性优 化 的难 度要 大得 多 ,所 以 ,目前 大部分 工作 集 中于基于单元 可靠 性的结构尺寸优化设计 。 本文 提出了一种结 合可 靠性 的桁架 结构 形状 与尺 寸组
式 中, 置、 置 和x 分 别为设计 变量 、 设计变量 的下 限值 和
上限值 。 由公式 ( 6 )可得 :
≤ ≤ …( i= 1 , n )
( 3 )
≤ ‘
( 4 )
{ } =[ D ] 。 [ ] 。 { “ } 。 ( e=1 , 2 …n )
( 1 O )
卢[ C ( x , Y )≤0 ]≥ ‘
( 5 )
式 中,[ u ] 为 e单元 结点位 移列阵 ;[ D] 。 、 [ B] 分别
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题目:十杆桁架结构优化设计日期:2013.09.16目录1设计题目 (1)2设计过程 (2)2.1一、运用Abaqus求解各杆轴力应力 (2)2.1.1Abaqus计算流程 (2)2.1.2结果 (3)2.2二、利用材料力学知识求解 (4)2.2.1基本思路 (4)2.2.2解题过程 (4)2.2.3结果 (5)2.3三、编写有限元程序求解 (6)2.3.1程序基本步骤 (6)2.3.2Vs2012 中重要的程序段 (6)2.3.3程序输出文件 (9)2.3.4材料力学、有限元程序、Abaqus结果比较 (10)2.4四、装配应力计算 (11)2.4.1处理技巧 (11)2.4.2Abaqus处理技巧 (11)2.4.3不加外力(P1,P2,P3)时材力,Ansys与Abaqus结果 (12)2.4.4不加外力(P1,P2,P3)时材力,Ansys与Abaqus误差分析 (12)2.4.5加外力(P1,P2,P3)时 Ansys与Abaqus结果 (12)2.5五、优化设计 (14)2.5.1设计中变量的概念 (14)2.5.2优化步骤运用VS2012编写复合形法进行约束优化。
(14)2.5.3VS2012优化程序 (16)2.5.4优化结果 (20)2.5.5结果说明 (20)3设计感想 (20)4备注 (20)4.1参考书目 (20)4.2说明 (20)十字桁架结构优化设计现有十字桁架结构见图1,材料泊松比为0.3,E=2.1e11,密度为7.8×103kg/m3, 许用应力为160Mpa,P1=600k N ,P2=900k N ,P3=600k N,杆1-6面积为A1=0.03m2,杆7-10面积为A2=0.02m。
1、利用Abaqus计算各杆的应力;2、利用材料力学的知识求解,并与1计算出的结果做比较;3、编写有限元程序求解,与1和2计算结果进行比较;4、若杆5制作时短了0.001m,试求各杆的应力;5、若令2节点的位移小于0.005m,A1、A2为0.005~0.05m2,试对结构进行优化,使其重量最小。
(同材料力学优化结果比较)。
图1十杆桁架2.1 一、运用Abaqus 求解各杆轴力应力利用Abaqus 求解,十字桁架结构可用2Dtruss 单元模拟。
单元参数为:弹性模量112.110E Pa =⨯,1-6杆截面面积210.03A m =,7-10杆截面面积220.02A m =。
加载求解输出各杆应力,结点位移。
2.1.1 Abaqus 计算流程Part:创建part trussmain,part45l,part45r,part trussmain,包涵除8,10杆外的所有杆,part45l 包涵8杆,part45r 包涵10杆。
Property :create Material:Elastic: 弹性模量112.110E Pa =⨯,泊松比0.3Create Section :beam\Truss :Section A1,截面面积30000。
Section A2,截面面积20000。
并给各杆赋材料属性。
Assembly :组装part trussmain,part45l,part45r 。
Step:创建一个分析步,step1。
Interaction:用Tie把part trussmain,part45l,part45r,绑定。
Load: create load:5,6点加铰接约束,固定x,y方向位移。
Create boundary Condition:2,4点加相应力。
Mesh:划分网格,一个杆为一个单元。
Element tape,选trussJob:创建一个job,Write Input,Data Check,Submit,通过Result来查看应力云图。
2.1.2结果图 2Abaqus各杆应力云图2.2 二、利用材料力学知识求解 2.2.1 基本思路显然题目中的十字桁架结构是两次静不定问题。
对于一次静不定问题,材料力学给出了两类解法:①去掉约束加力,找位移协调关系解题;②力则方程求解。
对于多次静不定,特别是上述桁架问题,找出其协调关系基本上是不可能的,而力则方程更适合于解这种结构。
如图3所示,去掉多余约束,建立力则方程:2.2.2 解题过程分别求出外力作用下各杆力和单位力作用下的各杆力,为计算方便,将其结果列入下表1中。
应用莫尔积分定理有:杆号 L P1 P2 P3 Fi1 Fi21 a 0 -2P2 0 1 -12 a 0 0 0 0 13 a 1P P2 P3 1 -14 a 0 P2 P3 0 15 a 0 0 0 1 06 a 0 0 0 0 17 2a 21P - 0 02- 2 8 2a 0 2P2 0 2-2 9 2a 0 2P2- 0 02- 10 2a 0 0 0 02- 11111221P11P21P322112222P12P22P3=0=0X X X X δδδδ∆=++∆+∆+∆⎧⎨∆=++∆+∆+∆⎩图 3 去多余约束2.2.3结果杆号轴力F(N) 应力S(MPa)1 1580569 52.672 347433.1 11.583 -1119431 -37.314 47433 1.585 128002.1 4.276 347433.1 11.587 1158850.4 57.948 -962469.9 -48.129 781447.6 39.0710 -491344.6 -24.572.3 三、编写有限元程序求解 2.3.1 程序基本步骤① 计算单元刚度矩阵 单元坐标系下刚度矩阵:1 0 1 00 0 0 01 0 1 00 0 0 0e EA K l --⎡⎤⎢⎥⎢⎥=⎢⎥-⎢⎥⎣⎦结构坐标下刚度矩阵:Te e K T K T -=cos sin 0 0-sin cos 0 00 0 cos sin 0 0 -sin cos T αααααααα⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦②组装总的刚度矩阵③边界条件处理(固定约束,直接去掉约束对应的行和列) ④计算位移向量 ⑤计算单元应力2.3.2 Vs2012 中重要的程序段'计算结点位移Private Sub Button1_Click(sender As Object , e As EventArgs ) Handles Button1.Click'桁架结点位移计算 '形成总刚度矩阵Dim TK(12, 12) As Double '总体刚度矩阵 TK = Matrix .STIFFSOfAllTK()Dim TKH(11, 11) As Double '去除0行0列 For I = 1 To 12For J = 1 To 12TKH(I - 1, J - 1) = TK(I, J)Next JNext I'输入结点载荷P(I)Dim P(12) As DoubleP = Data.NodeLoadData()Dim PH(11) As DoubleFor I = 1 To 12PH(I - 1) = P(I)Next I'边界条件处理For I = 8 To 11For J = 1 To 11TKH(I, J) = 0.0Next JNext IFor J = 8 To 11TKH(J, J) = 1.0Next JFor J = 8 To 11PH(J) = 0.0Next J'计算结点位移Dim Z(11) As Double'结点位移Dim TKHT(11, 11) As Double'去除0行0列TKHT = Matrix.InversionOfMatrix(TKH)Z = Matrix.MatrixMultipleVector(TKHT, PH)'输出结点位移IO.Output(Z)End SubPrivate Sub Button2_Click(sender As Object, e As EventArgs) Handles Button2.Click'桁架单元力'计算总体坐标架单元新节点位移XNEW(6,2)Dim XNEW(6, 2) As DoubleDim ZNEW(6, 2) As DoubleDim X(6, 2) As DoubleX = Data.PositionData()Dim Z(12) As Double'结点位移Z = Matrix.Displacement()For I = 1 To 6ZNEW(I, 1) = Z(2 * I - 2)ZNEW(I, 2) = Z(2 * I - 1)Next IXNEW = Matrix.Add(X, ZNEW)'计算变形后杆长Dim DDELTAX(10) As DoubleDim NEWDDELTAX(10) As DoubleDim D(10) As DoubleDim A(10) As DoubleDim E1 As IntegerA = Data.AreaDataE1 = Data.EDataDim N(10) As Double'单元力For I = 1 To 10X = Data.PositionData()'单元结点编号Dim NX(2, 10) As DoubleNX = Data.NodeData()NEWDDELTAX(I) = Math.Sqrt((XNEW(NX(1, I), 1) - XNEW(NX(2, I), 1)) ^ 2 + (XNEW(NX(1, I), 2) - XNEW(NX(2, I), 2)) ^ 2)DDELTAX(I) = Matrix.ElementLongger(I)D(I) = NEWDDELTAX(I) - DDELTAX(I)'计算单元力N(I) = D(I) * E1 * A(I) / DDELTAX(I)Next I' 输出单元力 NIO.Output(N)End Sub'计算单元应力过程Private Sub Button3_Click(sender As Object, e As EventArgs) Handles Button3.ClickDim S(10) As DoubleDim F(10) As DoubleDim A(10) As DoubleA = Data.AreaDataF = Matrix.FORCEFor I = 1 To 10S(I) = F(I) / A(I)Next I' 输出单元应力 SIO.Output(S)End Sub2.3.3程序输出文件图 5 有限元位移结果图 6有限元应力结果图 7有限元轴力结果2.3.4材料力学、有限元程序、Abaqus结果比较表 3 材力、有限元、Abaqus计算结果比较表 4 材力、有限元、Abaqus计算误差分析通过误差图显示,最大误差在4%,在误差允许围。
