高频电子线路公式大全

合集下载

13个常用的电路基础公式，电气人必备！

13个常用的电路基础公式，电气人必备！01欧姆定律计算计算电阻电路中电流、电压、电阻和功率之间的关系。

▶欧姆定律解释：欧姆定律解释了电压、电流和电阻之间的关系，即通过导体两点间的电流与这两点间的电势差成正比。

说明两点间的电压差、流经该两点的电流和该电流路径电阻之间关系的定律。

该定律的数学表达式为V=IR，其中V是电压差，I是以安培为单位的电流，R是以欧姆为单位的电阻。

若电压已知，则电阻越大，电流越小。

02计算多个串联或并联连接的电阻的总阻值03计算多个串联或并联连接的电容器的总容值04电阻分压计算计算电阻分压器电路的输出电压，以实现既定的阻值和电源电压组合。

什么是分压器？分压器是一个无源线性电路，能产生一个是其输入电压(V1)一部分的输出电压(Vout)。

分压器用于调整信号电平，实现有源器件和放大器偏置，以及用于测量电压。

欧姆定律解释了电压、电流和电阻之间的关系，即通过两点间导体的电流与这两点间的电势差成正比。

这是一个说明两点间的电压差、流经该两点的电流和该电流路径电阻之间关系的定律。

该定律的数学表达式为V=IR，其中V是电压差，I是以安培为单位的电流，R是以欧姆为单位的电阻。

若电压已知，则电阻越大，电流越小。

05电流分流器-电阻计算计算连接到电流源的多至10个并联电阻上流过的电流：06电抗计算计算指定频率下电感器或电容器的电抗或导纳大小。

1）感抗/导纳2）容抗/导纳07RC时间常数计算计算电阻与电容的积，亦称RC时间常数。

该数值在描述电容通过电阻器进行充电或放电的方程式中出现，表示在改变施加到电路的电压后，电容器两端的电压达到其最终值约63%所需的时间。

同时该计算器也会计算电容器充电到指定电压所存储的总能量。

如何计算时间常数：时间常数(T)可由电容(C)和负载电阻(R)的值确定。

电容器(E)中存储的能量(E)由两个输入确定，即由电压(V)和电容(C)决定。

08LED串联电阻器计算器计算在指定电流水平下通过电压源驱动一个或多个串联LED所需的电阻。

电路公式知识点总结

电路公式知识点总结电路是电子学的基础，它是由连接在一起的电子元件组成的。

电路可以分为两种类型：串联电路和并联电路。

在电路中，存在许多重要的公式和定律，这些公式和定律是电路分析和设计过程中至关重要的工具。

本文将对电路中常用的公式和定律进行总结，并介绍它们的用途和推导过程。

1. 电压、电流和阻抗在电路中，电压、电流和阻抗是最基础且最重要的概念。

电压是指电路中流动的电荷单位电荷所具有的能量。

电压可以通过下面的公式计算：V = IR其中V是电压，I是电流，R是电阻。

这个公式叫做欧姆定律，它指出了电压、电流和阻抗之间的关系。

利用欧姆定律，我们可以计算出电路中的电压和电流，并且通过改变电阻的大小来控制电路中的电压和电流。

2. 电阻和电阻率电阻是电路中的一个重要参数，它指的是电路中对电流的阻碍。

电阻的大小可以通过以下公式计算：R = ρL/A其中R是电阻，ρ是电阻率，L是电阻长度，A是电阻横截面积。

这个公式指出了电阻与电阻率、长度和横截面积之间的关系。

通过控制电阻的大小，我们可以调节电路中的电流和电压。

3. 串联电路和并联电路串联电路和并联电路是电路中两种基本的连接方式。

串联电路中元件按顺序连接在一起，电流只有一条路径可走。

并联电路中元件平行连接在一起，电流有多条路径可走。

在电路分析中，我们可以利用串联电路和并联电路的公式来计算电路中的电压和电流。

4. 电路中的功率功率是电路中另一个重要的物理量。

功率可以通过以下公式计算：P = IV其中P是功率，I是电流，V是电压。

这个公式指出了功率与电流和电压之间的关系。

利用功率公式，我们可以计算出电路中的功率，并且通过改变电路中的电流和电压来控制功率的大小。

5. 电感和电容电感和电容是电路中的两种被动元件，它们分别储存电磁能量和静电能量。

电感的大小可以通过以下公式计算：L = NΦ/I其中L是电感，N是匝数，Φ是磁通量，I是电流。

电容的大小可以通过以下公式计算：C = Q/V其中C是电容，Q是电荷，V是电压。

(完整版)高频电子线路简答及计算

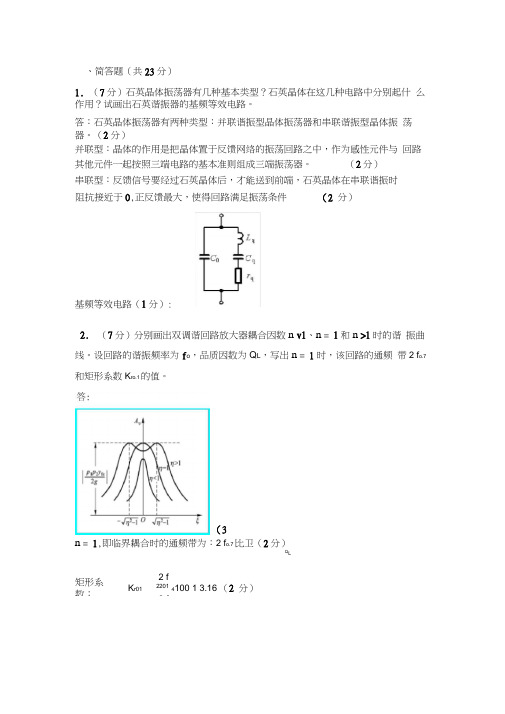
、简答题（共23分）1.（7分）石英晶体振荡器有几种基本类型？石英晶体在这几种电路中分别起什么作用？试画出石英谐振器的基频等效电路。

答：石英晶体振荡器有两种类型：并联谐振型晶体振荡器和串联谐振型晶体振荡器。

（2分）并联型：晶体的作用是把晶体置于反馈网络的振荡回路之中，作为感性元件与回路其他元件一起按照三端电路的基本准则组成三端振荡器。

（2分）串联型：反馈信号要经过石英晶体后，才能送到前端，石英晶体在串联谐振时2.（7分）分别画出双调谐回路放大器耦合因数n v1、n = 1和n >1时的谐振曲线。

设回路的谐振频率为f o，品质因数为Q L，写出n = 1时，该回路的通频带2 f o.7和矩形系数K ro.1的值。

n = 1,即临界耦合时的通频带为：2 f o.7 比卫（2分）Q L矩形系数：2 fK r0122014100 1 3.16 （2 分）2 f阻抗接近于0,正反馈最大，使得回路满足振荡条件（2 分）基频等效电路（1分）:（3分）3. (9分)分别写出正弦波振荡器起振条件、平衡条件和稳定条件的表达式。

如成分?答：高频已调波信号和本机振荡信号经过混频后，信号中包含直流分量、基波分量、谐波、和频、差频分量，通过 LC 并联谐振回路这一带通滤波器取出差频分量，完成混频。

5. 画出锁相环路的组成框图并简述各部分的作用，分析系统的工作过程。

解：锁相环路的系统框图如下图所示。

锁相环路是由鉴相器 PD(Phase Detector)、环路滤波器 LF(Loop Filter) 和压控振荡器VCQ 组成的，其中LF 为低通滤波器。

各部分功能如下： (1)鉴相器PD 鉴相器是一个相位比较器，完成对输入信号相位与 VCC 输出信号相位进行比较，得误差相位e(t) i (t) o (t)。

图所示三端式振荡器的交流等效电路中假设L 1C 1L 2C 2L 3C 3，试问该电路能a( 0) a(由于 L 1C 1 L 2C 2 L 3C 3, f( 0) 2n nf( ) 2n n(2 分)1 L|C1L 2C 2与L 1C 1均呈感性，L 3C 3呈容性，电路成为电感反馈三端电因此一1 -L 3C 31,L 2C 2当 321时，路，可以振荡。

高频电子线路第2章-高频电路基础

1 1 L= 2 = ω0 C (2π ) 2 f 02C
以兆赫兹(MHz)为单位Ｃ以皮法为单位, 以皮法(pF)为单位 L以为单位, 将f0以兆赫兹为单位为单位以微亨（）为单位，上式可变为一实用计算公式：微亨（µH）为单位，上式可变为一实用计算公式：
1 2 1 25330 6 L = ( ) 2 × 10 = 2 2π f 0 C f0 C
(3) 求满足求满足0.5 MHz带宽的并联电阻。设回路上并联带宽的并联电阻。带宽的并联电阻电阻为R 并联后的总电阻为R 电阻为 1, 并联后的总电阻为 1∥R0, 总的回路有载品 f0 质因数为Q 由带宽公式, 质因数为 L。由带宽公式有 Q =
L
B
此时要求的带宽B=0.5 MHz, 故 QL = 20 此时要求的带宽回路总电阻为
主要包括电台、工业、空间电磁、天电等主要包括电台、工业、空间电磁、
内部产生的一般称为噪声
人为:接地回路耦合等人为接地,回路耦合等接地系统内:电阻电子器件等的热噪声等系统内电阻,电子器件等的热噪声等电阻
电子噪声：电子线路中普遍存在。电子噪声：电子线路中普遍存在。指电子线路中的随机起伏的电信号，与电子扰动有关。机起伏的电信号，与电子扰动有关。当噪声,干扰与信号可比拟时称信号被噪声淹没当噪声干扰与信号可比拟时,称信号被噪声淹没干扰与信号可比拟时称信号被噪声淹没.
ωM M = 对于互感耦合: 对于互感耦合 k = 2 L1L2 ω L1L2
通常情况: 通常情况
M L1 = L2 = L 则 k = L
CC k= 对于电容耦合: 对于电容耦合 (C1 + CC )(C2 + CC )

高频电路基础

只有一个回路的振荡电路称为简单振荡回路或单振荡回路。简单振荡回路的阻抗在某一特定频率上具有最大或最小
值的特性称为谐振特性，这个特定频率称为谐振频率。
《高频电子线路》
第2章高频电路基础
(1)、并联谐振回路 1）电路结构
.
LC
Is
+
L
• Uo
. Is
r
C
–
L 的等效损耗电阻
Z
Zp
Uo Is

第2章高频电路基础
第2章高频电路基础
2.1 高频电路中的元器件 2.2 高频电路中的基本电路 2.3 电子噪声 2.4 噪声系数和噪声温度
《高频电子线路》
1
第2章高频电路基础
概述
• 基本元器件（无源元件、有源器件） • 基本电路（谐振回路、石英晶体振荡器、变压器等） • 基本问题（选频滤波、阻抗变换） • 基本方法（线性、非线性） • 基本指标（小信号时的噪声系数、大信号时的非线性
《高频电子线路》
8
第2章高频电路基础
2、晶体管与场效应管（FET）在高频中应用的晶体管仍然是双极晶体管和各种场效应
管，通常这些管子比用于低频的管子性能更好, 在外形结构方面也有所不同。
高频晶体管有两大类型: (1) 一类是作小信号放大的高频小功率管, 对它们的主
要要求是高增益和低噪声; (2) 另一类为高频功率放大管, 除了增益外, 要求其在高
(r jL) / jC r jL 1/ jC

L/C
r j(L 1 / C )
当 ωL 1 / ωC 时，回路并联谐振 r <<ωL
《高频电子线路》
第2章高频电路基础

电路常用公式范文

电路常用公式范文电路是通电子流的路径，电子流通过电路时会遵循一定的物理规律和数学公式。

掌握电路常用的公式可以帮助我们分析和解决电路方面的问题。

本文将介绍一些电路常用的公式，包括欧姆定律、串联电阻和并联电阻、功率公式、电流分流和电压分压定律等。

1.欧姆定律欧姆定律是电路中最基本的公式之一，描述了电压、电流和电阻之间的关系。

根据欧姆定律，电流(I)等于电压(V)除以电阻(R)。

公式为：I=V/R。

这个公式说明了在一个电阻中通过的电流与电压成反比，与电阻成正比。

2.串联电阻和并联电阻当电阻器或其他电子元件按照连接的顺序相继连接起来时，称为串联。

串联电阻的总阻值等于各个电阻之和。

如果有两个串联的电阻R1和R2，总阻值(Rt)等于R1+R2、公式为：Rt=R1+R2而当电阻器或其他电子元件由两个或多个平行连接的分支组成时，称为并联。

并联电阻的总阻值等于各个电阻的倒数之和的倒数。

如果有两个并联的电阻R1和R2，总阻值(Rt)等于1/(1/R1+1/R2)。

公式为：1/Rt=1/R1+1/R23.功率公式电路中的功率用来描述电能转化或消耗的速率。

功率(P)等于电流(I)乘以电压(V)。

公式为：P=I*V。

这个公式说明了功率与电流和电压成正比。

4.电流分流定律电路中的电流在分流点分成几个分支后，再汇流回到一点。

根据电流分流定律，分流点处的电流等于各个分支电流之和。

公式为：It=I1+I2+...+In。

这个公式说明了电流在分流点处的守恒性。

5.电压分压定律电路中的电压在分压点分成几个分支后，再汇合到一点。

根据电压分压定律，分压点处的电压等于各个分支电压之和。

公式为：Vt=V1+V2+...+Vn。

这个公式说明了电压在分压点处的守恒性。

6.电阻功率公式电阻器上产生的功率等于电流的平方乘以电阻的大小。

公式为：P=I^2*R。

这个公式说明了电阻功率与电流的平方和电阻成正比。

7.电能公式电能是电压和电流的乘积，用来描述电路中电能的转化和消耗。

高频电子线路第五版课后答案

0
f 1 j f
f f
02 1 0
则
f f 0 1 j 1 j f f （）
0

0
0

0
1 （ f 0 2 ） f
f 1MHz , 49 f 20 MHz , 12.1 f 50 MHz , 5
第2章习题
C 50 pF 通频带 2f0.7 150kHz 。试 2.7.给定并联谐振回路的 f0 5MHz ，求电感 L 、品质因数 Q 0 以及对信号源频率为5.5MHz时的失调。又若把 2f0.7 加宽至300KHz，应在回路两端再并联上一个阻值多大的电阻？
解、失调 f f f0 5.5 5 0.5MHz
p1 p2 y fe G'
12.3
图3.1a
图、 K1 1 QL Q 0
1.43
Y 'L
2
图3.1d
(5)、GL (
g s gie goe GL 1 2 g s gie goe GL S 1.26 1
g ie 2860 S , Cie 18 pF
g oe 200 S ; C oe 7 pF ; |y fe | 45mS ; fe 54; | yre | 0.31mS ; re 88.5;
解：图3.1的等效图为图3.1a和图3.1b。其中 p1 N 2~3 0.25, p2 N 4~5 0.25,
所以，需并联上一个阻值约为21 k 的电阻。
f0 G, 0C
B0.7 300 150 150kHz R 1 21k B0.7 2 C

《电工电子学基础常用公式总汇》

《电工电子学基础常用公式总汇》1.电流公式：
电流（I）=电荷（Q）/时间（t）
2.电压公式：
电压（V）=电流（I）x电阻（R）
3.电阻公式：
电阻（R）=电压（V）/电流（I）
4.电功率公式：
功率（P）=电流（I）x电压（V）
5.电能公式：
能量（W）=功率（P）x时间（t）
6.电感公式：
电感（L）= 电压（V） / (dI / dt)
7.电容公式：
电容（C）=电荷（Q）/电压（V）
8.电阻串联公式：
总电阻（Rt）=R1+R2+R3+...
9.电阻并联公式：
总电阻（Rt）=1/(1/R1+1/R2+1/R3+...)
10.电流分压公式：
电压（V1）=电阻（R1）/(电阻（R1）+电阻（R2）)x电压（V）11.电阻性能：
功率损耗（Pd）=电流（I）²x电阻（R）
12.串联电感公式：
总电感（Lt）=L1+L2+L3+...
13.并联电感公式：
总电感（Lt）=1/(1/L1+1/L2+1/L3+...)
14.串联电容公式：
总电容（Ct）=1/(1/C1+1/C2+1/C3+...)
15.并联电容公式：
总电容（Ct）=C1+C2+C3+...
以上是电工电子学中常用的一些基础公式，这些公式对于理解和计算电路中的各种参数具有重要的作用。

在实际应用中，我们可以根据具体的电路问题来选择合适的公式进行计算。

同时，这些公式也为我们提供了设计和优化电路的方法和依据。

因此，对于学习电工电子学的人来说，掌握这些公式是非常重要的。

电工电子学基础常用公式总表更新版

L是电感量，是磁链，I是电流，N是匝数或叫圈数，是磁通量，H是享利，还有（毫享mH，微享uH）。
电感串联公式
H
是总电感量，L是电感，H是享利，还有（毫享mH，微享uH）；电感串联计算时、电感与电感之间不互相干扰才比较准确。
电感并联公式
H
是总电感量，L是电感，H是享利，还有（毫享mH，微享uH）；电感并联计算时，电感与电感之间不互相干扰才比较准确。
U1U2是初次级线圈绕组的电压比，
N1N2是初次级线圈绕组的匝数比。
I1I2是初次级线圈绕组的电流比，
U2U1是次级初级线圈绕组的电压比。
U1U2是初次级线圈绕组的电压比，
N1N2是初次级线圈绕组的匝数比，
I2I1是次级初级线圈绕组的电流比。
工频变压器铁芯
截面积计算公式
Cm2
S 是铁路芯的截面积，K是系数,，P1是输入的视在功率，单位（VI伏安）一般输入功率10VA以下，系数K=2；10VA---50VA，系数K=2---1.5；50VA—1000VA，系数K=1.5---1； cm2是平方厘米。
±0.5﹪
±0.25﹪
±0.1﹪
±5﹪
±10﹪
±20﹪
四色环电阻：1、2环表示是有效数照写，3环表示是乘数（就是要乘与这个乘数），4环表示是精确度。
五色环电阻：1、2、3环表示是有效数照写，4环表示是乘数（就是要乘与这个乘数），5环表示是精确度。
例：四色环电阻五色环电阻
1 2 103±10﹪2 0 3 101±5﹪
是效率，公式也可用 = X100﹪。
用电量公式
用电量
KWh
（度）
K=1000，W是瓦特，h=时间、单位（小时），
1千瓦时=1度电。

电路公式总结知识点

电路公式总结知识点在电路的研究和设计中，有许多重要的公式和定律帮助工程师和研究人员理解电路的行为和特性。

本文将对一些重要的电路公式进行总结，并解释它们的用途和意义。

1. 电流和电压的关系在电路中，电流和电压是两个基本的物理量，它们之间的关系由欧姆定律给出：V = I * R在这个公式中，V代表电压，单位是伏特（V），I代表电流，单位是安培（A），R代表电阻，单位是欧姆（Ω）。

欧姆定律说的是，电压和电流成正比，而比例常数即为电阻。

这个公式是电路分析中最基本的公式之一，可用于计算电路中的电压、电流和电阻的关系。

2. 串联电路中电阻的计算在串联电路中，多个电阻依次连接在一起，形成一个电阻链。

串联电路中电阻的总和可以通过以下公式计算得出：R_total = R1 + R2 + ... + Rn在这个公式中，R_total代表串联电路的总电阻，R1, R2, ... Rn分别代表串联电路中每个电阻的电阻值。

通过这个公式，我们可以快速地计算出串联电路的总电阻，从而理解整个电路的特性。

3. 并联电路中电阻的计算在并联电路中，多个电阻并联连接在一起，形成一个并联结构。

并联电路中电阻的总和可以通过以下公式计算得出：1/R_total = 1/R1 + 1/R2 + ... + 1/Rn在这个公式中，R_total代表并联电路的总电阻，R1, R2, ... Rn分别代表并联电路中每个电阻的电阻值。

通过这个公式，我们可以快速地计算出并联电路的总电阻，从而理解整个电路的特性。

4. 电压分压公式在电路中，当多个电阻连接在一起时，电压会根据各个电阻的电阻比例进行分压。

这个分压公式可以通过以下公式计算得出：V_out = V_in * (R2 / (R1 + R2))在这个公式中，V_out代表电路中的输出电压，V_in代表电路中的输入电压，R1和R2分别代表电路中的两个电阻。

这个公式常用于分析电压分压器、电平转换器等电路结构。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一、单级单调谐放大器:
谐振频率 0f LCf210 C为总电容 C)f(L2021

通频带7.0BW eQfBW07.0 eQ为LC回路的有载品质因素
有载品质因素eQ CRLRQe00 R为总电阻，002f
矩形系数1.0K 1.07.01.0BWBWK
二、多级单调谐放大器: 各级电压增益相同，即unuuAAA32u1A
总电压增益为：nuunuuuAAAAA)(A1321u

总通频带为：enQfBW017.012（ eQf0为单级单调谐放大器的通频带）
三、丙类谐振功率放大器:
效率 )(21)()(2121P12101OgVUVIUIPCCcmCCccmmcDC

CC
cm
V

U


称为集电极电压利用系数；)()()(01011cmcIIg称为集电极电流利用系数或波形系数。

集电极耗散功率ODCCPPP
功率增益iOPPPA iP为基极输入功率
导电角imBBthUVU 输出功率PmccmmcORIUIP1212121
集电极直流电源供给功率CCcDCVIP0
集电极基波分量分函数表达式 )(00CMciI )(11CMmciI )(nCMcnmiI
其中)(0为直流分量分解系数；)(1为基波分量分解系数。

四、丙类倍频器：输出功率cnmcnmonUIP21 效率CCccnmcnmDCnVIUIP0on21P
正弦波振荡器平衡的条件 ①相位平衡条件：φA+φF＝2nπ(n＝0,1,2,3,···) ②振幅平衡条件：AF＝1
正弦波振荡器起振的条件 ①相位平衡条件：φA+φF＝2nπ(n＝0,1,2,3,···) ②振幅平衡条件：AF＞1

振荡频率的准确度和稳定度绝对准确度f 0fff

相对准确度 000fffff（0ff称为相对频率准确度或相对频率偏差）

C
Q
R000
振荡频率的稳定度=
五、电容三点式振荡器：
振荡频率0f LCffp210 其中2121CCCCC
振荡反馈系数
六、电感三点式振荡器：
振荡频率CMLLffp)2(21210
振荡反馈系数
七、克拉泼(Clapp)振荡器：振荡频率3021LCf

八、西勒(Seiler)振荡器：振荡频率)C(21430CLf
九、石英晶体振荡器：串联谐振频率

并联谐振频率
十、RC串并联选频网络：
反馈系数 )RC1-RCj(31F

幅频特性 200)-j(31F （RC10）

相频特性 3-arctan00F
十一、调幅波的基本性质：
低频调制信号 FtUtUtumm2coscos)(

高频载波信号 tfUtUtuccmccmc2coscos)(

调幅信号

调幅系数 minmaxminmaxUUUUma

时间间隔/
0
max

f

of
/UUF
21
/CC

of
/UUF
)/()(12MLML

qq
s
21CL

f

q0
q0
q

p
21CCCCL

f


0

q
s
1CCf

)(AMtu
ttUkUcmaCmcos)cos(


ttmUcacmcos)cos1(
双边带 ttUmttukuccmacaDSBcoscoscos)(
单边带

不失真条件 aaLLmFmCmax221R
十二、调频波与调相波的比较：
调制信号 tUtumcos)( 载波信号 tUtuccmccos)(
调频信号调相信号

瞬时角频率 )()(tuktfc dttduktpc)()(
tmccos

tmcsin


瞬时相位 tcdttutt0)()( )()(tukttpc
tmtfcsin

tmtpccos


最大角频偏 mfmUk mpmUk
fm
m
f2

pm

调制指数（或最大相移m）



mfm




mf
Uk

F
fm


mppUkm



数学表达式 ])(cos[)(0FMtfccmdttuktUtu )](cos[)(PMtuktUtuPccm
]sincos[tmtUfccm

]coscos[tmtUPccm


最大频偏=2m ；m为最大角频偏；调角波频偏的宽度 )(2FfBWm
fm的单位是rad ；f
k
的单位是VHz FmBW)1(2

tUmtUmu)cos(21)cos(21ccmaccmaDSB

tUmu)cos(21)(ccmaSSB上边带