北师大数学分析法课件
合集下载
1.2 综合法与分析法 课件1 (北师大选修2-2)

练习2:求证:
3- 2>
6- 5
练习3:设a,b为互不相等的正数,且a+b=1, 证明: 1 + 1 > 4
a b
变题: 已知 a, b, c R ,且 a b c 1
1 求证:(1)a b c ; 3 (2) a b c 3.
2 2 2
例2.如图,四棱锥 P ABCD 中,
2.分析法
从问题的结论出发,追溯导致结论的成 立的条件,逐步上溯,直到使结论成立的 条件和已知条件吻合为止.
其推证过程为:
结论 已知条件
特点:
从“未知”看“需知”,逐步靠拢 “已知”
3.直接证明
直接从原命题的条件逐步推得命题成立.
(综合法和分析法是直接证明的两种基本方法)
注:直接证明的一般形式为:
2 2
证: 求
直接证明
π 1 例. 已知α, β≠ kπ+ (k Z),且 2 sinθ+ cosθ= 2sinα sinθcosθ= sin 2 β 1 - tan α 1 - tan β = . 2 2 1 + tan α 2(1 + tan β)
2 2
证: 求
练习1:平行四边形ABCD中,AE⊥BD,垂足为E, CF⊥BD,垂足为F, 求证:AE=CF C D E F A B
PC 平面ABCD, PC 2,
在四边形 ABCD 中,点M 在PB上,
PB与平面ABC成 30 角.
CM // 面PAD; (1)求证:
面PAB 面PAD. (2)求证:
例3.已知数列 {an }的通项 an 为3,公差为1的等差数列.
2020北师大版高中数学选修1-2:第三章 分析法

−
������������
<
(������-������)2 8������
成立.
题型一
题型二
题型三
题型四
典例透析
反思由于题目中条件比较简单,结论比较复杂,用综合法比较困难, 可以从结论出发,逐步反推,寻求使当前命题成立的充分条件.
典例透析
题型一
题型二
题型三
题型四
【变式训练 1】 已知 a,b,c 是不全相等的正数,
=
4.
所以
������-������ ������-������
+
������������--������������≥4,即
1 ������-������
+
1 ������-������
≥
4 ������-������
,
当且仅当b-c=a-b,
即2b=a+c时,等号成立.故选C.
答案:C
题型一
题型二
求证:lg
������+������ 2
+
lg
������+������ 2
+
lg
������+������ 2
>
lg
������
+
lg
������
+
lg
������.
证明:要证
lg
������+������ 2
+
lg
������+������ 2
+
lg
������+������ 2
>
lg
a+lg
(北师大版文)2021届高考数学复习课件:综合法、分析法与反证法

证明
思维升华
(1)逆向思考是用分析法证题的主要思想,通过反推,逐步寻找使结论 成立的充分条件.正确把握转化方向是使问题顺利解决的关键. (2)证明较复杂的问题时,可以采用两头凑的办法,即通过分析法找出 某个与结论等价(或充分)的中间结论,然后通过综合法证明这个中间结 论,从而使原命题得证.
跟踪训练 已知非零向量 a,b,且 a⊥b,求证:|a|a|+ +|bb||≤ 2. 证明 由 a⊥b 得,a·b=0,要证|a|a|+ +|bb||≤ 2, 只需证|a|+|b|≤ 2|a+b|,
123456
解析 答案
题组三 易错自纠
4.若a,b,c为实数,且a<b<0,则下列命题正确的是
A.ac2<bc2 11
C.a<b
√ B.a2>ab>b2
ba D.a>b
解析 a2-ab=a(a-b),
∵a<b<0,∴a-b<0,∴a2-ab>0,
∴a2>ab.
①
又ab-b2=b(a-b)>0,∴ab>b2,
解析 P2=2a+13+2 a2+13a+42,
(a≥0),则P,Q的大小
Q2=2a+13+2 a2+13a+40,
∴P2>Q2,又∵P>0,Q>0,∴P>Q.
123456
解析 答案
3.设实数a,b,c成等比数列,非零实数x,y分别为a与b,b与c的等差 中项,则 ax+cy 等于
A.1
√B.2
C.4 D.6
解析 答案
3.(2018·武汉月考)若a,b,c是不全相等的正数,求证: a+b b+c c+a
lg 2 +lg 2 +lg 2 >lg a+lg b+lg c.
思维升华
(1)逆向思考是用分析法证题的主要思想,通过反推,逐步寻找使结论 成立的充分条件.正确把握转化方向是使问题顺利解决的关键. (2)证明较复杂的问题时,可以采用两头凑的办法,即通过分析法找出 某个与结论等价(或充分)的中间结论,然后通过综合法证明这个中间结 论,从而使原命题得证.
跟踪训练 已知非零向量 a,b,且 a⊥b,求证:|a|a|+ +|bb||≤ 2. 证明 由 a⊥b 得,a·b=0,要证|a|a|+ +|bb||≤ 2, 只需证|a|+|b|≤ 2|a+b|,
123456
解析 答案
题组三 易错自纠
4.若a,b,c为实数,且a<b<0,则下列命题正确的是
A.ac2<bc2 11
C.a<b
√ B.a2>ab>b2
ba D.a>b
解析 a2-ab=a(a-b),
∵a<b<0,∴a-b<0,∴a2-ab>0,
∴a2>ab.
①
又ab-b2=b(a-b)>0,∴ab>b2,
解析 P2=2a+13+2 a2+13a+42,
(a≥0),则P,Q的大小
Q2=2a+13+2 a2+13a+40,
∴P2>Q2,又∵P>0,Q>0,∴P>Q.
123456
解析 答案
3.设实数a,b,c成等比数列,非零实数x,y分别为a与b,b与c的等差 中项,则 ax+cy 等于
A.1
√B.2
C.4 D.6
解析 答案
3.(2018·武汉月考)若a,b,c是不全相等的正数,求证: a+b b+c c+a
lg 2 +lg 2 +lg 2 >lg a+lg b+lg c.
1.2 综合法与分析法 课件(北师大选修2-2)
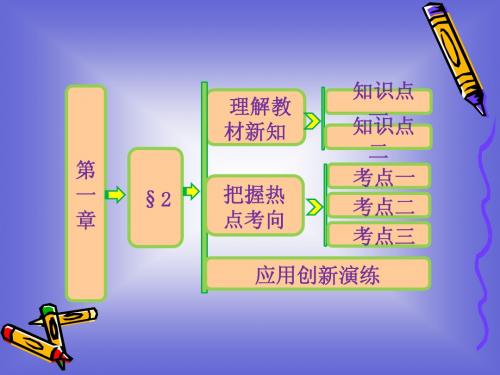
2.已知点P是直角三角形ABC所在平面外的一点,O是斜边 AB的中点,并且PA=PB=PC. 求证:PO⊥平面ABC.
证明:连接OC,如图所示,
∵AB是Rt△ABC的斜边,O是AB的中点, ∴OA=OB=OC. 又∵PA=PB=PC,∴PO⊥AB, 且△POA≌△POC, ∴∠POA=∠POC. ∴∠POC=90°. 即PO⊥AB,PO⊥OC,且AB∩OC=O,所以PO⊥ 平面ABC.
分析法与综合法的优缺点: 综合法和分析法是直接证明的两种基本方法,两种方 法各有优缺点.分析法解题方向较为明确,容易寻找到解
题的思路和方法,缺点是思路逆行,叙述较繁;综合法从
条件推出结论,较简捷地解决问题,但不便于思考.实际 证题时常常两法兼用,先用分析法探索证明途径,然后用 综合法有条理地表述解题过程.
提示:基本不等式.
问题 2:本题证明顺序是什么?
提示:从已知到结论.
综合法
(1)含义:从命题的 条件 出发,利用定义、公理、定理 及运算法则,通过 演绎 推理,一步一步地接近要证明 的 结论 ,直到完成命题的证明的思维方法,称为综合法. (2)思路:综合法用以下的框图表示:
1 2 即证 a +b ≥ (a +b2+2ab),即证 a2+b2≥2ab. 2 因为 a2+b2≥2ab 对一切实数恒成立, 2 所以 a +b ≥ (a+b)成立. 2
2 2
[一点通]
分析法是“执果索因”,一步步寻找结论成
立的充分条件.它是从求证的结论出发,逆着分析,由未
知想需知,由需知逐渐地靠近已知,这种证明的方法关键
AC cos B 1.在△ABC 中,AB= ,证明 B=C. cos C
sin B cos B 证明: 在△ABC 中, 由正弦定理及已知得 = . sin C cos C 于是 sin Bcos C-cos Bsin C=0,即 sin(B-C)=0, 因为-π<B-C<π,从而 B-C=0,所以 B=C.
高中数学第一章推理与证明1.2综合法与分析法课件北师大选修2_2

探究一
探究二
探究三
规范解答
变式训练
1
已知
a,b,c
都是正数,求证:21������
+
1 2������
+
1 2������
≥
1 ������+������
+
1 ������+������
+
������+1 ������.
证明:因为√������������ ≤ ������+2������,所以√1������������ ≥ ������+2������.
“×”.
(1)综合法是由因导果的顺推证法. ( √ ) (2)分析法是执果索因的逆推证法. ( √ ) (3) 分析法的推理过程要比综合法优越. ( × ) (4)所有证明的题目均可使用分析法证明. ( × )
(5)欲证√2 − √3 < √6 − √7成立,只需证(√2 − √3)2<(√6 − √7)2 成立即可. ( × )
探究三
规范解答
(2)∵由(1)知A=60°,且A+B+C=180°, ∴B+C=120°. 又 sin B+sin C=√3, ∴sin B+sin (120°-B)=√3,
即 sin B+(sin 120°cos B-cos 120°sin B)=√3.
∴32sin B+√23cos B=√3,即 sin (B+30°)=1. ∵0°<B<120°,∴30°<B+30°<150°. ∴B+30°=90°,即B=60°. ∴A=B=C=60°.因此△ABC为等边三角形.
1.2综合法和分析法 课件(北师大版选修2-2)
菜 单
课 时 作 业
教 师 备 课 资 源
BS·数学 选修2-2
教 学 教 法 分 析 教 学 方 案 设 计 课 前 自 主 导 学 课 堂 互 动 探 究
2.过程与方法 结合学生已学过的数学知识,通过实例引导学生分析 综合法与分析法的思考过程与特点,并归纳出操作流程. 3.情感、态度与价值观 (1)通过本节的学习,使学生在以后的学习和生活中, 能自觉地、有意识地运用这些方法进行数学证明,养成言 之有理、论证有据的习惯; (2)通过本节的学习和运用实践,体会数学问题解决过 程中的思维方式.
思 想 方 法 技 巧 当 堂 双 基 达 标
课 时 作 业
【提示】
条件:x+y=1;结论:2x+2y≥2 2.
教 师 备 课 资 源
菜
单
BS·数学 选修2-2
教 学 教 法 分 析 教 学 方 案 设 计 课 前 自 主 导 学 课 堂 互 动 探 究 菜 单 思 想 方 法 技 巧 当 堂 双 基 达 标
课 时 作 业
教 师 备 课 资 源
菜
单
BS·数学 选修2-2
教 学 教 法 分 析 教 学 方 案 设 计 课 前 自 主 导 学 课 堂 互 动 探 究 思 想 方 法 技 巧 当 堂 双 基 达 标
●教学建议 在以前的学习中,学生已积累了较多的综合法、分析 法证明数学问题的经验,但这些经验是零散的,不系统 的.由此,借助学生熟悉的数学实例,引导学生归纳总结 两种方法的特点,促使他们形成对两种方法的较完整认 识.所以本节课宜采取自主探究与师生交流相结合的教学 模式,充分暴露学生思维,总结共性,形成规律.
课 时 作 业
教 师 备 课 资 源
BS·数学 选修2-2
课 时 作 业
教 师 备 课 资 源
BS·数学 选修2-2
教 学 教 法 分 析 教 学 方 案 设 计 课 前 自 主 导 学 课 堂 互 动 探 究
2.过程与方法 结合学生已学过的数学知识,通过实例引导学生分析 综合法与分析法的思考过程与特点,并归纳出操作流程. 3.情感、态度与价值观 (1)通过本节的学习,使学生在以后的学习和生活中, 能自觉地、有意识地运用这些方法进行数学证明,养成言 之有理、论证有据的习惯; (2)通过本节的学习和运用实践,体会数学问题解决过 程中的思维方式.
思 想 方 法 技 巧 当 堂 双 基 达 标
课 时 作 业
【提示】
条件:x+y=1;结论:2x+2y≥2 2.
教 师 备 课 资 源
菜
单
BS·数学 选修2-2
教 学 教 法 分 析 教 学 方 案 设 计 课 前 自 主 导 学 课 堂 互 动 探 究 菜 单 思 想 方 法 技 巧 当 堂 双 基 达 标
课 时 作 业
教 师 备 课 资 源
菜
单
BS·数学 选修2-2
教 学 教 法 分 析 教 学 方 案 设 计 课 前 自 主 导 学 课 堂 互 动 探 究 思 想 方 法 技 巧 当 堂 双 基 达 标
●教学建议 在以前的学习中,学生已积累了较多的综合法、分析 法证明数学问题的经验,但这些经验是零散的,不系统 的.由此,借助学生熟悉的数学实例,引导学生归纳总结 两种方法的特点,促使他们形成对两种方法的较完整认 识.所以本节课宜采取自主探究与师生交流相结合的教学 模式,充分暴露学生思维,总结共性,形成规律.
课 时 作 业
教 师 备 课 资 源
BS·数学 选修2-2
3.3综合法与分析法 课件(北师大版选修1-2)

证 法2:∵a、b、c为 不相等正数 ,且abc = 1,
1 1 1 ∴ a+ b+ c = + + bc ca ab 1 1 1 1 1 1 + + + 1 < b c+c a+a b = + 2 2 2 a
1 1 + . b c 1 1 1 ∴ a + b + c < + + 成立. a b c
例:有下列各式: 1 1> , 2 1 1 1+ + > 1, 2 3 1 1 1 1 1 1 3 1+ + + + + + > , 2 3 4 5 6 7 2 1 1 1 1 1 1 1 1+ + + + + + + + >2 2 3 4 5 6 7 15 你能得到怎样的一般不等式,并加以证明。
又因为已知任何三条直线不过同一点,所以上面的k个 交点两两不相同,且与平面内其他的k(k-1)/2个 交点也两两不相同. 从而平面内交点的个数是 k(k-1)/2+k=k[(k-1)+2]/2 =(k+1)[(k+1)-1]/2. 这就是说,当n=k+1时,k+1条直线的交点个数为: f(k+1)=(k+1)[(k+1)-1]/2. 根据(1)、(2)可知,命题对一切大于1的正整数都成立. 说明:用数学归纳法证明几何问题,重难点是处理好当 n=k+1时利用假设结合几何知识证明命题成立.
注:在上例的题设条件下还可以有如下二个结论: (1)设这n条直线互相分割成f(n)条线段或射线, ---则: f(n)=n2. (2)这n条直线把平面分成(n2+n+2)/2个区域. 练习1:凸n边形有f(n)条对角线,则凸n+1边形的对角线 n-1 ------的条数f(n+1)=f(n)+_________. 练习2:设有通过一点的k个平面,其中任何三个平面或 三个以上的平面不共有一条直线,这k个平面将 空间分成f(k)个区域,则k+1个平面将空间分成 2k f(k+1)=f(k)+__________个区域.
【精编】北师大版高中数学选修2-2课件第一章《推理与证明》分析法-精心整理

11
故s<2a成立.
小结:
分析法和综合法是思维方向相反的两种思考方 法。在数学解题中,分析法是从数学题的待证 结论或需求问题出发,一步一步地探索下去, 最后达到题设的已知条件。综合法则是从数学 题的已知条件出发,经过逐步的逻辑推理,最 后达到待证结论或需求问题。对于解答证明来 说,分析法表现为执果索因,综合法表现为由 果导因,它们是寻求解题思路的两种基本思考 方法,应用十分广泛。
5
例2、求证: 8 7 5 10
证明:要证明 8 7 5 10 只需证明 ( 8 7 )2 ( 5 10)2
即 8 7 2 56 5 10 2 50
只需证明 56 50 即 56>50,这显然成立。
这样就证明了 8 7 5 10
证上式成立。这样就证明了命题的结论。
4
从要证明的结论出发,逐步寻求推证过程中,使 每一步结论成立的充分条件,直至最后,把要 证明的结论归结为判定一个明显成立的条件为 止,这种证明的方法叫做分析法.
这个明显成立的条件可以是: 已知条件、定理、定义、公理等
特点: 执果索因 即: 要证结果Q,只需证条件P
例3、求证:函数 f (x) 2x2 12x 16 在区间
(3,+∞)上是增加的。
6
证明:要证明函数 f (x) 2x2 12x 16
在区间(3,+∞)上是增加的,
只需证明对于任意 x1,x2 ∈(3,+∞),且 x1 > x2 时,有 f (x1) f (x2 ) 0 ,
2
综合法:
复习
①利用已知条件和已知的定义、定理、公理等,
②经过一系列的推理、论证,
③最后推导出所要证明的结论成立的证明方法
故s<2a成立.
小结:
分析法和综合法是思维方向相反的两种思考方 法。在数学解题中,分析法是从数学题的待证 结论或需求问题出发,一步一步地探索下去, 最后达到题设的已知条件。综合法则是从数学 题的已知条件出发,经过逐步的逻辑推理,最 后达到待证结论或需求问题。对于解答证明来 说,分析法表现为执果索因,综合法表现为由 果导因,它们是寻求解题思路的两种基本思考 方法,应用十分广泛。
5
例2、求证: 8 7 5 10
证明:要证明 8 7 5 10 只需证明 ( 8 7 )2 ( 5 10)2
即 8 7 2 56 5 10 2 50
只需证明 56 50 即 56>50,这显然成立。
这样就证明了 8 7 5 10
证上式成立。这样就证明了命题的结论。
4
从要证明的结论出发,逐步寻求推证过程中,使 每一步结论成立的充分条件,直至最后,把要 证明的结论归结为判定一个明显成立的条件为 止,这种证明的方法叫做分析法.
这个明显成立的条件可以是: 已知条件、定理、定义、公理等
特点: 执果索因 即: 要证结果Q,只需证条件P
例3、求证:函数 f (x) 2x2 12x 16 在区间
(3,+∞)上是增加的。
6
证明:要证明函数 f (x) 2x2 12x 16
在区间(3,+∞)上是增加的,
只需证明对于任意 x1,x2 ∈(3,+∞),且 x1 > x2 时,有 f (x1) f (x2 ) 0 ,
2
综合法:
复习
①利用已知条件和已知的定义、定理、公理等,
②经过一系列的推理、论证,
③最后推导出所要证明的结论成立的证明方法
