假设检验与t检验 ppt课件
合集下载
西北工业大学《概率论与数理统计》课件-第七章 假设检验
分析: 用 和 分别表示这一天袋
装糖重总体 X 的均值和标准差,
由长期实践可知, 标准差较稳定, 设 0.015,
则 X ~ N (, 0.0152 ), 其中 未知.
问题: 根据样本值判断 0.5 还是 0.5 ？
解 1º提出两个对立假设
H0 : 0 0.5 和 H1 : 0 . 2º X 是 的无偏估计量,
则我们拒绝 H0,
反之, 如果 u
x
/
0
n
u，则称 x 与0的差异是 2
不显著的, 则我们接受 H0,
上述关于 x 与 0 有无显著差异的判断是在显 著性水平 之下作出的.
2. 检验统计量
用于检验假设的统计量，称为检验统计量.
如：对于例2, 统计量 U X 0 / n
— 检验统计量.
3. 原假设与备择假设
1 假设 H0 : 0, H1 : 0 ;
2º取检验统计量
U X 0 ~ N (0,1), / n
(当H0为真时)
3º给定显著水平 ( 0< ≤ 0.05)
P{ U u }
2
由
(u
2
)
1
2
，查表可得
u
2
.
拒绝域： W1 {( x1, x2,, xn ) u u }, 2
u U ( x1, x2,, xn )
分析：从直观上分析，这批产品不能出厂. 因为抽样得到的次品率： 2 3% 10 然而，由于样本的随机性，如何才能根据抽
样结果判断总体(所有产品)的次品率是否≤3%?
解 用假设检验法，步骤：
1º提出假设 H0: p 0.03 其中 p为总体的次品率.
2º设
Xi
1, 0,
装糖重总体 X 的均值和标准差,
由长期实践可知, 标准差较稳定, 设 0.015,
则 X ~ N (, 0.0152 ), 其中 未知.
问题: 根据样本值判断 0.5 还是 0.5 ？
解 1º提出两个对立假设
H0 : 0 0.5 和 H1 : 0 . 2º X 是 的无偏估计量,
则我们拒绝 H0,
反之, 如果 u
x
/
0
n
u，则称 x 与0的差异是 2
不显著的, 则我们接受 H0,
上述关于 x 与 0 有无显著差异的判断是在显 著性水平 之下作出的.
2. 检验统计量
用于检验假设的统计量，称为检验统计量.
如：对于例2, 统计量 U X 0 / n
— 检验统计量.
3. 原假设与备择假设
1 假设 H0 : 0, H1 : 0 ;
2º取检验统计量
U X 0 ~ N (0,1), / n
(当H0为真时)
3º给定显著水平 ( 0< ≤ 0.05)
P{ U u }
2
由
(u
2
)
1
2
，查表可得
u
2
.
拒绝域： W1 {( x1, x2,, xn ) u u }, 2
u U ( x1, x2,, xn )
分析：从直观上分析，这批产品不能出厂. 因为抽样得到的次品率： 2 3% 10 然而，由于样本的随机性，如何才能根据抽
样结果判断总体(所有产品)的次品率是否≤3%?
解 用假设检验法，步骤：
1º提出假设 H0: p 0.03 其中 p为总体的次品率.
2º设
Xi
1, 0,
五章节假设检验HypothesisTesting104页PPT
• 硬币猜测游戏
正面朝上的概率
硬币0
0.5
硬币1
0.7
x 硬币0 硬币1
0
0.0010 0.0000
1
0.0098 0.0001
2
0.0439 0.0014
3
0.1172 0.0090
4
0.2051 0.0368
5
0.2461 0.1029
6
0.2051 0.2001
7
0.1172 0.2668
8
0.0439 0.2335
为假的时候接受H0
P(拒绝H0 | H0 ) P( X 6 | H0 ) 0.18
P(接受H0 | H1) P( X 6 | H1) 0.35
临界值c对错判概率的影响
• 假定c=0.1，即先验概率有差异
如果X 8，则接受H0
P(拒绝H0 | H0 ) P(X 8 | H0) 0.01 P(接受H0 | H1) P(X 6 | H1) 0.85
2.Neyman-Pearson范式
• 不用贝叶斯方法 • 规避了先验概率的决定 • 对两个假设区别对待，一个成为原假设
H假0设(nHul1l(ahlyteprontahteivseesh)y，p另ot一he个se成s)为备择
• 由此导致在有些场合下选择原假设的困难
Neyman-Pearson范式中的术语
• 一致最优检验
• 和假设检验有关的两个问题
• 置信区间和假设检验的对偶关系 • 如何选择原假设
• 广义似然比检验
– 广义似然比方法 – 多项分布的广义似然比检验 – 泊松分布的广义似然比检验
• 单样本检验的几个实例 • 两个样本的比较
第七章假设检验与t检验(终板)
1、假设检验中α值是检验水准，是拒绝 或不拒绝H0的概率标准。α的大小是人为 选定的，一般取0.05。
2、P值是指从H0所规定的总体中作随机 抽样,获得等于及大于 (或等于及小于)现有 样本统计量的概率。通过 P值与α 值的比 较来确定拒绝或不拒绝H0。
四、假设检验的应用注意事项
（1）研究设计要科学严密 （2）考虑假设检验方法的前提条件 （3）正确理解P值的含义 （4）假设检验的结论不能绝对化 （5）统计学意义与实际意义相互结合
的疗效时，如能根据专业知识认为新药 疗效不会比旧药差，只关心新药是否比 旧药好（疗效至少相同，绝对排除出现 相反的可能性），可用单侧检验。
双侧检验：在比较甲乙两种药物的疗效时， 事先不能确定哪种药的疗效较好，只关心两药 的疗效有无差别，要用双侧检验。双侧检验若 有差别，单侧检验肯定有差别；反之，单侧检 验若有差别，双侧检验不一定有差别。 单侧检验更容易得到有统计学意义的结论。
140 150 138 120 140 145 135 115 135 130 120 133 147 125 114 165 —
差值d （4）
27 25 12 -10 -10 0 0 10 7 -5 20 3 37 10 -6 10
d 130
d2 （5）
725 625 144 100 100 0 0 100 49 25 400 9 1369 100 36 100
2、选定检验方法和计算检验统计量
根据研究设计方案、资料类型、样本含量 大小及分析目的选用适当的检验方法，并根据 样本资料计算相应的检验统计量；不同的检验 方法要用不同的公式计算现有样本的检验统计 量（t ,u，F值）。检验统计量是在H0成立的前 提下计算出来。
3、确定P值，作出统计推断 P值是指由所规定的总体作随机抽样， 获得
2、P值是指从H0所规定的总体中作随机 抽样,获得等于及大于 (或等于及小于)现有 样本统计量的概率。通过 P值与α 值的比 较来确定拒绝或不拒绝H0。
四、假设检验的应用注意事项
（1）研究设计要科学严密 （2）考虑假设检验方法的前提条件 （3）正确理解P值的含义 （4）假设检验的结论不能绝对化 （5）统计学意义与实际意义相互结合
的疗效时，如能根据专业知识认为新药 疗效不会比旧药差，只关心新药是否比 旧药好（疗效至少相同，绝对排除出现 相反的可能性），可用单侧检验。
双侧检验：在比较甲乙两种药物的疗效时， 事先不能确定哪种药的疗效较好，只关心两药 的疗效有无差别，要用双侧检验。双侧检验若 有差别，单侧检验肯定有差别；反之，单侧检 验若有差别，双侧检验不一定有差别。 单侧检验更容易得到有统计学意义的结论。
140 150 138 120 140 145 135 115 135 130 120 133 147 125 114 165 —
差值d （4）
27 25 12 -10 -10 0 0 10 7 -5 20 3 37 10 -6 10
d 130
d2 （5）
725 625 144 100 100 0 0 100 49 25 400 9 1369 100 36 100
2、选定检验方法和计算检验统计量
根据研究设计方案、资料类型、样本含量 大小及分析目的选用适当的检验方法，并根据 样本资料计算相应的检验统计量；不同的检验 方法要用不同的公式计算现有样本的检验统计 量（t ,u，F值）。检验统计量是在H0成立的前 提下计算出来。
3、确定P值，作出统计推断 P值是指由所规定的总体作随机抽样， 获得
《生统》第五章 假设检验-t检验
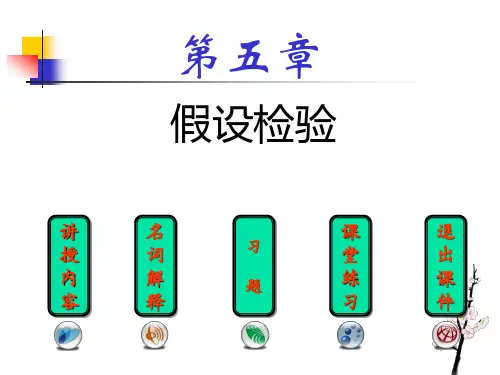
表5-4 粤黄鸡饲养试验增重 饲料 A B 8 8 ni 增 重（g） 720、710、735、680、690、705、700、705 680、695、700、715、708、685、698、688
ni
检验步骤：
1、提出无效假设与备择假设 H0：μ1=μ2，HA： μ1 ≠ μ2 2、计算 t 值
表5-2 非配对设计资料的一般形式
处理 1 2 观察值xij x11, x12,… x1j X21, x22,… x2j 样本含量ni n1 n2i 平均数 总体平均数 μ1 μ2
x1 x2
显著性检验的基本步骤:
（一）提出无效假设与备择假设 （二）计算值 计算公式为：
t x1 x 2 S x1 x2
结论：差异极显著
二、配对设计两样本平均数 差异显著性检验
1、自身配对 2、同源配对 配对设计两样本平均数差异显著性检验的基本步骤： （一）提出无效假设与备择假设 （二）计算 t 值
d t Sd
Sd Sd n
d d
n(n 1)
2
d
2
n(n 1)
( d ) 2 / n
检验步骤：
2、计算 t 值
S x1 x2
( x1 x1 ) 2 ( x2 x2 ) 2 ( 1
(n1 1) (n 2 1)
n1
1 ) n2
1、提出无效假设与备择假设
sx1 x2
2 S12 (n1 1) S2 (n2 1) 1 1 (n1 1) n2 1) n1 n2
|t|<t0.05， |t|≥ t0.01 ， 则 P>0.05 则 P≤0.01 差异不显著 差异显著 差异极显著 t0.01 ≤|t|< t0.05 ，则 0.01<P≤0.05
ni
检验步骤：
1、提出无效假设与备择假设 H0：μ1=μ2，HA： μ1 ≠ μ2 2、计算 t 值
表5-2 非配对设计资料的一般形式
处理 1 2 观察值xij x11, x12,… x1j X21, x22,… x2j 样本含量ni n1 n2i 平均数 总体平均数 μ1 μ2
x1 x2
显著性检验的基本步骤:
（一）提出无效假设与备择假设 （二）计算值 计算公式为：
t x1 x 2 S x1 x2
结论：差异极显著
二、配对设计两样本平均数 差异显著性检验
1、自身配对 2、同源配对 配对设计两样本平均数差异显著性检验的基本步骤： （一）提出无效假设与备择假设 （二）计算 t 值
d t Sd
Sd Sd n
d d
n(n 1)
2
d
2
n(n 1)
( d ) 2 / n
检验步骤：
2、计算 t 值
S x1 x2
( x1 x1 ) 2 ( x2 x2 ) 2 ( 1
(n1 1) (n 2 1)
n1
1 ) n2
1、提出无效假设与备择假设
sx1 x2
2 S12 (n1 1) S2 (n2 1) 1 1 (n1 1) n2 1) n1 n2
|t|<t0.05， |t|≥ t0.01 ， 则 P>0.05 则 P≤0.01 差异不显著 差异显著 差异极显著 t0.01 ≤|t|< t0.05 ，则 0.01<P≤0.05
第八章 假设检验 (《统计学》PPT课件)
与其，为选取“适当的”的而苦恼，不如干脆 把真正的（P值）算出来。
第二节 一个正态总体的假设检验
一、正态总体
设总体X ~ N(m, 2)，抽取容量为n的样本 x1, x2, xn
样本均值 X 与方差S2 计算公式分别为：
2
1 n 1
n i1
(xi
X)
我们将利用上述信息，来检验关于未知参数均值 和方差的假设。
总体参数
均值
方差
总体方差已知
z 检验
(单尾和双尾)
总体方差已知
t 检验
(单尾和双尾)
2 检验
(单尾和双尾)
第二节 一个正态总体的假设检验
二、均值m的假设检验
1.H0:m=m0
2.选择检验统计量：
2已知： Z X m0 ~ N(0，1)
/ n
2未知：
小样本： t X m0 ~ t(n 1)
这个值不像我 们应该得到的 样本均值 ...
...因此我们拒绝 原假设μ=50
... 如果这是总 体的假设均值
60
μ=80
H0
样本均值
第一节 假设检验概述
三、假设检验的程序
一个完整的假设检验过程，通常包括以下几个步骤：
首先，设立原假设H0与备选假设H1； 第二步，构造检验统计量，并根据样本观察数据
小样本：当 t t
2
，则拒绝原假设，反之则接受H0；
5.得出结论。
二、均值m的假设检验
6.例题分析
[例8.3] 某广告公司在广播电台做流行歌曲磁带广告 ，它的插播广告是针对平均年龄为21岁的年轻人的，标 准差为16。这家广告公司经理想了解其节目是否为目标 听众所接受。假定听众的年龄服从正态分布，现随机抽 取400多位听众进行调查，得出的样本结果为x 25 岁S2，18 。以0.05的显著水平判断广告公司的广告策划是否符合 实际？
第二节 一个正态总体的假设检验
一、正态总体
设总体X ~ N(m, 2)，抽取容量为n的样本 x1, x2, xn
样本均值 X 与方差S2 计算公式分别为：
2
1 n 1
n i1
(xi
X)
我们将利用上述信息，来检验关于未知参数均值 和方差的假设。
总体参数
均值
方差
总体方差已知
z 检验
(单尾和双尾)
总体方差已知
t 检验
(单尾和双尾)
2 检验
(单尾和双尾)
第二节 一个正态总体的假设检验
二、均值m的假设检验
1.H0:m=m0
2.选择检验统计量：
2已知： Z X m0 ~ N(0，1)
/ n
2未知：
小样本： t X m0 ~ t(n 1)
这个值不像我 们应该得到的 样本均值 ...
...因此我们拒绝 原假设μ=50
... 如果这是总 体的假设均值
60
μ=80
H0
样本均值
第一节 假设检验概述
三、假设检验的程序
一个完整的假设检验过程，通常包括以下几个步骤：
首先，设立原假设H0与备选假设H1； 第二步，构造检验统计量，并根据样本观察数据
小样本：当 t t
2
，则拒绝原假设，反之则接受H0；
5.得出结论。
二、均值m的假设检验
6.例题分析
[例8.3] 某广告公司在广播电台做流行歌曲磁带广告 ，它的插播广告是针对平均年龄为21岁的年轻人的，标 准差为16。这家广告公司经理想了解其节目是否为目标 听众所接受。假定听众的年龄服从正态分布，现随机抽 取400多位听众进行调查，得出的样本结果为x 25 岁S2，18 。以0.05的显著水平判断广告公司的广告策划是否符合 实际？
第五章 t检验
选择题：
1. 按α=0.10水准做t检验，P>0.10，不能认为两总体均 数不相等，此时若推断有错，其错误的概率为 （ ）。 A．大于0.10 B．β,而β未知 C．小于0.10 D．1-β,而β未知
2．某地正常成年男子红细胞的普查结果，均数为480 万/mm3，标准差为41.0万/mm3，后者反映（ ） A．个体变异 B．抽样误差 C．总体均数不同 D．均数间变异
(2) 当 p > , 不能拒绝 H0, 不能接受H1，按不能接受 H1下结论，也可能犯错误；
2、第 I 类错误和第 II 类错误
假设检验的结果有两种。
(1)
当拒绝 H0 时, 可能犯错误，可能拒绝了实际 上成立的H0， 称为 І 类错误（ “弃真”的错 误 ），其概率大小用 α 表示。 H0 时，也可能犯错误，没有拒绝 实际上不成立的H0 , 这类称为 II 类错误（ ”存 伪”的错误）, 其概率大小用 β 表示, β 值一般 不能确切的知道。
• .某市250名8岁男孩体重 有95%的人在18～30kg 范围内，由此可推知此 250名男孩体重的标准差 大约为 • A. 2 kg • B. 2.326 kg • C. 6.122 kg • D. 3.061 kg • E. 6 kg
• 同样性质的两项研究工作 中，都作两样本均数差别 的假设检验，结果均为P＜ 0.05，P值越小,则 • A. 两样本均数差别越大 • B. 两总体均数差别越大 • C. 越有理由说两总体均 数不同 • D. 越有理由说两样本均 数不同 • E. 越有理由说两总体均 数差别很大
3. 统计学中的差异显著或不显著，和日常生
活中所说的差异大小概念不同. （不仅区别于均
数差异的大小，还区别于均数变异的大小)
东华大学《概率论与数理统计》课件 第七章 假设检验
1. 2为已知, 关于的检验(U 检验 )
在上节中讨论过正态总体 N ( , 2 ) 当 2为已知时, 关于 = 0的检验问题 :
假设检验 H0 : = 0 , H1 : 0 ;
我们引入统计量U
=
− 0 0
，则U服从N(0,1)
n
对于给定的检验水平 (0 1)
由标准正态分布分位数定义知，
~
N (0,1),
由标准正态分布分位点的定义得 k = u1− / 2 ,
当 x − 0 / n
u1− / 2时, 拒绝H0 ,
x − 0 / n
u1− / 2时,
接受H0.
假设检验过程如下:
在实例中若取定 = 0.05, 则 k = u1− / 2 = u0.975 = 1.96, 又已知 n = 9, = 0.015, 由样本算得 x = 0.511, 即有 x − 0 = 2.2 1.96,
临界点为 − u1− / 2及u1− / 2.
3. 两类错误及记号
假设检验是根据样本的信息并依据小概率原
理，作出接受还是拒绝H0的判断。由于样本具有 随机性，因而假设检验所作出的结论有可能是错
误的. 这种错误有两类:
(1) 当原假设H0为真, 观察值却落入拒绝域, 而 作出了拒绝H0的判断, 称做第一类错误, 又叫弃
设 1,2, ,n 为来自总体 的样本,
因为 2 未知, 不能利用 − 0 来确定拒绝域. / n
因为 Sn*2 是 2 的无偏估计, 故用 Sn* 来取代 ,
即采用 T = − 0 来作为检验统计量.
Sn* / n
当H0为真时,
− 0 ~ t(n −1),
Sn* / n
由t分布分位数的定义知
(06)第6章 假设检验(T6)PPT课件
备择假设的方向为“<”，称为左侧检验 备择假设的方向为“>”，称为右侧检验
6 - 14
7/16/2020
统计学
STATISTICS (第六版)
双侧检验与单侧检验
(假设的形式)
以总体均值的检验为例
假设
双侧检验
单侧检验 左侧检验 右侧检验
原假设 H0 : =0 H0 : 0 H0 : 0
备择假设 H1 : ≠0 H1 : <0 H1 : >0
已经成了一种 37.1 36.2 36.3 37.5 36.9
共识。下面是 一个研究人员
37.0
36.7
36.9
37.0
37.1
测量的50个健 36.6 37.2 36.4 36.6 37.3
康成年人的体 36.1 37.1 37.0 36.6 36.9
温数据
36.7 37.2 36.3 37.1 36.7
2. 所表达的含义是总体参数发生了变化或变量之间 有某种关系或总体分布于某种理论分布有差异
3. 备择假设通常用于表达研究者自己倾向于支持的 看法，然后就是想办法收集证据拒绝原假设，以 支持备择假设
alternative 4. 总是有符号 , 或 H1 ： 某一数值 H1 ： 某一数值 H1 ： <某一数值
36.8 37.0 37.0 36.1 37.0
6-6
7/16/2020
统计学
STATISTICS (第六版)
正常人的平均体温是37oC吗？
➢ 根据样本数据计算的平均值是36.8oC ，标准差 为0.36oC
➢ 根据参数估计方法得到的健康成年人平均体温的 95%的置信区间为(36.7，36.9)。研究人员发现 这个区间内并没有包括37oC
6 - 14
7/16/2020
统计学
STATISTICS (第六版)
双侧检验与单侧检验
(假设的形式)
以总体均值的检验为例
假设
双侧检验
单侧检验 左侧检验 右侧检验
原假设 H0 : =0 H0 : 0 H0 : 0
备择假设 H1 : ≠0 H1 : <0 H1 : >0
已经成了一种 37.1 36.2 36.3 37.5 36.9
共识。下面是 一个研究人员
37.0
36.7
36.9
37.0
37.1
测量的50个健 36.6 37.2 36.4 36.6 37.3
康成年人的体 36.1 37.1 37.0 36.6 36.9
温数据
36.7 37.2 36.3 37.1 36.7
2. 所表达的含义是总体参数发生了变化或变量之间 有某种关系或总体分布于某种理论分布有差异
3. 备择假设通常用于表达研究者自己倾向于支持的 看法，然后就是想办法收集证据拒绝原假设，以 支持备择假设
alternative 4. 总是有符号 , 或 H1 ： 某一数值 H1 ： 某一数值 H1 ： <某一数值
36.8 37.0 37.0 36.1 37.0
6-6
7/16/2020
统计学
STATISTICS (第六版)
正常人的平均体温是37oC吗？
➢ 根据样本数据计算的平均值是36.8oC ，标准差 为0.36oC
➢ 根据参数估计方法得到的健康成年人平均体温的 95%的置信区间为(36.7，36.9)。研究人员发现 这个区间内并没有包括37oC