大学物理学-气体动理论基础教案
大学物理-气体分子动理论

v
v1 v2 v3 … …
N ΔN1 ΔN2 ΔN3 … …
速率为 vi 的概率为:
Pi
Ni N
长时间“观测”理想气体分子的速率 v :
v
0 ~ +∞ 连续分布
速率为 v → v + dv 的概率为:
Pv~vdv
dNv N
0
???
速率分布函数
Pv~vdv
dNv N
f (v)dv
f (v) dNv Ndv
刚性双原子分子的动能
分子动能
平动动能
t x
t y
t z
转动动能
r
r
t x
t y
t z
r
r
1 kT 2
t x
t y
t z
r
r
5 kT 2
温度较高时,双原子气体分子不能看作刚性分子,分子
平均能量更大,因为振动能量也参与能量均分
理想气体分子的平均能量
分子模型 刚性单原子分子 刚性双原子分子 刚性多原子分子
每个分子频繁地发生碰撞,速度也因此不断变化;
二、压强形成的微观解释
单个分子与器壁碰撞 冲力作用瞬间完成,大小、位置具有 偶然性;
大量分子(整个气体系统)与器壁碰撞 气体作用在器壁上是一个持续的、不 变的压力;
压强是气体分子给容器壁冲量的 统计平均量
三、理想气体的压强公式
建立三维直角坐标系 Oxyz
vz i N
气体处于平衡态时,气体分子沿各个方向运动的机会均等。
vx vy vz
气体分子速率平方的平均值
v v1 v2 v3 … …
N ΔN1 ΔN2 ΔN3 … …
v
大学物理第十二章气体动理论第6节 麦克斯韦气体分子速率分布律
解
m(H 2 ) m(O2 ) v p ( H 2 ) v p (O 2 )
vp (H2 ) 2 000m.s-1
2kT vp m
o
2 000
v/ ms
1
vp ( H 2 )
m( O 2 ) 32 4 v p (O 2 ) m( H 2 ) 2
vp (O2 ) 500m.s
f ( v)
dS
dN f ( v)dv dS N
v
第十二章 气体动理论
o
v v dv
概率密度
3
物理学
第五版
12-6 麦克斯韦气体分子速率分布律
f (v)dv物理意义
表示在温度为 T 的平衡状态下,速 率在 v 附近单位速率区间 的分子数占总 数的百分比 .
f (v)dv 的物理意义:
表示速率在 v v dv 区间的分 子数占总分子数的百分比.
第十二章 气体动理论
4
物理学
第五版
12-6 麦克斯韦气体分子速率分布律 麦克斯韦气体分子速率分布律 12-6
dN Nf ( v)dv 速率在 v v dv 内分子数: 速率位于 v1 v2区间的分子数: v2 N v N f (v)dv 1 速率位于 v1 v2 区间的分 f ( v)
-1
第十二章 气体动理论
17
f (v )
vp v v
2
第十二章 气体动理论
vp v 2 v
v
15
物理学
第五版
12-6 麦克斯韦气体分子速率分布律 麦克斯韦气体分子速率分布律 12-6
讨论 1 已知分子数 N ,分子质量 m ,分布函 数 f ( v) . 求 (1) 速率在 vp ~ v 间的分子 数;(2)速率在 vp ~ 间所有分子动能 之和 . 解 ( 1)
(大学物理课件)气体动理论

—气体压强公式
Ⅲ 温度的统计意义
由
p
2 3
n t
和p nkT
t
3 2
kT ,即T 和t
单值对应
由此给出温度的统计意义 —
T是大量分子热运动平均平动动能的量度。
t
1 2
mv 2
t
3 2
kT
v2 3kT m
3 RT
T,
v 2 称为方均根速率 (root-mean-square
Ⅳ 能量均分定理
2 . 理想气体
宏观上,满足理想气体状态方程的气体 微观假设: (1)大小 — 分子线度<<分子间平均距离; (2)分子力 — 除碰撞的瞬间,在分子之间
分子与器壁之间无作用力; (3)碰撞性质 — 弹性碰撞; (4)服从规律 — 牛顿力学。
二、等概率假设
(1)分子在各处出现的概率相同
ndNNcon.st dV V
dI dIi
(vix0)
1
2 i dIi
i
ni
mv
2 ix
d
t
d
A
(viy和viz可取任意值)
第4步:pd dF Add tdIA i nimvi2x
i
Ni V
mvi2x
V NmN Nivi2xnm v2x
1 nmv 2 3
由分子平均平动动能 t
1 2
mv 2
和p 1nmv2 3
有
p
2 3
n t
v — 振动自由度,
v=1
∴ 总自由度: i = t + r + v = 6
3. 多原子分子 (multi-atomic molecule)
如:H2O,NH3 ,…
A31_气体动理论

第一章
气体动理论
气体动理论是统计物理学最基本,最简单的内容, 气体动理论是统计物理学最基本,最简单的内容,它是从物质 是统计物理学最基本 的分子结构概念出发, 的分子结构概念出发,对气体分子运动及相互作用提出一定的 假设模型 再根据每个气体分子所遵从的力学规律 利用统计 模型, 力学规律, 假设模型,再根据每个气体分子所遵从的力学规律,利用统计 方法找出热运动的宏观量(如压强,温度等)与分子运动微观 找出热运动的宏观量 方法找出热运动的宏观量(如压强,温度等)与分子运动微观 量的统计平均值之间的关系 之间的关系. 量的统计平均值之间的关系.
六,热力学温标
P
液相 宏观上,用温度来表示物体的冷热程度, 宏观上,用温度来表示物体的冷热程度, 冷热程度 固相 临界点 微观上,温度的高低反映分子热运动激烈程度 分子热运动激烈程度. 微观上,温度的高低反映分子热运动激烈程度 609Pa 气相 温度的数值表示方法叫作温标,常用的有: 温度的数值表示方法叫作温标,常用的有 T (1)摄氏温标 ,单位:oC 1742年 瑞典 摄修斯273.16 K 摄氏温标t 单位: 摄氏温标 年 0oC——冰的熔点温度 100oC——水的沸腾点温度 冰的熔点温度 水的沸腾点温度 (2)华氏温标 , 单位0F 只有美国等少数国家仍在使用 华氏温标F, 华氏温标 1712年左右 1712年左右,德国物理学家华伦海特 年左右, 冰与盐混和后: ℉ 人体温度: ℉ 等分成100个刻度. 个刻度. 冰与盐混和后:0℉,人体温度:100℉,等分成 个刻度 320F ——水的冰点温度 水的冰点 2120F——水的沸点温度 水的冰点温度 水的沸点温度
3,热力学第零定律或热平衡定律 ,
A B A,B 两体系互不影响, , 两体系互不影响, 各自达到平衡态 绝热板 A B A,B 两体系的平衡态有联系, , 两体系的平衡态有联系, 达到共同的热平衡状态 导热板
大学物理第16章气体动理论

pA
lim N
NA N
1 2
抛硬币的 统计规律
2020/1/15
DUT 余 虹
4
16.1 理想气体的压强
一、分子的作用力与压强
总数N 个,分子质量m ,摩尔质量,
体积V,温度T。
F
气体分子频繁碰撞 容器壁——给容器
壁冲量。大量分子在t 时间内给予I
的冲量,宏观上表现为对器壁的平均
vf
v
d
v
0
f
vd v
0
vf
v d
v
麦克斯韦分布律
v 1.60 RT
2020/1/15
DUT 余 虹
21
(3)方均根速率 v 2
一段速率区间v1~v2的方均速率
f v
v122
v2 v 2 d N N v v2 2 f v d v
v1 v2 d N
作用力
F I t
气体对容器壁的压强
P F I S S t
2020/1/15
DUT 余 虹
5
二、P 与微观量 的关系
分子按速度区 间分组
第i 组: 速度 近vi 似~ 认vi 为 都dv是i v i
分子数N
i ,分子数密度
ni
Ni V
考察这组分子给面元A的冲量
一 碰壁前速度 vix viy viz
一、速率分布函数
处于平衡态的气体,每个分子 朝各个方向运动的概率均等。
可是大量分子速度分 量的方均值相等。
一个分子,某一时刻速度
v
通常 v xv y v z
v
大学物理,气体动理论14-06 麦克斯韦气体分子速率分布律

i ~ i 1
N i
N i N
5
14.6 麦克斯韦速率分布律
第14章 气体动理论
气体分子按速率分布的统计规律最早是由麦克 斯韦于1859年在概率论的基础上导出的,1877年玻 耳兹曼由经典统计力学导出。 由于技术条件的限制,测定气体分子速率分布 的实验,直到20世纪二十年代才实现。 1920年斯特 恩首先测出银蒸汽分子的速率分布;1934年我国物 理学家葛正权测出铋蒸汽分子的速率分布;1955年 密勒和库士测出钍蒸汽分子的速率分布。 斯特恩实验是历史上最早验证麦克斯韦速率分 布律的实验。实验证实了麦克斯韦的分子按速率分 布的统计规律。
14.6 麦克斯韦速率分布律
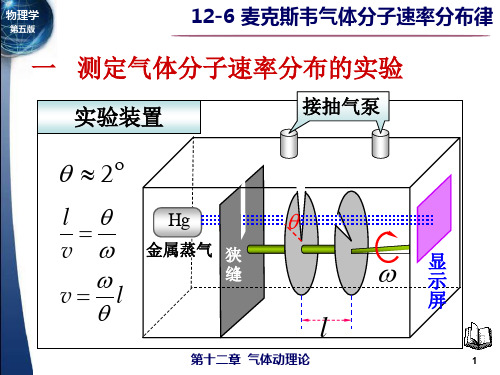
一 测定气体分子速率分布的实验
第14章 气体动理论
实验装置
接抽气泵
2
l v
Hg
金属蒸汽 狭 缝
v l
显 示 屏
8
l
14.6 麦克斯韦速率分布律
第14章 气体动理论
9
14.6 麦克斯韦速率分布律
测量原理
第14章 气体动理论
(1) 能通过细槽到达检测 器的分子所满足的条件 L v L v (2) 通过改变角速度ω的 大小,选择速率 v
28
14.6 麦克斯韦速率分布律
第14章 气体动理论
求:速率在 v1 ~ v2 之间的分子的平均速率。
(3) 通过细槽的宽度,选择不同的速率区间 L v v 2
(4) 沉积在检测器上相应的金属层厚度必定正比 相应速率下的分子数。
10
14.6 麦克斯韦速率分布律
速率区间 (m/s) 实验数据 氧分子在 273K时的 速率分布
河海大学《大学物理》第十四章 气体动理论2

S
N
v2
v1
N
f
(v)dv
o
v1 v2
v 速率位于v1 v2 区间的
分子数占总数的百分比:
N
N
v2 v1
f
(v)dv
二.麦克斯韦气体分子速率分布定律
麦氏分布函数
f (v) 4π(
m
) e v 3 2
mv 2 2kT
2
2πkT
f (v)
速率分布曲线图
o
v
三. 三种统计速率
(1)最概然速率 vp
C
x’
z’
x
单原子分子:一个原子构成一个分子
氦、氩等
三个自由度
双原子分子:两个原子构成一个分子
氢、氧、氮等
五个自由度
多原子分子:三个以上原子构成一个分子
水蒸汽、甲烷等
六个自由度
二.能量按自由度均分定理
1.理想气体分子的平均平动动能是
1 mv2 3 kT
2
2
式中
v2
v
2 x
v
2 y
vz2
在平衡态下
2.4910(4 J)
§14-5 麦克斯韦速度分
布律
一. 速率分布函数
1.定义
对于单个分子而言,其 运动方向,大小都具有偶然 性;对于大量分子而言,其 速率的分布却有其规律性;
偶然性
规律性
1859年,麦克斯韦从理论上导出了气体分子的速率 分布规律,——麦克斯韦速率分布律.
分子速率分布图 N : 分子总数
vp v v2
讨论
1 已知分子数 N ,分子质量 m ,分布函
数 f (v) . 求 (1) 速率在 vp ~ v 间的分子
大学物理(下)1气体动理论25页PPT

15、机会是不守纪律的。——雨果
16、业余生活要有意义,不要越轨。——华盛顿 17、一个人即使已登上顶峰,也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人,而用人最大的突破在于信任人。——马云 19、自己活着,就是为了使别人过得更美好。——雷锋 20、要掌握书,莫被书掌握;要为生而读,莫为读而生。——布尔沃
END
大学物理(下)1气体动理论
11、战争满足了,或曾经满足过人的 好斗的 本能, 但它同 时还满 足了人 对掠夺 ,破坏 以及残 酷的纪 律和专 制力的 欲望。 ——查·埃利奥 特 12、不应把纪律仅仅看成教育的手段 。纪律 是教育 过程的 结果, 首先是 学生集 体表现 在一切 生活领 域—— 生产、 日常生 活、学 校、文 化等领 域中努 力的结 果。— —马卡 连柯(名 言网)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
温度的分度方法叫温标,常用的有热力学温标(T)和摄氏温标(t).热力学温度与摄氏温度的关系为T=t+273.15三、理想气体状态方程当系统处于平衡态时,描写该平衡态下各个状态参量之间的关系式叫系统的状态方程。
1.理想气体:在压强不太大、温度不太低的条件下,严格遵守气体实验三定律的气体。
2.理想气体状态方程:一定质量的理想气体在平衡态下的状态方程为RTMMpVmol=, R=8.31J·mol-1·K-13.平衡态图示表示一个平衡态可由p-V图中对应的一个点来代表一条连续曲线代表一个由平衡态组成的变化过程,曲线上的箭头表示过程进行的方向。
平衡状态示意图§7.2 理想气体压强公式气体对器壁的压强应该是大量分子对容器不断碰撞的统计平均结果.一、理想气体分子模型和统计假设1.理想气体的分子模型(1) 分子可以看作质点。
(2) 除碰撞外,分子力可以略去不计。
(3) 分子间的碰撞是完全弹性的。
2.理想气体分子的统计假设在平衡态下:(1) 无外场时,气体分子在各处出现的概率相同。
(2) 由于碰撞,分子可以有各种不同的速度,速度取向各方向等概率。
222231vvvvvvvzyxzyx=====;二、理想气体的压强公式在平衡态下,大量理想气体分子弹性的自由运动的质点分子的数密度n处处相同气体压强公式的推导图1.先考察一个分子(如分子i )一次碰撞中给予器壁的冲量∆P mv mv mv ix ix ix ix =--=-()2由牛顿第三定律,分子i 给予器壁的冲量为2mv ix 2.分子i 在单位时间内施于A 1面的平均冲力单位时间内分子i 与A 1面碰撞的次数 v l ix21单位时间分子i 内施于A 1面的总冲量(冲力)221112mv v l l mv ix ix ix ⋅=3.所有分子在单位时间内对器壁的冲力──对i 求和F m l v m l v A i Nix ix i N 1112121====∑∑NNiix iiiix x ∑∑∑==222υυυ,表示分子在x 方向速度平方的平均值,于是所有分子在单位时间内施于A 1面的冲力为F m l N v A x 112= 4.求压强的统计平均值2321321xA v m l l l N l l F p == n Nl l l =123为分子数密度(即单位体积内的分子数)又由统计平均的观点有 222231υυυυ===z y xmolMRTmkTv332==∴(其数量级是102m/s)在0℃时,氢的方均根速率为1830m/s,氧为461m/s。
§7.4 能量均分定理理想气体的内能气体的能量与分子结构有关,为了确定分子各种运动形式的能量要引用力学中自由度的概念.一、自由度决定一个物体的空间位置所需要的独立坐标数,称为物体的自由度.1.单原子分子(如惰性气体),视作质点.平动自由度t= 3.分子自由度i=t=32.双原子分子(如H2、O2、N2等),可视作轻杆哑铃,刚性分子: 平动自由度:t =3, 转动自由度:r =2分子自由度i =t+r =5对于非刚性分子,增加1个振动自由度s=1,则i =t+r+s =63.多原子分子(如H2O、NH3等)刚性分子: 平动自由度:t =3, 转动自由度:r =3分子自由度i =t+r =6对于N个原子组成非刚性分子,i = t + r +s= 3N其中t =3, r =3,s = 3N - 6二、能量均分定理kTvm23212=v v v vx y z222213===∴有12121213121332122222mv mv mv mv kT kTx y z=====()()气体处于平衡态时,分子的任何一个自由度的平均动能都相等,均为12kT,这就是能量按自由度均分定理特殊情况除外,如对称性CO2分子§7.5 麦克斯韦分子速率分布定律一、气体分子的速率分布分布函数由于分无规则热运动,分子任一时刻的速度具有偶然性,但大量分子从整体上会出现一些统计规律.1.描写速率分布的方法有三种:(1)根据实验数据列表——分布表;(2)作出曲线——分布曲线;(3)找出函数关系——分布函数.把速率分成若干相等的区间.如教材表7.1, 气体在平衡状态下,分布在各个速率区间Δv之内的分子数ΔN,各占气体分子总数N的百分比。
气体分子速率分布曲线.如图,气体分子速率分布曲线2.速率分布函数:∆NN分布在相等间隔的速率区间υυυ∆+→内的分子数△N占总分子数的百分比,υ∆⋅∆NN,表示单位速率区间内分子数占总分子数的百分比.取极限, 即分子的速率分布函数:υυυddNNNNfv1lim)(==→∆∆∆它表示速率v附近的单位速率区间内的分子数占总分子数的百分比(比率).f(v)-v曲线叫做气体分子的速率分布曲线.速率分布函数满足归一化条件1)(=⎰∞υυdf二、麦克斯韦速率分布规律1860年,麦克斯韦从理论上导出平衡态理想气体在无外力场作用时,气体分子速率分布布函数f(v)222/32)2(4)(vekTmvf kTmv⋅⋅=-ππ式中T为气体的热力学温度;m为分子的质量;k为玻尔兹曼常量.麦克斯韦速率分布定律:dvvekTmkTmv222/32)2(4-⋅=ππNdN2.测定分子速率分布的实验测定分子速率分布的实验装置A为分子源,小缝S、以ω旋转的圆筒B,G为贴在圆筒内壁的玻璃板。
圆筒不转时,分子射在玻璃板的P处。
圆筒以ω旋转时,速率为v的分子通过从S到玻璃板的距离D需要的时间内,圆筒转过一个角度υDωθ⋅=。
故速率为v的分子落在玻璃板的p/处。
D为圆筒的直径,设pp/的弧长为l、显然有DωlωθυD2==或vωDl22=测量玻璃板上不同弧长l处沉积的厚度和分子速率,即可求得分子束中各种速率v附近的分子数占总分子数的比率,从而得出分子速率分布率。
三、分子速率的三个统计值1. 最概然速率v p分子速率分布函数的极大值对应的速率叫分子的最概然速率,用v p表示。
由极值条件0=dvdf可求得molmolp MRT.MRTmkTv41122≈==2.平均速率v⎰⎰⎰∞∞∞===0)(υυυυυυdfNdNNdN把麦克斯韦速率分布函数f(v)代入,可得理想气体速率从0到∞的算术平均速率为molmolMRT.MRTmkT60122≈==ππυ3.方均根速率__2v:分子速率平方值的平方根。
根据⎰⎰⎰∞∞∞===2222)(υυυυυυdfNdNNNd可得molmolMRT.MRTmkT73133__2≈==υ四、麦氏速度分布曲线的性质1.温度与分子速率同一种分子,温度越高最概然速率越大;速率分布曲线宽度越大、高度越小。
2.质量与分子速率在相同的温度下,质量大的气体分子最概然速率小;速率分布曲线宽度变窄、高度增大。
§7.7 分子平均碰撞频率和平均自由程一、平均碰撞次频率1.分子的有效直径d将分子看成是具有一定体积的弹性小球,分子的有效直径d定义为两个分子质心之间的所能允许的最小距离。
2.分子的平均碰撞频率z:一个分子在单位时间内与其它分子碰撞的平均次数为简单计,假定气体中只有一个分子(例如A分子)以平均相对速率u运动,而其它分子认为是静止不运动的。
这样,在A分子运动的路径上,分子中心与A 分子中心的距离小于或等于分子有效直径d的分子都会与A分子发生碰撞。
为此,以A分子中心的运动轨迹为曲线,以分子直径d为半径,做一曲折圆柱体。
则有vnππz2=可以证明:气体分子的平均相对速率u与平均速率v间有vu2=,故得v ndz⋅=22π。
