2010年高一下期人教A版必修3+必修4数学期末测试试卷

合集下载

人教版高一数学必修1必修4期末测试卷附答案

人教版高一数学必修1必修4期末测试卷附答案人教版高一数学必修1必修4期末测试卷姓名：__________ 班级：___________ 学号：____________ 分数：______________一、选择题（每题5分，共40分）1.集合A={x∈N*｜-1<x<3}的子集的个数是（。

）。

A。

4.B。

8.C。

16.D。

322.函数f(x)=1/(1-x)+lg(1+x)的定义域是（。

）。

A。

(-∞,-1)。

B。

(1,+∞)。

C。

(-1,1)U(1,+∞)。

D。

(-∞,+∞)3.设a=log2,c=5-1/3,b=ln22，则（。

）。

A。

a<b<c。

B。

b<c<a。

C。

c<a<b。

D。

c<b<a4.函数y=-x^2+4x+5的单调增区间是（。

）。

A。

(-∞,2]。

B。

[-1,2]。

C。

[2,+∞)。

D。

[2,5]5.已知函数f(x)=x^2-2ax+3在区间(-2,2)上为增函数，则a的取值范围是（。

）。

A。

a≤2.B。

-2≤a≤2.C。

a≤-2.D。

a≥26.下列函数中，既是偶函数，又在区间(0,+∞)上单调递减的函数是（。

）。

A。

y=x-2.B。

y=x-1.C。

y=x^2.D。

y=x^37.若函数f(x)=x/(2x+1)(x-a)为奇函数，则a=（。

）。

A。

1/2.B。

2/3.C。

3/4.D。

1/88.已知α是第四象限角，XXX(π-α)=5/12，则sinα=（。

）。

A。

1/5.B。

-1/5.C。

5.D。

-59.若tanα=3，则sinαcosα=（。

）。

A。

3.B。

3/2.C。

3/4.D。

9/410.sin600°的值为（。

）。

A。

3/2.B。

-3/2.C。

-1/2.D。

1/211.已知cosα=3/5，π/4<α<π，则XXX(α+π/4)=（。

）。

A。

1.B。

-1.C。

5/8.D。

-5/812.在△ABC中，sin(A+B)=sin(A-B)，则△ABC一定是（。

高中数学(人教A版)必修4第3章三角恒等变换测试题(含详解)

第三章测试(时间：120分钟，满分：150分)一、选择题(本大题共12小题，每题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．sin105°cos105°的值为( ) A.14 B ．－14C.34D ．－34解析原式＝12sin210°＝－12sin30°＝－14.答案 B2．若sin2α＝14，π4<α<π2，则cos α－sin α的值是( )A.32B ．－32C.34D ．－34解析 (cos α－sin α)2＝1－sin2α＝1－14＝34.又π4<α<π2， ∴cos α<sin α，cos α－sin α＝－34＝－32. 答案 B3．sin15°sin30°sin75°的值等于( ) A.14 B.34 C.18D.38解析 sin15°sin30°sin75° ＝sin15°cos15°sin30° ＝12sin30°sin30°＝12×12×12＝18. 答案 C4．在△ABC 中，∠A ＝15°，则 3sin A －cos(B ＋C )的值为( ) A. 2 B.22C.32D. 2解析在△ABC 中，∠A ＋∠B ＋∠C ＝π， 3sin A －cos(B ＋C ) ＝3sin A ＋cos A ＝2(32sin A ＋12cos A ) ＝2cos(60°－A )＝2cos45°＝ 2. 答案 A5．已知tan θ＝13，则cos 2θ＋12sin2θ等于( )A ．－65B ．－45C.45D.65解析原式＝cos 2θ＋sin θcos θcos 2θ＋sin 2θ＝1＋tan θ1＋tan 2θ＝65.答案 D6．在△ABC 中，已知sin A cos A ＝sin B cos B ，则△ABC 是( ) A ．等腰三角形 B ．直角三角形 C ．等腰直角三角形D ．等腰三角形或直角三角形解析 ∵sin2A ＝sin2B ，∴∠A ＝∠B ，或∠A ＋∠B ＝π2.答案 D 7．设a ＝22(sin17°＋cos17°)，b ＝2cos 213°－1，c ＝32，则( ) A ．c <a <b B ．b <c <a C ．a <b <c D ．b <a <c 解析 a ＝22sin17°＋22cos17°＝cos(45°－17°)＝cos28°，b ＝2cos 213°－1＝cos26°，c ＝32＝cos30°， ∵y ＝cos x 在(0,90°)内是减函数， ∴cos26°>cos28°>cos30°，即b >a >c . 答案 A8．三角形ABC 中，若∠C >90°，则tan A ·tan B 与1的大小关系为( ) A ．tan A ·tan B >1 B. tan A ·tan B <1 C ．tan A ·tan B ＝1D ．不能确定解析在三角形ABC 中，∵∠C >90°，∴∠A ，∠B 分别都为锐角．则有tan A >0，tan B >0，tan C <0. 又∵∠C ＝π－(∠A ＋∠B )，∴tan C ＝－tan(A ＋B )＝－tan A ＋tan B1－tan A ·tan B <0，易知1－tan A ·tan B >0，即tan A ·tan B <1. 答案 B9．函数f (x )＝sin 2⎝⎛⎭⎫x ＋π4－sin 2⎝⎛⎭⎫x －π4是( ) A ．周期为π的奇函数 B ．周期为π的偶函数 C ．周期为2π的奇函数 D ．周期为2π的偶函数解析 f (x )＝sin 2⎝⎛⎭⎫x ＋π4－sin 2⎝⎛⎭⎫x －π4 ＝cos 2⎝⎛⎭⎫π4－x －sin 2⎝⎛⎭⎫x －π4 ＝cos 2⎝⎛⎭⎫x －π4－sin 2⎝⎛⎭⎫x －π4 ＝cos ⎝⎛⎭⎫2x －π2 ＝sin2x . 答案 A10．y ＝cos x (cos x ＋sin x )的值域是( ) A ．[－2,2] B.⎣⎢⎡⎦⎥⎤1＋22，2C.⎣⎢⎡⎦⎥⎤1－22，1＋22D.⎣⎡⎦⎤－12，32 解析 y ＝cos 2x ＋cos x sin x ＝1＋cos2x 2＋12sin2x＝12＋22⎝⎛⎭⎫22sin2x ＋22cos2x ＝12＋22sin(2x ＋π4)．∵x ∈R ， ∴当sin ⎝⎛⎭⎫2x ＋π4＝1时，y 有最大值1＋22；当sin ⎝⎛⎭⎫2x ＋π4＝－1时，y 有最小值1－22. ∴值域为⎣⎢⎡⎦⎥⎤1－22，1＋22.答案 C11．已知θ为第二象限角，sin(π－θ)＝2425，则cos θ2的值为( )A.335 B.45 C ．±35D ．±45解析由sin(π－θ)＝2425，得sin θ＝2425.∵θ为第二象限的角，∴cos θ＝－725.∴cos θ2＝±1＋cos θ2＝± 1－7252＝±35. 答案 C12．若α，β为锐角，cos(α＋β)＝1213，cos(2α＋β)＝35，则cos α的值为( )A.5665 B.1665C.5665或1665D ．以上都不对解析 ∵0<α＋β<π，cos(α＋β)＝1213>0，∴0<α＋β<π2，sin(α＋β)＝513.∵0<2α＋β<π，cos(2α＋β)＝35>0，∴0<2α＋β<π2，sin(2α＋β)＝45.∴cos α＝cos [(2α＋β)－(α＋β)]＝cos(2α＋β)cos(α＋β)＋sin(2α＋β)sin(α＋β) ＝35×1213＋45×513＝5665. 答案 A二、填空题(本大题共4小题，每题5分，共20分．将答案填在题中横线上) 13．若1＋tan α1－tan α＝2012，则1cos2α＋tan2α＝______.解析1cos2α＋tan2α＝1＋sin2αcos2α＝sin 2α＋cos 2α＋2sin αcos αcos 2α－sin 2α＝tan 2α＋1＋2tan α1－tan 2α＝(tan α＋1)21－tan 2α＝1＋tan α1－tan α＝2012.答案 201214．已知cos2α＝13，则sin 4α＋cos 4α＝________.解 ∵cos2α＝13，∴sin 22α＝89.∴sin 4α＋cos 4α＝(sin 2α＋cos 2α)2－2sin 2αcos 2α ＝1－12sin 22α＝1－12×89＝59.答案 5915.sin (α＋30°)＋cos (α＋60°)2cos α＝________.解析 ∵sin(α＋30°)＋cos(α＋60°)＝sin αcos30°＋cos αsin30°＋cos αcos60°－sin αsin60°＝cos α，∴原式＝cos α2cos α＝12.答案 1216．关于函数f (x )＝cos(2x －π3)＋cos(2x ＋π6)，则下列命题：①y ＝f (x )的最大值为2； ②y ＝f (x )最小正周期是π；③y ＝f (x )在区间⎣⎡⎦⎤π24，13π24上是减函数；④将函数y ＝2cos2x 的图像向右平移π24个单位后，将与已知函数的图像重合．其中正确命题的序号是________．解析 f (x )＝cos ⎝⎛⎭⎫2x －π3＋cos ⎝⎛⎭⎫2x ＋π6 ＝cos ⎝⎛⎭⎫2x －π3＋sin ⎣⎡⎦⎤π2－⎝⎛⎭⎫2x ＋π6 ＝cos ⎝⎛⎭⎫2x －π3－sin ⎝⎛⎭⎫2x －π3 ＝2·⎣⎡⎦⎤22cos ⎝⎛⎭⎫2x －π3－22sin ⎝⎛⎭⎫2x －π3 ＝2cos ⎝⎛⎭⎫2x －π3＋π4 ＝2cos ⎝⎛⎭⎫2x －π12， ∴y ＝f (x )的最大值为2，最小正周期为π，故①，②正确．又当x ∈⎣⎡⎦⎤π24，13π24时，2x －π12∈[0，π]，∴y ＝f (x )在⎣⎡⎦⎤π24，13π24上是减函数，故③正确．由④得y ＝2cos2⎝⎛⎭⎫x －π24＝2cos ⎝⎛⎭⎫2x －π12，故④正确．答案 ①②③④三、解答题(本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤) 17．(10分)已知向量m ＝⎝⎛⎭⎫cos α－23，－1，n ＝(sin x,1)，m 与n 为共线向量，且α∈⎣⎡⎦⎤－π2，0.(1)求sin α＋cos α的值； (2)求sin2αsin α－cos α的值．解 (1)∵m 与n 为共线向量， ∴⎝⎛⎭⎫cos α－23×1－(－1)×sin α＝0，即sin α＋cos α＝23. (2)∵1＋sin2α＝(sin α＋cos α)2＝29，∴sin2α＝－79.∴(sin α－cos α)2＝1－sin2α＝169. 又∵α∈⎣⎡⎦⎤－π2，0，∴sin α－cos α<0. ∴sin α－cos α＝－43.∴sin2αsin α－cos α＝712. 18．(12分)求证：2－2sin ⎝⎛⎭⎫α＋3π4cos ⎝⎛⎭⎫α＋π4cos 4α－sin 4α＝1＋tan α1－tan α. 证明左边＝2－2sin ⎝⎛⎭⎫α＋π4＋π2cos ⎝⎛⎭⎫α＋π4(cos 2α＋sin 2α)(cos 2α－sin 2α) ＝2－2cos 2⎝⎛⎭⎫α＋π4cos 2α－sin 2α ＝1－cos ⎝⎛⎭⎫2α＋π2cos 2α－sin 2α＝1＋sin2αcos 2α－sin 2α＝(sin α＋cos α)2cos 2α－sin 2α＝cos α＋sin αcos α－sin α＝1＋tan α1－tan α. ∴原等式成立．19．(12分)已知函数f (x )＝2cos2x ＋sin 2x －4cos x . (1)求f ⎝⎛⎭⎫π3的值；(2)求f (x )的最大值和最小值．解 (1)f ⎝⎛⎭⎫π3＝2cos 2π3＋sin 2π3－4cos π3 ＝2×⎝⎛⎭⎫－12＋⎝⎛⎭⎫322－4×12 ＝－1＋34－2＝－94.(2)f (x )＝2(2cos 2x －1)＋(1－cos 2x )－4cos x ＝3cos 2x －4cos x －1＝3⎝⎛⎭⎫cos x －232－73， ∵x ∈R ，cos x ∈[－1,1]，∴当cos x ＝－1时，f (x )有最大值6；当cos x ＝23时，f (x )有最小值－73.20．(12分)已知cos ⎝⎛⎭⎫x －π4＝210，x ∈⎝⎛⎭⎫π2，3π4. (1)求sin x 的值； (2)求sin ⎝⎛⎭⎫2x ＋π3的值．解 (1)解法1：∵x ∈⎝⎛⎭⎫π2，3π4， ∴x －π4∈⎝⎛⎭⎫π4，π2，于是sin ⎝⎛⎭⎫x －π4＝ 1－cos 2⎝⎛⎭⎫x －π4＝7210.sin x ＝sin ⎣⎡⎦⎤⎝⎛⎭⎫x －π4＋π4＝sin ⎝⎛⎭⎫x －π4cos π4＋cos ⎝⎛⎭⎫x －π4sin π4 ＝7210×22＋210×22＝45. 解法2：由题设得22cos x ＋22sin x ＝210，即cos x ＋sin x ＝15.又sin 2x ＋cos 2x ＝1，从而25sin 2x －5sin x －12＝0，解得sin x ＝45，或sin x ＝－35，因为x ∈⎝⎛⎭⎫π2，3π4，所以sin x ＝45. (2)∵x ∈⎝⎛⎭⎫π2，3π4，故 cos x ＝－1－sin 2x ＝－1－⎝⎛⎭⎫452＝－35. sin2x ＝2sin x cos x ＝－2425.cos2x ＝2cos 2x －1＝－725.∴sin ⎝⎛⎭⎫2x ＋π3 ＝sin2x cos π3＋cos2x sin π3＝－24＋7350.21．(12分)已知函数 f (x )＝4cos x sin ⎝⎛⎭⎫x ＋π6－1. (1)求f (x )的最小正周期；(2)求f (x )在区间⎣⎡⎦⎤－π6，π4上的最大值和最小值．解 (1)因为f (x )＝4cos x sin ⎝⎛⎭⎫x ＋π6－1 ＝4cos x ⎝⎛⎭⎫32sin x ＋12cos x －1＝3sin2x ＋2cos 2x －1＝3sin2x ＋cos2x ＝2sin ⎝⎛⎭⎫2x ＋π6所以f (x )的最小正周期为π.(2)－π6≤x ≤π4，所以－π6≤2x ＋π6≤2π3，当2x ＋π6＝π2时，即x ＝π6，f (x )取得最大值2；当2x ＋π6＝－π6时，即x ＝－π6，f (x )取得最小值－1.22．(12分)已知函数f (x )＝sin ⎝⎛⎭⎫x ＋7π4＋cos ⎝⎛⎭⎫x －3π4，x ∈R . (1)求f (x )的最小正周期和最小值；(2)已知cos(β－α)＝45，cos(β＋α)＝－45，0<α<β≤π2，求证：[f (β)]2－2＝0.解 (1)∵f (x )＝sin ⎝⎛⎭⎫x ＋7π4－2π＋sin ⎝⎛⎭⎫x －3π4＋π2 ＝sin ⎝⎛⎭⎫x －π4＋sin ⎝⎛⎭⎫x －π4＝2sin ⎝⎛⎭⎫x －π4， ∴T ＝2π，f (x )的最小值为－2.(2)证明：由已知得cos βcos α＋sin βsin α＝45，cos βcos α－sin βsin α＝－45.两式相加，得2cos βcos α＝0， ∵0<α<β≤π2，∴β＝π2.∴[f (β)]2－2＝4sin 2π4－2＝0.。

河南省郑州市2012-2013高一下期期末数学试题(必修3+必修4)(含答案)(WORD版)

kg ）郑州市2012-2013学年下期期末试题高一数学第Ⅰ卷（选择题共60分）一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的） 1．tan 600的值是A．3-B ．3C ．D ．2．已知向量(4,2)a = ，向量(,3)b x =，且a ∥b ，则x 等于A ．9B ．6C ．5D ．33．某地区有300家商店，其中大型商店有30家，中型商店有75家，小型商店有195家．为了掌握各商店的营业情况，要从中抽取一个容量为20的样本．若采用分层抽样的方法，抽取的中型商店数是A ．2B ．3C ．5D ．134．下列各数化成10进制后最小的数是A ．85（9）B ．210（6）C ．1000（4）D ．111111（2）5．为了了解某地区高三学生的身体发育情况，抽查了该地区 100名年龄为17.5岁—18岁的男生体重（kg ），得到频率分布直方图如右：根据右图可得这 100名学生中体重在[56.5,64.5]的学生人数是 A ．20 B ．30C ．40D ．506．若△ABC 的内角A 满足2sin 23A =，则sin cos A A += AB ．C ．53D ．53-7．已知(,)2παπ∈，3sin 5α=，则tan()4πα+等于A ．17B ．7C ．17- D ．7-8．将函数sin()(0,||2y x πωϕωϕ=+>≤的图象沿x 轴方向向左平移3π则ω，ϕ的值分别为A ．1，3π B ．1，3π- C ．2，3πD ．2，3π-9．已知向量a 与b的夹角为120，||3a = ，||a b += ||b 等于A ．5BC ．2D ．410．要得到函数cos(2)4y x π=-的图象，只需将函数cos(23y x π=+的图象 A ．向左平移24π个单位长度B ．向右平移24π个单位长度C ．向左平移724π个单位长度D ．向右平移724π个单位长度11．已知(2sin cos )(32sin 2cos )0x x x x -++=，则2sin 22cos 1tan x xx++的值为A ．85B ．58C ．43D ．3412．已知sin ,0()(1)1,0x x f x f x x π<⎧=⎨-->⎩，则1111(()66f f -+的值为A ．0B ．12C ．1-D ．2-第Ⅱ卷（非选择题共90分）二、填空题（本大题共4小题，每小题5分，共20分．）13．若某程序框图如右图，则该程序运行后输出的k 的值为． 14．cos 43cos77sin 43cos167+的值为．15．已知向量(1,sin )a θ= ，(1,cos )b θ= ，则||a b - 的最大值为．16．对于下列命题：①函数sin()()y k x k Z π=-+∈为奇函数；。

人教A版高中数学必修3经典测试题及解析考点1 算法与程序框图

考点1 算法与程序框图1. （2010上海高一检测）图中所示的算法流程图,表达式为（）A．112399++++. B．1123100++++C．199D．1100【解析】选A。

2.(2010喀左高一检测)下面的程序框图，求输出的 y=0 那么输入的x为（）A．-3 、0 B．-3、-5 C．0、-5 D．-3、0、-5【解析】选A。

上面的程序框图表示的函数为3,05,00,0x xy x xx+<⎧⎪=+>⎨⎪=⎩，故若输出的 y=0 那么输入的x为-3。

3.(2010济南高一检测)如图给出的是计算201614121+⋅⋅⋅+++的值的一个程序框图，其中判断框内应填入的条件是（）A. i>10B. i<10C. i>20D. i<20【解析】选A 。

因为循环体对应“否”分支，因此填10i >。

4．（2010个旧高一检测）给出以下一个算法的程序框图，该程序框图的功能是（）A ．求出a, b, c 三数中的最大数B ．求出a, b, c 三数中的最小数C ．将a, b, c 按从小到大排列D ．将a, b, c 按从大到小排列【解析】选B 。

5．（2010济南高一检测）如图(1)、(2),它们都表示的是输出所有立方小于729的正整数的程序框图,那么判断框中应分别补充的条件为 ( )A.⑴3n ≥729 ? ⑵3n ＜729? B . ⑴3n ≤729 ? ⑵3n ＞729 ?C. ⑴3n ＜729 ? ⑵3n ≥729?D. ⑴3n ＜729 ? ⑵3n ＜729 ?【解析】选C 。

6. （2010银川高一检测）按如图所示的程序框图，在运行后输出的结果为（） A ．36 B ．45 C ．55 D ．56【解析】选C 。

上面程序表示求12310++++的算法。

2020-2021学年高一数学下学期期末测试卷01(人教A版必修3+必修4解析版).docx

2020-2021学年高一数学下学期期末测试卷01（人教A 版）一、选择题（每小题5分，共60分）1.若|«|=1, ”| = 2, |« + 2^| = 713,则方与万的夹角为 A.匹B.冬C.兰D.竺6323【答案】D 【分析】根据同=1,同=2,对|«+ 2&| = 713两边平方即可求出a-b=-l -从而可求出cos<a, b> = -^,这样即可求出力与方的夹角. 【详解】|a|=l,|fo|= 2,|a + 2Z?| = y/13 ；0 + 2 方）2 =F+4 戸+40•夕= 1 + 16 + 4Q •方= 13；又 0VV7, b> < 7i ■-• • a>方的夹角为-故选D. 【点睛】考查向量数量积的运算，向量夹角的余弦公式，以及已知三角函数值求角，属于基础题.7TA. 把曲线G 上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移亍个单位长度,cos<-a, 2. 已知曲线G :y = sinx,2x-y,则下列结论正确的是（）b>B.把曲线G上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移严个单位长度,得到曲线C?177C.把曲线G上各点的横坐标缩短到原来的土倍，纵坐标不变，再把得到的曲线向右平移一个单位长度,2 3得到曲线C?1TTD.把曲线G上各点的横坐标缩短到原来的土倍，纵坐标不变，再把得到的曲线向右平移严个单位长度,2 6得到曲线C?【答案】D【分析】根据三角函数的伸缩变换与平移变换原则，可直接得出结果.【详解】所以将y = sinx图象上各点的横坐标缩短为原来的* ,纵坐标不变，可得y = sin2x的图象，再将y = sin 2x的图象向右平移彳个单位，即可得到y = sin ］2x -彳］的图象.故选：D.3.某市A, B, C三个区共有高中学生20000人，其中A区高中学生7 000人，现采用分层抽样的方法从这三个区所有高中学生中抽取一个容量为600的样本进行“学习兴趣”调查，则在A区应抽取()A. 200 人B. 205 人C. 210 人D. 215 人【答案】C【解析】由题意知A区在样本中的比例为卫20000AA区应抽取的人数是7000 x600=210.20000故选C.4.在区间［-2, 3］上任取一个数x,贝IJ函数f(x) = y/2x-4有意义的概率为故选：D5.在△ ABC 中，P, 0 分别是边 AB, BC 上的点，S.AP = ^AB,BQ = ^BC.^AB = a> AC = b 则范1 - 1 r B.——a +—b 3 3 1 _ 1 rD. ——a ——b 3 3【答案】A【分析】__ , i ____ , __ . i ____ . _ , 2 __ . 由已知得到AP = -AB,BQ = -BC.利用丽=而_丽，得到PB = -AB,利用PQ = PB + BQ 及 BC =紀-而和平面向量的线性运算法则运算即得.【详解】____ . _______ • ________ ► _____ > 1 ________ > 2 ________ -PB = AB — AP = AB — — AB = -AB ,3 3PQ = PB + BQ = lAB + ~BC = -AB + -(AC-AB )= -AB + -AC = -a + -b. 33 3 3、丿 3333故选：A.【点睛】本题考查平面向量的线性运算，是基础题，只要熟练掌握平面向量的加减数乘运算法则，并注意将有关向量转化为基底向量表示，即可得解.6.下表是高一级甲，乙，丙三位同学在先后五次数学考试中的成绩折线图，那么下列说法正确的是（）2 A.- 53B. 一54C. 一51 D.-5【答案】D 【解析】x>2，又xw[-2, 3],所以xe[2, 3]-43-2 3-(-2)71 - 1 r A. — a —b3 3 1 _ 1 r C. — a — b3 3由已知可得丽-巫更冷岚考试步次A.甲平均分比丙要高；B.按趋势，第6次的考试成绩最高分必定是丙；C.每个人五次成绩的标准差最大的是乙；D.从第1次考试到第5次考试，进步幅度最大的是丙.【答案】D【分析】由折线图，观察各数据，均值、方差均要计算才能确定，前5次的成绩并不能代表第6次的成绩如何，但是第5次成绩与第1次成绩的差可以判断.由此可得结论.【详解】由于没有具体数据，因此平均分，方差无法比较，A、C不能确定，前5次成绩的变化趋势并不能代表第6 次的趋势，B也不能确定，但从图中可知第5次成绩与第一次成绩的差中丙的差最大，即丙进步幅度最大, D正确.故选：D.【点睛】本题考查折线图，考查样本数据的特征，属于基础题.7.已知扇形OAB的面积为1,周长为4,则弦AB的长度为（）A. 2B. 2/sinlC. 2siniD. sinl【答案】C【分析】设出圆心角和半径，由扇形的面积列方程组，解出圆心角和半径，进而计算出弦4B的长.【详解】画出扇形如下图所示，过0作OC丄佔，交4B于C,交AB于D.则C4 = CB.设圆心角fl 2 JZAOB = 2ZCOB = a,半径Q4 = OB = r,依题意〔2 ,解得a = 2/ = l.在心△OCB中,ar + 2r = 4a 2AB AB ,所以AB = 2 OB sin- = 2sinl.sin — = -- ---- =--------- 22OB 2OB故选：C【点睛】本小题主要考查扇形面积、周长和弦长的有关计算，属于基础题.8.总体由编号为01,02,03,50的50个个体组成，利用随机数表从中抽取5个个体，下面提供随机数表的第5行到第7行：931247795737891845503994557392296111609849657350984730309837377023104476914606792662206205229234若从表中第6行第6列开始向右依次读取，则抽取的第3个个体的编号是（）A. 09B. 03C. 35D. 37【答案】B【分析】从第6行第6列开始向右依次读取，注意：不在编号范围内的和重复的要去除.【详解】利用随机数表从第6行第6列开始向右读取，依次为09, 84 （去除），96 （去除），57 （去除），35, 09 （重复，去除），84 （去除），73 （去除），03,所以抽取的第3个个体的编号是03.故选：B.9.齐王与田忌赛马，田忌的上等马优于齐王的中等马，劣于齐王的上等马，田忌的中等马优于齐王的下等马，劣于齐王的中等马，田忌的下等马劣于齐王的下等马.某天，齐王与田忌赛马，双方约定：比赛三局，每局各出一匹，每匹马赛一次，赢得两局者为胜，则田忌获胜概率为（）.1111 A. —B. —C. —D.—126 4 3【答案】B 【分析】设齐王的三匹马分别为吗卫2卫3,田忌的三匹马分别为勺,爲03,列举所有比赛的情况，利用古典概型的概率公式计算即可得出结果. 【详解】设齐王的三匹马分别为厲卫2卫3，田忌的三匹马分别为b v b 2,b.,所有比赛的情况:：（匕,如、（色,方2）、（色，2），齐王获胜三局;(q,bj 、(a 2,b 3)y (a 3,b 2),齐王获胜两局;齐王获胜两局;田忌获胜两局;齐王获胜两局，共6种情况，则田忌胜1种情况，故概率为P = ~6故选：B 【点睛】本题考查了古典概型的概率计算问题，考查了理解辨析和数学运算能力，属于中档题目.10. 黄金分割比是指将整体一分为二，较大部分与整体得比值等于较小部分与较大部分得比值，该比值为“¥"6®这是公认的最能引起美感的比例•黄金分割比例得值还可以近似地表示为2SHU8。

高一数学测试卷(必修4第1、3章)

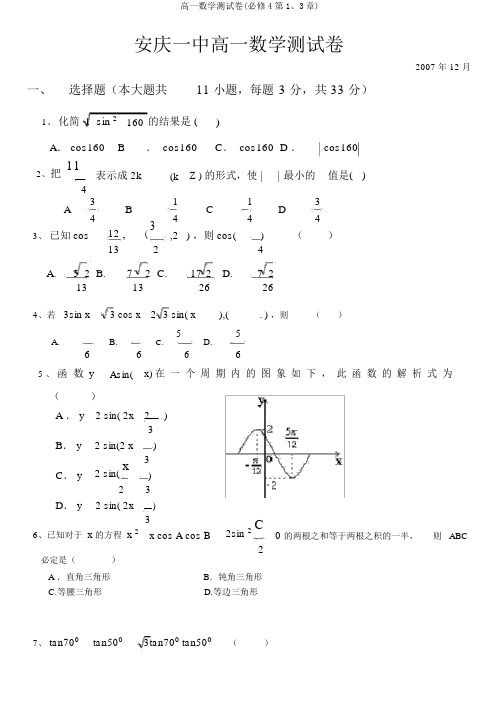
安庆一中高一数学测试卷2007 年 12 月一、选择题（本大题共 11 小题，每题 3 分，共 33 分）1、化简 1 sin 2160 的结果是 ()A ． cos160B ． cos160C ． cos160D ．cos1602、把11表示成 2k(k Z ) 的形式，使 || 最小的值是( )43113AB CD444412 , (33、已知 cos,2 ) ，则 cos() （）1324A.5 2 B. 7 2 C. 17 2 D. 7 2 13 13 26264、若 3sin x3 cos x 2 3 sin( x),(. ) ，则（）A.B.5 D.56 C.6665 、函数 yAsin( x) 在一个周期内的图象如下，此函数的解析式为（）A ． y 2 sin( 2x 2)3 B ． y2 sin(2 x )2 sin(x3 C ． y)23D ． y2 sin( 2x)32sin 2C6、已知对于 x 的方程 x 2x cos A cos B0 的两根之和等于两根之积的一半，则 ABC2必定是（）A ．直角三角形B ．钝角三角形 C.等腰三角形D.等边三角形7、 tan700 tan500 3tan700 tan500（）A.3B.3 C.3 33D.38、函数 ycos x sin 2 xcos2 x7 的最大值为（）441115B. 2C.A.4D.749、函数 y1 cos x）的周期是（sin xA ．B ．C ． 2D ． 4210、已知函数 f ( x) sin( x), g (x) cos(x) ，则以下结论中正确的选项是（）2 2A ．函数 y f ( x) g( x) 的最小正周期为 2B ．函数 y f ( x) g( x) 的最大值为 1C ．将函数 yf ( x) 的图象向左平移单位后得 y g ( x) 的图象2D ．将函数 yf ( x) 的图象向右平移单位后得 yg (x) 的图象211、 2002 年 8 月，在北京召开的国际数学家大会会标如下图，它是由 4 个同样的直角三角形与中间的小正方形拼成的一大正方形，若直角三角形中较小的锐角为，大正方形的面积是 1，小正方形的面积是1,则 sin 2cos 2 的值等于（）25A ． 1B ．24C．7D．72525 25安庆一中高一数学测试卷2007 年 12 月姓名 ____________班级 _____________得分 ______________一、选择题（本大题共11 小题，每题 3 分，共 33 分）题号1234567891011答案二、填空题（本大题共 4 小题，每题 3 分，共 12 分）12、函数y a sin x1的最大值是3，则它的最小值______________________ ；13、若tan 1 ，则 sin cos=；2 2 sin3 cos14、求值： 2cos100sin20 0=_______________；cos20 015、给出以下命题：① f ( x) 2 cos(72 x) 是奇函数；②若, 都是第一象限角且2，则 tan tan；③ x3是 y3sin(2x3) 的图像的一条对称轴；x 84④ f (x)3sin2 1 , 使f (x c) f ( x) 对随意实数 x 建立的正数 c 的最小值是2.2此中正确命题的序号是 _____________。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

中小学教育资源站（http://www.edudown.net)，百万资源免费下载，无须注册！
中小学教育资源站 http://www.edudown.net
高一数学下期期末测试试卷

(考试时间:120分钟满分:150分)
一、选择题(每小题5分,共60分)在每小题给出的四个选项中,只有一个是符合题
目要求的,请将正确选项的代号填在题后的括号中.)

1.给出下列关系式：sin1>sin2,cos(-21)>cos31,tan125°>tan70°,
sin1213π>cos1213π,其中正确的个数是（）
A、1 B、2 C、3 D、4

2.如果f(x+π)=f(-x),且f(x)= f(-x),则f(x)可能是( )
A、sin2x Bcosx C、sin|x| D、|sinx|
3.关于函数图象的变化，正确的结论是（）
A、将图象y=sin(2x-4)向右平移4，得图象y=sin2x

B、将图象y=sin(2x-4)上的每一点的纵坐标不变，横坐标变为原来的21，
得图象y=sin(x-4)
C、将图象y=f(x)按向量=(h,k)平移得图象y=f(x-h)-k
D、将图象y=f(x)先按向量平移，再按向量平移，且+=(-1,2)，则得
到的图象为y=f(x+1)+2

4.在△ABC中，A、B、C的对边分别是a、b、c，则acosB+bcosA等于（）
A、2cosC B、2sinC C、2ba D、c

5.不重合的四点A、B、C、D满足：2AB=3AC，AB =-2BD，则点D分
BC

之比为（）
中小学教育资源站（http://www.edudown.net)，百万资源免费下载，无须注册！
中小学教育资源站 http://www.edudown.net
A、3 B、-3 C、31 D、-31

6.设，，是任意的非零平面向量，且两两不共线，下列命题

其中正确的有（）
A、①② B、②③ C、③④ D、②④

7.已知OA=(-3,4),AB =(13,-4)，则AB在OA上的投影为（）
A、11 B、-11 C、18555 D、-18555

8.已知AB=(3,-2), AC=(k,3)，且△ABC为直角三角形，则实数k的值为
（）
A、2 B、319 C、不存在 D、2或319

9.在△ABC中，已知b2-bc-2c2=0，且a=6,cosA=87，则△ABC的面积为（）
A、215 B、15 C、2 D、3
10.在△ABC中,tanA+tanB+tanC>0,则△ABC是( )
A、锐角三角形 B、钝角三角形 C、直角三角形 D、任意三角形

11.已知m、n是夹角为60°的两个单位向量,则a=2m+n和b=-3m+2n的
夹角为（）

A、30° B、60° C、120° D、150°

12.在△ABC中,sinA:sinB:sinC=2:6:(3+1),则三角形的最小内角是
( )

A、60° B、45° C、30° D、以上答案都不对
中小学教育资源站（http://www.edudown.net)，百万资源免费下载，无须注册！
中小学教育资源站 http://www.edudown.net
二、填空题(每小题4分,共16分)请将你认为正确的答案直接填在题后的横线
上.
13.已知cos(4+x)=53,1217π14.计算cos15°cos75°+cos215°=_____________.
15.已知△ABC中，a=1,b=3，A=30°，则B=____________.
16.在正六边形ABCDEF中，若AB=a，CD =b，则CB=______________.
三、解答题(本题共6个小题,共74分)解答应写出文字说明、证明过程或演算
步骤).
17.(12 分) 已知△ABC三顶点的坐标分别为A(2,1),B(0,3),C(-1,5),AD为
边BC上的高。
①求AD的坐标。

②用向量BC，BA表示AD。
中小学教育资源站（http://www.edudown.net)，百万资源免费下载，无须注册！

中小学教育资源站 http://www.edudown.net
18.(12 分) 化简:1coscossinnnn (n∈Z).
中小学教育资源站（http://www.edudown.net)，百万资源免费下载，无须注册！

中小学教育资源站 http://www.edudown.net
19.(12分) 已知函数f(x)=sin2x+2sinxcosx+acos2x(a∈R)的图象按向量

m
=(-8,-2)平移得到函数y=2cos2x的图象。
①求实数a的值。

②求f(x)的最小正周期及函数图象的对称轴。
③指出f(x)的单调增区间，及f(x)=2+22时x的集合。
中小学教育资源站（http://www.edudown.net)，百万资源免费下载，无须注册！

中小学教育资源站 http://www.edudown.net
20.(12 分) 为了躲避台风，两海洋巡逻船分别抛锚在两荒岛C、D处，A、B

为两船舶基地，且相距km，现观察到：∠ACB=75°，∠BCD=45°，
∠ADC=30°，∠ADB=45°，求两荒岛C、D间的距离。

中小学教育资源站（http://www.edudown.net)，百万资源免费下载，无须注册！

中小学教育资源站 http://www.edudown.net
21.(12 分)
中小学教育资源站（http://www.edudown.net)，百万资源免费下载，无须注册！

中小学教育资源站 http://www.edudown.net
22.(14 分)
已知函数f(x)= a+bcosx+csinx 的图象经过A(0,1), B(2,1) 两点,当

函数f(x)的定义域为 [0, 2] 时, |f(x)|≤2 成立, 求实数a的取值范围.

答案
1—5 ADDDB
6—10 DBDAA
11—12 CB
13、7

14、433
15、60°或120°
16、—（ba）
17、（1）)56,512(AD
（2）BABCAD52
18、当n为偶数时原式 = sinα
当n为奇数时原式= －sinα
19、(1) a=3
(2) 最小正周期T=

对称轴 x=Zkk,28

(3) {x | x=Zkkxk,24724或}
20、3
21、(1) 提示：移项平方
（2）35352

22、—2≦a≦4+32
中小学教育资源站（http://www.edudown.net)，百万资源免费下载，无须注册！
中小学教育资源站 http://www.edudown.net