夏令营奥数14 巧算周长
三年级奥数《巧求周长》+《行程问题》

三年级奥数题《巧求周长》学习中我们已经会计算长方形和正方形的周长了,但是对于一些不是长方形,正方形而是多边形的图形,怎么求他的周长呢?今天给大家介绍如何把求多边形的周长转化为求长方形和正方形的周长。
例1如图13 — 1所示*求这个多边形的周长是多少厘米?分析要求这个多边形的周长,也就罡求线段AB ÷ BC +CD +DE+ ERn的和是多少,向在这大条线段中.只有砸利氐这两条线段的长度是己知的,其余四条线段的长度均是耒知的•当綿这个多边形的周长还是可以求的•眉一个大正方形把这个图形圈起来,如图捋一2所示,这个大正方形是ABCG•扌熨段原水平向上移动,移到CG边上,这样CD +EF的向上的DE边向左移动,移到AG边上.这样AF+ DE的长度正好与BC边的长度相等. 遗样虽然<K DE、EF.站这四条线段的长度不知道’但这四条线段的长度和我们可以求出耒.这样求这个多边形的周长就转化为求一个正方形的周长•这个多边形的周长就可以巧妙地求出来了。
解’ GX4=24〔厘氷)答;这个多边形的周⅜⅛24厘米。
匕度正好与抵■的长度相等■同样把竖直方B6.∣⅞>说明:本例图中的E 点在竖直方向上不论移动到什么位置(当然F 点也随着 上下移动),这个多边形的周长都不变,当然D 点在水平方向上移动(E 点也随 着移动).所得到的多边形周长也不变•这里点的移动不能超岀大正方形ABCG 这 个范围。
例2把长2厘米宽1厘氷的长方形一层、两层、三层地摆下去,摆気笫十五 层.这个图形的周长是多少厘米?分析 先观察图13-3,笫一层有一个长方形,第二层有两个长方形,笫三 层有三个长方形……找到规律,第十五层有十五个长方形•同样,用一个大长方 形把这个图形圈起亲•因此求这个多边形的周长就转化为求一个长为2×15=30 GS 米)、宽为1×15=15 (厘米)的长方形周长。
解:(2X15 + 1X15) ×2=45×2 = 90 (厘氷)答;这个图形的周长为90厘米。
(完整)小学奥数之巧求周长讲解及练习

巧求周长一、复习(1)正方形周长:边长×4(2)长方形周长:(长+宽)×2二、知识讲解考点1:平移变做已知把若干段不知道长度的线段通过平移变成知道长度的线段,化未知为已知。
考点2:分割变大周长将一个大长方形或正方形分割成若干个长方形和正方形,那么图形周长就会增加几个长或宽考点3:拼凑变小周长将若干个小长方形或正方形拼凑成一个大长方形或正方形,图形周长就会减少几个长或宽。
三、例题讲解例1:下图是一个楼梯的侧面图,求此图形的周长。
例2:下面图形是一个正方形和一个长方形组合在一起,求这个图形的周长。
558例5:下图是由6个边长为2厘米的正方形组成,求此图形的周长。
例3:下图是由6个边长2厘米的正方形拼成的。
这个图形的周长是多少厘米?例4:两个大小相同的正方形拼成一个长方形后,周长比原来两个正方形周长的和减少了6厘米。
原来一个正方形的周长是多少厘米?四、课堂运用1. 如下图所示,小明和小玲同时从学校到少儿书店,小明沿A路线行走,小玲沿B路线行走,如果两人速度一样,谁先到少儿书店?为什么?A B学校110米200米少儿书店2. 下面图形是两个长方形组合在一起,求这个图形的周长。
710103. 下面图形是两个长方形组合在一起,求这个大图形的周长。
71010720204. 下图是由5个边长为3厘米的正方形组成的图形,求此图形的周长。
5. 从一个边长是10厘米的正方形的一角剪去一边长是4厘米的小正方形,求剩下图形的周长。
4106. 把两个大小相同的正方形拼成一个长方形后,周长比原来两个正方形周长的和减少了10厘米,原来一个正方形的周长是多少厘米?7. 把一个正方形剪成两个大小相同的长方形后,两个长方形周长的和比原来正方形周长增加28分米,原来正方形的周长是多少分米?课后练习题1. 如图所示,一个大长方形被三条线段分成了四个小长方形,各条线段长度见图 (单位:厘米).求:图中四个小长方形的周长之和.2. 下图是由边长为 1厘米的 11个正方形堆成的“土”字图形.试求出其周长.3. 下图表示一块地,四周都用篱笆围起来,转弯处都是直角.已知西边篱笆长 17米,南边篱笆长 23米.四周篱笆长多少米?4. 求下图的周长.5. 用 9个相同的小长方形,组成一个大长方形,其中小长方形的长为25厘米,求这个大长方形的周长.6. (希望杯试题)右图中的阴影部分 BCGF是正方形,线段 FH长18厘米,线段 AC长24厘米,则长方形 ADHE的周长是厘米.7. 图⑴、图⑵都是由完全相同的正方形拼成的,并且图⑴的周长是 22厘米,那么图⑵的周长是多少厘米?(1) (2)。
小学奥数-巧求长方形、正方形周长

小学奥数-巧求长方形、正方形周长打开今日头条,查看更多精彩图片运用长方形和正方形的周长公式,可以很方便地求出一个长方形或正方形的周长。
有时,我们要将几个图形拼成一个长方形求其周长;或将一个图形分解成几个长方形,然后求新图形的周长;还有时,会遇到只求长方形一部分的周长的问题。
这就要求我们学会应用和掌握好转化的思考方法,把复杂的图形转化为标准的长方形和正方形,再运用求长方形和正方形周长的知识来巧求看起来不是长方形或正方形的图形的周长。
长方形的周长=(长+宽)×2 正方形的周长=边长×4精讲1:有3个边长为6厘米的正方形,通过重叠可形成图3-1所示的图形,你能求出这个图形的周长吗?解: 6×4×2=48(厘米)答:这个图形的周长是48厘米。
精讲2:在一个长12厘米,宽8厘米长方形内截图一个最大的正方形,求剩下的图形的周长。
解:12-8=4(厘米)(4+8)×2=24(厘米)答:剩下的图形的周长是24厘米。
平移法精讲3:你能用平移法求图3-10所示的阴影部分的周长吗?解:6×4=24(厘米)答:一个阴影部分的周长是24厘米。
精讲4:一个正方形被分成两个完全相同的长方形。
每个小长方形的周长是30厘米。
求原来正方形的周长是多少厘米?分析:小长方形不管怎么分两条边都等于正方形的边长,另外两条短边加起来等于一条正方形的边长。
所以小长方形的周长等于3倍的正方形边长,即正方形的边长为10厘米。
解:设正方形的边长为a,则长方形的宽为a/2(a+a/2)×2=30a=10正方形的周长=4a=4×10=40(厘米)答:正方形的周长是40厘米。
周长一条线,面积一大片精讲5:四个同样大的小长方形和一个周长为12厘米的小正方形,拼成一个边长为5厘米的大正方形,如图,每个小长方形的周长是多少?解:12÷4=3(厘米)(5-3)÷2=1(厘米)1+3=4(厘米)(4+1)× 2=10(厘米)答:每个小长方形的周长是10厘米。
小学奥数巧求周长

一、基本概念①周长:封闭图形一周的长度就是这个图形的周长.②面积:物体的表面或封闭图形的大小,叫做它们的面积.二、基本公式:①长方形的周长2=⨯(长+宽),面积=长⨯宽.②正方形的周长4=⨯边长,正方形的面积=边长⨯边长.三、常用方法:(1)对于基本的长方形和正方形图形,可以直接用公式求出它们的周长和面积,对于一些不规则的比较复杂的几何图形,我们可以采用转化的数学思想方法割补成基本图形,利用长方形、正方形周长及面积计算的公式求解.(2)转化是一种重要的数学思想方法,在转化过程中要抓住“变”与“不变”两个部分.转化后的图形虽然形状变了,但其周长和面积不应该改变,所以在求解过程中不能遗漏掉某些线段的长度或某部分图形的面积.转化的目标是将复杂的图形转化为周长或面积可求的图形.(3)寻求正确有效的解题思路,意味着寻找一条摆脱困境、绕过障碍的途径.因此,我们在解决数学问题时,思考的着重点就是要把所需解决的问题转化为已经能够解决的问题.也就是说,在直接求解不容易或很难找到解题途径的问题时,我们往往转化问题的形式,从侧面或反面寻找突破口,知道最终把它转化成一个或若干个能解决的问题.这种解决问题的思想在数学中叫“化归”,它是数学思维中重要的思想和方法.(4)在几何中,有许多图形是由一些基本图形组合、拼凑而成的.这样的图形我们称为不规则图形.不规则图形的面积往往无法直接应用公式计算.那么,不规则图形的面积怎样去计算呢?对称、旋转、平移这几种几何变换就是解决这类面积问题的手段.四、几个重要的解题思想 (1)平移在平面图形的计算中,常常要将一个平面图形移动到平面上的另一个位置进行计算.其中,将图形沿一个固定方向的移动叫做平移,一个图形经过平行移动不改变其形状与大小,所以图形面积是保持不变的.利用图形的平移,可以使面积计算问题的解法简捷明快,颇有新意.(2)割补割补法在我国古代叫“出入相补原理”,我国古代魏晋时期著名的数学家刘徽在《九章算术注》中就明确地提出“出入相补,各从其类”的出入相补原理.这个原理的内容是几何图形经过分、合、移、补所拼凑成的知识点拨4-2-2.巧求周长新图形,它的面积不变.(3)旋转在平面图形的割补中,有时要将一个图形绕定点旋转到一个新的位置,产生一种新的图形结构,图形在转动过程中形状大小不发生改变.利用这种新的图形结构可以帮我们解决面积的计算问题.(4)对称平面图形中有许多简单漂亮的图形都是轴对称图形.轴对称图形沿对称轴折叠,轴两侧可以完全重合.也就是说,如果一个图形是轴对称图形,那么对称轴平分这个图形的面积.熟悉轴对称图形这个性质,对面积计算会有很大帮助.(5)代换在几何计算中,对有关数量进行适当的等量代换也是解决问题的已知技巧.小结:本讲主要通过求一些不规则图形的周长,体会一种转化思想,重点在于把不规则图形转化为规则图形的方法,包括平移、旋转、割补、差不变原理,通过这些方法的学习,让学生体会求周长的技巧,提高学生的观察能力、动手操作能力、综合运用能力.例题精讲模块一、图形的周长和面积——割补法【例 1】求图中所有线段的总长(单位:厘米)D【考点】巧求周长【难度】2星【题型】填空【例 2】如图所示,点B是线段AD的中点,由A、B、C、D四个点所构成的所有线段的长度均为整数,若这些线段的长度之积为10500,则线段AB的长度是。
巧求周长奥数题三年级

巧求周长奥数题三年级
【最新版】
目录
1.题目概述
2.巧求周长的方法
3.例题解析
4.练习建议
正文
【1.题目概述】
巧求周长奥数题是针对三年级学生的一道经典数学题目,主要考察学生对周长概念的理解和计算能力。
在这类题目中,通常会给定一些图形,如长方形、正方形、圆形等,要求学生通过观察和分析,找到一种巧妙的方法来求解周长。
【2.巧求周长的方法】
在解决这类题目时,学生需要掌握一定的技巧,例如:长方形的周长公式是(长 + 宽)×2,正方形的周长公式是边长×4,圆形的周长公式是 2πr(其中 r 为半径)。
此外,还可以利用平移、切割等方法,将复杂的图形转化为简单的图形,从而简化计算过程。
【3.例题解析】
例题:一个长方形的长是 8 厘米,宽是 6 厘米,求这个长方形的周长。
解析:根据长方形的周长公式,周长=(长 + 宽)×2=(8+6)×2=28 厘米。
【4.练习建议】
对于这类题目,学生需要多做练习,提高自己的观察和分析能力。
可以从简单的图形入手,逐步增加难度,例如:组合图形、多边形等。
在解题过程中,要注重方法的灵活运用,善于总结和归纳,形成自己的解题技巧。
通过以上分析,我们可以看出,巧求周长奥数题虽然有一定难度,但只要掌握了基本的周长公式和解题技巧,就能够轻松应对。
奥数第七课《巧算周长》
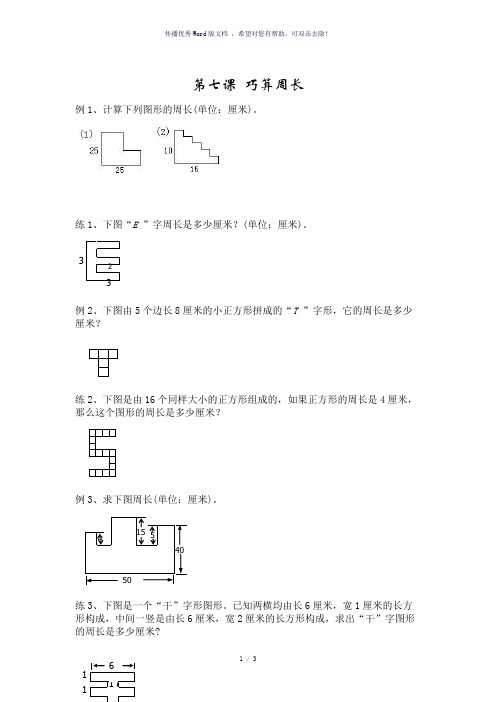
第七课巧算周长例1、计算下列图形的周长(单位:厘米)。
练1、下图“E ”字周长是多少厘米?(单位:厘米)。
例2、下图由5个边长8厘米的小正方形拼成的“T ”字形,它的周长是多少厘米?练2、下图是由16个同样大小的正方形组成的,如果正方形的周长是4厘米,那么这个图形的周长是多少厘米?例3、求下图周长(单位:厘米)。
练3、下图是一个“干”字形图形。
已知两横均由长6厘米,宽1厘米的长方形构成,中间一竖是由长6厘米,宽2厘米的长方形构成,求出“干”字图形的周长是多少厘米?23315 540504例4、下图是由3个边长为3厘米的小正方形组成,每个小正方形的顶点恰在另一个正方形的中心,且边相互平行,求这个图形的周长。
练4、下图是由七个长5厘米、宽3厘米的相同长方形经过竖放、横放而成的图形。
求这个图形的周长。
例5、把一块长20厘米,宽12厘米的长方形纸按右下图所示方法一层、二层、三层的摆下去,一共摆四层,摆好后图形周长是多少厘米?练5、把长2厘米、宽1厘米的长方形摆成如图的形状,求该图形的周长。
综合练习:1、下图是一块小麦地。
已知条件如图中所示,这块地的周长是多少米?50米50米2、下图是一块地,四周都用篱笆围起来,转弯处都是直角。
已知西边篱笆长17米,南边篱笆长23米,四周篱笆长多少米?17233、用15个边长2厘米的小正方形摆成如下图的形状,求图形周长是多少厘米?4、在4cm 7cm的正方形网格中,所有正方形的周长的和是多少cm?5、下图是一个零件的平面图,图中每一条最短线段均长5厘米,零件长35厘米,高30厘米,这个零件周长是多少厘米?30厘米。
三年级奥数(18)巧求周长
三年级奥数(14)巧求周长【类型一:不规则图形——平移】【例1】下图是由6个边长都是2厘米的正方形拼成的,你能算出这个图形的周长是多少厘米吗?变式1:计算下面各图的周长。
(单位:厘米)51015381053变式2:求下列图形的周长.(单位:米)1004040404040 80403020 13变式3:计算下面各图的周长(单位:厘米)11432852049【例2】把边长分别是厘米、厘米、厘米和厘米的个正方形按从大到小的顺序排109874成一行(如图),排成的图形周长是()厘米。
变式1:下图是一座楼房的平面图,图中不同字母表示长度不同的各条边.已知米,50b =米,米,这座楼房平面的周长是 米。
30c =10g =c=a=8b=3变式2:如图,线段厘米,厘米,厘米,图形的周长为()厘米。
10ac b12104变式3:一个长为厘米,宽为厘米的长方形,挖去一个边长为厘米的正方形补在另_____一边上(如图)。
所得图形的周长为厘米。
米,那么这个图形的周长是多少?变式1:如图所示,是由个边长为厘米的正方形组成的图形,你能求出这个图形的周长83吗?变式2:有一批长厘米,宽厘米的长方形按图所示方法:一层、二层、三层的摆下去,2016共要摆层,求摆好后图形的周长?80变式3:下图是一座古城堡的外观图,图中每条最短的线段长均为米,古城堡高米,212宽米,求这个外观图的周长是多少米?161612【例4】将张边长为分米的正方形纸片,按顺序一张一张地摆放在地板上,摆的时候,191要求后摆的纸片必须有一个顶点与前一张纸片的中心重合(图中表示已经摆好的张),地5板上摆好后图形的周长是多少?变式:李明将张扑克牌像下图那样摆放,已知扑克牌的长是毫米,宽毫米,那么这58656个摆成后的图形的周长是多少?【类型二:等量代换】884【例1】个同样的小长方形拼成一个大长方形,大长方形的周长是厘米,小长方形的周长是多少厘米?变式1:由个相等的小长方形拼成的大长方形,已知小长方形的宽是厘米,求大长方912形的周长是多少厘米?变式2:下图是由三个同样的长方形拼成的,求周长是多少?变式3:李明从走到再走到再到,走了米,马力从到再到再到走了A B C D 38B C D A 米,问此长方形的水池的周长是多少米?31ABCD CD B A【类型三:规则图形的变化】【例1】如图,一个正方形被分成6个大小、形状完全一样的长方形,每个长方形的周长都是14厘米。
巧求周长奥数题三年级
巧求周长奥数题三年级
摘要:
一、问题引入
二、解题思路
三、具体步骤
四、结论与反思
正文:
一、问题引入
在我们的日常生活中,计算周长是一个常见的数学问题。
今天,我将为大家讲解一个关于巧求周长的奥数题,适合三年级的学生挑战。
希望通过这个题目,大家能够巩固周长的计算方法,提高自己的数学思维能力。
二、解题思路
要解决这道题,我们需要灵活运用周长的计算公式,并掌握一些基本的数学思维方法,如观察、分析、归纳等。
三、具体步骤
假设有一个正方形,边长为a,我们需要求解它的周长。
根据正方形的性质,我们知道正方形的四条边长相等,所以周长C=4a。
现在,假设我们有一个长方形,长为a,宽为b。
我们同样需要求解它的周长。
根据长方形的性质,我们知道长方形的对边相等,所以周长
C=2a+2b。
然而,在现实生活中,我们常常会遇到一些不规则的图形,如一个边长为
a 的正方形和一个边长为
b 的长方形组成的图形。
对于这类图形,我们可以先将它们分割成若干个规则图形,如正方形和长方形,然后分别计算这些规则图形的周长,最后将它们相加得到整个图形的周长。
四、结论与反思
通过以上分析,我们可以得出结论:巧求周长的奥数题三年级主要考察了我们对周长计算公式的掌握程度以及对数学思维方法的运用。
在解题过程中,我们需要注意观察题目的特点,分析图形的性质,归纳总结规律,并灵活运用周长公式。
三年级奥数培优《巧求周长》
巧求周长专题简析:在解答比较复杂的关于长方形、正方形周长计算的问题时,生搬硬套公式往往行不通,这时灵活地运用所学知识在解题中显得相当的重要。
解答稍复杂的有关长方形、正方形周长的问题,首先要仔细观察,认真思考,想想已知条件和要求问题之间有什么联系,应该先求什么,再求什么,然后灵活运用长方形、正方形周长公式进行计算。
二、例题精讲例1.把长130厘米的铁丝围成一个长方形,接头处重合2厘米,要使长比宽多18厘米,长和宽各是多少厘米?例2.一根铁丝长80厘米,围成一个边长为8厘米的正方形,余下的铁丝围成一个长为14厘米的长方形。
这个长方形的宽是多少厘米?例3. 一个长方形的周长是正方形的2倍,正方形的边长与长方形的宽都是4厘米。
长方形的长是多少厘米?例4.四个同样大小的长方形正好拼成一个正方形,正方形的周长为64厘米,长方形周长是多少?例5.一张长方形的纸,长是28厘米,宽是15厘米,先剪下一个最大的正方形,再从余下的纸片中,再剪下一个最大的正方形。
最后余下的长方形周长是多少?二、课堂小测6.小华家给长方形的院子装上了篱笆墙,由于门宽2米,所以篱笆墙共长16米,而这个长方形的宽是长的一半。
长和宽各是多少米?7.如图:已知这个长方形的周长为38厘米,阴影部分为正方形,求长方形的长和宽。
8.一根绳子长78厘米,围成一个长12厘米,宽9厘米的长方形,余下的围成一个正方形。
这个正方形的边长是多少厘米?9.一个长方形的周长是正方形的2倍,正方形的边长与长方形的宽为10厘米。
长方形的长是多少厘米?10.六个同样大小的长方形正好拼成一个如下图的正方形,正方形周长为48厘米,每个长方形周长是多少?28厘米15厘米第二次剪下第一次剪下11.一张长为25厘米,宽为10厘米的长方形,先剪下一个最大的正方形,余下的长方形的周长是多少?12.一个周长为20厘米的正方形,从中间剪开成为两个大小相等的长方形。
这两个长方形周长共多少厘米?13.一根铁丝围成一个边长为7厘米的正方形,余下的正好围成一个长为12厘米、宽为10厘米的长方形。
小学奥数专题:巧求周长
第一讲巧求周长知识导航一、周长的基本概念周长:封闭图形一周的长度就是这个图形的周长。
二、周长的基本公式1.长方形的周长=(长+宽)×22.正方形的周长=边长×4三、计算周长的常用方法1.对于基本的长方形和正方形图形,可以直接用公式求出它们的周长和面积2.对于一些不规则的比较复杂的几何图形,我们可以采用转化的数学思想方法割补成基本图形,利用长方形、正方形的周长及面积的计算公式求解。
典型例题一(基本图形的周长)例1 下图由1个长方形和2个三角形拼成,线段长度如图所标,求图形的周长。
练习:如果所示,一个大长方形被三条线段分成了四个小长方形,各条线段长度已经标在图中。
求图中所有长方形的周长之和。
典型例题二(移补法求复杂图形的周长)例2 求如图所示的图形的周长。
(单位:厘米)练习如图所示,求图形的周长。
(单位:厘米)典型例题三(其他方法求复杂图形的周长)例3 下图中的阴影部分BCGF是正方形,线段FH长28厘米,线段AC长34厘米,则长方形ADHE的周长是多少厘米?练习如图所示,长方形ABCD被线段EG,HF分割成4个更小的长方形,已知长方形AEOH的周长为18厘米,CGOF的周长为16厘米,BFOE的周长为26厘米,求长方形ABCD的周长和长方形DHOG的周长。
课后巩固1.如图所示是由2个正方形和1个三角形组成的图形,线段长度见图中所标注,求该图形的周长。
(单位:厘米)2.如图所示,正方形ABCD的边长是6厘米,过正方形内的两点画直线,可把正方形分成9个小长方形。
这9个小长方形的周长之和是多少厘米?3.如图所示,是一个机器零件的侧面图,图中每一条最短线段长5厘米,这个零件高30厘米,求这个零件侧面的周长。
4.如图所示,在长方形ABCD中,EFGH是正方形。
已知AF的长为11厘米,HC的长为8厘米,求长方形ABCD的周长。
5.根据图中已标出线段的长度求如图所示图形的周长。
(单位:厘米)6.如图所示,用8个相同的长方形板砌成一个正方形边框。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6厘米
16 厘 米
24厘米
把5个相同的长方形拼成一 个大的长方形,每个长方形 的周长是60厘米,那么拼成 的长方形的周长是多少厘米?
练习作业
1、下图的周长是多少厘米? 30厘米 50 厘 米
2.下图的周长是多少分米?
8
43
10 (单位:分米)
3、下图是一幢楼房的平面图, 绕这幢楼的楼底走一圈是多 少米
7 7
16
40 (单位:米)
30厘米
模仿练习1
下图的周长是多少厘米?
35 厘 米
45厘米
拓展提升
一个正方形被分成3个大小、形状 完全一样的长方形,每个小长方形 的周长都是24厘米,求这个正方形 的周长?
变式练习
把一个正方形分成甲、乙两部 分,比较甲、乙两部分周长的 长短,并求出乙的周长? 甲
5
乙 (单位:分米)
思维发散
巧算周长
专题精析
对于求规则图形的周长,我们一般都直 接用公式来求:长方形的周长=(长+宽) ⅹ2;正方形的周长=边长ⅹ4.如果遇到 不规则的图形,我们可以用分割、平移、 旋转、拼接及合理的想象等技巧,使题 目化难为简,再利用基本公式解的周长是多少厘米? 24 厘 米
