第四章 多层感知器
100. 什么是深度学习中的多层感知器?

100. 什么是深度学习中的多层感知器?关键信息项:1、深度学习的定义2、多层感知器的概念3、多层感知器的组成结构4、多层感知器的工作原理5、多层感知器的训练方法6、多层感知器的优势7、多层感知器的局限性8、多层感知器的应用领域11 深度学习的定义深度学习是一种基于人工神经网络的机器学习技术,它试图模拟人脑的学习方式,通过构建多层的神经网络模型来自动从数据中提取特征和模式,以实现对复杂数据的准确预测和分类。
111 深度学习的特点深度学习具有以下几个显著特点:1111 强大的表示能力:能够处理高维度、复杂的数据,并自动学习数据中的隐藏特征和模式。
1112 端到端的学习:无需人工进行特征工程,直接从原始数据中学习到最终的预测或分类结果。
1113 大规模数据驱动:通常需要大量的数据来训练模型,以提高模型的性能和泛化能力。
12 多层感知器的概念多层感知器(Multilayer Perceptron,MLP)是一种常见的深度学习模型,它是由多个神经元组成的多层网络结构。
121 神经元的定义神经元是多层感知器的基本组成单元,它接收多个输入信号,并通过一个激活函数对输入进行加权求和和非线性变换,产生输出信号。
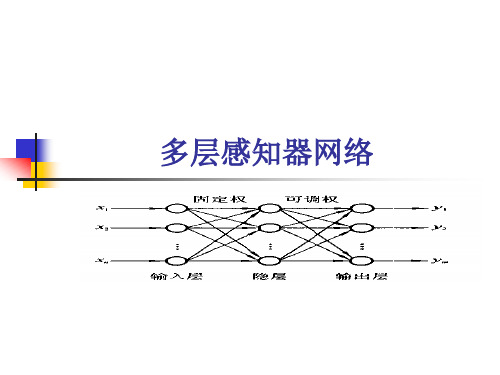
122 多层感知器的层次结构多层感知器通常包括输入层、隐藏层和输出层。
输入层接收外部输入数据,隐藏层用于对数据进行特征提取和变换,输出层产生最终的预测或分类结果。
13 多层感知器的组成结构131 输入层输入层的神经元数量取决于输入数据的特征维度,每个神经元对应一个输入特征。
132 隐藏层隐藏层可以有一层或多层,每层包含多个神经元。
隐藏层的神经元数量和层数是模型设计中的关键参数,它们决定了模型的学习能力和复杂度。
133 输出层输出层的神经元数量取决于任务的类型,例如对于二分类问题,输出层通常只有一个神经元;对于多分类问题,输出层的神经元数量等于类别数。
134 连接权重神经元之间通过连接权重进行连接,这些权重在训练过程中不断调整,以优化模型的性能。
多层感知器网络

多层感知器网络
权重优化与训练方法
权重优化与训练方法
权重初始化
1.权重初始化是训练多层感知器网络的重要步骤,可以防止模型在训练初期陷入局部最优解。常见 的初始化方法有随机初始化、Xavier初始化和He初始化等。 2.随机初始化将权重随机初始化为一个小值,可以保证模型在各个方向上的更新幅度大致相同,从 而提高模型的泛化能力。 3.Xavier初始化和He初始化则是针对特定激活函数提出的初始化方法,可以使得各层的激活值在进 行前向传播时能保持相同的分布。
学习率调整
1.学习率是影响多层感知器网络训练效果的重要因素之一,它决定了模型在每次更新时的步长大小 。 2.过大的学习率可能导致模型在训练过程中无法收敛,而过小的学习率则可能导致训练时间过长或 陷入局部最优解。 3.因此,在训练多层感知器网络时,需要根据模型的表现和训练轮数来动态调整学习率,以保证模 型的训练效果和收敛速度。
▪ L1正则化
1.L1正则化是在损失函数中加入模型参数的绝对值,通过约束 参数的范数来控制模型的复杂度。 2.L1正则化可以使一些参数变为零,从而起到特征选择的作用 ,有助于提高模型的泛化能力。 3.L1正则化的优化较为困难,需要使用一些特殊的优化算法, 如坐标下降法和近端梯度下降法等。
过拟合与正则化技术
权重优化与训练方法
▪ 批次归一化
1.批次归一化是一种提高多层感知器网络训练稳定性和收敛速 度的技术,它通过对每个批次的数据进行归一化处理来消除数 据间的差异。 2.批次归一化可以减少模型对初始权重的敏感性,提高模型的 泛化能力,同时也可以减少训练过程中出现的梯度消失和梯度 爆炸等问题。 3.在训练多层感知器网络时,加入批次归一化层可以有效地提 高模型的训练效果和收敛速度。
多层感知器算法原理

多层感知器算法原理多层感知器(Multilayer Perceptron,MLP)是一种前馈结构的人工神经网络,可以对一组输入向量进行非线性映射,从而实现分类或回归等任务。
MLP由多个节点层组成,每一层都与上一层和下一层相连,每个节点都是一个带有非线性激活函数的神经元。
MLP 的学习过程主要依赖于反向传播算法,即通过计算输出误差对网络权重进行反向调整,从而达到最优化的目的。
网络结构MLP的网络结构一般包括三层或以上,分别是输入层、隐藏层和输出层。
输入层接收外部输入的数据,输出层产生网络的预测结果,隐藏层位于输入层和输出层之间,可以有多个,用于提取输入数据的特征。
每一层中的节点都与相邻层中的所有节点相连,每条连接都有一个权重,表示该连接的强度。
每个节点除了接收来自上一层的加权输入外,还有一个偏置项,表示该节点的阈值。
每个节点的输出由其输入和激活函数共同决定,激活函数的作用是引入非线性,增强网络的表达能力。
常用的激活函数有Sigmoid函数、双曲正切函数、ReLU函数等。
学习过程MLP的学习过程主要分为两个阶段,即前向传播和反向传播。
前向传播是指从输入层到输出层逐层计算节点的输出,反向传播是指从输出层到输入层逐层计算节点的误差,并根据误差对权重进行更新。
具体步骤如下:前向传播从输入层开始,将输入数据乘以相应的权重,加上偏置项,得到每个节点的输入。
对每个节点的输入应用激活函数,得到每个节点的输出。
将每个节点的输出作为下一层的输入,重复上述过程,直到达到输出层。
在输出层,根据预测结果和真实标签,计算损失函数,评估网络的性能。
反向传播从输出层开始,根据损失函数对每个节点的输出求导,得到每个节点的误差。
对每个节点的误差乘以激活函数的导数,得到每个节点的梯度。
将每个节点的梯度作为上一层的误差,重复上述过程,直到达到输入层。
在每一层,根据节点的梯度和输入,计算权重的梯度,并根据学习率对权重进行更新。
MLP的学习过程可以采用批量梯度下降、随机梯度下降或小批量梯度下降等优化方法,也可以使用动量、自适应学习率或正则化等技术来提高收敛速度和泛化能力。
多层感知器的数据分类的过程

多层感知器的数据分类的过程多层感知器(Multilayer Perceptron,MLP)是一种基于人工神经网络的机器学习模型,常用于数据分类问题。
其主要由输入层、隐藏层和输出层组成。
下面将详细介绍多层感知器的数据分类过程。
注意:以下介绍以二分类任务为例。
1.数据准备与预处理:2.初始化网络参数:在训练多层感知器之前,需要初始化网络的权重和偏置。
这些初始值可以是随机生成的小数,或者根据先验知识给定的初始值。
3.前向传播:在多层感知器中,信息从输入层经过隐藏层传递到输出层,这个过程称为前向传播。
对于每个训练样本,我们将输入数据传递给输入层的每个神经元,然后将其加权求和,并通过激活函数进行非线性变换。
这些结果将作为下一层神经元的输入,并继续执行相同的计算。
在最后一个隐藏层后,我们将得到一个输出层,其结果表示了不同类别的概率。
通常,我们使用sigmoid函数、ReLU函数等作为激活函数。
4.计算损失函数:5.反向传播与参数更新:反向传播是通过计算损失函数相对于模型参数的梯度来更新网络参数的过程。
从输出层开始,我们根据链式法则计算每一层的梯度,并将这些梯度传播回输入层。
在每个层次上,我们使用梯度下降法来更新网络参数,以使损失函数最小化。
常用的优化算法有随机梯度下降法(SGD)、Adam 等。
6.重复步骤3-5:我们重复进行前向传播、计算损失函数和反向传播的步骤,以逐渐减小损失函数。
在每次迭代中,我们使用不同的训练样本来更新网络参数,直到达到预定的停止条件(如最大迭代次数、损失函数小于一些阈值等)。
7.模型评估与预测:在训练结束后,我们使用测试数据来评估训练得到的模型的性能。
通过将测试样本输入到模型中,根据输出值进行分类预测。
我们可以使用各种评估指标(如准确率、精确率、召回率、F1值等)来评估模型的性能。
8.模型优化与调参:根据模型评估的结果,我们可以进行模型优化和调参。
这可能包括改变网络结构、增加隐藏层、调整激活函数类型、选择合适的正则化方法等。
多层感知器网络
y(l ) j
j (v j (n))
如果神经元j是第一隐藏层,即l=1,置
y(0) j
(n)
xj
(n)
这里 xj (n)是输入向量X(n)的第j个元素。如果 神经元j在输出层,令
y(L) j
oj
(n)
计算误差信号
ej (n) d j (n) oj (n)
④、反向计算。
计算网络的局域梯度,定义为
这样做是因为设计受到感知器的学习 算法的限制,对于多层网络,当然有更 好的学习算法,比如BP网络学习算法。
1.在学习率知识点中提到的动量常数 在整个计 算中扮演什么样的角色?
2.假设隐藏层神经元个数一定,那么隐藏层的层数 取不同的值时,对于多层感知器的计算能力的影响是 怎样的?
3.动量和学习率参数随着训练迭代次数的增加而调 整(通常是减少的),为什么?
以图2所示两层感知器网络来实现, 其中隐层为随机感知器层(net1),神 经元数目设计为3,其权值和阈值是随机 的,它的输出作为输出层(分类层)的 输入;输出层为感知器层(net2),其 神经元数为1,这里仅对该层进行训练。
图4 例子中的两层感知器神经网络模型
(3)多层感知器神经网络的MATLAB程序实现
(l )
e(j L
)
(
n
)
' j
( v(j L
)
(
n
)),对输出层L的神经元j Nhomakorabean) j
' j
(
v(jl
)
(
n
))
k(l1) (n)k(jl1) (n),对隐藏层l的神经元j
k
多层感知器汇总.

( 1 (2) (2) j xi
)
)
不同处:局部误差δ计算。 (3) ' (3) d -f(s ) 和 f (s 乘积成正比 输出层, δ与 qj j j)
3) (3) ' (3) ( d f ( s ) f ( s j j j ) qj
隐含层, 局部误差δ由输出层的性能误差经反向传播而得。
Back Propagation)。
采用BP算法的MFNN是使用最广泛的神经网络,有时也称其 为BP神经网络。
1. 多层前馈网络的结构
1)多层前馈网络的组成 全连接的网络,由输入层,隐含层,输出层组成
2
输入层:仅起信息传递作用,激活函数相当于恒等函数。 输出即为输入, (0) (0)
x1 x1,xn0 xn0
输出层:由W(3)与第二隐含层全连接。激活函数可以是线性
函数或S函数。函数逼近多用线性函数。
y x (3) f ( s(3) ) f (W (3) x (2) )
5
2) 多层前馈网络的结构特点
(1)同一层神经元间无连接。
(2)相邻两层神经元之间全连接。
(3)信息传递有方向性。
前向计算时,由输入向输出逐层计算。
误差反向传播用以修正连接权时,则反向计算。
6
x
(1) (2)
f (s ) = f (W x )
() 1 (1) (0) (2) (2)
x = f( s ) f (W
x )
7
(1)
y x (3) f ( s(3) ) f (W (3) x (2) )
2. BP算法
1)算法推导
第q个样本加在网络上,定义性能指标
多层感知器AI技术中的多层感知器结构与模式识别

多层感知器AI技术中的多层感知器结构与模式识别多层感知器(Multi-Layer Perceptron, MLP)技术是人工智能(Artificial Intelligence, AI)领域中非常重要的一种技术。
它是一种前向人工神经网络,通过多个神经元层次的连接来模拟人脑中的神经元网络,并用于实现模式识别。
本文将介绍多层感知器的结构以及在模式识别中的应用。
一、多层感知器的结构多层感知器是由多个神经元层次组成的人工神经网络。
典型的多层感知器包括输入层、隐藏层和输出层。
1. 输入层输入层接收来自外部的数据输入,并将其传递到隐藏层。
输入层通常是根据具体问题设定的,可以是一组数字、图像或者其他形式的数据。
2. 隐藏层隐藏层是多层感知器中的核心部分。
它由多个神经元(节点)组成,每个神经元都与前一层的所有神经元相连。
隐藏层的层数以及每层的神经元数量都是可以调整的。
隐藏层通过对输入数据的加权求和和激活函数的作用,将处理后的数据输出到下一层。
3. 输出层输出层接收隐藏层的输出,并生成最终的输出结果。
输出层通常根据具体问题需要选择不同的激活函数,比如用于二分类问题的Sigmoid 函数或者用于多分类问题的Softmax函数。
二、多层感知器在模式识别中的应用多层感知器在模式识别领域有广泛的应用。
以下列举几个常见的应用场景。
1. 图像识别多层感知器可以用于图像识别任务,比如人脸识别、车牌识别等。
通过将图像数据输入到多层感知器中,隐藏层的神经元可以学习到图像的特征,输出层可以输出对应的分类结果。
2. 文本分类多层感知器可以用于文本分类任务,比如垃圾邮件过滤、情感分析等。
将文本数据表示成向量形式,输入到多层感知器中进行分类,可以实现对文本的自动分类。
3. 语音识别多层感知器可以用于语音识别任务,比如语音指令识别、语音转文字等。
将语音信号转换为频谱图或其他形式的特征表示,并输入到多层感知器进行识别,可以实现对语音的自动识别。
第4章 感知器

下面以两输入的但感知器为例,对区域的边界进行讨 论。
区域之间的判定边界使得净输入n为零的输入向量来 确定,即
11
《人工神经网络及应用》
为了可以具体说明判定边界的问题,假设权值和偏置
12
《人工神经网络及应用》
则该直线确定的判定边界在坐标系中的位 4 - 3 所示。
图 4 - 3 两输入感知器的判定边界图
图4-3 中的斜线表示净输入n 等于零的各点, 即
另外,为了确定图4 - 3 中直线的哪一侧的输出为1,
只需要检验空间中的某一点的网络输出值即可。选取输
入向量
,此时网络的输出为
《人工神经网络及应用》
此时,直线方程
将二维平面内的样本数据
分为两部分,处在直线上方的样本数据用“。”表示,
它们使净输入与偏置之和大于零,输出结果为+1;处在直
线下方的样本数据用“0 ”表示,它们使净输入与偏置之
和小于零,输出结果为一1,如 图 4 - 5 所示。
图 4 - 5 单层感知器对二维样本的分类
输出层第i个神经元的输出为 由于这里单层感知器的传递函数选用的是对称硬极限 函数,因此感知器的输出为 式中,W 为权值矩阵, x 为输入向量。 权值矩阵为
19
《人工神经网络及应用》
将权值矩阵W 中的第i个行向量定义为 则权值矩阵W 可表示为
式中,由 于iw表示第i个行向量,因此,WT 包含 时,感知器网络中第i个输出神经为
在n维空间内形成一个超平面,通过
改变感知器的权值和偏置值的大小,从而改变该超平面的
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、BP网络接受样本的顺序对训练结果有较大影 响。它更“偏爱”较后出现的样本 2、给集中的样本安排一个适当的顺序,是非常 困难的。 3、用 (X1,Y1),(X2,Y2),…,(Xs,Ys)的“总效 果”修改W(1) ,W(2) ,…,W(L)。 ∆w(k)ij=∑∆p w(k)ij
17
1 for k=1 to L do 1.1 初始化W(k); 2 初始化精度控制参数ε; 3 E=ε+1; 4 while E>ε do 4.1 E=0; 4.2 对所有的i,j,k:∆ w (k)ij=0;
3
o
f ′(net) 1
1 o net 1 e
net
0.25
(0,0.5)
0 (0,0) 0.5 1
o
– 应该将net的值尽量控制在收敛比较快的范围内 – 可以用其它的函数作为激活函数,只要该函数 是处处可导的
4
x1
W(1)
W(2)
W(3)
W(L)
o1
x2
o2
…
xn
…
…
…
…
…
… om
输入层
19
+ 较好地解决了因样本的顺序引起的精度问
题和训练的抖动问题 + 收敛速度:比较慢 + 偏移量:给每一个神经元增加一个偏移量 来加快收敛速度 + 冲量:联接权的本次修改要考虑上次修改 的影响,以减少抖动问题
20
+ Rumelhart等人1986年 – ∆wij=αδjoi+β∆wij′ – ∆wij′为上一次的修改量,β为冲量系数,一般可 取到0.9
25
+ 隐藏层的神经元的个数H作为一个输入参数
+ 同时将ε 、循环最大次数M等,作为算法的
输入参数 + 在调试阶段,最外层循环内,加一层控制, 以探测网络是否陷入了局部极小点
26
+ 基本假设 – 网络含有L层 – 联接矩阵: W(1) ,W(2) ,…,W(L) – 第k层的神经元:Hk个 – 自变量数: n*H1+H1*H2+H2*H3+…+HL*m – 样本集: S={ (X1,Y1),(X2,Y2),…,(Xs,Ys)} + 误差测度:
2、弱点:训练速度非常慢、局部极小点的逃离问题、 算法不一定收敛。 3、优点:广泛的适应性和有效性。
2
+ 4.2.1 网络的构成
神经元的网络输入: neti=x1w1i+x2w2i+…+xnwni 神经元的输出:
1 o f (net ) net 1 e
1 net 2 f (net) (e ) o o o(1 o) net 2 (1 e )
1 m 2 E (y k o k ) 2 k 1
29
取
E
E w ij w ij
E
wij
E >0,此时Δwij<0 w ij
E <0, 此时Δwij>0 w ij
wij
30
E E net j wij net j wij
而其中的
net j w kj o k
12
vhp=vhp+∆vhp ∆vhp=αδpk-1ohk-2 =αfk-1′(netp)(wp1δ1k+ wp2δ2k+…+ wpmδmk)ohk-2 =αopk-1(1-opk-1)(wp1δ1k+wp2δ2k+…+ pmδmk)ohk-2
wp1 ANh 第k-2层 δ1k
…
δqk ANq …
vhp
δpk-1
wpm ANp 第k-1层 wpq
δmk
第 k层
13
+ 样本集:S={(X1,Y1),(X2,Y2),…,(Xs,Ys)} + 基本思想 : – 逐一地根据样本集中的样本(Xk,Yk)计算出实际输出 Ok和误差测度E1,对W(1) ,W(2) ,…,W(L)各做一 次调整,重复这个循环,直到∑Ep<ε。 – 用输出层的误差调整输出层权矩阵,并用此误差 估计输出层的直接前导层的误差,再用输出层前 导层误差估计更前一层的误差。如此获得所有其 它各层的误差估计,并用这些估计实现对权矩阵 的修改。形成将输出端表现出的误差沿着与输入 信号相反的方向逐级向输入端传递的过程
14
1 for k=1 to L do 1.1 初始化W(k); 2 初始化精度控制参数ε; 3 E=ε+1; 4 while E>ε do 4.1 E=0;
15
4.2 对S中的每一个样本(Xp,Yp): 4.2.1 计算出Xp对应的实际输出Op; 4.2.2 计算出Ep; 4.2.3 E=E+Ep; 4.2.4 根据相应式子调整W(L); 4.2.5 k=L-1; 4.2.6 while k≠0 do 4.2.6.1 根据相应式子调整W(k); 4.2.6.2 k=k-1 4.3 E=E/2.0
22
1
2 3 4
用不同的小伪随机数初始化W,V; 初始化精度控制参数ε;学习率α ; 循环控制参数E=ε+1;循环最大次数M; 循环次数控制参数N=0; while E>ε & N<M do 4.1 N=N+1;E=0; 4.2 对每一个样本(X,Y),执行如下操作
23
4.2.1 计算:O1=F1(XV);O2=F2(O1W); 4.2.2 计算输出层的权修改量 for i=1 to m 4.2.2.1 ∆o[i]= O2 [i]*(1- O2 [i])*(Y[i]-O2 [i]); 4.2.3 计算输出误差:for i=1 to m 4.2.3.1 E=E+(Y[i]-O2 [i])2;
E 令 j net j
所以Δ wij=αδjoi
α为学习率
32
从而
oj=f(netj) 容易得到
E j net j E o j o j net j E f (net j ) o j
33
o j net j
f (net j )
1 m 2 yk ok 2 k 1 E o j o j 1 y j o j ( ) 2 o j
E
E
p 1
s
p
27
误差测度
E Ep
p 1
s
用E代表EP,用(X,Y)代表(XP,YP) X=(x1,x2,…,xn) Y=(y1,y2,…,ym) 该样本对应的实际输出为 O=(o1,o2,…,om)
28
E Ep
p 1
s
+ 用理想输出与实际输出的方差
作为相应的误差测度
隐藏层
输出层
5
1. BP网的结构 2. 输入向量、输出向量的维数、网络隐藏层
的层数和各个隐藏层神经元的个数的决定 3. 实验:增加隐藏层的层数和隐藏层神经元 个数不一定总能够提高网络精度和表达能 力。 4. BP网一般都选用二级网络。
6
x1
V
W
o1
x2
o2
… xn
…
…
… om
输入层
隐藏层
输出层
7
+ Sejnowski与Rosenberg ,1987年 – ∆wij=α((1-β)δjoi+β∆wij′) – ∆wij′也是上一次的修改量,β在0和1之间取值
21
+ 主要数据结构
W[H,m]——输出层的权矩阵; V[n,H]——输入(隐藏)层的权矩阵; ∆o[m]——输出层各联接权的修改量组成的向量; ∆h[H]——隐藏层各联接权的修改量组成的向量; O1——隐藏层的输出向量; O2——输出层的输出向量; (X,Y)——一个样本。
ik i
netk是 oj下一级的神 经元的网络输入
o1 oj o2 …
E H h E netk ( ) o j k 1 netk o j
H h1
w o ik i netk i 1 w jk o j o j
oHh
37
net E H h E k o j k 1 netk o j H h E w jk k 1 netk
样本:(输入向量,理想输出向量) 权初始化:“小随机数”与饱和状态;“不 同”保证网络可以学。 1、向前传播阶段: (1)从样本集中取一个样本(Xp,Yp),将Xp输 入网络; (2)计算相应的实际输出Op: Op=FL(…(F2(F1(XpW(1))W(2))…)W(L))
8
2、向后传播阶段——误差传播阶段: ( 1 )计算实际输出 Op 与相应的理想输出 Yp 的差; (2)按极小化误差的方式调整权矩阵。 (3)网络关于第p个样本的误差测度:
2
2 ( ( y j o j )) 2 (yj oj )
34
所以,
j
(y j o j )f (net j )
故,当ANj为输出层的神经元时,它对应 的联接权wij应该按照下列公式进行调整:
w ij (net j )(y j o j )o i
4.1 概述 4.2 基本BP算法 4.3 算法的改进 4.4 算法的实现 4.5 算法的理论基础 4.6 几个问题的讨论
1
1、BP算法的出现
非循环多级网络的训练算法 UCSD PDP 小组的 Rumelhart、Hinton 和 Williams1986 年独 立地给出了BP算法清楚而简单的描述 1982年,Paker就完成了相似的工作 1974年,Werbos已提出了该方法
35
E j net j E o j o j net j
